GraphMDL: Graph Pattern Selection Based on Minimum Description Length

Abstract

Many graph pattern mining algorithms have been designed to identify recurring structures in graphs. The main drawback of these approaches is that they often extract too many patterns for human analysis. Recently, pattern mining methods using the Minimum Description Length (MDL) principle have been proposed to select a characteristic subset of patterns from transactional, sequential and relational data. In this paper, we propose an MDL-based approach for selecting a characteristic subset of patterns on labeled graphs. A key notion in this paper is the introduction of ports to encode connections between pattern occurrences without any loss of information. Experiments show that the number of patterns is drastically reduced. The selected patterns have complex shapes and are representative of the data.

1 Introduction

Many fields have complex data that need labeled graphs, i.e. graphs where vertices and edges have labels, for an accurate representation. For instance, in chemistry and biology, molecules are represented as atoms and bonds; in linguistics, sentences are represented as words and dependency links; in the semantic web, knowledge graphs are represented as entities and relationships. Depending on the domain, graph datasets can be made of large graphs or large collections of graphs. Graphs are complex to analyze in order to extract knowledge, for instance to identify frequent structures in order to make them more intelligible.

In the field of pattern mining, there has been a number of proposals, namely graph mining approaches, to extract frequent subgraphs. Classical approaches to graph mining, e.g. gSpan [12] and Gaston [7], work on collections of graphs, and generate all patterns w.r.t. a frequency threshold. The major drawback of this kind of approach is the huge amount of generated patterns, which renders them difficult to analyze. Some approaches such as CloseGraph [13] reduce the number of patterns by only generating closed patterns. However, the set of closed patterns generally remains too large, with a lot of redundancy between patterns. Constraint-based approaches, such as gPrune [14], reduce the number of extracted patterns by extracting only the patterns following a certain acceptance rule. These algorithms generally manage to reduce the number of patterns, however they also limit their type. Additionally, if the acceptance rule is user-provided, the user needs some background knowledge on the data.

More effective approaches to reduce the number of patterns are those based on the Minimum Description Length (MDL) principle [3]. The MDL principle comes from information theory, and states that the model that describes the data the best is the one that compresses the data the best. It has been shown on sets of items [10], sequences [9] and relations [4] that an MDL-based approach can select a small and descriptive subset of patterns. Few MDL-based approaches have been proposed for graphs. SUBDUE [1] iteratively compresses a graph by replacing each occurrence of a pattern by a single vertex. At each step, the chosen pattern is the one that compresses the most. The drawback of SUBDUE is that the replacement of pattern occurrences by vertices entails a loss of information. VoG [5] summarizes graphs as a composition of predefined families of patterns (e.g., paths, stars). Like SUBDUE, VoG aims to only extract “interesting” patterns, but instead of evaluating each pattern individually like SUBDUE, it evaluates the set of extracted patterns as a whole. This allows the algorithm to find a “good set of patterns” instead of a “set of good patterns”. One limitation of VoG is that the type of patterns is restricted to predefined ones. Another limitation is that VoG works on unlabeled graphs, (e.g. network graphs), while we are interested in labeled graphs.

The contribution of this paper (Sect. 3) is a novel approach called GraphMDL, leveraging the MDL principle to select graph patterns from labeled graphs. Contrary to SUBDUE, GraphMDL ensures that there is no loss of information thanks to the introduction of the notion of ports associated to graph patterns. Ports represent how adjacent occurrences of patterns are connected. We evaluate our approach experimentally (Sect. 4) on two datasets with different kinds of graphs: one on AIDS-related molecules (few labels, many cycles), and the other one on dependency trees (many labels, no cycles). Experiments validate our approach by showing that the data can be significantly compressed, and that the number of selected patterns is drastically reduced compared to the number of candidate patterns. More so, we observe that the patterns can have complex and varied shapes, and are representative of the data.

2 Background Knowledge

2.1 The MDL Principle

The Minimum Description Length (MDL) principle [3] is a technique from the domain of information theory that allows to select the model, from a family of models, that best describes some data. The MDL principle states that the best model M for describing some data D is the one that minimizes the description length $L(M,D) = L(M) + L(D|M)$, where L(M) is the length of the model and L(D|M) the length of the data encoded with the model. The MDL principle does not define how to compute every possible description length. However, common primitives exist for data and distributions [6]:

• An element $x \in \mathcal {X}$ with uniform distribution has a code of $\log (|\mathcal {X}|)$ bits.

• An element $x \in \mathcal {X}$, appearing usage(x, D) times in some data D has a code of $L_{usage}^{\mathcal {X}}(x, D) = -log \left( \frac{usage(x, D)}{\sum _{x_i \in \mathcal {X}} usage(x_i, D)} \right)$ bits. This encoding is optimal.

• An integer $n \in \mathbb {N}$ without a known upper bound can be encoded with a universal integer encoding, whose size in bits is noted $L_{\mathbb {N}}(n)$¹.

Fig. 1.

A labeled undirected simple graph.

Fig. 2.

Embeddings of a pattern in the graph of Fig. 1.

Fig. 3.

Two singleton patterns.

Description lengths of elements that are common to all models are usually ignored, since they do not affect their comparison.

Krimp [10] is a pattern mining algorithm using the MDL principle to select a “characteristic” set of itemset patterns from a transactional database. Because of its good performances, Krimp has been adapted to other types of data, such as sequences [9] and relational databases [4]. In our approach we redefine Krimp’s key concepts on graphs, in order to apply a Krimp-like approach to graph mining.

2.2 Graphs and Graph Patterns

Definition 1

A labeled graph $G=(V,E,l_V, l_E)$ over two label sets $\mathcal {L}_V$ and $\mathcal {L}_E$ is a data structure composed of a set of vertices V, a set of edges $E \subseteq V \times V$, and two labeling functions $l_V \in V \rightarrow 2^{\mathcal {L}_V}$ and $l_E \in E \rightarrow \mathcal {L}_E$ that associate a set of labels to vertices, and one label to edges.

G is said undirected if E is symmetric, and simple if E is irreflexive.

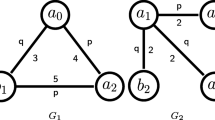
Although our approach applies to all labeled graphs, in the following we only consider undirected simple graphs, so as to compare ourselves with existing tools and benchmarks. Figure 1 shows an example of graph, with 8 vertices and 7 edges, defined over vertex label set $\{W,X,Y,Z\}$ and edge label set $\{a,b\}$. In our definition vertices can have several or no labels, unlike usual definitions in graph mining, because it makes it applicable to more datasets.

Definition 2

Let $G^P$ and $G^D$ be graphs. An embedding (or occurrence) of $G^P$ in $G^D$ is an injective function $\varepsilon \in V^P \rightarrow V^D$ such that: (1) $l^P_V(v) \subseteq l^D_V(\varepsilon (v))$ for all $v \in V^P$; (2) $(\varepsilon (u), \varepsilon (v)) \in E^D$ for all $(u, v) \in E^P$; and (3) $l^P_E(e) = l^D_E(\varepsilon (e))$ for all $e \in E^P$.

We define graph patterns as graphs $G^P$ having some occurrences in the data graph $G^D$. Figure 2 shows the three embeddings $\varepsilon _1, \varepsilon _2, \varepsilon _3$ of a two-vertices graph pattern into the graph of Fig. 1. We define singleton patterns as the elementary patterns. A vertex singleton pattern is a graph with one vertex having one label. An edge singleton pattern is a graph with two unlabeled vertices, connected by a single labeled edge. Figure 3 shows examples of singleton patterns.

Fig. 4.

Example of a GraphMDL code table over the graph of Fig. 1. Pattern and port usages, and code lengths have been added as illustration and are not part of the table definition. Unused singleton patterns are omitted.

3 GraphMDL: MDL for Graphs

In this section we present our contribution: the GraphMDL approach. This approach takes as input a graph—the original graph $G^o$—and a set of patterns extracted from that graph—the candidate patterns—and outputs the most descriptive subset of candidate patterns according to the MDL principle. The candidates can be generated with any graph mining algorithm, e.g. gSpan [12].

The intuition behind GraphMDL is that since data and patterns are both graphs, the data can be seen as a composition of pattern embeddings. Informally, we want a user analyzing the output of GraphMDL to be able to say “the data is composed of one occurrence of pattern A, connected to one occurrence of pattern B, which is itself connected to one occurrence of pattern C”. More so, we want the user to be able to tell how these structures are connected together: which vertices of each pattern are used to connect it to other patterns.

3.1 Model: A Code Table for Graph Patterns

Similarly to Krimp [10], we define our model as a Code Table (CT), i.e. a set $\mathcal{P}$ of patterns with associated coding information. A first difference with Krimp is that the patterns are graph patterns. A second difference is the need for additional coding information: a single code would not suffice since all the information related to connectivity between pattern occurrences would be lost.

We therefore introduce the notion of ports in order to represent how pattern embeddings connect to each other to form the original graph. The set of ports of a pattern is a subset of the vertices of the pattern. Intuitively, a pattern vertex is a port if at least one pattern embedding maps this vertex to a vertex in the original graph that is also used by another embedding (be it of the same pattern or a different one). For example, in Fig. 5a the three occurrences of pattern P1 are inter-connected through their middle vertex: this vertex is a port. Since port information increases the description length, we expect our approach to select patterns with few ports.

Figure 4 shows an example of CT associated to the graph of Fig. 1. Every row of the CT is composed of three parts, and contains information about a pattern $P \in \mathcal {P}$ (e.g. the first row contains information about pattern P1). The first part of a row is the graph $G^P$, which represents the structure of the pattern (e.g. P1 is a pattern with three labeled vertices and two labeled edges). The second part of a row is the code $c_P$, associated to the pattern. The third part of a row is the description of the port set of the pattern, $\varPi _P$, (e.g. P1 has two ports, its first two vertices, with codes of 2 and 0.42 bits²). We note $\varPi$ the set of all ports of all patterns. Like Krimp, the length of the code of a pattern or port depends on its usage in the encoding of the data, i.e. how many times it is used to describe the original graph $G^o$ (e.g. P1 has a code of 1 bit because it is used 3 times and the sum of pattern usages in the CT is 6, see Sects. 3.2 and 3.3).

Fig. 5.

How the data graph of Fig. 1 is encoded with the code table of Fig. 4. (a) Retained occurrences of CT patterns. (b) The rewritten graph. Blue squares are pattern embeddings (their label indicates the pattern), white circles are port vertices. Edge labels represent which pattern port correspond to each port vertex. (Color figure online)

3.2 Encoding the Data with a Code Table

The intuition behind GraphMDL is that we can represent the original graph $G^o$ (i.e. the data) as a set of pattern occurrences, connected via ports. Encoding the data with a CT consists in creating a structure that explicits which occurrences are used and how they interconnect to form the original graph. We call this structure the rewritten graph $G^r$.

Definition 3

A rewritten graph $G^r = (V^r, E^r, l^r_{V}, l^r_{E})$ is a graph where the set of vertices is $V^r = V^r_{emb} \cup V^r_{port}$: $V^r_{emb}$ is the set of pattern embedding vertices and $V^r_{port}$ is the set of port vertices. $E^r \subseteq V^r_{emb} \times V^r_{port}$ is the set of edges from embeddings to ports, $l^r_V \in V^r_{emb} \rightarrow \mathcal{P}$ and $l^r_E \in E^r \rightarrow \varPi$ are the labelings.

In order to compute the encoding of the data graph with a given CT, we start with an empty rewritten graph. One after another, we select patterns from the CT. For each pattern, we compute the occurrences of its graph $G^P$. Similarly to Krimp, we limit embeddings overlaps: we admit overlap on vertices (since it is the key notion behind ports), but we forbid edge overlaps.

Each retained embedding is represented in the rewritten graph by a pattern embedding vertex: a vertex $v_e \in V^r_{emb}$ with a label $P \in \mathcal{P}$ indicating which pattern it instantiates. Vertices that are shared by several embeddings are represented in the rewritten graph by a port vertex $v_p \in V^r_{port}$. We add an edge $(v_e, v_p) \in E^r$ between the pattern embedding vertex $v_e$ of a pattern P and the port vertex $v_p$, when the embedding associated to $v_e$ maps the pattern’s port $v_\pi \in \varPi _P$ to $v_p$. We label this edge $v_\pi$.

We make sure that code tables always include all singleton patterns, so that they can always encode any vertex and edge of the original graph.

Figure 5 shows the graph of Fig. 1 encoded with the CT of Fig. 4. Embeddings of CT patterns become pattern embedding vertices in the rewritten graph (blue squares). Vertices that are at the boundary between multiple embeddings become port vertices in the rewritten graph (white circles). When an embedding has a port, its pattern embedding vertex in the rewritten graph is connected to the corresponding port vertex and the edge label indicates which pattern’s port it is. For instance, the three retained occurrences of pattern P1 all share the same vertex labeled Y (middle of the original graph), thus in the rewritten graph the three corresponding pattern embedding vertices are connected to the same port vertex via port $v_2$.

3.3 Description Lengths

In this section we define how to compute the description length of the CT and the rewritten graph. Description lengths are used to compare CTs. Formulas are explained below and grouped in Fig. 6.

Fig. 6.

Formulas used for computing description lengths. The structure $G^P\,=\,(V^P, E^P, l_V^P, l_E^P)$ is shortened to $G\,=\,(V, E, l_V, l_E)$ for ease of reading.

Code Table. The description length $L(M) = L(CT)$ of a CT is the sum of the description lengths of its rows (skipping rows with unused patterns), and every row is composed of three parts: the pattern graph structure, the pattern code, and the pattern port description.

To describe the structure $G = G^P$ of a pattern (L(G)) we start by encoding the number of vertices of the pattern. Then we encode the vertices one after the other. For each vertex v, we encode its labels then its adjacent edges. To encode the vertex labels ($L_V(v,G)$) we specify their number first, then the labels themselves. To encode the adjacent edges ($L_E(v,G)$) we specify their number (between 0 and $|V| - 1$ in a simple graph), then for each edge, its destination vertex and its label. To avoid encoding twice the same edge, we decide—in undirected graphs—to encode edges with the vertex with the smallest identifier. Vertex and edge labels are encoded based on their relative usage in the original graph $G^o$ ($L_{ usage}^{\mathcal{L}_V}(l,G^o)$ and $L_{ usage}^{\mathcal{L}_E}(l_E(v,w),G^o)$). Since this encoding does not change between CTs, it is a meaningful way to compare them.

The second element of a CT row is the code $c_P$ associated to the pattern ($L(c_P)$). This code is based on the usage of the pattern in the rewritten graph.

The last element of a CT row is the description of the pattern’s ports ($L(\varPi _P)$). First, we encode the number of pattern’s ports (between 0 and |V|). Then we specify which vertices are ports: if there are k ports, then there are $\left( {\begin{array}{c}|V|\\ k\end{array}}\right)$ possibilities. Finally, we encode the port codes ($L(c_\pi , P)$): their code is based on the usage of the port in the rewritten graph w.r.t. other ports of the pattern.

Rewritten Graph. The rewritten graph has two types of vertices: port vertices and pattern embedding vertices. Port vertices do not have any associated information, so we just need to encode their number. The description length $L(D|M) = L(G^r)$ of the rewritten graph is the length needed for encoding the number of vertex ports plus the sum of the description lengths $L_{emb}(v, P, G^r)$ of the pattern embedding vertices v. Every pattern embedding vertex has a label $l^r_V(v)$ specifying its pattern P, encoded with the code $c_P$ of the pattern. We then encode the number of edges of the vertex i.e. the number of ports of this embedding in particular (between 0 and $|\varPi _P|$). Then for each edge we encode the port vertex to which it is connected and to which port it corresponds (using the port code $c_\pi$).

Table 1. Characteristics of the datasets used in the experiments

3.4 The GraphMDL Algorithm

In previous subsections we presented the different MDL definitions that GraphMDL uses to evaluate pattern sets (CT). A naive algorithm for finding the most descriptive pattern set (in the MDL sense) could be to create a CT for every possible subset of candidates and retain the one yielding the smallest description length. However, such an approach is often infeasible because of the large amount of possible subsets. That is why GraphMDL applies a greedy heuristic algorithm, adapting Krimp algorithm [10] to our MDL definitions.

Like Krimp, our algorithm starts with a CT composed of all singletons, which we call $CT_0$. One after the other, candidates are added to the CT if they allow to lower the description length. Two heuristics guide GraphMDL: the candidate order and the order of patterns in the CT. We use the same heuristics as Krimp, with the difference that we define the size of a pattern as its total number of labels (vertices and edges). We also implement Krimp’s “post-acceptance pruning”: after a pattern is accepted in the CT, GraphMDL verifies if the removal of some patterns from the CT allows to lower the description length L(M, D).

4 Experimental Evaluation

In order to evaluate our proposal, we developed a prototype of GraphMDL. The prototype was developed in Java 1.8 and is available as a git repository³.

4.1 Datasets

The first two datasets that we use, AIDS-CA and AIDS-CM, are part of the National Cancer Institute AIDS antiviral screen data⁴. They are collections of graphs often used to compare graph mining algorithms [11]. Graphs of this collection represent molecules: vertices are atoms and edges are bonds. We stripped all hydrogen atoms from the molecules, since their positions can be inferred.

We took our third dataset, UD-PUD-En, from the Universal Dependencies project⁵. This project curates a collection of trees describing dependency relationships between words of sentences of multiple corpora in multiple languages. We used the trees corresponding to the English version of the PUD corpus.

Table 1 presents the main characteristics of the three datasets that we use: the number of elementary graphs in the dataset, the total amount of vertices, the total amount of edges, the number of different vertex labels, and the number of different edge labels. Since GraphMDL works on a single graph instead of a collection, we aggregate collections into a single graph with multiple connected components when needed. We generate candidate patterns by using a gSpan implementation available on its author’s website⁶.

Table 2. Experimental results for different candidate sets

4.2 Quantitative Evaluation

Table 2 presents the results of the first experiment. For instance the first line tells that we ran GraphMDL on the AIDS-CA dataset, with as candidates the 2194 patterns generated by gSpan for a support threshold of 20%. It took 19 min for our approach to select a CT composed of 115 patterns, yielding a description length that is 24% of the description length obtained by the singleton-only $CT_0$. Selected patterns have a median of 9 labels and 3 ports.

We observe that the number of patterns of a CT is often significantly smaller than the number of candidates. This is particularly remarkable for experiments ran with small support thresholds, where GraphMDL reduces the number of patterns up to 300 times: patterns generated for these support thresholds probably contain a lot of redundancy, that GraphMDL avoids.

We also note that the description lengths of the CTs found by GraphMDL are between 20% and 40% of the lengths of the baseline code tables $CT_0$, which shows that our algorithm succeeds in finding regularities in the data. Description lengths are smaller when the number of candidates is higher: this may be because with more candidates, there are more chances of finding “good” candidates that allow to better reduce description lengths.

Fig. 7.

How GraphMDL (left) and SUBDUE (right) encode one of AIDS-CM graphs.

We observe that GraphMDL can find patterns of non-trivial size, as shown by the median label count in Table 2. Also, most patterns have few ports, which shows that GraphMDL manages to find models in which the original graph is described as a set of components without many connections between them. We think that a human will interpret such a model with more ease, as opposed to a model composed of “entangled” components.

4.3 Qualitative Evaluations

Interpretation of Rewritten Graphs. Figure 7 shows how GraphMDL uses patterns selected on the AIDS-CM dataset to encode one of the graphs of the dataset (more results are available in our git repository). It illustrates the key idea behind our approach: find a set of patterns so that each one describes part of the data, and connect their occurrences via ports to describe the whole data.

We observe that GraphMDL selects bigger patterns (such as P2), describing big chunks of data, as well as smaller patterns (such as P3, edge singleton), that can form bridges between pattern occurrences. Big patterns increase the description length of the CT, but describe more of the data in a single occurrence, whereas small patterns do the opposite. Following the MDL principle, GraphMDL finds a good balance between the two types of patterns.

It is interesting to note that pattern P1 in Fig. 7 corresponds to the carboxylic acid functional group, common in organic chemistry. GraphMDL selected this pattern without any prior knowledge of chemistry, solely by using MDL.

Comparison with SUBDUE. On the right of Fig. 7 we can observe the encoding found by SUBDUE on the same graph. The main disadvantage of SUBDUE is information loss: we can see that the data is composed of two occurrences of pattern P1, but not how these two occurrences are connected. Thanks to the notion of ports, GraphMDL does not suffer from this problem: the user can exactly know which atoms lie at the boundary of each pattern occurrence.

Table 3. Classification accuracies. Results of methods marked with * are from [8].

Assessing Patterns Through Classification. We showed in the previous experiments that GraphMDL manages to reduce the amount of patterns, and that the introduction of ports allows for a precise analysis of graphs. We now ask ourselves if the extracted patterns are characteristic of the data. To evaluate this aspect, we adopt the classification approach used by Krimp [10]. We apply GraphMDL independently on each class of a multi-class dataset, and then use the resulting CTs to classify each graph: we encode it with each of the CTs, and classify it in the class whose CT yields the smallest description length L(D|M). Since GraphMDL is not designed with the goal of classification in mind, we would expect existing classifiers to outperform GraphMDL. In particular, note that patterns are selected on each class independently of other classes. Indeed, GraphMDL follows a descriptive approach whereas classifiers generally follow a discriminative approach. Table 3 presents the results of this new experiment. We compare GraphMDL with graph classification algorithms found in the literature [8], and a baseline that classifies all graphs as belonging to the largest class. The AIDS-CA/CI dataset is composed of the CA class of the AIDS dataset and a same-size same-labels random sample from the CI class (corresponding to negative examples). The other datasets⁷ are from [8]. We performed a 10-fold validation repeated 10 times and report average accuracies and standard deviations.

GraphMDL clearly outperforms the baseline on two datasets, AIDS and Mutag, but is only comparable to the baseline for the PTC datasets. On Mutag, GraphMDL is less accurate than other classifiers but closer to them than to the baseline. On the PTC datasets, we hypothesize that the learned descriptions are not discriminative w.r.t. the chosen classes, although they are characteristic enough to reduce description length. Nonetheless results are still better than random guessing (accuracy would be 50%). An interesting point of GraphMDL classification is that it is explainable: the user can look at how the patterns of the two classes encode a graph (similarly to Fig. 7) and understand why one class is chosen over another.

5 Conclusion

In this paper, we have proposed GraphMDL, an MDL-based pattern mining approach to select a representative set of graph patterns on labeled graphs. We proposed MDL definitions allowing to compute description lengths necessary to apply the MDL principle. The originality of our approach lies in the notion of ports, which guarantee that the original graph can be perfectly reconstructed, i.e., without any loss of information. Our experiments show that GraphMDL significantly reduces the amount of patterns w.r.t. complete approaches. Further, the selected patterns can have complex shapes with simple connections. The introduction of the notion of ports facilitates interpretation w.r.t. to SUBDUE. We plan to apply our approach to more complex graphs, e.g. knowledge graphs.