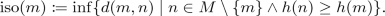Keywords

1 Introduction

Knowledge graphs (KG), such as DBpedia [15] or Wikidata [24], are the state of the art for storing information and to draw knowledge from. They represent knowledge through graphs and consist essentially of items which are related through properties and values. This enables them to fulfill the task of giving exact answers to exact questions. However, their ability to present a concise overview over collections of items with metric distances is limited. The number of such data sets in Wikidata is tremendous, e.g., the set of all cities of the world, including their geographic coordinates. Further examples are celestial bodies and their trajectories or, more general, feature spaces of data mining tasks.

One approach to understand such metric data is to identify outstanding elements, i.e., outstanding items. Based on such elements it is possible to compose or enhance item recommendations to users. For example, such recommendations could provide a set of the most relevant cities in the world with respect to being outstanding in their local surroundings. However, it is a challenging task to identify outstanding items in metric data sets. In cases where the metric space is equipped with an additional valuation function, this task becomes more feasible. Such functions, often called scores or height functions, are often naturally provided: cities may be ranked by population; the importance of scientific authors by the h-index [12]. A naïve approach for recommending relevant items in such settings would be: items with higher scores are more relevant items. As this method seems reasonable for many applications, some obstacles arise if the “highest” items concentrate into a specific region of the underlying metric space. For example, representing the cities of the world by the twenty most populated ones would include no western European city.Footnote 1 Recommending the 100 highest mountains would not lead to knowledge about the mountains outside of Asia.Footnote 2

Our novel approach shall overcome this problem: we combine the valuation measure (e.g., “height”) and distances, to provide new valuation functions on the set of items, called prominence and isolation. These functions do rate items based on their height in relation to the valuations of the surrounding items. This results in valuation functions on the set of items that reflect the extend to which an item is locally outstanding. The basic idea is the following: the prominence values an item based on the minimal descent (w.r.t. the height function) that is needed to get to another point of at least same height. The isolation, sometimes also called dominance radius, values the distance to the next higher point w.r.t. the metric (Fig. 1). These measures are adapted from the field of topography where isolation and prominence are used in order to identify outstanding mountain peaks. We base our approach on [22], where the authors proposed prominence and dominance for networks. We generalize these to the realm of bounded metric space.

Fig. 1.
figure 1

Isolation: minimal horizontal distance to another point of at least equal height. Prominence: minimal vertical descent to reach a point of at least equal height.

Full size image

We provide insights to the novel valuation functions and demonstrate their ability to identify relevant items for a given topic in metric knowledge graph applications. The contributions of this paper are as follows: \(\bullet \) We propose prominence and isolation for bounded metric spaces. For this we generalize the results in [22] and overcome the limitations to finite, undirected graphs. \(\bullet \) We demonstrate an artificial machine learning task for evaluating our novel valuation functions in metric data. \(\bullet \) We introduce an approach for using prominence and isolation to enrich metric data in knowledge graphs. We show empirically that this information helps to identify a set of representative items.

2 Related Work

Item recommendations for knowledge graphs is a contemporary topic of high interest in research. Investigations cover for example music recommendation using content and collaborative information [17] or movie recommendations using PageRank like methods [5]. The former is based on the common notion of embedding, i.e., embedding of the graph structure into d-dimensional real vector spaces. The latter operates on the relational structure itself. Our approach differs from those as it is based on combining a valuation measure with the metric of the data space. Nonetheless, given an embedding into an finite dimensional real vector space, one could apply isolation and prominence in those as well.

The novel valuation functions prominence and isolation are inspired by topographic measures, which have their origin in the classification of mountain peaks. The idea of ranking peaks solely by their absolute height was already deprecated in 1978 by Fry in his work [8]. The author introduced prominence for geographic mountains, a function still investigated in this realm, e.g., in Torres et al. [23], where the authors used deep learning methods to identify prominent mountain peaks. Another recent step for this was made in [14], where the authors investigated methods for discovering new ultra-prominent mountains. Isolation and more valuations functions motivated in the orometric realm are collected in [11]. A well-known procedure for identifying peaks and saddles in 3D terrain data is described in [6]. However, these approaches rely on data that approximates a continuous terrain surface via a regular square grid or a triangulation. Our data cannot fulfill this requirement. Recently the idea of transferring orometric functions to different realms of research gained attention: The authors of [16] used topographic prominence to identify population areas in several U.S. States. In [22] the authors Schmidt and Stumme transferred prominence and dominance, i.e., isolation, to co-author graphs in order to evaluate their potential of identifying ACM Fellows. We build on this for proposing our valuation functions on bounded metric data. This generalization results in a wide range of applications.

3 Mathematical Modeling

While the Wikidata knowledge graph itself could be analyzed with the prominence and isolation measures for networks, this paper focuses on bounded metric data sets. To analyze such data sets is more sufficient, since real world networks often suffer from a small average shortest path length [26]. This leads to a low amount of outstanding items: an item is outstanding if it is “higher” than the items that have a low distance to it. This leads to a strict measure for many real-world network data when the shortest path length is used as the metric function. Hence, we model our functions for bounded metric data instead of networks.

We consider the following scenario: We have a data set M, consisting of a set of items, in the following called points, equipped with a metric d and a valuation function h, in the following called height function. The goal of the orometric (topographic) measures prominence and isolation is, to provide measures that reflect the extent to which a point is locally outstanding in its neighborhood.

More precisely, let M be a non-empty set and \(d: M \times M \rightarrow \mathbb {R}_{\ge 0}\). We call d a metric on the set M iff \(\bullet \) \(\forall x,y \in M:d(x,y)=0\iff x=y\), and \(\bullet \) \(d(x,y)=d(y,x)\) for all \(x,y \in M\), called symmetry, and \(\bullet \) \(\forall x,y,z \in M: d(x,z) \le d(x,y) + d(y,z)\), called triangle inequality. If d is a metric on M, we call (M, d) a metric space and if M is finite we call (M, d) a finite metric space. If there exists a \(C\in \mathbb {R}_{\ge 0}\) such that we have \(d(m,n)\le C\) for all \(m,n \in M\), we call (M, d) bounded. For the rest of our work we assume that \(|M|>1\) and (M, d) is a bounded metric space. Additionally, we have that M is equipped with a height function (valuation/score function) \(h:M \rightarrow \mathbb {R}_{\ge 0}, m\mapsto h(m)\).

Definition 1

(Isolation). Let (M, d) be a bounded metric space and let \(h: M \rightarrow \mathbb {R}_{\ge 0}\) be a height function on M. The isolation of a point \(x \in M\) is then defined as follows:

  • If there is no point with at least equal height to m, than . The boundedness of M guarantees the existence of this supremum.

  • If there is at least one other point in M with at least equal height to m, we define its isolation by:

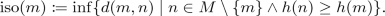
The isolation of a mountain peek is often called the dominance radius or sometimes the dominance. Since the term orometric dominance of a mountain sometimes refers to the quotient of prominence and height, we will stick to the term isolation to avoid confusion. While the isolation can be defined within the given setup, we have to equip our metric space with some more structure in order to transfer the notion of prominence. Informally, the prominence of a point is given by the minimal vertical distance one has to descend to get to a point of at least the same height. To adapt this measure to our given setup in metric spaces with a height function, we have to define what a path is. Structures that provide paths in a natural way are graph structures. For a given graph \(G=(V,E)\) with vertex set V and edge set \(E\subseteq {V\atopwithdelims (){2}}\), walks are defined as sequences of nodes \(\{v_i\}_{i=0}^n\) which satisfy \(\{v_{i-1},v_i\} \in E\) for all \(i \in \lbrace 1,...,n \rbrace \). If we also have \(v_i \ne v_j\) for \(i \ne j\), we call such a sequence a path. For \(v,w\in V\) we say v and w are connected iff there exists a path connecting them. Furthermore, we denote by G(v) the connected component of G containing v, i.e., .

To use the prominence measure as introduced by Schmidt and Stumme in [22], which is indeed defined on graphs, we have to derive an appropriate graph structure from our metric space. The topic of graphs embedded in finite dimensional vector spaces, so called spatial networks [2], is a topic of current interest. These networks appear in real world scenarios frequently, for example in the modeling of urban street networks [13]. Note that our setting, in contrast to the afore mentioned, is not based on a priori given graph structure. In our scenario the graph structure must be derived from the structure of the given metric space.

Our approach is, to construct a step size graph or threshold graph, where we consider points in the metric space as nodes and connect two points through an edge, iff their distance is smaller then a given threshold \(\delta \).

Definition 2

(\(\delta \)-Step Graph). Let (M, d) be a metric space and \(\delta > 0\). We define the \(\delta \)-step graph or \(\delta \)-threshold graph, denoted by \(G_{\delta }\), as the tuple \(\left( M,E_\delta \right) \) via

$$\begin{aligned} E_{\delta }:= \{ \{ m, n\} \in {M\atopwithdelims (){2}} \mid d(m,n) \le \delta \}. \end{aligned}$$
(1)

This approach is similar to the one found in the realm of random geometric graphs, where it is common sense to define random graphs by placing points uniformly in the plane and connect them via edges if their distance is less than a given threshold [21]. Since we introduced a possibility to derive a graph that just depends on the metric space, we use a slight modification of the definition of prominence compared to [22] for networks.

Definition 3

(Prominence in Networks). Let \(G=(V,E)\) be a graph and let \(h:V \rightarrow \mathbb {R}_{\ge 0}\) be a height function. The prominence \(\mathrm{prom}_G(v)\) of \(v\in V\) is defined by

(2)

where . The set \(P_{v}\) contains of all paths to vertices w with \(h(w)\ge h(v)\), i.e., , where P denotes the set of all paths of G.

Informally, \(\mathrm{mindesc}_{G}(v)\) reflects on the minimal descent in order to get to a vertex in G which has a height of at least h(v). For this the definition makes use of the fact that \(\inf \emptyset =\infty \). This case results in \(\mathrm{prom}_G(v)\) being the height of v. A distinction to the definition in [22] is, that we now consider all paths and not just shortest paths. This change better reflects the calculation of the prominence for mountains. Based on this we transfer the notions above to metric spaces.

Definition 4

(\(\delta \)-Prominence). Let (M, d) be a bounded metric space and \(h:M \rightarrow \mathbb {R}_{ \ge 0 }\) be a height function. We define the \(\delta \)-prominence \(\mathrm{prom}_\delta (m)\) of \(m \in M\) as \(\mathrm{prom}_{G_{\delta }}(v)\), i.e., the prominence of m in \(G_{\delta }\) from Definition 2.

We now have a prominence term for all metric spaces that depends on a parameter \(\delta \) to choose. For all knowledge procedures, choosing such a parameter is a demanding task. Hence, we want to provide in the following a natural choice for \(\delta \). We consider only those values for \(\delta \) such that corresponding \(G_{\delta }\) does not exhibit noise, i.e., there is no element without a neighbor.

Definition 5

(Minimal Threshold). For a bounded metric space (M, d) with \(|M|>1\) we define the minimal threshold \(\delta _M\) of M as

Based on this definition a natural notion of prominence for metric spaces (equipped with a height function) emerges via a limit process.

Lemma 1

Let M be a bounded metric space and \(\delta _M\) as in Definition 5. For \(m \in M\) the following descending limit exists:

$$\begin{aligned} \lim _{\delta \searrow \delta _M} \mathrm{prom}_\delta (m). \end{aligned}$$
(3)

Proof

Fix any \(\hat{\delta } > \delta _M\) and consider on the open interval from \(\delta _M\) to \(\hat{\delta }\) the function that maps \(\delta \) to \(\mathrm{prom}_\delta (m)\): \(\mathrm{prom}_{(.)}(m) :\ ]\delta _M, \hat{\delta }[ \rightarrow \mathbb {R}, \delta \mapsto \mathrm{prom}_\delta (m)\). It is known that it is sufficient to show that \(\mathrm{prom}_{(.)}(m)\) is monotone decreasing and bounded from above. Since we have for any \(\delta \) that \(\mathrm{prom}_\delta (m) \le h(m)\) holds, we need to show the monotony. Let \(\delta _1, \delta _2\) be in \(] \delta _M, \hat{\delta }[\) with \(\delta _1 \le \delta _2\). If we consider the corresponding graphs \((M,E_{\delta _1})\) and \((M, E_{\delta _2})\), it easy to see \(E_{\delta _1} \subseteq E_{\delta _2}\). Hence, we have to consider more paths in Eq. (2) for \(E_{\delta _2}\), resulting in a not larger value for the infimum. We obtain \(\mathrm{prom}_{\delta _1}(m) \ge \mathrm{prom}_{\delta _2}(m)\), as required.

Definition 6

(Prominence in Metric Spaces). If M is a bounded metric space with \(|M|>1\) and a height function h, the prominence \(\mathrm{prom}(m)\) of m is defined as:

Note, if we want to compute prominence on a real world finite metric data set, it is possible to directly compute the prominence values: in that case the supremum in Definition 5 can be replaced by a maximum and the infimum by a minimum, which leads to \(\mathrm{prom}(m)\) being equal to \(\mathrm{prom}_{\delta _M}(m)\). There are results for efficiently creating such step graphs [3]. However, for our needs in this work, in particular in the experiment section, a quadratic brute force approach for generating all edges is sufficient. We want to show that our prominence definition for bounded metric spaces is a natural generalization of Definition 3.

Lemma 2

Let \(G=(V,E)\) be a finite, connected graph with \( \left| V \right| \ge 2\). Consider V equipped with the shortest path metric as a metric space. Then the prominence \(\mathrm{prom}_{G}(\cdot )\) from Definition 3 and \(\mathrm{prom}(\cdot )\) from Definition 6 coincide.

Proof

Let be equipped with the shortest path metric d on G. As G is connected and has more than one node, we have \(\delta _M=1\). Hence, \((M,E_{\delta _M})\) from Definition 2 and G are equal. Therefore, the prominence terms coincide.

4 Application

Score Based Item Recommending. As an application we envisage a general approach for a score based item recommending process. The task of item recommending with knowledge graphs is a current research topic [17, 18]. However, most approaches are solely based on knowledge about preferences of the user and graph structural properties, often accessed through KG embeddings [19]. The idea of the recommendation process we imagine differs from those. We stipulate on a procedure that is based on the information entailed in the connection of the metric aspects of the data together with some (often naturally present) height function. We are aware that this limits our approach to metric data in KGs. Nonetheless, given the large amounts of metric item sets in prominent KGs, we claim the existence of a plenitude of applications. For example, while considering sets of cities, such a system could recommend a relevant subset, based on a height function, like population, and a metric, like geographical distances. By doing so, we introduce a source of information for recommending metric data in relational structures, like KGs. A common approach for analyzing and learning in KGs is embedding. There is an extensive amount of research about that, see for example [4, 25]. Since our novel methods rely solely on bounded metric spaces and some valuation function, one may apply those after the embedding step as well. In particular, one may use isolation and prominence for investigating or completing KG embeddings. This constitutes our second envisioned application. Finally, common item recommending scores/ranks can also be used as height functions in our sense. Hence, computing prominence and isolation for already setup recommendation systems is another possibility. Here, our valuation functions have the potential to enrich the recommendation process with additional information. In such a way our measures can provide a novel additional aspect to existing approaches. The realization and evaluation of our proposed recommendation approach is out of scope of this paper. Nonetheless, we want to provide some first insights for the applicability of valuation functions for item sets based on empirical experiments. As a first experiment, we will evaluate if isolation and prominence help to separate important and unimportant items in specific item sets in Wikidata. In detail, we evaluate if the valuation functions help to differentiate important and unimportant municipalities in France and Germany, solely based on their geographic metric properties and their population as height.

4.1 Resulting Questions

Given a bounded metric space M which represents the data set and a given height h. The following questions shall evaluate if our functions isolation and prominence provide useful information about the relevance of given points in the metric space. If (M, d, h) is a metric space equipped with an additional height function, let \(c:M \rightarrow \lbrace 0,1 \rbrace \) be a binary function that classifies the points in the data set as relevant (1) or not (0). We connect this to our running example using a function that classifies municipalities having a university (1) and municipalities that do not have an university (0). We admit that the underlying classification is not meaningful in itself. It treats a real geographic case while our model could also handle more abstract scenarios. However, since this setup is essentially a benchmark framework (in which we assume cities with universities to be more relevant) we refrain from employing a more meaningful classification task in favor of a controllable classification scenario. Our research questions are now: 1. Are prominence and isolation alone characteristical for relevance? We use isolation and/or prominence for a given set of data points as features. To which extend do these features improve learning a classification function for relevance? 2. Do prominence and isolation provide additional information, not catered by the absolute height? Do prominence and isolation improve the prediction performance of relevance compared to just using the height? Does a classifier that uses prominence and isolation as additional features produce better results than a classifier that just uses the height? We will evaluate the proposed setup in the realm of a KG and take on the questions stated above in the following section and present some experimental evidence.

5 Experiments

We extract information about municipalities in the countries of Germany and France from the Wikidata KG. This KG is a structure that stores knowledge via statements, linking entities via properties to values. A detailed description can be found in [24], while [9] gives an explicit mathematical structure to the Wikidata graph and shows how to use the graph for extracting implicational knowledge from Wikidata subsets. We investigate if prominence and isolation of a given municipality can be used as features to predict university locations in a classification setup. We use the query service of WikidataFootnote 3 to extract points in the country maps from Germany and France and to extract all their universities. We report all necessary SPAQRL queries employed on GitHub.Footnote 4

  • Wikidata provides different relations for extracting items that are instances of the notion city. The obvious choice is to employ the instance of (P31) property for the item city (Q515). Using this, including subclass of (P279), we find insufficient results. More specific, we find only 102 French cities and 2215 German cities.Footnote 5 For Germany, there exists a more commonly used item urban municipality of Germany (Q42744322) for extracting all cities, while to the best of our knowledge, a counterpart for France is not provided.

  • The preliminary investigation leads us to use municipality (Q15284), again including the subclass of (P279) property, with more than 5000 inhabitants.

  • Since there are multiple french municipalities that are not located in the mainland of France, we encounter problems for constructing the metric space. To cope with that we draw a basic approximating square around the mainland of France and consider only those municipalities inside.

  • We find the class of every municipality, i.e, university location or non-university location as follows. We use the properties located in the administrative territorial entity (P131) and headquarters location (P159) on the set of all universities and checked if these are set in Germany or France. An example of a University that has not set P131 is TU Dortmund (Q685557).Footnote 6

  • We match the municipalities with the university properties. This is necessary because some universities are not related to municipalities through P131, e.g., Hochschule Niederrhein (Q1318081) is located in the administrative location North Rhine-Westphalie (Q1198) (See footnote 6), which is a federal state containing multiple municipalities. For these cases we check the university locations manually. This results in 2064 municipalities (89 university loc.) in France and 2986 municipalities (160 university loc.) in Germany.

  • While constructing the data set we encounter twenty-two universities that are associated to a country having neither located in the administrative territorial entity (P131) nor headquarters location (P159). We check them manually and are able to discard them all for different reasons.

5.1 Binary Classification Task

Setup. We compute prominence and isolation for all data points and normalize them as well as the height. The data that is used for the classification task consists of the following information for each city: The height, the prominence, the isolation and the binary information whether the city has a university. Since our data set is highly imbalanced, common classifiers tend to simply predict the majority class. To overcome the imbalance, we use inverse penalty weights with respect to the class distribution. We want to stress out again that the goal for the to be introduced classification task is not to identify the best classifier. Rather we want to produce evidence for the applicability of employing isolation and prominence as features for learning a classification function. We decide to use logistic regression with \(L^2\) regularization and Support Vector Machines [7] with a radial kernel. For our experiment we use Scikit-Learn [20]. As penalty factor for the SVC we set \(C=1\), and experiment with \(C\in \{0.5,1,2,5,10,100\}\). For \(\gamma \) we rely on previous work by [1] and set it to one. For all combinations of population, isolation and prominence we use 100 iterations of 5-fold-cross-validation.

Evaluation. We use the g-mean (i.e., geometric mean) as evaluation function. Consider for this denotations TN (True Negative), FP (False Positive), FN (False Negative), and TP (True Positive). Overall accuracy is highly misleading for heavily imbalanced data. Therefore, we evaluate the classification decisions by using the geometric mean of the accuracy on the positive instances, \(acc_+ := \frac{TP}{TP+FN}\) and the accuracy on the negative instances \(acc_- :=\frac{TN}{TN+FP}\). Hence, the g-mean score is then defined by the formula \(g_{mean} :=\sqrt{acc_+ \cdot acc_-}\). The evaluation function g-mean is established in the topic of imbalanced data mining. It is mentioned in [10] and used for evaluation in [1]. We compare the values for g-mean for the following cases. First, we train a classifier function purely on the features population, prominence or isolation. Secondly, we try combinations of them for the training process. We consider the classifier trained using the population feature as baseline. An increase in g-mean while using prominence or isolation together with the population function is evidence for the utility of the introduced valuation functions. Even stronger evidence is a comparison of isolation/prominence trained classifiers versus baseline.

In our experiments, we are not expecting high g-mean values, since the placement of university locations depends on many additional features, including historical evolution of the country and political decisions. Still, the described evaluation setup is sufficient to demonstrate the potential of the novel features.

Table 1. Results of the classification task. We do 100 rounds of 5-fold-cross-validation and shuffle the data between the rounds. For all rounds we compute the g-mean value and then compute the average over the 100 rounds.
Full size table

Results. The results of the computations are depicted in Table 1. \(\bullet \) Isolation is a good indicator for structural relevance. For both countries and classifiers isolation outperforms population. \(\bullet \) Combining absolute height with our valuation functions leads to better results. \(\bullet \) Prominence is not useful as a solo indicator. We draw from our result that prominence solely is not a useful indicator. Prominence is a very strict valuation function: recall that we constructed the graphs by using distance margins as indicators for edges, leading to a dense graph structure in more dense parts of the metric space. Hence, a point in a more dense part has many neighbors and thus many potential paths that may lead to a very low prominence value. From Definition 3 we see that having a higher neighbor always leads to a prominence value of zero. This threshold is about 34 km for Germany and 54 km for France. Thus, a municipality has a not vanishing prominence if it is the most populated point in a radius of over 34 km, respectively 54 km. Only 75 municipalities of France have non zero prominence, with 40 of them being university locations. Germany has 104 municipalities with positive prominence with 72 of them being university locations. Thus, prominence alone as a feature is insufficient for the prediction of university locations. \(\bullet \) Support vector machine and logistic regression lead to similar results. To the question, whether our valuation functions improve the classification compared with the population feature, support vector machines and logistic regressions provide the same answer: isolation always outperforms population, a combination of all features is always better then using just the plain population feature. \(\bullet \) Support vector machine penalty parameter. Finally, for our last test we check the different results for support vector machines using the penalty parameters \(C\in \{0.5,1,2,5,10,100\}\). We observe that increasing the penalty results in better performance using the population feature. However, for lower values of C, i.e., less overfitting models, we see better performance in using the isolation feature. In short, the more the model overfits due to C, the less useful are the novel valuation functions we introduced in this paper.

6 Conclusion and Outlook

In this work, we presented a novel approach to identify outstanding elements in item sets. For this we employed orometric valuation functions, namely prominence and isolation. We investigated a computationally reasonable transfer to the realm of bounded metric spaces. In particular, we generalized previously known results that were researched in the field of finite networks.

The theoretical work was motivated by the observation that KGs, like Wikidata, do contain huge amounts of metric data. These are often equipped with some kind of height functions in a natural way. Based on this we proposed in this work the groundwork for a locally working item recommending scheme.

To evaluate the capabilities for identifying locally outstanding items we selected an artificial classification task. We identified all French and German municipalities from Wikidata and evaluated if a classifier can learn a meaningful connection between our valuation functions and the relevance of a municipality. To gain a binary classification task and to have a benchmark, we assumed that universities are primarily located at relevant municipalities. In consequence, we evaluated if a classifier can use prominence and isolation as features to predict university locations. Our results showed that isolation and prominence are indeed helpful for identifying relevant items.

For future work we propose to develop the conceptualized item recommender system and to investigate its practical usability in an empirical user study. Furthermore, we urge to research the transferability of other orometric based valuation functions.