Keywords

1 Introduction

Regression analysis provides a simple framework for predicting numerical target attributes from a set of independent predictive attributes. Addressing any problem using this framework requires designing models that fully capture the relations between predictive and target attributes. This has so far led to many classes of regression models being designed. For instance, multi-target regression models [11] consider predicting the value of multiple target attributes as opposed to basic regression models that aim at predicting only a single target attribute at a time. In another case, when one target variable is being predicted from a set of hierarchically ordered predictive attributes, the problem is known to be multi-level regression [5].

In this paper, we address the problem of regression for a class of problems where dependent variables are additionally hierarchically organized following different levels of aggregation. An example is the revenue forecasts per month and also per year of a given company. The forecasts for the new year can be the sum of the predictions done for each of the twelve months of the new year or can be done directly for the full new year. However, in many situations, it is important that the sum of the prediction per month is equal to the prediction for the full year. Moreover, relevant questions in this regard can arise. Can we obtain better predictions using both predictions for all months and for the full year? How may we reconcile the sum of the predictions done per month with the prediction done for the full year? Authors of [8] answered these questions for hierarchies of time series, i.e., a sequence of values, typically equally spaced, where this sequence can be aggregated by a given dimension.

This notion of hierarchy can also exist in the regression setting i.e., a problem with a set of n instances \((\mathbf {X_{i}, y_{i}}), i = 1, ..., n\). Each \((\mathbf {X_{i}}, y_{i})\) instance has a vector \(\mathbf {X_{i}}\) with p predictive attributes \((x_{i_1}, x_{i_2}, ..., x_{i_p})\) and a quantitative target attribute \(y_{i}\). The hierarchy can exist in this regression setting when, for instance, two of the p predictive attributes have a 1-to-many relation as referred to in relational databases. Addressing this problem in the regression setting leads to more flexible and robust solutions compared to the time series approach because: (1) any number of observations per time interval can be defined; (2) there are no limitations to the time interval between consecutive observations; and (3) any other type of predictive attribute can be used to better explain the target attribute.

In this work, we present an approach to reconcile predictions in the regression setting. We achieve this by proposing a new method named Reconciling for Regression (R4R). The R4R method is tested for the bus travel time prediction problem. This problem considers that buses run in predefined routes, and each route is composed of several links. Each link is the road stretch between two consecutive bus stops. Reconciling the predictions in this problem aims at reconciling the sum of the predictions done for each link with the prediction done for the full route. According to the authors’ knowledge, this is the first work on reconciling predictions in the regression setting. This work is also different from multi-target and multi-level variants being a combination of both (having multiple targets that are hierarchically ordered).

The R4R method can be applied to any other regression problem which exhibits a one-to-many relationship between instances, and also where the aggregated target value (the one) is the sum of the detailed target values (the many). In the previous example: (1) the revenue forecasts for the new year, the many component targets are the revenue forecasts per month, and the one component target is the revenue forecast for the full year; (2) in the bus travel time example, the many component targets are the link predictions while the one component target is the full route prediction. In this paper, we only discuss the sum as aggregation criterion (the one should be equal to the sum of the many), but the proposed method could be easily extended to other aggregation criteria, e.g., the average.

The remainder of this paper is organized as follows. In Sect. 2, we present the previous work on reconciling predictions. Section 3 elaborates the proposed methodology. In Sect. 4, we describe the case study. The results of the case study are presented and discussed in Sect. 5. Finally, the conclusions are presented in Sect. 6.

2 Literature Review

In this section, we review the previous research, both considering (i) the methods for forecasting for hierarchically organized time-series data and (ii) application area of travel time prediction.

Methods for Forecasting Hierarchically Organized Data: Common methods used to reconcile predictions for hierarchically organized time-series data can be further grouped into three categories: bottom-up, top-down and middle-out, based on the level which is predicted first. Bottom-up strategies forecast all the low-level target attributes and use the sum of these predictions as the forecast for the higher-level attribute. On the contrary, top-down approaches predict the top-level attribute and then splits up the predictions for the lower level attributes based on historical proportions that may be estimated. For time-series data with more than two levels of hierarchy, a middle-out approach can be used, combining both bottom-up and top-down approaches [3]. These methods form linear mappings from the initial predictions to reconciled estimates. As a consequence, the sum of the forecasts of the components of a hierarchical time series is equal to the forecast of the whole. However, this is achieved without guaranteeing an optimal solution. Authors of [8] presented a new framework for optimally reconciling forecasts of all series in a hierarchy to ensure they add up. The method first computes the forecast independently for each level of the hierarchy. Afterward, the method provides a means for optimally reconciling the base forecasts so that they aggregate appropriately across the hierarchy. The optimal reconciliation is based on a generalized least squares estimator and requires an estimation of the covariance matrix of the reconciliation errors. Using Australian domestic tourism data, authors of [8] compare their optimal method with bottom-up and conventional top-down forecast approaches. Results show that the optimal combinational approach and the bottom-up approach outperform the top-down method. The same authors extended, in [9], the previous work proposed in [8] to cover non-hierarchical groups of time series, as well as, large groups of time series data with a partial hierarchical structure. A new combinational forecasting approaches is proposed that incorporates the information from a full covariance matrix of forecast errors in obtaining a set of aggregate forecasts. They use a weighted least squares method due to the difficulty of estimating the covariance matrix for large hierarchies.

In [16], an alternative representation that involves inverting only a single matrix of a lower number of dimensions is used. The new combinational forecasting approach incorporates the information from a full covariance matrix of forecast errors in obtaining a set of aggregate consistent forecasts. The approach minimizes the mean squared error of the aggregate consistent forecasts across the entire collection of time series.

A game-theoretically optimal reconciliation method is proposed in [6]. The authors address the problem in two independent steps, by first computing the best possible forecasts for the time series without taking into account the hierarchical structure and next to a game-theoretic reconciliation procedure to make the forecasts aggregate consistent.

The previously mentioned methods are limited by the nature of the time-series approach they take. It is often impossible to take any advantage of additional features and attributes accompanying data with such an approach. Furthermore, many prevalent data imperfection problems such as missing data, lead to imperfect time-series. This fact reduces the applicability of time-series models that require equally distanced samples.

In our work, we take advantage of additional features and the structure of the grouped data to improve and reconcile predictions. Instead of forecasting each time series independently and then combine the predictions, in a regression setting, we can reconcile future events using only some past events. This leads to a solution suitable for online applications.

Application Area of Travel Time Prediction: There exists a considerable amount of research papers that address the problem of travel time prediction for transport applications. Accurate travel time information is essential as it attracts more commuters and increases commuter’s satisfaction [1]. The majority of these works are on short-term travel time prediction [19], aimed at applications in advanced traveler information systems. There are also works on long-term travel time prediction [13], which can be used as a planning tool for public transport companies or even for freight transports.

Link travel time prediction can be used for route guidance [17], for bus bunching detection [14], or to predict the bus arrival time at the next station [18] which can promote information services about it. More recently, Global Positioning System (GPS) data is becoming more and more available, allowing its use to predict travel times from GPS trajectories. These trajectories can be used to construct origin-destination matrices of travel times or traffic flows, an important tool for mobility purposes [2].

Using both link travel time predictions and the full trip travel time prediction in order to improve all those predictions is a contribution of this paper for the transportation field.

3 The R4R Method

3.1 Problem Definition

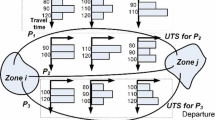
Consider a dataset \(D=\langle \mathbf{X} _, \mathbf{L} ,\mathbf{r} \rangle \). Note that \(\mathbf{X} \) in this tuple denotes the set of predictive attributes and is a matrix of size \(N \times Q\) representing a set of N number of instances each composed of Q number of predictive attributes. Furthermore, \(\mathbf{L} \) is the set of the many component targets and is a matrix of size \(N \times K\) with K being the number of elements of the many component target. \(\mathbf{r} \) representes the set of one component target and is a vector of length N. Elements of \(\{r_n \in \mathbf{r} \}\) represent the target attributes of the one component and each \(\{l_{n,k} \in \mathbf{L} \}\) is the kth target attribute of the many component. Also, consider \(r_{n}= \sum _{k=1}^{K} l_{n,k}\) denoting the sum of all the many component targets being equal to a corresponding one component target.

Defining the prediction of each \(l_{n,k}\) as \(p_{n,k}\), we are looking for a model that ensures that the sum of the predictions of the many component target are as close as possible to the \(r_{n}\). In other words, after making predictions, we want the following equation to hold:

$$\begin{aligned} \{ \displaystyle \sum _{k=1}^{K} p_{n,k} \thickapprox r_{n} | n \le N \} \end{aligned}$$
(1)

3.2 Methodology

In this section, we elaborate on our proposed method, Reconciling for Regression (R4R), to address the above-mentioned problem. R4R method is composed of two steps. In the first step, it learns models for prediction of the many component targets, separately. In the second step, it reconciles the many predictions with the one component.

In order to improve the individual \(p_{n,k}\) predictions such that Eq. 1 holds, our proposed framework uses a modified version of the least squares optimization method to compute a set of corrective coefficients (see Eq. 4), that are used to update the individual \(p_{n,k}\) predictions.

Step 1, Learning the Predictive Models: at the first step, the predictions of the many component targets are calculated using a specific base learning method. K different models are trained, one for each of the K elements of the many target component. It is possible to select a different learning method for each element to ensure higher accuracy. The resulting predictions for each of the K elements are referred to as \(p_{m,k}\), where m is the instance number, and k identifies elements of the many component targets. Algorithm 1 depicts these steps. As a result, this algorithm creates an output \(\mathbf{P} \), a matrix of size \( M \times K\) composed of predictions \(p_{m,k}\). \(\mathbf{P} \) is used in the second stage for reconciliation.

figure a

Step 2, Reconciling Predictions: In the second step, the framework updates the value of predictions resulted from the initial models used in Algorithm 1. This is achieved by estimating a corrective coefficient (\(\theta _k\)) for each element of the many target component (\(p_{m,k}\)). This coefficient needs to be multiplied with the model predictions to ensure minimized error from the actual one component target (\(r_m\)) and many component target (\(l_{m,k}\)). We achieve this goal using a least-squares method on the current training dataset and using the objective functions given by Eqs. 2 and 3 to estimate \(\varvec{\theta } = (\theta _{1}, ..., \theta _{K})\).

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{lb< \varvec{\theta } < ub} (\sum _{k=1}^{K}(\theta _{k} p_{m,k}) - r_m)^2 , m \le M \end{aligned}$$
(2)
$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{lb< \varvec{\theta } < ub} \sum _{k=1}^{K}(\theta _{k} p_{m,k} - l_{m,k})^2, m \le M \end{aligned}$$
(3)

The first objective function presented in Eq. 2 is attempting to optimize reconciliation based on the value of one component target. The second objective function presented in Eq. 3 aims at minimizing the error of the predictions based on the value of each element of the many component targets, separately. Both of these objective functions can be combined and expanded to Eq. 4. In Eq. 4, the first M rows are representing the objective function presented in Eq. 2. The remaining \(M \times (KM)\) rows represent the second objective function as provided in Eq. 3.

$$\begin{aligned} \begin{bmatrix} p_{1,1} &{} p_{1,2} &{} \cdots &{} p_{1,k} &{} \cdots &{} p_{1,K} \\ p_{2,1} &{} p_{2,2} &{} \cdots &{} p_{2,k} &{} \cdots &{} p_{2,K} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} &{} \vdots \\ p_{m,1} &{} p_{m,2} &{} \cdots &{} p_{m,k} &{} \cdots &{} p_{m,K} \\ p_{1,1} &{} 0 &{} \cdots &{} 0 &{} \cdots &{} 0 \\ 0 &{} p_{1,2} &{} \cdots &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 &{} \cdots &{} p_{1,K} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ p_{m,1} &{} 0 &{} \cdots &{} 0 &{} \cdots &{} 0 \\ 0 &{} p_{m,2} &{} \cdots &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} p_{m,k} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 &{} \cdots &{} p_{m,K} \end{bmatrix} \begin{bmatrix} \theta _{1} \\ \theta _{2} \\ \vdots \\ \theta _{K} \end{bmatrix} = \begin{bmatrix} r_{{1}} \\ r_{{2}} \\ \vdots \\ r_{{m}} \\ l_{1,1} \\ l_{1,2} \\ \vdots \\ l_{1,K} \\ \vdots \\ l_{m,1} \\ l_{m,2} \\ \vdots \\ l_{m,k} \\ \vdots \\ l_{m,K} \end{bmatrix} \end{aligned}$$
(4)

As seen in Eqs. 2 and 3 we have defined a constraint on the values of \(\varvec{\theta }\). The aim is to regularize the modifications to the predictions done for each element of the many component targets in a sensible manner (e.g. negative factors cannot be allowed when negative predictions are not meaningful). Therefore, we assume, without loss of generality, that all values of \(\varvec{\theta }\) are positive, with lower (lb) and upper (ub) bound constraints, \(0< lb< \theta _{k} < ub\). Both lb and ub are free input parameters. We reduce the number of free parameters to one (\(\alpha \)) by defining a symmetric bound region as \((lb,up) = (1 - \alpha , 1 + \alpha )\).

figure b

The process of reconciliation on predictions is explained in Algorithm 2. In the final step of this algorithm, the prediction matrix for all elements of the many component targets is updated using the corrective coefficients \(\varvec{\theta }\). A Least Squares method is used to calculate corrective coefficients. To allow robustness against outliers, we suggest using a nk number of nearest neighbors for estimating \(\varvec{\theta }\). We assume that similar trips from the past have the same behavior, as shown in [12]. The new predictions are defined as \(\mathbf{P} _{new}\). The algorithm takes into account the information of the predictions for both the many component elements and the one component predicted from similar instances in \(\mathbf{P} _{m,k}\), in order to verify Eq. 1 on reconciliation.

Table 1. Characteristics of tested STCP bus routes
Full size table

4 Case Study

To test the methodology explained in Sect. 3.2, we conduct a series of experiments using a real dataset that has our desired hierarchical organization of target values. Measuring travel time in public transport systems can produce such a dataset. Being able to perform accurate Travel Time Prediction (TTP) is an important goal for public transport companies. On the one hand, travel time prediction of the link between two consecutive stops (the many component targets in our model) allows timely informing the roadside users about the arrival of buses at bus stops (in the rest of this paper we refer to this value as link TTP). On the other hand, total trip travel time prediction (the one component in our model) is useful to better schedule drivers’ duty services (in the rest of this paper, we refer to this value as total TTP) [4].

The dataset used in this section is provided by the Sociedade de Transportes Colectivos do Porto (STCP), the main mass public transportation company in Porto, Portugal.

The experiments described in the following sections are based on the data collected during a period from January 1st to March 30th of 2010 from six bus routes (shown in Table 1). All the six selected bus routes operate between 5:30 a.m. to 2:00 a.m. However, we have considered only bus trips starting after 6 a.m.

The collected dataset has multiple nominal and ordinal attributes that make it suitable for defining a regression problem. We have selected five features that characterize each bus trip: (1) WEEKDAY: the day of the week \(\lbrace \)Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday\(\rbrace \); (2) DAYTYPE: the type of the day \(\lbrace \)holiday, normal, non-working day, weekend holiday\(\rbrace \); (3) Bus Day Month: \(\lbrace \)1,...,31\(\rbrace \); (4) Shift ID; (5) Travel ID.

We have implemented R4R using the R Software [15] and the lsq_linear routine from Scipy Python library [10]. For the first stage of R4R, as depicted in Algorithm 1, we use a simple multivariate linear regression as a base learning method. We refer to this base learning method as (Bas). We further split data according to the following format. A 30 days window length is used for selecting training samples, and a 60 days window length is considered for selecting test samples.

In our experiments, the parameter \(\alpha \) used for determining the lower and upper bound for the parameter for estimating \(\varvec{\theta }\) varies from 0.01 to 0.04, which corresponds to 0.96–1.04, minimum and maximum values that \(\varvec{\theta }\) can take, respectively.

5 Comparative Study

5.1 Can Reconciliation Be Achieved Using R4R?

Firstly, using the proposed R4R method, we try to answer the following question: is it possible to use the total trip travel time to improve the link TTPs guaranteeing a better reconciliation between the sum of the link TTPs and the total TTP simultaneously? To answer this question we measure the relative performance improvement achieved by R4R compared to a multivariate linear regression as the base learning method (denoted by Bas).

We evaluate the performance in predicting the following metrics (i) link travel time prediction (LP), the sum of link travel time predictions (SFP), and full trip time prediction (FP). Methods are compared based on Root Mean Square Error (RMSE) as defined in Eq. 5.

$$\begin{aligned} RMSE = \sqrt{\frac{1}{N_{test}} \displaystyle \sum _{i=1}^{N_{test}} (\hat{y}_{i} - y_{i})^2} \end{aligned}$$
(5)

where \(y_{i}\) and \(\hat{y}_{i}\) represent the target and predicted bus arrival times, for the ith example in the test set, respectively. \(N_{test}\) is the total number of test samples. For link travel time prediction indicator, LP, the mean of the RMSE of each bus link is considered.

Results of the comparison of R4R and Bas are presented in Fig. 1. Please note that relative gains are presented for the sake of readability of graphs. The duration of travel-times varies widely. This fact leads to unreadable graphs when actual data is presented.

As seem, R4R outperforms the base multivariate regression model in all cases. This comparison answers the question posed earlier. R4R improves predictions of the base regression learning method, guaranteeing a better reconciliation between the sum of the link TTPs and the total trip travel time, simultaneously.

Fig. 1.
figure 1

Relative improvement of R4R (Res) relative to Baseline (Bas) for mean LP - Link Prediction (red), sum of the link travel time predictions (green) and the full trip time prediction (blue). (Color figure online)

Full size image

5.2 How Does R4R Perform Against Baselines Made for Time Series Data?

We continue our experiments by comparing our proposed methodology R4R with the methods proposed by Hyndman et al. in the recent related works [8, 9, 16] denoted by (H2011, W2015, and H2016). To compare with these works, we used the available implementation in the R package [7]. It should be considered that these baseline models are designed for time-series data. Therefore, in order to perform comparisons with these approaches, we also define a time series problem using this dataset. This is achieved by representing data in the form of a time series with a resolution of a one-hour interval. We compute the mean link travel time for each hour between 6:00 a.m. to 2:00 a.m the next day, i.e. 20 data points in total for each “bus day". In the majority of the cases, each interval has more than one link travel time. For this reason we averaged the link travel times for each hour. Because the dataset has a considerable amount of missing values, interpolation was used to fill the missing links’ travel times. However, the results presented in the paper do not take into account the predictions done for intervals with no data.

The above-mentioned pre-processing tasks that were necessary in order to use the approaches proposed by Hyndman et al. already suggest that it is viable to propose methods such as R4R that perform in a more general and flexible regression setting. Indeed, the discretization of data into a time-series format implies the need to make predictions for intervals instead of point-wise predictions as done in the regression setting. Discretization also implies the necessity of filling missing data when the intervals have no data instances. This problem can be prevented by considering larger intervals. However, larger intervals imply loss of details. Moreover, the regression setting deals naturally with additional attributes that can partially explain the value of the target attribute.

Fig. 2.
figure 2

RMSE for each of the Link Travel Time Predictions of R4R against the methods proposed in H2011 [8], W2015 [16], H2016 [9] applied to bus route L305. SUM is the RMSE of the sum of the LTT prediction for the entire trip against the full trip time. This plot shows the results before the bus starts its journey.

Full size image
Table 2. Overall mean RMSE for each model, H2011 [8], W2015 [16], H2016 [9] and the new proposed approach R4R. BL - the Bus Line, LP - mean of the RMSE of Link Predictions, STP - RMSE of the sum of the LTT prediction for the entire trip against the full trip time.
Full size table

Figure 2 presents the results of predictions for bus route L305. It should be mentioned that we have chosen to show only results for \(\alpha = 0.01\), the parameter that consistently gave us the best performance in all the experiments we did. Indeed, the errors increase with increasing values of \(\alpha \) in all experiments we did. The results show very small differences between the methods under study.

The data provided is not homogeneous. This can adversely affect the performance of the least-squares method when outlying data is used to find the corrective coefficients \(\varvec{\theta }\). To avoid such problems, in our proposed framework, we select the nk number of nearest neighbors for each bus trip (also presented in Algorithm 2). Thus, after each link travel time prediction, it is necessary to recompute the whole process, i.e., to select a new set of similar bus trips and further find the coefficients using the least-squares method and update the predictions. Comparing with Hyndman et al. works, this process leads to a more computationally expensive solution. It is also important to find a suitable value for nk. During our experiments, we observed that the best results are achieved for \(nk = 3\). Therefore, all results presented in this paper are based on \(nk = 3\).

Table 2 shows the general results of predictions using this approach for all bus routes tested using multivariate linear regression as the base learning method (Bas). The results show that R4R outperforms Bas in all cases. There are a number of cases where a version of the time series model proposed by Hyndman. et al. perform better than R4R. These differences can be explained when considering the simple linear regression algorithm we used as a base learner in Algorithm 1. A linear model cannot find non-linear relations between features. Technically, the performance of R4R can be improved further as it allows using any other regression method. Furthermore, using extra features, such as weather conditions, could possibly improve the performance of R4R even further. However, the methods proposed by Hyndman et al. cannot benefit from using extra features.

6 Conclusion

In this paper, we study the problem of the reconciliation of predictions in a regression setting. We presented a two-stage prediction framework for prediction and reconciliation. In order to evaluate the performance and applicability of this method, we conduct a set of experiments using a real dataset collected from buses in Porto, Portugal. The results demonstrate that R4R improves the predictions of the base learning method. R4R is also able to further improve the reconciliation of the link TTPs after each iteration in an online manner. However, this is not shown due to space constraints. We also compare the results achieved in a regression setting with that of a time-series approach. In the case study discussed in this paper, R4R is able to reduce the error of link TTPs and increase reconciliation. An important advantage of the R4R method compared to time series variants is that it provides a flexible framework that can take advantage of any regression model and additional features accompanying data. Furthermore, R4R is not affected by data imperfection problems such as missing data, that reduce the applicability of time-series models that require equally distanced samples.