Transfer Learning by Learning Projections from Target to Source

Abstract

Using transfer learning to help in solving a new classification task where labeled data is scarce is becoming popular. Numerous experiments with deep neural networks, where the representation learned on a source task is transferred to learn a target neural network, have shown the benefits of the approach. This paper, similarly, deals with hypothesis transfer learning. However, it presents a new approach where, instead of transferring a representation, the source hypothesis is kept and this is a translation from the target domain to the source domain that is learned. In a way, a change of representation is learned. We show how this method performs very well on a classification of time series task where the space of time series is changed between source and target.

1 Introduction

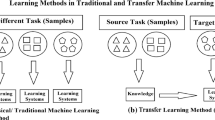
While transfer learning has a long history, dating back at least to the study of analogy reasoning, it has enjoyed a spectacular rise of interest in recent years, thanks largely to its use and effectiveness in learning new tasks with deep neural networks using an architecture learned on a source task. This approach is called Hypothesis Transfer Learning [6]. The justification for this strategy is that, in the absence of enough data in the target domain to learn anew a good hypothesis, it might be effective to transfer the intermediate representations learned on the source task. This is indeed the case, for instance, in face analysis when the source task is to guess the age of the person, and the target task is to recognize the gender. Technically, with neural networks, this amounts to keeping the first layers of the source neural network in the target network and learning only the last layers, the ones that combine intermediate representations of the examples in order to make a prediction.

Let $\mathcal X$, $\mathcal Y$ and $\mathcal Z$ be the input, output and feature spaces respectively. Let F be a class of representation functions, where $f \in F$: $\mathcal{X} \rightarrow \mathcal{Z}$. Let G be a class of decision functions that use descriptions of the examples in the feature space: $g \in G: \mathcal{Z} \rightarrow \mathcal{Y}$. Then, in the context of deep neural networks, the hypothesis class is $\mathcal{H} := \{h : \exists f \in F, g \in G$ st. $h = g \circ f\}$ and while f is kept (at least approximately) from the source problem to the target one, only g remains to be learned to solve the target problem.

In this paper, we adopt a dual perspective: we propose to keep the decision function g fixed, and learn translation functions from the target input space to the source input space, $\pi : \mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$, such that the target hypothesis space becomes $\mathcal{H}_\mathcal{T} := \{h_\mathcal{T} : \exists \pi \in \varPi , f \in F, g \in G ~\text {st.}~ h_\mathcal{T} = g \circ f \circ \pi \}$, which, given that $h_\mathcal{S} = g \circ f$ might be considered as the source hypothesis, may be re-expressed as: $\mathcal{H}_\mathcal{T} := \{h_\mathcal{T} : \exists \pi \in \varPi , f \in F, g \in G ~\text {st.}~ h_\mathcal{T} = h_\mathcal{S} \circ \pi \}$.

Indeed, for some problems, it might be much more easy to learn a translation (also called projections in this paper) from the target input space $\mathcal{X}_\mathcal{T}$ to the source input space $\mathcal{X}_\mathcal{S}$ than to learn a new target decision function. Furthermore, this allows one to tackle problems with different input spaces $\mathcal{X}_\mathcal{S}$ and $\mathcal{X}_\mathcal{T}$.

In the following, Sect. 2 presents TransBoost a new algorithm for transfer learning. The theoretical analysis of Sect. 3 provides a PAC-learning bound on the generalization error on the target domain. Controlled experiments are described in Sect. 4 together with an analysis of the results. The new approach is put in perspective in Sect. 5 before we conclude in Sect. 6.

2 A New Algorithm for Transfer Learning

Suppose that we have a system that is able to recognize poppy fields in satellite images. We might imagine that knowing how to translate a biopsy image into a satellite image, we could, using the recognition function defined on satellite image, decide if there is cancerous cells in the biopsy.

Ideally then, one could translate a target query: “what is the label of ${\mathbf{x}}^\mathcal{T} \in \mathcal{X}_\mathcal{T}$” into a source query “what is the label of $\pi ({\mathbf{x}}^\mathcal{T}) \in \mathcal{X}_\mathcal{S}$” where $h_\mathcal{S}$ is the source hypothesis which, applied to $\pi ({\mathbf{x}}^\mathcal{T}) \in \mathcal{X}_\mathcal{S}$, provides the answer we are looking for. Notice here that we suppose that $\mathcal{Y}_\mathcal{S} = \mathcal{Y}_\mathcal{T}$, but not $\mathcal{X}_\mathcal{S} = \mathcal{X}_\mathcal{T}$.

Fig. 1.

The principle of prediction using TransBoost. A given target example ${\mathbf{x}}_i^\mathcal{T}$ is projected in the source domain using a set of identified weak projections $\pi _j$ and the prediction for ${\mathbf{x}}_i^\mathcal{T}$ is computed as: $H_\mathcal{T}({\mathbf{x}}_i^\mathcal{T}) = \texttt {sign} \biggl \{ \sum _{j=1}^N \alpha _j h_\mathcal{S}\bigl (\pi _j({\mathbf{x}}_i^\mathcal{T})\bigr ) \biggr \}$.

The goal is then to learn a good translation $\pi : \mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$. However, defining a proper space of candidate projections $\varPi$ might be problematic, not to mention the risk of overfitting if the space of functions $h_\mathcal{S} \circ \varPi$ has too high a capacity. It might be more easy and manageable to discover “weak projections” from $\mathcal{X}_{\mathcal{T}}$ to $\mathcal{X}_{\mathcal{S}}$ using a boosting learning scheme.

Definition 1

A weak projection w.r.t. source decision function $h_\mathcal{S}$ is a function $\pi : \mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$ such that the decision function $h_\mathcal{S}\bigl (\pi ({\mathbf{x}}^\mathcal{T})\bigr )$ has better than random classification performance on the target training set $S_\mathcal{T}$.

In this setting, the training set $S_\mathcal{T} = \{({\mathbf{x}}^\mathcal{T}_i, y^\mathcal{T}_i)\}_{1 \le i \le m}$ is used to learn weak projections (Fig. 1).

Once the concept of weak projection is assumed, it is natural to use a boosting algorithm in order to learn a set of such weak projections and to combine them to get a final good classification on elements of $\mathcal{T}$. This is what does the TransBoost algorithm (see Algorithm 1). It does rely on the property of the boosting algorithm to find and combine weak rules to get a strong(er) rule.

3 Theoretical Analysis

Here, we study the question: can we get guarantees about the performance of the learned decision function $H_\mathcal{T}$ in the target space using TransBoost?

We tackle this question in two steps. First, we suppose that we learn a single projection function $\pi \in \varPi : \mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$ so that $h_\mathcal{T} = h_\mathcal{S} \circ \pi$, and we find bounds on the generalization error on the target domain given the generalization error on the source domain. Second, we turn to the TransBoost algorithm in order to justify the use of a boosting approach.

3.1 Generalization Error Bounds When Using a Single Projection

For this analysis, we suppose the existence of a source input distribution in addition to the target input distribution . We consider the binary classification setting $\mathcal{Y} = \{-1, +1\}$, and we note $\bar{h}_\mathcal{S}$ and $\bar{h}_\mathcal{T}$ respectively the source and the target labelling functions. We note $R_\mathcal{S}(h)$ (resp. $R_\mathcal{T}(h)$) the risk of a hypothesis h on the source (resp. target) domain: (resp. ). Let $\widehat{R}_\mathcal{S}(h)$ and $\widehat{R}_\mathcal{T}(h)$ be the corresponding empirical risks, with $m_\mathcal{S}$ training points for $\mathcal{S}$ and $m_\mathcal{T}$ training points for $\mathcal{T}$. Let $d_\mathcal{H}$ be the VC dimension of the hypothesis space $\mathcal{H}$.

In the following, what is learned is a projection $\pi \in \varPi : \mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$ in order to get a target hypothesis of the form $h_\mathcal{T} = \widehat{h}_\mathcal{S} \circ \pi$, where $\widehat{h}_\mathcal{S} = \mathop {\text {ArgMin}}\nolimits _{h \in \mathcal{H}_\mathcal{S}} \widehat{R}_\mathcal{S}(h)$ is the source hypothesis. Our aim is to upper-bound $R_\mathcal{T}(\widehat{h}_\mathcal{T})$, the risk of the learned hypothesis on the target domain in terms of:

• the empirical risk $\widehat{R}_\mathcal{S}(\widehat{h}_\mathcal{S})$ of the source hypothesis,

• the generalization error of a hypothesis $\widehat{h}_\mathcal{S}$ in $\mathcal{H}_\mathcal{S}$ learned from $m_\mathcal{S}$ examples, which depends on $d_{\mathcal{H}_\mathcal{S}}$,

• the generalization error of a hypothesis $\widehat{h}_\mathcal{T} = h_\mathcal{S} \circ \pi$ in $\mathcal{H}_\mathcal{T}$ learned from $m_\mathcal{T}$ examples, which depends on $d_{\mathcal{H}_\mathcal{T}} \, = \, d_{h_\mathcal{S} \circ \pi }$,

• a term that expresses the “proximity” between the source and the target problems.

For the latter term, we adapt the theoretical study of McNamara and Balcan [9] on the transfer of representation in deep neural networks. We suppose that $P_\mathcal{S}$, $P_\mathcal{T}$, $h_\mathcal{S}$, $h_\mathcal{T} = \widehat{h}_\mathcal{S} \circ \pi ~(\pi \in \varPi )$, $\widehat{h}_\mathcal{S}$ and $\varPi$ have the property:

$$\begin{aligned} \forall ~\widehat{h}_\mathcal{S} \in \mathcal{H}_\mathcal{S}: ~~\mathop {\text {Min}}\limits _{\pi \in \varPi } R_\mathcal{T}(\widehat{h}_\mathcal{S} \circ \pi ) \; \le \; \omega \bigl (R_\mathcal{S}(h_\mathcal{S})\bigr ) \end{aligned}$$

(2)

where is a non-decreasing function.

Equation (2) means that the best target hypothesis expressed using the learned source hypothesis has a true risk bounded by a non-decreasing function of the true risk on the source domain of the learned source hypothesis.

We are now in position to get the desired theorem.

Theorem 1

Let be a non-decreasing function. Suppose that $P_\mathcal{S}$, $P_\mathcal{T}$, $h_\mathcal{S}$, $h_\mathcal{T} = \widehat{h}_\mathcal{S} \circ \pi (\pi \in \varPi )$, $\widehat{h}_\mathcal{S}$ and $\varPi$ have the property given by Eq. (2). Let $\widehat{\pi } := \mathop {\text {ArgMin}}\nolimits _{\pi \in \varPi } \widehat{R}_\mathcal{T}(\widehat{h}_\mathcal{S} \circ \pi )$, be the best apparent projection.

Then, with probability at least $1 - \delta ~~ (\delta \in (0, 1))$ over pairs of training sets for tasks $\mathcal{S}$ and $\mathcal{T}$:

$$\begin{aligned} \begin{aligned} R_\mathcal{T}(\widehat{h}_\mathcal{T}) \;&\le \; \omega \bigl (\widehat{R}_\mathcal{S}(\widehat{h}_\mathcal{S}) \bigr ) \; + \; 2 \, \sqrt{\frac{2 \, d_{\mathcal{H}_\mathcal{S}} \log (2 e m_\mathcal{S} / d_\mathcal{H_\mathcal{S}}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{S}}} \; \\&~~ + \; 4 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta ) }{m_\mathcal{T}}} \end{aligned} \end{aligned}$$

(3)

Proof

Let $\pi ^* \; = \; \mathop {\text {ArgMin}}\nolimits _{\pi \in \varPi } R_\mathcal{T}(h_\mathcal{S} \circ \pi )$. With probability at least $1 - \delta$:

$$\begin{aligned} \begin{aligned} R_\mathcal{T}(h_\mathcal{S} \circ \widehat{\pi }) \;&\le \; \widehat{R}_\mathcal{T}(h_\mathcal{S} \circ \widehat{\pi }) \; + \; 2 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{T}}} \\&\le \; \widehat{R}_\mathcal{T}(h_\mathcal{S} \circ \pi ^*) \; + \; 2 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{T}}} \\&\le \; R_\mathcal{T}(h_\mathcal{S} \circ \pi ^*) \; + \; 4 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{T}}} \\&\le \; \omega \bigl (R_\mathcal{S} (\widehat{h}_\mathcal{S}) \bigr ) \; + \; 4 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{T}}} \\&\le \; \omega \bigl (\widehat{R}_\mathcal{S}(\widehat{h}_\mathcal{S}) \bigr ) \; + \; 2 \, \sqrt{\frac{2 \, d_{\mathcal{H}_\mathcal{S}} \log (2 e m_\mathcal{S} / d_\mathcal{H_\mathcal{S}}) \, + \, 2 \log (8 / \delta )}{m_\mathcal{S}}} \; \\&\qquad \qquad \qquad \;\;\!\!\!\! + \; 4 \, \sqrt{\frac{2 \, d_{h_{\mathcal{S} \circ \varPi }} \, \log (2 e m_\mathcal{T} / d_{h_{\mathcal{S} \circ \varPi }}) \, + \, 2 \log (8 / \delta ) }{m_\mathcal{T}}} \end{aligned} \end{aligned}$$

This follows from the fact that [10] (p. 48) using m training points and a hypothesis class of VC dimension d, with probability at least $1 - \delta$, for all hypotheses h simultaneously, the true risk R(h) and empirical risk $\widehat{R}(h)$ satisfy $|(R(h) - \widehat{R}(h)| \, \le \, 2 \, \sqrt{\frac{2 \, d \log (2 e m / d) + 2 \log (4 / \delta )}{m}}$. For $h_\mathcal{S} \circ \varPi$, this yields the first and third inequalities with probabilities at least $1 - \delta /2$. For $\mathcal{H}_\mathcal{S}$, this yields the fifth inequality with probability at least $1 - \delta /2$. Applying the union bound archives the desired results. The second inequality follows from the definition of $\widehat{\pi }$, and the fourth inequality is where we inject our assumption about the transferability (or proximity) between the source and the target problem.    $\square$

We can thus control the generalization error on the transfer domain by controlling $d_{h_{\mathcal{S} \circ \varPi }}$, $m_\mathcal{S}$ and $\omega$ which measures the link between the domain and the target domain. The number of target training data $m_\mathcal{T}$ is typically supposed to be small in transfer learning and thus cannot be employed to control the error.

3.2 Boosting Projections from Target to Source

The above analysis bounds the generalization error of the learned target hypothesis $h_\mathcal{S} \circ \widehat{\pi }$ in terms, among others, of the VC dimension of the space $h_\mathcal{S} \circ \varPi$. The problem of controlling the capacity of such a space of functions in order to prevent under or over-fitting is the same as in the traditional supervised learning setting. The difficulty lies in choosing the right space $\varPi$ of projection functions from $\mathcal{X}_\mathcal{T}$ to $\mathcal{X}_\mathcal{S}$.

The space of hypothesis functions considered is:

where $\varPi _B$ is a space of weak projections satisfying definition (1).

Now, from [11] (p. 109), the VC dimension of the space $h_\mathcal{S} \circ \varPi _{B}$ satisfies:

$$\begin{aligned} d_{L(h_\mathcal{S} \circ \varPi _{B})} \; \le \; N (d_{h_\mathcal{S} \circ \varPi _{B}} + 1) \, (3 \log (N(d_{h_\mathcal{S} \circ \varPi _{B}} + 1)) \, + \, 2) \end{aligned}$$

If $d_{h_\mathcal{S} \circ \varPi _{B}} \ll d_{h_\mathcal{S} \circ \varPi }$, then $d_{L(h_\mathcal{S} \circ \varPi _{B})}$ can also be much less than $d_{h_\mathcal{S} \circ \varPi }$, and theorem (1) provides tighter bounds.

Using the TransBoost method, we can thus gain both on the theoretical bounds on the generalization error and on the ease of finding an appropriate space of projections $\mathcal{X}_\mathcal{T} \rightarrow \mathcal{X}_\mathcal{S}$.

4 Design of the Experiments

4.1 The Main Dimensions of Experiments in Transfer Learning

There are two dimensions that can be expected to govern the efficiency of transfer learning:

• 1. The level of signal in the target data.

• 2. The relatedness between the source and the target domains.

Regarding the first dimension, one can expect that if there is no signal in the target data (i.e. the examples are labelled randomly), then no regularity can be extracted, directly or using transfer. In fact, only overfitting of the training data can potentially occur. If, on the contrary, the target learning task is easy, then there cannot be much advantage in using transfer learning. A question therefore arises as to whether there might be an optimal level of signal in the target data so as to maximally benefit from transfer learning.

The second dimension is tricky. Here, we intuitively expect that the closer the source and target domains (and problems), the more profitable transfer learning should be. However, how should we measure the “relatedness” of the source and target problems? In the domain adaptation setting, closeness can be measured through a measure of the divergence between the source distribution and the target one, since they are defined on the same input space. In transfer learning, the input spaces can be different, so that it is much more difficult to define a divergence between distributions. This is why we resorted to the function $\omega$ in our theoretical analysis. In our experiments, we control relatedness through the information shared between source and target (see below).

4.2 Experimental Setup

In our study, we devised an experimental setup that would allow us to control the two dimensions above.

In the target domain, the learning task is to classify time series of length $t_\mathcal{T}$ into two classes: . By controlling the level of noise and the difference between the distributions governing the two classes, we can control the signal level, that is the difficulty of extracting information from the target training data. We control the amount of information by varying the size $m_\mathcal{T}$ of the target training set.

Likewise, the source input space is the space of sequences of real measurements of length $t_\mathcal{S}$. Therefore, we have .

Varying $|t_\mathcal{S} - t_\mathcal{T}|$ is a way of controlling the information potentially shared in the two domains. With $t_\mathcal{S} = t_\mathcal{T}$, the two input domains are the same.

Note that learning to classify times series is not a trivial task. It has many applications, some of them involving to classify time series of length different from the length for which exists a classifier.

4.3 Description of the Experiments

Time series were generated according to the following equation:

$$\begin{aligned} x_t \; = \; \underbrace{t \times \text {slope} \times \text {class}}_{\text {information gain}} \; + \; \underbrace{\mathrm {x}_{max}\,\sin (\omega _i \times t \, + \, \varphi _j)}_{\text {sub shape within class}} \; + \; \underbrace{\eta (t)}_{\text {noise factor}} \end{aligned}$$

(4)

The fact that the noise factor is generated according to a Gaussian distribution induces a distribution over the data (class $\in \{-1, +1\}$).

The level of signal in the training data is governed by:

• 1. the slope factor: the higher the value of the slope factor, the easier the discrimination between the two classes at each additional time step

• 2. the number of different shapes in each class of sequences, each shape controlled by $\omega _i$ and $\phi _j$, and the importance of this factor in the equation being weighted by $\mathrm {x}_{max}$

• 3. the noise factor $\eta (t)$

• 4. the length of the time series, that is the number of measurements

• 5. the size of the training set

In our experiments, the noise factor is generated according to a Gaussian distribution of mean = 0 and standard deviation in $\{0.001, 0.002, 0.02, 0.2, 1\}$.

Figure 2 illustrates what can be obtained with slope $= 0.01$ with 3 subclasses in the $+1$ class, and 2 subclasses in the $-1$ class.

Fig. 2.

A synthetic data set $\mathcal S$ with 5 times series where $\eta$ is Gaussian $(\mu =0,\sigma =0.2)$.

In the experiments reported here, we kept the size of the training set constant. In each experiment, 900 times series of length 200 were generated according to the equation described above: 450 times series in each class $-1$ or $+1$. We varied the difficulty of learning by varying the slope from almost non existent: 0.001 to significant: 0.01. Similarly, we varied the length $t_\mathcal{T}$ of the target training set in $\{20, 50, 70, 100\}$ thus providing increasing levels of signal.

A target training data set of 300 time series was drawn equally balanced between the two classes. Note that this relatively small number corresponds to transfer learning scenarios where the training data is limited in the target domain. The remaining 600 time series were used as a test set. The source hypothesis was learned using the complete time series generated as explained above.

In these experiments, the set of projections $\varPi$ was chosen as a set of “hinge functions”, defined by three parameters, the slope of the first linear part, the time t where the hinge takes place, and the slope of the second linear part. The set is explored randomly by the algorithm and a projection is retained if its error rate on the current weighted data is lower than 0.45. We explored other, richer, spaces of projections without gaining superior performances. This simple set seems to be sufficient for this learning task.

In order to better assess the value of TransBoost, its performance was compared (1) to a classifier (Gaussian SVM as implemented in Scikit Learn) acting directly on the target training data, (2) to a boosting algorithm operating in the target domain with base classifiers being Gaussian SVMs, and (3) to a baseline transfer learning method that consists in finding a regression from the target input space to the source input space using a SVR regression. In this last method the regression acts as a translation from $\mathcal{X}_\mathcal{T}$ to $\mathcal{X}_\mathcal{S}$ and the class of an example ${\mathbf{x}}^\mathcal{T}$ is given by $h_\mathcal{S}\bigl (\text {regression}({\mathbf{x}}^\mathcal{T})\bigr )$.

Table 1. Comparison of the error rate (lower is better) between: learning directly in the target domain (columns $h_\mathcal{T}$ (train) and $h_\mathcal{T}$ (test)), using TransBoost (columns $H_\mathcal{T}$ (train) and $H_\mathcal{T}$ (test)), learning in the source domain (column $h_\mathcal{S}$ (test)) and, finally, mapping the time series with a SVR regression and using $h_\mathcal{S}$ (naïve transfer, column $H_\mathcal{T}^{\prime }(test)$). Test errors are highlighted in the orange columns. Bold numbers indicate where TransBoost significantly dominates both learning without transfer and learning with naïve transfer.

Table 1 provides representative examples of the results obtained. Each cell of the table shows the average performance (and the standard deviations) computed from 100 experiments repeated under the same conditions. The experimental conditions are organized according to the level of signal in the training data. In the experiments corresponding to this table, the source hypotheses were learned according to the first protocol defined above.

Several lessons can be drawn. First of all, in most situations, TransBoost brings very significant gains over learning without transfer or using transfer learning with regression. Figures 3 and 4 that sum up a larger set of experimental conditions make this even more striking. In both tables, the x-axis reports the error rate obtained using TransBoost, while the y-axis reports the error rate of the competing algorithm: either the hypothesis $h_\mathcal{T}$ learnt on the target training data alone (Fig. 3), or the hypothesis $H'_\mathcal{T}$ learned on the target data projected on the source input space using a SVR regression (Fig. 4). The remarkable efficiency of TransBoost in a large spectrum of situations is readily apparent.

Secondly, as expected, Transboost is less dominant when either the data is so noisy that no method can learn from the data (high level of noise or low slope): this is apparent on the right part of the graphs 3 and 4 (near the diagonal), or when the task is so easy (large slope and/or low noise) that nothing can be gained from transfer learning (left part of the two graphs).

We did not report here the results obtained with boosting directly in the target input space $\mathcal{X}_\mathcal{T}$ since the learning performance was almost the same as the performance as the one of the SVM classifier. This shows that this is not boosting in itself that brings a gain.

Fig. 3.

Comparison of error rates. y-axis: test error of the SVM classifier (without transfer). x-axis: test error of the TransBoost classifier with 10 boosting steps. The results of 75 experiments (each one repeated 100 times) are summed up in this graph.

Fig. 4.

Comparison of error rates. y-axis: test error of the “naïve” transfer method. x-axis: test error of the TransBoost classifier with 10 boosting steps. The results of 75 experiments (each one repeated 100 times) are summed up in this graph.

4.4 Additional Experiments

We show here, in Figs. 5, 6 and 7 qualitative results obtained on the classical half-moon problem. It is apparent that Transboost brings satisfying results.

Fig. 5.

Experiments on the half-moon problem.

5 Comparison to Previous Works

In the theoretical analysis of Ben-David et al. [1, 2], one central idea is that a common representation space should be found in which the projections of the source data $\{({\mathbf{x}}^\mathcal{S}_i)\}_{1 \le i \le m}$ and of the target data $\{({\mathbf{x}}^\mathcal{T}_i)\}_{1 \le i \le m}$ should be as undistinguishable as possible using discriminative functions from the hypothesis space $\mathcal{H}$. The intuition is that if the domains become indistinguishable, a classifier constructed for the source domain should work also for the target domain. It has been at the core of many proposed methods so far [3, 5, 7, 12].

Fig. 6.

A KNN model trained on the few target data points (in yellow). (Color figure online)

Fig. 7.

A KNN model transboosted on the few target data points.

In [8] a scenario in which multiple sources are available for a single target domain is studied. For each source $i \in \{1, \ldots , k\}$, the input distribution $D_i$ is known as well as a hypothesis $h_i$ with loss bounded by $\varepsilon$ on $D_i$. It is further assumed that the target input distribution is a mixture of the k source distributions $D_i$. The adaptation problem is thus seen as finding a combination of the hypotheses $h_i$. It is shown that guarantees on the loss of the combined target hypothesis can be given for some forms of combinations. However, the authors do not show how to learn the parameters of these combinations. In [4], the authors present a system called TrAdaboost, which uses a boosting scheme to eliminate data points that seem irrelevant for the new task defined over the same space $\mathcal{X}$. Despite the use of boosting, the scope is quite different from ours.

Finally, the authors in [6] study a scheme seemingly very close to ours. They define Hypothesis Transfer Learning algorithms as algorithms taking as input a training set in the target domain and a source hypothesis in the source domain, and producing a target hypothesis:

$$\begin{aligned} A^{\text {htl}} ~: ~ (\mathcal{X}_\mathcal{T} \times \mathcal{Y}_\mathcal{T})^m \; \times \; \mathcal{H}_\mathcal{S} \; \rightarrow \; \mathcal{H}_\mathcal{T} \subseteq \mathcal{Y}^\mathcal{X} \end{aligned}$$

One goal of the paper is to identify the effect of the source hypothesis on the generalization properties of $A^{\text {htl}}$. However, the scope of the analysis is limited in several ways. First, it focusses on linear regression with the Regularized Least Square algorithm. Second, the formal framework necessitates that in fact $\mathcal{X}_\mathcal{T} = \mathcal{X}_\mathcal{S}$ and $\mathcal{Y}_\mathcal{T} = \mathcal{Y}_\mathcal{S}$. It is thus more an analysis of domain adaptation than of transfer learning. Third, the transfer learning algorithm in effect tries to find a weight vector ${\mathbf{w}}^\mathcal{T}$ as close as possible to the source weight vector ${\mathbf{w}}^\mathcal{S}$ while fitting the target data set. There is therefore a parameter $\lambda$ to set. More importantly, the consequence is that the analysis singles out the performance of the source hypothesis on the target domain as the most significant factor controlling the expected error on the target problem. Again, therefore, the target hypothesis cannot be much different from the source one, which seems to defeat the whole purpose of transfer learning.

6 Conclusion

This paper has presented a new transfer learning algorithm, TransBoost, that uses the boosting mechanism in an original way by selecting and combining weak projections from the target domain to the source domain. The algorithm inherits some nice features from boosting. There is only one parameter to set: the number of boosting steps, and guarantees on the training error an on the test error are easily derived from the ones obtained in the theory of boosting.