A Lattice-Based Enhanced Privacy ID

Abstract

The Enhanced Privacy ID (EPID) scheme is currently used for hardware enclave attestation by an increasingly large number of platforms that implement Intel Software Guard Extensions (SGX). However, the scheme currently deployed by Intel is supported on Elliptic Curve Cryptography (ECC), and will become insecure should a large quantum computer become available. As part of National Institute of Standards and Technology (NIST)’s effort for the standardisation of post-quantum cryptography, there has been a great boost in research on lattice-based cryptography. As this type of cryptography is more widely used, one expects that hardware platforms start integrating specific instructions that accelerate its execution. In this article, a new EPID scheme is proposed, supported on lattice primitives, that may benefit not only from future research developments in post-quantum cryptography, but also from instructions that may extend Intel’s Instruction Set Architecture (ISA) in the future. This paper presents a new security model for EPID in the Universal Composability (UC) framework. The proposed Lattice-based EPID (LEPID) scheme is proved secure under the new model. Experimentally compared with a closely related Lattice-based Direct Anonymous Attestation (DAA) (LDAA) scheme from related art, it is shown that the private-key size is reduced 1.5 times, and that signature and verification times are sped up up to 1.4 and 1.1 times, respectively, for the considered parameters, when LEPID is compared with LDAA. Moreover, the signature size compares favourably to LDAA for small and medium-sized communities .

1 Introduction

The Enhanced Privacy ID (EPID) scheme is a fundamental part of the security model underpinning Software Guard Extensions (SGX)’s functioning [9]. It gives the ability to attest that a hardware enclave was successfully established on an Intel platform.

EPID can be seen as Direct Anonymous Attestation (DAA) with different linkability requirements [5]. The DAA scheme was built having the Trusted Platform Module (TPM) standard in mind. In this context, the TPM holds a representation of the host machine state, and wishes to provide a verifier with a signature of the state representation, without revealing their identity. During an offline phase, an issuer provisions the TPM and the host with membership credentials. Based on this cryptographic material, the TPM and the host jointly prove that they belong to the DAA community in zero-knowledge, while producing the above-mentioned signature. Unlike other privacy-preserving systems, like group signatures, DAA does not support the property of traceability, wherein a group manager can identify the signer from a given signature.

Alternatively, the DAA provides two approaches to prevent a malicious signer from abusing their anonymity. Firstly, when a private-key is leaked, anyone can check whether a specific DAA signature was created under this key or not. Secondly, two DAA signatures created by the same signer may or may not be linked from a verifier’s point of view. The linkability is controlled by a parameter called basename. When the same basename is used by the same signer for two signatures, they are linked; otherwise they are not. However, there are situations where this model does not suffice to prevent malicious actions. For instance, should an attacker corrupt a TPM and obtain the private-key without ever publishing it, there is no way to revoke it. While this latter problem can be mitigated by having TPMs use the same basename whenever they access a certain service, this option removes the anonymity for all uses with the same basename.

EPID is a more general scheme than DAA and thus does not split signers into TPMs and hosts, but also targets the creation of anonymous signatures. An EPID scheme consists of an issuer, signers, verifiers and a revocation manager. Like with DAA, one can check whether a certain signature was generated by a leaked private-key. Nonetheless, the ability to link signatures with the same basename is removed. Instead, whenever a signer is corrupted, they may be revoked by including one of their signatures as part of a revocation list. As a result, EPID is capable of revoking corrupted signers from the system, even when their private-key is kept hidden, whilst providing maximum privacy for the platforms. Enhanced Privacy ID signatures can also be constructed on the top of group signatures that allow members of a group to anonymously sign messages on behalf of the group, with the added property that a group manager can revoke the credentials of a misbehaving or compromised group member.

A post-quantum EPID scheme has been proposed in [3] built on hash and pseudorandom functions. More concretely, the EPID credential corresponds to a hash-based signature generated by the issuer, and proofs-of-knowledge are constructed from the Multi-Party Computation (MPC) in the head technique from Ishai et al. [8]. While [3] achieves signature sizes in the order of MBs, execution times are not considered. The main goal of this article is not to outperform [8], but rather to ignite research on lattice-based EPID partially propelled by the National Institute of Standards and Technology (NIST)’s effort on post-quantum cryptography standardisation [16]. By basing our construction on lattices, future versions of EPID might leverage the research resulting from this standardisation process to improve their efficiency. Moreover, since post-quantum cryptography is still in its infancy, it might be useful for implementers to consider multiple security assumptions, to mitigate the effects of cryptanalysis against one of them.

Lattices have proven to be a flexible tool in constructing cryptographic schemes, with applications ranging from digital signatures to public-key encryption and zero-knowledge proofs, while offering post-quantum security [1, 2, 13]. One expects that as this type of cryptography matures, an increasing number of platforms exploiting EPID ship with accelerators for lattice-based constructs [15]. Herein, by building from a recently proposed DAA scheme [10], the range of cryptographic constructs supported by lattice-based cryptography is extended to EPID. The LEPID signature size compares favourably to Latticebased DAA (LDAA) for small and medium-sized communities.

Organisation: The next section introduces the lattice-based hard problems and the two building blocks that support the proposed LEPID scheme, namely the LDAA scheme from [10] and the Zero Knowledge Proof of Knowledge (ZKPoK) of Ring-Learning With Errors (Ring-LWE) secrets from  [2]. Section 3 presents a new security model for EPID in the UC framework. The novel LEPID scheme is proposed in Sect. 4 and proven secure in Sect. 5. The performance of the LEPID scheme is discussed in Sect. 6. Finally, Sect. 7 concludes the paper.

2 Preliminaries

Throughout this paper we will use the polynomial rings ${\mathcal {R}_q=\mathbb {Z}_{q}[X]/\langle X^n + 1 \rangle }$, where $\mathbb {Z}_{q}$ is the quotient ring $\mathbb {Z}/q\mathbb {Z}$ and n a power of 2. We use names in bold, like $\varvec{a}$, both to denote elements of $\mathcal {R}_q$ and their coefficient embeddings in $\mathbb {Z}_{q}^n$. $\Vert \varvec{a}\Vert _{\infty }$ represents the infinity norm of a polynomial $\varvec{a}$, $\Vert \varvec{a}\Vert _{\infty }=\max _{i}| {a}^{i}|$, and where the ${a}^{i}$ are the coefficients of ${\varvec{a}}$. $\hat{A}=(\varvec{a}_{1},\ldots , \varvec{a}_{m})$ denotes a vector where m is a positive integer and $\varvec{a}_{1},\ldots , \varvec{a}_{m}$ are polynomials. $\Vert \hat{A}\Vert _{\infty }$ denotes the infinity norm of $\hat{A}$, defined as $\Vert \hat{A}\Vert _{\infty }=\max _{i}\Vert \mathbf{a} _{i}\Vert _{\infty }$. $B_{3d}$ represents the set of vectors $\varvec{u} \in \{-1, 0, 1\}^{3d}$ having exactly d coordinates equal to −1, d coordinates equal to 0, and d coordinates equal to 1. We represent a challenge set by , where $\bar{\mathcal {C}}$ denotes the set of differences $\mathcal {C}- \mathcal {C}$ except 0. $\mathcal {D}^{h}_{s}$ represents the discrete Gaussian distribution of standard deviation s, s.t. Pr$_{{\varvec{x}} \leftarrow \mathcal {D}^{h}_{s}} [ \Vert {\varvec{x}}\Vert > \sqrt{2h}s]\le 2^{-h/4}$. We define the following rejection sampling algorithm from [14] to avoid the dependency of ${\varvec{z}}$ on the secret ${\varvec{b}}$, $\mathtt {rej}({\varvec{z}},{\varvec{b}}, \xi )$ : Let $u \leftarrow [0,1)$; if $u>$ 1/3 exp return 0, else return 1, with $\xi$ representing a standard deviation of some distribution.

Definition 1

(The Ring Short Integer Solution Problem ($\mathbf {Ring}\hbox {-}\mathbf {SIS}_{n,m,q,\beta }$)[17]). Given m uniformly random elements ${\varvec{a}}_{i} \in \mathcal {R}_{q}$ defining a vector $\hat{A}=({\varvec{a}}_{1},{ \varvec{a}}_{2}, \ldots , {\varvec{a}}_{m})$, find a nonzero vector of polynomials $\hat{Z} \in \mathcal {R}^{m}_{q}$ of norm $\Vert \hat{Z}\Vert _{\infty } \le \beta$ such that: $f_{\hat{A}}(\hat{Z})= \sum _{i \in [m]} {\varvec{a}}_{i} {\varvec{z}}_{i} =\mathbf 0 \in \mathcal {R}_{q}$. The Ring Inhomogeneous Short Integer Solution ($Ring-ISIS_{n,m,q,\beta })$ problem asks to find $\hat{Z}$ of norm $\Vert \hat{Z}\Vert _{\infty } \le \beta$, and such that:$f_{\hat{A}}(\hat{Z})=\mathbf{y} \in \mathcal {R}_{q}$ for some uniform random polynomial $\mathbf{y }$.

Definition 2

(The Ring Learning With Error Problem (Ring-LWE) [18]). Let $\chi$ be an error distribution defined over $\mathcal {R}$ and ${\varvec{s}}\leftarrow \mathcal {R}_{q}$ a uniformly random ring element, the Ring-LWE distribution $A_{s,\chi }$ over $\mathcal {R}_{q} \times \mathcal {R}_{q}$ is sampled by choosing ${\varvec{a}} \in \mathcal {R}_{q}$ uniformly at random, randomly choosing the noise ${\varvec{e}} \leftarrow \chi$ and outputting $({\varvec{a}}, {\varvec{b}})=( {\varvec{a}},\ {\varvec{s} a}+ {\varvec{e}} \mod q) \in \mathcal {R}_{q} \times \mathcal {R}_{q}$. Let ${\varvec{u}}$ be uniformly sampled from $\mathcal {R}_{q}$. The decision problem of Ring-LWE asks to distinguish between $({\varvec{a}},{\varvec{b}}) \leftarrow A_{s,\chi }$ and $(\varvec{a}, \varvec{u})$ for a uniformly sampled secret ${\varvec{s}} \leftarrow \mathcal {R}_{q}$. The search Ring-LWE problem asks to return the secret vector ${\varvec{s}} \in \mathcal {R}_{q}$ given a Ring-LWE sample $({\varvec{a}},{\varvec{b}}) \leftarrow A_{s,\chi }$.

2.1 Lattice-Based Direct Anonymous Attestation

The DAA scheme proposed in [10] can be split at a high level into three parts. In a first part, a TPM-host pair with identifier $\mathsf{id} = (\mathsf{id}_1, ..., \mathsf{id}_{\ell }) \in \{0, 1\}^{\ell }$ joins a DAA community. This consists of the TPM sampling small $\hat{X}_t = (\varvec{x}_1, \ldots , \varvec{x}_m) \in \mathcal {R}_q^m$, and sending ${\varvec{u}}_t = \hat{A}_t \hat{X}_t$ to the issuer, where $\hat{A}_t \in \mathcal {R}_q^m$ is part of the issuer’s public-key. A signature proof of knowledge based on [12], showing that ${\varvec{u}}$ is well formed is also sent, along with a link token that prevents two TPMs from having the same secret-key. Using its private-key, the issuer then samples small $\hat{X}_h = (x_{m+1}, \ldots , x_{3m}) \in \mathcal {R}_q^{2m}$ such that $\hat{A}_h \hat{X}_h = {\varvec{u}} - {\varvec{u}}_t$, where $\hat{A}_h = [ \hat{A}_{\mathcal {I}} | \hat{A}_0 + \sum _{i = 1}^l \text {id}_i \hat{A}_i] \in \mathcal {R}_q^{2m}$, and ${\varvec{u}} \in \mathcal {R}_q$, $\hat{A}_{\mathcal {I}} \in \mathcal {R}_q^m$ and $\hat{A}_i \in \mathcal {R}_q^m\ \forall i \in \{0, \ldots , l\}$ are part of the issuer’s public-key. The vector $\hat{X}_h$ is sent back to the host. After this process, the TPM and host own small key-shares satisfying

$$\begin{aligned}{}[X_t | X_h] [\hat{A}_t | \hat{A}_h] = {\varvec{u}}. \end{aligned}$$

(1)

In a second part, the TPM and the host jointly generate a signature with respect to a message $\mu$. The signature corresponds to a tuple $(\mathsf {nym}, bsn , \pi )$, where $\text {nym}$ is a link token, $bsn$ is the basename, and $\pi$ is a signature-based proof:

$$\begin{aligned}\begin{gathered} \pi = \mathsf {SPK}\Big \{ \mathsf{public}:=\{\mathsf {pp}, \mathsf {nym}, bsn \}, \mathsf{witness}:=\{ \hat{X} = ({\varvec{x}}_1, \ldots , {\varvec{x}}_{3m}), \text {id}, \ {\varvec{e}} \}: \\ {\varvec{u}} = \hat{X} [\hat{A}_t | \hat{A}_h] \bmod q \ \wedge \ \Vert \hat{X} \Vert _{\infty } \le \beta \ \wedge \ \mathsf {nym} = \mathcal {H}( bsn ) {\varvec{x}_1} + {\varvec{e}} \bmod q \ \wedge \ \Vert {\varvec{e}} \Vert _{\infty } \le \beta \Big \}(\mu ) \end{gathered}\end{aligned}$$

demonstrating not only (1) but also that $\mathsf {nym}= \mathcal {H}( bsn ){\varvec{x}_1} + {\varvec{e}} \mod q$, where $\mathcal {H}$ is a random oracle mapping $bsn$ to a polynomial and ${\varvec{e}}$ is small.

A final part deals with signature verification. First, $\pi$ is verified. Then, the verifier iterates over the list of revoked private-keys, consisting of the elements $\varvec{x}_1^{(i)}$ of the $\hat{X}_t^{(i)}$ in (1) of the corrupt signers. In the case that $\Vert \mathsf {nym} - \mathcal {H}( bsn ) {\varvec{x}}_1^{(i)} \Vert _{\infty }$ is small, the signature has been generated by the i-th revoked user and is rejected. Similarly, two signatures $(\mathsf {nym}, bsn , \pi )$ and $(\mathsf {nym}', bsn , \pi ')$ having the same basename are linked when $\Vert \mathsf {nym} - \mathsf {nym}' \Vert _{\infty }$ is small.

2.2 Zero Knowledge Proof of the Ring-LWE Secrets

The technique presented in [2] will herein be used to modify the LDAA and support the more effective revocation method of EPID. This techniques allows one to efficiently prove in zero-knowledge possession of $\varvec{s}$ and $\varvec{e}$, with $2\varvec{s}$ and $2\varvec{e}$ being short, such that $2\varvec{y} = 2\varvec{a}\varvec{s} + 2\varvec{e}$, for public $\varvec{a}$ and $\varvec{y}$. Random $\varvec{r}_s, \varvec{r}_e \leftarrow \mathcal {D}_s$ are initially produced, and $\varvec{t} = \varvec{a} \varvec{r}_s + \varvec{r}_e$ is computed. A challenge $c = H(\varvec{t}) \in \{0, 1, \ldots , 2n-1\}$ is generated and $\varvec{s}_s = \varvec{r}_s + X^c \varvec{s}$, $\varvec{s}_e = \varvec{r}_e + X^c \varvec{e}$ are outputted in response with probability ${\text{ P }}(\varvec{s}_s, \varvec{s}_e)$, where ${\text{ P }}$ is chosen in a way that prevents $\varvec{s}_s$ and $\varvec{s}_e$ from depending on the prover’s secret inputs.

3 UC Based Security Model for EPID

The security model for the DAA [7] has been modified by replacing linkability with a revocation interface, adding the signature revocation check from [6], and introducing other modifications that results in a new EPID security model in the UC framework. Our new security definition is given in the UC model with respect to an ideal functionality $\mathcal {F}^l_{\mathsf {EPID}}$. In UC, an environment $\mathcal {E}$ should not be able to distinguish with a non-negligible probability between two worlds: the real world, where each party in the EPID protocol $\varPi$ executes its assigned part of the protocol and the network is controlled by an adversary $\mathcal {A}$ that communicates with $\mathcal {E}$; and the ideal world, in which all parties forward their inputs to $\mathcal {F}^l_{\mathsf {EPID}}$, which internally performs all the required tasks and creates the party’s outputs. A protocol $\varPi$ is said to securely realise $\mathcal {F}^l_{\mathsf {EPID}}$ if, for every adversary $\mathcal {A}$ performing an attack in the real world, there is an ideal world adversary $\mathcal {S}$ that performs the same attack in the ideal world.

An EPID scheme should satisfy: (i) unforgeability, i.e. no adversary can output a valid signature on a message $\mu$ without knowing the signer’s secret key; (ii) correctness, i.e. honestly generated signatures are always valid; and (iii) anonymity, i.e. even for a corrupt issuer, no adversary can tell whether two honestly generated signatures were produced by the same signer. The UC framework allows us to focus on the analysis of a single protocol instance with a globally unique session identifier $sid$. $\mathcal {F}^l_{\mathsf {EPID}}$ uses session identifiers of the form $sid = (\mathcal {I}, sid ')$ for some issuer $\mathcal {I}$ and a unique string $sid '$. In the procedures, functions $\mathsf{CheckTtdHonest}$ and $\mathsf{CheckTtdCorrupt}$ are used that return ‘1’ when a key belongs to a honest signer that has produced no signature, and when a key belongs to a corrupt user such that there is no signature simultaneously linking back to the inputted key and another one, respectively; and return ‘0’ otherwise. We label the checks that are done by the ideal functionality in roman numerals.

$\mathcal {F}^l_{\mathsf {EPID}}$ Setup: On input $(\text {SETUP}, sid$) from the issuer ${\mathcal {I}}$, $\mathcal {F}^l_{\mathsf {EPID}}$ verifies that $(\mathcal {I}, sid ')= sid$ and outputs $(\text {SETUP}, sid$) to $\mathcal {S}$. $\mathcal {F}^l_{\mathsf {EPID}}$ receives from the simulator $\mathcal {S}$ the algorithms Kgen, sig, ver, identify and revoke. These algorithms are responsible for generating keys for honest signers, creating signatures for honest signers, verifying the validity of signatures, checking whether a signature was generated by a given key, and updating the revocation lists respectively. $\mathcal {F}^l_{\mathsf {EPID}}$ stores the algorithms, checks that the algorithms ver, identify and revoke are deterministic [Check-I], and outputs $(\text {SETUPDONE}, sid$) to $\mathcal {I}$.

$\mathcal {F}^l_{\mathsf {EPID}}$ Join:

• 1. JOIN REQUEST: On input $(\text{ JOIN }, sid , jsid$) from a signer $\mathcal {M}_i$, create a join session $\langle jsid, \mathcal {M}_{i}, \text {request} \rangle$. Output $(\text {JOINSTART}, { sid , jsid},\mathcal {M}_{i}$) to $\mathcal {S}$.

• 2. JOIN REQUEST DELIVERY: Proceed upon receiving delivery notification from $\mathcal {S}$ by updating the session record to $\langle {jsid},\mathcal {M}_{i}, \text {delivery}\rangle$. If $\mathcal {I}$ or $\mathcal {M}_{i}$ is honest and $\langle \mathcal {M}_{i}, \star , \star \rangle$ is already in Member List $\texttt {ML}$, output $\bot$ [Check II]. Otherwise, output $(\text {JOINPROCEED}, { sid , jsid}, \mathcal {M}_i$) to $\mathcal {I}$.

• 3. JOIN PROCEED: Upon receiving an approval from $\mathcal {I}$, $\mathcal {F}^l_{\mathsf {EPID}}$ updates the session record to $\langle {jsid, sid }, \mathcal {M}_{i}, \text {complete}\rangle$. Then it outputs (JOINCOMPLETE, sid, jsid) to $\mathcal {S}$.

• 4. KEY GENERATION: On input $(\text {JOINCOMPLETE}, { sid , jsid}, { tsk }$) from $\mathcal {S}$.

  • If the signer is honest, set ${ tsk }=\bot$, else verify that the provided ${ tsk }$ is eligible by performing the following two checks that are described above: $\mathsf{{CheckTtdHonest}}({ tsk })$=1 [Check III]; $\mathsf{{CheckTtdCorrupt}}({ tsk })$=1 [Check IV].

  • Insert $\langle \mathcal {M}_{i},{ tsk }\rangle$ into Member List $\texttt {ML}$, and output JOINED.

$\mathcal {F}^l_{\mathsf {EPID}}$ Sign:

• 1. SIGN REQUEST: On input $(\text {SIGN}, { sid , ssid}, \mathcal {M}_{i}, \mu , {\varvec{p}}$) from the signer on a message $\mu$ with respect to ${\varvec{p}}$, the ideal functionality aborts if $\mathcal {I}$ is honest and no entry $\langle \mathcal {M}_{i}, \star \rangle$ exists in $\texttt {ML}$, else creates a sign session $\langle ssid,\mathcal {M}_{i}, \mu , { \varvec{p}},$ request$\rangle$ and outputs $(\text {SIGNSTART}, {sid, ssid},\mathcal {M}_{i}, l(\mu , {\varvec{p}})$) to $\mathcal {S}$.

• 2. SIGN REQUEST DELIVERY: On input $(\text {SIGNSTART}, sid , ssid$) from $\mathcal {S}$, update the session to $\langle ssid,\mathcal {M}_{i}, \mu ,{\varvec{p}},$ delivered$\rangle$, and output $(\text {SIGNPROCEED}, sid ,ssid, \mu ,{\varvec{p}}$) to $\mathcal {M}_{i}$.

• 3. SIGN PROCEED: On input $(\text {SIGNPROCEED}, {sid, ssid}$) from $\mathcal {M}_{i}$, $\mathcal {F}^l_{\mathsf {EPID}}$ updates the records $\langle {ssid}, \mathcal {M}_{i}, \mu , {\varvec{p}}, \text {delivered}\rangle$, and outputs $(\text {SIGNCOMPLETE},sid,ssid, \texttt {KRL} , \texttt {SRL} )$ to $\mathcal {S}$, where $\texttt {KRL}$ and $\texttt {SRL}$ represent the key and the signature revocation lists respectively.

• 4. SIGNATURE GENERATION: On input $(\text {SIGNCOMPLETE}, { sid , ssid}, \sigma ,$$\texttt {KRL} , \texttt {SRL} )$ from $\mathcal {S}$, if $\mathcal {M}_{i}$ is honest then $\mathcal {F}^l_{\mathsf {EPID}}$ will:

  • Ignore an adversary’s signature $\sigma$, and generate the signature for a fresh or established ${ tsk }$.

  • Check $\mathsf{{CheckTtdHonest}}({ tsk })$ =1 [Check V], and store $\langle {\mathcal {M}_{i}},{ tsk }\rangle$ in DomainKeys.

  • Generate the signature $\sigma \leftarrow \text {sig}({ tsk }, \mu , {\varvec{p}})$.

  • Check ver($\sigma , \mu , { \varvec{p}}, \texttt {KRL} , \texttt {SRL}$)=1 [Check VI], and check identify$(\sigma ,\mu ,{\varvec{p}},$${ tsk })=1$ [Check VII].

  • Check that there is no signer other than $\mathcal {M}_{i}$ with key ${ tsk }'$ registered in Members or DomainKeys such that identify($\sigma , \mu ,{ { \varvec{p}}}, { tsk }'$)=1 [Check VIII].

  • For all $( \sigma ^{*}, \mu ^{*}, {\varvec{p}}^{*}) \in { \texttt {SRL} }$, find all $({ tsk }^{*}, \mathcal {M}^{*})$ from Members and DomainKeys such that identify($\sigma ^{*}, \mu ^{*}, {\varvec{p}}^{*}, \star ,{ tsk }^{*})\,=\,1$

    • Check that no two distinct keys ${ tsk }^{*}$ trace back to $\sigma ^{*}$.

    • Check that no pair $({ tsk }^{*},\mathcal {M}_{i})$ was found.

  • If $\mathcal {M}_{i}$ is honest, then store $\langle \sigma ,\mu ,\mathcal {M}_{i}, {\varvec{p}} \rangle$ in Signed and output $(\text {SIGNATURE}, sid ,ssid,\sigma , \texttt {KRL} , \texttt {SRL} )$.

$\mathcal {F}^l_{\mathsf {EPID}}$ Verify: On input $(\text {VERIFY}, sid , \mu , \varvec{p}, \sigma , \texttt {KRL} , \texttt {SRL} )$, from a party $\mathcal {V}$ to check whether $\sigma$ is a valid signature on a message $\mu$ with respect to ${ \varvec{p}}$, $\texttt {KRL}$ and $\texttt {SRL}$, the ideal functionality does the following:

• Extract all pairs $({ tsk }_i,\mathcal {M}_{i})$ from the DomainKeys and $\texttt {ML}$, for which identify($\sigma , \mu , {\varvec{p}},{ tsk }_{i})=1$. Set $b=0$ if any of the following holds:

  • More than one key ${ tsk }_i$ was found [Check IX].

  • $\mathcal {I}$ is honest and no pair (${ tsk }_i,\mathcal {M}_i$) was found [Check X].

  • An honest $\mathcal {M}_i$ was found, but no entry $\langle \star , \mu ,\mathcal {M}_i, { \varvec{p}} \rangle$ was found in Signed [Check XI].

  • There is a key ${ tsk }^{*} \in \texttt {KRL}$, such that identify($\sigma , \mu , {\varvec{p}},{ tsk }^{*}$) = 1 and no pair (${ tsk },\mathcal {M}_{i}$) for an honest $\mathcal {M}_{i}$ was found [Check XII].

  • For matching ${ tsk }_{i}$ and ($\sigma ^{*}, \mu ^{*}, {\varvec{p}}^{*}) \in {\texttt {SRL} }$, identify($\sigma ^{*}, \mu ^{*}, { \varvec{p}}^{*},{ tsk }_{i})=1.$

• If $b \ne 0$, set $b \leftarrow$ver$(\sigma , \mu , {\varvec{p}}, \texttt {SRL} , \texttt {KRL} )$. [Check XIII]

• Add $\langle \sigma , \mu , {\varvec{p}}, \texttt {KRL} , \texttt {SRL} , b \rangle$ to VerResults, and output $(\text {VERIFIED}, { sid}, b)$ to $\mathcal {V}$.

$\mathcal {F}^l_{\mathsf {EPID}}$ Revoke: On input $({ tsk }^{*}, \texttt {KRL} )$, the ideal functionality replaces $\texttt {KRL}$ with $\texttt {KRL} \cup { tsk }^{*}$. On input $(\sigma ^{*}, \mu ^{*}, \texttt {SRL} )$, the ideal functionality replaces $\texttt {SRL}$ with $\texttt {SRL} \cup \sigma ^{*}$ after verifying $\sigma ^{*}$.

4 The Proposed LEPID Scheme

The DAA scheme proposed in [10] is herein modified so as to support the security model described in Sect. 3. We give a general overview of the proposed Latticebased EPID (LEPID) scheme in Subsect. 4.1 before proceeding with the details in Subsect. 4.2.

4.1 High Level Description of the LEPID Scheme

The first part of the DAA protocol described in Subsect. 2.1 is herein mirrored, with the exception that the TPM and the host are fused into a single signer. In particular, the issuer makes one further polynomial $\varvec{b}$ available in Procedure 1. When requesting to join a DAA community in Procedure 2, the signer with identifier $\mathsf{id} = (\mathsf{id}_1, ..., \mathsf{id}_{\ell }) \in \{0, 1\}^{\ell }$ samples a small $\hat{X}_t= (\varvec{x}_1, \ldots , \varvec{x}_{m + 1}) \in \mathcal {R}_q^{m+1}$ and sends $\varvec{u}_t = [b | \hat{A}_{\mathcal {I}}] \hat{X}_t \bmod q$ to the issuer, along with a link token $\mathsf {nym}_{\mathcal {I}} = \mathcal {H}( bsn _{\mathcal {I}}) \varvec{x}_1 + \varvec{e}_{\mathcal {I}}$ and a zero-knowledge proof $\pi _{\varvec{u}_t}$ from [10] showing that $\varvec{u}_t$ is well formed. Upon receiving this message, the issuer uses $\text {nym}_{\mathcal {I}}$ to check that no other signer has the same $\varvec{x}_1$, verifies $\pi _{\varvec{u}_t}$ and samples small $\hat{X}_h = [\hat{X}_{h_1} | \hat{X}_{h_2}] = (\varvec{y}_2, \ldots , \varvec{y}_{2m + 1}) \in \mathcal {R}_q^m \times \mathcal {R}_q^m$ such that $\hat{A}_h \hat{X}_h = \varvec{u} - \varvec{u}_t \bmod q$, with $\hat{A}_h = [\hat{A}_{\mathcal {I}} | \hat{A}_0 + \sum _{i = 1}^l \text {id}_i \hat{A}_i] \in \mathcal {R}_q^{2m}$. $\hat{X}_h$ is sent back to the signer, that updates their key as $\hat{X} = (\varvec{x}_1, \forall _{i=(2, \ldots , m+1)} \varvec{x}_i := \varvec{x}_i + \varvec{y}_i, \forall _{i=(m+2, \ldots , 2m+1)} \varvec{x}_i := \varvec{y}_i)$ in Procedure 3.

Signatures are generated in Procedures 4 and 5 as in Subsect. 2.1 for the DAA, but the basename is always chosen at random, generating link tokens $\mathsf {nym}= \varvec{p} \varvec{x}_1 + \varvec{e} \bmod q$ for a uniformly random $\varvec{p}$, and the proof-of-knowledge $\pi$ is as described in the Appendix of the full version of this paper [11]. In particular, this allows one to maintain linkability in the case of leaked private-keys, whilst maintaining full anonymity. In addition, when signing a message, the signer is presented with a list of signatures from revoked users and proves in zero-knowledge that their underlying $\varvec{x}_1$ was not used to produce any of those signatures. We achieve this by firstly randomising the $(\mathsf {nym}^{*}_i = \varvec{p}^{*}_i \varvec{f}_i + \varvec{l}_i, \varvec{p}^{*}_i)$ pairs from the list of revoked signatures, where $\varvec{f}_i$ corresponds to the $\varvec{x}_1$ polynomial of the i-th revoked user and $\varvec{l}_i$ has small norm, as

$$\begin{aligned} \varvec{d}_i= & {} \mathsf {nym}^{*}_i \varvec{q}_{i} + \varvec{l}_{i}^{'''}\end{aligned}$$

(2)

$$\begin{aligned} \varvec{o}_{i}= & {} \varvec{p}^{*}_i \varvec{q}_{i} + \varvec{l}_{i}^{'} \end{aligned}$$

(3)

for small $\varvec{q}_{i}$, $\varvec{l}_{i}^{'''}$ and $\varvec{l}_{i}^{'}$ sampled from a Gaussian distribution. Note that $\varvec{d}_{i} = \varvec{o}_{i} \cdot \varvec{f}_i + \varvec{e}_i$ for a small $\varvec{e}_{i}$. The signature includes not only $\varvec{d}_{i}$ and $\varvec{o}_{i}$, but also $\varvec{k}_{i} = \varvec{o}_{i} \varvec{x}_1 + \varvec{l}_i^{''}$ along with a zero-knowledge proof of the construction of $\varvec{d}_{i}$, $\varvec{o}_{i}$ and $\varvec{k}_{i}$. This zero-knowledge proof is an adaptation of the one described in Subsect. 2.2, the details of which can be found in the Appendix of the full version of this paper [11].

Signature verification in Procedure 6 is similar to that of the DAA, with the difference that now the proof of the shape of $\varvec{d}_{i}$, $\varvec{o}_{i}$ and $\varvec{k}_{i}$ is verified, and the norm of $\varvec{d}_{i} - \varvec{k}_{i}$ is assessed to ascertain whether the $\varvec{x}_1$ used to produce the signature under verification is the same as the one used to produce the i-th revoked signature. Finally, the community revocation manager may revoke users by updating the list of revoked private-keys ($\texttt {KRL}$) or the list of signatures of revoked users ($\texttt {SRL}$) using Procedure 7.

4.2 Detailed Description of the LEPID Scheme

We now present our LEPID scheme in detail. We start by recalling some standard functionalities that are used in the UC model of the DAA [7]:

• is a common certificate authority functionality that is available to all parties.

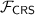• is a common reference string functionality that provides participants with all system parameters.

• is a special authenticated communication functionality that provides an authenticated channel between the issuer and the signer.

The LEPID scheme includes the Setup, Join, Sign, Verify and Revoke procedures that are as follows.

Procedure 1

(Setup). creates the system parameters: $\mathsf {sp} = (\lambda , t,q, n,m, \mathcal {R}_q, \beta , \ell , r, s,\xi )$, where $\lambda , t$ are positive integer security parameters, $\beta$ is a positive real number such that $\beta <q$, $\ell$ is the length of the users’ identifiers, and r, s and $\xi$ represent standard deviations of Gaussian distributions.

Upon input $(\text {SETUP}, sid )$, where $sid$ is a unique session identifier, the issuer first checks that ${ sid }=(\mathcal {I}, { sid '})$ for some ${ sid '}$, then creates its key pair. The Issuer’s public key is $\mathsf {pp} = (\mathsf {sp}, {\varvec{b}}, \hat{ A}_{\mathcal {I}}, \hat{ A}_0, \hat{ A}_1, \dots , \hat{ A}_{\ell }, {\varvec{u}},\mathcal {H}_{0}, \mathcal {H}, H)$, where $\hat{ A}_{\mathcal {I}}, \hat{ A}_i (i = 0,1, \ldots , \ell ) \in \mathcal {R}_q^m$, ${\varvec{b}}, {\varvec{u}} \in \mathcal {R}_q$, $\mathcal {H}_{0}: \{0, 1\}^* \rightarrow \{1,2,3\}^{t}$, $\mathcal {H}: \{0, 1\}^* \rightarrow \mathcal {R}_q$, and $H: \{0, 1\}^* \rightarrow \{0,1, 2,\ldots , 2n-1\}$. The Issuer’s private key is $\hat{T}_{\mathcal {I}}$, which is the trapdoor of $\hat{ A}_{\mathcal {I}}$ with $\Vert \hat{T}_{\mathcal {I}} \Vert _\infty \le \beta$.

The issuer initialises the Member List $\texttt {ML} \leftarrow \emptyset$. The issuer proves that his secret key is well formed in $\pi _{\mathcal {I}}$, and registers the key $(\hat{T}_{\mathcal {I}}, \pi _{\mathcal {I}})$ with and outputs $(\text {SETUPDONE}, sid )$.

Procedure 2

(Join Request). On input query $(\text {JOIN}, sid ,jsid,\mathcal {M})$, the signer $\mathcal {M}$ forwards $(\text {JOIN}, sid , jsid)$ to $\mathcal {I}$, who replies by sending $({ sid , jsid}, \rho , { bsn }_{\mathcal {I}})$ back to the signer, where $\rho$ is a uniform random nonce $\rho \leftarrow \{0,1\}^\lambda$, and ${ bsn }_{\mathcal {I}}$ is the issuer’s base name. The signer $\mathcal {M}$ proceeds as follows:

• 1. It checks that no such entry exists in its storage.

• 2. It samples a private key: ${\varvec{x}}_{1} \leftarrow {\mathcal D}_{s}$ and $({\varvec{x}}_2, \ldots , {\varvec{x}}_{m+1}) \leftarrow {\mathcal D}^{m}_{r}$. Let $\hat{X}_t= ({\varvec{x}}_{1}, \ldots , {\varvec{x}}_{m+1})$ correspond to $\mathcal {M}$’s secret key with the condition $\Vert (\varvec{x}_2, \ldots , \varvec{x}_{m+1}) \Vert _{\infty }\le \beta /2$ and $\Vert {\varvec{x}}_{1}\Vert _{\infty } \le \beta$. $\mathcal {M}$ stores its key as (${ sid }, \hat{X}_{t}$), and computes the corresponding public key ${\varvec{u}}_t = [{\varvec{b}} | \hat{ A}_{\mathcal {I}}] \hat{X}_t \mod q$, a link token $\mathsf {nym}_{\mathcal {I}} = \mathcal {H}({ bsn }_{\mathcal {I}}) {\varvec{x}}_1 + {\varvec{e}}_{\mathcal {I}} \mod q$ for some error ${\varvec{e}}_{\mathcal {I}} \leftarrow {\mathcal D}_{s}$ such that $\Vert {\varvec{e}}_{\mathcal {I}}\Vert _{\infty } \le \beta$, and generates a signature based proof:

  $$\begin{aligned} \pi _{{\varvec{u}}_t}&= \mathsf {SPK}\Big \{ \mathsf{public}:=\{\mathsf {pp}, {\varvec{u}}_t, bsn _{\mathcal {I}}, \mathsf {nym}_{\mathcal {I}} \}, \mathsf{witness}:=\{ \hat{X}_{t}= ({\varvec{x}}_1, \ldots , {\varvec{x}}_{m+1}),\\&{\varvec{e}}_{\mathcal {I}} \},\ {\varvec{u}}_t = [{\varvec{b}} | \hat{A}_{\mathcal {I}}] \hat{X}_{t} \mod q \wedge \ \Vert \hat{X}_{t} /{\varvec{x}}_{1} \Vert _{\infty } \le \beta /2 \ \wedge \Vert {\varvec{x}}_{1}\Vert \le \beta \\&\qquad \qquad \quad \wedge \mathsf{nym}_{\mathcal {I}}= \mathcal {H}( bsn _{\mathcal {I}}) {\varvec{x}}_1 + {\varvec{e}}_{\mathcal {I}} \mod q \ \wedge \ \Vert {\varvec{e}}_{\mathcal {I}} \Vert _{\infty } \le \beta \Big \}(\rho ). \end{aligned}$$

• 3. It sends ($\mathsf{nym}_{\mathcal {I}}, {\varvec{u}}_t, \pi _{{\varvec{u}}_t}$) to the issuer by giving an input $(\text {SEND},\mathsf{nym}_{\mathcal {I}},\pi _{{\varvec{u}}_t},{ sid },{jsid})$.

$\mathcal {I}$, upon receiving $(\text {SENT}, \mathsf{nym}_{\mathcal {I}}, \pi _{{\varvec{u}}_t}, { sid }, { jsid}, \mathcal {M})$ from , verifies the proof $\pi _{{\varvec{u}}_t}$ and makes sure that the signer $\mathcal {M}\notin \texttt {ML}$. $\mathcal {I}$ stores $({jsid}, \mathsf{nym}_{\mathcal {I}}, \pi _{{\varvec{u}}_t},\mathcal {M})$, and generates the message $(\text {JOINPROCEED}, { sid }, {jsid}, \mathsf{id}, \pi _{{\varvec{u}}_t})$, for some identity $\mathsf{id} \in \{0,1\}^{\ell }$ assigned to $\mathcal {M}$, and not used before by any joined member.

Procedure 3

(Join Proceed). If the signer chooses to proceed with the Join session, the message $(\text {JOINPROCEED}, { sid , jsid})$ is sent to the issuer, who performs as follows:

• 1. It checks the record $({ jsid}, \mathsf{nym}_{\mathcal {I}}, \mathsf{id}, {\mathcal {M}}, \pi _{{\varvec{u}}_t})$. For all $\ \mathsf{nym}'_{\mathcal {I}}$ from the previous Join records, the issuer checks whether $\Vert \mathsf{nym}_{\mathcal {I}} - \mathsf{nym}'_{\mathcal {I}}\Vert _{\infty } \le 2\beta$ holds; if yes, the issuer further checks if ${\varvec{u}}_t = {\varvec{u}}'_t$. If the equality ${\varvec{u}}_t = {\varvec{u}}'_t$ holds, the issuer will jump to Step 4 returning $\hat{X}_h = \hat{X}'_h$, if not the issuer will abort. Note that this double check will make sure that no two EPID keys will include the same ${\varvec{x}}_1$ value.

• 2. For all $\mathsf{nym}^{*}_{\mathcal {I}}$ in the Issuer’s Revocation record $\texttt {IR}$, the issuer checks whether the equation

  $$\Vert \mathsf{nym}_{\mathcal {I}} - \mathsf{nym}^{*}_{\mathcal {I}}\Vert _{\infty } \le 2\beta $$

  holds, if yes the issuer aborts.

• 3. It calculates the vector of polynomials $\hat{{ A}}_{h} = [\hat{ A}_{\mathcal {I}}| \hat{ A}_0 + \sum _{i = 1}^{\ell } \mathsf {id}_i \hat{{ A}}_{i} ] \in \mathcal {R}_q^{2m}$.

• 4. It samples, using the issuer’s private key $\hat{T}_{\mathcal {I}}$, a preimage $\hat{X}_h=[\hat{X}_{h_{1}}|\hat{X}_{h_{2}}] = ({\varvec{y}}_{2}, ...,$ ${\varvec{y}}_{2m+1}) \in \mathcal {D}_{r}^{m} \times \mathcal {D}_{s}^{m}$ of ${\varvec{u}} - {\varvec{u}}_t$ such that $\hat{{ A}}_{h} \hat{X}_h = {\varvec{u}} _h = {\varvec{u}} - {\varvec{u}}_t \mod q$ and $\Vert \hat{X}_{h_{1}}\Vert _{\infty } \le \beta /2$ and $\Vert \hat{X}_{h_{2}}\Vert _{\infty } \le \beta$.

• 5. The issuer adds ($\mathsf{nym}_{\mathcal {I}}, \mathsf{id},{\mathcal {M}}, \pi _{{\varvec{u}}_t}$) to his data base, and sends (${ sid , jsid}, \hat{X}_h$) to $\mathcal {M}$ via .

When $\mathcal {M}$ receives the message $({ sid , jsid},\hat{X}_h)$, it checks that the equations $\hat{{ A}}_{h} \hat{X}_h = {\varvec{u}} _h \mod q$ and ${\varvec{u}} = {\varvec{u}}_t + {\varvec{u}}_h$ are satisfied with $\Vert \hat{X}_{h_1}\Vert _{\infty } \le \beta /2$ and $\Vert \hat{X}_{h_{2}}\Vert _{\infty } \le \beta$. It stores (${ sid }, \mathcal {M}, \mathsf{id}, \hat{X}_h, {\varvec{u}}_t$) and outputs (JOINED, ${ sid , jsid}$). $\mathcal {M}$ then computes $\hat{X}=({\varvec{x}}_1,\forall _{i = (2, ..., m+1)}{\varvec{x}}_i:={\varvec{x}}_i+{\varvec{y}}_i,\forall _{i = (m+2, ..., 2m+1)}{\varvec{x}}_i:={\varvec{y}}_i)$, where $\Vert \hat{X}\Vert _{\infty } \le \beta$.

Procedure 4

(Sign Request). Upon input $(\text {SIGN}, { sid ,ssid},\mathcal {M}, \mu )$, the signer does the following:

• 1. It makes sure to have a Join record $( sid , \mathsf{id}, \hat{X},\mathcal {M})$.

• 2. It generates a sign entry $({ sid , ssid}, \mu )$ in its record.

• 3. Finally it outputs $(\text {SIGNPROCEED},{ sid , ssid}, \mu )$.

Procedure 5

(Sign Proceed). When $\mathcal {M}$ gets permission to proceed for ssid, the signer proceeds as follows:

• 1. It retrieves the records $( sid , \mathsf{id}, \pi _{{\varvec{u}}_t})$ and $({ sid , ssid}, \mu )$.

• 2. $\mathcal {M}$ samples a random polynomial ${\varvec{p}}$ and computes the polynomial $\mathsf{nym} = {\varvec{p}} {\varvec{x}}_1 + {\varvec{e}} \mod q$, for an error term ${\varvec{e}} \leftarrow \mathcal {D}_{s}$ such that $\Vert {\varvec{e}} \Vert _{\infty } \le \beta$. $\mathcal {M}$ then generates a signature based knowledge proof $\pi$.

  $$\begin{aligned}\begin{gathered} \pi = \mathsf {SPK}\Big \{\mathsf {public} := \{ \mathsf {pp},\mathsf{nym}, {\varvec{p}} \}, \\ \mathsf {witness} := \{ \hat{ X} = ({\varvec{x}}_{1}, ..., {\varvec{x}}_{2m+1}), \mathsf{id}, {\varvec{e}}\} : \\ [{\varvec{b}} | \hat{A}_{h}] \hat{X} = {\varvec{u}} \ \wedge \ \Vert \hat{ X}\Vert _{\infty } \le \beta \ \wedge \ \mathsf{nym} = {\varvec{p}} {\varvec{x}}_{1} + {\varvec{e}} \ \wedge \ \Vert {\varvec{e}}\Vert _{\infty } \le \beta \Big \}(\mu ). \end{gathered}\end{aligned}$$

  The details of the proof $\pi$ are presented in the Appendix of the full version of this paper [11].

• 3. The signer proves that it is not using any of the keys that produced a revoked signature $(\sigma _{i}^{*}, {\varvec{p}}^{*}_{i}, \mathsf{nym}^{*}_{i})$ in the signature revocation list (more details about the proof can be found in the Appendix of the full version of this paper [11]).

  • Let $\mathsf{nym}^{*}_{i}={\varvec{p}}^{*}_{i} {\varvec{f}}_{i} + {\varvec{l}}_i$, where (${\varvec{f}}_{i}, {\varvec{l}}_i$) were used before to create $\mathsf{nym}^{*}_{i}$ by some $\mathcal {M}{_i}{^*}$ that generated a revoked signature $\sigma _{i}^* \in \texttt {SRL}$. $\mathcal {M}$ proceeds as follows:

    • 

    • ${\varvec{o}}_{i}={\varvec{p}}^{*}_{i}{\varvec{q}}_{i}+ {\varvec{l}}'_i$, ${\varvec{k}}_{i}={\varvec{o}}_{i} {\varvec{x}}_{1}+ {\varvec{l}}''_i$, ${\varvec{d}}_{i}=\mathsf{nym}^{*}_{i}{\varvec{q}}_{i}+{\varvec{l}}'''_i$

    • ${\varvec{r}}_{{ x}_{1}}, {\varvec{r}}_{ e}, {\varvec{r}}_{{ q}_{i}}, {\varvec{r}}_{{ l}'_{i}}, {\varvec{r}}_{{l}''_{i}}, {\varvec{r}}_{{ l}'''_i} \leftarrow {\mathcal D}_{s}$

    • ${\varvec{t}}_\mathsf{nym}= {\varvec{p}} {\varvec{r}}_{{ x}_{1}}+ {\varvec{r}}_{ e}$, ${\varvec{t}}_{{ o}_{i}}= {\varvec{p}}^{*}_{i} {\varvec{r}}_{{ q}_{i}}+ {\varvec{r}}_{{ l}'_{i}}$, ${\varvec{t}}_{{ k}_{i}}= {\varvec{o}}_{i}{\varvec{r}}_{{ x}_{1}}+ {\varvec{r}}_{{l}''_{i}}$, ${\varvec{t}}_{{ d}_{i}}= \mathsf{nym}^{*}_{i}{\varvec{r}}_{{ q}_{i}}+{\varvec{r}}_{{ l}'''_i}$.

  • Calculates the challenge ${ c}_{v}= H({\varvec{t}}_\mathsf{nym}| {\varvec{t}}_{{ o}_{i}}| {\varvec{t}}_{{ k}_{i}}| {\varvec{t}}_{{d}_{i}}|\mu ) \in \{0,1,2,\ldots , 2n-1\}$.

  • The following responses are computed:

    • ${\varvec{s}}_{x_{1}}={\varvec{r}}_{x_{1}}+ { X}^{c_{v}} {\varvec{x}}_{1}$, ${\varvec{s}}_{e}={\varvec{r}}_{e}+ { X}^{c_{v}}{\varvec{e}}$, ${\varvec{s}}_{q_i}={\varvec{r}}_{q_i}+{X}^{c_v}{\varvec{q}}_{i}$,

      ${\varvec{s}}_{l'_i}={\varvec{r}}_{l'_i}+{X}^{c_v} {\varvec{l}}'_i$, ${\varvec{s}}_{l''_i}={\varvec{r}}_{l''_i}+X^{c_v}{\varvec{l}}''_i$, ${\varvec{s}}_{l'''_i}={\varvec{r}}_{l'''_i}+X^{c_v}{\varvec{l}}'''_i$.

    Abort if any of these rejection samples outputs 1:

    • $\mathtt {rej}( {\varvec{s}}_{x_{1}},{ X}^{c_{v}} {\varvec{x}}_{1}, \xi )$, $\mathtt {rej}( {\varvec{s}}_{e}, { X}^{c_{v}}{\varvec{e}}, \xi )$, $\mathtt {rej}({\varvec{s}}_{q_i}, {X}^{c_v}{\varvec{q}}_{i}, \xi )$,

      $\mathtt {rej}({\varvec{s}}_{l'_i}, {X}^{c_v} {\varvec{l}}'_i, \xi )$, $\mathtt {rej}({\varvec{s}}_{l''_i}, {X}^{c_v} {\varvec{l}}''_i, \xi )$ or $\mathtt {rej}({\varvec{s}}_{l'''_i}, {X}^{c_v} {\varvec{l}}'''_i, \xi )$.

• 4. Finally, $\mathcal {M}$ outputs $\sigma =(\pi , \mathsf{nym}, {\varvec{o}}_{i}, {\varvec{k}}_{i},{\varvec{d}}_{i},{\varvec{s}}_{x_{1}},{\varvec{s}}_{e}, {\varvec{s}}_{q_i},{\varvec{s}}_{l'_i},{\varvec{s}}_{l''_i},{\varvec{s}}_{l'''_i},c_{v},\texttt {KRL} ,\texttt {SRL} )$.

Procedure 6

(Verify). Let ${ \texttt {KRL} }$ denotes the revocation list with all the rogue signer’s secret keys ${\varvec{x}}^{*}_{1}$. Upon input $(\text {VERIFY}, { sid },\sigma , \mu , \texttt {KRL} , \texttt {SRL} )$, the verifier proceeds as follows:

• 1. It checks the zero-knowledge proof regarding the statement: $\{[{\varvec{b}} |\hat{A}_{h}] \hat{ X}\,=\,{\varvec{u}}\wedge \Vert \hat{{X}}\Vert _{\infty }\le \beta \wedge \mathsf{nym}\,=\,{\varvec{p}}{ \varvec{x}}_1+{\varvec{e}}\mod q\wedge \Vert {\varvec{e}}\Vert _{\infty }\le \beta .\}$

• 2. For all ${\varvec{x}}^{*}_1 \in {\texttt {KRL} }$, if $\Vert {\varvec{p}} {\varvec{x}}^{*}_1 -\mathsf{nym}\Vert _{\infty } \le \beta$ the verifier outputs 0.

• 3. For all $\sigma _{i}^{*} = (\pi _{\mathsf{nym}^{*}_{i}}, \mathsf{nym}_{i}^{*}, {\varvec{p}}_{i}^{*}) \in \texttt {SRL}$, the verifier

  • (a) computes:

    • ${\varvec{t}'}_{k_i}\,{=}\, {\varvec{o}}_{i}{\varvec{s}}_{x_{1}}+{\varvec{s}}_{l''_i}-X^{{ c}_{v}}{{\varvec{k}}_i}$, ${\varvec{t}'}_{d_i}\,{=}\, \mathsf{nym}^{*}_{i}{\varvec{s}}_{q_{i}}+{\varvec{s}}_{l'''_i}-X^{{ c}_{v}}{{\varvec{d}}_i}$,

      ${\varvec{t}'}_{o_i}\,{=}\, {\varvec{p}}^{*}_{i}{\varvec{s}}_{q_{i}}+{\varvec{s}}_{l'_i}-X^{{ c}_{v}}{{\varvec{o}}_i}$, ${\varvec{t}'}_\mathsf{nym}\,{=}\, {\varvec{p}}{\varvec{s}}_{x_{1}}+{\varvec{s}}_{e}-X^{{ c}_{v}}{\mathsf{nym}}$.

  • (b) checks ${c_v}\overset{?}{=}H({\varvec{t}'}_\mathsf{nym}| {\varvec{t}'}_{o_{i}}|{\varvec{t}'}_{k_i}|{\varvec{t}'}_{d_{i}}|\mu )$ and that all the following norms satisfy $\Vert {\varvec{s}}_{{\varvec{x}}_1}\Vert _{\infty }$, $\Vert {\varvec{s}}_{e}\Vert _{\infty }, \Vert {\varvec{s}}_{q_i}\Vert _{\infty }, \Vert {\varvec{s}}_{l'_i}\Vert _{\infty }, \Vert {\varvec{s}}_{l''_i}\Vert _{\infty }, \Vert {\varvec{s}}_{l'''_i}\Vert _{\infty } \le \beta + \sqrt{n}\beta .$

• 4. For all $\sigma _{i}^{*} = (\pi _{\mathsf{nym}^{*}_{i}}, \mathsf{nym}^{*}_{i}, {\varvec{p}}_{i}^{*})$, the verifier checks $2\Vert {\varvec{d}}_{i}-{ \varvec{k}}_{i}\Vert < \varGamma$, where $\varGamma$ is a function of $\beta$. If $2\Vert {\varvec{d}}_{i}-{ \varvec{k}}_{i}\Vert < \varGamma$ the verifier outputs 0, otherwise 1.

Procedure 7

(Revoke). On input $(\text {Revoke}, sid, {\varvec{x}}_{1}^{*}, \texttt {KRL} )$ or $(\text {Revoke}, sid, \sigma ^{*}, \mu ^{*}, \texttt {SRL} )$, the revocation manager adds ${\varvec{x}}_{1}^{*}$ to $\texttt {KRL}$ or $\sigma ^{*}$ to $\texttt {SRL}$ after verifying $\sigma ^{*}$.

5 A Sketched Security Proof for LEPID

In this section, we provide a sketch of the security proof of the LEPID scheme. A detailed security proof is presented in the Appendix of the full version of this paper [11]. A variant of the sequence of games of [7] is presented, showing that no environment $\mathcal {E}$ can distinguish the real world protocol $\varPi$ with an adversary $\mathcal {A}$, from the ideal world $\mathcal {F}^l_{\mathsf {EPID}}$ with a simulator $\mathcal {S}$. Starting with the real world protocol game, we change the protocol game by game in a computationally indistinguishable way, finally ending with the ideal world protocol.

Game 1

This is the real world protocol.

Game 2

An entity C is introduced, that receives all inputs from the honest parties and simulates $\varPi$ for them. This is equivalent to Game 1.

Game 3

C is split into $\mathcal {F}$ and $\mathcal {S}$. $\mathcal {F}$ behaves as an ideal functionality, receiving all inputs and forwarding them to $\mathcal {S}$, who simulates the real world protocol for honest parties. $\mathcal {S}$ sends the outputs to F, who forwards them to $\mathcal {E}$. This game is similar to Game 2, but with a different structure.

Game 4

$\mathcal {F}$ now behaves differently in the setup interface. It stores the algorithms for the issuer $\mathcal {I}$, and checks that the structure of $sid$ is correct for an honest $\mathcal {I}$, aborting if not. In case $\mathcal {I}$ is corrupt, $\mathcal {S}$ extracts the secret key for $\mathcal {I}$ and proceeds in the setup interface on behalf of $\mathcal {I}$. Clearly $\mathcal {E}$ will notice no change.

Game 5

$\mathcal {F}$ now performs the verification and key revokation checks instead of forwarding them to $\mathcal {S}$. There are no protocol messages and the outputs are exactly as the real world protocol. However, the verification algorithm that $\mathcal {F}$ uses does not contain any key or signature revocation checks. $\mathcal {F}$ can perform this check separately, so the outcomes are equal.

Game 6

$\mathcal {F}$ stores in its records the members that have joined. If $\mathcal {I}$ is honest, $\mathcal {F}$ stores the secret key tsk, extracted from $\mathcal {S}$, for corrupt platforms. $\mathcal {S}$ always has enough information to simulate the real world protocol except when the issuer is the only honest party. In this case, $\mathcal {S}$ does not know who initiated the join, and so cannot make a join query with $\mathcal {F}$ on the signer’s behalf. Thus, to deal with this case, $\mathcal {F}$ can safely choose any corrupt signer and put it into Members. The identities of signers are only used for creating signatures for honest signers, so corrupted signers do not matter. In the case that the signer is already registered in Members, $\mathcal {F}$ would abort the protocol, but $\mathcal {I}$ will have already tested this case before continuing with the query JOINPROCEED. Hence $\mathcal {F}$ will not abort. Thus in all cases, $\mathcal {F}$ and $\mathcal {S}$ can interact to simulate the real world protocol.

Game 7

(Anonymity). In this game, $\mathcal {F}$ creates anonymous signatures for honest platforms by running the algorithms defined in the setup interface. Let us start by defining Game $7.k.k'$. In this game $\mathcal {F}$ handles the first $k'$ signing inputs of ${\mathcal {M}}_{i}$ for $i < k$ using algorithms, and subsequent inputs are forwarded to $\mathcal S$ who creates signatures as before. We note that Game 7.0.0=Game 6. For increasing $k'$, Game $7.k.k'$ will be at some stage equal to Game $7.k+1.0$, this is because there can only be a polynomial number of signing queries to be processed. Therefore, for large enough k and $k'$, $\mathcal {F}$ handles all the signing queries of all signers, and Game 7 is indistinguishable from Game $7.k.k'$. To prove that Game $7.k.k'+1$ is indistinguishable from Game $7.k.k'$, suppose that there exists an environment that can distinguish a signature of an honest party using ${ tsk }={\varvec{x}}_{1}$ from a signature using a different ${ tsk }^{j}={ \varvec{x}}^{j}_{1}$, then the environment can solve the Decision Ring -LWE Problem.

The first $j \le k'$ signing queries on behalf of ${\mathcal {M}}_{k}$ are handled by $\mathcal {F}$ using the algorithms, and subsequent inputs are then forwarded to $\mathcal {S}$ as before. Now suppose that F outputs the tuples $( \mathsf {nym}^{j}, {\varvec{p}}^{j}, {\varvec{o}}_{i}^{j}, {\varvec{k}}_{i}^{j}, {\varvec{d}}_{i}^{j}, {\varvec{s}}^{j}_{x_{1}}, {\varvec{s}}^{j}_{e}, {\varvec{s}}^{j}_{q_i}, {\varvec{s}}^{j}_{l'_i}, {\varvec{s}}^{j}_{l''_i}, {\varvec{s}}^{j}_{l'''_i}, c^{j}_{v}, \texttt {SRL} )$ for $j \le k'$, with $\mathsf{nym}^{j}={\varvec{p}}^{j}{\varvec{x}}_{1}+{\varvec{e}}^{j}$, for an error term ${\varvec{e}}_{j} \leftarrow \mathcal {D}_{s}$, and the remaining proofs are honestly generated. The $j=k'+1$-th query for $\mathcal {M}_{k}$ is as follows: $( \mathsf {nym}^{\mathcal S}, {\varvec{p}}^{\mathcal S}, {\varvec{o}}^{\mathcal S}_{i}, {\varvec{k}}^{s}_{i}, {\varvec{d}}^{\mathcal S}_{i}, {\varvec{s}}^{\mathcal S}_{x_{1}}, {\varvec{s}}^{\mathcal S}_{e}, {\varvec{s}}^{\mathcal S}_{q_i}, {\varvec{s}}^{\mathcal S}_{l'_i}, {\varvec{s}}^{\mathcal S}_{l''_i}, {\varvec{s}}^{\mathcal S}_{l'''_i}, c^{\mathcal S}_{v},\mu ^{\mathcal S}, \texttt {SRL} )$. $\mathcal S$ is challenged to decide if $( \mathsf {nym}^{\mathcal S}, {\varvec{p}}^{\mathcal S}, {\varvec{o}}^{\mathcal S}_{i}, {\varvec{k}}^{s}_{i}, {\varvec{d}}^{\mathcal S}_{i}, {\varvec{s}}^{\mathcal S}_{x_{1}}, {\varvec{s}}^{\mathcal S}_{e}, {\varvec{s}}^{\mathcal S}_{q_i}, {\varvec{s}}^{\mathcal S}_{l'_i}, {\varvec{s}}^{\mathcal S}_{l''_i}, {\varvec{s}}^{\mathcal S}_{l'''_i}, c^{\mathcal S}_{v}, \mu ^{\mathcal S}, \texttt {SRL} )$ is chosen from a Ring LWE distribution for some secret ${ \varvec{x}}_{1}$ or uniformly at random. $\mathcal {S}$ proceeds in simulating the signer without knowing the secret ${ \varvec{x}}_{1}$. $\mathcal {S}$ can answer all the H queries, as $\mathcal {S}$ is controlling . $\mathcal S$ sets: ${\varvec{t}}^{\mathcal S}_{k_i}{=} {\varvec{o}}^{\mathcal S}_{i}{\varvec{s}}^{\mathcal S}_{x_{1}}+{\varvec{s}}^{\mathcal S}_{l''_i}-X^{{ c}^{\mathcal S}_{v}}{{\varvec{k}}^{\mathcal S}_{i}}$; ${\varvec{t}}^{\mathcal S}_{d_i}{=} \mathsf{nym}^{{*}}_{i}{\varvec{s}}^{\mathcal S}_{q_{i}}+{\varvec{s}}^{\mathcal S}_{l'''_i}-X^{{ c}^{\mathcal S}_{v}}{{\varvec{d}}^{\mathcal S}_{i}}$; ${\varvec{t}}^{\mathcal S}_{o_i}{=} {\varvec{p}}^{*}_{i}{\varvec{s}}^{\mathcal S}_{q_{i}}+{\varvec{s}}^{\mathcal S}_{l'_i}-X^{{ c}^{\mathcal S}_{v}}{{\varvec{o}}^{\mathcal S}_{i}}$; ${\varvec{t}}^{\mathcal S}_\mathsf{nym}{=} {\varvec{p}}^{\mathcal S}{\varvec{s}}^{\mathcal S}_{x_{1}}+{\varvec{s}}^{\mathcal S}_{e}-X^{{ c}^{\mathcal S}_{v}}{\mathsf{nym}^{\mathcal S}}$; and, finally, $c^{\mathcal S}_{v}:{=}H({\varvec{t}}^{\mathcal S}_\mathsf{nym}| {\varvec{t}}^{\mathcal S}_{o_{i}}|{\varvec{t}}^{\mathcal S}_{k_i}|{\varvec{t}}^{\mathcal S}_{d_{i}}|\mu ^{\mathcal S})$. For $i> k'+1$, $\mathcal {S}$ outputs the tuples $(\mathsf {nym}^{j},{\varvec{p}}^{j},{\varvec{o}}_{i}^{j},{\varvec{k}}_{i}^{j},{\varvec{d}}_{i}^{j},{\varvec{s}}^{j}_{x_{1}},{\varvec{s}}^{j}_{e},{\varvec{s}}^{j}_{q_i},{\varvec{s}}^{j}_{l'_i},{\varvec{s}}^{j}_{l''_i},{\varvec{s}}^{j}_{l'''_i}, c^{j}_{v},\mu ^{j},\texttt {SRL} )$, with $\mathsf{nym}^{j}={\varvec{p}}^{j}{\varvec{x}}^{j}_{1}+{\varvec{e}}^{j} \mod q$, for some freshly generated secret ${\varvec{x}}_{1}^{j}$ and error term ${\varvec{e}}^{j} \leftarrow \mathcal {D}_{s}$. For each case, ${\mathcal {M}}_{k}$ can provide a simulated proof as follows. $\mathcal S$ sets ${\varvec{t}}^{j}_{k_i}{=} {\varvec{o}}^{j}_{i}{\varvec{s}}^{j}_{x_{1}}+{\varvec{s}}^{j}_{l''_i}-X^{{ c}^{j}_{v}}{{\varvec{k}}^{j}_{i}}$; ${\varvec{t}}^{j}_{d_i}{=} \mathsf{nym}^{{*}}_{i}{\varvec{s}}^{j}_{q_{i}}+{\varvec{s}}^{j}_{l'''_i}-X^{{ c}^{j}_{v}}{{\varvec{d}}^{j}_{i}}$; ${\varvec{t}}^{j}_{o_i}{=} {\varvec{p}}^{*}_{i}{\varvec{s}}^{j}_{q_{i}}+{\varvec{s}}^{j}_{l'_i}-X^{{ c}^{j}_{v}}{{\varvec{o}}^{j}_{i}}$; ${\varvec{t}}^{j}_\mathsf{nym}{=} {\varvec{p}}^{j}{\varvec{s}}^{j}_{x_{1}}+{\varvec{s}}^{j}_{e}-X^{{ c}^{j}_{v}}{\mathsf{nym}^{j}}$; and, finally, $c^{j}_{v}:{=}H({\varvec{t}}^{j}_\mathsf{nym}| {\varvec{t}}^{j}_{o_{i}}|{\varvec{t}}^{j}_{k_i}|{\varvec{t}}^{j}_{d_{i}}|\mu ^{j})$.

Thus, any distinguisher between Game $7.k.k'$ and Game $7.k.k'+1$ can solve the Decision Ring LWE Problem.

Game 8

$\mathcal {F}$ now no longer informs $\mathcal {S}$ about the message and ${\varvec{p}}$ that are being signed. If the signer $\mathcal {M}$ is honest, then $\mathcal {S}$ can learn nothing about the message $\mu$ and $\varvec{p}$. Instead, $\mathcal {S}$ knows only the leakage $l(\mu , {\varvec{p}})$. To simulate the real world, $\mathcal {S}$ chooses a pair $(\mu ', {\varvec{p}}')$ such that $l(\mu ', {\varvec{p}}')$=$l(\mu , {\varvec{p}})$. An environment $\mathcal {E}$ observes no difference, and thus Game 8 = Game 7.

Game 9

If $\mathcal {I}$ is honest, then $\mathcal {F}$ now only allows members that joined to sign. An honest signer will always check whether it has joined before signing in the real world protocol, so there is no difference for honest signers. Therefore Game 9 = Game 8.

Game 10

When storing a new $tsk={\varvec{x}}_{1}$, $\mathcal {F}$ checks =1 or =1. We want to show that these checks will always pass. In fact, valid signatures always satisfy $\mathsf{nym}={\varvec{p}}{\varvec{x}}_{1}+ \varvec{e}$ where $\Vert {\varvec{x}}_{1}\Vert _{\infty } \le \beta$ and $\Vert \varvec{e}\Vert _{\infty } \le \beta$. By the unique Shortest Vector Problem, there exists only one tuple $({\varvec{x}}_{1}, \varvec{e})$ such that $\Vert {\varvec{x}}_{1}\Vert _{\infty } \le \beta$ and $\Vert \varvec{e}\Vert _{\infty } \le \beta$ for small enough $\beta$. Thus, will always give the correct output. Also, due to the large min-entropy of discrete Gaussians the probability of sampling ${\varvec{x}}'_{1}= {\varvec{x}}_{1}$, and thus of having a signature already using the same $tsk= {\varvec{x}}_{1}$, is negligible, which implies that will give the correct output with overwhelming probability. Hence Game 10 = Game 9.

Game 11

(Completeness). In this game, $\mathcal {F}$ checks that honestly generated signatures are always valid. This is true as sig algorithm always produces signatures passing through verification checks. Those signatures satisfy $\mathsf{identify}(tsk, \sigma , \mu , {\varvec{p}})=1$, which is checked via $\mathsf {nym}$. $\mathcal {F}$ also makes sure, using its internal records Members and DomainKeys that honest users are not sharing the same secret key ${ tsk }$. If there exists a key ${ tsk }'= {\varvec{x}}'_{1}$ in Members and DomainKeys such that $\Vert \mathsf{nym}- {\varvec{p}} {\varvec{x}}'_{1}\Vert _{\infty } \le \beta$, then this breaks search Ring-LWE.

Game 12

Check-IX is added to ensure that there are no multiple ${ tsk }$ tracing back to the same signature. Since there exists only one pair (${\varvec{x}}_{1}, {\varvec{e}}_{\mathcal {I}}$), $\Vert {\varvec{x}}_{1}\Vert _{\infty } \le \beta$, $\Vert {\varvec{e}}_{\mathcal {I}}\Vert _{\infty } \le \beta$, satisfying $\mathsf{nym}_{\mathcal {I}}=\mathcal {H}({ bsn }_{\mathcal {I}}) {\varvec{x}}_{1}+ {\varvec{e}}_{\mathcal {I}}$, two different signers cannot share the same ${\varvec{x}}_{1}$, thus any valid signature traces back to a single ${ tsk }$.

Game 13

(Unforgeability). To prevent accepting signatures that were issued by the use of join credentials not issued by an honest issuer, $\mathcal {F}$ further adds Check-X. This is due to the unforgeability of Boyen signatures [4].

Game 14

(Unforgeability). Check-XI is added to $\mathcal {F}$, preventing the forging of signatures with honest tsk and credentials. If a valid signature is given on a message that the signer has never signed, the proof could not have been simulated. ${\varvec{x}}_{1}$ would be extracted and Ring-LWE would be broken. So Game 14 = Game 13.

Game 15

Check-XII is added to $\mathcal {F}$, ensuring that honest signers keys are not being revoked. If an honest signer is simulated by means of the Ring-LWE problem instance and a proper key $\texttt {KRL}$ is found, it must be the secret key of the target instance. This is equivalent to solving the search Ring-LWE problem.

Game 16

$\mathcal {F}$ now performs signature based revocation when verifying signatures. $\mathcal {F}$ checks that there is no $(\sigma ^{*}, \mathsf{nym}^{*}, {\varvec{p}}^{*}) \in \texttt {SRL}$ such that for some matching ${ tsk }_{i}$ and ($\sigma ^{*}, \mu ^{*}, {\varvec{p}}^{*}) \in {\texttt {SRL} }$, we have identify($\sigma ^{*}, \mu ^{*}, { \varvec{p}}^{*},{ tsk }_{i})=1$. By the soundness of the proof presented in the Appendix of the full version of this paper [11], this check will always pass with overwhelming probability.$\square$

6 Experimental Results

Let $q \ge 2$ represents an integer modulus such that $q=poly(n)$. For correctness, we require the main hardness parameter n, to be large enough (e.g., $n\ge 100$) and $q> \beta$ as both being at least a small polynomial in n. We also let $m=O(\log {q})$ as in  [17]. A concrete choice of parameters can be as follows: $n=512,\ l=32,\ q=8380417,\ m =24,$ and $\beta =275$.

Both LDAA and LEPID were implemented in C, emulating all entities in a single machine. The code was compiled with gcc 4.8.5 with the -O3 and -march=native flags and executed on an Intel i9 7900X CPU with 64 GB running at 3.3 GHz operated by CentOS 7.5. The obtained experimental results can be found in Table 1. Note that the measured times for signing and verification do not take into account transfer times between the entities or object creation and destruction.

By construing the signer as a single entity instead of two as in the LDAA, the proposed LEPID scheme achieves a reduction of the private-key size of 1.5 times. While the comparison in signatures sizes between both schemes yields favourably for the proposed LEPID scheme with a small amount of rejected users, as the number of users in the SRL increases, its signature size increases linearly at a rate of 18 kB per rejected user (9 polynomials and an integer). When the SRL contains 500 users, the LEPID signature size closely matches that of the LDAA scheme. Should LEPID signing be implemented on a device with limited computational resources like the TPM, its constrained memory resources and the cost of data transfer might limit its application to small and medium-sized communities. In particular, if one considers a revocation rate of 0.1%, LEPID signatures will compare favourably in size to LDAA signatures for communities with fewer than 500,000 users.

The signing time in the LEPID scheme is dominated by the signature based knowledge proof $\pi$. The addition of the SRL, and consequently of 13 polynomial multiplications per rejected user, shows no meaningful impact in the final signing time, where LEPID maintains a speedup of 1.4 over the LDAA scheme. Likewise, in the verification time, the additional 2 polynomial multiplications per rejected user incurred by the SRL are negligible compared to the verification of $\pi$. Hence, the proposed LEPID scheme achieves a speedup of 1.1 when compared with the LDAA scheme across both small and medium rejection lists. For the computational complexity introduced by the SRL to be meaningful, the number of rejected users must be in the order of millions. Once more, the proposed LEPID scheme shows improved signature and verification times for small and medium communities when compared with the LDAA.

Table 1. Experimental results for the proposed LEPID and LDAA [10] for $n = 512$, $q = 8380417$, $l = 32$, $m = 24$ and $\beta = 256$ obtained on an Intel i9 7900X

7 Conclusion

While EPID plays a determinant role in the security of SGX, the scheme currently deployed by Intel will become insecure in the event that a large-scale quantum-computer is produced. Herein, a novel EPID scheme is proposed, supported on lattice-based security assumptions, and achieving presumed quantum resistance. A security model for EPID is presented for the first time in the UC framework, and the proposed scheme is proven secure under this model. When compared with a closely related LDAA scheme from related art, the proposed LEPID achieves a reduction in the private-key size of 1.5 times, and of the signature and verification times of 1.4 and 1.1 times, respectively, when no users have been revoked. It is furthermore shown, experimentally, that the overhead introduced by the more effective revocation method of LEPID is minimal for small to medium-sized communities. Finally, it is expected that the proposed LEPID may benefit from theoretical developments and hardware accelerators that result from the increased interest that lattice-based cryptography has gathered in the last few years.