Introduction

Recently, the discussion on gene drives is gaining momentum (Fischer 2018; Groß 2016; Jacobs 2015). The deliberate release of genetically modified organisms (GMOs) equipped with genetic systems to overcome the patterns of Mendelian inheritance, able to either drive desired traits into a wild population or suppress the population altogether. This harbours wide implications concerning economy, ethics, genetics and ecology. To explore implications of the latter we constructed a series of model concepts around the putative target organism, the olive fruit fly Bactrocera oleae. We discuss the different modelling approaches in their current prototype stages and want to stress the importance of model simulations in order to identify ecological hazards prior to the release of potentially adverse agents such as artificial self-reproducing.

The GeneTip project works on the conception and design modelling of population dynamics influenced by gene drives. In this pursuit, multiple different approaches and concepts have been developed to on one hand, be able to cover a broad perspective on the topic but on the other hand to also focus on different key aspects. In the following we present seven concepts based on different modelling approaches. In these model concepts our model organism is the olive fruit fly (Bactrocera oleae), which is a major pest species in agricultural olive production.

Female olive flies oviposit their eggs into the ripening olive fruits right beneath the outer skin (Nardi et al. 2005), thereby they lay one egg per fruit and are able lay 250–350 eggs within a lifetime (Genç and Nation 2008). From an egg, a monodietary larva hatches which eats its way through the fruit pulp to the center of the olive (Daane and Johnson 2010; Sharaf 1980). Olive flies may have three to five overlapping generations per year (Bocaccio and Petacchi 2009; Comins and Fletcher 1988; Kokkari et al. 2017; Pontikakos et al. 2010; Voulgaris et al. 2013) and thereby cause annual net losses estimated to be as high 5% of global olive production translating into 800 million US-Dollar per year (Montiel Bueno and Jones 2002). Due to their role as an agricultural pest species, the olive fly is considered a target species for diverse pest control methods.

Until now they have been the target for the sterile insect technique (SIT) (Knipling 1955). Wherein, laboratory-reared sterile males are mass-released into the wild. The sterile males outnumber the fertile wild males and thus reduce the number of offspring in the subsequent generation. However, prolonged SIT applications proved costly and showed only limited success, since the decimated population rebounds quickly to their former size once the sterile male releases seize. Therefore, the application of a gene drive might be feasible (For a more comprehensive information on the olive fly review Chap. 4, case study 1).

A gene drive is a phenomenon that increases the prevalence of certain gene, or set of genes within a population. Artificial gene drive systems may be released with the intention to spread desired genes in a population, these genes may either confer a certain trait such as reduced fertility or a bias in the sex ratio of a population, but may also simply kill potential offspring. Such gene drives, may however harbour unforeseen ecological consequences, due to the multifactorial set-up of ecosystems. For instance, a potent gene drive aimed at suppression might cause an eradication of the target species which may affect interconnected species and the ecosystem’s food web. Therefore, it is important to predict potential effects of gene drives on a population and their habitat by various modelling approaches.

First, the possibilities to model population dynamics based on a stock-flow model will be explored. This model will consider the temperature dependent mortality of the different life stages of the flies. Another stock flow model was developed to simulate the population dynamics of a single-locus Underdominance gene drive as presented by Reeves et al. (2014). Then a differential-equation based concept which further considers a gene drive released into a wild population of olive flies will be introduced. The following stochastic, recurrence equation-based model will further consider the variability enhancing effects of ecological disturbances such as winter population bottlenecks on an olive fly population that is already exposed to a gene drive. Finally, this chapter will conclude with an outlook onto an individual-based model which also considers the spatio-temporal dynamics of an olive fly population exposed to gene drive-carrying flies.

Stock-Flow Model of an Olive Fly Population

The stock flow model was put together with the isee systems STELLA® Professional Version 1.1.2 software. In its current state, it considers the temperature-dependent mortality data from the literature (Genç and Nation 2008; Sánchez-Ramos et al. 2013; Tsiropoulos 1972; Tsitsipis 1980) compared to the average annual temperatures encountered on the Greek island of Crete between 1961 and 1990 (German Weather Service).

This model (depicted in Fig. 6.1) was conceived as a means to visualize the growth and development of an olive fly population on an olive orchard. As datasets for this approach the collated data from the literature on B. oleae were used. In its current form, each life stage is integrated as a stock. The life cycle begins in the “Egg”-stock. The egg stock is limited by an estimated number of 100 million olives on the orchard. Influenced by the operator “Egg mortality”, each egg may either die or follow the “Hatching”-flow to the next stage, depicted in the “Larva”-stock. From there, it goes on over the “Pupa”-stock to the “Male Adult” and “Female Adult”-stocks. Until the adult stage, the sex of the organisms is unimportant. During each life stage, the individual may either die or proceed to the next life stage. Each life stage is represented by a different stock. The mortality rates of the different life stages in relation to the temperature as encountered in the cycle of the years on the Greek island of Crete were integrated into the model as the sole time dependent factor. The decision whether to follow the respective “Death” or “Growth”-flow is influenced by the “Mortality”-Operators. Note, that in its current form, the durations of the different life stages all equal one month. The adult flies, again may either die or unite in the “Mating”-stock. Since the “Mating”-stock’s only outflow “Mate only once” leads to a sink, the model assumes a single mating per adult fly. The number of individuals in the “Mating”-stock stimulate the “Egg-Laying”-inflow into the “Egg”-stock. The “Number of Eggs/Mating”-operator adds a stochastic factor, as each mating produces between 150 and 400 eggs. Figure 6.2 shows a simulation run for 60 months. The initial population was set to contain only 1000 male- and 1000 female adult flies. From which it develops quickly and before the end of the second year the number of eggs for the first time reaches the maximum threshold of 100 million, which was set as the number of olives available for oviposition. Clear annual cycles are visible in the various life stage populations which are due to the variable temperature dependent mortality rates. The population seems to undergo stable cycles. Further planned implementations into the model entail variable life stage durations, multiple matings per generation and a seasonal change in the number of olives available for oviposition.

Fig. 6.1
figure 1

Stock-flow model of an olive fly population. The flies undergo the different stages of egg, larva, and pupa, up to male and female adults. Each life stage is represented by a different stock. Male and female adults unite in the “Mating”-stock which stimulates the inflow into the “Egg”-stock. At each stage, the individual organism may either die due to temperature or transition to the next stage

Full size image
Fig. 6.2
figure 2

Wild type population dynamics over a simulated time of 60 months. Note, that in this simplified model, the duration of each life stage equals one month. The maximum number of eggs is limited by the number of olives, which were set to 100 million. The population started with 1000 male and 1000 female adult flies. The life stage populations seem to reach stable annual cycles

Full size image

The next step for this model would be to include applications of different gene drive techniques in order to examine the effects on the population dynamics. The gene drive techniques planned to implement are Medea (Akbari et al. 2014), two-locus Underdominance (Akbari et al. 2013), Y-linked X-Shredder (Galizi et al. 2014), CRISPR/Cas-based gene drives (Burt et al. 2018; Esvelt et al. 2014; Hammond et al. 2016) and Killer-Rescue (Gould et al. 2008).

Stock-Flow Model of a Single-Locus Underdominance Gene Drive

Underdominance, aka heterozygosity inferiority is a phenomenon in which heterozygous carriers of an underdominant gene suffer a higher fitness penalty than homozygous carriers. Modelling the population dynamics of a single-locus Underdominance gene drive requires the implementation of three genotypic subpopulations, wild types (W/W), homozygous (W/U) and heterozygous gene drive-carriers (U/U). These subpopulations are depicted as stocks as illustrated in Fig. 6.3.

Fig. 6.3
figure 3

Model structure of the stock-flow model for single-locus Underdominance gene drive population dynamics

Full size image

This simple model only assumes static growth by a fixed growth variable, determining the number of offspring per mating. However, the number of gene drive carrying offspring is further affected by the respective fitness variables, included in the form of operators. Furthermore, growth of all subpopulations is limited by a universal capacity limit. Besides growing, the subpopulations can of course also decline due to mortality which was assumed equal for all subpopulations in this model. A sex ratio of 1:1 and random mating are assumed and therefore the number and genotypes of offspring are directly dependent on the size of the respective subpopulations. Adhering to the inheritance scheme of single-locus Underdominance, the Mendelian genotype ratios are derived. From which the following equations for the growth of each subpopulation are deductible.

$${P}_{W/W}=+\frac{\left({N}_{W/W}*{N}_{W/W}\right)+\left(\frac{1}{2}*{N}_{W/U}*{N}_{W/W}\right)+\left(\frac{1}{4}*{N}_{W/U}*{N}_{W/U}\right)}{{N}_{W/W}+{N}_{W/U}+{N}_{U/U}}$$
(6.1)
$${P}_{W/U}=+\frac{\left({\frac{1}{2}*N}_{W/U}*{N}_{W/U}\right)+\left(\frac{1}{2}*{N}_{W/U}*{N}_{U/U}\right)+\left(\frac{1}{2}*{N}_{W/U}*{N}_{W/W}\right)+\left(\frac{1}{2}*{N}_{W/W}*{N}_{U/U}\right)}{{N}_{W/W}+{N}_{W/U}+{N}_{U/U}}$$
(6.2)
$${P}_{U/U}=+\frac{\left({N}_{U/U}*{N}_{U/U}\right)+\left(\frac{1}{2}*{N}_\frac{W}{U}*{N}_{U/U}\right)+\left(\frac{1}{4}*{N}_\frac{W}{U}*{N}_{W/U}\right)}{{N}_{W/W}+{N}_{W/U}+{N}_{U/U}}$$
(6.3)

where PX/X represent the probabilities of offspring with the certain genotype and NX/X the number of individuals with that genotype in the population. This model is suited to examine the invasiveness of a single-locus Underdominance gene drive, without the affliction of ecological factors.

Stock-Flow Model of a Medea Gene Drive

Similar but more complex than Underdominance in its inheritance, the Medea gene drive technique can be simulated in a stock-flow model. The model structure is depicted in Fig. 6.4. Just as in the Underdominance model each genotypic subpopulation is represented as a stock. Furthermore, the different sexes become important as Medea’s lethality is induced maternally. Hence, the model revolves around six stocks representing both sexes of three different genotypes. Each genotypic subpopulation’s growth is regulated by a respective “Birth Rate”-converter, while the mortality of all subpopulations is regulated by a single “Mortality”-converter set to 1. The birth rate is set to 100 offspring per mating. As before with Underdominance, mating is assumed to be random and dependent on the size of the respective subpopulations. Obviously, male and female mating partners are required for reproduction, thus the number of mating events is equal to the number of the rarer mating partner (i.e. 50 WT males and 25 WT females will amount to 25 matings).

Fig. 6.4
figure 4

Model structure of the stock-flow model representing Medea-gene drive population dynamics

Full size image

The populations’ growth is also limited by the growth capacity already defined in the previous model in Eq. 6.4. In this model as well the capacity limit K was set to 10 million. The carrier subpopulations are furthermore affected in their growth by their respective fitness-converters. The homozygotes’ fitness was assumed as 0.35 and the heterozygotes’ fitness as 0.72, according to Buchman et al. (2018). The most important factor in the propagation of the gene drive is of course based on genetics. Only the offspring of a heterozygous Medea-carrying mother that do not possess a copy of the gene drive will die. Out of 36 different gamete combinations three are lethal, six are wild type, eighteen are heterozygous and nine are homozygous carriers.

From the inheritance scheme, the growth for each subpopulation can be deducted as shown in the following equations (Eqs. 6.4–6.6) and included in the model into the respective “Birth Rate”-converters. Similar to the model concept of Underdominance, this model is suited to simulate the invasiveness of Medea gene drives.

(6.4)
(6.5)
(6.6)

As before, PX/X denotes the probability of a certain offspring genotype, while NX/X is the number of genotypic individuals within the population, in this model divided by sex.

Deterministic Recurrence-Based Calculations on the Inheritance Schemes of Different Gene Drive Techniques

The model is based on the inheritance schemes of the various gene drive techniques. The probability of the occurrence of a particular genotype was multiplied by its respective fitness. A random mating was assumed based on the respective genotypes in the infinite population. The genotype fitness and the initial population share can be selected by the user. To calculate the invasiveness of gene drive techniques, the variation in fitness and population parameters for a given generation was automated and presented in a color-coded graph in which population percentages are assigned different colours depending on the thresholds selected. The purpose of this survey is to describe the ability of gene drives to achieve population replacements. For this purpose, a simple population genetic model was chosen that provides the percentage of genotype as a function of fitness and the relative release size of gene drive organisms (GDOs). Models with a similar approach have also been described by Gould et al. (2008), Ward et al. (2011) and Dhole et al. (2018).Footnote 1

As a basis, our underlying recurrence-based, deterministic model utilizes inheritance schemes in a hypothetical population of infinite size. Therefore, it is impossible to achieve a population suppression or eradication in this model. All genotypic subpopulations are regarded as relative percentages of the whole population.

Two-locus Underdominance, Medea, a CRISPR/Cas-mediated GD including resistance allele formation, Killer-Rescue and a Y-linked X-Shredder were chosen for a quantitative comparison of their invasiveness. As positive and negative controls, the spread of two different transgenes lacking the GD-specific functionality of super-Mendelian inheritance were calculated: a female specific release of insects carrying a dominant lethal (fsRIDL, Fu et al. 2010) a fitness gain conferring transgene e.g. a pesticide resistance, respectively. For the calculations, the following assumptions were made that should be taken into account for a critical discussion of the presented results on the invasiveness:

  • fsRIDL (negative control): Female lethality is 100% regardless of zygosity. Cumulative fitness penalty for each allele was assumed.

  • Transgene with fitness loss/gain (negative/positive control): Cumulative fitness loss/gain for each allele was assumed.

  • X-Shredder: A Y-linked X-Shredder system with a male biased sex ratio of 95% was assumed according to Galizi et al. (2014). Since the ratio of females cannot decrease below 5%, due to the assumptions of our model, the thresholds were adapted for this approach to 7 and 93% in the cross section computation.

  • Killer-Rescue: Cumulative fitness penalties were assumed per allele regardless of killer or rescue.

  • Medea: Fitness penalty was assumed being cumulative for hetero- and homozygous Medea-carriers.

  • Underdominance: A two-locus autosomal Underdominance system similar to UDmel (Akbari et al. 2013) was modelled. Female-carriers kill offspring that do not inherit at least one copy of each construct. It was assumed that heterozygosity for each of the Underdominance alleles confers a 15% fitness penalty. Therefore, the double hetero UD genotype’s fitness is 30% lower than that of the double homo genotype. Whereas homozygosity in one construct but lack of the other results in half the fitness penalty of the double homozygotes.

  • CRISPR/Cas-mediated gene drive: The homing rate was assumed to be 98% similar to data presented by DiCarlo et al. (2015). Resistance formation rates were assumed as the direct reciprocals of the homing rates, i.e. 2%. Fitness penalties were assumed to be half for heterozygous GDOs. Each resistance allele was assumed to confer a 10% fitness penalty. Homozygously resistant population percentages above 95% are depicted in green in the overlays.

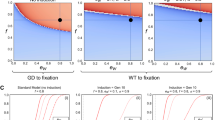
Figure 6.5 shows positive and negative control approaches for the model as transparent overlays of cross sections for up to 60 generations post release, in 5-generational steps. Negative controls are represented by the complete fading of fsRIDL-carriers from a population within five generations and the spread of a transgene which confers a fitness loss. The spread of a transgene which confers a fitness gain represents a positive control. The blue areas represent combinations of fitness and population percentage at a given generation post-release at which more than 95% of the population is of wild type genotype. Red areas represent fitness and population percentage combinations at given generations resulting in less than 5% wild type genotypes in the population.

Fig. 6.5
figure 5

Cross sections of the negative controls for the model represented on the fsRIDL technique and the fade of a transgene conferring a fitness loss. Red = Wild type population percentage below 5%; Blue = Wild type population percentage above 95%. Black numbers and lines represent the respective generation post-release. Lines were inserted by hand for clarity

Full size image

Figure 6.6 shows the allele frequency of gene drives. The depicted generations post-release range from 5 to a maximum of 60, in 5-generational steps.

Fig. 6.6
figure 6

Cross section overlays of fitness and initial release population percentage for different gene drive techniques. Red = Wild type population percentage below 5%; Blue = Wild type population percentage above 95%. Green = Population homozygous for resistance alleles above 95%. Black numbers and lines represent the respective generation post-release. Black lines were inserted by hand for clarity

Full size image

Stochastic Model Considering an Olive Fly Population with Gene Drive and Bottlenecks

For this model, a gene drive technique was assumed resembling a CRISPR/Cas-based gene drive carrying a female specific lethal cargo-gene, similar to the RIDL [Release of Insects carrying a Dominant Lethal gene (Thomas et al. 2000)]. Therefore, it was assumed that 99% of the offspring resulting from a mating of a wild type and an AG parent will also be altered gene individuals. This corresponds a conversion rate similar to findings reported by DiCarlo et al. in wild yeast (DiCarlo et al. 2015). Furthermore, it is assumed that if these offspring are female, they are non-viable and die at larval stage. Mating between two wild type individuals will of course result in 100% wild type offspring. And lastly, a winter bottleneck was assumed to take place after every sixth generation, thereby killing 98% of the population regardless of genetic constitution.

The model was implemented in the statistical programming language “R”, using the RLab and LaPlaces Demon Library packages. It was designed to display the size and demographic characteristics of the wild type B. oleae population and the genetically modified population at different computational time steps. Stochastic formulations are employed for the simulation of mating and gene inheritance, as well as for sex determination. Information required for the modulation of the initial population and the released gene drive population was acquired via literature review and expert surveys. The initial population consists of a certain number of wild type (WT) males and females, as well as of individuals carrying an altered gene (AG). The model assumes a certain percentage of females to mate, which are selected using a Bernoulli distribution for each mating event. In order to select a male for mating with a specific female, random mating and monogamy were assumed.

Two different simulation scenarios were run, one with regularly occurring bottlenecks and as a control a scenario without winter bottlenecks. In both scenarios, an initial wild population of 200,000 olive fruit flies (sex ratio 1:1) was assumed. A total of 400,000 gene drive-carrying males were released. Ten replicate simulation runs were performed; each comprises a simulation for 24 generations.

Results of these model scenarios are depicted in Fig. 6.7a and 23 Without the occurrence of a population bottleneck, the release of altered gene flies induces a constant reduction of population densities over the course of the first 11 simulated generations. Thereafter, the fly population recovers and increases from generation to generation. Figure 6.7b shows that a similar outcome is obtained for each simulation run. Figure 6.8 shows that the occurrence of a bottleneck after six generations further reduces the number of flies which is already on decline due to the release of gene drive-carrying individuals. While altered gene flies exhibit a high proportion of the entire population after the first bottleneck, wild type flies dominate the population after the second and third bottleneck. Very different outcomes are displayed by single model runs: in some cases, the wild type population is driven to extinction, in other model runs it recovers at various rates.

Fig. 6.7
figure 7

Simulation result for an olive fruit fly population that does not experience population bottlenecks. a Arithmetic mean of ten model runs; b development of the wild type fly population in each single model run

Full size image
Fig. 6.8
figure 8

Simulation result for an olive fruit fly population regularly experiencing population bottlenecks. a The arithmetic mean of ten model runs; b development of the wild type fly population for each single model run. The bottles indicate the regular occurrence of population bottlenecks after every sixth generation

Full size image

These results indicate that the occurrence of population bottlenecks reduces the predictability of the effect of gene drive releases to natural olive fruit fly populations. Therefore, the consideration of ecological properties at the population biological level for a comprehensive risk assessment prior to the release of genetically altered organisms to wild ecosystems is strongly recommended.

Differential Equation-Based Modelling of an Olive Fly Population with a Gene Drive

Differential equations are frequently used in population ecology. They can be considered as a standard to study spatially homogeneous conditions, where the calculation of non-overlapping generations is not applicable. The results from both approaches can substantially differ, since the causality-derived determinism requires an absence of trajectories crossing, whereas in difference equations, the systems state is only defined for certain points in time.

For this deterministic approach, the following assumptions have been made: The population grows exponentially up to an environmentally set carrying capacity limit. The individuals of the population die following an exponential decline. Just as before, the sex ratio of the wild type population is assumed to be 1:1. The gene drive, similar to the one in the stochastic model, is assumed to be propagated to all offspring as long as one of the mating partners carries the gene drive and the gene drive causes female lethality.

For the two sub-populations the following equations were established:

$$\begin{aligned} \text{Wild type population}\,\,\frac{dW}{dt}& =r*W*\frac{0.5* W}{\frac{1}{2}W+Mg}*\frac{K-\left(W+Mg\right)}{K}-mf*FF*W \end{aligned}$$
(6.7)
$$\begin{aligned} \text{Male gene drive population}\,\,\frac{dMg}{dt} & =r*W*\frac{Mg}{\frac{1}{2}W+Mg}*\frac{K -\left(W+Mg\right)}{K}-mf*Mg\end{aligned}$$
(6.8)

where r denotes the exponential growth and is assumed to be 0.5; W is the population of the wild types, Mg is the population of the male gene drive-carriers; K is the carrying capacity of the ecosystem and is assumed to be 2000; mf is the mortality factor, assumed to be 0.1; and FF is the fitness factor which represents the fitness difference between the populations, it was varied during simulation runs between 0.1 and 0.9.

During the simulation runs in which not only the FF but also the initial population values W and Mg have been varied, an interesting phenomenon could be observed. The isoclines vary depending on the FF value. In Fig. 6.9, these isoclines are shown in direction fields. Depending on the isoclines, either an extinction of the gene drive males occurs or the gene drive males get extinct and the wild type population persists. The delimitation between both alternatives occurs at a value of 0.5 for FF. In that case, a marginal stability prevails.

Fig. 6.9
figure 9

Direction fields showing the wild type versus the male gene drive-carrying population. Dependent on the FF isoclines form, which regardless of the initial population settings lead to the population’s extinction for a fitness factor (FF above 0.5 and to wild type persistence for FF < 0.5. A marginal stability can be observed for FF = 0.5. X- and Y axes scale from 0.1 to 2000

Full size image

This illustrates how important transgene-induced fitness can be at the expense of the outcome of a gene drive application.

Individual-Based Model of an Olive Fly Population with Gene Drive

Individual-based models (IBM) represent activity, interaction and states of single organisms as data structures in a simulation. In most applications, they are spatially explicit and consider environmental structures and temporal variability of environmental states. Therefore, the approach is suitable to analyse the contribution of single aspects and components of the spatial context as well as behaviour and states of organisms to particular results on higher integration levels (e.g. population level), which result from an aggregation of individual activities. In particular, IBM can facilitate a deeper and more detailed understanding of the conditions for specific population dynamic phenomena (Breckling et al. 2006).

Since the possible releases of SPAGE in natural populations pose qualitatively new questions for risk assessment, it was reasonable to demonstrate the utility of the approach also in the context with genetic aspects. Hence, a prototypical IBM structure with regard to the olive fly case study was drafted.

The focus was to prepare a model outline rather than implementing a complete parameterization in any relevant detail. In the current stage of development, the model consists of characteristic features, linking spatial, behavioural and crucial physiological aspects of olive flies. The following features were implemented (Fig. 6.10):

  • Spatial structures of the environment, in particular relevant resources like olive tree locations,

  • distribution of the individual olive flies as well as aspects of their movement behaviour,

  • Temporal characteristics of the development process: Eggs, maggots, pupae and imago,

  • Temperature sensitivity of individual development, bottlenecks through low or high temperatures,

  • Mating behaviour,

  • and we represent a gene drive influence, the distinction of male individuals carrying a gene that leads to the death of females prior to maturity.

Fig. 6.10
figure 10

Three different test runs with identical parametrisation but different random seed. Each model run results in a different outcome. a, c and e show the population dynamics over time. Beneath the title line temperature regimes are depicted as a colour bar with blue inducing population decline due to cold conditions and brown marks times of heat decline. b, d and f show the spatial distribution of the population at the final time step. a and b Simulation run with 59 as start of random number generation: Wild-type and gene drive males persist in a spatially heterogeneous setting. While wild types dispersed, gene drive males largely remain active in the part of the simulated area where they were started. c and d Simulation run with 67 as start of random number generation: Gene drive males died out, and the wild type population dispersed throughout the simulated area. e and f Simulation run with 97 as start of random number generation: Gene drive males limited the population expansion and prevented a further dispersal. The population density remains on a low level. The colour code for the individual olive flies is either brown for different immature stages. For the mature stages purple is used for females, blue for males and red for gene drive males (left and right side). Green circles represent trees

Full size image

The model was written in SIMULA (Dahl et al. 1970; Kirkerud 1989) and compiled with the CIM (SIMULA-to-C) precompiler (https://www.gnu.org/software/cim/). The executable was run on a Lenovo ThinkPad Personal Computer under SUSE Linux. The graphic output was generated using GRPS as an external class.

Since each individual and its specific state is represented, spatial structures as well as the temporal development of the population can be visualized. The simulation was initiated with twelve wild type females, wild type males and gene drive-males each. They were located in a partially overlapping area within direct interaction distance. In the graphic simulation output, green circles mark the location of olive trees, dots show the position of mature and immature life stages. Since random movement processes influence the dispersal process across the simulation area, the results of each model run are unique, however, in terms of probability, typical development trends can be identified. Repeating identical model runs with the only difference in the starting value for the random generator can lead to qualitatively different results of single runs. Random numbers are used to determine co-ordinates of individual movement steps surrounding the current position and mortality events according to temperature dependent conditions. The preliminary simulation results show (Fig. 6.10), that it is important to explore the heterogeneous structure of the response space. Statistical assessment would be a further step to identify result type frequencies in a larger number of model re-runs.

As qualitatively different results of the simulation runs, which were carried out for 630 time steps so far, we observed cases where the gene drive persists while the population expands throughout the available area. Another simulation run revealed the result, that the population level can be higher when the gene drive carrying individuals died out. Finally, it was observed that under the same parameterization the gene drive males can hinder an expansion across the simulation area and arrest the population density on a comparatively low level. As a preliminary result we can conclude, that there is the potential that under given spatial conditions and under identical physiological specifications, random influences can contribute to a variety of qualitatively distinct outcome in relatively short observation times.

Model studies with the current implementation showed, that the specification is crucially influencing how pronounced the population bottlenecks occur. If phases of exceptionally low or high temperature vary in extent, it would add another significant dimension of uncertainty to the population development.

We suggest to employ individual-based models to analyse in particular how behavioural aspects and spatial heterogeneities contribute to dispersal and persistence processes and how the probability structure of the response space can be understood.

Conclusion

The introduced model concepts give insights how to analyse and understand underlying implications in various aspects of gene drives and population dynamics. It is however important to note, that a model is always a simplification of otherwise highly complex processes. Therefore, a model’s applicability to real life is limited. Each model, has its own focal points while even completely dismissing other factor that in reality might have an important influence on the observed process. Although models may facilitate various analyses, they are heavily reliant on what was built into them. Thus, emergent properties of the model were already implied in the model assumptions. Due to this, we did not focus on only one model approach but approached the topic from various sides to allow for a broader view on the vast subject and some of its key aspects.

Nevertheless, models allow insights into complex dynamic processes and furthermore help to discover emergent properties that would have remained undisclosed otherwise. Especially in the context of gene drive releases, which may cause unpredictable consequences, it is important to identify possible hazards and adverse ecological effects on an ecosystem before real-life test trials. To this end, simulations and modelling approaches play a pivotal role.