Abstract
In July 2012 the ATLAS and CMS experiments announced the discovery of a Higgs boson, confirming the conjecture put forward in the 1960’s. This article briefly traces the history of the Brout-Englert-Higgs mechanism, its impact on the elucidation of the standard model, the design and construction of the ATLAS and CMS experiments, and finally the discovery of the Higgs boson. The article outlines some of the challenges faced during the construction of the Large Hadron Collider and its experiments, and their operation and performance. In particular, recent results relating to the properties and couplings of the Higgs boson will be discussed as well future prospects at the LHC.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
6.1 Introduction and the Standard Model
The standard model of particle physics (SM) is a theory that is based upon principles of great beauty and simplicity. The theory comprises the building blocks of visible matter, the fundamental fermions: quarks and leptons, and the fundamental bosons that mediate three of the four fundamental interactions; photons for electromagnetism, the W and Z bosons for the weak interaction and gluons for the strong interaction (Fig. 6.1).
The SM provides a very successful description of the visible universe and has been verified in many experiments to a very high precision. It has an enormous range of applicability and validity. So far no significant deviations have been observed experimentally.
The possibility of installing a proton-proton accelerator in the LEP tunnel, after the e+e− programme, was being discussed in the 1980’s. At the time there were many profound open questions in particle physics, and several are still present. In simple terms these are: what is the origin of mass i.e. how do fundamental particles acquire mass, and why do they have the masses that they have? Why is there more matter than anti-matter? What is dark matter? What is the path towards unification of all forces? Do we live in a world with more space-time dimensions than the familiar four? The LHC [1, 2] was conceived to address or shed light on these questions.
The question of how fundamental particles acquire mass was first posed in the following form: how does the photon remain massless, giving the electromagnetic force an infinite range, whilst the W and Z bosons acquire a seemingly large mass, explaining the short-range of the weak nuclear force.
In 1964 three groups of physicists, Englert and Brout; Higgs; and Guralnik, Hagen, and Kibble [3,4,5,6,7], proposed that there exists an omnipresent field, pervading the universe, and fundamental particles can acquire mass by interacting with this field. At the heart of the mechanism endowing mass was spontaneous symmetry breaking of a local gauge symmetry, through the field’s non-zero vacuum expectation value. The new field being a quantum field had an associated quantum, which became known as the Higgs boson.
Today, it seems remarkable that not much attention was paid to the papers [3,4,5,6,7], and even less to the associated Higgs boson. This was partly due to the fact that in the early 1960’s most particle physicists were trying to make sense of a plethora of new particles being discovered.
In 1967 Kibble [8] generalized his earlier work with Guralnik and Hagen and brought the mechanism of spontaneous symmetry breaking closer to its application to the description of the real world, one in which the photon remains massless and the W and Z particles become massive [9]. This vein of work reached fruition in the seminal papers of Weinberg [10] and Salam [11], which raised the prospect of the unification of electromagnetism and weak interactions, now labeled the electro-weak theory. Earlier work on a similar model had been carried out by S. Glashow [12]. Weinberg and Salam assumed that W and Z bosons acquired mass by interacting with the field introduced in the earlier papers [3,4,5,6,7].
Both Weinberg and Salam conjectured that such a model would be renormalizable i.e. calculations would give finite answers. The key prediction of their theory was the existence of the Z0 boson, in addition to the long-known charged W bosons. Again not much attention was paid to these papers.
The situation changed dramatically in 1971. t’Hooft in a tour de force, using methods developed by Veltman, outlined the proof that, indeed, the electro-weak theory would be renormalizable [13]. The electro-weak theory started being taken very seriously, so much so that Weinberg’s paper [10] has now become the most cited paper in physics.
Experimentally, the 1973 discovery of weak neutral currents [14], mediated by the Z0 boson, provided strong evidence for the verity of the electro-weak theory.
In parallel much progress had been made in understanding the particles that were being discovered in the 1950s and 1960s. Eventually, these were understood through an underlying gauge field theory, where the “charge” of strong interactions was labeled “colour”, and the interactions of coloured quarks are mediated by gluons. The theory [15, 16] displayed two main properties: colour confinement, resulting in the hadrons being colourless, and asymptotic freedom, leading to a steady decrease in the strength of the interaction between quarks and gluons as the interaction energy scale increases. The latter enabled the use of perturbation theory for calculating strong interaction processes at high energies, which has been key to understanding the physics at the LHC.
Further major discoveries included those of new quarks and the gluon meant that the discovery, in 1983, of the W and Z bosons [17, 18] at CERN set the stage for the search for the Higgs boson. The Higgs boson, that earlier had been considered to be a minor and uninteresting feature of the spontaneous breaking mechanism, became to assume a role of central importance as the still missing key particle of the SM. The SM worked so well that the Higgs boson, or something else doing the same job, more or less had to be present.
In 1984, one year after the discovery of the W and Z bosons, a workshop was held in Lausanne where first ideas were discussed about a possible proton-proton collider and associated experiments to make a search for such a particle. The aim was to reuse the LEP tunnel after the end of the electron-positron programme. Amongst the leading protagonists were the scientists from UA1 and UA2 experiments. An exploratory machine was required to cover the wide range of mass values possible for the SM Higgs boson, its diverse decay signatures and production mechanisms and to discover any new high-mass particles at a centre-of-mass energy ten times higher than previously probed. A hadron (proton-proton) collider is such a machine as long as the proton energy is high enough and the instantaneous luminosity, ℒ, measured in cm−2 s−1, is sufficiently large. The rate of production of a given particle is determined by ℒ × σ where σ is the cross section of the production reaction, measured in units of cm2. The most interesting and easily detectable final states at a hadron collider involve charged leptons and photons and have a low σ × BR, where BR is the branching ratio into the decay mode of interest.
A major goal of the LHC thus became the elucidation of the mechanism for electroweak symmetry breaking. It also was clear that a search had to be made for new physics at the TeV energy scale as the SM is logically incomplete; it does not incorporate gravity. A promising avenue is the superstring theory, an attempt towards a unified theory with dramatic predictions of extra space dimensions and supersymmetry.
The LHC and its experiments were designed to find new particles, new forces and new symmetries amongst which could be the Higgs boson(s), supersymmetric particles, Z′ bosons, or evidence of extra space dimensions. An experiment that could cover the detection of all these hypothesized but yet undiscovered particles would provide the best opportunity to discover whatever else might be produced at LHC energies.
In July 2012 the ATLAS and CMS collaborations discovered a Higgs boson [19, 20].
This paper is based on the previous articles [1, 21,22,23] written by the authors, some with M. Della Negra, using the recently published results from the ATLAS and CMS Collaborations on the measurements of the properties of the Higgs boson.
6.2 The SM Higgs Boson
In the early 1990’s the search for the SM Higgs boson played a pivotal role in the design of the ATLAS and CMS experiments. The mass of the Higgs boson (mH) is not predicted by theory, but from general considerations, mH < 1 TeV. At the start of the LHC operation, direct searches for the Higgs boson carried out at the LEP collider led to a lower bound of mH > 114.4 GeV at 95% CL [24], whilst precision electroweak constraints, including LEP data, implied that m H < 152 GeV at 95% confidence level (CL) [25]. At time of the discovery at CERN, CDF and D0 experiments operating the Tevatron proton antiproton collider, detected an excess of events in the range 120–135 GeV [26].
It is known that quantum corrections make the mass of any fundamental scalar particle, such as the SM Higgs boson, float up to the next highest mass scale present in the theory, which in the absence of extensions to the SM, can be as high as 1015 GeV. Hence finding the scalar Higgs boson would immediately raise a more puzzling question: Why should it have a mass in the range between 100 GeV and 1 TeV? One appealing hypothesis, much discussed at the time, and still being investigated, predicts a new symmetry labeled supersymmetry. For every known SM particle there would be a partner with spin differing by half a unit; fermions would have boson superpartners and vice versa, thus doubling the number of fundamental particles. The contributions from the boson and fermion superpartners, and vice a versa, with amplitudes of opposite signs, would lead to their cancellation, and allow a low mass for the Higgs boson. In supersymmetry five Higgs bosons are predicted to exist with one resembling the SM Higgs boson with a mass below about 140 GeV. The lightest of this new species of superparticles could be the candidate for dark matter whose presence, by mass, in the universe is around five times more abundant than ordinary matter.
In 1975, physicists had already started to turn their attention to how a putative Higgs boson would manifest itself in experiments [27].
The search for the SM Higgs boson provided a stringent benchmark for evaluating the physics performance of various experiment designs under consideration in the early 1990s and heavily influenced the conceptual design of the general-purpose experiments, ATLAS and CMS.
6.2.1 Higgs Boson: Production and Decay
Although the mass of the Higgs boson is not predicted by theory, at a given mass all of its other properties are precisely predicted within the SM. The SM Higgs boson is short-lived (10−23 s) and hence the experiments only detect the decay products.
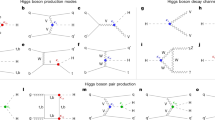
The cross sections for differing production mechanisms and the branching fractions for differing decay modes of the SM Higgs boson, as a function of mass, are illustrated in Fig. 6.2a, b, respectively [28], and the principal ones for mH = 125 GeV and at √s = 14 TeV are tabulated in Table 6.1. The uncertainties on these numbers can be found in the twiki in Reference [28].
(a) SM Higgs boson production cross sections as a function of the centre-of-mass energy, √s, for pp. collisions. The VBF process is indicated here as qqH [28]. The theoretical uncertainties are indicated as bands. (b) Branching ratios for the main decays of the SM Higgs boson near mH = 125GeV [28]. The theoretical uncertainties are indicated as bands
The dominant Higgs-boson production mechanism, labeled pp. → H in Fig. 6.2a (for masses up to ≈ 700 GeV) is gluon–gluon fusion.
The vector boson fusion (VBF) mechanism (WW(∗) or ZZ(∗)), labeled pp. → qqH in Fig. 6.2a, becomes important for the production of higher-mass Higgs bosons. Here, the quarks that emit the W or Z bosons have transverse momenta of the order of W and Z masses. The detection of the resulting high-energy jets in the forward pseudorapidityFootnote 1 regions, 2.0 < |η| < 5.0, can be used to tag the reaction, improving the signal-to-noise ratio. Tagging of forward jets from the VBF process has turned out to be very important in the measurements of many of the properties of the Higgs boson.
The production of the Higgs boson in association with W and Z boson, labeled pp. → W or Z H in Fig. 6.2a, or the production via the t-tbar fusion, has a much lower cross section, but nevertheless has been important for the final states with large backgrounds such as b-bbar, τ+τ− or μ+μ−.
The Higgs boson decays in one of several ways (decay modes) into known SM particles, the types depending on its mass. Hence a search had to be envisaged not only over a large range of masses but also many possible decay modes: into pairs of photons, Z bosons, W bosons, τ leptons, and b quarks.
In the mass interval 110 < m H < 150 GeV, early detailed studies indicated that the two-photon decay would be the main channel likely to give a significant signal [29]. Detailed studies of another mode, H → ZZ(∗) → ℓℓℓℓ, where ℓ stands for a charged electron or a muon, dubbed the “golden” mode, suggested that it could be used to cleanly detect the Higgs boson over a wide range of masses starting around m H = 130 GeV [30]. One or both of the Z bosons would be virtual for m H < 180 GeV, and the upper end of the detection range was indicated to be about m H < 600 GeV.
In the region 700 < m H < 1000 GeV the cross-section decreases so Higgs boson decays via W and Z decays, where the W and Z decays are to channels with higher branching fractions, have to be employed.
6.3 The Large Hadron Collider
6.3.1 The Road to the LHC
With the prospect of ground-breaking physics at the LHC, several workshops and conferences followed, where the formidable experimental challenges started to appear manageable, provided that enough R&D work on detectors could be carried out. In 1987 the workshop in La Thuile of the so-called “Rubbia Long-Range Planning Committee” resulted in the recommendation of a proton-proton collider, labeled the Large Hadron Collider (LHC), as the next accelerator for CERN. Meetings of note were the ECFA LHC Workshop in Aachen in 1990 [31], and “Towards the LHC Experimental Programme” [32] which took place in Evian-les-Bains, France in March 1992. At Evian several proto-collaborations presented their designs in “Expressions of Interest”. In addition, from the early 1990s, CERN’s LHC Detector R&D Committee (DRDC), which reviewed and steered R&D groupings, greatly stimulated innovative developments in detector technology.
Table 6.2 lists the major steps on the long road to the discovery of the Higgs boson.
6.3.2 The Challenges of the LHC Accelerator
In this section we outline some of the features and the technological challenges of the LHC [1].
Protons are accelerated by high electric fields generated in superconducting r.f. cavities and are guided around the accelerator by powerful superconducting dipole magnets. The dipole magnets are designed to operate at 8.3 Tesla, allowing the proton beams to be accelerated to 7 TeV, with the current carrying conductor cooled down to 1.9 K in a bath of superfluid helium. The beam pipe in which the protons circulate is under a better vacuum, and at a lower temperature, than that found in inter-planetary space.
The choices of two-in-one high-field superconducting dipole magnets operating at a temperature of 1.9 K, cooled by super-fluid helium were critical to a competitive and affordable design. The LHC could only be competitive with the Superconducting Super Collider (SSC), whose construction had started in the early 1990s in Texas, U.S.A, if the instantaneous luminosity could be an order of magnitude higher (at 1034 cm−2 s−1). However, the SSC was later cancelled in October 1993.
The main challenges for the accelerator were to build more than one thousand two hundred 15 m long superconducting dipoles able to reach the required magnetic field, the large distributed cryogenic plant to cool the magnets and other superconducting accelerator structures, and the control of the beams, whose stored energy will reach, in design operation, a value of 350 MJ. This magnitude requires extraordinary precautions for beam handling, since if, for any reason this beam is lost in an uncontrolled way, it can do considerable damage to the machine elements, which would result in months of down time.
The counter-rotating LHC beams are organized in 2808 bunches, each of ~1011 protons per bunch separated by 25 ns, leading to a bunch crossing rate of ~40 MHz.
Proton beams were first circulated in the LHC in September 2008, and in the days that followed, rapid progress was made in getting a beam to circulate with very good lifetime. Soon after the start a technical incident occurred in the last of the eight sectors to be tested as it was being ramped up to the pre-agreed start-up energy of 5 TeV. The root cause was a failure of one of the 50,000 soldered joints. Substantial damage was done to a large part of the sector involved. After repairs lasting about a year, the LHC started operating again in November 2009. Collisions took place at the injection energy (450 GeV per beam), followed in 2010 and 2011, by a very successful operation at a centre-of-mass energy of 7 TeV. In 2012 the centre-of-mass energy was increased to 8 TeV. The performance surpassed expectations and an integrated luminosity of ~25 fb−1, corresponding to 2 × 1015 proton-proton interactions, was delivered. This is labeled Run 1.
During the period 2015–2018 the LHC operated at a proton-proton centre-of-mass energy of 13 TeV and delivered a total of over 150 fb−1 of integrated luminosity. The collider performed close to, or beyond, its design values in many parameters, operating at 13 TeV and reaching peak luminosities of 2 × 1034 cm−2 s−1, twice the design value. This period of operation is labeled Run 2. The achieved performance at the time of writing (2018) can be found in Table 6.3.
6.4 The ATLAS and CMS Experiments
Not only was the putative SM Higgs boson to be rarely produced in the proton collisions, but also it decays into particles (isolated photons, electrons, and muons) that are the best identifiable signatures of its production at the LHC also was expected to be rare. The rarity is illustrated by the fact that Higgs boson production and decay to one such distinguishable signature (H → ZZ(∗) → 4 l) happens roughly once in 1013 proton-proton collisions. So a vast number of proton-proton collisions per second have to be delivered by the accelerator and examined by the experiments. At the end of 2018, the LHC was operating at a collision rate of around 109 per second. The ATLAS and CMS detectors operate in the harsh environment created by this huge rate of proton-proton collisions. The challenges posed are discussed in reference [33, 34].
6.4.1 The Challenges for ATLAS and CMS Experiments
At the Aachen workshop the physics case for the LHC was thoroughly examined. The experimental search for the Higgs boson across the entire possible range of mass was fully explored for the first time. There was a prevalent prejudice of the protagonists of supersymmetry that mH should be smaller than 135 GeV. As the decay width of the SM Higgs boson is about 5.5 MeV at mH = 100 GeV, and 8.3 MeV at 150 GeV, the width of the reconstructed invariant (γγ or 4 l) mass distribution, and hence the signal/background ratio, would be limited by the electron/photon energy resolution of the electromagnetic calorimeter, and the charged particle momentum resolution of the inner tracker and the muon spectrometer. This lower end of the remaining open mass range was considered to be especially difficult in hadron colliders. Hence the LHC experiments had to pay particular attention to the performance requirements imposed by the search for the Higgs boson in this low mass range. As a consequence much importance was placed on the tracking (inner and muon), as well as the magnetic field strength, and the electromagnetic calorimeters.
The search for the high-mass Higgs boson, particles predicted by SUSY, and other exotic states mentioned above, required excellent resolution for jets and missing transverse momentum (pT miss), requiring full solid angle calorimeter coverage.
A saying prevalent in the late 1980’s and early 1990’s captured the challenge: ‘We think we know how to build a high energy, high luminosity hadron collider—but we don’t have the technology to build a detector for it’. Making discoveries in the unprecedented high collision rate environment, generated by around one billion proton-proton interactions per second, with several tens of simultaneous collisions per bunch crossing, would require extraordinary detectors. Many technical, financial, industrial and human challenges lay ahead, which were all overcome, to yield experiments of unprecedented complexity and power. A flavour can be attained from articles in reference [35].
At the Evian meeting in 1992 four experiment designs were presented: two deploying toroids (one with a superconducting magnet in the barrel) and two deploying superconducting high-field solenoids. The choice of the magnetic field configuration determined the overall design of the experiments.
The collaborations deploying toroids merged to form the ATLAS Collaboration. The ATLAS design [35] was based on a very large superconducting air-core toroid for the measurement of muons, and supplemented by a superconducting 2 Tesla solenoid to provide the magnetic field for inner tracking and by a liquid-argon/lead electromagnetic calorimeter with a novel “accordion” geometry. The CMS design [36] was based on a single large-bore, long, high-field solenoid for analyzing muons, together with powerful microstrip-based inner tracking and an electromagnetic calorimeter comprising scintillating crystals.
On top of the selected event of interest, an average of up to around 40 other proton-proton events are superimposed. These superposed events are referred to as minimum-bias events, because no selection is made. Thus thousands of particles emerge from the interaction region every 25 ns where one nanosecond (ns) = 10−9 s. Hence the products of an interaction under study can be confused with those from other interactions in the same bunch crossing. This problem, known as pileup, clearly becomes more severe if the response time of a detector element and its electronic signal is longer than 25 ns. The effect of pileup can be reduced by using highly granular detectors with fast, short duration, signals, giving low occupancy (i.e., a low probability that a detector element will give a signal) at the expense of having large numbers of detector channels. The resulting millions of electronic channels require very good time synchronization.
The large flux of particles emanating from the interaction region creates a high-radiation environment requiring radiation-hard detectors and front-end electronics. Access for maintenance is very difficult, time consuming, and highly restricted. Hence, a high degree of long-term operational reliability had to be attained, comparable to that which is usually associated with instruments flying on space missions.
The event selection process (called the trigger) must select among the billion interactions that occur each second since no more than a thousand events per second can be stored for subsequent analysis. The short time between bunch crossings, 25 ns, has major implications for the design of the readout and trigger systems. It takes a long time to make a trigger decision, yet new events occur in every crossing and a trigger decision must be made for every crossing; the selection process is split in several levels. The first of these is the Level-1 trigger decision, which takes about 3 μs and selects, on average, one crossing out of 400. During this time the data must be stored in pipelines integrated into the front-end electronics. In CMS, the data from these selected events are then moved into a commercial farm of CPUs to select and store about one thousand/s of the most interesting events for subsequent analysis.
It cannot be stressed enough how important were the many years of R&D and prototyping that preceded the start of detector construction. Technologies had to be developed far beyond what was the state-of-the-art in early 1990s, in terms of granularity, speed of readout, radiation tolerance, reliability, and very importantly cost. For many detector subsystems, there were initially several technologies considered, as it was far from certain which technologies would be able to attain the required performance. In many cases several variants were developed, prototyped and tested, before choosing the one best able to fulfill the stringent requirements. This involved building and testing increasingly more realistic and larger prototypes, in a process that involved industry from the outset. This took place over a number of years before construction commenced in the second half of the 1990s.
In the 1990’s the two collaborations, ATLAS and CMS, grew rapidly in terms of people and institutes. Today each comprises over 3500 scientists and engineers, from over 150 institutions in more than 40 countries. The talents and resources of all these scientists were needed to build the experiments, which are now performing extraordinarily well at the LHC.
The single most important aspect of the experiment design and layout is the magnetic field configuration for the identification of muons and the measurement of their momentum. Large bending power is needed to measure precisely the momentum of charged particles. This forces a choice of superconducting technology for the magnets. The design configurations chosen by ATLAS and CMS are discussed below.
6.4.2 The ATLAS Detector
The design of the ATLAS detector [35], shown in Fig. 6.3 (top), is based on a novel superconducting air-core toroid magnet system, containing ~80 km of superconductor cable, in eight separate barrel coils (each 25 × 5 m2 in a ‘racetrack’ shape) and two matching endcap toroid systems. A field of ~0.5 Tesla is generated over a large volume. The toroids are complemented with a thin superconducting central solenoid (2.4 m diameter, 5.3 m length) that provides an axial magnetic field of 2 Tesla.
The electromagnetic calorimeter consists of a lead/liquid-argon sampling calorimeter in a novel ‘accordion’ geometry. A plastic scintillator—iron sampling hadron calorimeter, also with a novel geometry, is used in the barrel part of the experiment. Liquid-argon hadronic calorimeters are employed in the endcap regions near the beam axis. The electromagnetic and hadronic calorimeters have almost 200,000 and 20,000 cells, respectively, and are in an almost field-free region between the toroids and the solenoid.
The momentum of the muons is precisely measured after traversing the calorimeters in the air-core toroid field over a distance of ~5 m. About 1200 large muon chambers of various shapes, with a total area of 5000 m2, measure the impact position with an accuracy of better than 0.1 mm. Another set of about 4200 fast chambers is used to provide the “trigger”.
The reconstruction of all charged particles, and that of displaced vertices, is achieved in the inner detector, which combines highly granular pixel (50 × 400 μm2 elements, leading to 80 million channels) and microstrip (13 cm × 80 μm elements, leading to six million channels) silicon semiconductor sensors placed close to the beam axis, and a ‘straw tube’ gaseous detector (350,000 channels) which provides about 30–40 signal hits per track. The latter also helps in the identification of electrons using information from the effects of transition radiation.
The air-core magnet system allows a relatively lightweight overall structure leading to a detector weighing 7000 tons. The muon spectrometer defines the overall diameter of 25 m and length of 44 m of the ATLAS detector.
6.4.3 The CMS Detector
The design of the CMS detector [36], shown in Fig. 6.3 (bottom), is based on a state-of-the-art superconducting high-field solenoid, which first reached the design field of 4 Tesla in 2006.
The solenoid generates a uniform magnetic field parallel to the direction of the LHC beams. The field is produced by a current of 20 kA flowing through a reinforced Nb-Ti superconducting coil built in four layers. Economic and transportation constraints limited the outer radius of the coil to 3 m and its length to 13 m. The field is returned through a 1.5 m thick iron yoke, which houses four muon stations to ensure robustness of identification and measurement and full geometric coverage.
The CMS design was first optimized to cleanly identify, trigger and measure muons, e.g. arising from processes such as H → ZZ(∗) → 4 μ and few TeV mass Z’ → 2 μ, over a wide range of momenta. The muons trace a spiral path in the magnetic field and are identified and reconstructed in ~3000 m2 of gas chambers interleaved with the iron plates in the return yoke. Another ~500 fast chambers are used to provide a second system of detectors for the Level-1 muon trigger.
The next design priority was driven by the search for the decay of the SM Higgs boson into two photons. A new type of scintillating crystal was selected: lead-tungstate (PbWO4) crystal.
The solution to charged particle tracking was to opt for a small number of precise position measurements of each charged track (~13 each with a position resolution of ~15 μm per measurement) leading to a large number of cells distributed inside a cylindrical volume 5.8 m long and 2.5 m in diameter: 66 million 100 × 150 μm2 silicon pixels and 9.3 million silicon microstrips ranging from ~10 cm × 80 μm to ~20 cm × 180 μm. The 198 m2 area of active silicon of the CMS tracker is by far the largest silicon tracker ever built.
Finally the hadron calorimeter, comprising ~3000 projective towers covering almost the full solid angle, is built from alternate plates of ~5 cm brass absorber and ~4 mm thick scintillator plates that sample the energy. The scintillation light is detected by photodetectors (hybrid photodiodes) that can operate in the strong magnetic field.
6.4.4 Installation and Commissioning
The two very different and complementary detector concepts, ATLAS and CMS, resulted in two different strategies for the underground installation of these experiments.
Given its size and its magnet structure, the ATLAS detector had to be assembled directly in the underground cavern. The installation process began in summer 2003 (after the completion of civil engineering work that started in 1998) and ended in summer 2008. Figure 6.4 (top) shows the completion of the barrel toroid magnet system with the insertion of the barrel calorimeters. Figure 6.4 (bottom) shows one end of the cylindrical barrel detector after 3.5 years of installation work, 1.5 years before completion. The ends of four of the barrel toroid coils are visible, illustrating the eightfold symmetry of the structure.
(top) Photograph of the barrel toroid magnet system after the completion of the the installation of the eight coils, (bottom) Photograph of one end of the ATLAS detector barrel with the calorimeter end-cap still retracted before its insertion into the barrel toroid magnet structure (February 2007 during the installation phase)
The iron yoke of the CMS detector is divided into five barrel-wheels and three endcap disks at each end, giving a total weight of 12,500 tons. This structure enabled the detector to be assembled and tested in a large surface hall while the underground cavern was being prepared. The sections, weighing between 350 tons and 2000 tons, were then lowered sequentially between October 2006 and January 2008, using a dedicated gantry system equipped with strand jacks: a pioneering use of this technology to simplify the underground assembly of large experiments. Figure 6.5 top shows the lowering of the heaviest and central section, supporting the superconducting coil. Figure 6.5 bottom shows the transverse section of the barrel part of CMS illustrating the successive layers of detection starting from the centre where the collisions occur: the inner tracker, the crystal calorimeter, the hadron calorimeter, the superconducting coil, and the iron yoke instrumented with the four muon stations. The last muon station is at a radius of 7.4 m.
Individual detector components (e.g. chambers) of both experiments were built and assembled in a distributed way all around the globe in the numerous participating institutes and were typically first tested at their production sites, then after delivery to CERN, and finally again after their installation in the underground caverns. The collaborations also invested enormous effort in testing representative samples of the detectors in test beams at CERN and other accelerator laboratories around the world. These test-beam campaigns not only verified that performance criteria were met over the several years of production of detector components, but also were used to prepare the calibration and alignment data for LHC operation. The so-called large combined test-beam setups, which represented whole ‘slices’ of the different detector layers of the final detectors, proved to be very important.
During the installation, the experiments made extensive use of the constant flow of cosmic rays impinging on Earth providing a reasonable flux of muons even at a depth of 100 m underground. Typically a few hundred per second traverse the detectors. These muons were used to check the whole chain from sub-detector hardware to analysis programs of the experiments, and to align the detector elements and calibrate their response prior to the proton-proton collisions. In particular, after the LHC incident on 19th September 2008 the experiments used the 15 months LHC down time, before the first collisions on 23rd November 2009, to run the full detectors in very extensive cosmic-ray campaigns, collecting many hundreds of millions of muon events. These runs allowed both ATLAS and CMS to be ready for physics operation, with pre-calibrated and pre-aligned detectors, by the time of the first pp collisions.
6.5 Experiment Software and LHC Worldwide Computing Grid
The experiment collaborations themselves develop the software that enables reconstruction, from raw data, of analyzable objects such as electrons, photons, jets, b jets, muons, and other charged tracks, and their energies or momenta. Algorithms have to be run to calibrate the energy deposits; align the hits from charged particles; and correct for changes in detector response arising from irradiation, variation in environmental parameters such as temperature, or changes in the position of detecting elements. The software packages must also simulate the response of the detectors to the passage of particles generated in simulated events occurring in bunch crossings that contain interesting physics processes, as well as simple backgrounds. These include processes such as the production of W or Z bosons, QCD jets, or Higgs bosons and their decays. Such simulations helped prepare, prior to the first collisions, the experiments’ end-to-end processing and analysis chains, which were crucial for the rapid delivery of physics results of outstanding quality and quantity soon after the first collisions.
The LHC computing system, termed the LHC Worldwide Computing Grid (WLCG) [1], was conceived to make effective use of distributed resources, work on a large scale, and enable all the experiments’ scientists, wherever they were based, to have access to LHC data, and without regard to the extent of the resources they themselves could afford. The WLCG provided the backbone for the analysis capabilities of the experiments. The global WLCG has continued to grow, now encompassing around 170 computing centers in 42 countries, with an infrastructure that provides access to some 600,000 computing cores, around 500 PB of storage (50% on disk and 50% on tape), and a network that frequently runs at 100 Gb s−1 between larger sites and at 10 Gb s−1 between smaller sites. The security of access have been instrumental for building a truly federated computing infrastructure for science. Although the individual computing tasks described above were already familiar in particle physics, the scope, scale, and geographical spread of the LHC computing and data analysis are unprecedented.
6.6 Operation of the LHC: The Start of Data Taking
On the tenth of September 2008 first beams circulated in the Large Hadron Collider. Nine days later, during the powering test of the last octant, alarms reached the LHC accelerator’s control room and safety systems were activated to protect the accelerator. It turned out that one of the 50,000 soldered joints had malfunctioned. This led to an electrical arc that pierced the vacuum enclosure of a superconducting dipole bending magnet leading a massive escape of helium, the pressure wave of which caused considerable damage. The accelerator went offline for repairs. The ATLAS and CMS experiments continued to run round-the-clock for a few months recording billions of traversals of muons from cosmic rays. These data demonstrated that the experiments were in a good shape to take collision data. After a few tweaks the ATLAS and CMS experiments were even better prepared for first collisions, which came on 23rd November 2009. The first collision data were rapidly distributed, analysed and physics results produced.
Following a preliminary low-energy run in the autumn of 2009, the ATLAS and CMS experiments started recording high-energy proton-proton collisions in March 2010 at √s = 7 TeV. Some 45 pb−1 of data were recorded, sufficient to demonstrate that the experiments were working well, according to the ambitious design specifications and the results they were producing were consistent with the predictions from known SM physics. Many parameters were examined, including the efficiency of identification and reconstruction of physics objects, the measured energy and momentum resolutions, the resolution of peaks in invariant mass distribution, and more. An example of the performance from the CMS experiment is the comparison of the observed width of Y particle with the design mass resolution. The width is expected to be dominated by instrumental resolution. Figure 6.6 shows that the observed width is measured to be 70 MeV consistent with the design value. Also observed in such di-muon invariant mass distributions is a history of decades of particle physics indicating the excellent performance of the experiments. The next step was to see if known physics could be measured as per the predictions of the SM, extrapolated to the new energies.
The distribution of the invariant mass for di-muon events, shown here from CMS, displays the various well-known resonant states of the SM. The inset illustrates the excellent mass resolution for the three states of the Y family. The mass resolutions in the central region are; 28 MeV (0.9%) for J/ψ, 69 MeV (0.7%) for Υ(1S), both dominated by instrumental resolution and Γ = 2.5 GeV for the Z dominated by its natural width, and are equal to the design values
6.6.1 Measurement of SM Processes to Verify Experiment Performance
Observation and accurate measurement of the production of known SM particles at the LHC collision energies is a pre-requisite for the exploration of new physics, including the search for the Higgs boson. The SM processes, such as W and Z production, are often considered to be ‘standard candles’ for the experiments.
In the ATLAS and CMS experiments, SM physics can be studied with unprecedented precision, allowing comparison with the predictions of the SM with small instrumental systematic errors. The data collected so far have enabled many precise measurements of SM processes, including the production of light quarks and gluons, bottom and top quarks, and W and Z bosons, singly and in pairs, and with varying numbers of jets resulting from higher order processes. A summary of such studies is shown in Fig. 6.7, where measurements of cross sections for various selected electroweak and QCD processes are compared with predictions from the SM. These very diverse measurements, probing cross-sections over a range of many orders of magnitude, established that the experiments were “physics commissioned” and ready for discoveries. The detector performance was well understood and known SM processes were correctly observed, crucially important as they often constitute large backgrounds to signatures of new physics, such as those expected for the Higgs boson.
The speed with which these measurements verified the SM predictions for known physics is a tribute to the large amount of work done by many groups, including theorists, other collider experiments at LEP, Tevatron, HERA, b-factories and to the good preparation of the ATLAS and CMS experiments.
In what follows the production of b-bar, τ+τ−, W+W−, etc. will be denoted by bb, ττ, WW(∗), etc.
Using all the data so far collected extensive searches for new physics, beyond the standard model, have been performed. No new physics beyond the SM has yet been discovered. Limits have been set on e.g. quark substructure, supersymmetric particles (e.g. disfavouring gluino masses below 1.5 TeV in simple models of supersymmetry), potential new bosons (e.g disfavouring new heavy SSM W′ and Z′ bosons with masses below 3 TeV for couplings similar to the ones for the known W and Z bosons) and semi-classical black holes in the context of large extra dimensions (with masses below 10 TeV).
6.7 The Discovery and Properties of a Higgs Boson
Undoubtedly, the most striking result to emerge from the ATLAS and CMS experiments is the discovery of the Higgs boson at a mass of ~125 GeV [19] and [20], respectively.
The SM Higgs boson couples to the different pairs of particles in a set proportion i.e. for fermions (f) proportional to mf 2, and for bosons (V) proportional mV 4/v 2 where v is the vacuum expectation value of the scalar field (v = 246 GeV). Once produced the Higgs boson disintegrates immediately into known SM particles. Both the production modes and decay modes and rates are precisely predicted in the SM. A search had to be made over a large range of masses and the many possible decay modes with differing branching ratios as shown in Fig. 6.2 and Table 6.1. For example, at mH = 125 GeV the SM boson is predicted to decay into pairs of photons with branching fraction (BR) of 2.2 × 10−3, into Z bosons and then four electrons or muons or two muons and two electrons with BR = 1.25 × 10−4, into a pair of W bosons and then into llνν with BR ~1%, etc.
For a given Higgs boson mass hypothesis, the sensitivity of the search depends on:
-
the mass of the Higgs boson
-
the Higgs boson production cross section (Fig. 6.2a and Table 6.1),
-
the decay branching fraction into the selected final state (Fig. 6.2b and Table 6.1),
-
the signal selection efficiency,
-
the observed Higgs boson mass resolution, and
-
the level of backgrounds with the same or a similar final state.
Comparisons with the expectations from the SM for the various combinations of production and decay modes are usually cast in terms of modifiers such as signal strength, μ, that is the ratio of the measured production × decay rate of the signal and the SM expectation i.e. μ = σ.BR/(σ.BR)SM. Signal strength of one would be indicative of the SM Higgs boson.
CMS and ATLAS increasingly use global event reconstruction algorithms, labeled particle-flow reconstruction, that attempt to identify, reconstruct and provide the measurement of the energy of particles by combining information from the inner tracker, the calorimeters and the muon system in an optimized manner. Hadronic jets are clustered from the reconstructed particles using the infrared- and collinear-safe anti-kT algorithm with a distance parameter usually set at 0.4. The jet momenta are measured by summing vectorially the momenta of all particles in the jet. Jets originating from b-jets are identified by discriminants that include the presence of particles originating from vertices displaced from the primary interaction vertex. A typical b-jet efficiency of around 70% is attained for a 1% misidentification probability for light quarks and gluons. The missing transverse momentum vector is taken as the negative of the vector sum of the momenta of all reconstructed particles in the event; its magnitude is labeled pT miss.
By the end of 2012 (LHC Run 1) the total amount of data that had been examined corresponded to an integrated luminosities of ~5 fb−1 at √s = 7 TeV and ~ 20 fb−1 at √s = 8 TeV, equating to the examination of some 2 × 1015 proton-proton collisions.
By the end of the Run 2 (2018) the total amount of data that had been recorded corresponded to an integrated luminosities ~150 fb−1 at √s = 13 TeV, equating to some 1.5 × 1016 proton-proton collisions.
6.7.1 Event and Physics Objects Reconstruction and Analysis Techniques
It is convenient to subdivide the analysis of data relating to Higgs bosons according to the decay channel, using datasets where the data have been selected to contain a particular set of final state particles. To improve the sensitivity, the events in this dataset are usually separated into categories that are intended to reflect the expected signal-to-background ratio. Several multivariate methods are used in the analyses
-
to improve event reconstruction, estimates of the energies/momenta of physics objects (e.g. photons and electrons, etc.),
-
to identify physics objects (such as electrons, photons, b-quarks, tau leptons, etc.)
-
to categorize events according to particular production (e.g. ggH, VBF, VH, ttH etc.), decay mode, or expected signal-to-background ratio.
The reader can find the exact description of the multivariate methods used within the individual papers referenced in the sections below.
Charged leptons and photons originating from the fundamental partonic processes tend to be “isolated” i.e. no other particles surround the one of interest. A relative isolation condition is applied on such particles. The sum of transverse momenta of accompanying particles, within an angular radius of approximately 0.3, around the particle of interest, is divided by the transverse momentum of the particle of interest. A cut on this ratio is made, the value of which is separately optimized for electrons, muons or photons. A correction to the accompanying energy is applied when the instantaneous luminosity is high and undesirable energy from pileup interactions is accidentally captured in the region.
6.7.2 The Discovery: Results from the 2011 and Partial 2012 Datasets
In the 2011 data-taking run the ATLAS and CMS experiments recorded data at √s = 7 TeV corresponding to an integrated luminosity of ~5 fb−1. In December 2011, the first “tantalizing hints” of a new particle from both the CMS and ATLAS experiments were shown at CERN. The general conclusion was that both experiments were seeing an excess of unusual events at roughly the same place in mass (in the mass range 120–130 GeV) in two different decay channels. That set the stage for data taking in 2012.
In January 2012 it was decided to slightly increase the energy of the protons from 3.5 to 4 TeV, giving a centre of mass energy of 8 TeV. By June 2012 the number of high-energy collisions examined had doubled and both CMS and ATLAS had greatly improved their analyses so it was decided to look at the area which had shown the excess of events but only after all the algorithms and selection procedures had been agreed, in case a bias was inadvertently introduced. These data led to the discovery of a Higgs boson, independently in both the ATLAS and CMS experiments in July 2012.
In this section we shall concentrate on the region of low mass (114.4 < mH < 150 GeV) where the two channels particularly suited for unambiguous discovery are the decays to two photons and to two Z bosons, where one or both of the Z bosons could be virtual, subsequently decaying into four electrons, four muons or two electrons and two muons. These two decay modes are particularly suited for discovery as the observed mass resolution (~1% of mH) is the best and the backgrounds are manageable or small.
6.7.2.1 The H → γγ Decay Mode
In the H → γγ analysis a search is made for a narrow peak in the diphoton invariant mass distribution in the mass range 110–150 GeV, on a large irreducible background from QCD production of two photons (via quark-antiquark annihilation and the gluon-fusion or “box” diagrams). There is also a reducible background where one or more of the reconstructed photon candidates originate from misidentification of jet fragments, with the process of QCD Compton scattering dominating. The relative fractions of these backgrounds in the selected events are illustrated in Fig. 6.9a.
The event selection requires two “isolated” photon candidates satisfying p T and photon identification criteria. As an example, CMS applies a threshold of p T = m γγ/3 (m γγ/4) to the leading (sub-leading) photon in p T, where m γγ is the diphoton invariant mass. Scaling the p T thresholds in this way avoids distortion of the shape of the m γγ distribution. The background is estimated from data, without the use of MC simulation, by fitting the diphoton invariant mass distribution in a range (100 < m γγ < 180 GeV).
The results from the CMS experiments are shown in Fig. 6.8a [20]. A clear peak at a diphoton mass of around 125 GeV is seen. A similar result was obtained in the ATLAS experiment [19].
(a) The two-photon invariant mass distribution of selected candidates in the CMS experiment, weighted by S/B of the category in which it falls. The lines represent the fitted background and the expected signal contribution (m H = 125 GeV). (b) The four-lepton invariant mass distribution in the ATLAS experiment for selected candidates relative to the background expectation. The expected signal contribution (m H = 125 GeV) is also shown
6.7.2.2 The H → ZZ(∗) → 4 l Decay Mode
In the H → ZZ(∗) → 4 l decay mode a search is made for a narrow four-charged lepton mass peak in the presence of a small continuum background. The background sources include an irreducible four-lepton contribution from direct ZZ(∗) production via quark-antiquark and gluon–gluon processes. Reducible background contributions arise from Z + bb and tt production where the final states contain two isolated leptons and two b-quark jets producing secondary leptons.
The event selection requires two pairs of same-flavour, oppositely charged isolated leptons. Since there are differences in the reducible background rates and mass resolutions between the sub-channels 4e, 4 μ, and 2e2μ, they are analysed separately. Electrons are typically required to have p T > 7 GeV. The corresponding requirements for muons are p T > 5 GeV. Both electrons and muons are required to be isolated. The pair with invariant mass closest to the Z boson mass is required to have a mass in the range 40–120 GeV and the other pair is required to have a mass in the range 12–120 GeV. The ZZ(∗) background, which is dominant, is evaluated from Monte Carlo simulation studies.
The m 4l distribution is shown in Fig. 6.8b for the ATLAS experiment [19]. A clear peak is observed at ~125 GeV in addition to the one at the Z mass. The latter is due to the conversion of an inner bremstrahlung photon emitted simultaneously with the dilepton pair. A similar result was obtained by the CMS experiment [20].
6.7.2.3 Combinations
A search was also made in other decay modes of a possible Higgs boson and combined to yield the final results published in August 2012 by ATLAS [19] and CMS [20] experiments. Both ATLAS and CMS independently discovered a new heavy boson at approximately the same mass, clearly evident in the two different decay modes, γγ and ZZ(∗). The observed (expected) local significances were 6.0σ (5.0σ) and 5.0σ (5.8σ) in ATLAS and CMS respectively, indicating that a new particle had been discovered.
The decay into two bosons (two photons; two Z bosons or two W bosons) implied that the new particle is a boson with spin different from one, and its decay into two photons that it carries either spin-0 or spin-2.
The results presented by both ATLAS and CMS collaborations were consistent, within uncertainties, with the expectations for a SM Higgs boson. Both noted that collection of more data would enable a more rigorous test of this conclusion and an investigation of whether the properties of the new particle imply physics beyond the SM.
6.7.3 Results from the Data Recorded Subsequent to the Discovery
The combined results from the ATLAS and CMS experiment from Run 1 on the Higgs boson production, decay rates and constraints on its couplings were published in 2016 [37]. These results have been superseded by the ones presented below. Results are presented from the most recently published papers (in journals or submitted to the hep arXiv) from the two collaborations. The integrated luminosity differs from one result to another and is indicated in the legends of the plots presented.
The LHC centre of mass energy was increased from √s = 8 TeV to √s = 13 TeV in 2015. At the higher value of √s the predicted cross-sections for the dominant ggH production mode and the rare ttH production mode increased by factors of ~2.3 and ~ 3.8, respectively. This and the larger datasets from Run 2 allow a more precise comparison of the properties of the Higgs boson with respect to those predicted by the SM. In addition, since the discovery, the theoretical predictions have become more accurate with the inclusion of further (higher) order corrections. Details can be found below in the references included in the individual papers of the two collaborations.
The two collaborations have also improved the reconstruction of physics objects and the methods of analysis. Event categorization and machine learning methods are deployed to study almost all the different production and decay modes. The analyses described below divide events into multiple categories reflecting the different Higgs boson production channels to improve the sensitivity of the measurements. Associated production processes (WH and ZH), or the ttH production process, are tagged by requiring the presence of additional leptons or jets. The VBF process is tagged using distinctive kinematic properties such the presence of two jets with a large separation in pseudorapidity and a large invariant jet-jet mass. In some cases the kinematic characteristics of the whole event, such as large missing pT, are used to preferentially select events e.g. arising from ZH production where the Z boson decays to neutrinos.
6.7.3.1 The H → γγ
As the H → γγ decay proceeds via W-boson and top-quark loops, it is especially sensitive to the presence of any undiscovered heavy charged fermions and bosons. Any significant deviation from the precise SM prediction for the cross section would be indicative of new physics.
The H → γγ mode provides good sensitivity to almost all Higgs boson production processes. The interference between W-loop and top-loops provides sensitivity to the relative sign of the fermion and boson couplings.
It is common to use a dedicated boosted decision tree discriminator to select and categorize events; it is constrained using the diphoton kinematic variables, photon isolation and identification variables, and per-event estimated diphoton mass resolution for the pair of photons in the event.
ATLAS has measured the properties of the H → γγ mode using 79.8 fb−1 of collision data recorded at √s = 13 TeV [38]. The properties measured include the signal strength, the cross section measurements for the production of a Higgs boson through gluon–gluon fusion, vector boson fusion, and in association with a vector boson or a top-quark pair. They are found to be compatible with the predictions of the SM. The signal strength is measured to be μ = 1.06 ± 0.08 (stat), +0.08 –0.07 (exp), +0.07 –0.06 (theo), improving on the precision of the previous ATLAS measurement at √s = 7 and 8 TeV by over a factor of three. The cross section for the production of the Higgs boson decaying to two isolated photons in the fiducial region of the selection of photons is measured to be 60.4 ± 6.1 (stat) ± 6.0 (exp) ± 60.3 (theo) fb, in good agreement with the SM value of 63.5 ± 3.3 fb. The differential cross section, sensitive to higher order QCD corrections and properties of the Higgs boson, such as its spin and CP quantum numbers, is illustrated in Fig. 6.9b and no significant deviation from a wide array of SM predictions is observed.
CMS has reported results from the H → γγ decay channel based on data collected at √s = 13 TeV corresponding to an integrated luminosity of 35.6 fb−1 [39]. The diphoton invariant mass distribution, observed in CMS, is shown in Fig. 6.10a. The measured signal strength is found to be 1.18 +0.17 –0.14, largely insensitive to the precise mass value assigned to the Higgs boson. Signal strengths associated with the different Higgs boson production mechanisms are shown in Fig. 6.10b and found to be compatible with the expectations from the SM.
(a) Data and signal-plus-background model fits for all categories summed, weighted by their sensitivity. The one (green) and two (yellow) standard deviation bands include the uncertainties in the background component of the fit. The lower panel shows the residuals after the background subtraction. (b) Cross section ratios measured for each process (black points) compared to the SM expectations and their uncertainties (blue band). The signal strength modifiers are constrained to be nonnegative, as indicated by the vertical line and hashed pattern at zero
6.7.3.2 H → ZZ(∗) → 4 l Decay Mode
The Higgs boson decay H → ZZ(∗) → 4 l is the most significant process in constraining the HZZ coupling. To study the differing production mechanisms involved, the events are categorized on the basis of the presence of jets, b-tagged jets, leptons, pT miss, and various matrix element discriminants that make use of the information about the additional objects: VBF (1- and 2-jet), VH hadronic, VH leptonic, ttH, VH pT miss, and untagged categories.
ATLAS has studied the coupling properties of the Higgs boson in the four-lepton (e,μ) decay channel using 36.1 fb−1 of pp. collision data recorded at √s = 13TeV [40]. The four-lepton invariant mass distribution is illustrated in Fig. 6.11a. Cross sections are measured for the main production modes and the ratio of sigma.BR/(sigma.BR)SM are plotted in Fig. 6.11b. The inclusive cross section times branching fraction for H → ZZ(∗) decay and for a Higgs boson absolute rapidity below 2.5 is measured to be 1.73+0.24 –0.23 pb, the statistical error dominating, compared to the SM prediction of 1.34 ± 0.09 pb.
(a) Distribution of the four-lepton reconstructed invariant mass m4l in the full mass range, combining data from 2016 an 2017. Points with error bars represent the data and stacked histograms represent expected distributions of the signal and background processes. The ZZ(∗) backgrounds are normalized to the SM expectation, the Z + X background to the estimation from data. (b) Result of the 2D likelihood scan for the μ(ggH, ttH, bbH, tqH) and μ(VBF,VH) signal-strength modifiers
CMS has studied the coupling properties using 77.4 fb−1 of pp. collision data recorded at √s = 13TeV [41]. The four-lepton invariant mass distribution is illustrated in Fig. 6.12a. The signal strength is measured to be μ = 1.06+0.15 –0.13 at mH = 125.09 GeV, the combined ATLAS and CMS measurement of the Higgs boson mass [42]. The result of a 2D likelihood scan of the signal strengths for the individual Higgs boson production modes are also measured and are shown in Fig. 6.12b. All measurements are consistent with the expectations from the SM.
6.7.3.3 H → WW(∗) → 2 l 2ν Decay Mode
The H → WW(∗) decay mode has a large branching fraction (~20%) and a relatively low-background final state. The study of this final state in which both W bosons decay leptonically is based on the signature with two isolated, oppositely charged, high p T leptons (electrons or muons) and large missing transverse momentum, E T miss, due to the undetected neutrinos. The signal sensitivity is improved by separating events according to lepton flavor; into e+e−, μ+μ−, and eμ samples and according to jet multiplicity into 0-jet and 1-jet samples. The dominant background arises from irreducible non-resonant WW(∗) production, and the dominant uncertainties arise from the estimation, using the data themselves, of the backgrounds from top quark pair, WW(∗) and DY production.
The final states are categorized according to the number of associated jets, with the 0-jet category dominating the overall sensitivity. Events are selected that contain two leptons of either different or the same flavour. The large background from tt production, the different and same flavour final states are further categorized with 0, 1 and 2 associated jets. In the different-flavour final state, dedicated 2-jet categories are included to enhance the sensitivity to VBF and VH production mechanisms.
ATLAS has presented measurements of the inclusive cross section of Higgs boson production via the gluon–gluon fusion (ggF) and vector-boson fusion (VBF) modes [43], based on an integrated luminosity of 36.1 fb−1 recorded at √s = 13 TeV in 2015–2016. The combined transverse mass distribution for Njet ≤ 1 is shown in Fig. 6.13a. The ggF and VBF cross-sections times the H → WW(∗) branching ratio are measured to be 12.6 ± 1.0(stat) +1.9 –1.8 (syst) pb and 0.50 ± 0.24 (stat) ±0.18 (syst) pb, respectively, in agreement with the SM predictions, as illustrated in Fig. 6.13b.
(a) Post-fit combined transverse mass distribution for Njet ≤ 1. The bottom panel shows the difference between the data and the estimated background compared to the distribution for a SM Higgs boson with mH = 125GeV. The HVBF contribution is too small to be visible. (b) 68% and 95% confidence level two-dimensional likelihood contours of σggF·BH → WW(∗) vs. σVBF· BH → WW(∗), compared to the SM prediction shown by the red marker
CMS has published results on the decay mode H → WW(∗) using data corresponding to an integrated luminosity of 35.9 fb−1, collected at √s = 13 TeV during 2016 [44]. The expected relative fraction of different Higgs boson production mechanisms in each category is shown in Fig. 6.14a, together with the expected signal yield. Combining all channels, the observed cross section times branching fraction is 1.28+0.18 –0.17 times the SM prediction for the Higgs boson with a mass of 125.09 GeV. The ratio of the observed and the predicted cross sections for the main Higgs boson production modes is shown in Fig. 6.14b. All are consistent with the predictions from the SM.
(a) Expected relative fraction of different Higgs boson production mechanisms in each category included in the combination, together with the expected signal yield. (b) Observed cross sections for the main Higgs boson production modes, normalized to the SM predictions. The vertical line and band correspond to the SM prediction and associated theoretical uncertainty
6.7.3.4 The H → ττ Decay Mode
All of the decay modes discussed so far test the direct coupling of the Higgs boson to bosons, and only indirectly probe, through quantum loops, its coupling to fermions. The H → ττ mode provides the best sensitivity for the direct measurement for Higgs boson coupling to fermions. It benefits from a relatively large branching fraction, a moderate mass resolution (~10–20%) and provides good sensitivity to both the ggH and VBF production processes.
The H → ττ mode is studied via tau decays to eμ, μμ, eτ h, μτ h, τ hτ h, where electrons and muons arise from leptonic τ-decays and τ h denotes a τ lepton decaying hadronically. Each of these categories is further divided into three sub-categories labeled 0-jet, boosted and VBF. The 0-jet category helps constrain background normalisation, identification efficiencies, and energy scales, and systematic uncertainties in the background model. The main irreducible background, Z → ττ production, and the largest reducible backgrounds (W + jets, QCD multijet production, and top quark pair) are evaluated from control samples in data.
(a) Distribution of the decimal logarithm of the ratio between the expected signal and the sum of expected signal and expected. The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. (b) Best fit signal strength per category
CMS has observed the H → ττ mode using a data sample corresponding to an integrated luminosity of 35.9fb−1 at √s = 13 TeV [45]. Figure 6.15a shows the distribution of the decimal logarithm of the ratio of the expected signal and the sum of expected signal and expected background in each bin of the mass distributions used to extract the results, in all signal regions. The background contributions are separated by decay channel. The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. The best fit of the product of the observed H → ττ signal production cross section and branching fraction is 1.09+0.27 –0.26 times the SM expectation. The combination with the corresponding measurement performed with data collected by the CMS experiment at center-of-mass energies of 7 and 8 TeV leads to an observed significance of 5.9 standard deviations, equal to the expected significance. Figure 6.15b right plots the signal strength per category for m H = 125.09 GeV.
ATLAS has observed the H → ττ mode using 36.1 fb−1 of data recorded at √s = 13 TeV [46]. All combinations of leptonic and hadronic tau decays were considered. Combining all data taken at √s = 7, 8 and 13 TeV, the observed (expected) significance is found to be 6.4 (5.4) standard deviations. Using the data taken at √s = 13 TeV, the total cross section, in the H → ττ decay channel, is measured to be 3.71 ± 0.59 (stat) +0.87 –0.74 (syst) pb, for mH = 125 GeV, assuming the relative contributions of its production modes predicted by the SM. Total cross sections are determined separately for vector boson fusion production and gluon–gluon fusion production to be σ(VBF, H → ττ) = 0.28 ± 0:09 (stat) +0.11 –0.09 (syst) pb and σ(ggF, H → ττ) = 3.0 ± 1.0 (stat.) +1.6 –1.2 (syst) pb, respectively. The measured values for σ(H → ττ), when only the data of individual channels are used, are shown in Fig. 6.16a, along with the result from the combined fit. The theory uncertainty in the predicted signal cross section is shown by the yellow band. Figure 6.16b shows the likelihood contours in the variables (ggF, H → ττ) and (VBF, H → ττ) for the combination of all channels. The 68% and 95% CL contours are shown as dashed and solid lines, respectively, for mH = 125 GeV. The SM expectation is indicated by a plus symbol and the best fit to the data is shown as a star. All measurements are in agreement with SM expectations.
(a) Measured values for σ(H → ττ) when only the data of individual channels are used. Also shown is the result from the combined fit. The total ± 1σ uncertainty in the measurement is indicated in black, with the individual contribution from the statistical uncertainty in blue. (b) Likelihood contours for the combination of all channels in the [(ggF, H → ττ) v/s (VBF, H → ττ)] plane. The SM expectation is indicated by a plus symbol and the best fit to the data is shown as a star
6.7.3.5 H→ \( b\overline{b} \) Decay Mode
In the SM, fermions couple directly to the Higgs boson via the Yukawa interaction. A clear test of this hypothesis would be the measurement of the H→ \( b\overline{b} \) coupling.
The H → bb decay mode has by far the largest branching ratio (~58%). However, this is the most difficult decay channel to observe, since bottom quark pairs are prolifically produced by QCD processes and give rise to a formidable background. The cross section for b-quark pair production, σbb(QCD), is ~107 × σ(H → bb). Therefore the search concentrates on Higgs boson production in association with a W or Z boson using the following decay modes: W → eν/μν and Z → ee or μμ or νν. The Z → νν decay is identified by the requirement of a large missing transverse energy. The Higgs boson candidate is reconstructed by requiring two b-tagged jets.
(a) Distribution of mbb in data after subtraction of all backgrounds except for the WZ and ZZ diboson processes, as obtained with the dijet-mass analysis. (b) Fitted values of the Higgs boson signal strength, μ, for mH = 125 GeV for the WH and ZH processes and their combination, using the 7 TeV, 8 TeV and 13 TeV data
Events are selected in 0-, 1- and 2-charged lepton (e or μ) channels, to explore the ZH → ννbb, WH → lνbb, ZH → llbb signatures, respectively. Both experiments introduced several improvements since the initial searches including more efficient identification of b-jets, better dijet mass resolution and use of multivariate discriminants that better separate signal from background. Multivariate discriminants, built from variables that describe the kinematics of the selected events, are used to maximise the sensitivity to the Higgs boson signal. The signal extraction method is validated with, for example, the diboson analysis where the nominal multivariate analysis is modified to extract the VZ, Z → bb diboson process.
ATLAS has observed the mode H → bb by analyzing the combined data from Run 1 and Run 2 [47], corresponding to an integrated luminosity of 80fb−1 yielding an observed (expected) significance of 5.4 (5.5) standard deviations, thus providing direct observation of the Higgs boson decay into b-quarks. The signal strength is measured to be 1.01 ± 0.12(stat) +0.16 –0.15(syst). Figure 6.17a shows the distribution of mbb in data after subtraction of all backgrounds except for the WZ and ZZ(∗) diboson processes using data taken at √s = 13 TeV. The contributions from all lepton channels, pV T regions, and number-of-jets categories are summed and weighted by their respective S/B, with S being the total fitted signal and B the total fitted background in each region. The expected contribution of the associated WH and ZH production of a SM Higgs boson with mH = 125 GeV is shown, scaled by the measured signal strength (μ =1.06). The size of the combined statistical and systematic uncertainty for the fitted background is indicated by the hatched band. Figure 6.17b shows the fitted values of the Higgs boson signal strength, where μ(VHbb) = 0.98 +0.22 –0.21 for mH = 125 GeV for the WH and ZH processes and their combination, using the 7 TeV, 8 TeV and 13 TeV data.
CMS has observed the mode H → bb. Figure 6.18a shows the weighted dijet invariant mass distribution for events weighted by S/(S + B) in all channels combined in the 2016 and 2017 data sets [48]. The data (points), the fitted VH signal (red) and VZ background (grey) distributions, with all other fitted background processes subtracted, except that from dibosons are shown in Fig. 6.18a. Figure 6.18b shows the best-fit value of the H → bb signal strength for the five individual production modes considered, as well as the overall combined result. The vertical dashed line indicates the SM expectation. All results are extracted from a single fit with mH = 125.09 GeV. CMS has made measurements, using data collected at √s = 7, 8, and 13 TeV, and observes an excess of events at mH = 125 GeV with a significance of 5.6 standard deviations, where the expectation for the SM Higgs boson is 5.5, and a signal strength of 1.04 ± 0.14 (stat.) ±0.14 (syst.).
(a) Dijet invariant mass distribution for events weighted by S/(S + B) in all channels combined in the 2016 and 2017 data sets. The error bar for each bin represents the presubtraction 1σ statistical uncertainty on the data, while the gray hatching indicates the 1σ total uncertainty on the signal and all background components. (b) Best-fit value of the H → bb signal strength with its 1σ systematic (red) and total (blue) uncertainties for the five individual production modes considered, as well as the overall combined result. The vertical dashed line indicates the SM expectation
6.7.3.6 H → μμ Decay Mode
The H → μ+μ− decay mode extends the test of the Higgs boson’s coupling to the second generation of fermions. Several scenarios beyond the SM predict a higher branching fraction than the one predicted in the SM (2.2 × 10−4 at mH = 125 GeV).
The dominant and irreducible background arises from the Z/γ∗ → μμ process that has a rate several orders of magnitude larger than that from the SM Higgs boson signal. However, due to the precise muon momentum measurement achieved by ATLAS and CMS, the dimuon mass resolution is excellent (≈ 2–3%). A search is performed for a narrow peak over a large but smoothly falling background. For optimal search sensitivity, events are divided into several categories. Taking advantage of the superior muon momentum measurement in the central region events can be subdivided by the pseudorapidity of the muons, or by selections aiming at specific production processes. A category selecting the vector boson fusion process with its distinctive signature and relatively large cross section is particularly useful.
ATLAS has performed this search using data corresponding to an integrated luminosity of 36.1 fb−1 collected at √s = 13 TeV [49]. No significant excess is observed above the expected background. When combined with the data taken at √s = 7 and 8 TeV, the observed (expected) cross-section upper limit is 2.8 (2.9) times the SM prediction.
The search in CMS, using an integrated luminosity corresponding to 35.9 fb−1 recorded at √s = 13 TeV [50], and combining with data taken at √s = 7 and 8 TeV, yielded an observed (expected) cross-section upper limit is 2.92 (2.16) times the Standard Model prediction.
6.7.3.7 ttbar H Production Mode
As mt > mH the Yukawa coupling of the Higgs boson to top quarks cannot be tested directly. However, it can be measured through the measurement in the pp. → ttH production process. The coupling of the Higgs boson to the top quark, the heaviest particle in the SM, could be very sensitive to the effects of physics beyond the SM.
Although the pp. → ttH production process only contributes around 1% of the total Higgs-boson production cross section, the top quarks in the final state offer a distinctive signature and allow many Higgs-boson decay modes to be accessed. Of these, the decay to two b-quarks, the Higgs boson decay mode with the largest branching fraction, also is sensitive to the b-quark’s Yukawa coupling, the second largest in the SM.
A top quark decays almost exclusively to a bottom quark and a W boson, with the W boson subsequently decaying either to a quark and an antiquark or to a charged lepton and its associated neutrino. The Higgs boson has a rich spectrum of decay modes, and ttH production is studied using a wide variety of final state event topologies, with the Higgs boson decaying into bb, WW (∗), ττ, γγ, and ZZ (∗) pairs.
ATLAS has observed this production mode using data taken at √s = 7 TeV, 8 TeV and 13 TeV corresponding to integrated luminosities up to 79.8 fb−1. The Higgs boson decays included comprise bb, WW \( ^* \), τ + τ−, γγ, and ZZ \( ^* \). The observed significance is 6.3σ, compared to an expectation of 5.1σ [51]. Assuming SM branching fractions, the total ttH production cross section at √s = 13 TeV is measured to be 670 ± 90(stat.) +110 −100(syst.) fb, in agreement with the SM prediction. Figure 6.19a shows the observed event yields in all analysis categories. The background yields correspond to the observed fit results, and the signal yields are shown for both the observed results (μ = 1.32) and the SM prediction (μ = 1). The ranking of the discriminant bins is carried out by log10(S/B), where S is the extracted signal yield and B the extracted background yield. Figure 6.19b shows the combined ttH production cross section, as well as cross sections measured in the individual analyses, divided by the SM prediction. The black lines show the total uncertainties, and the bands indicate the statistical and systematic uncertainties. The red vertical line indicates the SM cross-section prediction, and the grey band represents the PDF and α S uncertainties and the uncertainties due to missing higher-order corrections.
(a) Observed event yields in all analysis categories in up to 79.8fb−1 of 13 TeV data. The lower panel shows the ratio of the data to the background estimated from the fit with freely floating signal, compared to the expected distribution including the signal assuming μ = 1.32 (full red) and μ = 1 (dashed orange). The error bars on the data are statistical. (b) Combined ttH production cross section, as well as cross sections measured in the individual analyses, divided by the SM prediction
CMS has observed ttH production in a combined analysis of data at √s = 7, 8, and 13 TeV, corresponding to integrated luminosities of up to 5.1, 19.7, and 35.9 fb−1, respectively [52]. An excess of events is observed with an observed (expected) significance of 5.2 (4.2) standard deviations, over the expectation from the background-only hypothesis for mH = 125.09. The combined best-fit signal strength normalized to the standard model prediction is 1.26+0.31 –0.26. Figure 6.20a shows the distribution of events as a function of the decimal logarithm of S/B, where S and B are the expected postfit signal (with μttH = 1) and background yields, respectively, in each bin of the distributions considered in this combination. The shaded histogram shows the expected background distribution. The two hatched histograms, each stacked on top of the background histogram, show the signal expectation for the SM (μttH = 1) and the observed (μttH = 1.26) signal strengths. The lower panel shows the ratios of the expected signal and observed results relative to the expected background. Figure 6.20b plots the ttH signal strength modifiers, μttH, for the various selections and the overall combined result. The SM expectation is shown as a dashed vertical line.
(a) Distribution of events as a function of the decimal logarithm of S/B. The shaded histogram shows the expected background distribution. The two hatched histograms, each stacked on top of the background histogram, show the signal expectation for the SM (μttH = 1) and the observed (μttH = 1.26) signal strengths. The lower panel shows the ratios of the expected signal and observed results relative to the expected background. (b) Best fit value of the ttH signal strength modifier μttH, with its 1σ and 2σ confidence intervals for upper section) the five individual decay channels considered, middle section) the combined result for 7 + 8 TeV alone and for 13 TeV alone, and lower section) the overall combined result. The SM expectation is shown as a dashed vertical line
6.7.4 Combining the Results
6.7.4.1 Mass of the Observed State
The mass of the Higgs boson is measured using the two decay channels that give the best mass resolutions namely H → γγ and H → ZZ(∗) → 4 l. ATLAS and CMS have combined their results from Run 1 [53]. The results were obtained from a simultaneous fit to the reconstructed invariant mass peaks in the two channels and for the two experiments. The measured masses from the individual channels and the two experiments were found to be consistent amongst themselves. The combined measured mass of the Higgs boson was found to be mH = 125.09 ± 0.21 (stat.) ± 0.11 (syst.) GeV, a value subsequently used in many of the analyses discussed above. The results of these measurements and more recent ones are shown in Fig. 6.21 [54].
Summary of the CMS and ATLAS mass measurements in the γγ and ZZ(∗) channels in Run 1 and Run 2. Particle Data Group [54]
The mass of the Higgs boson, combined with the measured top quark mass, has cosmological implications. The current measurement of mH, along with that of the top quark mass [mt = 173.21 ± 0.51 (stat) ±0.71 (syst)] indicate that our universe is in a metastable state, which eventually will tunnel through the potential barrier to the true vacuum in which space collapses, albeit over a period of time that is many orders of magnitude larger than the lifetime of the universe so far.
6.7.4.2 Compatibility of the Observed State with the SM Higgs Boson Hypothesis: Signal Strength
In the SM, the Higgs boson is a fundamental scalar particle with spin-parity JP = 0+, and couples to fundamental fermions as mf 2/v 2 and to fundamental bosons as mV 4/v 2 where v = 246 GeV. Several individual tests of compatibility with expectations from the SM have been discussed above.
Here we discuss the signal strength, μ, as determined by the combination of results from all channels. ATLAS and CMS combined their data from Run 1 [37] from the analysis of five production processes, namely gluon fusion, vector boson fusion, and associated production with a W or a Z boson or a pair of top quarks, and of the five decay modes H → γγ, ZZ(∗), WW(∗), bb, and ττ. All results are reported assuming a value of 125.09 GeV for the Higgs boson mass. The Higgs boson production and decay rates measured by the two experiments are combined within the context of three generic parameterisations: two based on cross sections and branching fractions, and one on ratios of coupling modifiers. Several interpretations of the measurements with more model-dependent parameterisations are also given. The combined signal yield relative to the SM prediction is measured to be 1.09 ± 0.11. The error is broken down as ±0.07 (statistical), ±0.04 (experimental systematic), ±0.03 (theoretical on background) and ± 0.07 (theoretical on signal).
The most recent measured values of μ, using the above-mentioned channels, are:
-
ATLAS: μ = 1.13 +0.09 –0.08, using 79.8 fb−1 at √s = 13 TeV [55],
-
CMS: μ = 1.17 ± 0.1, using 35.9 fb−1 at √s = 13 TeV [56].
The error in the measurement from ATLAS has the following breakdown: ±0.05 (statistical), ±0.05 (experimental systematic), ±0.03 (theoretical on background) and (+0.05, −0.04) (theoretical on signal). This should give a flavor of the possibilities for extrapolation into the future.
6.7.4.3 Compatibility of the Observed State with the SM Higgs Boson Hypothesis: Couplings
The 25 products, μ i × μ f, where i (f) is the production (decay) index can also be considered as free parameters. This can be viewed as the measurements of cross sections times branching fractions, sigma×BR, by production mechanism and decay mode. The results from the ATLAS and CMS have been combined and are illustrated in Fig. 6.22 from the Particle Data Group [54] showing compatibility with the SM.
Figure 6.23a, from the ATLAS experiment [55], illustrates the dependence of the Higgs boson couplings on mass of the decay particles (μ, τ, b-quark, W, Z and t-quark). The plot is made for reduced coupling strength modifiers, κ, using κF(mF/v) for fermions and (√κV)(mV/v) for vector bosons, where v = 246.22 GeV. The couplings modifiers κF and κV are measured assuming no BSM contributions to the Higgs boson decays, and the SM structure of loop processes. The line is the expectation from the SM.
(a) Reduced coupling strength modifiers κF(mF/v) for fermions (t, b, τ, μ) and (√κV)(mV/v) for vector bosons (W, Z) as a function of their masses mF and mV, respectively. The SM prediction for both cases is also shown (dotted line). (b) Likelihood scan in the M-ε plane. The best-fit point and, 1σ, 2σ CL regions are shown, along with the SM prediction
CMS has made a similar fit, shown in Fig. 6.23b [56], using a phenomenological parameterization relating the masses of the fermions and vector bosons to the corresponding κ modifiers using two parameters, denoted M and ε. In such a model one can relate the coupling modifiers to M and ε as \( {\kappa}_{\mathrm{F}}=\mbox{\textit{v}}\;{m}_f^{\in }/{M}^{1+\in } \) for fermions, and \( {\kappa}_{\mathrm{V}}=\mbox{\textit{v}}\,\,{m}_{\mathrm{V}}^{2\in }/{M}^{1+2\in } \) for vector bosons. The SM expectation, κi = 1, is recovered when (M, ε) = (v, 0).
Both Fig. 6.23a and b demonstrate good compatibility with the SM within the errors on the measurements.
6.7.4.4 Compatibility of the Observed State with the SM Higgs Boson Hypothesis: Quantum Numbers
Ascertaining the quantum numbers of the Higgs boson is essential to the understanding of its nature and its coupling properties. According to the Landau-Yang theorem the observations made in the diphoton channel excludes the spin-1 hypothesis and restricts possibilities for the boson to have spin-0 or -2. The diphoton decay mode also implies that the boson has charge conjugation has C-even.
To identify the spin-parity of the Higgs boson the production and decay processes are examined in several analyses. The angular distributions of the decay particles can be used to test various spin hypotheses.
Much can be gleaned from the decay mode H → ZZ(∗) → 4 l, where the full final state is reconstructed, including the angular variables sensitive to the spin-parity, along with a very favourable signal/background ratio. CMS has used the information from the five angles (see Fig. 6.24a) and the two dilepton pair masses combined to form a discriminant based on the 0+ nature of the Higgs boson [57].
(a) Illustration of the production and decay of a particle X → Z1Z2 → 4 l with the two production angles θ∗ and Φ1 shown in the X rest frame and three decay angles θ 1, θ 2, and Φ shown in the Zi and X rest frames, respectively. (b) Examples of distributions of the test statistic (˜q) defined in for the combination of decay channels left) 0+ versus 0− right) 0+ versus the spin-2 model. The observed values are indicated by the vertical solid line and the expected medians by the dashed lines. The shaded areas correspond to the integrals of the expected distributions used for the rejection of each hypothesis
ATLAS has also tested various JP hypotheses, and in particular 0+ and 0−.
In all scenarios investigated by both CMS [57] and ATLAS [58] experiments, the data are compatible with the 0+ hypothesis, excluding a pseudoscalar nature at CLS levels of 99.8% and 98.0%, respectively. The expected distribution in ATLAS of the test statistic for the SM hypothesis (in blue) and several alternative spin and parity hypotheses is compared in Fig. 6.24b. The combination of the three decay processes allows the exclusion of all considered non-SM hypotheses at amore than 99.9% CL in favour of the SM spin-0 hypothesis.
6.8 Conclusions and Outlook
In July 2012 the ATLAS and CMS experiments announced the discovery of a Higgs boson, confirming the conjecture put forward in the 1960s. Further results from the two experiments show that, within the current measurement precision, the Higgs boson has the properties predicted by the SM. However, several theories of physics beyond the SM (BSM) predict the existence of more than one Higgs boson, and one of these would only be subtly different from that predicted in the SM one, with signal strengths differing by between 0.5–5%, depending on the model in question, indicative of the required level of sensitivity to distinguish it from a SM Higgs boson.
In Run 2 (2015–2018) the LHC provided proton-proton collisions at √s = 13 TeV with a peak instantaneous luminosity of 2 × 1034 cm−2 s−1, a factor of two beyond the design value. It is intended to operate the accelerator at √s = 14 TeV after the next long shutdown (2019–2020) and to integrate a luminosity corresponding to some 300 fb−1 by the end of Run 3 (2021–2024). More precise measurements of the properties of the new boson will be made, as well as a more extensive exploration of physics beyond the SM, for which many possibilities are conjectured including supersymmetry, extra dimensions, unified theories, superstrings etc.
The results presented in Chap. 6 are still mostly dominated by statistical errors. The ATLAS and CMS experiments continually update their results that can be found through their websites quoted in references [36, 37]. Much more data need to be collected to enable rigorous testing of the compatibility of the Higgs boson with the SM and to get clues to physics lying beyond the SM in case of a significant deviation. This is one of the main motivations for the high luminosity LHC project, labeled the HL-LHC.
Europe’s topmost priority in particle physics calls for the exploitation of the full potential of the LHC, including the high-luminosity upgrade of the accelerator and detectors with a view to collecting ten times more data than in the initial design. It is planned to increase the instantaneous luminosity of the LHC to 5 × 1034 cm−2 s−1, and record, by around 2035, an integrated luminosity corresponding to ~3000 fb−1 (ten times larger than the original design value). Such an integrated luminosity also requires substantial upgrades of the ATLAS and CMS experiments, now underway, to allow a very precise measurement of the properties of the Higgs boson the study of its rare decay modes and self-coupling, in addition to the search for physics beyond the SM. Many theories beyond the SM make different predictions for the properties of one or more Higgs bosons.
Summary plot from CMS showing the total expected ±1σ uncertainties in S1 and S2 on the per-decay mode signal strength parameters for 300 fb−1 (left) and 3000 fb−1 (centre). The statistical-only component of the uncertainty is also shown. (right) Expected uncertainty on the branching ratio measurements in ATLAS for the gg, ZZ(∗), WW(∗), tt, bb, μμ and Zγ decay channels normalized to their SM predictions assuming SM production cross section for scenarios S1 (red) and S2 (black)
Based on the currently analysed data ATLAS and CMS experiments have recently made projections of the attainable sensitivity for such measurements by the end of the HL-LHC phase [59, 60]. As around 150 million Higgs bosons will be produced a search can also be made for exotic and rare decays of the boson. Figures 6.25 and 6.26 show two sets of projections; Scenario 1 (S1) using the current theoretical errors or Scenario 2 (S2) where the theoretical errors are halved. The extrapolations show the possibility of measuring the individual signal strengths with a precision of between 5–10% for an integrated luminosity of 300 fb−1, and a few percent for a dataset corresponding to 3000 fb−1 per experiment, dominated by theoretical erros. The per-production mode signal strength parameters are projected to be measurable with uncertainties of between 3–6% for a dataset corresponding to 3000 fb−1 per experiment. Of particular note, in view of a future electron-positron collider, is the projection for the measurement of the ttH coupling with a precision of ~5% per experiment.
(a) Expected uncertainty on the measurement of cross sections in ATLAS for the ggF, VBF, WH, ZH and ttH production modes normalized to their SM predictions assuming SM branching fractions for Scenarios S1 (red) and S2 (black). (b) Summary plot from CMS showing the total expected ±1σ uncertainties in S1 and S2 on the cross section measurements for 300 fb−1 (left) and 3000 fb−1 (right). The statistical-only component of the uncertainty is also shown
The discovery of a Higgs boson implies the discovery of a fundamental scalar field that pervades the universe. Astronomical and astrophysical measurements point to the following composition of energy-matter in the universe: ~4% normal matter that “shines”, ~23% dark matter, and the rest in the form of “dark energy.” Dark matter is weakly and gravitationally interacting matter with no electromagnetic or strong interactions. These are the properties carried by the lightest supersymmetic particle. Hence the question: Is dark matter supersymmetric in nature? Fundamental scalar fields could well have played a critical role in the conjectured inflation of our universe immediately after the Big Bang, and in the recently observed accelerating expansion of the universe that, among other measurements, signals the presence of dark energy in our universe.
The discovery of the Higgs boson could turn out to be a portal to physics beyond the SM. Physicists at the LHC are eagerly looking forward to further running of the LHC, and the HL-LHC, and to establishing the true nature of the Higgs boson, to find clues or answers to some of the other fundamental open questions in particle physics and cosmology. The exploitation of the LHC is in its infancy, having recorded a small fraction of the finally anticipated integrated luminosity, and the expectations for other discoveries in the coming decades are high.
Notes
- 1.
The pseudorapidity η = −ln[tan(θ/2)] where and θ is the polar angle measured from the positive z axis (along the beam direction).
References
L. Evans (ed.), The Large Hadron Collider, a Marvel of Technology, EPFL Press, 2nd Edition, 2018;
L. Evans, P. Bryant (ed.) and LHC Machine, JINST 03 (2008) S08001.
F. Englert and R. Brout, Phys. Rev. Lett. 13 (1964) 321.
P.W. Higgs, Phys. Lett. 12 (1964) 132.
P.W. Higgs, Phys. Rev. Lett. 13 (1964) 508.
G.S. Guralnik, C.R. Hagen, and T.W.B. Kibble, Phys. Rev. Lett. 13 (1964) 585.
P.W. Higgs, Phys. Rev. 145 (1966) 1156.
T.W.B. Kibble, Phys. Rev. 155 (1967) 1554.
The Infinity Puzzle, Frank Close, Basic Books (2011).
S. Weinberg, Phys. Rev. Lett. 19 (1967) 1264.
A. Salam, Proceedings of the eighth Nobel symposium, ed. N. Svartholm, p. 367. Almqvist & Wiskell, 1968.
S.L. Glashow, Nucl. Phys. 22 (1961) 579.
G. t’Hooft and M. Veltman, Nucl. Phys. B44(1972)189.
F. J. Hasert et al., Phys. Lett. B46(1973)38.
D. Gross and F.Wilczek, Phys. Rev. Lett. 30(1973)1343.
D. H. Politzer, Phys. Rev. Lett. 30(1973)1346.
UA1 Collaboration, Experimental Observation of isolated large transverse energy electrons with associated missing energy at √s=540 GeV, Phys. Lett. B122 (1983) 103; Experimental Observation of Lepton Pairs of Invariant Mass Around 95 GeV/c2 at the CERN SPS Collider, Phys. Lett. 126B (1983) 398.
UA2 Collaboration, Observation of single isolated electrons of high transverse momentum in events with missing transverse energy at the CERN p-pbar collider, Phys. Lett. B122 (1983) 476; Evidence for Z0 → e+e− at the CERN anti-p – p Collider, Phys. Lett. 129B (1983) 130.
ATLAS Collaboration, Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC, Phys. Lett. B716 (2012) 1.
CMS Collaboration, Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC, Phys. Lett. B716 (2012) 30.
M. Della Negra, P. Jenni and T.S. Virdee, Journey in the Search of the Higgs Boson: The ATLAS and CMS Experiments at eth Large Hadron Collider, Science Vol. 338 no. 6114 (2012) 1560.
P. Jenni and T.S. Virdee, The Discovery of the Higgs Boson at the LHC, in “60 Years of CERN Experiments”, Ed. H. Schopper and L. Di Lella (World Scientific, 2015), 978-981-4644-14-3.
M. Della Negra, P. Jenni and T. S. Virdee, The Construction of ATLAS and CMS, Ann. Rev. Part. Sci. 68 (2018) 183.
ALEPH, DELPHI, L3, OPAL Collaborations, and LEP Working Group for Higgs Boson Searches, Phys. Lett. B 565 (2003) 61.
ALEPH, CDF, D0, DELPHI, L3, OPAL, SLD Collaborations, the LEP Electroweak Working Group, the Tevatron Electroweak Working Group, and the SLD Electroweak and Heavy Flavour Groups, Precision electroweak measurements and constraints on the standard model, CERN PH-EP-2010-095, http://lepewwg.web.cern.ch/LEPEWWG/plots/winter2012/, arXiv:1012.2367, 2010, http://cdsweb.cern.ch/record/1313716.
CDF and D0 Collaborations, Evidence for a Particle Produced in Association with Weak Bosons and Decaying to Bottom-Antibottom Quark Pair in Higgs Boson Searches at the Tevatron, Phys. Rev. Lett. 109, 071894 (2012).
J.R. Ellis, M.K. Gaillard, D.V. Nanopoulos, Nucl. Phys. B 106 (1976) 292.
LHC Higgs Cross Section Working Group, https://twiki.cern.ch/twiki/bin/view/LHCPhysics/LHCHXSWG, http://arxiv.org/abs/1101.0593 (2011), http://arxiv.org/abs/1201.3084 (2012), http://arXiv:1307.1347 (2013), http://arXiv:1610.07922 (2016).
C.J. Seez, T.S. Virdee, L. Di Lella, R.H. Kleiss, Z. Kunszt, W.J. Stirling, in: G. Jarlskog, D. Rein (Eds.), Proceedings of the Large Hadron Collider Workshop, Aachen, Germany, 1990, p. 474, CERN 90-10-V-2/ECFA 90-133-Vol-2.
M. Della Negra, D. Froidevaux, K. Jakobs, R. Kinnunen, R. Kleiss, A. Nisati, T. Sjostrand, in: G. Jarlskog, D. Rein (Eds.), Proceedings of the Large Hadron Collider Workshop, Aachen, Germany, 1990, p. 509, CERN 90-10-V-2/ECFA 90-133-Vol-2.
Proceedings of the Large Hadron Collider Workshop, Aachen, Germany, 1990, CERN 90-10-V-2/ECFA 90-133.
G. Flugge, ed. Proceedings of the General Meeting on LHC Physics Detectors: Towards the LHC Experimental Programme, Geneva: ECFA/CERN (1992).
N. Ellis, T. S. Virdee, Ann. Rev. Nucl. Sci. 44 (1994) 609.
The LHC Detector Challenge, Physics World, Vol. 17, No. 9, (2004); Detectors at LHC, Phys. Rep. 403-404 (2004) 401.
ATLAS Collaboration, https://atlas.cern/discover/about, Letter of Intent, CERN-LHCC-92-004 (1992); Technical Proposal, CERN-LHCC-1994-043 (1994); JINST 3 (2008) S08003.
CMS Collaboration, https://cms.cern/, Letter of Intent, CERN-LHCC-92-003 (1992); Technical Proposal, CERN-LHCC-1994-038 (1994); JINST 3 (2008) S08004.
ATLAS and CMS Collaborations, Measurement of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analyss of the LHC pp collision data at √s=7 and 8 TeV, JHEP08 (2016) 045.
ATLAS Collaboration, Measurements of the Higgs boson properties in the diphoton decay channel using 80 fb−1 of pp collision data with the ATLAS detector, ATLAS-CONF-2018-028 (2018).
CMS Collaboration, Measurements of Higgs boson properties in the diphoton decay channel in proton-proton collisions at √s = 13 TeV, JHEP11 (2018) 185.
ATLAS Collaboration, Measurements of Higgs boson coupling properties in the H → ZZ\( ^* \) → 4l decay channel at √s = 13 TeV with the ATLAS detector, JHEP03 (2018) 095.
CMS Collaboration, Measurements of the properties of Higgs boson decaying in the four-lepton final state at √s = 13 TeV, CMS PAS HIG-18-001.
ATLAS and CMS Collaborations, Combined measurement of the Higgs Boson Mass in pp Collisions at √s=7 and 8 TeV with the ATLAS and CMS Experiments, Phys. Rev. Lett. 114 191803 (2015).
ATLAS Collaboration, Measurements of gluon–gluon fusion and vector-boson fusion Higgs boson production cross-sections in the H→WW∗→eνμν decay channel in pp collisions at √s=13TeV with the ATLAS detector, Phys. Lett. B 789 (2019) 508.
CMS Collaboration, Measurements of the properties of Higgs boson decaying to a W boson pair in pp collisions at √s = 13 TeV, Phys. Lett. B 791 (2019) 96.
CMS Collaboration, Observation of the Higgs boson decay to a pair of τ leptons with the CMS detector, Phys. Lett. B 779 (2018) 283.
ATLAS Collaboration, Cross-section measurements of the Higgs boson decaying to a pair of tau leptons in proton-proton collisions at √s=13 TeV with the ATLAS detector, Phys. Rev. D 99, 072001 (2019).
ATLAS Collaboration, Observation of H→ \( b\overline{b} \) decays and VH production with the ATLAS detector, Phy. Lett. B786 (2018) 59.
CMS Collaboration, Observation of the Higgs Boson decay to Bottom Quarks, Phys. Rev. Lett. 121, 121801 (2018).
ATLAS Collaboration, Search for the Dimuon Decay of the Higgs Boson in pp Collisions at √s=13 TeV with the ATLAS detector, Phys. Rev. Lett. 119, 051802 (2017).
CMS Collaboration, Search for Higgs boson decaying to two muons in proton-proton collisions at √s=13 TeV, Phys. Rev. Lett. 122, 021801 (2019).
ATLAS Collaboration, Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector, Phys. Lett. B 784 (2018) 173.
CMS Collaboration, Observation of ttH Production, Phys. Rev. Lett 120, 231801 (2018).
ATLAS and CMS Collaborations, Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using collisions at 7 and 8 TeV, Eur. Phys. J. C (2015) 75:212.
C. Patrignani et al., Particle Physics Group, Chin. Phys. C, 40 100001 (2016)
ATLAS Collaboration, Combined measurements of Higgs boson production and decay in proton-proton collision date at √s=13 TeV, ATLAS-CONF-2018-031 (2018).
CMS Collaboration, Combined measurements of Higgs boson couplings in proton-proton collisions at √s=13 TeV, Eur. Phys. J. C 79 (2019) 421.
CMS Collaboration, Study of the mass and spin-parity of the Higgs boson candidate via its decays to Z boson pairs, Phys. Rev. Lett., 110 (2013) 081803.
ATLAS Collaboration, Study of the spin of the Higgs boson in diboson decays with the ATLAS detector, Eur. Phys. J C75 (2016) 476.
ATLAS Collaboration, Projections for measurements of Higgs boson cross sections, branching fractions, coupling parameters and mass with the ATLAS detector, ATL-PHY-PUB-2018-054.
CMS Collaboration, Sensitivity projections for Higgs boson properties measurements at the HL-LHC, CMS PAS FTR-18-011 (2018).
Acknowledgements
The construction, and now the operation and exploitation, of the large and complex ATLAS and CMS experiments have required the talents, the resources, and the dedication of thousands of scientists, engineers and technicians worldwide. This paper is dedicated to all who have worked on these experiments. The superb construction, and efficient operation of the LHC accelerator and the WLCG computing are gratefully acknowledged.
The authors are greatly indebted to C. Seez for careful reading of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this chapter
Cite this chapter
Jenni, P., Virdee, T.S. (2020). The Discovery of the Higgs Boson at the LHC. In: Schopper, H. (eds) Particle Physics Reference Library. Springer, Cham. https://doi.org/10.1007/978-3-030-38207-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-38207-0_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-38206-3
Online ISBN: 978-3-030-38207-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)