Abstract
We can define the traditional trigonometric functions in several different ways: via differential equations, via an arclength definition on the unit circle x 2 + y 2 = 1, or via an analytic approach. In this project, we adapt these approaches to define analogous functions for a unit squircle |x|p + |y|p = 1, p ≥ 1. As we develop these functions using only elementary calculus, we will ponder the importance and role of π, and glimpse some very deep ideas in elliptic integrals, special functions, non-Euclidean geometry, number theory, and complex analysis.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Adler, C.L., Tanton, J.: π is the minimum value of Pi. College Mathematics Journal 31(2), 102–106 (2000)
Andrews, G., Askey, R., Roy, R.: Special Functions (Encyclopedia of Mathematics and its Applications). Cambridge University Press (1999). https://doi.org/10.1017/CBO9781107325937
Blåjö, V.: The Isoperimetric Problem. The American Mathematical Monthly 112 (6), 526–566 (2005)
Borwein, J., Bailey, D.: Mathematics by Experiment: Plausible Reasoning in the 21st Century. A K Peters (2003)
Boyce, W., DiPrima, R.: Elementary Differential Equations, 9th edition. Wiley (2008)
Callahan, J., Cox, D., Hoffman, K., O’Shea, D., Pollatsek, H., Senechal, L.: Calculus in Context: The Five College Calculus Project. W.H. Freeman (1995)
Cha, B.: Transcendental Functions and Initial Value Problems: A Different Approach to Calculus II. College Mathematics Journal 38(4), 288–296 (2007)
Euler, R., Sadek, J.: The π’s go full circle, Mathematics Magazine 72, 59–63 (1999)
R. Grammel: Eine Verallgemeinerung der Kreis- und Hyperbelfunktionen, (German) Ing.-Arch. 16, 188–200 (1948)
Hardy, G., Littlewood, J., Pólya, G., Inequalities, Cambridge Univ. Press (1934)
Keller, J., Vakil, R.:
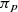 , the Value of π in
, the Value of π in 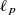 . The American Mathematical Monthly, 116(10), 931–935 (2009). https://doi.org/10.4169/000298909X477069
. The American Mathematical Monthly, 116(10), 931–935 (2009). https://doi.org/10.4169/000298909X477069
Krause, E.: Taxicab Geometry: Adventures in Non-Euclidean Geometry. Dover (1987)
Lang, J., Edmunds, D.: Eigenvalues, Embeddings and Generalised Trigonometric Functions, Springer Lecture Notes in Mathematics (2016)
Levin, A.: A Geometric Interpretation of an Infinite Product for the Lemniscate Constant. The American Mathematical Monthly, 113(6), 510–520 (2006). https://doi.org/10.2307/27641976
Lindqvist, P., Peetre, J.: p-arclength of the q-circle, Math. Student 72 (1–4) 139–145(2003)
Maican, C.C: Integral Evaluations Using the Gamma and Beta Functions and Elliptic Integrals in Engineering: A Self-Study Approach, International Press, 2005.
Markushevich, A.I.: The Remarkable Sine Functions, Elsevier (1966)
Poodiack, R.: Squigonometry, Hyperellipses, and Supereggs, Mathematics Magazine, 89(2) 92–102 (2016)
Shelupsky, D.: A Generalization of the Trigonometric Functions, The American Mathematical Monthly, 66(10), 879-884 (1959). https://doi.org/10.1080/00029890.1959.11989425
Singh, S.: Fermat’s last theorem: the story of a riddle that confounded the world’s greatest minds for 358 years. Harper Perennial (2007)
Weisstein, E.W.: Gamma Function. From Mathworld – A Wolfram Web Resource. http://mathworld.wolfram.com/GammaFunction.html
Weisstein, E.W.: Elliptic Integral Singular Value. From Mathworld – A Wolfram Web Resource. http://mathworld.wolfram.com/EllipticIntegralSingularValue.html
Wood, W.: Squigonometry, Mathematics Magazine, 84(4): 257–265 (2011)
Young, R.M. Excursions in Calculus: An Interplay of the Continuous and the Discrete, Cambridge Univ. Press (1992)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Wood, W.E., Poodiack, R.D. (2020). Squigonometry: Trigonometry in the p-Norm. In: Harris, P., Insko, E., Wootton, A. (eds) A Project-Based Guide to Undergraduate Research in Mathematics. Foundations for Undergraduate Research in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-37853-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-37853-0_9
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-37852-3
Online ISBN: 978-3-030-37853-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


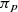 , the Value of π in
, the Value of π in 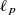 . The American Mathematical Monthly, 116(10), 931–935 (2009).
. The American Mathematical Monthly, 116(10), 931–935 (2009).