1 Introduction

An orthogonal drawing of a planar graph G is a planar drawing where each edge is drawn as a chain of horizontal and vertical segments; see Fig. 1a. Orthogonal drawings are among the most investigated research subjects in graph drawing, see, e.g., [3,4,5, 11, 13, 17, 25, 28, 30, 31] for a limited list of references, and also [12, 23] for surveys. The OrthogonalPlanarity problem asks whether G admits an orthogonal drawing with at most b bends in total, for a given \(b \in \mathbb {N}\).

In a seminal paper, Garg and Tamassia [25] proved that OrthogonalPlanarity is NP-complete when \(b=0\), which implies that minimizing the number of bends is also NP-hard. In fact, it is even NP-hard to approximate the minimum number of bends in an orthogonal drawing with an \(O(n^{1-\varepsilon })\) error for any \(\varepsilon > 0\) [25]. On the positive side, Tamassia [30] showed that OrthogonalPlanarity can be decided in polynomial time if the input graph is plane, i.e., it has a fixed embedding in the plane. When a planar embedding is not given as part of the input, polynomial-time algorithms exist for some restricted cases, namely subcubic planar graphs and series-parallel graphs, see, e.g., [11, 13, 17, 28, 31].

Given the hardness result for OrthogonalPlanarity, a natural research direction is to investigate its parameterized complexity [19]. Despite the rich literature about orthogonal drawings, this direction has been surprisingly disregarded. The only exception is a result by Didimo and Liotta [16], who described an algorithm for biconnected planar graphs that runs in \(O(6^{r} n^4 \log n)\) time, where r is the number of degree-4 vertices. We recall that FPT algorithms have been proposed for other graph drawing problems, such as upward planarity [10, 15, 26], layered drawings [20], linear layouts [2, 21, 22], and 1-planarity [1].

Contribution. We describe an FPT algorithm for OrthogonalPlanarity whose parameters are the number of bends, the treewidth and the number of degree-2 vertices of the input graph. We recall that the notion of treewidth [29] is commonly used as a parameter in the parameterized complexity analysis (see also Sect. 2). The algorithm works for planar graphs of degree four with no restriction on the connectivity. Our main contribution is summarized as follows.

Theorem 1

Let G be an n-vertex planar graph with \(\sigma \) degree-2 vertices and let \(b \in \mathbb {N}\). Given a tree-decomposition of G of width k, there is an algorithm that decides OrthogonalPlanarity in \(f(k,\sigma , b) \cdot n\) time, where \(f(k,\sigma , b)=k^{O(k)}(\sigma +b)^{k}\log (\sigma +b)\). The algorithm computes a drawing of G, if one exists.

For an n-vertex graph G of treewidth k, a tree-decomposition of G of width k can be found in \(k^{O(k^3)} \, n\) time [7], while a tree-decomposition of width O(k) can be computed in \(2^{O(k)} \, n\) time [9]. The function \(f(k,\sigma ,b)\) depends exponentially on neither \(\sigma \) nor b. Since both \(\sigma \) and b are O(n) [3], OrthogonalPlanarity can be solved in time \(n^{g(k)}\) for some polynomial function g(k), and thus it belongs to the XP class when parameterized by treewidth [19]. Moreover, since the number of bends in a bend-minimum orthogonal drawing is O(n), the next result follows from Theorem 1, performing a binary search on b.

Corollary 1

Let G be an n-vertex planar graph. Given a tree-decomposition of G of width k, there is an algorithm that decides OrthogonalPlanarity in \(k^{O(k)}n^{k+1}\log n\) time. Also, a bend-minimum orthogonal drawing of G can be computed in \(k^{O(k)}n^{k+1}\log ^2 n\) time.

By Corollary 1 OrthogonalPlanarity can be decided in \(O(n^{3} \log n)\) time for graphs of treewidth two, and hence bend-minimum orthogonal drawings can be computed in \(O(n^{3} \log ^2 n)\) time. We remark that the best previous result for these graph, dating back to twenty years ago, is an \(O(n^4)\) algorithm by Di Battista et al. [13] which however is restricted to biconnected graphs (whereas ours is not).

Our FPT approach can be applied to related problems, namely to HV-Planarity and FlexDraw. HV-Planarity takes as input a planar graph G whose edges are each labeled H (horizontal) or V (vertical) and it asks whether G admits an orthogonal drawing with no bends and in which the direction of each edge is consistent with its label. As a corollary of our results, we can decide HV-Planarity in \(O(n^3\log n)\) time for series-parallel graphs, which improves a recent \(O(n^4)\) bound by Didimo et al. [18] and addresses one of the open problems in that paper. FlexDraw takes as input a planar graph G whose edges have integer weights and it asks whether G admits an orthogonal drawing where each edge has a number of bends that is at most its weight [5, 6].

Proof Strategy and Paper Organization. The first ingredient of our approach is a well-known combinatorial characterization of orthogonal drawings (see [12, 30]) that transforms OrthogonalPlanarity to the problem of testing the existence of a planar embedding along with a suitable angle assignment to each vertex-face and edge-face incidence (see Sect. 2). The second ingredient is the definition of a suitable data structure, called orthogonal sketch es, that encodes sufficient information about any such combinatorial representation, and in particular it makes it possible to decide whether the representation can be extended with further vertices incident to a given vertex cutset of the graph (see Sect. 3). The proposed algorithm (see Sect. 4) traverses a tree-decomposition of the input graph and stores a limited number of orthogonal sketch es for each node of the tree, rather than all its possible orthogonal drawings. This number depends on the width of the tree-decomposition, on the number of bends, and on the number of degree-2 vertices. The key observation is that a vertex of degree greater than two may correspond to a right turn when walking clockwise along the boundary of a face but not to a left turn, while a degree-2 vertex may correspond to both a left or a right turn. Thus, the number of degree-2 vertices, as well as the number of bends, have an impact in how much a face can “roll-up” in the drawing, which in our approach translates in possible weights that can be assigned to the edges of an orthogonal sketch. The extensions of our approach can be found in Sect. 5, while conclusions and open problems are in Sect. 6. For reasons of space, some proofs have been omitted and can be found in [14] (the corresponding statements are marked with an asterisk (*)).

2 Preliminaries

Embeddings. We assume familiarity with basic notions about graph drawings. A planar drawing of a planar graph G subdivides the plane into topologically connected regions, called faces. The infinite region is the outer face. A planar embedding of G is an equivalence class of planar drawings that define the same set of faces and with the same outer face. A planar embedding of a connected graph can be uniquely identified by specifying its rotation system, i.e., the clockwise circular order of the edges around each vertex, and the outer face. A plane graph G is a planar graph with a given planar embedding. The number of vertices encountered in a closed walk along the boundary of a face f of G is the degree of f, denoted as \(\delta (f)\). If G is not 2-connected, a vertex may be encountered more than once, thus contributing more than one unit to the degree of the face.

Orthogonal Representations. Let \(G=(V,E)\) be a planar graph with vertex degree at most four. A planar drawing \(\varGamma \) of G is orthogonal if each edge is a polygonal chain consisting of horizontal and vertical segments. A bend of an edge e in \(\varGamma \) is a point shared by two consecutive segments of e. An angle formed by two consecutive segments incident to the same vertex (resp. bend) is a vertex-angle (resp. bend-angle). An orthogonal representation of G can be derived from \(\varGamma \) and it specifies the values of all vertex- and bend-angles (see [12, 30]). More formally, let \(\mathcal E\) be a planar embedding of G, and let \(e=(u,v)\) be an edge that belongs to the boundary of a face f of \(\mathcal E\). The two possible orientations (u, v) and (v, u) of e are called darts. A dart is counterclockwise with respect to f, if f is on the left side when walking along the dart following its orientation. Let D(u) be the set of darts exiting from u and let D(f) be the set of counterclockwise darts with respect to f.

Definition 1

Let \(G=(V,E)\) be a planar graph with vertex degree at most four. An orthogonal representation H of G is a planar embedding \(\mathcal E\) of G and an assignment to each dart (u, v) of two values \(\alpha (u,v) = c_{\alpha } \cdot \frac{\pi }{2}\) and \(\beta (u,v) = c_{\beta } \cdot \frac{\pi }{2}\), where \(c_{\alpha } \in \{1,2,3,4\}\) and \(c_{\beta } \in \mathbb {N}\), that satisfies the following conditions.

  • C1. For each vertex u: \(\sum \limits _{(u,v) \in D(u)}\alpha (u,v)=2\pi \);

  • C2. For each internal face f: \(\sum \limits _{(u,v) \in D(f)}(\alpha (u,v)+\beta (v,u)-\beta (u,v))=\pi (\delta (f)-2)\);

  • C3. For the outer face \(f_{o}\): \(\sum \limits _{(u,v) \in D(f_{o})}(\alpha (u,v)+\beta (v,u)-\beta (u,v))=\pi (\delta (f_{o})+2)\).

Let f be the face counterclockwise with respect to dart (u, v). The value \(\alpha (u,v)\) represents the vertex-angle that dart (u, v) forms with the dart following it in the circular counterclockwise order around u; we say that \(\alpha (u,v)\) is a vertex-angle of u in f. The value \(\beta (u,v)\) represents the sum of the \(\frac{\pi }{2}\) bend-angles that dart (u, v) forms in f. Condition C1 guarantees that the sum of angles around each vertex is valid, while C2 (respectively, C3) guarantees that the sum of the angles at the vertices and at the bends of an internal face (respectively, outer face) is also valid. Given an orthogonal representation of an n-vertex graph G, a corresponding orthogonal drawing can be computed in O(n) time [30].

Tree-Decompositions. Let \((\mathcal {X},T)\) be a pair such that \(\mathcal {X}=\{X_1,X_2,\dots ,X_\ell \}\) is a collection of subsets of vertices of a graph G called bags, and T is a tree whose nodes are in a one-to-one mapping with the elements of \(\mathcal X\). With a slight abuse of notation, \(X_i\) will denote both a bag of \(\mathcal {X}\) and the node of T whose corresponding bag is \(X_i\). The pair \((\mathcal {X},T)\) is a tree-decomposition of G if : (i) For every edge (u, v) of G, there exists a bag \(X_i\) that contains both u and v, and (ii) For every vertex v of G, the set of nodes of T whose bags contain v induces a non-empty (connected) subtree of T. The width of a tree-decomposition \((\mathcal {X},T)\) of G is \(\max _{i=1}^\ell {|X_i| - 1}\), and the treewidth of G is the minimum width of any tree-decomposition of G. We use a particular tree-decomposition (which always exists [27]) that limits the number of possible transitions between bags.

Definition 2

[27]. A tree-decomposition \((\mathcal {X},T)\) of G is nice if T is a rooted tree and: (a) Every node of T has at most two children, (b) If a node \(X_i\) of T has two children whose bags are \(X_j\) and \(X_{j'}\), then \(X_i=X_j=X_{j'}\), (c) If a node \(X_i\) of T has only one child \(X_j\), then there exists a vertex \(v \in G\) such that either \(X_i = X_j \cup \{v\}\) or \(X_i \cup \{v\} = X_j\). In the former case of (c) we say that \(X_i\) introduces v, while in the latter case \(X_i\) forgets v.

3 Orthogonal Sketches

Recall that an orthogonal representation of a planar graph G corresponds to a planar embedding of G and to an assignment of vertex- and bend-angles in each face of G. A fundamental observation for our approach is that the conditions that make an assignment of such angles a valid orthogonal representation of G can be verified for each vertex and for each face independently. In what follows we define two equivalence relations on the set of orthogonal representations of G that yields a set of equivalence classes whose size is bounded by some function of the width of T, of the number of degree-2 vertices of G, and of the number of bends.

Fig. 1.
figure 1

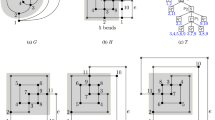
(a) An orthogonal drawing \(\varGamma \) of a graph \(G=(V,E)\) with 8 bends; the white vertices define a set \(X \subseteq V\). (b) The representing cycles of the active faces of H with respect to X, where H denotes the orthogonal representation of \(\varGamma \). (c) The connected sketched embedding \(C^*(H,G)\). (d) The orthogonal sketch \(\langle C(H,X), \phi ,\rho \rangle \).

Full size image

Sketched Embeddings. Let H be an orthogonal representation of a planar graph \(G=(V,E)\) and let \(X \subseteq V\); see for example Fig. 1a. The vertices in X are called active. A face f of H is active if it contains at least one active vertex. A representing cycle \(C_f\) of an active face f is an oriented cycle such that: (i) It contains all and only the active vertices of f in the order they appear in a closed walk along the boundary of f. (ii) \(C_f\) is counterclockwise with respect to f, that is, \(C_f\) is oriented coherently with the counterclockwise darts of face f. Notice that \(C_f\) may be non-simple because a cut-vertex may appear multiple times when walking along \(C_f\). Also, if H contains distinct components, the outer face of each component is considered independently. See Fig. 1b for an illustration.

Let H be an orthogonal representation of a planar graph G. We may conveniently focus on an orthogonal drawing \(\varGamma \) that falls in the equivalence class of drawings having H as an orthogonal representation. Assume first that H is connected. The sketched embedding of H with respect to X is the plane graph C(H, X) constructed as follows. For each active face f we draw in \(\varGamma \) its representing cycle \(C_f\) by identifying the vertices of \(C_f\) with the corresponding vertices of f and by drawing the edges of \(C_f\) inside f without creating crossings. Graph C(H, X) is the embedded graph formed by the edges that we drew inside the active faces. This is a plane graph by construction, it may be disconnected, and it may contain self-loops and multiple edges. Graph C(H, X) has a face \(f'\) for each representing cycle \(C_f\) of an active face f of H; we call \(f'\) an active face of C(H, X). If H is not connected, a sketched embedding \(C(H_i,X)\) is computed for each connected component \(H_i\) of H (\(i=1,\dots ,h\)) and the sketched embedding of H is \(C(H,X)= \bigcup _{i=1}^{h} C(H_i,X)\). See for example Fig. 1b.

Definition 3

Let \(G=(V,E)\) be a planar graph and let \(X \subseteq V\). Let \(H_1\) and \(H_2\) be two orthogonal representations of G. \(H_1\) and \(H_2\) are X-equivalent if they have the same sketched embedding.

Suppose that H is connected. We now aim at computing a connected supergraph of C(H, X). By construction, the active faces of C(H, X) may share vertices but not edges and hence C(H, X) also contains faces that are not active. For each non-active face g of C(H, X), we add a dummy vertex \(v_g\) in its interior and we connect it to all vertices on the boundary of g by adding dummy edges. This turns C(H, X) to a connected plane graph \(C^*(H,X)\), which we call a connected sketched embedding of H with respect to X. If H is not connected, a connected sketched embedding \(C^*(H_i,X)\) is computed for each \(C(H_i,X)\) independently, and the connected sketched embedding of H is \(C^*(H,X) = \bigcup _{i=1}^{h} C^*(H_i,X)\). Figure 1c shows a connected sketched embedding obtained from Fig. 1b. Observe that it may be possible to construct different connected sketched embedding s of the same sketched embedding. However, any connected sketched embedding encodes the information about the global structure of H that is sufficient for the purposes of our algorithm. \(C^*(H,X)\) (and hence C(H, X)) has a number of vertices that is O(|X|) and a number of edges that is also O(|X|) because \(C^*(H,X)\) is planar and the multiplicity of an edge in \(C^*(H,X)\) is at most four.

Lemma 1 (*)

Let \(G=(V,E)\) be a planar graph and let \(X \subseteq V\). Let \(\mathcal {H}\) be the set of all possible orthogonal representations of G. The X-equivalent relation partitions \(\mathcal {H}\) in at most \(w^{O(w)}\) equivalence classes, where \(w=|X|\).

Orthogonal Sketches. Let H be an orthogonal representation of a plane graph \(G=(V,E)\) and let \(X \subseteq V\). Let C(H, X) be a sketched embedding of H with respect to X. Recall that H is defined by two functions, \(\alpha \) and \(\beta \), that assign the vertex- and bend-angles made by darts inside their faces. The shape of C(H, X) consists of two functions \(\phi \) and \(\rho \) defined as follows. Let (u, v) be a dart of C(H, X), which corresponds to a path \(\varPi _{uv}\) in H. Let z be the vertex of \(\varPi _{uv}\) adjacent to u (possibly \(z=v\)). We set \(\phi (u,v) = \alpha (u,z)\); the value \(\phi (u,v)\) still represents the vertex-angle that u makes in the face on the left of (u, v). Function \(\rho \) assigns to each dart (u, v) of C(H, X) a number that describes the shape of \(\varPi _{uv}\) in H. More precisely, for each representing cycle \(C_f\) and for each dart (u, v) of \(C_f\), \(\rho (u,v,f)=n_\frac{\pi }{2}(u,v)-n_\frac{3\pi }{2}(u,v)-2n_{2\pi }(u,v)\), where \(n_a(u,v)\) (\(a \in \{\frac{\pi }{2},\frac{3\pi }{2},2\pi \}\)) is the number of vertex- and bend-angles between u and v whose value is a. For example, Fig. 1d shows a sketched embedding together with its shape. We call \(\rho (u,v,f)\) the roll-up numberFootnote 1 of (u, v) in f. If \(\phi (u,v)>\frac{\pi }{2}\) and f is the counterclockwise face with respect to dart (u, v), we say that u is attachable in f. Two X-equivalent sketched embedding s have the same shape, if they have the same values of \(\phi \) and \(\rho \). A sketched embedding C(H, X), together with its shape \(\langle \phi , \rho \rangle \), is called an orthogonal sketch and it is denoted by \(\langle C(H,X), \phi , \rho \rangle \).

Definition 4

Let \(G=(V,E)\) be a planar graph and let \(X \subseteq V\). Let \(H_1\) and \(H_2\) be two orthogonal representations of G. \(H_1\) and \(H_2\) are shape-equivalent if they are X-equivalent and their orthogonal sketch es have the same shape.

Lemma 2 (*)

Let \(\langle C(H,X), \phi , \rho \rangle \) be an orthogonal sketch. Let \(C_f\) be a representing cycle of C(H, X) and consider a closed walk along its boundary. Let \(\rho ^*\) be the sum of the roll-up numbers over all the traversed edges, and let \(n_a\) be the number of encountered vertex-angles with value \(a \in \{\frac{\pi }{2}, \frac{3\pi }{2}, 2\pi \}\). Then \(\rho ^*+n_\frac{\pi }{2}-n_\frac{3\pi }{2}-2n_{2\pi }=c\), with \(c=4\) (\(c=-4\)) if f is an inner (the outer) face.

Lemma 3 (*)

Let \(G=(V,E)\) be a planar graph with \(\sigma \) vertices of degree two. Let \(\mathcal {H}\) be the set of all possible orthogonal representations of G with at most b bends in total. The shape-equivalent relation partitions \(\mathcal {H}\) in at most \(w^{O(w)} \cdot (\sigma +b)^{w-1}\) equivalence classes, where \(w=|X|\).

Proof sketch

We shall prove that \(n_X \cdot n_S \le w^{O(w)} \cdot (\sigma +b)^{w-1}\), where \(n_X\) is the number of X-equivalent classes and \(n_S\) is the number of possible shapes for each X-equivalent class. By Lemma 1, \(n_X \le w^{O(w)}\); we can show that \(n_S \le w^{O(w)}(\sigma +b)^{w-1}\). For a fixed sketched embedding C(H, X), a shape is defined by assigning to each dart (u, v) of C(H, X) the two values \(\phi (u,v)\) and \(\rho (u,v,f)\). The number of choices for the values \(\phi (u,v)\) is at most \(4^{4w} \le w^{O(w)}\). As for the possible choices for \(\rho (u,v,f)\), we claim that \(-(\sigma +b) \le \rho (u,v,f) \le \sigma +b+4\) based on two observations. (1) The number of vertices and bends forming an angle of \(\frac{3\pi }{2}\) inside a face cannot be greater than \(b + \sigma \). (2) For each vertex forming an angle of \(2\pi \) inside a face there are two vertex-angles of \(\frac{\pi }{2}\) inside the same face. Finally, once the vertex-angles are fixed, the number of darts for which the roll-up number can be fixed independently is at most \(w-1\). Thus, we have \(w-1\) values to choose and \(2(\sigma +b)+5\) choices for each of them.    \(\square \)

4 The Parameterized Algorithm

Overview. We describe an algorithm, called OrthoPlanTester, that decides whether a planar graph G admits an orthogonal drawing with at most b bends in total, by using a dynamic programming approach on a nice tree-decomposition T of G. The algorithm traverses T bottom-up and decides whether the subgraph associated with each subtree admits an orthogonal drawing with at most b bends. For each bag X, it stores all possible orthogonal sketch es and, for each of them, the minimum number of bends of any orthogonal representation encoded by that orthogonal sketch. To generate this record, OrthoPlanTester executes one of three possible procedures based on the type of transition with respect to the children of X in T. If the execution of the procedure results in at least one orthogonal sketch, then the algorithm proceeds, otherwise it halts and returns a negative answer. If the root bag contains at least one orthogonal sketch, then the algorithm returns a positive answer. In the positive case, the information corresponding to the embedding of the graph and to the vertex- and bend-angles can be reconstructed through a top-down traversal of T so to obtain an orthogonal representation of G, and consequently an orthogonal drawing [30].

The Algorithm. Let G be an n-vertex planar graph with vertex degree at most four and with \(\sigma \) vertices of degree two, and let \((\mathcal {X},T)\) be a nice tree-decomposition of G of width k. Following a bottom-up traversal of T, let \(X_i\) be the next bag to be visited and let \(B_i\) the set of all orthogonal sketch es of \(X_i\). Let \(w=k+1\) and recall that \(|X_i| \le w\). Let \(T_i\) be the subtree of T rooted at \(X_i\). Let \(G_i\) be the subgraph of G induced by all the vertices that belong to the bags in \(T_i\). We distinguish the following four cases.

\(\varvec{X_i}\) is a Leaf. Without loss of generality, we can assume that \(X_i\) contains only one vertex v (as otherwise we can root in \(X_i\) a chain of bags that introduce the vertices of \(X_i\) one by one). Thus, \(G_i\) contains only v and it admits exactly one orthogonal representation with no bends. In particular, there is a unique sketched embedding consisting of a single representing cycle \(C_f\) having v and no edges on its boundary. Also, the functions \(\phi \) and \(\rho \) are undefined.

\(\varvec{X_i}\) Forgets a Vertex. Let v be the vertex forgotten by \(X_i\). Let \(X_j\) be the child of \(X_i\) in T. In this case \(G_i = G_j\) and we generate the orthogonal sketch es for \(B_i\) by suitably updating those in \(B_j\). For each orthogonal sketch \(\langle C(H,X_j), \phi , \rho \rangle \) in \(B_j\) and for each representing cycle \(C_f\) of \(C(H,X_j)\) containing v, we apply the following operation. If v is the only vertex of \(C_f\), we remove \(C_f\) from C(H, X). Otherwise there are at most eight edges of \(C_f\) incident to v, based on whether v appears one or more times in a closed walk along \(C_f\). We first remove all self-loops incident to v, if any. Let \((u_1,v)\), \((v,u_2)\) be any two edges of \(C_f\) incident to v that appear consecutively in a counterclockwise walk along \(C_f\). For any such pair of edges we apply the following procedure. We remove the edges \((u_1,v)\), \((v,u_2)\) from \(C_f\) and we add an edge \((u_1,u_2)\). We assign to the dart \((u_1,u_2)\) roll-up number equal to the sum of the roll-up numbers of darts \((u_1,v)\) and \((v,u_2)\) plus a constant c defined as follows. If \(\phi (v,u_2)=\pi \), then \(c=0\); if \(\phi (v,u_2)=\frac{\pi }{2}\), then \(c=1\); if \(\phi (v,u_2)=\frac{3\pi }{2}\), then \(c=-1\); if \(\phi (v,u_2)=2\pi \), then \(c=-2\). Once all consecutive pairs of edges incident to v have been processed, v is removed from \(C_f\). It is immediate to verify that Lemma 2 holds for \(C_f\) after applying this operation. See Fig. 2a and b for an illustration.

Fig. 2.
figure 2

A portion of a orthogonal sketch before and after removing the bigger vertices.

Full size image

The above operation does not change the number of bends associated with the resulting orthogonal sketch es, but it may create duplicated orthogonal sketch es for \(B_i\), which we delete. When deleting the duplicates, we shall pay attention on pairs of orthogonal sketch es that are the same but with a different number of bends. To see this, let (u, v) be a dart of an orthogonal sketch \(\langle C(H,X_j), \phi , \rho \rangle \), which corresponds to a path \(\varPi _{uv}\) in H, and let f be the face on the left of this path in H. An angle along \(\varPi _{uv}\) in f may be both a vertex-angle or a bend-angle. Hence, removing v from different orthogonal sketch es (with different numbers of bends) may result in a set of orthogonal sketch es that differ only in the number of bends. In this case, the algorithm stores the one with fewer bends, because in every step of the algorithm (see also the next two cases), the information about the total number of bends of an orthogonal sketch is only used to verify that it does not exceed the given parameter b.

\(\varvec{X_i}\) Introduces a Vertex. Let v be the vertex introduced in \(X_i\). Let \(X_j\) be the child of \(X_i\) in T. If v does not have neighbors in \(X_i\), then \(B_i\) is the union of \(B_j\) and the (unique) orthogonal sketch of the graph with the single vertex v (see the leaf case). Otherwise, let \(u_1,\dots ,u_h\) be the neighbors of v in \(X_i\), with \(h \le w\). We generate \(B_i\) from \(B_j\) by applying the following procedure. At a high level, we first update each sketched embedding that can be extracted from an orthogonal sketch in \(B_j\) by adding v, we then generate all shapes for the resulting sketched embedding s, and we finally discard those shapes that are not valid.

Let \(C(H,X_j)\) be a sketched embedding for which there is at least one orthogonal sketch in \(B_j\). Suppose first that \(u_1,\dots ,u_h\) all belong to the same component of \(C(H,X_j)\). By planarity, an orthogonal representation of \(G_j\), whose sketched embedding is \(C(H,X_j)\), can be extended with v only if it contains at least one face having all of v’s neighbors on its boundary. This corresponds to verifying first the existence of a representing cycle \(C_f\) in \(C(H,X_j)\) with all of v’s neighbors on its boundary. We thus identify the representing cycles in which vertex v can be inserted and connected to its neighbors. We consider each possible choice independently; for each choice we duplicate \(C(H,X_j)\) and insert v accordingly. For each of the resulting sketched embedding s, we generate all possible shapes. Namely, for each representing cycle, we generate all possible vertex-angle assignments for its vertices and all possible roll-up numbers for its edges that satisfy Lemma 2. Next, for every such assignment, denoted by \(\langle \overline{\phi },\overline{\rho } \rangle \), we verify its validity. Let \(S_j\) be the set of orthogonal sketch es \(\langle C(H,X_j), \phi , \rho \rangle \) of \(B_j\) such that the restriction of \(\langle \overline{\phi },\overline{\rho } \rangle \) to the edges of \(C(H,X_j)\) corresponds to \(\langle \phi , \rho \rangle \). If \(S_j\) is empty, \(\langle \overline{\phi },\overline{\rho } \rangle \) is discarded as it would not be possible to obtain it from \(B_j\). Furthermore, observe that \(\overline{\rho }(v,u_i)\) corresponds to the number of bends along the edge \((v,u_i)\). Thus, we should ensure that \(b^*+\sum _{i=1}^h \overline{\rho }(v,u_i) \le b\), where \(b^*\) is the number of bends of \(\langle C(H,X_j), \phi , \rho \rangle \). If this is not the case, again the shape is discarded. Finally, among the putative orthogonal sketch es generated, we store in \(B_i\) only those for which Lemma 2 holds for each of its representing cycles.

\(\varvec{X_i}\) Has Two Children. Let \(X_j\) and \(X_{j'}\) be the children of \(X_i\) in T. Recall that these three bags are all the same, although \(G_j\) and \(G_{j'}\) differ. The only orthogonal representations of \(G_i\) are those that can be obtained by merging at the common vertices of \(X_i\) an orthogonal representation of \(G_j\) with an orthogonal representation of \(G_{j'}\) in such a way that the resulting representation has a planar embedding, it has at most b bends in total, and it satisfies Definition 1. At a high level, this can be done by merging two connected sketched embedding s (one in \(B_j\) and one in \(B_{j'}\)) and then by verifying that there is a planar embedding for the merged graph such that Lemma 2 is verified for each representing cycle, and the overall number of bends is at most b. We split this procedure in two phases.

Let \(C(H,X_j)\) be a sketched embedding for which there is at least one orthogonal sketch in \(B_j\) and let \(C(H',X_{j'})\) be a sketched embedding for which there is at least one orthogonal sketch in \(B_{j'}\). We first compute a connected sketched embedding \(C^*(H,X_j)\) and a connected sketched embedding \(C^*(H',X_{j'})\). Let \(\overline{C}\) be the union of these two graphs disregarding the rotation system and the choice of the outer face. For each connected component of \(\overline{C}\), we generate all possible planar embeddings. (The embeddings of \(\overline{C}\) that are not planar are discarded because they correspond to non-planar embeddings of \(G_i\).) For each planar embedding of \(\overline{C}\), we verify that the planar embedding of \(\overline{C}\) restricted to the edges of \(C(H,X_{j})\) corresponds to the planar embedding of \(C(H,X_{j})\) and the same holds for the edges of \(C(H',X_{j'})\). This condition ensures that the embedding of \(\overline{C}\) can be obtained from those of \(C(H,X_j)\) and \(C(H',X_{j'})\). We then remove the dummy vertices and the dummy edges from \(\overline{C}\) and we analyze each face of the resulting plane graph to verify whether the orientation of its edges is consistent. Namely, a face of a sketched embedding contains only edges that are either all counterclockwise or clockwise with respect to it. If this condition is not satisfied, the candidate sketched embedding is discarded.

In the second phase, for each generated sketched embedding, we compute all of its possible shapes and test the validity of each of them. Let \(\overline{C}\) be a sketched embedding. For each representing cycle of \(\overline{C}\), we generate all possible vertex-angle assignments for its vertices and roll-up numbers for its edges, keeping only those that satisfy Lemma 2. For every such assignment \(\langle \overline{\phi },\overline{\rho } \rangle \), let \(S_j\) be the set of orthogonal sketch es \(\langle C(H,X_j), \phi , \rho \rangle \) of \(B_j\) such that the restriction of \(\langle \overline{\phi },\overline{\rho } \rangle \) to the edges of \(C(H,X_j)\) corresponds to \(\langle \phi , \rho \rangle \). Similarly, let \(S_{j'}\) be the set of orthogonal sketch es \(\langle C(H',X_{j'}), \phi ', \rho ' \rangle \) of \(B_{j'}\) such that the restriction of \(\langle \overline{\phi },\overline{\rho } \rangle \) to the edges of \(C(H',X_{j'})\) corresponds to \(\langle \phi ', \rho ' \rangle \). If any of \(S_j\) and \(S_{j'}\) is empty, \(\langle \overline{\phi },\overline{\rho } \rangle \) is discarded as it would not be possible to obtain it from \(B_j\) and \(B_{j'}\). Finally, let \(b^*_j\) and \(b^*_{j'}\) be the minimum number of bends among the orthogonal sketch es of \(S_j\) and \(S_{j'}\), respectively. The set \(E_i\) of edges shared by \(C(H,X_j)\) and \(C(H',X_{j'})\) contains edges (if any) that connect pairs of vertices of \(X_i\) and that belong to G. In particular, for each edge in \(E_i\), the absolute value of its roll-up number corresponds to the number of bends along it. Hence, we verify that \(b^*_j+b^*_{j'}-\sum _{(u,v) \in E_i} |\rho (u,v)| \le b\), otherwise we discard \(\langle \overline{\phi },\overline{\rho } \rangle \). We conclude:

Lemma 4

Graph G admits an orthogonal drawing with at most b bends if and only if algorithm OrthoPlanTester returns a positive answer.

Lemma 5 (*)

Algorithm OrthoPlanTester runs in \(k^{O(k)}(b+\sigma )^{k}\log (b+\sigma ) \cdot n\) time, where k is the treewidth of G, \(\sigma \) is the number of degree-two vertices of G, and b is the maximum number of bends.

Proof sketch

Let \(T'\) be a tree-decomposition of G of width k and with O(n) nodes. We compute, in \(O(k \cdot n)\) time, a nice tree-decomposition T of G of width k and O(n) nodes [8, 27]. In what follows, we prove that OrthoPlanTester spends \(k^{O(k)}(b+\sigma )^{k}\log (b+\sigma )\) time for each bag \(X_i\) of T. The claim trivially follows if \(X_i\) is a leaf of T. If \(X_i\) forgets a vertex v, OrthoPlanTester considers each orthogonal sketch of the child bag \(X_j\), which are \(k^{O(k)} \cdot (b+\sigma )^{k}\) by Lemma 3 (a bag of T has at most \(k+1\) vertices). For each orthogonal sketch, OrthoPlanTester removes v from each of its O(1) representing cycles. Clearly, this can be done in O(1) time. Also, OrthoPlanTester removes possible duplicates in \(B_i\). Note that, before removing the duplicates, the elements in \(B_i\) are at most as many as those in \(B_j\). To efficiently remove the duplicates in \(B_i\), we represent each orthogonal sketch as a concatenation of three arrays, encoding its sketched embedding (i.e., the rotation system and the outer face), its function \(\phi \), and its function \(\rho \). Thus we have a set of \(N=k^{O(k)}(b+\sigma )^{k}\) arrays each of size O(k). Sorting the elements of this set, and hence deleting all duplicates, takes \(O(k) \cdot N \log N\) time, which, with some manipulations, can be rewritten as \(k^{O(k)}(b+\sigma )^{k}\log (b+\sigma )\). If \(X_i\) introduces a vertex v, OrthoPlanTester considers each sketched embedding that can be extracted from \(B_j\). Each of them, is then extended with v in all possible ways, which are \(k^{O(k)}\) (observe that \(|X_j| \le k-1\)). Next OrthoPlanTester generates at most \(k^{O(k)}(\sigma +b)^{k}\) orthogonal sketch es. We remark that, as explained in the proof of Lemma 3, for each cycle of length \(w \le k+1\) it suffices to generate the roll-up numbers of \(w-1\) edges. Moreover, for the edges incident to v the roll-up number is restricted to the range \([-b,+b]\) and it is subject to the additional constraint that the total number of bends should not exceed b. For each generated shape, OrthoPlanTester checks whether the corresponding subsets of the values of \(\phi \) and \(\rho \) exist in the orthogonal sketch es of \(B_j\) having the fixed sketched embedding. This can be done by encoding the values of \(\phi \) and \(\rho \) as two concatenated arrays, each of size O(k), by sorting the set of arrays, and by searching among this set. Since the number of orthogonal sketch es is \(N=k^{O(k)}(\sigma +b)^{k}\), this can be done in \(O(k) \cdot N\log N=O(k) \cdot k^{O(k)}(\sigma +b)^{k} \, O(k)\log (k(\sigma +b))=k^{O(k)} (\sigma +b)^k \log (\sigma +b)\) for a fixed sketched embedding, and in \(k^{O(k)} (\sigma +b)^{k}\log (\sigma +b)\) time in total. Finally, it remains to check Lemma 2 for each representing cycle, which takes \(O(k^2)\) time for each of the \(k^{O(k)} \cdot (\sigma +b)^{k}\) orthogonal sketch es in \(B_i\).    \(\square \)

Lemmas 4 and 5 imply Theorem 1 and Corollary 1.

5 Applications

HV Planarity. Let G be a graph such that each edge is labeled H (horizontal) or V (vertical). HV-Planarity asks whether G has a planar drawing such that each edge is drawn as a horizontal or vertical segment according to its label, called a HV-drawing (see, e.g., [18, 24]). This problem is NP-complete [18]. The next theorem follows from our approach.

Theorem 2 (*)

Let G be an n-vertex planar graph with \(\sigma \) vertices of degree two. Given a tree-decomposition of G of width k, there is an algorithm that solves HV-Planarity in \(k^{O(k)}\sigma ^{k}\log \sigma \cdot n\) time.

The next corollary improves the \(O(n^4)\) bound in [18].

Corollary 2

Let G be an n-vertex series-parallel graph. There is a \(O(n^3 \log n)\)-time algorithm that solves HV-Planarity.

Flexible Drawings. Let \(G=(V,E)\) be a planar graph with vertex degree at most four, and let \(\psi : E \rightarrow \mathbb {N}\). The FlexDraw problem [5, 6] asks whether G admits an orthogonal drawing such that for each edge \(e \in E\) the number of bends of e is \(b(e) \le \psi (e)\). The problem becomes tractable when \(\psi (e) \ge 1\) [5] for all edges, while it can be parameterized by the number of edges e such that \(\psi (e)=0\) [6]. By subdividing \(\psi (e)\) times each edge e, we can conclude the following.

Theorem 3 (*)

Let \(G=(V,E)\) be an n-vertex planar graph, and let \(\psi : E \rightarrow \mathbb {N}\). Given a tree-decomposition of G of width k, there is an algorithm that solves FlexDraw in \(k^{O(k)}(n \cdot b^*)^{k+1}\log (n \cdot b^*)\) time, where \(b^* = \max _{e \in E}\psi (e)\).

6 Open Problems

The results in this paper suggest some interesting questions. First, we ask whether OrthogonalPlanarity is FPT when parameterized by the number of bends and by treewidth. Improving the time complexity of Corollary 1 is also an interesting problem on its own. Since HV-Planarity is NP-complete even for graphs with vertex degree at most three [18], another research direction is to devise new FPT approaches for HV-Planarity on subcubic planar graphs.