Neutrino Detectors Under Water and Ice

Abstract

Underwater/ice neutrino telescopes are multi-purpose detectors covering astrophysical, particle physics and environmental aspects. Among them, the detection of the feeble fluxes of astrophysical neutrinos which should accompany the production of high energy cosmic rays is the clear primary goal. Since these neutrinos can escape much denser celestial bodies than light, they can trace processes hidden to traditional astronomy. Different to gamma rays, neutrinos provide incontrovertible evidence for hadronic acceleration. On the other hand, their extremely low interaction cross section makes their detection extraordinarily difficult.

17.1 Introduction

Underwater/ice neutrino telescopes are multi-purpose detectors covering astrophysical, particle physics and environmental aspects [1,2,3]. Among them, the detection of the feeble fluxes of astrophysical neutrinos which should accompany the production of high energy cosmic rays is the clear primary goal [4, 5]. Since these neutrinos can escape much denser celestial bodies than light, they can trace processes hidden to traditional astronomy. Different to gamma rays, neutrinos provide incontrovertible evidence for hadronic acceleration. On the other hand, their extremely low interaction cross section makes their detection extraordinarily difficult.

Figure 17.1 shows a compilation of the spectra of dominant natural and artificial neutrino fluxes. Solar neutrinos, burst neutrinos from SN-1987A, reactor neutrinos, terrestrial neutrinos from radioactive decay processes in the Earth and neutrinos generated in cosmic ray interactions in the Earth atmosphere (“atmospheric neutrinos”) have been already detected. Two guaranteed—although not yet detected—fluxes are the diffuse flux of neutrinos from past supernovae (marked “background from old supernovae”) and the flux of neutrinos generated in collisions of ultra-energetic protons with the 3 K cosmic microwave background [6] (marked GZK after Greisen, Zatsepin and Kuzmin [7] who first considered such collisions). These neutrinos will hopefully be detected in the next decade. Neutrinos in the TeV-PeV range emerging from acceleration sites of cosmic rays (marked AGN after “Active Galactic Nuclei”) have been detected in 2013 with IceCube [8]. No practicable idea exists how to detect 1.9 K cosmological neutrinos.

Fig. 17.1

Spectra of natural and reactor neutrinos

The energy range below 5 GeV is the clear domain of underground detectors, notably water Cherenkov, liquid scintillator and radio-chemical detectors (see chapter C4 and [9]) which led to the discovery of solar and atmospheric neutrinos, of neutrino oscillations and of neutrinos from Supernova SN1987A. These detectors, presently with maximal geometrical cross sections of about 1000 m², have turned out to be too small to detect the feeble fluxes of astrophysical neutrinos from cosmic acceleration sites. The high energy frontier of TeV and PeV energies is being tackled by much larger, expandable detectors installed in open water or ice, a principle first proposed by M. Markov in 1959 [10]. They consist of arrays of photomultipliers recording the Cherenkov light from charged particles produced in neutrino interactions. Towards even higher energies, novel detectors aim at detecting the coherent Cherenkov radio signals (ice, salt) or acoustic signals (water, ice, salt) from neutrino-induced particle showers. Air shower detectors search for showers with a “neutrino signature”. The very highest energies are covered by balloon-borne detectors recording radio emission in terrestrial ice masses, by ground-based radio antennas sensitive to radio emission in the moon crust, or by satellite detectors searching for fluorescence light or radio signals from neutrino-induced air showers. This article focuses on optical detectors in water and ice. The methods for higher energies are sketched in Sect. 17.8. Table 17.1 gives an overview over past, present and future optical detectors in water and ice.

Table 17.1 Past, present (2018) and future neutrino telescope projects and their main parameters

Underwater/ice detectors—apart from searching for neutrinos from cosmic ray sources—also address a variety of particle physics questions (see for reviews [12, 13]). With their huge event statistics, large neutrino telescopes have opened a new perspective for oscillation physics with atmospheric neutrinos, and actually can compete with accelerator experiments [14]. Another example for a particle physics task is the search for muons produced by neutrinos from dark matter annihilation in the Sun or in the center of the Earth. These searches are sensitive to super-symmetric WIMPs (Weak Interacting Massive Particles) as dark matter candidates. Underwater/ice detectors can also search for relativistic magnetic monopoles, with a light emission 8300 times stronger than that of a bare muon and therefore providing a very clear signature. Other tasks include the search for super-heavy particles like GUT monopoles, super-symmetric Q-balls or nuclearites which would propagate with less than a thousandth of the speed of light and emit light by heating up the medium or by catalyzing proton decays.

The classical operation of neutrino telescopes underground, underwater and in deep ice is recording upward travelling muons generated in a charged current neutrino interaction. The upward signature guarantees the neutrino origin of the muon since no other particle can cross the Earth. A neutrino telescope should be arranged at > 1 km depth in order to suppress the background from misreconstructed downward moving muons which may mimic upward moving ones (Fig. 17.2).

Fig. 17.2

Sources of muons in deep underwater/ice detectors. Cosmic nuclei—protons(p), α-particles(He), etc.—interact in the Earth atmosphere (light-colored). Sufficiently energetic muons produced in these interactions (“atmospheric muons”) can reach the detector (white box) from above. Muons from the lower hemisphere must have been produced in neutrino interactions

The identification of extraterrestrial neutrino events faces three sources of backgrounds:

• down-going punch-through muons from cosmic-ray interactions in the atmosphere (“atmospheric muons”). This background can be reduced by going deeper.

• random backgrounds due to photomultiplier (PMT) dark counts,⁴⁰K decays (mainly in sea water) or bioluminescence (only water), which impact adversely on event recognition and reconstruction. This background can be mitigated by local coincidences of PMTs.

• neutrinos from cosmic-ray interactions in the atmosphere (“atmospheric neutrinos”). Extraterrestrial neutrinos can be separated from atmospheric neutrinos on a statistical basis (due to their harder energy spectrum). For down-going neutrinos interacting within the detector, atmospheric neutrinos can be largely rejected by vetoing accompanying atmospheric muons from the same shower as the atmospheric neutrino.

Atmospheric neutrinos, of course, have an own scientific value: at medium and high energies they are a well-understood “standard candle” to calibrate the detector, at low energies they allow for investigating neutrino oscillations.

17.2 Neutrino Interactions

The behaviour of the neutrino cross section can be approximated by a linear dependence for E _ν < 5 TeV, for energies larger than 5 TeV by an $E_{\nu }^{0.4}$ dependence [1]. The absolute value of the cross section at 1 TeV is about 10⁻³⁵ cm².

The final state lepton follows the initial neutrino direction with a mean mismatch angle θ decreasing with the square root of the neutrino energy [4]:

$$\displaystyle \begin{aligned} {<}\theta{>} \approx \frac{1.5^{\circ}}{{\sqrt{E_{\nu}[\mathrm{TeV}]}}} \end{aligned} $$

(17.1)

This on the one hand principally enables source tracing with charged current muon neutrinos, but on the other hand sets a kinematical limit to the ultimate angular resolution. It is worse than for high energy gamma astronomy and particularly worse than for conventional astronomy.

The probability $P_{\nu \rightarrow \mu }(E_{\nu },E_{\mu }^{min})$ to produce, in a charged current interaction of a muon neutrino with energy E _ν, a muon reaching the detector with a minimum detectable energy $E_{\mu }^{min}$ depends on the cross section $d \sigma _{\nu N}^{CC} (E_{\nu }, E_{\mu })/dE_{\mu }$ and the effective muon range R _eff, which is defined as the range after which the muon energy has decreased to $E_{\mu }^{min}$ [4]:

$$\displaystyle \begin{aligned} P_{\nu \rightarrow \mu} (E_{\nu},E_{\mu}^{min}) = N_A \int^{E_{\nu}}_{E_{\mu,min}} dE_{\mu} \frac{d\sigma_{\nu N}^{CC}(E_{\nu},E_{\mu})} {dE_{\mu}} \cdot R_{eff} (E_{\mu}^{min}, E_{\mu}) \end{aligned} $$

(17.2)

with N _A being the Avogadro constant. For water and $E_{\mu }^{min} \approx$ 1 GeV one can approximate [4]

$$\displaystyle \begin{aligned} \begin{array}{rcl} P_{\nu \rightarrow \mu} &\displaystyle = &\displaystyle 1.3 \cdot 10^{-6} \cdot E_{\nu}^{2.2} \ \mathrm{for}\ \mathrm{E}_{\nu} < 1\, \mathrm{TeV} \end{array} \end{aligned} $$

(17.3)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle = &\displaystyle 1.3 \cdot 10^{-6} \cdot E_{\nu}^{0.8} \ \mathrm{for}\ \mathrm{E}_{\nu} > 1\, \mathrm{TeV} \end{array} \end{aligned} $$

(17.4)

(with E _ν given in TeV). This means, that a telescope can detect a muon neutrino with 1 TeV energy with a probability of about 10⁻⁶, if the telescope is on the neutrino’s path.

The number of events from a flux Φ_ν recorded by a detector with area A within a time T under a zenith angle 𝜗 is then given by

(17.5)

Here Z(δ) is the matter column in the Earth crossed by the neutrino. For sub-TeV energies, absorption in the Earth is negligible and the exponential term ∼1 (see Fig. 17.5).

17.3 Principle of Underwater/Ice Neutrino Telescopes

Underwater/ice neutrino telescopes consist of a lattice of photomultipliers (PMs) housed in transparent pressure spheres which are spread over a large volume in oceans, lakes or glacial ice. The PMs record arrival time and amplitude, sometimes even the full waveform, of Cherenkov light emitted by muons or particle cascades.

In most designs the spheres are attached to strings which—in the case of water detectors—are moored at the ground and held vertically by buoys. The typical spacing along a string is 10–25 m, and between strings 60–200 m. The spacing is incomparably large compared to Super-Kamiokande (see chapter C4). This allows covering large volumes but makes the detector practically blind with respect to phenomena below 10 GeV. An exception are planned high-density detectors under water and ice which are tailored to oscillation physics and to the determination of the mass hierarchy of neutrinos [15, 16].

17.3.1 Cherenkov Light

Charged particles moving faster than the speed of light in a medium with index of refraction n, v ≥ c∕n, emit Cherenkov light. The index of refraction depends on the frequency ν of the emitted photons, n = n(ν). The total amount of released energy is given by

(17.6)

with α being the fine structure constant and β = v∕c. In the transparency window of water, i.e. for wavelength 400 nm ≤ λ ≤ 700 nm, the index of refraction for water is n ≈ 1.33, yielding about 400 eV/cm, or ≈200 Cherenkov photons per cm. The spectral distribution of Cherenkov photons is given by

(17.7)

The photons are emitted under an angle Θ_C given by

(17.8)

For water, Θ_C = 41.2^∘.

17.3.2 Light Propagation

The propagation of light in water is governed by absorption and scattering. In the first case the photon is lost, in the second case it changes its direction. Multiple scattering effectively delays the propagation of photons. The parameters generally chosen as a measure for these phenomena are [17, 18]:

• (a) The absorption length L _a(λ)—or the absorption coefficient a(λ) = 1∕L _a—with λ being the wavelength. It describes the exponential decrease of the number N of non-absorbed photons as a function of distance r, N = N ₀ ⋅exp(−r∕L _a).

• (b) The scattering length L _b(λ) and scattering coefficient b(λ), defined in analogy to L _a(λ) and a(λ).

• (c) The scattering function χ(θ, λ), i.e. the distribution in scattering angle θ.

• (d) Often instead of the “geometrical” scattering length L _b(λ), the effective scattering length L _eff is used: $L_{eff} = L{{ }_b}/(1-\langle \cos \theta \rangle )$ with $\langle \cos \theta \rangle$ being the mean cosine of the scattering angle. L _eff “normalizes” scattering lengths for different distributions χ(θ, λ) of the scattering angle to one with $\langle \cos \theta \rangle = 0$, i.e. L _eff is a kind of isotropization length. For $\langle \cos \theta \rangle \sim 0.8\text{-}0.95$, as for all media considered here, photon delay effects in media with the same L _eff are approximately the same.

Table 17.2 summarizes typical values for Lake Baikal [19, 20], oceans [21, 22] and Antarctic ice [23, 24], each are given for the wavelength of their maximum.

Table 17.2 Absorption length and effective scattering length for different sites

Scattering and absorption in water and ice are determined with artificial light sources. The scattering coefficient in water changes only weakly with wavelength. The dependence on depth over the vertical dimensions of a neutrino telescope in water is small, but parameters may change in time, due to transient water inflows loaded with bio-matter or dust, or due to seasonal changes in water parameters. They must therefore be permanently monitored. In glacial ice at the South Pole, the situation is different. The parameters are constant in time but strongly change with depth (see Sect. 17.6.3).

Strong absorption leads to reduced photon collection, strong scattering deteriorates the time information which is essential for the reconstruction of tracks and showers (see Sects. 17.6 and 17.7).

17.3.3 Detection of Muon Tracks and Cascades

Neutrinos can interact with target nucleons N through charged current, CC (ν _l + N → l + X, with l denoting the charged parter lepton of the neutrino) or neutral current, NC (ν _l + N → ν _l + X) processes. A CC reaction of a ν _μ produces a muon track and a hadronic particle cascade, whereas all NC reactions and CC reactions of ν _e produce particle cascades only. CC interactions of ν _τ can have either signature, depending on the τ decay mode.

In most astrophysical models, neutrinos are expected to be produced through the π∕K → μ → e decay chain, i.e. with a flavour ratio ν _e : ν _μ : ν _τ ≈ 1 : 2 : 0. For sources outside the solar system, neutrino oscillations turn this ratio to ν _e : ν _μ : ν _τ ≈ 1 : 1 : 1 upon arrival on Earth. That means that about 2/3 of the charged current interactions appear as cascades.

Figure 17.3 sketches the two basic detection modes of underwater/ice neutrino telescopes.

Fig. 17.3

Detection of muon tracks (left) and cascades (right) in underwater detectors

Fig. 17.4

Typical muon tracks and charged secondaries in water above the Cherenkov threshold, for different muon energies (a) 10 TeV (box), and zoomed: 10 TeV, 1 TeV and 100 GeV [26]

17.3.3.1 Muon Tracks

In the muon-track mode, high energy neutrinos are inferred from the Cherenkov cone accompanying muons which enter the detector from below or which strat inside the detector. The upward signature guarantees the neutrino origin of the muon since no other particle can cross the Earth. The effective volume considerably exceeds the actual detector volume due to the large range of muons (about 1 km at 300 GeV and 24 km at 1 PeV [4]).

The muon looses energy via ionization, pair production, bremsstrahlung and photonuclear reactions. The energy loss can be parameterized by [4, 25]

(17.9)

For water, the ionization loss is given by a = 2 MeV/cm, the energy loss from pair production, bremsstrahlung and photonuclear reactions is described by b = (1.7 + 1.3 + 0.4) ⋅ 10⁻⁶ cm⁻¹ = 3.4 ⋅ 10⁻⁶ cm⁻¹ and rises linearly with energy [25]. Figure 17.4 shows muons tracks with the corresponding secondaries from the last three processes [26]. A detailed description of the muon propagation through matter has to take into account the stochastic character of the individual energy loss processes, which leads to separated cascades of secondaries along the muon track.

Fig. 17.5

Transmission of the Earth for neutrinos of different energy, as a function of zenith angle [27]

Underwater/ice telescopes are optimized for the detection of muon tracks and for energies of a TeV or above, by the following reasons:

• (a) The flux of neutrinos from cosmic accelerators is expected to be harder than that of atmospheric neutrinos, yielding a better signal-to-background ratio at higher energies.

• (b) Neutrino cross section and muon range increase with energy. The larger the muon range, the larger the effective detector volume.

• (c) The mean angle between muon an neutrino decreases with energy like E ^−0.5, resulting in better source tracing and signal-to-background ratio at high energy.

• (d) For energies above a TeV, the increasing light emission allows estimating the muon energy with an accuracy of σ(logE _μ) ∼ 0.3. By unfolding procedures, a muon energy spectrum can be translated into a neutrino energy spectrum.

Muons which have been generated in the Earth’s atmosphere above the detector and punch through the water or ice down to the detector outnumber neutrino-induced upward moving muons by several orders of magnitude (about 10⁶ at 1 km depth and 10⁴ at 4 km depth) and have to be removed by careful up/down assignment.

At energies above a few hundred TeV, where the Earth is going to become opaque even to neutrinos, neutrino-generated muons arrive preferentially from directions close to the horizon, at EeV energies essentially only from the upper hemisphere (Fig. 17.5). The high energy deposition of muons from PeV-EeV extraterrestrial neutrinos provides a handle to distinguish them—on a statistical basis—from downward going atmospheric muons (those with a spectrum decreasing rather steeply with energy). A different case are down-going muon tracks or cascades starting within the detector. They must be due to neutrino interactions. If the neutrino has been generated in the atmosphere, it will be accompanied in most cases by muons from the same air shower, the higher the energy, the more frequently. Therefore one can apply a veto against accompanying down-going muons and thereby remove most atmospheric neutrinos. This method has been first applied in [8].

17.3.3.2 Cascades

Neutral current interactions and charged current interactions of electron and (most) tau neutrinos do not lead to high energy muons but to electromagnetic or hadronic cascades. Their length increases only like the logarithm of the cascade energy (Fig. 17.6). Cascade events are therefore typically “contained” events.

Fig. 17.6

Typical electromagnetic cascades in fresh water for 10 GeV, 100 GeV and 1 TeV [26]

With 5–20 m length in water, and a diameter of the order of 10–20 cm, cascades may be considered as quasi point-like compared to the spacing of the strings along which the PMs are arranged (again with the exception of high-density arrays tailored to oscillation physics). The effective volume for the clear identification of isolated cascades from neutrino interactions is close to the geometrical volume of the detector. For first-generation neutrino telescopes it is therefore much smaller than that for muon detection. However, for kilometer-scale detectors and not too large energies it can reach the same order of magnitude as the latter. The total amount of light is proportional to the energy of the cascade. Since the cascades are “contained”, they do not only provide a dE∕dx measurement (like muons) but an E-measurement. Therefore, in charged current ν _e and ν _τ interactions, the neutrino energy can be determined with an accuracy of 10–30% (depending on energy and PM spacing). While this is much better than for muons, the directional accuracy is worse since the lever arm for fitting the direction is negligibly small. The background from atmospheric electron neutrinos is much smaller than in the case of extraterrestrial muon neutrinos and atmospheric muon neutrinos. All this taken together, makes the cascade channel particularly interesting for searches for diffuse high-energy excesses of extraterrestrial neutrinos over atmospheric neutrinos.

17.4 Effective Area and Sensitivity

The detection efficiency of a neutrino telescope is quantified by its effective area, e.g., the fictitious area for which the full incoming neutrino flux would be recorded. Fig. 17.7 shows the effective area of the IceCube detector for the detection mode of through-going muons. The increase with E _ν is due to the rise of neutrino cross section and muon range, while neutrino absorption in the Earth causes the decrease at large zenith angle θ. Identification of downward-going neutrinos requires strong cuts against atmospheric muons, hence the cut-off towards low E _ν.

Fig. 17.7

Effective area of the IceCube detector for neutrinos, A _eff(ν), assuming the detection mode of through-going muons. The zenith angle θ is counted 0^∘/180^∘ for vertically downward/upward moving muons. The effective area is strongly increasing with energy due to increasing neutrino cross section and muon range. The decrease at high energy and large zenith angles is due to the opacity of the Earth to neutrinos with energies above ≈100 TeV. Identification of downward-going neutrinos requires strong cuts against atmospheric muons, hence the cut-off towards low E _ν for θ < 30^∘

Due to the small cross section, the effective area is many orders of magnitude smaller than the geometrical dimension of the detector; a muon neutrino with 1 TeV, e.g., can be detected with a probability of the order 10⁻⁶ if the telescope is on its path. Note that the detection efficiency for cascades or muons starting within the detector are much smaller since these detection modes do not profit from the potentially large range of muons coming from outside.

Even cubic kilometer neutrino telescopes reach only effective areas between a few square meters and a few hundred square meters, depending on energy. This has to be compared to several ten thousand square meters typical for air Cherenkov telescopes which detect gamma ray-initiated air showers. A ratio 1:1000 (10 m²:10 000 m²) may appear desperately small. However, one has to take into account that Cherenkov gamma telescopes can only observe one source at a time, and that their observations are restricted to moon-less, cloud-less nights. Neutrino telescopes observe a full hemisphere, 24 h per day. Therefore, cubic kilometer detectors reach a flux sensitivity similar to that which first-generation Cherenkov gamma telescopes like Whipple and HEGRA [28, 29] had reached for TeV gamma rays, namely Φ(> 1 TeV) ≈10⁻¹² cm⁻² s⁻¹.

17.5 Reconstruction

In this section, some relevant aspects of event reconstruction are demonstrated for the case of muons tracks [30, 31]. For cascades, see [32, 33]. The reconstruction procedure for a muon track consists of several consecutive steps:

• 1. Rejection of noise hits

• 2. Simple pre-fit procedures providing a first-guess estimate for the following iterative maximum-likelihood reconstructions

• 3. Maximum-likelihood reconstruction

• 4. Quality cuts in order to reduce background contaminations and to enrich the sample with signal events. This step is strongly dependent of the actual analysis—diffuse fluxes at high energies, searches for steady point sources, searches for transient sources etc.

An infinitely long muon track can be described by an arbitrary point $\vec {r}_0$ on the track which is passed by the muon at time t ₀, with a direction $\vec {p}$ and energy E ₀. Photons propagating under the Cherenkov angle θ _c and on a straight path (“direct photons”) are expected to arrive at PM i located at $\vec {r}_i$ at a time

$$\displaystyle \begin{aligned} t_{geo} = t_0 + \frac{\vec{p}\cdot (\vec{r}_i - \vec{r}_0) + d \cdot \tan\theta_c}{c}, \end{aligned} $$

(17.10)

where d is the closest distance between PM i and the track, and c the vacuum speed of light. The time residual t _res is given by the difference between the measured hit time t _hit and the hit time expected for a direct photon t _geo:

$$\displaystyle \begin{aligned} t_{res} = t_{hit} - t_{geo}. \end{aligned} $$

(17.11)

Schematic distributions for time residuals are given in Fig. 17.8. An unavoidable symmetric contribution in the range of a nanosecond comes from the PM/electronics time jitter, σ _t. An admixture of noise hits to the true hits from a muon track adds a flat pedestal contribution like shown in top right of Fig. 17.8. Electromagnetic cascades along the track lead to a tail towards larger (and only larger) time residuals (bottom left). Scattering of photons which propagate in water loaded with bio-matter and dust or in ice can lead to an even stronger delay of the arrival time (bottom right). These residuals must be properly implemented in the probability density function for the arrival times.

Fig. 17.8

Schematic distributions of arrival times for different cases (see text)

The simplest likelihood function is based exclusively on the measured arrival times. It is the product of all N _hit probability density functions p _i to observe, for a given value of track parameters {a}, photons at times t _i at the location of the hit PMs:

$$\displaystyle \begin{aligned} L_{time} = \prod^{Nhit}_{i=1} p(t_{res,i}| \{a\}) \end{aligned} $$

(17.12)

More complicated likelihoods include the probability of hit PMs to be hit and of non-hit PMs to be not hit, or the amplitudes of hit PMs. Instead for referring only to the arrival time of the first photon for a given track hypothesis, and the amplitude for a given energy hypothesis, one may also refer to the full waveform from multiple photons hitting the PM. For efficient background suppression, the likelihood may also incorporate information about the zenith angular dependence of background and signal (Bayesian probability). The reconstruction procedure finds the best track hypothesis by maximizing the likelihood.

17.6 First Generation Neutrino Telescopes

The development of the field was pioneered by the project DUMAND (Deep Underwater Muon And Neutrino Detection Array) close to Hawaii [34]. First activities started in 1975. With the final goal of a cubic kilometre array, the envisaged first step was a configuration with 216 optical modules at 9 strings, 30 km offshore the Big Island of Hawaii, at a depth of 4.8 km. A test string with 7 optical modules (OMs) was deployed in 1987 from a ship, took data at different depths for several hours and measured the depth dependence of the muon flux [35]. A shore cable for a stationary array was laid in 1993 and a first string with 24 OMs deployed. It failed due to water leakages. Financial and technical difficulties led to the official termination of the project in 1996. Therefore the eventual breakthrough and proof of principle came from the other pioneering experiment located in Lake Baikal. See for the history of neutrino telescopes [36].

17.6.1 The Baikal Neutrino Telescope NT200

The Baikal Neutrino Telescope NT200 was installed in the Southern part of Lake Baikal [37]. The distance to shore is 3.6 km, the depth of the lake at this location is 1366 m, the depth of the detector about 1.1 km.

The BAIKAL collaboration was not only the first to deploy three strings (as necessary for full spatial reconstruction), but also reported the first atmospheric neutrinos detected underwater [38, 39] (see also Fig. 17.9, right).

Fig. 17.9

Left: The Baikal Neutrino Telescope NT200. Right: One of the first upward moving muons from a neutrino interaction recorded with the 4-string stage of the Lake Baikal detector in 1996 [40]. The muon fires 19 channels

NT200 was an array of 192 optical modules (OMs), completed in April 1998. It is sketched in Fig. 17.9, left. The OMs were attached to eight strings carried by an umbrella-like frame consisting of 7 arms each 21.5 m in length. The strings were anchored by weights at the bottom and held in a vertical position by buoys at various depths. The geometrical dimensions of the configuration were 72 m (height) and 43 m (diameter). Detectors in Lake Baikal are deployed (or hauled up for repairs) within 6–7 weeks in February/April, when the lake is covered with a thick ice layer providing an ideal, stable working platform. They are connected to shore by several cables which allow operation over the full year.

The time calibration of NT200 was done with several nitrogen lasers, one sending short light pulses via optical fibres of equal length to each individual OM pair (top of Fig. 17.9), the other, the light pulses of the other laser below the array (not shown in the figure) propagate to the OMs through the water.

The OMs consisted of a pressure glass housing equipped with a QUASAR-370 phototube and were grouped pair-wise along a string. In order to suppress accidental hits from dark noise (∼30 kHz) and bio-luminescence (typically 50 kHz but seasonally raising up to hundreds of kHz), the two PMs of a pair were switched in coincidence, defining a channel, with only ∼0.25 kHz noise rate. The basic cell of NT200 consisted of a svjaska (Russian for “bundle”), comprising two OM pairs and an electronics module which was responsible for time and amplitude conversion and slow control functions (Fig. 17.9, left). A majority trigger was formed if ≥m channels were fired within a time window of 500 ns (this is about twice the time a relativistic particle needed to cross the NT200 array), with m typically set to 4. Trigger and inter-string synchronization electronics were housed in an array electronics module at the top of the umbrella frame. This is less than 100 m away from the OMs, allowing for easy nanosecond synchronization over copper cable.

Figure 17.10 shows the phototube and the full OM [41]. The QUASAR-370 consisted of an electro-optical preamplifier followed by a conventional PM (type UGON). In this hybrid scheme, photoelectrons from a large hemispherical cathode (K₂CsSb) with >2π viewing angle are accelerated by 25 kV to a fast, high gain scintillator which is placed near the centre of the glass bulb. The light from the scintillator is read out by the small conventional PM. One photoelectron emerging from the hemispherical photocathode yields typically 20 photoelectrons in the conventional PM. This high multiplication factor results in an excellent single electron resolution of 70%, a small time jitter (2 ns) and a small sensitivity to the Earth’s magnetic field. The OM contains the QUASAR, the HV supply for the small PM (2 kV) and the large tube (25 kV) and a LED. The signal from the last dynode and the anode is read out via two penetrators, the two other penetrators pass the signal driving the calibration LED and the low voltages for the HV system and the preamplifiers. The optical contact between QUASAR bulb and glass housing is made by liquid glycerine sealed with a layer of polyurethane, in later versions with a silicon gel.

Fig. 17.10

Left: The QUASAR phototube. Right: a full Baikal optical module [41]

Due to the small lever arm, the angular resolution of NT200 for muon tracks was only 3–4^∘. On the other hand, the small spacing of modules led to a comparably low energy threshold for muon detection of ∼15 GeV. The total number of upward muon events collected over 5 years was only about 400, due not only to the small dimensions of the array, but also to its unstable operation. Still, NT200 could compete for some time with the much larger AMANDA, by searching for high energy cascades below NT200, surveying a volume about ten times as large as NT200 itself [42].

17.6.2 AMANDA

Rather than water, AMANDA (Antarctic Muon And Neutrino Detection Array) was using the 3 km thick ice layer at the South Pole as target and detection medium [43, 44]. AMANDA was (actually still is, although switched off) located some hundred meters away from the Amundsen–Scott station which provides the necessary infrastructure. Holes of 60 cm diameter were drilled with pressurized hot water, and strings with OMs were deployed in the column of molten water and frozen into the ice. South Pole installation operations are performed in the Antarctic summer, November to February, when temperatures rise to up to − 25^∘C. For the rest of the time, two operators (of a winter-over crew of 30–40 persons in total) maintain the detector, connected to the outside world via satellite communication.

Figure 17.11, left, shows the configuration of AMANDA. A first shallow test array with 80 OMs at 4 strings (not shown in the figure) was deployed in the Antarctic season 1993/1994, at depths between 800 and 1000 m [45]. It turned out that the effective scattering length L _eff was desperately small, 40 cm at 830 m depth, but increased with depth (80 cm at 970 m depth). The scattering was due to remnant bubbles and made track reconstruction impossible. The tendency of scattering decreasing with depth, as well as results from ice core analyses at other places in Antarctica, suggested that bubbles should disappear below 1300 m. This expectation was confirmed with a second 4-string array which was deployed in 1995/1996. The effect of bubbles disappeared, with the remaining scattering being mostly due to dust (see Fig. 17.11, right). The scattering length averaged over 1500–2000 m depth is L _eff ≈ 20 m, still considerably worse than for water but sufficient for track reconstruction [30, 46]. The array was upgraded stepwise, completed in January 2000 and eventually comprised 19 strings with a total of 677 OM, most of them at depth between 1500 and 2000 m.

Fig. 17.11

Left: The AMANDA configuration. Three of the 19 strings have been sparsely equipped towards larger and smaller depth in order to explore ice properties, one string got stuck during deployment at too shallow depth and was not used in analyses. Right: scattering coefficient (top) and absorption coefficient (bottom) as a function of depth and wavelength

Figure 17.11, right, gives absorption and scattering coefficient as a function of depth and wavelength for glacial ice at the South Pole. The variations with depth are due to (a) bubble remnants at shallow depth leading to very strong scattering, (b) dust and other scattering and absorbing material transported in varying climate epochs to Antarctica. The depth dependence complicates the evaluation of the experimental data. Furthermore, the strong scattering leads to strong delays in photon propagation, resulting in worse angular resolution of deep ice detectors compared to water. On the other hand, the large absorption length, with a cut-off below 300 nm instead at 350–400 nm (water), results in better photon collection than in water. The quality of the ice improves substantially below a major dust layer at 2000–2100 m, with a value for the scattering length about twice as large as for the shallower region above 2000 m.

The short distance between OM and surface electronics allowed for a unique technical solution: the analogue PM anode signals were not digitized in the depth, but driven over 2 km cable to surface. This requires a large output signal of the PM, a specification met by the 8-inch R5912-2 from Hamamatsu with 14 dynodes and an internal amplification of 10⁹. The first ten strings used coaxial (string 1–4) and twisted pair (string 6–10) cables for both HV supply and signal transmission, for the last 9 strings the anode signal was fed to an LED, and the light signal transmitted via optical fibre to surface. Naturally, the electrical signal transmission suffered from strong dispersion, widening the anode signal to several 100 ns. However, applying an amplitude correction to time flags from a constant fraction discriminator, a time jitter of 5–7 ns was achieved. Given the strong smearing of photon arrival times due to light scattering in ice, this jitter appeared to be acceptable. For optical signals, dispersion was negligible. An event was defined by a majority trigger formed in the surface counting house, requesting ≥8 hits within a sliding window of 2 μs.

Time calibration of the AMANDA array was performed with a YAG laser at surface (wavelengths > 450 nm), sending short pulses via optical fibres of well defined length to each OM. This laser system was also used to measure the delay of optical pulses propagating between strings and to determine the ice properties as well as the inter-string distances. A nitrogen laser (337 nm) at 1850 m depth, halogen lamps (350 and 380 nm) and LED beacons (450 nm) extended the information about ice properties across a large range of wavelengths (see Fig. 17.11, right). The measured time delays were fitted and the resulting parameterizations implemented in the probability density functions for the residual times t _res.

One big advantage compared to underwater detectors is the small PM noise rate, about 1 kHz in an 8-inch PM, compared to 20–40 kHz due to K ⁴⁰ decays and bio-luminescence in lakes and oceans. The contribution of noise hits to the true hits from a particle interaction is therefore small and makes hit cleaning procedures much easier than in water.

The angular resolution of AMANDA for muon tracks was 2–2.5^∘, with an energy threshold of ≈50 GeV. Although better than for Lake Baikal (3–4^∘), it was much worse than for ANTARES (<0.5^∘, see below). This is the result of the strong light scattering which deteriorates the original information contained in the Cherenkov cone. The effect is even worse for cascades, where the angular resolution achieved with algorithms of that time was only ≈25 deg  (compared to 5–8^∘ in ANTARES).

In 2008, AMANDA had established a series of record upper limits, e.g. for diffuse extraterrestrial neutrino fluxes using muon as well as cascade searches, for the flux of relativistic magnetic monopoles or for neutrinos from point sources (see for a review [47]). The final AMANDA point source analysis was based on 6595 neutrinos collected in the years 2000–2006 [48]. AMANDA was switched off in 2009.

17.6.3 Mediterranean Projects: ANTARES

Mediterranean efforts to build an underwater neutrino telescope are related to three locations:

• (a) a site close to Pylos at the Peloponnesus, with available depths ranging from 3.5 to 5 km for distances to shore of 30–50 km,

• (b) a site close to Capo Passero, Sicily, at a depth of 3.5 km and 70 km, distance to shore,

• (c) a site close to Toulon, at a depth of 2.5 km and 40 km distance to shore.

All of these sites are considered locations for a future distributed infrastructure of a total volume of few cubic kilometres. All sites have physics and infrastructural pros and cons. For instance, large depth is a challenge for long-term ocean technology and bears corresponding risks, but has convincing physics advantages: less background from punch-through muons from above, less bio-luminescence, less sedimentation.

Historically, the first Mediterranean project was NESTOR [49] off the Greek coast. It was conceived as a tower-like structure with 12 floors, 300 m in height and 32 m in diameter. A prototype hexagonal floor with 14 PMs (15-inch Hamamatsu) was deployed in 2004 and took data for a few weeks. The project is terminated meanwhile. NEMO, close to Sicily [50], focused on technology development and feasibility studies for a cubic kilometer array. The basic unit of NEMO have been towers composed by a sequence of floors. The floors consist of rigid horizontal structures, 15 m long, each equipped with four 10-inch PMs. The floors are tilted against each other and form a three-dimensional structure.

In the following, ANTARES [51, 52] is described, being the one of the three projects which made it to a full telescope of AMANDA-size.

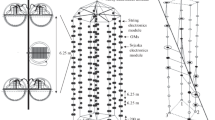
Figure 17.12 shows a schematic view of the detector. It consists of 12 strings, each anchored at the seabed and kept vertical by a top buoy. The minimum distance between the strings is 60 m. Each string is composed of 25 storeys. A storey is equipped with three 10-inch PMs Hamamatsu R7091-20 housed in 13-inch glass spheres. The PMs are oriented at 45^∘ with respect to the vertical. A mu-metal grid reduces the influence of the Earth magnetic field. The storeys are spaced by 14.5 m, the lowest being located about 100 m above seabed. The storeys are connected by an electro-optical cable, including 21 optical fibres for digital communications [53, 54].

Fig. 17.12

Right: Schematic view of the ANTARES detector, with 12 detector lines L1–L12, and an extra-line with environmental equipment (IL07). L12 and ILO7 carry test equipment for basic tests toward acoustic neutrino detection. Left: A storey with three optical modules and the metallic cylinder housing the Local Control Module (LCM). Every fifth storey carries a LED beacon (above the LCM) and a hydrophone (bottom left) for acoustic triangulation[52]

From a functional point of view, each string is divided into five sectors, each containing five storeys. A storey is controlled by a Local Control Module (LCM) which maintains the data communication between its sector and the shore. A String Controller Module (SCM), located at the basis of each string, interfaces the string to the rest of the detector. The string cables are led to a junction box to which the shore cable is connected.

The signals from the PMTs are digitized by an Analogue Ring Sampler (ARS). The ARS produces “hits” by time-stamping the PMT signal and by integrating the PMT anode current over a programmable time interval (25–80 ns). The time stamp is provided by the local clock of the LCM. The master clock signal of 20 MHz is generated at shore and distributed through optical fibres to the LCM clocks. Sub-nanosecond precision is achieved by a time-to-voltage converter which allows interpolation between two subsequent clock pulses. The output voltage is digitized with an 8-bit ADC. The maximally achievable time resolution is therefore 1/(20 MHz × 256) ∼ 0.2 ns.

The timing calibration is performed with calibration pulses between shore clock and LMC clocks, and with LED beacons which fire both the ARS (electrically) and the PMT (optically) and correct for the varying PMT transit time. The position calibration is particularly import since the string positions change due to water current. It is performed with compasses and tiltmeters along the strings, and with a acoustic triangulation system based on transmitters at the bottom of the strings and hydrophones along the strings. The relative positions of the OMs can be determined with an accuracy of a few centimetres.

The Monte Carlo angular resolution for muons is 0.2^∘ at 10 TeV. At low energies the neutrino tracing is limited by the angle between muon and neutrino, 0.7^∘ at 1 TeV and 1.8^∘ at 100 GeV (median mismatch angle for those muons triggering the detector [55]).

Naturally, the angular resolution for cascades is worse than for muons. Simple reconstruction algorithms give 10^∘ median mismatch angle above 5 TeV, however, with proper quality cuts, values below 4^∘ can be achieved, with 20–40% passing rates for signals [33].

ANTARES is operated in its full configuration since 2008 and is planned to continue data taking until the follow-up project KM3NeT has surpassed ANTARES w.r.t. to its sensitivity, i.e. at least through 2018.

17.7 Second Generation Neutrino Telescopes

17.7.1 IceCube

IceCube [56] is the successor of AMANDA. It consists of 5160 digital optical modules (DOMs) installed on 86 strings at depths between 1450 and 2450 m in the Antarctic ice [57], and 320 DOMs installed in IceTop [58], detectors in pairs on the ice surface directly above the strings (see Fig. 17.13). AMANDA was integrated into IceCube as a low-energy sub-detector, but later was replaced by DeepCore, a high density, six-string sub-array at large depths (i.e. in best ice) at the centre of IceCube. The energy threshold is about 100 GeV for the full IceCube array and about 10 GeV for DeepCore.

Fig. 17.13

Schematic view of the IceCube Neutrino Observatory. Since 2009, AMANDA is replaced by DeepCore, a nested low-threshold array. At the surface are the air shower detector IceTop and the IceCube counting house

The thermal power of hot-water drill factory is increased to 5 MW, compared to 2 MW for AMANDA, reducing the average time to drill a 60 cm hole to 2450 m depth down to ≈35 h. The subsequent installation of a string with 60 DOMs requires typically 12 h. A record number of 20 strings was deployed in the season 2009/2010. The detector was completed in December 2010.

The components are not accessible after refreezing of the holes. Therefore—as for AMANDA—the architecture has to avoid single-point failures in the ice. A string carries 60 DOMs, with 30 twisted copper pair cables providing power and communication. Two sensors are operated on the same wire pair. Neighbouring DOMs are connected to enable fast local coincidence triggering in the ice [57].

A schematic view of a DOM is shown in Fig. 17.14. A 10-inch PMT Hamamatsu R7081-02 is embedded in a 13-inch glass pressure sphere [59]. A mu-metal grid reduces the influence of the Earth’s magnetic field. The programmable high voltage is generated inside the DOM. The average PMT gain is set to 10⁷. Signals are digitized by a fast analogue transient waveform recorder (ATWD, 3.3 ns sampling) and by a FADC (25 ns sampling). The PM signal is amplified by 3 different gains to extend the dynamic range of the ATWD to 16 bits, resulting in a linear dynamic range of 400 photoelectrons in 15 ns; the dynamic range integrated over 2 μs is about 5000 photoelectrons.

Fig. 17.14

Schematic view of an IceCube digital optical module

The digital electronic on the main board are based on a field-programmable gate array (FPGA). It communicate with the surface electronics, new programs can be downloaded. The LEDs on the flasher board emit calibration pulses at 405 nm which can be adjusted over a wide range up to ∼10¹¹ photons.

All digitized PM pulses are sent to the surface. The full waveform, however, is only sent for pulses from local (neighbour or next to neighbour) coincidences in order to apply data compression for isolated hits which are mostly noise pulses. All DOMs have precise quartz oscillators providing local clock signals, which are synchronized every few seconds to a central GPS clock. The time resolution is about 2 ns. The noise rate for DOMs in the deep ice is ∼540 Hz, if a deadtime of 250 μs is applied only ∼280 Hz. The very low noise rates are critical for the detection of the low-energy neutrino emission associated with a supernova collapse (see below).

At the surface, 8 custom PCI cards per string provide power, communication and time calibration. Subsequent processors sort and buffer hits until the array trigger and event builder process is completed [61]. The architecture allows deadtime free operation. The design raw data rate of the full array is of the order of 100 GB/day which are written to tapes. Online processing in a computer farm allows extraction of interesting event classes, like all upgoing muon candidates, high-energy events, IceTop/IceCube coincidences, cascade events, events from the direction of the muon or events in coincidence with Gamma Ray Bursts (GRB). The filtered data stream (∼20 GB/day) is then transmitted via satellite to the Northern hemisphere.

The muon angular resolution is about 1^∘ for 1 TeV tracks and below <0.5^∘ for energies of 10 TeV and higher. The very good ice below 2100 m has a particular potential for improved resolution. This will be even more important for the angular reconstruction of cascades. The presently achieved angular resolution for cascades is only 25^∘, much worse than for water, with the inferiority being mainly due to light scattering in ice.

IceCube is the only detector which can be permanently operated together with a surface air shower array, IceTop [58]. It consists of tanks filled with ice, each instrumented with 2 DOMs. The comparison of air shower directions measured with IceTop and directions of muons from these showers in IceCube allows an angular calibration of IceCube (absolute pointing and angular resolution). IceTop can measure the spectrum air showers up to primary particle energies of ∼10¹⁸ eV. Combination of IceTop information (reflecting dominantly the electron component of the air shower) and IceCube information (muons from the hadronic component) allows estimating the mass range of the primary particle.

Last but not least, IceCube allows for another mode of operation which is essentially only possible in ice: the detection of burst neutrinos from a supernova [60]. The low dark counting rate of PMs (∼280 Hz, see above) allows detecting of the feeble increase of the summed count rates of all PMs during several seconds, which would be produced by millions of MeV neutrino interactions from a supernova burst. IceCube records the counting rate of all PMs in millisecond steps. A supernova in the centre of the Galaxy would be detected with extremely high confidence and the onset of the pulse could be measured in unprecedented detail. Even a 1987A-type supernova in the Large Magellanic Cloud would result in a 5σ effect and be sufficient to provide a trigger to the SuperNova Early Warning System, SNEWS [62].

The following figures show displays of some events recorded with IceCube. Figure 17.15, left, is a typical muon track crossing the detector from below. The event on the right side is a cascade event, actually the fully contained cascade event with the highest energy recorded, about 2 PeV. The analysis employed containment conditions and an atmospheric muon veto for suppression of down-going atmospheric neutrinos (“High-Energy Starting Event” analysis, HESE). The HESE events cannot be explained by atmospheric neutrinos and misidentified atmospheric muons alone: with 6 years of data, the excess has a significance of > 7σ, i.e. a flux of extraterrestrial neutrinos could be safely confirmed.

Fig. 17.15

Left: A through-going upward muon track. Right: The highest-energy cascade event detected (status 2018) with IceCube, with ≈2 PeV energy released in the detector [68]. The size of the symbols reflect the recorded amount of light, the color indicates the signal timing (red: early; green: late), see the scale at the bottom

Also, events with through-going muons show a corresponding excess of cosmic origin [69]—see the display of the highest-energy track-like neutrino event in Fig. 17.16.

Fig. 17.16

Left: Event view of the PeV track-like event recorded by IceCube on June 11, 2014. Color code like in the previous figure. Note that the scaling is non-linear and a doubling in sphere size corresponds to one hundred times the measured charge. This event deposited an energy of 2.6 ± 0.3 PeV in the detector volume. Right: Probability distribution of primary neutrino energies that could result in the observed multi-PeV track-like event, assuming an $E_{\nu }^{-2}$ spectrum. The total probabilities for the different flavors are 87.7, 10.9 and 1.4% for ν _μ, ν _e and ν _τ, respectively. The most probable energy of the primary neutrino is between 8 and 9 PeV

In its final configuration, IceCube takes data since spring 2011, with a duty cycle of more than 99%. It collects almost 10⁵ clean neutrino events per year, with nearly 99.9% of them being of atmospheric origin. The failure rate of DOMs is only about one per year, out of more than 5000.

17.7.2 KM3NeT

KM3NeT has two main, independent objectives: (a) the discovery and subsequent observation of high-energy cosmic neutrino sources and (b) precise oscillation measurements and the determination of the mass hierarchy of neutrinos [63, 64]. For these purposes the KM3NeT Collaboration plans to build an infrastructure distributed over three sites: off-shore Toulon (France), Capo Passero (Sicily, Italy) and Pylos (Peloponnese, Greece). In a configuration to be realized until 2021/2022, KM3NeT will consist of three so-called building blocks (“KM3NeT Phase-2”).

A building block comprises 115 strings, each string with 18 optical modules.Two building blocks will be sparsely configured to fully explore the IceCube signal with a comparable instrumented volume, different methodology, improved resolution and complementary field of view, including the Galactic plane. These two blocks will be deployed at the Capo Passero site and are referred to as ARCA: Astroparticle Research with Cosmics in the Abyss. The third building block will be densely configured to precisely measure atmospheric neutrino oscillations. This block, being deployed at the Toulon site, is referred to as ORCA: Oscillation Research with Cosmics in the Abyss (see Fig. 17.17).

Fig. 17.17

The two incarnations of KM3NeT. The two ARCA blocks (top) have diameters of 1 km and a height of about 600 m and focus to high-energy neutrino astronomy. ORCA (bottom) is a shrinked version of ARCA with only 200 m diameter and 100 m height. Both ARCA and ORCA have 115 strings with 18 optical modules (OMs) per string

A novel concept has been chosen for the KM3NeT optical module: The 43 cm glass spheres of the DOMs will be equipped with 31 PMs of 7.5 cm diameter, with the following advantages: (a) The overall photocathode area exceeds that of a 25 cm PM by more than a factor three; (b) The individual readout of the PMs results in a very good separation between one- and two-photoelectron signals which is essential for online data filtering; (c) some directional information is provided. This technical design has been validated with in situ prototypes. A view and a cross-sectional drawing of the DOM are shown at the top of Fig. 17.18.

Fig. 17.18

View and a cross-sectional drawing of a KM3NeT-DOM with its 31 small PMs inside [64]

Rather than digitizing the full waveform (like for the one large PM per DOM in IceCube), for each of the analogue pulses from 31 small PMs which pass a preset threshold, the time of the leading edge and the time over threshold are digitized (referred to as a hit). Each hit corresponds to 6 Bytes of data (1 B for PM address, 4 B for time and 1 B for time over threshold, with the least significant bit of the time information corresponding to 1 ns). All hits are sent to shore (all-data-to-shore concept). The total rate for a single building block with its 64,170 PMTs amounts to about 25 Gb/s which are sent via optical fibers to shore. To limit the number of fibres, wavelength multiplexing is used.

At shore, the physics events are filtered from the background. To maintain all available information for the offline analysis, each event contains a snapshot of all the data during that event. The filtered data (with a rate reduced by a factor of about 10⁵ with respect to the data arriving at shore), are stored at disks.

KM3NeT-ARCA is conceived as the European counterpart to IceCube and will preferentially observe the Southern instead of the Northern hemisphere, including the Galactic Centre [63]. With a fully equipped ARCA, IceCube’s cosmic neutrino flux could be detected with high-significance within 1 year of operation. In practise the detector will be deployed in stages allowing to reach the 1 year sensitivity of two clusters much before the second cluster is fully installed.

ORCA will continue along the venue opened by IceCube-DeepCore and perform precision measurements of neutrino oscillations. In particular, it could determine the neutrino mass hierarchy with at least 3σ significance after 3 years of operation.

17.7.3 GVD

Based on the long-term experience with the NT200 detector and on extended prototype tests, the Baikal Collaboration has started the stepwise installation of a kilometer-scale array in Lake Baikal, the Giant Volume Detector, GVD [65, 66].

The optical modules of Baikal-GVD are equipped with 10-inch PMs of the type Hamamatsu R7081-100, with a quantum efficiency of ≈35%. The OMs are mounted on vertical strings, fixed to the bottom with anchors. Each eight strings form a cluster, with 36 OMs per string, i.e. 288 OMs per cluster. Each cluster is a full functional detector which is capable of detecting a physical event both in standalone mode and as part of the full-scale array. The first phase of GVD (GVD-1) is planned to be be completed by 2021, with eight clusters carrying ≈2.3 × 10³ OMs in total and a volume of 0.3–0.4 km³. Figure 17.19 shows a schematic view of GVD-1. In a second phase, Baikal-GVD is conceived to be extended to an array of about 10⁴ OMs with an instrumented volume of 1–2 km³.

Fig. 17.19

Schematic view of phase-1 of Baikal-GVD, consisting of 8 clusters, each with 120 m diameter and 520 m height. A cluster consists of eight strings with 36 optical modules along each string

The OMs are vertically spaced by 15 m, with the lowest OM at a depth of 1275 m (about 100 m above the bottom of the lake) and the top OM at 750 m below the lake surface. The seven strings of a cluster are arranged at a radius of 60 m around a central string. The distances between the centers of the clusters are 300 m.

A string is composed of three sections, each comprising 12 OMs with analog outputs. A Central section Module (CM) converts the analog signals into a digital code, using a 12-bit ADC with a sampling frequency of 200 MHz. Coincidences of signals from any pairs of neighbouring OMs are used as a local trigger of the section (signal request), with average frequencies of the section request signals in the range of 2–10 Hz, dependent on signal thresholds and level of water luminescence. The request signals from three sections are combined in the Control Module of the string (CoM) and transferred to the cluster Cluster DAQ center where a global trigger is formed. The Cluster DAQ center is arranged close to the water surface at a depth of 25 m and connected to the Shore DAQ Center by hybrid electro-optical cable.

Calibration is performed by LEDs and lasers. LEDs installed in each OM provide amplitude and time calibration of the OMs, separate underwater modules equipped with LEDs are used for time calibration between sections. A high-power laser is used arranged between clusters ensures calibration of the cluster as a whole and calibration between neighboured clusters. The coordinates of the optical modules are determined using an acoustic positioning. Each cluster has its own acoustic positioning system, with four acoustic modems per string, the lowest at the bottom of the string, the highest 538 m higher. The transit time between acoustic sources at the lake bed and the acoustic modems gives the coordinates of the acoustic modems with an accuracy of ≈2 cm.

17.7.4 IceCube-Gen2

The progress from IceCube will be limited by the modest numbers of cosmic neutrinos measured, even in a cubic kilometer array. In [67] a vision for the next-generation IceCube neutrino observatory is presented. At its heart is an expanded array of optical modules with a volume of 7–10 km³. This high-energy array will mainly address the 100 TeV to 100 PeV scale. For point sources, it will have five times better sensitivity than IceCube, and the rate for events at energies above a few hundred TeV will be ten times higher than for IceCube. It has the potential to deliver first GZK neutrinos, of anti-electron neutrinos produced via the Glashow resonance, and of PeV tau neutrinos, where both particle showers associated with the production and decay of the tau are observed (“double bang events”).

Another possible component of IceCube-Gen2 is the PINGU sub-array. It targets—similar to ORCA—precision measurements of the atmospheric oscillation parameters and the determination of the neutrino mass hierarchy. The facility’s reach would further be enhanced by exploiting the air-shower measurement and vetoing capabilities of an extended surface array. Moreover, a radio array (“ARA”, for Askarian Radio Array, see below) will achieve improved sensitivity to neutrinos in the 10¹⁶-10²⁰ eV energy range, including GZK neutrinos.

17.8 Physics Results: A 2018 Snapshot

The 2018 status of the field is dominantly defined by the IceCube results. ANTARES significantly contributes to searches for neutrinos from the Southern hemisphere and the central parts of the Galaxy. These are the main results obtained over the last 5 years:

• Both IceCube and ANTARES have measured the flux of “conventional” atmospheric neutrinos from π and K decay up to a few hundred TeV and found it in agreement with predictions [70, 71]. Tight upper limits have been set for the flux of “prompt” atmospheric neutrinos from charm and bottom decays.

• At energies below 50 GeV, the oscillation of atmospheric neutrinos passing through the Earth has been observed both by IceCube and ANTARES. The IceCube constraints on the neutrino mixing parameters are meanwhile as tight as those derived from accelerator experiments [72].

• In 2013, IceCube has detected a diffuse flux of astrophysical neutrinos with a very high confidence (meanwhile larger than 7σ). This observation can be considered a real breakthrough, 53 years after the first ideas on underwater neutrino detectors have been proposed [73].

• ANTARES and IceCube have jointly analysed their data to identify a neutrino excess from the Galactic Plane and can exclude that more than 8.5% of the observed diffuse astrophysical flux comes from the Galactic plane [74].

• No steady neutrino point sources could be identified, neither using 8 years of IceCube data, with 497,000 upward muons from neutrino interactions, nor with ANTARES data. The derived limits on point source fluxes are a fantastic factor 3000 below those obtained in 2000 with AMANDA data [75].

• Also, various analyses where many sources belonging to a certain source class are “stacked” did not yield significant excesses. For instance, latest IceCube results exclude that more 6% of the observed diffuse astrophysical muon neutrino flux could come from blazars (active galaxies with their jet pointing to the Earth) [76]. Blazars have been considered since long as top-candidate neutrino sources. The same applies to neutrinos from Gamma Ray Bursts (GRB). IceCube could exclude at more than 90% confidence those models which assume that GRBs are the dominant source of the measured cosmic-ray flux at highest energies [77].

• An alert issued by IceCube on September 22, 2017, led to the first coincident observation of a high-energy energy neutrino with X-ray, gamma-ray and optical information. These electromagnetic follow-up observations identified a blazar named TXS 0506+ 056 in its active state as the likely source of the neutrino. IceCube examined its archival data in the direction of TXS 0606+ 056 and found an additional 3.5σ evidence for a flare of 13 neutrinos starting at the end of 2014 and lasting about 4 months. This is considered the first compelling evidence for flaring source of neutrinos [78, 79].

• No neutrinos from cosmic-ray interactions with the 3K-microwave background radiation could yet be identified. Their observation will need multi-km³ detectors like IceCube-Gen2 or even radio detectors as discussed in the next Sect. [80].

• Record limits have been derived for neutrino fluxes from dark matter annihilations in the Earth, the Sun or the Galactic halo and for the flux of magnetic monopoles (which, if at relativistic velocity, could be identified via their high light emission) and to the coupling of hypothetical sterile neutrinos to normal neutrino states (see [81] for a review of results on particle physics with IceCube).

17.9 Technologies for Extremely High Energies

The technologies described in this section are tailored to signals which propagate with km-scale attenuation. Consequently, they allow for the observation of much larger volumes than those typical for optical neutrino telescopes. 100 km³ scale detectors are necessary, for instance, to record more than just a few GZK neutrinos, with a typical energy range of 100 PeV to 10 EeV.

17.9.1 Detection via Air Showers

At energies above 10¹⁷ eV, large extensive air shower arrays like the Pierre Auger detector in Argentina [82] or the Telescope Array in Utah/USA [83] are seeking for horizontal air showers due to neutrino interactions deep in the atmosphere (showers induced by charged cosmic rays start on top of the atmosphere). Figure 17.20 explains the principle. AUGER consists of an array of water tanks spanning an area of 3000 km² and recording the Cherenkov light of air-shower particles crossing the tanks. It is combined with telescopes looking for the atmospheric fluorescence light from air showers (see chapter on cosmic ray detectors). The optimum sensitivity window for this method is at 1–100 EeV, the effective detector mass is up to 20 Giga-tons. An even better sensitivity might be obtained for tau neutrinos, ν _τ, scratching the Earth and interacting close to the array [84, 85]. The charged τ lepton produced in the interaction can escape the rock around the array, in contrast to electrons, and in contrast to muons it decays after a short path into hadrons. If this decay happens above the array or in the field of view of the fluorescence telescopes, the decay cascade can be recorded. Provided the experimental pattern allows clear identification, the acceptance for this kind of signals can be large. For the optimal energy scale of EeV, the present differential single-flavor limit (2017) is about $2 \times 10^{-8} E_{\nu }^{-2}$ GeV⁻¹ cm⁻² s⁻¹ sr⁻¹ [86].

Fig. 17.20

Detection of particles or fluorescence light emitted by horizontal or upward directed air showers from neutrino interactions

A variation of this idea is to search for tau lepton cascades which are produced by horizontal PeV neutrinos hitting a mountain and then decay in a valley between target mountain and an “observer” mountain [87].

17.9.2 Radio Detection

Electromagnetic cascades generated by high energy neutrino interactions in ice or salt emit coherent Cherenkov radiation at radio frequencies. The effect was predicted in 1962 [88] and confirmed by measurements at accelerators [89, 90]. Electrons are swept into the developing shower, which acquires an electric net charge from the added shell electrons. This charge propagates like a relativistic pancake of 1 cm thickness and 10 cm diameter. Each particle emits Cherenkov radiation, with the total signal being the convolution of the overlapping Cherenkov cones. For wavelengths larger than the cascade diameter, coherence is observed and the signal rises proportional to $E_{\nu }^2$, making the method attractive for high energy cascades. The bipolar radio pulse has a width of 1–2 ns. In ice, attenuation lengths of up to a kilometer are observed, depending on the frequency band and the ice temperature. Thus, for energies above a few ten PeV, radio detection becomes competitive or superior to optical detection (with its attenuation length of ∼100 m) [91].

A prototype Cherenkov radio detector called RICE was operated at the South Pole, with 20 receivers and emitters buried at depths between 120 and 300 m. From the non-observation of very large pulses, limits on the diffuse flux of neutrinos with E> 100 PeV and on the flux of relativistic magnetic monopoles have been derived [92].

Three groups are working towards detectors with 100–300 km³ active volume: The Askarian Radio Array (ARA [93]) at the South Pole, the Antarctic Ross Iceshelf Antenna Neutrino Array (ARIANNA [94]) on the Antarctic Ross ice shelf—both in the phase of tests with engineering arrays—and the Greenland Neutrino Observatory (GNO [96]) which is conceived to be deployed near the USA Summit Station in Greenland.

The current ARA proposal [93] envisages and array of 37 stations, each consisting of 16 antennas, buried up to 200 m depth below the firn ice. The stations are spaced by 2 km. As of 2018, five of them are deployed. ARIANNA [94] will observe the 570 m thick ice covering the Ross Sea. The smooth ice-seawater interface reflects radio waves; therefore ARIANNA might have a better sensitivity for downward moving and horizontal neutrinos. However, the ice is warmer than at the South Pole, reducing the attenuation length for GHz radio waves from 800–900 m (South Pole) to about 400 m (ice shelf). ARIANNA antennas face downward and are arranged just below the ice surface, with about thousand antennas for the ultimate array, spread over an area of ≈1000 km². One can reasonably expect that only one of these two projects can be funded in its full size.

ANITA (Antarctic Impulsive Transient Array [95] is an array of radio antennas which has been flown at a balloon on an Antarctic circumpolar path in 2006 and 2008/2009 (see Fig. 17.21).

Fig. 17.21

Principle of the ANITA balloon experiment

From 35 km altitude it searches for radio pulses from neutrino interactions in the thick ice cover and monitored, with a threshold in the EeV range and a volume of the order of 10⁶ Gigatons. This corresponds to a much larger volume than that of ARA and ARIANNA and can be achieved only for the price of an energy threshold about two orders of magnitude above that of ARA and ARIANNA. With its dual-polarization horn antennas it scanned the ice out to 650 km away. Neutrino signals would be vertically polarized, while background signals from down-going cosmic-ray induced air showers are preferentially horizontally polarized. Signals pointing to known or suspected areas of human activity are rejected. The ANITA 90% C.L. integral flux limit on a pure E ⁻² spectrum, integrating over 10¹⁸-10^23.5 eV, is E ² × 1.3 ⋅ 10⁻⁷ GeV cm⁻² s⁻¹ sr⁻¹, presently (2018) the most stringent limit on the GZK neutrino flux.

Even higher energies are are addressed when searching for radio emission from particle cascades induced by neutrinos or cosmic rays skimming the moon surface. An example is the GLUE project (Goldstone Ultra-high Energy Neutrino Experiment [97]) which used two NASA antennas and reached maximum sensitivity at several ZeV (1 ZeV =  1000 EeV). With the same method, the NUMOON experiment at the Westerbork Radio Telescope searched for extremely energetic neutrinos [98], and the LUNASKA experiment which uses the Parkes and ATCA radio telescopes [99]. LUNASKA stands for “Lunar Ultra-high Neutrino Astrophysics with the SKA”, indicating the final purpose: to use the Square Kilometer Array SKA to perfrom a lunar neutrino search.

17.9.3 Acoustic Detection

Production of pressure waves by fast particles passing through liquids was predicted in 1957 [100] and experimentally proven with high intensity proton beams two decades later [101]. A high energy cascade deposits energy into the medium via ionization losses which is immediately converted into heat. The effect is a fast expansion, generating a bipolar acoustic pulse with a width of a few 10 μs in water or ice (Fig. 17.22). Transversely to the pencil-like cascade, the radiation propagates within a disk of about 10 m thickness (the length of the cascade) into the medium. The signal power peaks at 20 kHz where the attenuation length of sea water is a few kilometres, compared to 50 m for light. The threshold of this method is however very high, in the several-EeV range. Acoustic detection was also considered an option for ice, where the signal itself is higher and ambient noise is lower than in water. A test array, SPATS (South Pole Acoustic Test Setup), has been deployed at the South Pole in order to determine attenuation length and ambient noise [102]. Another test configuration has been deployed together with the ANTARES detector (see Fig. 17.22). Tests are also performed close to Sicily, close to Scotland and in Lake Baikal. Another project has been using a very large hydrophone array of the US Navy, close to the Bahamas [109]. The existing array of hydrophones spans an area of 250 km and has good sensitivity at 1–500 kHz and can trigger on events above 100 EeV with a tolerable false rate.

Fig. 17.22

Acoustic emission of a particle cascade

17.9.4 Hybrid Arrays

Best signal identification would be obtained by combining signatures from two of the three methods, optical, radio and acoustic [110]. Naturally, radio detection does not work in water. The threshold for acoustic detection is so high that coincidences from a 100 km³ acoustic array and a 1 km³ optical array would be rare and a true hybrid approach not promising. The hybrid principle may be applicable at the South Pole, since the overlap between optical and radio methods (threshold for radio ∼10–100 PeV) is significant. A nested hybrid array with optical-radio coincidences is therefore be conceivable and is actually part of the IceCube-Gen2 proposal (see previous section).

Overviews on acoustic and radio detection can be found in the proceedings of the workshops on “Acoustic and Radio EeV Neutrino Detection Activities” (ARENA) [103,104,105,106,107,108].