Abstract
The phase retrieval problem has a long and rich history with applications in physics and engineering such as crystallography, astronomy, and laser optics. Usually, the phase retrieval consists in recovering a real-valued or complex-valued signal from the intensity measurements of its Fourier transform. If the complete phase information in frequency domain is lost then the problem of signal reconstruction is severelly ill-posed and possesses many non-trivial ambiguities. Therefore, it can only be solved using appropriate additional signal information. We restrict ourselves to one-dimensional discrete-time phase retrieval from Fourier intensities and particularly consider signals with finite support. In the first part of this section, we study the structure of the arising ambiguities of the phase retrieval problem and show how they can be characterized using the given Fourier intensity. Employing these observations, in the second part, we study different kinds of a priori assumptions on the signal, where we are especially interested in their ability to reduce the non-trivial ambiguities or even to ensure uniqueness of the solution. In particular, we consider the assumption of non-negativity of the solution signal, additional magnitudes or phases of some signal components in time domain, or additional intensities of interference measurements in frequency domain. Finally, we transfer our results to phase retrieval problems where the intensity measurements arise, for example, from the Fresnel or fractional Fourier transform.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- discrete one-dimensional phase retrieval for complex signals
- autocorrelation polynomial
- ambiguities of discrete phase retrieval
- non-negative signals
- compact support
- interference measurements
2010 Mathematics Subject Classification:
1 Introduction
In the classical phase retrieval problem, one is usually faced with the recovery of a complex-valued signal from intensity measurements of its Fourier transform. Recovery problems of this kind have many interesting applications in physics and engineering like crystallography [1,2,3], astronomy [4, 5], and laser optics [6, 7]. We particularly refer to Chap. 2. Without further information about the unknown signal, the phase retrieval problem is highly ambiguous such that the recovery of the true solution within the solution set is nearly hopeless.
In this chapter, we consider the one-dimensional discrete-time variant of the phase retrieval problem, where we restrict ourselves to the recovery of complex-valued signals with finite support length. The solution set of this problem can be characterized by investigating and factorizing the related autocorrelation function, which coincides with the squared given Fourier intensity, see [4, 8, 9]. As a consequence of this characterization, we show how ambiguities of the discrete-time phase retrieval problem are related to the true solution signal. Trivial ambiguities are caused by multiplication with a unimodular constant, time-shifts, and reflection and conjugation. Non-trivial ambiguities are essentially obtained by conjugation of linear factors of the algebraic polynomial being defined by the signal values [8]. The number of these non-trivial ambiguities essentially depends on the structure of the given intensities [10].
Depending on the application, one can incorporate different a priori conditions or further information about the unknown signal in order to get rid of the unwanted ambiguities. One approach to reduce the solution set is to assume that the unknown signal is real-valued and non-negative. The non-negativity condition is usually employed if the original signal represents an intensity or a probability density, see for instance [3, 4, 11]. The a priori non-negativity is, moreover, exploited by a variety of numerical methods like the alternating projection algorithm [5, 11,12,13] or adapted multilevel Gauß–Newton methods [6]. In the one-dimensional case considered here, the non-negativity constraint is, however, very erratic [14]. In special cases, the restricted phase retrieval problem can become uniquely solvable. However, in many situations, the non-negativity assumption may either not reduce the solution set at all or may lead to an empty solution set.
Sometimes, like in wave front sensing and laser optics [7], one has additionally access to the magnitudes of the unknown signal itself. The obtained restricted one-dimensional phase retrieval problem with a priori magnitude information in time domain can be efficiently solved by multilevel Gauß–Newton methods [6, 15, 16]. While these numerical methods work well in certain cases, their stability strongly depends on the given Fourier intensities [17]. Moreover, the algorithms can converge to approximate solutions which essentially differ from the true solution signal. On the basis of these numerical observations, we study the question whether the knowledge of magnitudes of the signal components can guarantee uniqueness. Our findings imply that the related phase retrieval problems are uniquely solvable for almost all finite-length signals [8, 18]. But there also exist instances of non-unique phase retrieval problems with given magnitudes of the signal components [10]. Our results on uniqueness of solutions can be transferred to phase retrieval problems with additional phase information in time domain [18].
A further approach to reduce the solution set or to ensure uniqueness is to exploit additional measurements in frequency domain, which arise from the interference of the unknown true signal with an appropriate reference signal. If the reference signal is known beforehand, the solution set of the discrete phase retrieval problem is reduced to at most two different signals [8, 19, 20]. Under mild assumptions, one can also use an unknown reference signal to guarantee uniqueness [8, 21,22,23]. Besides employing known or unknown reference signals that are not related to the unknown true signal, it is also possible to use a modulation of the unknown signal itself as a reference [24, 25].
One possible generalization of the classical phase retrieval problem is to replace the discrete-time Fourier transform by some other signal transform. If we restrict the one-dimensional discrete phase retrieval problem to signals with fixed support \(\{0,\dots , M-1\}\), which can be represented as M-dimensional vectors, then the Fourier intensities \(|\widehat{x}(\omega _k)|\) at different points \(\omega _k \in [-\pi , \pi ]\) can be written as magnitudes \(|\left\langle x,v_k\right\rangle |\) with \(v_k := (\mathrm {e}^{\mathrm{i}\omega _k m})^{M-1}_{m=0}\). If we now replace the the Fourier vectors \(v_k\) by elements of an arbitrary frame of \({\mathbb C}^{M}\), the question arises how to choose the frame vectors to ensure a unique recovery of the true signal. This question has been studied, for instance, in [26,27,28,29]. Further generalizations, where the Fourier transform is replaced by the signed Fourier transform or by the short-time Fourier transform, have been studied in [30] and [31,32,33] respectively, see also the references therein.
The generalization of the Fourier phase retrieval problem with respect to a suitable frame often goes hand in hand with the a priori assumption that the true signal possesses a sparse representation in the frame. Phase retrieval problems of this kind have been studied for the shearlet frame [34] and for the translation invariant Haar pyramid tight frame [35]. Certainly, the sparsity assumption is not restricted to frame representations. If the sparsity of the true signal is sufficiently strong, this a priori condition guarantees uniqueness in the classical phase retrieval problem too, see [31] and references therein. Moreover, the sparsity of the true signal plays a key role in the recovery of spike and spline functions [36, 37] as well as in the reconstruction of structured functions [38].
This chapter is organized as follows. In the first part, Sects. 24.2 and 24.3, we introduce the one-dimensional discrete-time phase retrieval problem in more detail and derive a characterization of the entire solution set by factorizing the autocorrelation function—the squared Fourier intensity—suitably. Using this characterization, we show that each ambiguity is caused by rotation, time-shift, and conjugation and reflection of the factors in a convolution representation of the true signal.
In the second part—Sects. 24.4–24.6—we exploit our findings on the solution set to investigate different a priori assumptions and additional information about the signal with respect to their capability to ensure a unique recovery of the unknown true signal. In particular, we study the three a priori assumptions: non-negativity, additionally known direct measurements or intensity measurements in time domain, and additional intensity measurements in the frequency domain. Here the measurements in the frequency domain arise from the interference of the true signal with another signal. We particularly study the interference with a known reference signal, the interference with an unknown reference signal, and interference with modulations of the unknown solution signal.
Finally, in Sect. 24.7, we briefly discuss a generalization of the discrete-time phase retrieval problem where the Fourier transform is replaced by a so-called linear canonical transform. The linear canonical transform covers an entire class of well-known transforms like the Fresnel and the fractional Fourier transform. Due to the structure of these transforms the characterization of the solution set and uniqueness guarantees can be easily transferred to the new setting.
2 The Discrete-Time Phase Retrieval Problem
The central task in phase retrieval is the recovery of an unknown complex-valued signal from the measured intensity of its Fourier transform. In other words, we have completely lost the phase information in the frequency domain. Although the Fourier transform itself is a well-understood isometric isomorphism, the missing phase significantly hampers the reconstruction process and turns the phase retrieval problem into an ill-posed, quadratic inverse problem.
In this chapter, we consider the discrete-time version of the phase retrieval problem that can be stated as follows: recover an unknown complex-valued signal \(x := (x[n])_{n \in \mathrm {\mathbb {Z}}}\) from its Fourier intensity
Throughout the paper, we assume that the true signal x has a finite support, which means that only finitely many components x[n] are non-zero. We say that the signal x has a support of length N if there exists an integer \(n_{0}\) such that \(x[n_{0}]\) and \(x[n_{0}+N-1]\) are non-zero and \(x[n]=0\) for all \(n \not \in \{ n_{0}, \ldots , n_{0}+N-1 \}\). Since the exponential sum in (24.1) has only finitely many terms, the Fourier intensity \(|\widehat{x}|\) is here always well-defined.
The Fourier intensity \(|\widehat{x}|\) is closely related to the autocorrelation signal \(a := (a[n])_{n \in \mathrm {\mathbb {Z}}}\) of x given by
The coefficients of the autocorrelation signal are conjugate symmetric, which means \(a[n] = \overline{a[-n]}\) for all n in \(\mathrm {\mathbb {Z}}\). Further, the support of the autocorrelation signal is always \(\{-N+1, \dots , N-1\}\), where N again denotes the support length of the original signal x, and does not depend on the actual position of the non-zero elements of the true signal x.
Using the definition of the autocorrelation signal, we observe
where \(\widehat{a}\) is called the autocorrelation function of x. The phase retrieval problem is thus equivalent to the recovery of the true signal x from its autocorrelation signal a. Due to the support \(\{-N+1, \dots , N-1\}\) of the autocorrelation signal a, the squared intensity \(|\widehat{x}|^2\) is here a trigonometric polynomial of degree \(N-1\), which implies that the Fourier intensity \(|\widehat{x}|\) is already completely determined by \(2N-1\) measurements in \([-\pi ,\pi )\). For convenience, we nevertheless assume that the entire Fourier intensity is given.
3 Trivial and Non-trivial Ambiguities
The unknown phase of \(\widehat{x}\) in the frequency domain cannot be completely arbitrary since the squared Fourier intensity is a trigonometric polynomial. However, without further information, the phase retrieval problem is never uniquely solvable. The simplest occurring ambiguities are
-
1.
rotated signals \((\mathrm {e}^{-\mathrm{i}\alpha } \, x[n])_{n \in \mathrm {\mathbb {Z}}}\) with \(\alpha \in \mathrm {\mathbb {R}}\),
-
2.
time-shifted signals \((x[n-n_0])_{n \in \mathrm {\mathbb {Z}}}\) with \(n_0 \in \mathrm {\mathbb {Z}}\), and
-
3.
the reflected and conjugated signal \((\overline{x[-n]})_{n \in \mathrm {\mathbb {Z}}}\),
which obviously have the same Fourier intensity \(|\widehat{x}|\) as the true signal x. Since these signals are, however, closely related to the true signal x, we call these ambiguities trivial.
In the following, we are interested in all non-trivial solutions of the discrete-time phase retrieval problem. Before we give an explicit characterization, let us start with the following observation. If our true signal x can be represented as a convolution \(x = x_1 * x_2\) defined by
where \(x_1\) and \(x_2\) are two signals with finite support, than the Fourier convolution theorem implies that the signal
with \(\alpha \in \mathrm {\mathbb {R}}\) and \(n_0 \in \mathrm {\mathbb {Z}}\) has the same Fourier intensity \(|\widehat{x}|\). Differently from the trivial ambiguities, the constructed signal in (24.2) can have a completely different structure than the original signal x. In this section, we will show that all ambiguities—trivial and non-trivial—in discrete-time phase retrieval can be written as in (24.2), which means that they are caused by rotation, time-shifts, and reflection and conjugation of the single factors with respect to an appropriate convolution.
For this purpose, we will derive a suitable factorization of the given autocorrelation function \(\widehat{a}\) by exploiting that the trigonometric polynomial \(\widehat{a}\) is closely related to the algebraic polynomial \(P_a\) of degree \(2N-2\) defined by
More precisely, we have
In the following, we call \(P_{a}\) the algebraic polynomial associated to \(\widehat{a}\).
Due to the conjugate symmetry \(a[n]=\overline{a[-n]}\) for \(n=0, \ldots , N-1\), the polynomial \(P_a\) is here conjugate palindromic, which implies that all roots occur in pairs of the form \((\gamma , \overline{\gamma }^{\,-1})\), where \(\gamma \) and \(\overline{\gamma }^{\,-1}\) have exactly the same multiplicity. Moreover, zeros on the unit circle have an even multiplicity. Hence, the associated polynomial can be written as
Using the identity
we obtain the factorization
The square root of \(\widehat{a}\) now yields the Fourier transform of a finitely supported signal, and hence a solution of the phase retrieval problem with respect to the autocorrelation function \(\widehat{a}\). Interchanging the role of \(\gamma _j\) and \(\overline{\gamma }_j^{\,-1}\) in (24.4), we can explicitly construct further non-trivial solutions of the problem. With this idea in mind, we can characterize all solutions x of the discrete-time phase retrieval problem with given squared Fourier intensity \(|\widehat{x}|^{2} = \widehat{a}\).
Theorem 24.1
([8]) Let \(\widehat{a} :\mathrm {\mathbb {R}}\rightarrow [0, \infty )\) be an arbitrary non-negative trigonometric polynomial of degree \(N-1\). The Fourier transform of every finitely supported signal x with \(|\widehat{x}|^2=\widehat{a}\) can be written in the form
where \(\alpha \) is a real number, \(n_0\) is an integer, and \(\beta _j\) is chosen from the zero pair \((\gamma _j^{\,}, \overline{\gamma }_j^{\,-1})\) of the associated polynomial \(P_a\).
In Theorem 24.1, the trivial rotation ambiguity is covered by the factor \({\mathrm e}^{\mathrm{i}\alpha }\), and the time-shift ambiguity by the factor \(\mathrm {e}^{\mathrm{i}n_{0}\omega }\). Further, if the true signal x corresponds to the zero set \(\{\beta _1, \dots , \beta _{N-1}\}\), then the reflected and conjugated signal \(\overline{x[-\cdot ]}\) corresponds to the zero set \(\{\overline{\beta }_1^{-1}, \dots , \overline{\beta }_{N-1}^{-1}\}\). Consequently, the trivial reflection and conjugation ambiguity is also covered.
Employing the representation (24.5) of all ambiguities in the frequency domain, we can finally show that every non-trivial solution x of the phase retrieval problem \(|\widehat{x} |^{2} = \widehat{a}\) can be described by a suitable convolution factorization of the true signal x.
Theorem 24.2
([8]) Let x and y be two discrete-time signals with finite support and the same Fourier intensity \(|\widehat{x}|\). Then there exist two finitely supported signals \(x_1\) and \(x_2\) such that
and
where \(\alpha \) is a suitable real number and \(n_0\) is a suitable integer.
Using the characterization of all solutions in Theorem 24.1, we can construct \(2^{N-1}\) zero sets \(\{ \beta _{1}, \ldots , \beta _{N-1} \}\) by choosing either \(\beta _j = \gamma _j\) or \(\beta _j = \overline{\gamma }_j^{\,-1}\) for \(j=1, \ldots , N-1\), and each zero set determines a solution \(\widehat{x}\) of the phase retrieval problem \(|\widehat{x}|^{2} = \widehat{a}\). Remembering that the reflection of all zeros on the unit circle corresponds to the reflection and conjugation of the related signal, we can therefore have at most \(2^{N-2}\) different non-trivial solutions.
The true number of non-trivially different solutions \(\widehat{x}\) can, however, be much smaller and depends on the number of different zero sets \(\{\beta _1, \dots , \beta _{N-1}\}\) that can be constructed. If all zeros lie on the unit circle, then \(\gamma _j\) and \(\overline{\gamma }_j^{\,-1}\) coincide for all \(j=1,\dots ,N-1\), and the solution is thus unique. A similar observation holds if some zero pairs \((\gamma _\ell , \overline{\gamma }_\ell ^{\,-1})\) have a higher multiplicity \(m_\ell >1\), where the number of pairwise different zero sets \(\{\beta _1, \dots , \beta _{N-1}\}\) is then reduced accordingly.
Theorem 24.3
([10]) Let x be a discrete-time signal with finite support. Furthermore, let L be the number of distinct zero pairs \((\gamma _\ell ^{\,}, \overline{\gamma }_\ell ^{\,-1})\) of the associated polynomial \(P_a\) to the autocorrelation function \(\widehat{a}\) not lying on the unit circle, and let \(m_\ell \) be the multiplicity of these zero pairs. The corresponding phase retrieval problem to recover the signal x exactly has
non-trivial ambiguities.
Example 24.1
The actual number of non-trivial ambiguities in phase retrieval strongly depends on the zeros of the autocorrelation function. For example, the phase retrieval problem related to the autocorrelation function given by
has exactly three non-trivially different solutions, namely
and
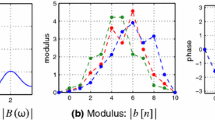
Reflecting more than two zeros at the unit circle from \(\nicefrac 12\) to 2 only produces further trivial ambiguities caused by conjugation of the linear factors. The absolute value and the coefficients of the three non-trivially different solutions \(x_1\), \(x_2\), and \(x_3\) are shown in Fig. 24.1. \(\square \)
4 Non-negative Signals
As we have seen in Theorem 24.3, the solution set of the discrete-time phase retrieval problem usually consists of a vast number of non-trivially different solutions that strongly differ in shape and form. To recover the true signal x within the solution set, we have to rely on further a priori knowledge on the desired signal. In many applications, we can assume that the unknown signal is real-valued and non-negative, see for instance [3, 4, 11]. Therefore, we study the problem: how many non-trivial real-valued non-negative signals exist satisfying \(|\widehat{x}|^{2} = \widehat{a}\) for a given autocorrelation function? In other words, can the a priori assumption that x is real-valued and non-negative help us to find a unique solution or at least essentially reduce the number of non-trivial ambiguities?
Let us now assume that x has a finite support of the form \(\{ 0, \ldots , N-1 \}\), and that all components x[n] with \(n \in \{0, \ldots , N-1\}\) are real and non-negative. The representation (24.5) in Theorem 24.1 without rotations and time-shifts—with \(\alpha =0\) and \(n_{0}=0\)—yields the solution
The non-negativity of x is now equivalent with the condition that the coefficients of the algebraic polynomial Q given by
are non-negative. Since the zeros \(\beta _j\) are always non-zero, the leading coefficient and the absolute term of Q have even to be strictly positive. Algebraic polynomials of this kind are usually called positive polynomials.
A closer inspection shows that the non-negativity condition does not always reduce the number of non-trivial ambiguities of the phase retrieval problem.
Theorem 24.4
([14]) Let x be a real-valued discrete-time signal with finite support. If the zero set \(\{ \beta _{1}, \ldots , \beta _{N-1} \}\) corresponding to \(\widehat{x}\) in (24.6) is contained in the left half plane, which means that \({\text {Re}}\beta _{j} < 0\) for all \(j=1, \ldots , N-1\), then all occurring real-valued non-trivial ambiguities of the corresponding phase retrieval problem are non-negative.
Proof
Since the polynomial Q in (24.7) is real-valued, the zeros \(\beta _{j}\) have to be real or have to come in conjugated pairs \((\beta _{j}, \overline{\beta _{j}})\). The corresponding linear or quadratic factors have the form
By assumption all coefficients in these factors are non-negative. Therefore, also all coefficients of the polynomial Q are non-negative, and Q therefore always leads to a non-negative solution x of the phase retrieval problem. \(\square \)
However, if the assumption of Theorem 24.4 is not satisfied, the number of non-negative non-trivial ambiguities of the discrete-time phase retrieval problem is usually reduced.
Non-reduced non-negative solution set for the phase retrieval problem \(\widehat{a} = | \widehat{x} |^2\), see [10]
Example 24.2
Figures 24.2, and 24.4 show some different cases which can occur under the restriction of non-negativity. Figure 24.2 presents all non-trivial solutions that can be constructed from the autocorrelation function \(| \widehat{x}|^{2}\), where x is the marked signal of length 6 being determined by the zero set
As shown in Theorem 24.4, all non-trivial solutions being constructed via (24.6) are real and non-negative. The solution set is presented without reflected, conjugated signals. In this example, we have \(2^4 = 16\) different solutions, which is the maximal number of non-trivial ambiguities by Theorem 24.3.
In the second example, see Fig. 24.3, the condition of nonnegativity is strong enough to ensure uniqueness of the phase retrieval problem. Here, the unique non-negative solution \(x_1\) corresponds to the zero set
Note that the problem has only four non-trivial ambiguities since the complex zeros of the characterization (24.5) additionally have to be chosen as complex conjugated pairs.
In the last example, Fig. 24.4, the restriction of non-negativity is too strong since every solution of the phase retrieval problem possesses some negative coefficients, which means that the given phase retrieval problem cannot be solved by a real-valued non-negative signal. The signal \(x_1\) in Fig. 24.4b here corresponds to the zero set
\(\square \)
Unique non-negative solution of the phase retrieval problem \(\widehat{a} = | \widehat{x} |^2\), see [10]
Empty non-negative solution set for the phase retrieval problem \(\widehat{a} = | \widehat{x}|^2\), see [10]
Since the coefficients of an algebraic polynomial continuously depend on the zero set \(\{ \beta _1, \dots , \beta _{N-1} \}\), the number of non-negative non-trivial ambiguities around a true signal x with non-zero components remains unchanged in a certain (small) neighbourhood of the zero set. On the basis of this observation, one can show that neither the signals that are uniquely defined by their Fourier intensity and the a priori known non-negativity nor the signals that are not uniquely defined by these conditions form negligible sets. Unfortunately, there is no simple way to decide from the given intensity data whether the a priori condition of non-negativity is helpful for reducing the number of ambiguities of the discrete-time phase retrieval problem. Mathematically, we can show the following result.
Theorem 24.5
([14]) The set of real-valued discrete-time signals with support \(\{0, \ldots , N-1\}\) of length \(N>0\) that can be recovered uniquely up to reflection as well as the set of signals that cannot be recovered uniquely from their Fourier intensities employing the non-negativity constraint are both unbounded sets containing a cone of infinite Lebesgue measure.
In other words, the non-negativity of the true signal is not an appropriate a priori assumption in order to guarantee uniqueness of the solution of the related one-dimensional phase retrieval problem.
5 Additional Data in Time-Domain
In certain applications like electron microscopy, wave front sensing and laser optics [6], we may have direct access to one or more signal values x[n] or to magnitudes |x[n]| in the time domain. In order to exploit these additional information, we need to know the position of the measurements within the support of the true signal. To simplify the following considerations, we restrict ourselves to finite discrete-time signals \(x = (x[n])_{n\in \mathrm {\mathbb {Z}}}\) with support \(\{ 0, \ldots , N-1 \}\). These signals may be interpreted as complex-valued vectors \(x = (x[n])_{n=0}^{N-1}\) in \({\mathbb C}^{N}\). If x[0] and \(x[N-1]\) are additionally non-zero, then we call the support of the signal x with length N normalized.
Xu et al. already considered the a priori constraint that, besides \(| \widehat{x} |\) for a real-valued signal, also the endpoint \(x[N-1]\) is known [40], which almost always enforces uniqueness. In [18], these ideas have been generalized to discrete-time phase retrieval problems with given magnitudes of the form |x[n]| or partial phase information \(\arg (x[n])\) in the time domain.
Again, the question arises whether a priori information of this type is sufficient to determine a unique solution of the discrete-time phase retrieval problem (up to trivial ambiguities).
5.1 Using an Additional Signal Value
In order to get a heuristic idea, we start with the following question: for a given non-negative trigonometric polynomial \(\widehat{a}\) of degree \(N-1\) as in Theorem 24.1 and a given constant \(C \in {\mathbb C}\), how many non-trivial solutions x with support \(\{ 0, \ldots , N-1\}\) exist for the constrained phase retrieval problem
As we know already from Theorem 24.1, there exist at most \(2^{N-2}\) non-trivially different signals \(x= (x[n])_{n\in \mathrm {\mathbb {Z}}}\) with Fourier intensity \(| \widehat{x}|^{2} = \widehat{a}\). But how many of these solutions also satisfy the side condition \(x[N-1] = C\)?
To answer this question, we employ our knowledge about the structure of the solutions in (24.5). Recalling that \(\widehat{x} (\omega ) = \sum _{n=0}^{N-1} x[n] \, {\mathrm e}^{- \mathrm{i}\omega n}\), we notice that the coefficient \(x[N-1]\) in (24.5) with \(n_{0}=0\) is given by
We therefore derive the consistency condition
If this condition is not satisfied, there will be no solution signal satisfying the side condition \(x[N-1]=C\). Assuming that (24.9) is satisfied for some zero set \(\{\beta _{1}, \ldots , \beta _{N-1} \}\), we find at least one solution of (24.8), where we take \(\alpha \) according to the phase of the complex value C. By Theorem 24.1, all further solutions with Fourier intensity \(| \widehat{x}|^{2} = \widehat{a}\) are obtained by reflecting zeros from \(\beta _{j}\) to \(\overline{\beta }_{j}^{-1}\) at the unit circle for some indices \(j \in \{1, \ldots , N-1 \}\) in the representation (24.5).
Let us now assume that there is indeed a second solution \(\tilde{x}\) of (24.8) satisfying (24.9), and let \(\{ \tilde{\beta }_{1}, \ldots , \tilde{\beta }_{N-1} \}\) be the corresponding zero set in (24.5). Then we can assume without loss of generality that the corresponding zeros are given by
for some \(L \in \{1, \ldots , N-1 \}\). The consistency condition (24.9) now implies
and thus \(\prod _{j=1}^{L} | \beta _{j} |^{2} = 1\). We can therefore state the following theorem.
Theorem 24.6
([8]) Let x be a complex-valued discrete-time signal with normalized support of length N, i.e., \(\widehat{x}\) is of the form (24.5) with \(n_{0}=0\). Then the constrained phase retrieval problem to recover the signal x from its Fourier intensity \(|\widehat{x}|\) and the signal value \(x[N-1]\) is uniquely solvable if and only if
for each non-empty subset \(\Lambda \) of B, where B denotes the set of values in the corresponding zero set of x not lying on the unit circle.
Since the support of x is normalized to \(\{ 0, \ldots , N-1 \}\), and since the rotation factor \(\alpha \) in (24.5) is here fixed by the phase of the given constant C, we have no trivial ambiguities caused by rotation or shift. Moreover, the reflection and conjugation ambiguity cannot occur since we have here particularly assumed \(\prod _{j=1}^{N-1} | \beta _{j} |^{2} \ne 1\). The simplification of the set of zeros to those with modulus different from 1 can be done since the reflection of zeros on the unit circle does not lead to further non-trivial solutions.
5.2 Using Additional Magnitude Values of the Signal
Next, we generalize the problem considered in (24.8) and assume that, besides the Fourier intensity \(| \widehat{x} |^{2}\), either all or at least some of the magnitudes |x[n]| with \(n=0, \ldots , N-1\) are given. Phase retrieval problems with these constraints have been considered for example in [6, 15, 16]. The numerical approaches to find the phase retrieval solution in [15] are based on multilevel Gauß–Newton methods. However, these algorithms are not always stable and sometimes reconstruct signals that are different from the desired solution.
We therefore study the uniqueness of solutions of the following constrained phase retrieval problem: for a given non-negative trigonometric polynomial \(\widehat{a}\) of degree \(N-1\) as in Theorem 24.1 and a given \(C >0\), how many non-trivial solutions x with support \(\{ 0, \ldots , N-1\}\) exist to the constrained phase retrieval problem
To characterize the solutions of (24.10), we can proceed similarly as in Sect. 24.5.1. Doing so, we obtain the same consistency condition (24.9) but, obviously, the given absolute value \(|x[N-1]|\) will give us no information how to choose the rotation factor \({\mathrm e}^{{\mathrm{i}\alpha }}\); so we cannot get rid of the rotation ambiguity.
Corollary 24.1
([8]) Let x be a complex-valued discrete-time signal with normalized support of length N, i.e., \(\widehat{x}\) is of the form (24.5) with \(n_{0}=0\). Then the constrained phase retrieval problem to recover the signal x from its Fourier intensity \(|\widehat{x}|\) and the absolute value \(|x[N-1]|\) is uniquely solvable up to rotations if and only if
for each non-empty subset \(\Lambda \) of B, where B denotes the set of values in the corresponding zero set of x not lying on the unit circle.
In [18], we have generalized these observations to the constrained phase retrieval problem of the form
for some \(n \in \{0, \ldots , N-1\}\). Similarly as before, one can derive a consistency condition and a condition in terms of the zeros of the autocorrelation function \(\widehat{a}\) such that uniqueness of a solution x of (24.11) is guaranteed up to trivial ambiguities. However, the corresponding conditions are more complex and require an extensive investigation of the \((N-1)\)-variate elementary symmetric polynomials, which are related to the components of the true signal x by Vieta’s formulae. The important outcome of these investigations can be summarized as follows.
Theorem 24.7
([18]) Let x be a complex-valued discrete-time signal with normalized support of length N, and let \(\ell \) be an arbitrary integer between 0 and \(N-1\). The phase retrieval problem to recover the signal x from its Fourier intensity \(|\widehat{x}|\) and the absolute value \(|x[N-1-\ell ]|\) is almost always uniquely solvable up to rotations whenever \(\ell \ne \nicefrac {(N-1)}{2}\). In the special case that \(\ell =\nicefrac {(N-1)}{2}\), the reconstruction is almost always unique up to rotations and conjugate reflections.
‘Almost always’ means here that the union of all signals with normalized support of length N, which permit a further non-trivial solution, corresponds to the union of finitely many algebraic varieties with Lebesgue measure zero in \({\mathrm {\mathbb {R}}}^{2N}\), see [18]. In particular, we almost always obtain uniqueness if the magnitudes of all signal values |x[n]|, \(n=0, \ldots , N-1\), are given.
Corollary 24.2
([10]) Let x be a complex-valued discrete-time signal x with normalized support of length N. The phase retrieval problem to recover the signal x from its Fourier intensity \(|\widehat{x}|\) and its moduli \((|x[n]|)_{n\in \mathrm {\mathbb {Z}}}\) is almost always uniquely solvable up to rotations.
Obviously, Corollary 24.2 is a simple consequence of Theorem 24.7. But the following question remains: is the knowledge of all magnitudes |x[n]| with \(n=0, \ldots , N-1\) already sufficient to obtain a unique solution of the constrained problem
up to rotation ambiguities? The following example shows that this is unfortunately not the case.
Example 24.3
We consider the complex-valued signal x determined by th corresponding zeros
and by \(\alpha =0\) and \(n_{0}=0\) in the representation (24.5). Knowing the autocorrelation function \(\widehat{a} \left( \omega \right) = |\widehat{x} \left( \omega \right) |^2\) for \(\omega \in \mathrm {\mathbb {R}}\) and the moduli of all components \(| x \left[ n \right] |\) for \(n \in \mathrm {\mathbb {Z}}\), we still cannot recover x uniquely. In this specific example, we find, up to rotations, three non-trivial solutions that are presented in Fig. 24.5.
It is possible to construct further examples with several non-trivial solutions for all dimensions N of the problem, see [10]. Hence, the a priori known moduli of the components strongly reduce the set of ambiguities, but we cannot ensure uniqueness (up to trivial ambiguities) for every signal. \(\square \)
Using an analogous approach, one can study the restricted discrete-time phase retrieval problem where the knowledge of additional magnitudes in time domain is replaced by a priori phase information in time domain. Due to the trivial rotation ambiguity, we can only expect to reduce the non-trivial solution set if we have given the phase of at least two signal components.
Theorem 24.8
([18]) Let x be a complex-valued discrete-time signal with normalized support of length N, and let \(\ell _1\) and \(\ell _2\) be different integers between 0 and \(N-1\). The phase retrieval problem to recover the signal x from its Fourier intensity and the two phases \(\arg x[N-1-\ell _1]\) and \(\arg x[N-1-\ell _2]\) is almost always uniquely solvable whenever \(\ell _1 + \ell _2\ne N-1\). If \(\ell _1+\ell _2=N-1\), then the reconstruction is only unique up to conjugate reflections, except for the special case where \(\ell _1\) and \(\ell _2\) correspond to the two endpoints.
6 Interference Measurements
Another possibility to reduce the ambiguities in the considered discrete-time phase retrieval problem is to exploit additional reference measurements of the form \(| \mathop {\mathcal {F}}\nolimits [x + h]|\), where h is a suitable reference signal with finite support. We consider here two cases, either the reference signal h is known beforehand, or it is also unknown. In the first case, we will show that the corresponding phase retrieval problem with given intensities \(|{\mathop {\mathcal {F}}\nolimits [x]}|\) and \(| \mathop {\mathcal {F}}\nolimits [x + h]|\) has at most two non-trivial solutions. If h is unknown, we assume that the Fourier intensities \(|{\mathop {\mathcal {F}}\nolimits [x]}|\), \(|{\mathop {\mathcal {F}}\nolimits [h]}|\), and \(| \mathop {\mathcal {F}}\nolimits [x + h]|\) are given and show unique recovery results under suitable side conditions. Finally, we will examine the special case where the unknown reference signal is a modulated version of the true signal x itself.
6.1 Interference with a Known Reference Signal
Let us assume that the considered reference signal \(h= (h[n])_{n\in {\mathbb Z}}\) has finite support and is completely known beforehand. The corresponding phase retrieval problem is then nearly unique solvable up to at most one ambiguity, see [8, 20].
Theorem 24.9
([8]) Let x and h be two discrete-time signals with finite support, where the non-vanishing reference signal h is known beforehand. Then the signal x can be recovered from the Fourier intensities
except for at most one ambiguity. This ambiguity ist trivial if h possesses a linear phase.
Proof
Let \(y=x+h\) be the interference between the unknown signal x and the known reference signal h. Then y is a finite length signal with known Fourier intensity \(|\mathop {\mathcal {F}}\nolimits [y]| = |\mathop {\mathcal {F}}\nolimits \left[ x + h \right]|\). Further, with \(\widehat{x}(\omega ) = |\widehat{x}(\omega )| \, {\mathrm e}^{\mathrm{i}\phi (\omega )}\) and \(\widehat{h}(\omega ) = |\widehat{h}(\omega )| \, {\mathrm e}^{\mathrm{i}\psi (\omega )}\), it follows
such that we can extract the phase difference \(\phi (\omega ) - \psi (\omega ) \) up to the sign and a multiple of \(2\pi \) for every \(\omega \in \mathrm {\mathbb {R}}\). Due to the piecewise continuity of the phases \(\phi \) and \(\psi \), there is an open interval where the sign has to be either plus or minus everywhere. Since each trigonometric polynomial is completely determined by its values on an open set, we conclude that there can be at most two different solutions. If we write these solutions x and \(\tilde{x}\) in the form \(\widehat{x}(\omega ) = |\widehat{x}(\omega )| \, {\mathrm e}^{\mathrm{i}\phi _{1}(\omega )}\) and \(\widehat{\tilde{x}}(\omega ) = |\widehat{x}(\omega )| \, {\mathrm e}^{\mathrm{i}\phi _{2}(\omega )}\), then the phases \(\phi _{1}\) and \(\phi _{2}\) are related by
i.e., \( \phi _{2}(\omega ) = - \phi _{1}(\omega ) + 2 \psi (\omega ) + 2 \pi \, \ell _\omega \). If the reference h has linear phase, which means that the phase \(\psi \) is of the form \( \psi (\omega ) = n_{0}\omega + \alpha \) for some \(n_{0} \in {\mathbb Z}\) and \( \alpha \in {\mathbb R}\), then \(\tilde{x}\) is a trivial ambiguity of x obtained by support shift and rotation. \(\square \)
If the signal h does not have linear phase, then the ambiguity \(\tilde{x}\) can be non-trivially different as discussed in the next example.
Example 24.4
Let us consider the discrete-time phase retrieval problem to recover the true signal
from the Fourier intensities \(|\mathop {\mathcal {F}}\nolimits [x]|\) and \(|\mathop {\mathcal {F}}\nolimits [x+h]|\), where h is the known reference signal
Here, we have underlined the entry with index 0. Since h does not possess a linear phase, cf. Fig. 24.6c, there may exist a further non-trivially different solution by Theorem 24.9, and, indeed, the signal
yields the same Fourier intensities. The signals and the given Fourier intensities are presented in Fig. 24.6. \(\square \)
Discrete-time phase retrieval problem to recover x from the Fourier intensities \(|\mathop {\mathcal {F}}\nolimits [x]|\) and \(|\mathop {\mathcal {F}}\nolimits [x+h]|\), where h is a known reference signal as in Example 24.4. Besides the true solution x, the non-trivial ambiguity \(\breve{x}\) is the only further solution of the problem, see [10]
6.2 Interference with an Unknown Reference Signal
Let us now consider the case where the finitely supported signal h is also unknown. For real signals, this problem has already been studied in [21]. For complex signals, we want to refer to the work of Raz et al. [22], where, besides the three Fourier intensities in the next theorem, a fourth intensity of the form \(| \widehat{x}(\omega ) + \mathrm{i}\widehat{h} (\omega ) |\) was used for the recovery of x. From a theoretical point of view, this intensity is not needed to ensure uniqueness, but this additional information allows the derivation of an explicit analytic solution.
Theorem 24.10
([8]) Let x and h be two discrete-time signals with finite support. If the corresponding zero sets of the signals x and h are disjoint, then the two signals x and h can be recovered from the Fourier intensities
uniquely up to common trivial ambiguities.
‘Common trivial ambiguities’ means here that we can multiply the two signals x and h with the same unimodular constant \({\mathrm e}^{{\mathrm i} \alpha }\) or shift the two signals with the same integer \(n_{0}\) or take the reflection and conjugation for both signals, and all these actions do not change the given Fourier intensities in Theorem 24.10. For a detailed proof of this theorem, we refer to [8]. The main part of the proof is heavily based on the result of Theorem 24.2, where we have shown that each further solution \((\tilde{x}, \tilde{h})\) with Fourier intensities \(|\mathop {\mathcal {F}}\nolimits [\tilde{x}]| = |\mathop {\mathcal {F}}\nolimits x]|\) and \(|\mathop {\mathcal {F}}\nolimits [\tilde{h}]| = |\mathop {\mathcal {F}}\nolimits [h]|\) is related to the true solution (x, h) by some factorization
and
with rotations \(\alpha _{1}, \, \alpha _{2} \in [-\pi , \pi )\) and shifts \(n_{1}, \, n_{2} \in {\mathbb Z}\). The assertion then follows from a detailed comparison of the third Fourier intensity
by incorporating the product representations of the signals.
If the assumption of Theorem 24.10 is violated and x and h have common zeros in the defining zero sets in representation (24.5), then we may find more non-trivial solutions, as shown in the following example.
Example 24.5
We want to recover the signal x in Example 24.4, which corresponds to the zero set
in the representation (24.5) of \(\widehat{x}\). Further, we choose the reference signal h with the corresponding zero set
If both signals are unknown, we have to recover x and h from the Fourier intensities \(|\mathop {\mathcal {F}}\nolimits [x]|\), \(|\mathop {\mathcal {F}}\nolimits [h]|\), and \(|\mathop {\mathcal {F}}\nolimits [x+h]|\). The intersection of the corresponding zero sets of x and h is here given by
such that the uniqueness of the solution is not covered by Theorem 24.10. Indeed, reflecting the zeros \(\nicefrac 14 \, (1+\mathrm{i})\) and \(\nicefrac 14 \, (4+4\mathrm{i})\) in the representations (24.5) of both signals at the unit circle, we find a second non-trivial solution \((\breve{x}, \breve{h})\). Both solutions (x, h) and \((\breve{x}, \breve{h})\) are presented in Fig. 24.7. \(\square \)
Discrete-time phase retrieval problem to recover x and h from the Fourier intensities \(|\mathop {\mathcal {F}}\nolimits [x]|\), \(|\mathop {\mathcal {F}}\nolimits [h]|\) and \(|\mathop {\mathcal {F}}\nolimits [x+h]|\), where h is an unknown reference signal as in Example 24.5. Besides the true solution (x, h), the non-trivial ambiguity \((\breve{x}, \breve{h})\) is also a solution of the problem, see [10]
6.3 Interference with the Modulated Signal
Finally we consider the model, where the unknown reference signal is a modulated version of the signal x itself. Similar approaches for the (periodic) discrete Fourier transform have already been studied in [25, 41]. We here especially rely on the results in [24]. The discrete-time phase retrieval problem can be now posed as follows: recover a finitely supported signal x from its Fourier intensity \(| \widehat{x} |\) and a set of interference measurements
where the modulations and rotations are described by \(\mu \in {\mathbb R}\) and \(\alpha \in [0, \, 2\pi )\). In order to guarantee uniqueness, besides the Fourier intensity \(|\widehat{x}|\), we merely need two additional interference signals.
Theorem 24.11
([24]) Let x be a discrete-time signal with finite support of length N. If \(\mu \) satisfies the assumption that \(k\mu \not \equiv 0 \, \text {mod} \, 2\pi \) for all \(k=1, \ldots , 2N-1\), then the signal x can be uniquely recovered up to a rotation ambiguity from its Fourier intensity \(|\widehat{x}|\) and the Fourier intensities of two interference signals
where \(\alpha _1\) and \(\alpha _2\) are two real numbers satisfying \(\alpha _1 - \alpha _2 \ne \pi k\) for all \(k \in {\mathbb Z}\).
Proof
Writing the unknown Fourier-transformed signal in the form \(\widehat{x}(\omega ) = | \widehat{x}(\omega ) | \, {\mathrm e}^{\mathrm{i}\phi (\omega )}\), we only need to recover the phase \(\phi (\omega )\) to solve the given phase retrieval problem. The Fourier intensity measurements of the first interference signal yield
and thus the cosine of the relative phase
Analogously, we can extract \(\cos (\phi (\omega -\mu )-\phi (\omega )+\alpha _{2})\) from the Fourier intensity measurements of the second interference signal. Since \(\alpha _1 - \alpha _2 \ne \pi k\) for all \(k \in {\mathbb Z}\), we can therefore uniquely determine the phase difference \(\phi (\omega -\mu )-\phi (\omega )\) for every \(\omega \in \mathrm {\mathbb {R}}\). Obviously, the solution can be only recovered up to rotations. Taking an arbitrary phase \(\phi (\omega _{0})\), we can compute the corresponding phases \(\phi (\omega _{0} +\mu k)\) for \(k=0, \ldots , 2N-1\) and thus the Fourier values \(\widehat{x}(\omega _{0}+ \mu k)\) for \(k=0, \ldots , 2N-1\). It remains to recover the signal x and especially the unknown support from these Fourier values. Due to the support length N, the Fourier transform \(\widehat{x}\) can be written in the form
with \(c_{n}:= x[n+n_{0}]\). Using the found Fourier values, we obtain the equation system
with \(d_{n}:=c_{n} {\mathrm e}^{-\mathrm{i}\omega _{0}(n+n_{0})}\) and \(z_{n}:= {\mathrm e}^{-\mathrm{i}\mu (n+n_{0})}\). This system can be solved by Prony’s method if the values \(\omega _{0} + \mu k \, \text {mod} \, 2\pi \) are pairwise different for \(k=0, \ldots , 2N-1\), which means that \(k\mu \) is not a multiple of \(2\pi \) for all \(k=1, \ldots , 2N-1\), see for instance [42]. \(\square \)
7 Linear Canonical Phase Retrieval
Up to this point, we have assumed that the given measurements in the frequency domain arise from the Fourier-transformed true signal. These measurements can be seen as intensities in the so-called far field in Fourier optics. In this section, we briefly investigate the question: how do the established uniqueness guarantees change if we replace the far field intensity measurements for example by near field intensity measurements—what happens if we replace the Fourier transform by the Fresnel or fractional Fourier transform?
The discrete-time Fourier, fractional Fourier, and Fresnel transform are special cases of the so-called linear canonical transform. Referring to [43, 44], for the real parameters a, b, c, and d with \(ad-bc = 1\) and \(b \ne 0\), we define the discrete-time linear canonical transform of the signal \(x := (x[n])_{n\in \mathrm {\mathbb {Z}}}\) by
where the kernel \(K_{(a,b,c,d)}\) is given by
The inverse discrete-time linear canonical transform is given by
see [43, 44]. The classical discrete-time Fourier transform \(\mathop {\mathcal {F}}\nolimits \) coincides with the linear canonical transform \(\mathcal C_{(0,1,-1,0)}\) up to a multiplicative constant \(\theta := \theta _{(a,b,c,d)} := \nicefrac {1}{\sqrt{2 \pi b}} \, \mathrm {e}^{\nicefrac {-\mathrm{i}\pi }{4}}\). The discrete-time Fresnel transform [45] and the fractional Fourier transform [46] are covered by the linear canonical transforms \(\mathcal C_{(1, \nicefrac {1}{2\alpha },0,1)}\) and \(\mathcal C_{(\cos \alpha , \sin \alpha , - \sin \alpha , \cos \alpha )}\) with \(\alpha \in \mathrm {\mathbb {R}}\), respectively.
Since \(b \ne 0\) by assumption, we can rewrite the linear canonical transform with respect to the discrete-time Fourier transform as
Let us now consider the linear canonical phase retrieval problem, where we wish to recover a complex-valued discrete-time signal \(x := (x[n])_{n \in \mathrm {\mathbb {N}}}\) with finite support from the intensity \(|\mathcal C_{(a,b,c,d)} [x]|\) of its linear canonical transform. Similarly to the Fourier phase retrieval problem, we are particularly interested in the arising ambiguities and in uniqueness guarantees. Using the alternative formulation (24.12) that relates the linear canonical transform to the discrete-time Fourier transform, it can be simply seen that the linear canonical phase retrieval problem to recover the true signal x is also solved by
-
1.
the rotated signal \(\mathrm {e}^{\mathrm{i}\alpha } \, x\) with \(\alpha \in \mathrm {\mathbb {R}}\),
-
2.
the shifted signal \(\mathrm {e}^{- \nicefrac {\mathrm{i}a n_0 \cdot }{b}} \, x[\cdot - n_0]\) with \(n_0 \in \mathrm {\mathbb {Z}}\), and
-
3.
the conjugated and reflected signal \(\mathrm {e}^{- \nicefrac {\mathrm{i}a \cdot ^2}{b}} \, \overline{x[-\cdot ]}\).
Again, these trivial ambiguities are of minor interest.
The representation (24.12) implies that the linear canonical phase retrieval problem to recover x from \(|\mathcal C_{(a,b,c,d)}[x]|\) is equivalent to the recovery of the signal \((x[n] \, \mathrm {e}^{\nicefrac {\mathrm{i}a n^2}{2b}})_{n \in \mathrm {\mathbb {N}}}\) from the Fourier intensity \(|\mathop {\mathcal {F}}\nolimits [x[\cdot ] \, \mathrm {e}^{\nicefrac {\mathrm{i}a \cdot ^2}{2b}}]|\), and we can immediately transfer the characterization of the complete solution set in Theorem 24.1 to the new setting.
Theorem 24.12
([44]) Let x be a discrete-time signal with finite support. Then each signal y with finite support satisfying
is characterized by
where \(\alpha \) is a real number, \(n_0\) is an integer, and \(\beta _j\) is chosen from the zero pair \((\gamma _j, \overline{\gamma }_j^{\,-1})\) of the associated polynomial \(P_a\) with respect to the autocorrelation signal of \(\theta \, \mathrm {e}^{\nicefrac {\mathrm{i}a \cdot ^2}{2b}} x[\cdot ]\).
With the characterization of trivial and non-trivial ambiguities, the linear canonical phase retrieval problem also inherits the uniqueness guarantees of the discrete-time Fourier phase retrieval problem; so the solutions in linear canonical phase retrieval are almost always unique (up to trivial ambiguities) if we have access to further magnitudes or phases in the time-domain, cf. Sect. 24.5, or if further interference measurements are available, cf. Sect. 24.6.
References
Hauptman, H.A.: The phase problem of X-ray crystallography. Rep. Progr. Phys. 54(11), 1427–1454 (1991)
Kim, W., Hayes, M.H.: The phase retrieval problem in X-ray crystallography. In: IEEE International Conference on Acoustics, Speech and Signal Processing. Proceedings: ICASSP 91, May 14–17, vol. 3, pp. 1765–1768. IEEE Signal Processing Society (1991)
Millane, R.P.: Phase retrieval in crystallography and optics. J. Opt. Soc. Am. A 7(3), 394–411 (1990)
Bruck, Y.M., Sodin, L.G.: On the ambiguity of the image reconstruction problem. Opt. Commun. 30(3), 304–308 (1979)
Dainty, J.C., Fienup, J.R.: Phase retrieval and image reconstruction for astronomy. In: Stark, H. (ed.) Image Recovery: Theory and Application, pp. 231–275. Academic Press, Orlando (Florida) (1987)
Seifert, B., Stolz, H., Donatelli, M., Langemann, D., Tasche, M.: Multilevel Gauss-Newton methods for phase retrieval problems. J. Phys. A, Math. Gen. 39(16), 4191–4206 (2006)
Seifert, B., Stolz, H., Tasche, M.: Nontrivial ambiguities for blind frequency-resolved optical gating and the problem of uniqueness. J. Opt. Soc. Amer. B Opt. Phys. 21(5), 1089–1097 (2004)
Beinert, R., Plonka, G.: Ambiguities in one-dimensional discrete phase retrieval from Fourier magnitudes. J. Fourier Anal. Appl. 21(6), 169–1198 (2015)
Oppenheim, A.V., Schafer, R.W.: Discrete-Time Signal Processing. Prentice Hall Signal Processing Series. Prentice Hall, Englewood Cliffs, NJ (1989)
Beinert, R.: Ambiguities in one-dimensional phase retrieval from Fourier magnitudes. Dissertation, University of Göttingen (2015)
Fienup, J.R.: Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 3(1), 27–29 (1978)
Adams, D., Martin, L.S., Seaberg, M.D., Gardner, D., Kapteyn, H., Murnane, M.: A generalization for optimized phase retrieval algorithms. Opt. Express 20(22), 24,778–24,790 (2012)
Bauschke, H.H., Combettes, P.L., Luke, D.: Hybrid projection-reflection method for phase retrieval. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 20(6), 1025–1034 (2003)
Beinert, R.: Non-negativity constraints in the one-dimensional discrete-time phase retrieval problem. Inf. Inference 6(2), 213–224 (2017)
Langemann, D., Tasche, M.: Phase reconstruction by a multilevel iteratively regularized Gauss-Newton method. Inverse Probl. 24(3), 035006(26) (2008)
Langemann, D., Tasche, M.: Multilevel phase reconstruction for a rapidly decreasing interpolating function. Results Math. 53(3–4), 333–340 (2009)
Beinert, R.: Multilevel Gauss-Newton-Methoden zur Phasenrekonstruktion. Master thesis, University of Göttingen (2013)
Beinert, R., Plonka, G.: Enforcing uniqueness in one-dimensional phase retrieval by additional signal information in time domain. Appl. Comput. Harmon. Anal. 45(3), 505–525 (2018)
Kim, W., Hayes, M.H.: Iterative phase retrieval using two Fourier transform intensities. In: IEEE International Conference on Acoustics, Speech and Signal Processing. Proceedings: ICASSP, 90, Apr 3–6, vol. 3, pp. 1563–1566. IEEE Signal Processing Society (1990)
Kim, W., Hayes, M.H.: Phase retrieval using two Fourier-transform intensities. J. Opt. Soc. Am. A 7(3), 441–449 (1990)
Kim, W., Hayes, M.H.: Phase retrieval using a window function. IEEE Trans. Signal Process. 41(3), 1409–1412 (1993)
Raz, O., Dudovich, N., Nadler, B.: Vectorial phase retrieval of 1-d signals. IEEE Trans. Signal Process. 61(7), 1632–1643 (2013)
Raz, O., Schwartz, O., Austin, D., Wyatt, A.S., Schiavi, A., Smirnova, O., Nadler, B., Walmsley, I.A., Oron, D., Dudovich, N.: Vectorial phase retrieval for linear characterization of attosecond pulses. Phys. Rev. Lett. 107(13), 133902(5) (2011)
Beinert, R.: One-dimensional phase retrieval with additional interference measurements. Results Math. 72(1), 1–24 (2017)
Candès, E.J., Eldar, Y.C., Strohmer, T., Voroninski, V.: Phase retrieval via matrix completion. SIAM J. Imaging Sci. 6(1), 199–225 (2013)
Balan, R., Bodmann, B.G., Casazza, P.G., Edidin, D.: Painless reconstruction from magnitudes of frame coefficients. J. Fourier Anal. Appl. 15(4), 488–501 (2009)
Balan, R., Casazza, P.G., Edidin, D.: On signal reconstruction without phase. Appl. Comput. Harmon. Anal. 20(3), 345–356 (2006)
Bandeira, A.S., Chen, Y., Mixon, D.G.: Phase retrieval from power spectra of masked signals. Inf. Inference 3(2), 83–102 (2014)
Bodmann, B.G., Hammen, N.: Stable phase retrieval with low-redundancy frames. Adv. Comput. Math. 41(2), 317–331 (2015)
van Hove, P., Hayes, M.H., Lim, J.S., Oppenheim, A.V.: Signal reconstruction from signed Fourier transform magnitude. IEEE Trans. Acoust. Speech Signal Process. ASSP 31(5), 1286–1293 (1983)
Bendory, T., Beinert, R., Eldar, Y.: Fourier phase retrieval: uniqueness and algorithms. In: Boche, H., Caire, G., Calderbank, R., März, M., Kutyniok, G., Mathar, R. (eds.) Compressed Sensing and Its Applications, pp. 231–275. Birkhäuser (2017)
Nawab, S., Quatieri, T.F., Lim, J.S.: Algorithms for signal reconstruction from short-time Fourier transform magnitude. In: IEEE International Conference on Acoustics, Speech, and Signal. Proceedings: ICASSP 83, vol. 8, pp. 800–803. IEEE (1983)
Nawab, S., Quatieri, T.F., Lim, J.S.: Signal reconstruction from short-time Fourier transform magnitude. IEEE Trans. Acoust. Speech Signal Process. ASSP 31(4), 986–998 (1983)
Loock, S., Plonka, G.: Phase retrieval for Fresnel measurements using a shearlet sparsity constraint. Inverse Probl. 30(5), 055005(17) (2014)
Shi, B., Lian, Q., Chen, S.: Sparse representation utilizing tight frame for phase retrieval. EURASIP J. Adv. Signal Process. 96 (2015)
Beinert, R., Plonka, G.: Sparse phase retrieval of one-dimensional signals by Prony’s method. Front. Appl. Math. Stat. 3(5) (2017)
Ranieri, J., Chebira, A., Lu, Y.M., Vetterli, M.: Phase retrieval for sparse signals: uniqueness conditions (2013). Preprint, arXiv:1308.3058v2
Beinert, R., Plonka, G.: Sparse phase retrieval of structured signals by Prony’s method. PAMM. Proc. Appl. Math. Mech. 17(1), 829–830 (2017)
Fejér, L.: Über trigonometrische Polynome. J. Reine Angew. Math. 146(2), 53–82 (1916)
Xu, L., Yan, P., Chang, T.: Almost unique specification of discrete finite length signal: from its end point and Fourier transform magnitude. In: IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings: ICASSP 87, vol. 12, pp. 2097–2100. IEEE (1987)
Alexeev, B., Bandeira, A.S., Fickus, M., Mixon, D.G.: Phase retrieval with polarization. SIAM J. Imaging Sci. 7(1), 235–66 (2014)
Plonka, G., Tasche, M.: Prony methods for recovery of structured functions. GAMM-Mitt. 37(2), 239–258 (2014)
Wolf, K.B.: Integral Transforms in Science and Engineering. Plenum Press, New York (1979)
Beinert, R.: Ambiguities in one-dimensional phase retrieval from magnitudes of a linear canonical transform. ZAMM Z. Angew. Math. Mech. 97(9), 1078–1082 (2017)
Gori, F.: Fresnel transform and sampling theorem. Opt. Commun. 39(5), 293–297 (1981)
Pei, S.C., Ding, J.J.: Relations between fractional operations and time-frequency distributions, and their applications. IEEE Trans. Signal Process. 49(8), 1638–1655 (2001)
Acknowledgements
The first author gratefully acknowledges the funding of this work by the Austrian Science Fund (FWF) within the project P28858. The Institute of Mathematics and Scientific Computing of the University of Graz, with which the first author is affiliated, is a member of NAWI Graz (http://www.nawigraz.at/).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this chapter
Cite this chapter
Beinert, R., Plonka, G. (2020). One-Dimensional Discrete-Time Phase Retrieval. In: Salditt, T., Egner, A., Luke, D.R. (eds) Nanoscale Photonic Imaging. Topics in Applied Physics, vol 134. Springer, Cham. https://doi.org/10.1007/978-3-030-34413-9_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-34413-9_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34412-2
Online ISBN: 978-3-030-34413-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)