Abstract
This chapter briefly summarizes some main concepts of coherent X-ray imaging. More specifically, we consider lensless X-ray imaging based on free-space propagation. It is meant as primer and tutorial which should help to understand later chapters of this book devoted to X-ray imaging, phase contrast methods, and optical inverse problems. We start by an introduction to scalar wave propagation, first in free space, followed by propagation of short wavelength radiation within matter. This provides the basic tools to consider the mechanisms of coherent image formation in a lensless X-ray microscope. The recorded intensities are inline holograms created by self-interference behind the object. We then present single-step and iterative fixed-point techniques based on alternating projections onto constraint sets as tools to decode the measured intensities (phase retrieval). The chapter closes with a brief generalization of two dimensional coherent imaging to three dimensional imaging by tomography.
Science, for me, gives a partial explanation for life. In so far as it goes, it is based on fact, experience and experiment.
– Rosalind Franklin
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 X-ray Propagation
Coherent X-ray imaging is based on wave-optical propagation of electromagnetic waves, including free-space propagation and the interaction of short wavelength light with matter. Here we present an overview of fundamental principles of X-ray imaging and field propagation, with references to relevant literature. We first justify the use of scalar wave theory and approximations of paraxial (parabolic) wave equations. Then we show how to compute the wavefield at a distance d along the optical axis z with respect to a known field distribution in a plane at \(z=0\), assuming free space between planes \(z=0\) and \(z=d\). Next, we address the projection approximation which is ubiquitous in X-ray imaging to describe the complex transmission function of an optically thin object. Finally, we present finite difference equations as a more general tool to treat X-ray propagation in matter and objects which cannot be approximated as thin.
1.1 Scalar Diffraction Theory and Wave Equations
Propagation of stationary X-ray fields in matter can be described by the well-known Helmholtz equation (HE)
with vacuum wave number \(k = \omega / c\), vacuum speed of light c, angular frequency \(\omega \), and the complex refractive index n of the propagation medium. Here, \({\mathbf {E}}(\mathbf {r}, \omega )\) denotes the time-domain Fourier transform of the electric vector field \(\mathbf { \mathcal {E} } (\mathbf {r}, t)\)
The HE in the homogeneous form of (2.1) is derived from Maxwell’s equations for stationary fields in media, which are homogeneous, isotropic, non-magnetic, non-conductive, and do not contain free charges. Further, the field intensity has to be sufficiently small to neglect the non-linear response of matter. While this derivation assumes a constant or at least piecewise constant index of refraction, the HE is still an excellent description even for \(n \rightarrow n({\mathbf {r}})\), i.e. spatially varying distributions of matter as in an object to be imaged or in an optical device (refractive lens, zone plate, waveguide). Also in a crystal, where the continuum approximation of the index of refraction \(n({\mathbf {r}})\) must certainly break down, Fourier expansion with respect to the lattice vectors, still allows using (2.1). Indeed, propagation in a source-less but inhomogeneous medium with spatially varying dielectric function \(\epsilon ({\mathbf {r}})\) (equivalently magnetic permeability \(\mu ({\mathbf {r}})\)) is well described by (2.1). This is surprising, since inhomogeneous media result in an inhomogeneous wave equation with corresponding source terms on the right hand side of (2.1). Certainly, in an inhomogeneous medium \(\epsilon ({\mathbf {r}})\) is not a slowly varying function on scales of the X-ray wavelength. However, the approximations used to derive the HE are rescued by the simple fact that the X-ray index of refraction in matter is very close to the vacuum index of refraction, i.e. \(\epsilon \simeq \epsilon _0\) and \(\mu \simeq \mu _0\) for X-rays. This is both a curse and a blessing. It is a blessing, because the weak interactions result in the bulk penetration capability for which hard X-rays are famous, as well as the beneficial approximation of kinematic diffraction, which often warrants a quantitative reconstruction. Note that multiple scattering events can be safely neglected in most X-ray imaging applications, contrary to electron and visible light optics. Yet, at the same time, weak interaction is a curse, because it severely limits our ability to create efficient optical elements such as focusing devices.
Let us therefore briefly consider the (continuous) index of refraction \(n (\mathbf {r})= 1-\delta (\mathbf {r}) +i\beta (\mathbf {r})\). Compared to other regions in the electromagnetic spectrum, the high frequency of X-rays manifests itself in extremely small dispersion \(\delta \ll 1\) and absorption decrements \(\beta \ll 1\), describing the phase shifts and absorption in matter, respectively. For a given element and atom density \(\rho _a\), the refractive index is given in terms of the atomic form factor
where Z is the atomic number, \(r_e= {2.82 \cdot 10^{-15}}\mathrm{\,m}\) the Thomson scattering length; \(f^{\prime }(\omega ) \ll Z\) and \(f^{\prime \prime }(\omega ) \ll Z\) are the dispersion and absorption corrections. For mixed elemental composition, the indices are weighted averages according to the local stoichiometry of elements.
Next, we want to justify scalar wave theory for X-rays. Strictly speaking, we have to solve the HE for all components of the electric and magnetic field: \(\forall \, \psi \in \left\{ E_x, E_y, E_z, B_x,B_y,B_z \right\} \). In general, the field components are coupled (since they have to obey the full Maxwell system and/or different boundary conditions). For example, given the HE for the electric field in (2.1), the solution must also fulfill
Instead, in scalar wave theory, one often treats only a single component
Note that this form can be further simplified to a second-order ordinary differential equation, if one takes a two-dimensional Fourier transform with respect to the perpendicular space directions \(\mathbf {r}_\perp := (x ,\; y)^T\)
with \(\tilde{ \psi } = \mathcal {F}_{\mathbf {r}_\perp }[\psi ](\mathbf {k}_\perp )\) and \(\beta := \sqrt{k^2 n^2 - k_\perp ^2 }\) [1]. Scalar wave theory is ubiquitous in X-ray optics and X-ray imaging, but permissible only if polarization effects can be neglected and field propagation of different polarization states is equivalent. This is the case for many applications (apart from propagation in crystals for example), since the relevant diffraction angles are much smaller than the Brewster angle.
Given a solution \(\psi \) of the scalar HE in (2.5), how do we obtain meaningful solutions and permissible polarisation states in terms of \(\mathbf {\mathcal {E}}\) and \(\mathbf {\mathcal {B}}\)? As shown in [1], one can construct solutions of the Maxwell system by setting \({{\psi }} = \psi \, \mathbf {e}_p\) for any unit vector \(\mathbf {e}_p\), and then compute
General solutions can be constructed from linear combinations of three independent scalar potentials \(\psi _x,\psi _y,\psi _z\) so that \(\psi = \psi _x \mathbf {e}_x + \psi _y \mathbf {e}_y + \psi _z \mathbf {e}_z\). For the special case of paraxial waves which can be written as the product of a slowly varying envelope \(u(\mathbf {r})\) and a fast oscillating term (see Fig. 2.1) with the wavevector pointing in direction of the optical axis \(\mathbf {e}_z\), i.e. \(\mathbf {k} = k \mathbf {e}_z\), i.e. propagation axis along z, we have
and the corresponding electromagnetic field vectors are \({\mathbf {E}} \approx n \psi \, \mathbf {e}_x\) and \({\mathbf {B}} \approx \frac{n^2}{c} \psi \, \mathbf {e}_y\) [1]. Given the numerically computed scalar field, the local (time-averaged) energy flux density also follows from the full electromagnetic field [1] via the Poynting vector
where \(\mu _0\) is the free-space permeability. The energy flux density (averaged or integrated over the exposure time) is often denoted as the optical intensity. For time-harmonic fields and requiring Hermitian symmetry \({\mathbf {E}}(-\omega ) = {\mathbf {E}}^*(\omega )\), one can write the field based on a discrete sum of frequencies \(\omega _i\) for \(i \in \mathbb {N}\)
and the equivalent expression for \(\mathbf {\mathcal {B}}\), which is a starting point to compute \(\mathbf {S}\). When the fields are constructed from a single scalar potential \(\psi \), which is slowly varying in direction of \(\mathbf {e}_p\) such that \(\Vert \mathbf {\nabla }(\mathbf {e}_p \cdot \mathbf {\nabla }\psi ) \Vert \ll |n^2 k^2 \psi |\), the time-averaged Poynting vector can be approximated as [1]
with \(k_i = \omega _i / c\). For paraxial beams it then follows
Hence, for a monochromatic paraxial beam, the magnitude of the time-averaged Poynting vector, i.e. the optical intensity I, can be written as [1]
with an energy flow oriented in direction of the phase gradient.
The above approximation of the Poynting vector was derived under the assumption of paraxial waves. Indeed, many X-ray optical problems are well described by forward directed paraxial diffraction. Thus, we can further approximate the scalar HE and arrive at the parabolic wave equation. To this end, we start with a separation ansatz for solutions of the HE in case of waves \(\psi (\mathbf {r})\) propagating along the optical axis z
where \(u(\mathbf {r})\) is the (slowly varying) envelope of the wave field \(\psi (\mathbf {r})\). For X-rays in particular, we are often not interested in the rapidly oscillating term which changes sign on atomic length scales, and which is as irrelevant as the time-harmonic term. Instead, in numerical computation and plots, we are only interested in phases and amplitudes of \(u(\mathbf {r})\), which are well suited to monitor the small phase and intensity changes building up over many hundreds and thousands of atoms, see Fig. 2.1. Inserting (2.13) into the HE yields a differential equation for the envelope u
Working out the differential operators of the left-hand term
and dividing by \(\mathrm {e}^{ikz}\), we obtain
For paraxial beams, the second order derivative in z can be neglected, given \( \left| \frac{\partial ^2 u}{\partial z^2} \right| \ll \left| k \frac{\partial u}{\partial z} \right| \) since \(\partial _z^2 u \ll k^2 u\), leading to the paraxial (or parabolic) wave equation
The parabolic wave equation reduces to
in free space with Gaussian beams as a well known family of solutions. Compared to the elliptic Helmholtz equation, its parabolic approximations offer higher numerical stability. Furthermore, solutions are more easily accessible in terms of boundary conditions. Initial values have to be specified in a plane at small z along with lateral boundary conditions, but no values at the high z boundary of the computational domain are required. For these reasons, paraxial approximations have become an important tool in X-ray optics [2,3,4], including generalizations to time-dependent propagation problems via the spectral approach [1]. As in Schrödinger’s equation, the parabolic wave equation can be rearranged to
This form of the paraxial wave equation is typically used in X-ray optics.
Turning back to the Helmholtz equation formulated as in (2.6), we complete this section by presenting a slightly different form of the parabolic wave equation, put forward in [1] and based on the approach in [5]. Due to the less restrictive approximations necessary for its derivation, we expect this form to have a larger range of validity. In particular, the assumption \( \left| \frac{\partial ^2 u}{\partial z^2} \right| \ll \left| k \frac{\partial u}{\partial z} \right| \) (or correspondingly \(\partial _z^2 u \ll k^2 u\)) is not required anymore. The differential operator in (2.6) can be written as a product of two operators
The scalar HE is hence solved by a solution \(\tilde{\psi }\) of either of the differential equations (forward and backward HE)
In the context of paraxial beams, we are interested in the right equation describing a wave vector oriented in \(\mathbf {e}_z\) direction. Further, for paraxial beams, the support of \(\tilde{\psi }\) is constrained to low spatial frequencies with \(k_\perp ^2 \ll k^2\). Therefore, one can approximate the square root in \(\beta \) through its first-order Taylor series around \(k_\perp ^2 = 0\) [1]
Substitution into (2.20) (right) and transforming back to real space results in [1]
Equation (2.21) can again be formulated for the envelope u, defined by \(\psi = u \, \exp (- i k z)\) [1]
For \(n= 1\), (2.22) and (2.19) become identical. As a consequence in the regime of hard X-rays, solution of equations (2.22) and (2.19) will not differ. Yet, for soft X-rays, the difference could become relevant.
1.2 Propagation in Free Space
We first address the propagation in free space, following the angular spectrum approach as presented in the textbook of Paganin [6]. Again, we assume a time independent, monochromatic wave, i.e. we treat a single component \(\psi _\omega (\mathbf {r})\) of the spectrum with angular frequency \(\omega \) and corresponding wavelength \(\lambda \). A general time-dependent field of finite bandwidth is then computed as superposition of its monochromatic components by
As discussed above, the single spectral component \(\psi _\omega (\mathbf {r})\) must obey the free-space Helmholtz equation
where we have dropped the subscript \(\psi _\omega \rightarrow \psi \) for simplicity of notation. Particular solutions of the Helmholtz equation are plane waves
where \(k^2 = k_x^2 + k_y^2 + k_z^2 = \frac{4 \pi ^2}{\lambda ^2}\). The z-dependent part of the plane wave can be separated by
The last equation entails an important message: Knowing the plane wave in the source plane \(\psi _P (x,y,z=0)= \exp \left[ i(k_x x + k_y y) \right] \), the electromagnetic field at any distance z can be calculated by a simple multiplication with the so-called “free-space propagator”\(~\exp \left[ iz \sqrt{k^2-k_x^2-k_y^2} \right] \). To propagate an arbitrary wave field \(\psi \), we express \(\psi \) given in plane \(z=0\) by its Fourier transform \(\hat{\psi }( k_x, k_y, z=0 )\)
This Fourier transform can be read as a superposition of plane waves. Since we can expand (almost) any wave field of interest in such a Fourier integral in the source plane and since we know how to propagate plane waves, we also know how to propagate general wave fields. It is thus possible to compute the field at any distance z from the given field in the xy-plane at \(z=0\). This allows interpreting an electromagnetic disturbance in a plane at \(z=0\) as a superposition of plane waves of fixed modulus of the wavevector leaving the plane of interest under different angles
Angular spectrum approach for propagation of arbitrary wavefields. A wavefield in the source plane is decomposed into plane waves propagating under different angles (2.28) with respect to the optical axis. Each plane wave can be propagated by application of the free-space propagator
see also Fig. 2.2 and [7]. Each of these plane waves can be propagated from \(z=0\) to any distance \(z>0\) by multiplication with the free-space propagator
Next, we restrict the wave fields of interest to paraxial waves, i.e. those which propagate at small angles with respect to the optical axis z. In this case, \(k_x\) and \(k_y\) are much smaller compared to \(k_z\). As a consequence, we can approximate the free-space propagator by
where
Using (2.30) and formulating (2.29) as an operator-equation the propagated field at distance z is
where \(\mathcal {F}\) is the Fourier transform with respect to the xy-plane. Application of the Fourier convolution theorem to (2.32) and expansion of the exponent in the integrand leads to the Fresnel diffraction integral
The chirp function \(\exp \left[ \frac{ik}{2z} \left( x^{\prime 2} + y^{\prime 2}\right) \right] \) merits a closer look. Reformulating the argument of the exponential function results in
The term \((x^{\prime 2} + y^{\prime 2})\) ‘measures’ the squared spatial cross-section of features in the input wavefield. Let a be the smallest such structure of interest, so that the argument of the exponential, the so-called chirp, is governed by the dimensionless ratio \(\frac{a^2}{\lambda z} =:F\) called the Fresnel number. For large propagation distances (compared to wavelength and a), the Fresnel number approaches zero and hence the chirp function is close to unity: The Fresnel diffraction integral becomes the Fourier transform of the wavefield. This limiting case is known as the Fraunhofer far field approximation. Fresnel numbers close to one indicate the optical near field: The chirp function cannot be neglected. Indeed, as we will see below, it is the chirp function that makes numerical free-space propagation challenging. Importantly, paraxial propagation is governed only by a single parameter F, so that all simulations can be carried out in natural units of pixel size and with a single unitless parameter F.
Before we turn to numerical implementation, however, a brief comment on the choice of relevant feature size a is reasonable. A natural choice in the discrete setting of numerical calculations is the pixel size \(a=\varDelta x\). The Fraunhofer regime \(F\ll 1 \) is then quickly reached with increasing z. These ‘far field’ holograms, however, do not look like far field diffraction patterns (squared Fourier transform of the object), which is usually associated with the Fraunhofer approximation. The reason is that there is always another length scale a to be considered, namely the beam size. Only when the Fresnel number—computed for all object length scales and the length scale of the beam—is much smaller than one, we get the conventional Fraunhofer diffraction pattern without mixing of object wave and primary wave.
a Illustration of the hologram created by a single point in plane wave illumination (parallel beam), and b the equivalent for spherical wave illumination (cone beam). According to the Fresnel scaling theorem, the holograms are identical up to a simple variable transformation, including the geometric magnification M and an effective defocus distance \(z_\text {eff}\). c Cone beam geometry in unitless variables, taking a Gaussian beam as an example for a coherent and divergent beam, see text for explanations
1.3 The Fresnel Scaling Theorem
Consider a setting where an object is illuminated by the incident wavefield \(\psi _i\). Two limiting cases of the illumination geometry are of particular importance: plane wave illumination and spherical wave illumination. The spherical beam geometry (also denoted as cone-beam geometry) can be used to implement radiography at the nanoscale, well below the resolution limit of the detector pixel size \(\varDelta x\). As sketched in Fig. 2.3a, b, this requires X-ray nano-focusing optics [8, 9], as presented in Chap. 3 and a defocus geometry with object and detector positioned behind the focus at distances \(z_{01}\) and \(z_{02}\), respectively, see also Chap. 13. Focusing serves two purposes: Firstly, the photon density is increased in the object plane, as long as the defocus position is smaller than the focal length of the optic \(z_{01} \le f\). Secondly, it magnifies the near field pattern (hologram) and thus enables a resolution below the detector pixel size \(\varDelta x\). To discuss the effect of the spherical illumination function \(\psi _i\) and following the projection approximation, we slightly rewrite the input wavefield as a product of illumination and a complex-valued object transfer function \(\psi _\omega (x^\prime ,y^\prime ,0) = \psi _i (x^\prime ,y^\prime ,0) \tau (x^\prime ,y^\prime )\) and insert it in (2.33) yielding
where \(z_{12} := z_{02} - z_{01}\) denotes the distance between object and detector. For simplicity of notation, the subscript \(\omega \) was skipped, and the prefactors were abbreviated by the complex valued \(A(\mathbf {r})\). The factorization underlying the projection approximation will be justified further below. Equation (2.33) essentially describes the case of a plane wave incident illumination \(\psi _i=e^{ikz}\) with \(\tau (x^\prime ,y^\prime ,0)=\psi (x^\prime ,y^\prime ,0)\), i.e. no sample in the beam path. However, for point source illumination with
the integral becomes
where \(A(\mathbf {r})\) may also account for the amplitude decrease of the spherical wave. With the geometric magnification given by
and the definition of an effective propagation distance \(z_\text {eff}\)
we obtain
i.e. wave propagation is equivalent in plane and spherical geometry, if a simple coordinate transformation is performed. This result is known as the Fresnel Scaling Theorem (FST). Following the FST, numerical propagation which will be discussed in the next section, is always performed in the effective parallel beam coordinate system. But before doing so, we note down an immediate consequence of spherical beam propagation, which is also illustrated in Fig. 2.3. While the Fresnel number F decreases with increasing distance between object and detector, the opposite is true for the divergent beam setting. As \(z_{01}\) is reduced (at constant \(z_{02}\)), the imaging regime becomes more and more holographic (decrease in F) since the decrease in effective pixels size \(\varDelta x_\text {eff}=\varDelta x/M\) enters quadratically and outweighs the effect of \(z_\text {eff}\). For the minima of the contrast transfer function, which will be discussed further below, this means that their number increases as \(z_{01}\) is decreased (or equivalently M is increased), see the dashed lines in Fig. 2.3c. In order to plot the divergent beam geometry in unitless variables, the intensity of a Gaussian illumination can serve as a model for the diffraction limited beam
with waist \(w_0\), \(w(z)=w_0 \sqrt{1+(z/z_R)^2}\) and Rayleigh length \(z_R=w_0^2 \pi /\lambda \). Next, we parameterize the position of the object along the optical axis by \(Z=z_{01}/z_{02}=1/M\), such that this inverse magnification varies between \(1/M_\text {max}=z_R/z_{02}\) and one. The corresponding lateral width of the beam varies between \(w_0\) and \(w_\text {max}= \alpha z_{02}\), with divergence \(\alpha \) defining the numerical aperture. In unitless variables we designate the beam width by \(W=w(Z)/w_\text {max}\), and plot W as a function of 1/M on double-logarithmic scale, see Fig. 2.3c. Accordingly, the blue line shows the increase in beam width, while the orange line designates the effective pixel size \(\varDelta x_\text {eff}= (\varDelta x/z_{02}) z_{01}\), i.e. the demagnification size of a single detector pixel. In unitless variables this line reaches \(W=\varDelta x/w_\text {max}\) for \(Z=1\) and crosses the dashed red horizontal line at \(Z=w_0/\varDelta x\). The dashed red line separates lateral length scales which can be resolved (above) from those which are unresolved (below), based on the limited numerical aperture (N.A.).
1.4 Numerical Implementation of Free-Space Propagation
The numerical implementation of free-space propagation is not trivial. In particular, sufficient sampling of chirp functions has to be guaranteed. Extensive literature can be found at [7, 10, 11]. There are two main options to implement propagation. The first uses two Fourier transformations and has equal coordinate systems in source and destination plane, the second is based on a single transformation and can work with differently sized and sampled planes. We start with the first option, which is based on (2.29), according to which propagation can be designed as a filter operation of the wavefield in Fourier space. The corresponding filter is the free-space propagator, which is given by (2.31) in paraxial approximation \(G_k(k_x, k_y; z)\) as a function in reciprocal space. The propagator function can also be written down analytically in real space (called the impulse response function), and then be numerically Fourier transformed. Importantly, the coordinate system of input and output field are identical, and the propagation is based on two fast Fourier transform (FFT) operations. For the second approach, the propagation can be directly calculated based on (2.33), involving a single Fourier transform, either by a single FFT or by other numerical solutions of the Fourier integral, e.g. for non-equidistant sampling. This approach is well suited for cases where the pixel sizes between input and output must vary, e.g. to cover the field of view in a detector after diffraction broadening.
Next, we consider the sampling criteria for the first method. In order to correctly sample the free-space propagator or reciprocal space chirp, the real space sampling interval \(\varDelta x\) has to be [11]
where L is the field of view consisting of N pixels: \(L = N \varDelta x\). Hence, only a large number N of pixels or a short propagation distance result in aliasing-free sampling of the propagated field. To find a remedy, one can artificially increase the number of pixels. Yet, this drastically decreases the computational speed. Alternatively, one can also write down the impulse response function, i.e. the real space counterpart of the reciprocal space chirp:
The corresponding sampling criterion is [11]
Violation of the last equation results in periodic copies of the chirp interfering with each other. A way out is to use a suitable window function to limit the chirp [7, 12]. Following (2.28) and [7], the highest angle under which plane waves can be emitted is given by
In the discrete version of the Fourier transform, the Shannon sampling theorem is fulfilled by the relation
The highest resolvable spatial frequency corresponds to an oscillation that extends over two real space pixels, or equivalently
Hence, the largest properly sampled angle \(\theta _\text {max}\) under which radiation is emitted is given by
A useful window function to be multiplied with the real space chirp is [7]
Finally, we consider the sampling requirement for the second propagation approach, based directly on the Fresnel diffraction integral. This requires sampling of chirp functions in the source plane.
In fact, if only intensity in the destination plane is of interest, the observation chirp does not need to be sampled. Further, instead of a destination plane, the output field should be regarded as a function of spatial frequencies, rather than spatial coordinates of the detector. In this way one can dispense of the observation chirp altogether.
1.5 X-ray Propagation in Matter
After considering propagation in free space, the next challenge is to conceptualize the interaction of X-rays and matter as well as to give suitable approximations to compute stationary wave propagation in matter. For wave propagation, we are not interested in incoherent and inelastic interaction processes such as Compton scattering, nor in the cascade of processes following photo absorption of X-ray photons [13, 14], but only in the elastic scattering events of atoms which collectively result in diffraction and refraction effects. For X-ray imaging, matter mainly has two functions: either optical component or sample/object of interest. If objects and optical components are sufficiently thin so that propagation effects (also called volume effects) can be neglected, the propagation effects can be described by a simple multiplication, as shown below. For a more general case, (2.16) or (2.17) have to be solved for the paraxial case. This is a formidable task and analytical solutions only exist for a few very special cases (sphere, slab waveguide). Neglecting atomic-scale variations which would become important only for perfect crystals, we can write the index of refraction in continuum approximation as in (2.3) with the real-valued decrement or dispersion term \(\delta \) given by [13]
where \(\rho _a\) is the number density of atoms, \(r_0=2.82 \cdot 10^{-15}\)m the Thomson scattering length, Z the number of electrons in the atom and \(f^{\prime }(E)\) the real part of the atomic form factor correction at energy E. For the imaginary part (absorption term) \(\beta \) we have
with \(f^{\prime \prime }(E)\) being the imaginary part of the atomic form factor. Note that form factors and their dependence on photon energy E are tabulated for each element in the International Tables for Crystallography and are also available online.Footnote 1 Away from absorption edges, the real part of \(n(\mathbf {r})\) only depends on the total electron density (summed over all elements)
Due to the small value of the Thomson scattering length resulting in \(\delta \ll 1\), diffraction and refraction effects in the X-ray spectral range are weak, and hence there is ample room for approximations, notably the ansatz by Born or the ansatz by Rytov, which are discussed in view of X-ray propagation in [15,16,17].
Within the first order of the Born approximation, we can neglect multiple scattering if the sample is sufficiently thin and consider the scattering \(\psi _s(\mathbf {r})\) as a small additive correction to the primary wave \(\psi _0(\mathbf {r})\), i.e.
For a far field observation point, the scattered wave is given as a Fourier transform of the scattering length density, i.e. \(r_0 \rho \), with \(\rho \) being the electron density and \(r_0\) the Thomson scattering length
where \(\mathbf {q}\) is the scattering vector. Alternatively, according to the Rytov ansatz, we can also write the solution in a multiplicative form as
where \(\varphi _s(\mathbf {r})\) is the complex-valued phase of the scattered field and \(\psi _0(\mathbf {r})\) again the primary wave amplitude without perturbation by the object. Rytov’s approximation then requires \(\vert (\nabla \varphi _s)^2 \vert \ll \vert \tau \vert \), with the object function defined as \(\tau (\mathbf {r}) = k_0^2 (1-n(\mathbf {r}))\), where \(k_0=2\pi /\lambda \). One can compute \(\varphi _s\) from \(\tau \) using the Green’s function \(G(\mathbf {r}) = \exp ( ikr) / (4\pi r)\) [17]
which in frequency space gives [17]
For paraxial propagation with \(\sqrt{k_0^2-k_x^2 -k_y^2} \simeq k_0 \left( 1-\frac{k_x^2}{2 k_0^2} - \frac{k_y^2}{2 k_0^2} \right) \), and for objects with thickness \(\varDelta z\) sufficiently small it can be shown that [17]
This last idea of considering the limit of small object thickness, is extremely useful and shall be approached in even simpler terms. To this end, let us first consider a plane wave \(\exp (ikz)\) incident at \(z = 0\) onto a homogeneous slab of thickness \(\varDelta z\), the wavefield behind the object (outgoing wave) can then be written as
where \(\exp (-ik_0 \delta \varDelta z)\) describes phase shift and \(\exp (-k_0 \beta \varDelta z)= \exp (-\mu \varDelta z /2)\) absorption of the wave in the medium (absorption coefficient \(\mu \)). For an inhomogeneous medium and negligible diffraction inside the specimen, the complex-valued transmission function of a slab can then be expressed by the integral along the optical path
The underlying approximation is known as the projection approximation. Its basic assumption is that the value of the wavefield is entirely determined by the phase and amplitude shifts accumulated along streamlines of the unscattered beam. In doing so, the spread of the wave by diffraction inside the sample is ignored. Thus, this is correct only down to a certain sample size, depending on the resolution element and photon energy E. The projection approximation is valid for sufficiently small spatial frequencies, fulfilling
where \(\varDelta T\) denotes the thickness of the object. Propagation through arbitrary objects can be treated by sequences of small projection and propagation steps, as if matter came in form of thin slices lined up along the optical axis (multi-slice approach). For further details of this method see [1, 18]. A different approach to solve propagation through matter is propagation by finite difference equations which is presented below. Finite difference propagation and the multi-slice approach have been compared in [1].
1.6 Propagation by Finite Difference Equations
Next, we will present the basic scheme of finite difference equations (FD) for propagation in the framework of the paraxial wave equation. As the paraxial wave equation is a parabolic partial differential equation, initial and boundary data are required for its solution. But in contrast to elliptic equations such as the Helmholtz equation, there is no data required on a closed boundary. In other words, we can propagate from left to right along the optical axis, and we expect causality in the sense that the field is only determined by what has happened upstream, but not downstream. For two dimensional propagation problems (one dimension for the optical axis z plus a single lateral direction x), i.e. if the index of refraction is independent of y, following (2.19), the parabolic wave equation can be written as
where
a Three dimensional distribution of the refractive index in a voxelated space. The optical axis is parallel to the z axis and X-rays (wavevector \(\mathbf {k}\)) are impinging on the sample. b Wave propagation using finite difference equations solved by the Crank-Nicolson algorithm. Boundary conditions/initial values are represented by thick gray lines. Colored regions denote regions of different refractive index. Note that because the parabolic wave equation is used, no boundary conditions for \(u(x,z_{N_z}+1)\) need to be set. In order to compute \(u_k^{n+1}\), the values \(u_k^{n},\,u_{k-1}^{n},\,u_{k+1}^{n},\,u_{k-1}^{n+1},\,u_{k+1}^{n+1}\) are required
with boundary conditions
where \(u_0(x,0)\) is the field in the initial plane, while \(u_0(x_0,z)\) and \(u_0(x_{N_x},z)\) are the bottom and top boundary conditions to be specified along lines parallel to the optical axis, at the sides of the computational field of view. The computational field of view is modeled such that it has \(N_x+1\) grid points in the lateral direction x, and \(N_z+1\) grid points along the optical axis. Importantly, and contrarily to elliptical partial differential equations, no values have to be set for \(u_0(x,N_z+1)\). The initial-boundary-value problem given in (2.63) and (2.66) can be solved numerically using finite-difference schemes [3, 19]. Here, the crucial point is the update scheme (‘stencil’), see Fig. 2.4b. For the two dimensional case (one dimension for the optical axis, one lateral dimension), the stencil introduced by Crank and Nicolson [20] gives second order accuracy in steps \(\varDelta z\) along the optical axis and \(\varDelta x\) perpendicular to the optical axis [21]. Accordingly, (2.63) is approximated by the following finite-difference expressions [3]
with \(u_k^n=u(x_k,z_n)\) and \(C_k^{n+\frac{1}{2}}=C(x_k,z_{n+\frac{1}{2}})\), resulting in the finite-difference equation [3]
Furthermore, we abbreviate
and (2.70) may now be written as a system of \(N_x-1\) linear equations [3]
with
and
Since \(\mathbf {d}^n\) has no field values with index \(n+1\) except for \(u_0^{n+1}\) and \(u_{N_x}^{n+1}\), which are set by the boundary conditions (2.65) and (2.66), it is possible to compute the field in plane \(n+1\) from plane n, by solving a system of \(N_z-1\) linear equations. Furthermore, because \(M^n\) is tridiagonal, this can be carried out with \(\mathcal O(N_x)\) operations [21]. Finally, the process is repeated sequentially for all \(N_z\) grid points, resulting in numerical complexity \(\mathcal O(N_x\times N_z)\). The update scheme for propagation in three dimensions (3d) (i.e. 2d \(+\) 1d) is described in [1, 22, 23].
2 Coherent Image Formation
In early years, electron microscopy was severely limited by aberrations of electromagnetic objective lenses. To overcome these difficulties, D. Gabor proposed lens-less imaging by inline holography in 1948, inspired by L. Bragg’s ideas of a coherent projection X-ray microscope, see [24] for a historical perspective. Gabor demonstrated his idea of coherent imaging without optics with visible light [25]. Instead of recording sharp images with a lens-based system, the (near field) interference pattern behind a (semi-transparent) object was recorded on a photographic plate. The pattern originates from interference of the direct beam passing through the object with the secondary waves diffracted by the object. Illuminating the (reversed) photographic plate, i.e. using the photographic plate as an object resulted in a clear image of the sample. In Gabor’s time, this type of holographic reconstruction was by necessity of analogue optical nature, whereas nowadays a hologram recorded by a detection device can be reconstructed numerically.
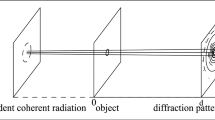
Illustration of coherent diffractive imaging (optical far field) and holographic full field imaging (optical near field). a In conventional diffraction from crystalline or non-crystalline specimen, intensity scattered to high angles is measured and the direct beam is blocked. b Contrarily, holography uses the interference between diffracted waves and the direct beam, such that phase information is encoded in the intensity pattern. Note that the techniques require different detectors: single photon counting detectors with a large numerical aperture are preferred for (a), while (b) requires high resolution detection devices such as scintillator-based cameras
While in electron microscopy the lens problems were eventually overcome, a similar challenge appeared in X-ray microscopy: X-ray lenses (diffractive or refractive) lack the efficiency and numerical aperture which we are used to from visible light lenses. At the same time, X-rays are attractive as a microscopy probe owing to short wavelength and hence potentially high resolution as well as high penetration power. Therefore, Gabor’s idea of coherent lens-less imaging re-emerged in X-ray optics and microscopy, once that radiation of high brilliance and sufficient coherence became available by synchrotron sources, in particular after the invention of undulators. In contrast to coherent diffractive imaging (CDI), where the primary beam is blocked behind the sample and the diffracted radiation is recorded without interference with the primary or reference wave, and in direct analogy to Gabor’s setup, X-ray holography is based on the interference between primary and scattered waves on the detector (see Fig. 2.5).
2.1 Holographic Imaging in Full Field Setting
Inline holography is a full field imaging technique, in which many resolution elements of object and detector are illuminated in parallel, typically employing a mega-pixel detector with sufficiently small pixel size to record the fine interference fringes between scattered and primary waves. While the field of view (FOV) can of course be further increased by lateral scanning, an image of large FOV can be acquired in a single exposure. This is in contrast to coherent techniques which are based on scanning the object in a focused beam, or which require a fully coherent illumination and are therefore limited to a correspondingly small field of view. For this reason, holographic imaging is of significant advantage in particular for tomography, where compared to the net counting time, motor overhead and detector readout for three degrees of freedom become a dominant time factor in recording data. Furthermore, time-resolved imaging is more easily implemented in parallel than serial acquisition.
Two geometries are commonly used for inline X-ray holography: (quasi-) parallel and (quasi-)spherical illumination. The first case is implemented at synchrotron beamlines using almost the full undulator beam without focusing. The divergence is then small enough so that in the object and detector plane the beam is almost of the same lateral size. The FOV is adjusted by slits upstream from the object. This geometry is used for holography/tomography of large objects with resolution elements at the size of the detector pixels.
The second case is cone beam illumination used for high resolution holographic imaging, since it offers variable geometric magnification and FOV by adjusting the distance between focus and object, the so-called defocus distance. Resolution elements are of the detector pixel size scaled by the inverse geometric magnification. Figure 2.6 illustrates magnification and contrast evolution for a phantom consisting of an assembly of spheres. The Fresnel scaling theorem was used to compute the contrast in an effective parallel beam setup which is numerically more convenient.
a Cone-beam setting for holographic full field imaging. The object is illuminated by diverging wavefronts. b Placing the sample at different defocus positions results in oscillatory contrast of spatial frequencies in the recorded holograms. c–e Illustration of the effect of geometrical magnification: Placing the sample close to the focus (c) increases magnification and the number of contrast oscillations when plotting the CTF as a function of spatial frequency (dark blue curve in b). Placing the sample closer to the detector (d–e) decreases magnification and reduces the number of contrast oscillations (light blue and cyan curves in b)
2.2 Contrast in X-ray Holograms
As discussed above, elastic interaction of light and matter can be accounted for by the complex-valued index of refraction, which we rewrite here as
to stress its wavelength dependency. For forward scattered radiation and away from absorption edges, \(\delta \) is directly proportional to the electron density \(\rho \) of the sample [13]
with the classical electron radius \(r_0\). In this (often warranted) approximation, \(\delta \) varies quadratically with wavelength, independent of sample stoichiometry, in contrast to the imaginary part of the index of refraction \(\beta (\lambda )\), which strongly depends on the elemental composition and also exhibits much larger jump discontinuities at absorption edges. For hard X-rays and low-Z materials such as in soft and biological matter, \(\delta (\lambda )\) is up to three orders of magnitude larger than \(\beta (\lambda )\). For this reason, interference contrast in holograms due to phase shift often dominates over absorption contrast. By enhancing radiographic imaging with phase contrast, fine details of weakly absorbing components become detectable, which would otherwise be invisible in classical absorption based X-ray radiography. The effect of the object on the phase of the so-called exit wave \(\psi _\lambda (x,y)\) directly behind the object, becomes apparent by considering a monochromatic plane wave (wavelength \(\lambda \)) passing through an object which is homogeneous in z and has a thickness \(\varDelta T\):
where \(k=\frac{2\pi }{\lambda }\) and \(\mu (\lambda , x,y)\) is the absorption coefficient with \(\mu = 2k\beta \). Neglecting absorption and replacing \(\delta \) by (2.74) results in
Phase retrieval techniques aim at recovering the phase in the exit plane
from measured intensity distributions. By (2.77), it becomes clear that the phase of the exit plane is directly proportional to the local electron density, if the object is homogeneous in z. More generally, for inhomogeneous (thin) objects, the phase is proportional to the projected electron density, as \(\int \rho (x,y,z) dz\).
The lateral distribution of \(\varphi (x,y)\) then results in diffraction behind the object, and as the wave propagates, the phase information is converted to an intensity pattern. The relative contrast of features on different length scales (spatial frequencies) is found to change in a characteristic manner with the free-space propagation distance between object and detector, or more generally with Fresnel number. This evolution of contrast can be analyzed by inspecting the Fourier transform of the hologram. What one finds is an oscillatory contrast as a function of spatial frequency. For an optically weak object (i.e. weakly varying phase and small absorption) it can be shown that in Fourier space, intensity is given as a linear combination of the object’s phase and absorption map [26,27,28,29]
with z the distance between sample and detector and \(k=2\pi \nu \) the angular spatial frequency in the object plane. To obtain this linear relationship, the signal is normalized to the incident plane, subtracted by one. If the diffraction of the illuminating wave is neglected, the expression can be generalized to an inhomogeneous illumination field \( I_0 \rightarrow I(x,y,0)\), see [30, 31] for a discussion of empty beam division. The structure of (2.78) suggests to define linear filter functions describing the evolution of contrast. For the case of weak phase objects (i.e. with weakly varying phase and negligible absorption), the contrast transfer function (CTF) can be defined as
where \(\mathcal {F}\left[ \varphi (x,y,\lambda )\right] \) is the Fourier transform of the object function and
If phase and absorption are proportional in each pixel (single material object), this can be generalized to [26, 28, 29]
Once absorption becomes important, the cosine term is non-negligible including a scaling with the ratio \(\frac{\beta }{\delta }\), i.e. the ratio between energy dependent absorbing and phase shifting properties of the sample [28, 29]. Note also that spatial frequencies \((\nu _x,\nu _y)\) are now expressed in natural dimensionless units, by \(\nu =k a/2\pi \) with a the pixel size. In this way, the dependence on the Fresnel number \(F = \frac{a^2}{\lambda z}\) is highlighted. The spacing of discrete sampling points in reciprocal space is \(\varDelta \nu = 1/N\), with N being the number of pixels in horizontal or vertical direction. An illustration is provided in Fig. 2.6, showing holograms simulated for different distances and magnification in cone-beam geometry (a), with corresponding phase \(\text {CTF}_p\) (only the sine part of the CTF) for the three indicated positions or equivalently F (b). Holograms for the three object positions are shown in (c–e). When the Fresnel number is large, the image contrast is dominated by edges (edge enhancement). For example, the cyan curve in (b) is maximal at high spatial frequencies and hence edges in (e) are enhanced with respect to areas. Shifting the sample closer to the source (light blue and dark blue curves in (b) and holograms in (c–d) shows oscillating contrast for lower image frequencies than in (e).
3 Solving the Phase Problem in the Holographic Regime
Consider holographic intensity distributions as shown in Fig. 2.6. If phase and amplitude were directly measurable by a detector, the complex wavefield could be numerically back-propagated to obtain the wavefield in the exit plane of the object, where the phase represents a sharp image of the projected electron density. Measurement of the phase is of course completely impossible as the frequency of hard X-rays is on the order of \(10^{18}\) Hz. However, the intensity pattern in the detection plane is directly related to the phase in the exit plane. Unfortunately, the corresponding set of equations is way too large to be solved directly, as it equals to the number of pixels. Furthermore, the interference between primary and scattered wave and the self-interference of the scattered wave render the equations non-linear. Finally, given a single detector image, the system of equations is under-determined, because the amplitude and phase maps in the exit plane contain twice as many unknowns as the available (real-valued) intensity map in the detection plane. The first concern of holographic imaging must therefore be to design the experiment such that the measured data is sufficient, i.e. to achieve uniqueness. Several detector images with sufficient diversity in the data can be generated by variation of the Fresnel number, but in practice a second strategy is more common: The number of unknowns is reduced when sufficient constraints can be formulated, restricting the solution. For example when the phase map can be set be zero outside a known support (support constraint), or when absorption in the object is negligible and the amplitude can be assumed to be one everywhere (pure phase contrast constraint), or finally when the object is approximated to have identical stoichiometry resulting in a coupling of phase and absorption (single material constraint), the phase problem becomes manageable.
Once this first concern of sufficient data and constraints is met, the second concern is to decode the holographic images and retrieve the phase map, i.e. the solution of the phase problem as an inverse problem. This phase retrieval process requires knowledge about image formation (i.e. the forward problem based on the wave equation), including all experimental parameters, as well as about the constraints which can be formulated based on properties of the object. In the following, two basic approaches of phase retrieval will be introduced: Deterministic single step and iterative algorithms using alternating projections onto constraint sets.
3.1 Single-Step Phase Retrieval
Single-step deterministic reconstruction techniques invert the process of holographic image formation under certain approximations. An example is phase retrieval based on the contrast transfer function (CTF) given in (2.81). In cases where the Fourier transform of a hologram can be expressed as a product of the object function and the oscillating CTF
a simple ansatz is to divide the Fourier transformed intensities by the analytically determined CTF [28]:
This separation firstly requires one of the following three constraints: pure phase contrast, pure amplitude contrast, or single material (coupled contrast). Secondly, an analytical expression for the CTF is only possible by linearization of the optical properties of the sample. Note that the original assumption of a weak phase shift in the derivation of the CTF was later lifted to a weakly varying phase [27]. Furthermore, even if the assumptions are justified, proper implementation of CTF-based phase retrieval requires regularization in order to compensate for the zero-crossings of the CTF [26, 28, 29]. A detailed description on the implementation of the CTF formalism including the extension to multi-distances can be found in [32].
3.2 Iterative Phase Retrieval
Analytic, single step reconstruction techniques are quick but come at a price: They require very restrictive assumptions or approximations, as detailed above. The applicability of phase retrieval can be significantly extended by iterative methods which are computationally expensive but compatible with a wider range of constraints and valid for more general X-ray optical properties of the object. Iterative algorithms cycle between object and detector plane, and are alternatively subjected to an object constraint and the constraint that the solution has to satisfy the measured data. In the following, some of the most common constraints will be introduced.
Compatibility with the measured data is assured by the so-called magnitude constraint: A solution to the phase problem must satisfy the measured intensity distribution of the hologram I(x, y). To this end, the wavefield \(\psi (x,y)\) is modified such that
Note that in order to formulate phase retrieval only in terms of projections and to treat all constraints on equal footing, the Fresnel propagation \(\mathcal {D}_z\) of the wavefield between object and detector (and back) is incorporated into the projection operator.
Next, we need at least a second constraint, notably in the object plane (or more precisely the exit plane). A very general constraint is the range constraint, which sets the magnitude behind the object strictly equal to one (after normalization to incoming intensity). In other words, one assumes the object to be of pure phase contrast. In a more general setting one solely requires the amplitude to be smaller than one (i.e. thereby fixing the range of the amplitude). This is justified, since right behind the object, no interference effects have yet evolved, the wavefield amplitudes can only be smaller (absorbing components in the object) than or equal (transparent components) to unity
However, some caution is advised. Application of the range constraint requires normalization of intensity by an independent measurement of the empty beam intensity and not just normalization by the mean intensity.
Another straightforward but not always suitable constraint is the support constraint. The reconstructed sample is only allowed to cover a limited part D of the field of view
In phase retrieval, this constraint is very powerful, for example in view of recovering spatial frequencies corresponding to zeros in the CTF [33]. Unfortunately, it is not applicable to extended samples.
A compact support can be regarded as a special case of sparsity. Obviously, the pixels with non-zero density are sparse, if the support is small. More generally, the object may be sparse in very different ways, i.e. the object or its projection may be specified by a set of independent values much smaller than the number of pixels (voxels). Sparsity constraints enforce image properties to be sparse in some sense, without being too restrictive and specific. A suitable way to enforce sparsity for X-ray holography is the shearlet constraint [34]. Shearlets are deformed (scaled, translated and sheared) wavelet-type basis functions [35, 36]. They are particularly useful to represent so-called cartoon-like images (compactly supported and twice continuously differentiable functions) [37,38,39]. Hence, in case that amplitude and phase of the object’s transmission function can be categorized as cartoon-like, a sparse representation by a linear combination of shearlets is possible, and this information can be used as an additional constraint for phase retrieval [34]. Yet the applicability of the shearlet constraint is not limited to cartoon-like objects, but the set of shearlets required is much smaller in this case, and the constraint can therefore be formulated more ‘strictly’, and will thus be more powerful for phase retrieval.
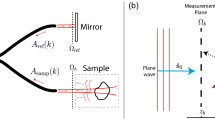
If no reasonable constraint can be formulated for the object, i.e. if the object is extended, exhibits uncoupled variations in phase and amplitude and is not sparse, additional data has to be acquired and used as input for phase retrieval. One way to do this is by translations of the object or detector (either longitudinal or lateral) and successive image acquisitions. Alternating projections on such multi-measurements by various update schemes are denoted as multi-magnitude projection (mmp) [30, 40, 41]. In mmp, the illumination (probe) has to be perfect or known beforehand, for example by a complete mmp series acquired at different detector positions [40]. This is often difficult to accomplish.
A suitable alternative is to generate multi-measurements by translation of the object and to use ptychographic algorithms for phasing by enforcing separability of object and probe afterwards. This so-called separability constraint enables simultaneous phase retrieval of object and probe, and can thereby account for the fact that aberrations inherent in the illumination interfere with the modulations imposed by the sample, which otherwise result in degradation of image quality and resolution [30, 31]. The separability constraint is key in all ptychographic algorithms [42,43,44], and was introduced in X-ray holography in several different ways, based on using either a wavefront diffuser and lateral translations [45], or longitudinal translations [46], or a combination of lateral and longitudinal translations [47]. Note that the last case is least restrictive in terms of probe properties, see also [48] for a detailed comparison and discussion.
Illustration of iterative phase retrieval: An initially guessed wavefield \(\psi \) exiting the object of interest (1.) is forced to fulfill constraints right behind the sample (2.), has to fulfill the wave equation (3. and 5.), has to match the measured intensities (4.) and is updated to form a new guessed field \(\psi \) (6.)
Figure 2.7 presents a schematic of an iterative phase retrieval algorithm. It is composed of alternating projections and reflections onto sets of functions that fulfill two or more constrains. The final goal is to ultimately decode the holographic intensities and reveal a solution proportional to the electron density distribution of the sample. The precise update scheme of a specific reconstruction algorithm (step 6 in Fig. 2.7), has significant effect on the convergence. As an illustration, three common update techniques will be briefly introduced.
The oldest such schemes are known as Gerchberg-Saxton-type (GS) algorithms [49] and consist of alternating projections onto sets of functions fulfilling magnitude or range-constraints as given in (2.84). Holograms \(M_1(x,y)\) and \(M_2(x,y)\) recorded at two different defocus positions provide the required data, but a single measurement can be sufficient, for example in case of pure phase contrast. The complete algorithm can be written as
Alternating projections are stopped, once a fixed point solution \(\psi ^{(n+1)}(x,y) = \psi ^{(n)}(x,y)\) is found. In case of a pure phase object, the range constraint for the object domain is replaced by (2.85). It can be shown that the GS algorithm corresponds to a local optimization, which is therefore highly dependent on the initial guess. A very similar algorithm based on the iterative application of two projections is the Error Reduction Algorithm which alternates the magnitude (measurement) constraint and a support constraint.
To avoid stagnation in side minima, a more general update scheme can be formulated, with non-local search properties. The first such example was provided by the Hybrid-Input-Output algorithm, which was originally formulated for far field coherent diffractive imaging and objects limited to a finite support [50]. The main idea is to formulate the update as a linear combination of the wavefield of the previous iterate (the input), and the wavefield resulting from projection onto the measurement and application of a support constraint (the output). This linear combination is governed by the parameter \(\beta \in \left[ 0,1 \right] \), gradually pulling the wavefield outside D to zero
As a consequence, the solution \(\psi ^{(n+1)}(x,y)\) does neither exactly fulfill the magnitude constraint, nor does it fulfill the support constraint. Yet, it can overcome stagnation and finally find a solution that is consistent with both, support and range. Whereas the classical HIO algorithm was designed for far field imaging (i.e. the propagated wavefields are calculated by Fourier transforms), a modified Hybrid-Input-Output algorithm was formulated for full field holography [33]. The differences to its original version are the replacement of the Fourier transforms by the Fresnel near field propagator and the fact that both phase and amplitude of the wavefield outside the support are subjected to a support constraint [33] pulling the amplitudes to one and the phases to zero.
The Relaxed-Averaged-Alternating-Reflections (RAAR) algorithm [51] combines projections \(\mathcal {P}\) and reflections \(\mathcal {R}=2\cdot \mathcal {P} - 1\). It is designed such that
The parameter \(\lambda _n\) is a relaxation parameter. As above the index M refers to projections/reflections on the set of functions reproducing the measured intensities, whereas the subscript O indicates operations fulfilling constraints in the object domain. These can be range constraints, sparsity/shearlet constraints, separability constraints or support constraints. For more details on this algorithm see Chaps. 6 and 23.
a Simulated holographic intensities of a sample consisting of multi-material spheres. b True projected phases of the sample. c Line profiles through the phantom and the reconstructions shown in (d–f). d Reconstructed phase by the CTF-based single step technique. e Phase retrieval result by the modified Hybrid-Input-Output algorithm (mHIO). f Phase retrieval result by the Relaxed-Averaged-Alternating-Reflections (RAAR) algorithm
Figure 2.8 depicts the results of three different phase retrieval methods applied to the simulated holographic intensities in (a). The phantom shown in (b) consists of spheres with radii between 50 and 200 nm of different materials (Al, Al\(_2\)O\(_3\), Ca) inside a volume. The incoming illumination was simulated as a plane wave with photon energy of 7keV. The fact that the spheres are not made of a single material violates the assumptions required to derive single step CTF-based phase retrieval (2.79). Hence, the reconstruction shown in (d) depicts blurry regions (absorbing and phase shifting components \(\beta \) and \(\delta \) were set to the mean values of the given materials). The iterative modified Hybrid-Input-Output (e) and the Relaxed-Averaged-Alternating-Reflections algorithm can reveal features of the projected phase more distinctly and with less blur. A detailed comparison between iterative and analytic phase retrieval for experimental data can be found in [52].
4 From Two to Three Dimensions: Tomography and Phase Retrieval
Inverting the holographic intensity distributions via phase retrieval techniques, one arrives at a two dimensional (2d) image proportional to the projected index variation, or equivalently—when considering the real part only—the projected electron density. But for a three dimensional (3d) object f(x, y, z), we would also like to find the 3d structure as given by the refractive index \(n(\mathbf {r})\). For this purpose, many projections of the sample have to be recorded under different angles, see Fig. 2.9a. Projected gray values onto a single line s under an angle \(\theta \) shown in Fig. 2.9b correspond to
where \(\mathbf {r}\) is a vector in a 2d hyper-plane of the 3d volume, \(\delta _\text {Dirac}\) is the Dirac delta distribution and \(\mathbf {n_\theta }\) is the unit length vector pointing in direction of s. The operator \(\mathcal {R}\left[ f(\mathbf {r})\right] (s)\) is denoted as the Radon transform. It results in the 1d projection of the sample onto the line s. Figure 2.9b illustrates the discrete version of (2.90) (integral is replaced by sum). It shows the top view of a selected slice (xy-plane) through the sample f (gray shaded region). The operator \(\mathcal {R}\left[ f(\mathbf {r})\right] (s)\) computes line integrals through the object: Whenever the scalar product \(\mathbf {r} \cdot \mathbf {n_\theta }\) equals a distinct value s (here: \(s_a\) and \(s_b\)) corresponding to the projection of \(\mathbf {r}\) (here illustrated by \(\mathbf {a_n}\), \(\mathbf {a_{n+m}}\), \(\mathbf {b_n}\), \(\mathbf {b_{n+m}}\)) onto \(\mathbf {n_\theta }\), the value of the object \(f(\mathbf {r})\) contributes to the projected gray value in a specific bin of the detector (here: the gray values at \(s_a\) and \(s_b\)).
There are different techniques to invert the Radon transform, i.e. to reconstruct \(f(\mathbf {r})\) from a set of projections. The most popular and widely used method is the so-called filtered back-projection. Its basic ingredients are a Fourier-filtering step of the projection data by a ramp filter and the back-projection or smearing out of the filtered projection values along straight lines equal to the paths of the line integrals of the Radon transform. In-depth literature about tomography can be found in [14, 53, 54]. Finally, Fig. 2.9c summarizes the basic steps of three-dimensional holographic X-ray imaging (holographic tomography): A small sample is rotated in a (partially) coherent beam (see Fig. 2.6a), and for each angle a holographic intensity distribution is recorded. Each of the holograms needs to be processed by a suitable phase retrieval technique resulting in an image proportional to the object’s projected electron density. Finally, the 3d object is computed using the information collected by all of the projections.
From two to three dimensions: a Projections of a sample (consisting of spheres) are recorded under different angles. This can be realized by either rotating the sample or the detector. b Illustration of (2.90): The delta-distribution in combination with the scalar product \(\mathbf {r}\cdot \mathbf {n_\theta }\) selects points with a component of length s in direction of \(\mathbf {n_\theta }\). These point lie on lines pointing to the detector under the angle \(\theta \). The summed values of f (shaded region) along these lines are recorded by the detector. Note that (b) illustrates a single plane/slice through the three dimensional object perpendicular to the axis of rotation—see outermost right sketch in (c) for clarity. c Holographic X-ray microscopy is used for high resolution tomography. Holographic intensity distributions are collected under different angles. Each single projection is processed by phase retrieval algorithms. The reconstructed phases are used for inversion of the Radon transform, i.e. for three dimensional tomographic reconstruction
A different approach is to combine phase retrieval and tomographic reconstruction. Instead of performing phase retrieval of all projections first and in a second step the inverse Radon transform (e.g. filtered back-projection), these two steps can be intertwined iteratively: Iterative Reprojection Phase retrieval (IRP) [55]. In this way, an iterate of the full 3d object exists at all times during the process, which ensures tomographic consistency of all projections. This was found to facilitate phase retrieval, effectively acting as a constraint of its own.
Since IRP is computationally very involved, another simultaneous operation of tomographic reconstruction and phase retrieval by CTF was proposed, which also couples the two previously sequential operations [56]. It relies on propagation of the transmission function of an entire 3d object—the propagated object—and requires linearization of the object’s optical properties. If this approximation is justified, the concept of propagating the entire 3d object in parallel is extremely useful for holo-tomography, an shall be briefly introduced here, following [56].
To this end, let us consider a plane wave \(\psi _0\) along the optical axis z impinging on a 3d object, parameterized by the spatial distribution of the index of refraction \(n(\mathbf {r})\). If the projection approximation holds, the exit wave \(\psi (x,y,z=0)\) is determined by the projection of the index of refraction onto a plane perpendicular to the optical axis, which can be written in terms of the Radon operator \(\mathcal {R}(n-1) := \int (n-1)\) dz as
where the approximation of an optically weak object with \(|k_0 \mathcal {R} (n-1)| \ll 1\) was used to linearize the exponential function. Following the angular spectrum approach in Sect. 2.1.2, the free-space propagation to the detector plane at distance z (using the propagator \(P_z\)) can be formulated as
with the radially symmetric free-space propagator function \(P_{2d}(k_x,k_y,z):=\exp (i z [k_0^2-k_x^2 - k_y^2]^{1/2})\) (Fourier space coordinates \(k_x\), \(k_y\) and wavenumber \(k_0= 2\pi /\lambda \)), followed by a 2d Fourier back-transformation \(\mathcal {F}^{-1}_{2d}\). Next, we consider the 2d Fourier transform of a projection of the object, e.g. along z, which can be rewritten as
From (2.93), it can be inferred that the central slice of the 3d Fourier transform of the object (given by \(n-1\)), equals the 2d Fourier transform of a projection normal to the slice. This is an important geometric relation in tomography, known as the Fourier slice theorem. Here we use it to show that the order of projection and propagation \(\mathcal {D}\) can be inverted [56]. We consider the 2d propagation \(\mathcal {D}_{2d}\) of the projection \(\mathcal {R} (n-1)\) [56]
The term \(P_{3d} =\exp \left[ i \varDelta \sqrt{k_0^2-k_x^2-k_y^2-k_z^2} \,\right] \) is the 3d propagator function. As detailed in [56], this result is the starting point to perform CTF approximations and fast iterative phase retrieval directly in 3d, i.e. simultaneously with tomographic reconstruction. Within a few iterations, tomographic consistency can be enforced and serves as constraint for phase retrieval.
References
Melchior, L., Salditt, T.: Finite difference methods for stationary and time-dependent X-ray propagation. Opt. Express 25, 32090–32109 (2017)
Bergemann, C., Keymeulen, H., van der Veen, J.F.: Focusing x-ray beams to nanometer dimensions. Phys. Rev. Lett. 91(20), 204801 (2003)
Fuhse, C., Salditt, T.: Finite-difference field calculations for one-dimensionally confined X-ray waveguides. Phys. B 357(1–2), 57–60 (2005)
Kopylov, Y.V., Popov, A.V., Vinogradov, A.V.: Application of the parabolic wave equation to X-ray diffraction optics. Opt. Commun. 118(5–6), 619–636 (1995)
Husakou, A.: Nonlinear phenomena of ultrabroadband radiation in photonic crystal fibers and hollow waveguides. Ph.D. thesis, Freie Universität Berlin (2002)
Paganin, D.M.: Coherent X-ray Optics. Oxford University, New York (2006)
Ruhlandt, A.: Time-resolved x-ray phase-contrast tomography. Ph.D. thesis, Universität Göttingen (2018)
Bartels, M., Krenkel, M., Haber, J., Wilke, R.N., Salditt, T.: X-ray holographic imaging of hydrated biological cells in solution. Phys. Rev. Lett. 114, 048103 (2015)
Döring, F., Robisch, A.L., Eberl, C., Osterhoff, M., Ruhlandt, A., Liese, T., Schlenkrich, F., Hoffmann, S., Bartels, M., Salditt, T., Krebs, H.U.: Sub-5 nm hard x-ray point focusing by a combined Kirkpatrick-Baez mirror and multilayer zone plate. Opt. Express 21(16), 19311–19323 (2013)
Voelz, D.G.: Computational Fourier Optics: A MATLAB Tutorial (SPIE Tutorial Texts Vol. TT89). SPIE press (2011)
Voelz, D.G., Roggemann, M.C.: Digital simulation of scalar optical diffraction: revisiting chirp function sampling criteria and consequences. Appl. Opt. 48(32), 6132–6142 (2009)
Matsushima, K., Shimobaba, T.: Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Opt. Express 17(22), 19662–19673 (2009)
Als-Nielsen, J., McMorrow, D.: Elements of Modern X-ray Physics, 2nd edn. Wiley (2011)
Salditt, T., Aspelmeier, T., Aeffner, S.: Biomedical Imaging: Principles of Radiography, Tomography and Medical Physics. Walter de Gruyter GmbH & Co KG (2017)
Davis, T.J.: Dynamical X-ray diffraction from imperfect crystals: a solution based on the Fokker-Planck equation. Acta Crystallogr. Sec. A 50(2), 224–231 (1994)
Gureyev, T.E., Davis, T.J., Pogany, A., Mayo, S.C., Wilkins, S.W.: Optical phase retrieval by use of first Born- and Rytov-type approximations. Appl. Opt. 43(12), 2418–2430 (2004)
Sung, Y., Barbastathis, G.: Rytov approximation for x-ray phase imaging. Opt. Express 21(3), 2674–2682 (2013)
Li, K., Wojcik, M., Jacobsen, C.: Multislice does it all-calculating the performance of nanofocusing x-ray optics. Opt. Express 25(3), 1831–1846 (2017)
Scarmozzino, R., Osgood, R.M.J.: Comparison of finite-difference and Fourier-transform solutions of the parabolic wave equation with emphasis on integrated-optics applications. J. Opt. Soc. Am. A 8(5), 724–731 (1991)
Crank, J., Nicolson, P.: A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Proc. Camb. Philos. Soc. 43, 55–67 (1947)
Thomas, J.W.: Numerical Partial Differential Equations: Finite Difference Methods, vol. 22. Springer Science & Business Media (2013)
Fuhse, C.: X-ray waveguides and waveguide-based lensless imaging. Ph.D. thesis (2006)
Fuhse, C., Salditt, T.: Finite-difference field calculations for two-dimensionally confined x-ray waveguides. Appl. Opt. 45(19), 4603–4608 (2006)
Spence, J.C.: Lawrence Bragg, microdiffraction and X-ray lasers. Acta Crystallogr. Sect. A Found. Crystallogr. 69(1), 25–33 (2013)
Gabor, D.: A new microscopic principle. Nature 161, 777–778 (1948)
Cloetens, P., Ludwig, W., Baruchel, J., Guigay, J.P., Pernot-Rejmankova, P., Salome-Pateyron, M., Schlenker, M., Buffiere, J.Y., Maire, E., Peix, G.: Hard x-ray phase imaging using simple propagation of a coherent synchrotron radiation beam. J. Phys. D 32(10A), A145–A151 (1999)
Guigay, J.P.: Fourier transform analysis of Fresnel diffraction patterns and in-line holograms. Optik 49(1), 121–125 (1977)
Turner, L.D., Dhal, B.B., Hayes, J.P., Mancuso, A.P., Nugent, K.A., Paterson, D., Scholten, R.E., Tran, C.Q., Peele, A.G.: X-ray phase imaging: demonstration of extended conditions for homogeneous objects. Opt. Express 12(13), 2960–2965 (2004)
Zabler, S., Cloetens, P., Guigay, J.P., Baruchel, J., Schlenker, M.: Optimization of phase contrast imaging using hard x rays. Rev. Sci. Instrum. 76(7), 073705 (2005)
Hagemann, J., Robisch, A.-L., Luke, D.R., Homann, C., Hohage, T., Cloetens, P., Suhonen, H., Salditt, T.: Reconstruction of wave front and object for inline holography from a set of detection planes. Opt. Express 22(10), 11552–11569 (2014)
Homann, C., Hohage, T., Hagemann, J., Robisch, A.-L., Salditt, T.: Validity of the empty-beam correction in near-field imaging. Phys. Rev. A 91, 013821 (2015)
Krenkel, M.: Cone-beam x-ray phase-contrast tomography for the observation of single cells in whole organs. Ph.D. thesis, Universität Göttingen (2015)
Giewekemeyer, K., Krüger, S.P., Kalbfleisch, S., Bartels, M., Beta, C., Salditt, T.: X-ray propagation microscopy of biological cells using waveguides as a quasipoint source. Phys. Rev. A 83(2), 023804 (2011)
Loock, S., Plonka, G.: Phase retrieval for Fresnel measurements using a shearlet sparsity constraint. Inverse Probl. 30(5), 055005 (2014)
Guo, K., Kutyniok, G., Labate, D.: Sparse multidimensional representations using anisotropic dilation and shear operators. In: Chen, G., Lai, M. (eds.) Wavelets and Splines. Nashboro Press, pp. 189–201 (2006)
Labate, D., Lim, W.Q., Kutyniok, G., Weiss, G.: Sparse multidimensional representation using shearlets. In: Papadakis, M., Laine, A.F., Unser M.A. (eds.) Wavelets XI, Proceedings of the SPIE, vol. 5914, pp. 254–262 (2005)
Donoho, D.L.: Sparse components of images and optimal atomic decomposition. Constr. Approx. 17, 353–382 (2001)
Kutyniok, G., Labate, D. (eds.): Shearlets: Multiscale Analysis for Multivariate Data. Birkhäuser (2012)
Pein, A., Loock, S., Plonka, G., Salditt, T.: Using sparsity information for iterative phase retrieval in x-ray propagation imaging. Opt. Express 24(8), 8332–8343 (2016)
Hagemann, J., Robisch, A.-L., Osterhoff, M., Salditt, T.: Probe reconstruction for holographic X-ray imaging. J. Synchrotron Rad. 24(2), 498–505 (2017)
Hagemann, J., Salditt, T.: Divide and update: towards single-shot object and probe retrieval for near-field holography. Opt. Express 25(18), 20953–20968 (2017)
Guizar-Sicairos, M., Fienup, J.R.: Phase retrieval with transverse translation diversity: a nonlinear optimization approach. Opt. Express 16(10), 7264–7278 (2008)
Maiden, A.M., Rodenburg, J.M.: An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 109(10), 1256–1262 (2009)
Thibault, P., Dierolf, M., Menzel, A., Bunk, O., David, C., Pfeiffer, F.: High-resolution scanning x-ray diffraction microscopy. Science 321(5887), 379–382 (2008)
Stockmar, M., Cloetens, P., Zanette, I., Enders, B., Dierolf, M., Pfeiffer, F., Thibault, P.: Near-field ptychography: phase retrieval for inline holography using a structured illumination. Sci. Rep. 3, 1927 (2013)
Robisch, A.-L., Salditt, T.: Phase retrieval for object and probe using a series of defocus near-field images. Opt. Express 21(20), 23345–23357 (2013)
Robisch, A.-L., Kröger, K., Rack, A., Salditt, T.: Near-field ptychography using lateral and longitudinal shifts. New J. Phys. 17(7), 073033 (2015)
Robisch, A.-L.: Phase retrieval for object and probe in the optical near-field. Ph.D. thesis, Universität Göttingen (2016)
Gerchberg, R.W., Saxton, W.O.: A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35(2), 237–246 (1972)
Fienup, J.R.: Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 3(1), 27–29 (1978)
Luke, D.R.: Relaxed averaged alternating reflections for diffraction imaging. Inverse Probl. 21(1), 37 (2005)
Krenkel, M., Toepperwien, M., Alves, F., Salditt, T.: Three-dimensional single-cell imaging with X-ray waveguides in the holographic regime. Acta Crystallogr. Sec. A 73(4), 282–292 (2017)
Buzug, T.: Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Springer (2008)
Natterer, F.: The Mathematics of Computerized Tomography. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (2001)
Ruhlandt, A., Krenkel, M., Bartels, M., Salditt, T.: Three-dimensional phase retrieval in propagation-based phase-contrast imaging. Phys. Rev. A 89, 033847 (2014)
Ruhlandt, A., Salditt, T.: Three-dimensional propagation in near-field tomographic X-ray phase retrieval. Acta Crystallogr. Sec. A 72(2), 215–221 (2016)
Acknowledgements
We thank present and past group members for insights and discussions, in particular Lars Melchior, Aike Ruhlandt and Johannes Hagemann, for the progress they have provided in FD propagation (L.M.), numerical free-space propagators and 3d propagation (A.R.), and in iterative methods of holographic phase retrieval (J.H.). We also acknowledge the fruitful exchange with our colleagues from mathematics, in particular Russell Luke, Thorsten Hohage, Carolin Homann, Gerlind Plonka-Hoch, Stefan Look, and Simon Maretzke.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this chapter
Cite this chapter
Salditt, T., Robisch, AL. (2020). Coherent X-ray Imaging. In: Salditt, T., Egner, A., Luke, D.R. (eds) Nanoscale Photonic Imaging. Topics in Applied Physics, vol 134. Springer, Cham. https://doi.org/10.1007/978-3-030-34413-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-34413-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34412-2
Online ISBN: 978-3-030-34413-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)