Single Particle Imaging with FEL Using Photon Correlations

Abstract

Scattering experiments with femtosecond high-intensity free-electron laser pulses provide a new route to macromolecular structure determination without the need for crystallization at low material usage. In these experiments, the X-ray pulses are scattered with high repetition on a stream of identical single biomolecules and the scattered photons are recorded on a pixelized detector. The main challenges are the unknown random orientation of the molecule in each shot and the extremely low signal to noise ratio due to the very low expected photon count per scattering image, typically well below the number of over 100 photons required by available analysis methods. The latter currently limits the scattering experiments to nano-crystals or larger virus particles, but the ultimate goal remains to retrieve the atomic structure of single biomolecules. Here, we use photon correlations to overcome the issue with low photon counts and present an approach that can determine the molecular structure de novo from as few as three coherently scattered photons per image. We further validate the method with a small protein (46 residues), show that near-atomic resolution of $3.3~{\AA }$ is within experimental reach and demonstrate structure determination in the presence of isotropic noise from various sources, indicating that the number of disordered solvent molecules attached to the macromolecular surface should be kept at a minimum. Our correlation method allows to infer structure from images containing multiple particles, potentially opening the method to other types of experiments such as fluctuation X-ray scattering (FXS).

1 The Single Molecule Scattering Experiment

Despite the great effort in biomolecular structure determination, the structures of less than 1% ($\sim$160,000) of the more than 21 million transcribed proteins [1] have been determined to high resolution [2]. Over the past years existing structure determination methods such as X-ray crystallography and NMR have been stagnating, leaving room for novel methods that can extend the knowledge of biomolecular structures. To this end, X-ray scattering experiments with single biomolecules have been proposed by Neutze et al. as a new de novo structure determination approach for proteins without the need for crystallization [3,4,5,6,7]. Single molecule X-ray imaging becomes possible due to newly-developed free electron laser that produce very high-intensity femtosecond-short X-ray pulses with a focus size of down to 100 nm.

Fig. 16.1

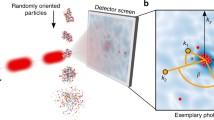
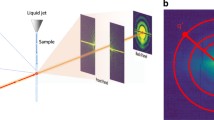
Experimental setup of single molecule scattering imaging. A stream of randomly-oriented particles is injected into the high-intensity short-pulsed FEL beam, hit sequentially by femtosecond X-ray pulses, and the few coherently scattered photons (red dots) are recorded on the pixel detector. The spatial distribution of the photons follows the Fourier intensity of the molecule which is depicted here in light blue in the background of the photon pattern. After illumination, ionization effects charge the molecules and the resulting Coulomb forces quickly disintegrate the molecule

As illustrated in Fig. 16.1, in the experiment, a stream of (typically) hydrated and randomly oriented proteins enters the pulsed X-ray beam at a rate of one molecule per pulse. Despite the high photon flux of the incident beam, only a few photons are scattered by the molecules and recorded on the pixelized detector.

Sample delivery is non-trivial due to the nanoscopic size of the biomolecules and several solutions have been proposed, e.g., using electrospraying techniques [8], gas focused liquid jets [9], oil/water droplet immersion jets [10] or embedding the molecules into polymers (lipidic cubic phase injector) to save material [11]. In each sample delivery method, it is important that the single molecules stay in their physiological environment in order to observe the their natural conformations.

In the scattering process, ionization (Auger decay) charges the atoms in the molecule and leads to Coulomb explosion, coining the method as a “diffract and destroy” experiment. In fact, only 10% of all photons are scattered coherently, all others are absorbed due to the photo-electric effect and expelled shortly after from the molecules at lower energies. However, the short pulses, usually less than 100 fs long, outrun the severe radiation damage because the molecular motion in response to the changed electronic configuration is estimated to take longer than 100 fs [7, 12] and the incident photons are scattered by the unperturbed structure before the molecule disintegrates.

Like in conventional X-ray crystallography, only the intensities and not the phases are measured. In the absence of crystals, the measured signal is the continuous Fourier transformation of the molecule, rendering the phase problem accessible to established ab initio phase-retrieval methods [13].

Whereas previous X-ray sources, including synchrotron sources, have primarily engaged in studies of static structures, X-ray FELs are by their nature suited for studying dynamic systems at the time and length scales of atomic interactions. In contrast to methods that measure a structure ensemble (NMR, SAXS, FRET), this method gives access to single molecule images and, with a seed model, the images could be e.g., sorted probabilistically to distinguish between different native conformations. Further, similar to nano-crystallography, in systems where reactions can be easily induced, e.g., by light, a sequence of structures at different reaction times may be recorded which opens the window to molecular movies as a long-standing dream [14]. Even without sorting, the variance of the native conformations can be assessed via the variance of the determined electron density in which flexible regions would be smeared out more than rigid protein motifs.

2 Structure Determination Using Few Photons

Single molecule scattering images sample spherical dissections (Ewald sphere ) of the continuous 3D Fourier intensity, $I(\mathbf {k})=\left| \mathcal {F}[\rho (\mathbf {x})]\right| ^{2}$ and the orientation of the dissection depends on the orientation of the molecule at the time of illumination. The structure determination from these single molecule images faces two major challenges. First, the orientation of the molecule at the time of illumination is unknown and hard to control because it is usually injected into the “reaction chamber” via electro-spraying in which the molecules tumble inside a solvent bubble. Second, only a low number of photons is coherently scattered (as a statistical Poisson process following the Fourier intensity) and the additional background noise from, e.g., inelastic scattering, the photo-electric effect or background radiation leads to very low signal-to-noise levels. In fact, we estimated that a rather small protein (46 residues) scatters only 20 photons coherently at realistic beam parameters of the next generation European XFEL which add an additional layer of complexity to the structure determination problem due to the additional Poisson noise (shot noise).

Over the past years, several structure determination methods have been proposed and demonstrated which mainly fall into two major classes. The first class of methods predicts the orientation of the molecules at the time of illumination for each scattering image either explicitly or implicitly e.g., through statistical similarities between images or by using a coarse seed model. Images that belong to the same orientation are averaged and these averages are assembled into the 3D intensity similar to cryo-EM. However, almost all of the orientation classification methods are limited to scattering datasets with usually many more than 100 average photons per image.

The second class of methods forgoes the classification of orientations by using photon correlations as an averaged summary statistics of the entire image dataset that is independent of the individual orientations and will be covered in this Chapter. Previous attempts have focused on extracting as much as possible information from two correlated photons using additional knowledge such as symmetry or molecular rotations around a fixed axis. From early work by Kam on electron micrograph images, it is known that two-photon correlations do not carry sufficient information to retrieve the full 3D intensity ab initio [15, 16]. Motivated by these observation, we suspected and eventually validated the claim that three photon suffice and therefore developed a method method that allows for de novo structure determination from as few as three coherently scattered photons per single molecule X-ray scattering image. The main idea is to determine the molecule’s intensity $I(\mathbf {k})$ from the full three-photon correlation $t(k_1,k_2,k_3,\alpha ,\beta )$ which is accumulated from all photon triplets in the recorded scattering images, independent of the respective molecular orientations and therefore free of errors associated with the classification of the orientations.

2.1 Theoretical Background on Three-Photon Correlations

A single photon triplet is characterized by the angles $\alpha$ and $\beta$ between the photons and the distances of the photons to the detector center (Fig. 16.2). Each triplet is comprised of three correlated doublets $(k_1,k_2, \alpha ,)$, $(k_2, k_3, \beta )$ and $(k_1, k_3, \alpha +\beta )$ and the angles are chosen as the minimum difference between the pairs, $\alpha ,\beta \in [0,\pi ]$. The probability of observing a coherently scattered photon at pixel position $\mathbf {k}^{\star }$ is proportional to the intensity $I(\mathbf {k}^{\star })$ at this pixel which lies on the projection of the intensity $I(\mathbf {k})$ on the Ewald sphere in 3D Fourier space. The full three-photon correlation $t(k_{1},k_{2},k_{3},\alpha ,\beta )$ is the sum over all possible triplets which is equivalent to the orientational average $\left\langle \right\rangle _{\omega }$ of the product between three intensities $I(\mathbf {k})$ that lie on the intersection between the Ewald sphere and the 3D Fourier density,

$$\begin{aligned} t(k_{1},k_{2},k_{3},\alpha ,\beta )_{I(\mathbf {k})} = \left\langle I_{\omega }\left( \mathbf {k}^{\star }_1(k_{1},0)\right) \cdot I_{\omega }\left( \mathbf {k}^{\star }_2(k_{2},\alpha )\right) \cdot I_{\omega }^{*}\left( \mathbf {k}^{\star }_3(k_{3},\beta )\right) \right\rangle _{\omega }. \end{aligned}$$

(16.1)

Here, without loss of generality, the three vectors $\mathbf {k_1}^{\star }$, $\mathbf {k_1}^{\star }$ and $\mathbf {k_1}^{\star }$ are the projection onto the Ewald sphere of the three photon positions $\mathbf {k_1}=(k_1,0,0)$, $\mathbf {k_2}=k_2(\cos \alpha ,\sin \alpha ,0)$ and $\mathbf {k_3}=k_3(\cos \beta ,\sin \beta ,0)$ in the detector plane. These positions are chosen as one arbitrary realization of the tuple $(k_{1},k_{2},k_{3},\alpha ,\beta )$.

Fig. 16.2

Schematic depiction of the three-photon correlation using an exemplary synthetic single molecule scattering image of Crambin with only coherently scattered photons. In the detector plane $k_xk_y$ the recorded photons are grouped into triplets, each of which is characterized by distances $k_1,k_2,k_3$ to the detector center (orange lines) and the angles $\alpha$ and $\beta$ between the respective photons (orange circular arcs)

For the orientational average $\left\langle \right\rangle _{\omega }$ it is assumed that in the experiment the orientation of the molecule is unknown and uniformly sampled. Note that the orientational average can either be expressed as an average over all rotations of $I_{\omega }(\mathbf {k})$ for fixed $\mathbf {k}_{1,2,3}$ (our approach) or as an average over all rotations of the vectors $\mathbf {k}_{1,2,3,\omega }$ for a fixed $I(\mathbf {k})$.

The orientational integral over all possible triple products of 3D intensities $I(\mathbf {k})$ in 16.1 is challenging to calculate and may be simplified by decomposing $I(\mathbf {k})$ into spherical shells with radius k and by expanding each shell using a spherical harmonics basis [17],

$$\begin{aligned} I\left( \mathbf {k}\right) =\sum _{lm}A_{lm}\left( k\right) Y_{lm}\left( \theta ,\varphi \right) . \end{aligned}$$

(16.2)

The coefficients $A_{lm}(k)$ describe the intensity function on the respective shells and are non-zero only for even $l\in \left\{ 0,2,4,...,L\right\}$ because of the symmetry of $I(\mathbf {k})=I(-\mathbf {k})$ (Friedel’s law). In this description, a 3D Euler rotation $\omega$ of $I(\mathbf {k})$ is expressed by transforming the spherical harmonics coefficients according to $A_{lm}^{\mathrm {rot}}(k)=\sum _{mm\prime }D_{mm\prime }^{l}A_{lm\prime }^{\mathrm {unrot}}(k)$, using the rotation operators $D_{m'm}^{l}$ which are composed of elements of the Wigner D-matrix as defined, e.g., in  [17], yielding the rotated intensity,

$$\begin{aligned} I_{\omega }\left( \mathbf {k}\right) =\sum _{lmm'}A_{lm}\left( k\right) Y_{lm'}\left( \theta ,\varphi \right) D_{m'm}^{l}\left( \omega \right) . \end{aligned}$$

(16.3)

Inserting the spherical harmonics expansion of the rotated intensity $I_{\omega }\left( \mathbf {k}\right)$, evaluated at positions $\mathbf {k}_1^{\star }$, $\mathbf {k}_2^{\star }$ and $\mathbf {k}_3^{\star }$ on the Ewald sphere ($\theta _i=\cos ^{-1}(\dfrac{k_i\lambda }{4\pi })$), into the expression for the three-photon correlation, (16.1), yields

$$\begin{aligned}&t(k_{1},k_{2},k_{3},\alpha ,\beta )_{\left\{ A_{lm}(k)\right\} } = \nonumber \\&\qquad \sum _{l_{1}\,l_{2}\,l_{3}}\sum _{m_{1}\,m_{2}\,m_{3}}\sum _{m_{1}'\,m_{2}'\,m_{3}'}A_{l_{1}m_{1}}\left( k_{1}\right) A_{l_{2}m_{2}}\left( k_{2}\right) A_{l_{3}m_{3}}^{*}\left( k_{3}\right) \nonumber \\&\qquad \qquad Y_{l_{1}m_{1}'}\left( \theta _1(k_1),0\right) \cdot Y_{l_{2}m_{2}'}\left( \theta _2(k_2),\alpha \right) \cdot Y_{l_{3}m_{3}'}^{*}\left( \theta _3(k_3),\beta \right) \nonumber \\&\qquad \qquad \left\langle D_{m_{1}m_{1}'}^{l_1}\cdot D_{m_{2}m_{2}'}^{l_2}\cdot D_{m_{3}m_{3}'}^{l_3{*}}\right\rangle _{\omega }, \end{aligned}$$

(16.4)

such that the orientational average only involves the elements of the Wigner D-matrix $D_{mm\prime }^{l}$.

Using the Wigner-3j symbols $\left( \begin{array}{ccc} l_{1} &{} l_{2} &{} L\\ m_{1} &{} m_{2} &{} -M \end{array}\right)$ [18], the product of two rotation elements $D_{mm\prime }^{l}$ reads

$$\begin{aligned} D_{m_{1}m_{1}'}^{l_{1}}D_{m_{2}m_{2}'}^{l_{2}}= & {} \sum _{L=\left| l_{1}-l_{2}\right| }^{l_{1}+l_{2}}\sum _{MM'}(2L+1)\left( -1\right) ^{M-M'}\\&\left( \begin{array}{ccc} l_{1} &{} l_{2} &{} L\\ m_{1} &{} m_{2} &{} -M \end{array} \right) \nonumber \\&\left( \begin{array}{ccc} l_{1} &{} l_{2} &{} L\\ m'_{1} &{} m'_{2} &{} -M' \end{array} \right) D_{MM'}^{L}.\nonumber \end{aligned}$$

(16.5)

With the orthogonality theorem for orientational averages of the product of two Wigner D operators,

$$\begin{aligned} \left\langle D_{MM'}^{L}D_{m_{3}m_{3}'}^{l_{3}*}\right\rangle _{\omega }=\dfrac{1}{2L+1}\delta _{l_{3}L}\delta _{m_{3}M}\delta _{m_{3}'M'}, \end{aligned}$$

(16.6)

the three-photon correlation finally reads

$$\begin{aligned} t(k_{1},k_{2},k_{3},\alpha ,\beta )_{\left\{ A_{lm}(k)\right\} }= & {} \sum _{l_{1}\,l_{2}\,l_{3}}\sum _{m_{1}\,m_{2}\,m_{3}}A_{l_{1}m_{1}}\left( k_{1}\right) A_{l_{2}m_{2}}\left( k_{2}\right) A_{l_{3}m_{3}}^{*}\left( k_{3}\right) \\&\left( \begin{array}{ccc} l_{1} &{} l_{2} &{} l_{3}\\ m_{1} &{} m_{2} &{} -m_{3} \end{array} \right) \nonumber \\&\sum _{m_{1}'\,m_{2}'\,m_{3}'}\left( -1\right) ^{m_{3}-m_{3}'}\left( \begin{array}{ccc} l_{1} &{} l_{2} &{} l_{3}\\ m'_{1} &{} m'_{2} &{} -m_{3}' \end{array} \right) \nonumber \\&Y_{l_{1}m_{1}'}\left( \theta _1(k_1),0\right) Y_{l_{2}m_{2}'}\left( \theta _2(k_2),\alpha \right) Y_{l_{3}m_{3}'}^{*}\left( \theta _3(k_3),\beta \right) .\nonumber \end{aligned}$$

(16.7)

This expression only involves sums of products of three spherical harmonics coefficients $A_{lm}(k)$ with known Wigner-3j symbols and spherical harmonics basis functions $Y_{lm}(\theta ,\varphi )$. The numerical calculation of the three photon correlation (forward model) is the computationally limiting step in the structure determination approach. The correlations, expressed in spherical harmonics terms, are faster to calculate than e.g., the numerical integration, and they allow for adapting the number $K(L^2+3L+2)/2$ of spherical harmonics basis functions to the target resolution via the largest considered wave number $k_{\mathrm {cut}}$, the number K of used shells between $0...k_{\mathrm {cut}}$, and the expansion order L. The hierarchical properties of spherical harmonics basis functions further allow to determine the structure first with low angular resolution and then to successively refine it to higher resolutions and higher expansion limits, respectively.

2.2 Bayesian Structure Determination

Currently no analytic inversion of the three-photon correlation in (16.7) is known, and the number of unknowns (e.g., 4940 for $K=26$, $L=18$) is too large for a straightforward numeric solution. Instead we have developed a probabilistic approach [19] in which we asked which intensity $I(\mathbf {k})$ is most likely to have generated the complete set of measured scattering images and triplets, respectively. To this end, we considered the Bayesian probability p (with uniform prior) that a given intensity $I(\mathbf {k})$, expressed in spherical harmonics by $\left\{ A_{lm}(k)\right\}$, generated the set of triplets, $\left\{ k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i\right\} _{i=1...T}$,

$$\begin{aligned} p\left( \left\{ k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i\right\} _{i=1...T}\right| \left\{ A_{lm}(k)\right\} ) = \prod _{i=1}^T{\tilde{t}(k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i)_{\left\{ A_{lm}(k)\right\} }}. \end{aligned}$$

(16.8)

Due to the statistical independence of the triplets, this probability p is a product over the probabilities $\tilde{t}(k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i)$ of observing the individual triplets i which is given by the normalized three-photon correlation $\tilde{t}\left( k_{1},k_{2},k_{3},\alpha ,\beta \right)$. Here, $\tilde{t}\left( k_{1},k_{2},k_{3},\alpha ,\beta \right)$ is calculated using (16.7) for varying intensity coefficients $\left\{ A_{lm}(k)\right\}$ and the coefficients that maximized $p\left( \left\{ k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i\right\} \right)$ are determined using a Monte Carlo scheme as discussed in Sect. 16.2.4.

In contrast to the direct inversion, the probabilistic approach has the benefit of fully accounting for the Poissonian shot noise implied by the limited number of photon triplets that are extracted from the given scattering images. We note that this approach also circumvents the limitation faced in previous works on degenerate three photons correlations by Kam [16], where only triples are considered, in which two photons are recorded at the same detector position. Because all other triples had to be discarded, Kam’s approach is limited to very high beam intensities, and cannot be applied in the present extreme Poisson regime.

Calculating the probability from (16.8) (and energy in the Monte Carlo scheme) is computationally expensive due to the typically large number of triples T. We therefore approximated this product by grouping triplets with similar $\alpha ,\beta$ angles and distances k into bins and calculated the function $t(k_1,k_2,k_3,\alpha ,\beta )$ for each bin only once, denoted $t_{k_1,k_2,k_3,\alpha ,\beta }$, thus markedly reducing the number of function evaluations to the number of bins. To improve the statistics for each bin, the intrinsic symmetry of the triple correlation function was also used. In particular, all triplets were mapped into the sub-region of the triple correlation that satisfies $k_{1}\ge k_{2}\ge k_{3}$. In this mapping, special care was taken to correct for the fact that triplets with $k_{1}=k_{2}\ne k_{3}$ or $k_{1}\ne k_{2}=k_{3}$ or $k_{1}=k_{3}\ne k_{2}$ occur 3 times more often than $k_{1}=k_{2}=k_{3}$ and triplets with $k_{1}\ne k_{2}\ne k_{3}$ occur 6 times more often. To compensate for different binsizes, each bin was normalized by $k_1k_2k_3$.

2.3 Reduction of Search Space Using Two-Photon Correlations

The high-dimensional search space may be reduced by utilizing the structural information contained within the two-photon correlation. In analogy to the three-photon correlation, the two photon-correlation is expressed as a sum over products of spherical harmonics coefficients $A_{lm}(k)$ weighted with Legendre polynomials $P_{l}$ [16, 20],

$$\begin{aligned} c_{k_{1},k_{2},\alpha }=\sum _{l}P_{l}\left( \cos \left( \alpha \right) \right) \sum _{m}A_{lm}\left( k_{1}\right) \left( \omega \right) A_{lm}^{*}\left( k_{2}\right) . \end{aligned}$$

(16.9)

Please note that the $\alpha$ which is seen on the detector is different from the angle $\alpha ^{\star }=cos^{-1}(\sin (\theta _1)\sin (\theta _2)\cos (\alpha ) + cos(\theta _1)\cos (\theta _2))$ between the two points in 3D intensity space due to the Ewald curvature ($\theta =\cos ^{-1}(k\lambda /4\pi )$.

The inversion yields coefficient vectors $\mathbf {A}_{l}^{0}(k) = (A_{l-m}^{0},...,A_{lm}^{0})$ for all $l \le L \le K_{\mathrm {max}}/2$ and $-l<m<l$, as first demonstrated by Kam [16]. However, all rotations in the $2l+1$-dimensional coefficient eigenspaces of $\mathbf {A}_{l}^{0}(k)$ by $\mathbf {U}_{l}$ are also solutions,

$$\begin{aligned} \mathbf {A}_{l}\left( k\right) =\mathbf {U}_{l}\mathbf {A}_{l}^{0}\left( k\right) . \end{aligned}$$

(16.10)

The result implies that the inversion only gives a degenerate solution for the coefficients and the intensity cannot be determined solely from two photons. Note that the maximum L, corresponding to the angular resolution of the intensity model, scales with the number of shells $K_{\mathrm {max}}$ (or the inverse of the shell spacing $\varDelta k$ respectively) used for the two-photon inversion.

2.4 Optimizing the Probability Using Monte Carlo

In our method, we decided to maximize the probability p from (16.8) with a Monte Carlo/simulated annealing approach on the ‘energy’ function

$$\begin{aligned}&E\left( \left\{ k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i\right\} | \left\{ A_{lm}(k)\right\} \right) \nonumber \\&\qquad = -\log {p\left( \left\{ k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i\right\} \right| \left\{ A_{lm}(k)\right\} )} \nonumber \\&\qquad = -\sum _i{\log \tilde{t}(k_1^i,k_2^i,k_3^i,\alpha ^i,\beta ^i)}_{\left\{ A_{lm}(k)\right\} }, \end{aligned}$$

(16.11)

in the space of all rotations $\mathbf {U}_{l}$ given by the inversion of the two-photon correlation discussed in the previous Section.

Each Monte Carlo run is initialized with a random set of rotations $\left\{ \mathbf {U}_{l}\right\}$ and the set of unaligned coefficients $\left\{ \mathbf {A}_{l}^{0}\right\}$. In each Monte Carlo step j, all rotations $\mathbf {U}^{j}_{l}$ are varied by small random rotations $\varvec{\Delta }_{l}(\beta _l)$ such that the updated rotations for each l ($l \le L$) read $\mathbf {U}^{j+1}_{l}=\varvec{\Delta }_{l}(\beta _l)\cdot \mathbf {U}^{j}_{l}$ using stepsizes $\beta _l$. In order to escape local minima, a simulated annealing is performed using an exponentially decaying temperature protocol, $T(j)=T_{\mathrm {init}} \exp (j/\tau )$. Steps with an increased energy were also accepted according to the Boltzmann factor $\exp (-\varDelta E/T)$. We further used adaptive stepsizes such that all $\beta (l)$ were increased or decreased by a factor $\mu$ when accepting or rejecting the proposed steps, respectively. Convergence was improved by using a hierarchical approach in which the intensity was first determined with low angular resolution and further increased to high resolution. To this end, the variations of low-resolution features were “frozen out” faster than the variations of high-resolution features.

The random rotations $\left\{ \mathbf {U}_{l}\in R^{2l+1\times 2l+1}\right\}$ were generated using QR decompositions of matrices whose entries were drawn from a normal distribution as described by Mezzadri [21]. The rotational variations $\varvec{\Delta }_{l}\left( \beta \right)$ were calculated via the basis transformation

$$\begin{aligned} \varvec{\Delta }_{l}\left( \beta \right) =\mathbf {R}_{l}\mathbf {S}_{l}\left( \beta \right) \mathbf {R}_{l}^{-1} \end{aligned}$$

(16.12)

with

$$\begin{aligned} \mathbf {S}_{l}\left( \beta \right) =\left( \begin{array}{ccccc} \cos \left( \beta \right) &{} -\sin \left( \beta \right) &{} 0 &{} ... &{} 0\\ \sin \left( \beta \right) &{} \cos \left( \beta \right) &{} 0 &{} ... &{} 0\\ 0 &{} 0 &{} I_{2l+1-2}\\ ... &{} ...\\ 0 &{} 0 \end{array}\right) \end{aligned}$$

(16.13)

and random rotation matrices $\mathbf {R}_{l}$ [22]. Here, sub-matrix $\mathbf {I}_{2l-1}$ in $\mathbf {S}_{l}$ is a $2l-1$-dimensional unity matrix.

By using the small rotational variations $\varvec{\Delta }_{l}\left( \beta \right)$, the SO(n) is sampled ergodically. Approximately $[1/(2 - 2\cos (\beta ))]n\cdot \log (n)$ steps are necessary to achieve sufficient sampling aaccording to [22]. For the largest search space of $L=18$ with a rotation dimension of $n=37$ ($n=2L+1$) and a minimum stepsize of $\beta =0.025~\mathrm {rad}$, 213,777 steps are required to sample rotations in SO(37) sufficiently dense. To ensure that the search space is exhaustively explored, we aimed at an optimization length of over 200,000 Monte Carlo steps. To this end, a time constant for the temperature decrease of $\tau =50000$ steps was chosen. The initial temperature $T_{\mathrm {init}}$ was calculated as 10% of the standard deviation of the energy within 50 random steps away from the starting structure using the initial stepsizes. Further, we used a factor $\mu =1.01$ for the adaptive stepsizes. The hierarchical approach was implemented by distributing the initial stepsizes according to $\beta (l)=(l-1)\pi$ such that spherical harmonics coefficients with larger expansion orders l are always varied with a larger stepsize $\beta (l)$ than coefficients with lower orders.

3 Method Validation

Currently, experimental single molecule scattering data is only available for very large icosahedral viruses and in the absence of single molecule scattering images of smaller bio-molcules such as proteins, we have resorted to synthetic scattering experiments to validate our method. Thus, we have tested the method with a Crambin molecule for which we have estimated approx. 20 coherently scattered photons per image at realistic beam parameters. To stay below the estimate of approximately 20 photons per image, we generated up to $3.3\times 10^9$ synthetic scattering images with only 10 photons on average, totalling up to $3.3\times 10^{10}$ recorded photons. With an expected XFEL repetition rate of up to 27 kHz [23], and assuming a hit-rate of 10%, this data can be collected within a few days. However, the data acquisition time substantially decreases to e.g., approx. 30 min when on average 100 photons per image are recorded, reducing the total number of required photons by a factor 100 to $3.3\times 10^{8}$ (and reducing the number of images by a factor 1000 to $3.3\times 10^{6}$).

For the synthetic image generation, we approximated the 3D electron density $\rho (\mathbf {x})$ by a sum of Gaussian functions centered at the atomic positions $\mathbf {x}_i$,

$$\begin{aligned} \rho (\mathbf {x}) = \sum _{i=1}^{N_{atoms}} N_i \exp ^{-\left( \mathbf {x}-\mathbf {x}_i\right) ^2/\left( 2\sigma _i^2\right) }. \end{aligned}$$

(16.14)

The heights and variances of the Gaussian spheres depend on the type of atom i. The variances $\sigma _i$ correspond to the size of the atoms with respect to their scattering cross-section and the height is determined by $N_i$, the number of electrons which are the potential targets for scattering.

The absolute square of the electron densities’ Fourier transformation $I(\mathbf {k})=\left| \mathcal {F}[\rho (\mathbf {x})]\right| ^{2}$ was used to generate the images. In each synthetic scattering experiment, In each shot, the molecule, and thus also $I(\mathbf {k})$, was randomly oriented and on average P photons per image were generated according to the distribution given by the dissection of the randomly oriented Ewald sphere and the intensity $I_{\omega }(\mathbf {K})$.

To generate the distributions numerically, first, a random set of $N_{\mathrm {pos}}$ positions $\left\{ \mathbf {K}_i\right\}$ in the $k_xk_y$-plane was generated according to a 2D Gaussian distribution $G(\mathbf {K})$ with width $\sigma =1.05\,{\AA }^{-1}$ (specific to the Crambin intensity). Given a random 3D rotation $\mathbf {U}$, rejection sampling was used to accept or reject each position according to $\xi < I_{\omega }(\mathbf {U} \cdot \mathbf {K}_i)/( M \cdot G(\mathbf {K}_i))$ using uniformly-distributed random numbers $\xi \in [0,1]$ each. Here, the constant M was chosen as $I_{\mathrm {max}} \cdot \max (G(\mathbf {K}))$ such that the ratio $I_{\omega }(\mathbf {U}\cdot \mathbf {K}_i)/( M\cdot G(\mathbf {K}_i))$ is below 1 for all $\mathbf {K}$.

In accordance with our most conservative estimate, the number of positions $N_{\mathrm {pos}}$ was chosen such that on average 10 scattered photons were generated. For assessing the dependency of the resolution on the number of scattered photons, additional image sets with 25, 50 or 100 scattered photons were also generated (see Sect. 16.3.2).

3.1 Resolution Scaling with Photon Counts

Starting from the histograms obtained from $3.3\times 10^9$ synthetic scattering images with 10 photons, we performed 20 independent structure determination runs. For all runs we used an expansion order $L=18$, $K=26$ shells and a cutoff $k_{\mathrm {cut}}=2.15\,{\AA }^{-1}$, thus setting the maximum achievable resolution to $2.9~{\AA }$. To assess the achievable resolution of the determined Fourier intensities, we calculated 20 real space electron density maps using the relaxed averaged alternating reflections (RAAR) iterative phase retrieval algorithm by Luke [13]. Figure 16.3 compares the average of the 20 retrieved densities (a, green shaded structure) with the the reference electron density (b, blue shaded structure) which has been calculated from the Fourier density (including phases) with same cutoff $k_{\mathrm {cut}}$ as (a). The cross-correlation between the two densities is 0.9.

The resolution of the phased electron densities was characterized by the Fourier shell correlation (FSC),

$$\begin{aligned} \mathrm {FSC}(k)= & {} \frac{\displaystyle \sum _{k_i \in k}{ F_1(k_i) \cdot F_2(k_i)^{*} }}{\displaystyle \sqrt{\sum _{k_i \in k}{ \left| F_1(k_i)\right| ^2} \cdot \sum _{k_i \in k}{\left| F_2(k_i)\right| ^2}}}. \end{aligned}$$

(16.15)

We have adopted the common definition of the resolution from cryo-EM [24] for cases in which the reference density is known. The resolution is then defined as the scattering angle $k_{\mathrm {res}}$ at which $\mathrm {FSC}(k)=0.5$, yielding a radial resolution $\Delta r=2\pi /k_{\mathrm {res}}$. In cases where the two densities in the FSC come from densities retrieved from independent image-sets (cross-validation), a lower cut-off $\mathrm {FSC}(k)=0.143$ is typically used. Here, we have achieved a near-atomic resolution of $3.3~{\AA }$ from the correlation derived from $3.3\times 10^9$ images.

Fig. 16.3

Comparison of the retrieved electron density (a) and the reference electron density (b). The reference density (b) was calculated from the known Fourier density using the same cutoff $k_{\mathrm {cut}}=2.15\,{\AA }^{-1}$ in reciprocal space as (a). The resolution of the retrieved density is $3.3~{\AA }$, the resolution of the reference density is $2.9~{\AA }$ and the cross-correlation between the two densities is 0.9

Next, we have determined the structure from increasing number of images to asses how the resolution scales with the total number of observed photons and, hence, the number of recorded images. To this end, electron densities were calculated and averaged as above starting from $1.3\times 10^{6}$ and going up to $3.3\times 10^{9}$ images ($4.7\times 10^{8}$ up to $1.2\times 10^{12}$ triplets).

Fig. 16.4

Fourier shell correlations (FSC) of densities retrieved from $1.3\times 10^{7}$ to $3.3\times 10^{10}$ photons ($4.7\times 10^{8}$–$1.2\times 10^{12}$ triplets) and infinite photon number. As a reference, the “optimal” FSC is shown (dashed grey), which was calculated directly from the known intensity using the same expansion parameters. The inset shows the corresponding resolutions estimated from $\mathrm {FSC}(k_{\mathrm {res}})=0.5$

Fig. 16.5

Electron densities retrieved from a $2.0\times 10^{8}$, b $8.2\times 10^{8}$, c $3.3\times 10^{9}$ and d $3.3\times 10^{10}$ photons

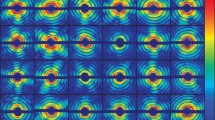
Figure 16.4 shows the FSC curves of all retrieved (averaged) densities along with the 0.5 cutoff (vertical dashed line) and the corresponding resolutions (inset). In Fig. 16.5 visualizes how the resolution improves with the increasing number of detected photons by comparing four electron densities that were retrieved from histograms with $2.0\times 10^{8}$ to $3.3\times 10^{10}$ photons.

As mentioned before, the best electron density was retrieved with a near-atomic resolution of $3.3~{\AA }$ (Fig. 16.5a) from the histograms that was derived from a total of $3.3\times 10^{10}$ photons. Decreasing the number of photons by a factor of 10 decreased the resolution only slightly by 0.4–$3.7~{\AA }$ (Fig. 16.5c), which indicates that very likely fewer than $3.3\times 10^{10}$ photons suffice to achieve near-atomic resolution. If much fewer photons are recorded, e.g. $2.0\times 10^8$, the resolution decreased markedly to $7.8~{\AA }$ (Fig. 16.5a) and even $14~{\AA }$ resolution for $1.3\times 10^7$ photons. For comparison, the diameter of Crambin is $17~{\AA }$.

To address the question how much further the resolution can be increased, we mimicked an experiment with infinite number of photons by determining the intensity from the analytically calculated three-photon correlation. As can be seen in Fig. 16.4 (purple line), the resolution only slightly improved by $0.1~{\AA }$ to about $3.2~{\AA }$ indicating that at this point either the expansion order L or insufficient convergence of the Monte Carlo based structure search became resolution limiting. To distinguish between these two possible causes, we phased the electron density directly from the reference intensity, using the same expansion order $L=18$ as in the other experiments.

The reference intensity is free from convergence issues of the Monte Carlo structure determination and the resulting electron density only includes the phasing errors introduced by the limited angular resolution of the spherical harmonics expansion in Fourier space. The FSC curve of the “optimal phasing” (grey dashed) shows only a minor increase in resolution to $3.1~{\AA }$ indicating that the Monte Carlo search decreases the resolution by $0.1~{\AA }$. The remaining $0.2~{\AA }$ difference to the optimal resolution of $2.9~{\AA }$ at the given $k_{\mathrm {cut}}$ (not shown) is attributed to the finite expansion order L and the corresponding phasing errors.

We have also independently assessed the overall phasing error by calculating the intensity shell correlation (ISC) between the intensities of the phased electron densities $I_{\mathrm {phased}}=|\mathcal {F}[\rho _{\mathrm {retrieved}}]|^2$ and the intensities before phasing $I_{\mathrm {retrieved}}$. The phasing method does not markedly deteriorate the structures.

3.2 Impact of the Photon Counts per Image

The maximum number of triplets T that can be collected from an image with P photons is $T=P\cdot (P-1)\cdot (P-2)/6$. However, these triplets are not all statistically independent; instead, starting from 3 photons, each additional photon adds only two real numbers to the triple correlation: a new angle $\beta$ (with respect to another photon) and a new distance k to the detector center.

The sampling of the three-photon correlation is improved by either collecting more photons per image P or by collecting more images I. However, because for each image, the orientation (3 Euler angles) needs to be inferred, the total amount of information that remains available for structure determination increases with the number of photons per image. Therefore, for every structure determination method, including ours, increasing P is preferred over increasing I, especially at low photon counts. For larger photon counts, the ratio between the 3 Euler angles and P becomes small and hence also the information asymmetry between P and I.

Fig. 16.6

The resolution as a function of the total number of photons collected from images with 10, 25, 50 and 100 photons on average

To assess this effect, we asked how the resolution depends on the number of images I and the photons per image P and therefore carried out additional synthetic experiments using image sets with 10, 25, 50 and 100 average photons P per shot at different image counts yielding different total number of photons. In Fig. 16.6, the achieved resolutions are shown as a function of the number of collected photons for four different $P=[10,25,50,100]$. For the best achievable resolution of $3.3~{\AA }$, e.g., the total number of required photons decreases by a factor of 100 from $3.3\times 10^{10}$ to $3.3\times 10^{8}$ photons (and the number of images decreased by a factor of 1000 from $3.3\times 10^{9}$ to $3.3\times 10^{6}$ images) when increasing the photons per image from 10 to 100, thus substantially decreasing the data acquisition time from over 20.000 min to only 30 min.

3.3 Structure Results in the Presence of Non-Poissonian Noise

To asses how additional noise (beyond the Poisson noise due to low photon counts) affects the achievable resolution, we have carried out synthetic scattering experiments including Gaussian distributed photons, $G(\mathbf {k}, \sigma ) = (2\pi \sigma ^2)^{-1/2}\exp \left( -|\mathbf {k}|^2/2\sigma ^2\right)$ (see Fig. 16.7), as a simple noise model. From the generated scattering images, intensities $S(\mathbf {k})$ were determined with the discussed structure determination scheme.

Fig. 16.7

Comparison of linear cuts through the normalized intensities of noise distributed according to Gaussian functions with widths $\sigma =[0.5,0.75,1.125,2.5]\,{\AA }^{-1}$ (purple shades and black), noise from Compton scattering (grey) and noise from the a disordered water shell of $5~{\AA }$ thickness (aqua). A cut through the Crambin intensity without noise (green) is given for reference. Note that, due to the normalization in 3D, the noise intensities are shown at a signal to noise ratio $\gamma =100\%$; at different signal to noise ratios, the noise intensities are shifted vertically with respect to the Crambin intensity

Assuming that the noise is independent of the molecular structure, the obtained intensities $S(\mathbf {k}) = I(\mathbf {k}) + \gamma N(\mathbf {k})$ are a linear superposition of the molecules’ intensity $I(\mathbf {k})$ and the intensity of the unknown noise $N(\mathbf {k})$. Accordingly, the noise was subtracted from $S(\mathbf {k})$ in 3D Fourier space using our noise model $N(\mathbf {k})=G(\mathbf {k}, \sigma )$ and the estimated signal to noise ratio $\gamma$. Since the spherical harmonics expansion of a Gaussian distribution is described by a single coefficient $G_{l=0,m=0}(k) = G\left( k,\sigma \right)$ on each shell k, the noise subtraction simplified to $A_{l=0,m=0}^{\mathrm {noise-free}}(k) = A_{l=0,m=0}^{\mathrm {noisy}}(k) - \gamma G\left( k,\sigma \right)$.

As discussed in the main text, we assessed the effect of noise for different Gaussian widths ($\sigma =[0.5,0.75,1.125,2.5]\,{\AA }^{-1}$ and several signal to noise ratios $\gamma \in [10\%,...,50\%]$. Figure 16.7 compares the Crambin intensity (green) with the different Gaussian distributions (puples shades, black) at signal to noise ratio of $\gamma =100\%$.

The Figure also shows the noise expected from Compton scattering (grey), which was estimated using the Klein-Nishina differential cross-section [25].

$$\begin{aligned} \mathrm d\sigma = \frac{1}{2} \frac{\alpha ^2}{m^2} \left( \frac{E'}{E}\right) ^2 \left[ \frac{E'}{E} + \frac{E}{E'} - \sin ^2 \theta \right] \mathrm d \varOmega , \end{aligned}$$

(16.16)

with the scattering angle $\theta$, the energy of the incoming photons E, the energy of the scattered photon $E^\prime =E/(1+{\frac{E}{m}}(1-\cos \theta ))$, the fine structure constant $\alpha = 1/137.04$ and the electron resting mass $m_e=511\ \mathrm {keV} /c^{2}$. As can be seen, the noise from Compton scattering (grey) is described well by a Gaussian distributions with width $\sigma =2.5\,{\AA }^{-1}$ (black), and thus was used to approximate incoherent scattering.

Finally, we also estimated the noise from the disordered fraction of the water shell by averaging the intensities of 100 Crambin structures with different $5~{\AA }$-thick water shells. The resulting intensity (aqua) is similar to the reference intensity with fewer signal in the intermediate regions ($0.2\,{\AA }^{-1}< k < 1.0\,{\AA }^{-1}$) and more signal in the center and the high-resolution regions ($k>1.0\,{\AA }^{-1}$). Since the noise of the water shell depends on the structure of the biomolecule, potentially combined with ordered water molecules, it is unlikely to be well described by our simple Gaussian model. Therefore, simple noise subtraction will be challenging, and more advanced iterative techniques will be required.

In Fig. 16.8, the electron densities from the discussed runs are compared to each other.

Fig. 16.8

Comparison of the electron densities retrieved from images containing noise of different levels $\gamma \in [10\%,...,50\%]$ and widths $\sigma \in [0.5, 0.75, 1.125, 2.5]$

4 Structure Determination from Multi-Particle Images

Structure determination approaches are usually limited by the total number of single molecule shots that can be recorded. Remarkably, our method can process images with multiple illuminated particles because the two- and three-photon correlations of these images are connected to the correlations of the single particle shots. In order to show this relation, here, we derived the connection for the two-particle case.

The intensity of an image containing two randomly oriented particles $I_2(\mathbf {k})$ is the superposition of the the individual particle intensities’ with the relative orientation being random,

$$\begin{aligned} I_2(\mathbf {k})= & {} \langle I(\mathbf {k}) + I_{\omega }(\mathbf {k})\rangle _{\omega }\\= & {} I(\mathbf {k}) + \langle I_{\omega }(\mathbf {k})\rangle \nonumber \\= & {} I(\mathbf {k}) + I^{1}(k)\nonumber . \end{aligned}$$

(16.17)

The two-photon correlation then reads,

$$\begin{aligned} c_{k_1,k_2,\alpha }^{(2)}= & {} \langle I_2(\mathbf {K}_1)I_2(\mathbf {K}_2)\rangle>_{\omega }\\= & {} \langle I(\mathbf {K}_1)I(\mathbf {K}_2) + I(\mathbf {K}_1)I^1(k_2) + I^1(k_1)I(\mathbf {K}_2) + I^1(k_1)I^1(k_2)\rangle >_{\omega }\nonumber \\= & {} c_{k_1,k_2,\alpha }^{(1)} + 3I^1(k_1)I^1(k_2)\nonumber \end{aligned}$$

(16.18)

and the three-photon correlation of the two-particle case is calculated as,

$$\begin{aligned} t_{k_1,k_2,k_3,\alpha ,\beta }^{(2)}= & {} \langle I_2(\mathbf {K}_1)I_2(\mathbf {K}_2)I_2(\mathbf {K}_3)\rangle _\omega \\= & {} \left\langle (I(\mathbf {K}_1) + I^{1}(k_1))(I(\mathbf {K}_2) + I^{1}(k_2))(I(\mathbf {K}_3) + I^{1}(k_3))\right\rangle _\omega \nonumber \\= & {} \left\langle I(\mathbf {K}_1)I(\mathbf {K}_2)I(\mathbf {K}_3) + I^{1}(k_1)I(\mathbf {K}_2)I(\mathbf {K}_3) + \right. \nonumber \\&I(\mathbf {K}_1)I^{1}(k_2)I(\mathbf {K}_3) + I(\mathbf {K}_1)I(\mathbf {K}_2)I^{1}(k_3) + \nonumber \\&I^{1}(k_1)I^{1}(k_2)I(\mathbf {K}_3) + I^{1}(k_1)I(\mathbf {K}_2)I^{1}(k_3) + \nonumber \\&\left. I(\mathbf {K}_1)I^{1}(k_2)I^{1}(k_3) + I^{1}(k_1)I^{1}(k_2)I^{1}(k_3)\right\rangle _\omega \nonumber \\= & {} t_{k_1,k_2,k_3,\alpha ,\beta }^{(2)} + I^1(k_2)c_{k_1,k_3,\beta }^{(1)} + I^1(k_1)c_{k_2,k_3,(\alpha -\beta )}^{(1)} + \nonumber \\&I^1(k_3)c_{k_1,k_2,\alpha }^{(1)} + 4I^1(k_1)I^1(k_2)I^1(k_3)\nonumber \end{aligned}$$

(16.19)

The expressions above are readily generalized to the N-particle case and the only remaining unknowns are the mixture ratios $\gamma _i$ for the $N_i$-particles, i.e. the fraction of images containing $N_i$ particles. These ratios are equivalent to the ratios between the integrated intensities of the individual images which identifies the total number of particle in each image and therefore can be calculated from the experimental data without additional effort.

The robustness of the two- and three-photon correlation in the presence of multiple particles in the beam potentially makes our method also interesting for other types of experiments such as fluctuation X-ray scattering (FXS) [26, 27] which is similar to solution scattering. In conventional solution scattering, the orientational averaging that occurs during the X-ray illumination results in signal which carries only 1-dimensional (radial) intensity information and all angular information is averaged out. In FXS experiments, however, the X-ray pulses from synchronous or free electron lasers are much shorter than the orientational diffusion times of the molecules such that they appear to be fixed in space. In each image multiple particles with different orientations are recorded and as a result speckle patterns emerge from which angular correlations can be calculated as described above.