RSP-QL$^{\star }\!$: Enabling Statement-Level Annotations in RDF Streams

Abstract

RSP-QL was developed by the W3C RDF Stream Processing (RSP) community group as a common way to express and query RDF streams. However, RSP-QL does not provide any way of annotating data on the statement level, for example, to express the uncertainty that is often associated with streaming information. Instead, the only way to provide such information has been to use RDF reification, which adds additional complexity to query processing, and is syntactically verbose. In this paper, we define an extension of RSP-QL, called RSP-QL$^{\star }\!$, that provides an intuitive way for supporting statement-level annotations in RSP. The approach leverages the concepts previously described for RDF* and SPARQL*. We illustrate the proposed approach based on a scenario from a research project in e-health. An open-source implementation of the proposal is provided and compared to the baseline approach of using RDF reification. The results show that this way of dealing with statement-level annotations offers advantages with respect to both data transfer bandwidth and query execution performance.

1 Introduction

Recent years have seen an increasing interest in processing and analyzing streaming information as it is generated by applications, services, sensors, and smart devices. RDF Stream Processing (RSP) leverages the principles of Linked Data and the Semantic Web to cope with heterogeneity in data, but employs strategies inspired from stream processing to cope with high velocity data streams. During the last decade, several RSP systems and models have been proposed, which have all provided their own syntax, semantics, and underlying assumptions about the nature of RDF streams [6, 7]. The RSP community group¹ was formed to define a common model for producing, transmitting and continuously querying RDF streams. The first version of this common query model (RSP-QL) was proposed by Dell’Aglio et al. in 2014 [7], and the draft of the abstract syntax and semantics was published by the RSP community group in 2016 [2].

Data generated by sensors is almost always coupled with provenance information, or a level of uncertainty representing, for instance, lack of precision or a knowledge gap. For example, all values reported by a temperature sensor may be associated with some error describing a probability distribution. The RDF specification provides a vocabulary that allows metadata to be represented about RDF triples using RDF reification [11]. In practice, however, this is not widely adopted as a standard for representing and managing such metadata on the Semantic Web [8]. RDF$^\star$ was recently proposed as a way to support a concise representation of statement-level metadata, while remaining backwards compatible with standard RDF [9, 10]. By enclosing a triple using the strings ‘ ’ and ‘ ’, the extension allows it to be used in the subject or object position of other triples. This allows statement-level metadata to be provided directly. For example, the triple :bob :knows :alice could be annotated with the source wikipedia as follows: :bob :knows :alice :source :wikipedia. Similarly, the authors’ propose SPARQL$^\star$ as an extension of SPARQL for querying RDF$^\star$ data, where SPARQL$^\star$ supports similar nesting of triple patterns.

We propose an extension to RSP-QL that leverages RDF$^\star$/SPARQL$^\star$ for annotating and querying streaming data. We show that the proposed approach has several benefits over RDF reification when it comes to statement-level annotations. The approach is motivated based on a use case from a current research project, where we attempt to detect abnormal situations in an e-health scenario.

The rest of the paper is organized as follows. Section 2 briefly discusses the relevant related work, while Sect. 3 describes a use-case scenario that both motivates the proposed approach and exemplifies the requirements addressed by the proposal. Section 4 describes the proposed approach informally, and Sects. 5 and 6 provide the necessary formal definitions, where Sect. 5 defines the data model and Sect. 6 defines the syntax and semantics of the proposed RSP-QL extension. Section 7 provides an application-based evaluation of the approach. Section 8 describes a prototype implementation and a performance evaluation of the implemented system. Section 9 discusses the impact of the presented work and Sect. 10 summarizes the main conclusions of the paper.

2 Related Work

Over the past decade, there has been a growing interest in providing models and languages for combining the principles of the Semantic Web with streaming information. RDF Stream Processing (RSP) systems aim to provide extensions to RDF and SPARQL for representing and querying streaming data. However, though several RSP systems have emerged that provide extensions and operators for this purpose [1, 3, 4, 13, 18], they typically provide different languages, constructs, operators, and evaluation semantics [7]. The W3C RSP community group was formed to define a common model for representing and querying streaming RDF data. The proposed model and language, RSP-QL [7], can be used to model the behavior of most of the current RSP systems, and provides well-defined semantics for explaining query execution. However, none of the existing RSP approaches have given much attention to aspects related to representing metadata in streams, such as uncertainty or provenance. The RSP-QL stream model allows such annotations to be provided on the graph level, but annotations on the triple level are not supported.

The term statement-level metadata refers to data that captures information about a single statement or fact. The RDF specification includes the notion of RDF reification that lets a set of RDF triples describe some other RDF triple [11]. The approach requires the inclusion of four additional RDF triples for every statement where metadata is to be provided. Another approach is to leverage named graphs, where the identifier of the graphs can be used to attach metadata to statements [12]. However, this approach has the disadvantage of inhibiting the application of named graphs for other uses. Finally, singleton properties have been proposed as an alternative approach, where a distinct property is provided for each triple to be annotated [15]. The singleton properties proposal introduces a large number of unique predicates, which is atypical for RDF data, and disadvantageous for common SPARQL optimization techniques [19]. Additionally, these approaches result in verbose queries [9]. For standard RDF, there therefore exists no convenient way of annotating data with metadata on the statement level [10]. The RDF$^\star$/SPARQL$^\star$ approach was proposed as a way of supporting a more intuitive representation, by allowing triples in the subject and object positions of RDF statements [9, 10]. In this paper, we propose to extend RSP-QL based on this approach.

3 Use-Case Scenario

In this section, we describe a use-case scenario to exemplify the kinds of requirements that may be addressed by combining RSP-QL with RDF$^\star$/SPARQL$^\star$. The scenario originates from an ongoing research project, E-care@home², in which the aim is to develop privacy-preserving AI-solutions for home care of elderly patients. In addition to developing technical solutions, the project has put great emphasis on studying the requirements of stakeholders. These requirements have been documented in a project deliverable [14]. As part of this deliverable, a number of personas and use-case scenarios were also developed, including the following description of a scenario involving the patient Rut who has advanced chronic obstructive pulmonary disease (COPD) and is multimorbid.

“The system can automatically sense abnormal situations, e.g. when certain health parameters deviate from the normal values, or when the overall situation as assessed by a multitude of sensors appears abnormal. When the system detects such situations, it sends out an alarm to a suitable recipient based on the severity of the deviation (e.g., emergency dispatch for a life-threatening deviation, the patient’s physician if no immediate action is required, or next-of-kin if suitable). [...] Today the system has detected an abnormal state. Rut appears to have been sitting in the same position in a chair in the living room for an unusually long time given that there are no entertainment devices turned on at the moment. Her heart rate is above normal, but her breathing is slower than normal. Small motions indicate that she is not asleep, yet she is not moving much. Her oxygen levels are about normal. The system decides to classify this as a low-emergency abnormal state. The system also knows that Rut’s partner has left the house a few hours ago. It therefore sends an alert to him [...] the alert reaches Rut’s partner as he is already on his way home. He hurries home and opens the door only to find out that Rut is in good health and has been enjoying a paperback copy of the latest crime novel by a famous Swedish author for the past few hours” [14].

Like any health-care system, the one envisioned by E-care@home sets high requirements in terms of patient safety, system reliability, and transparency. To this end, all the data that the system uses to draw conclusions and to generate suggestions, or even to take action, must be accompanied by some assessed confidence. For instance, in the scenario above, to put patient safety first the system cannot afford to miss an abnormal and highly dangerous situation, but on the other hand it needs to be able to disregard observations that are not reliable. As an example, whenever a pulse oxymeter reports the oxygen saturation of a patient, the system also needs to know the confidence that the system can put in this value. The sensor may have a fixed confidence value, but the system may also derive an adjusted value that takes into account contextual factors of the measurement, such as the position of the sensor and the activity of the patient at measurement time. Regardless of how the confidence value is derived, it needs to be reported as part of the reported observation.

4 Overview of RSP-QL$^{\star }\!$

The main difference between RSP and traditional RDF/SPARQL processing is that the former introduces a time dimension to processing [6]. The time dimension in RSP-QL is managed by allowing windows to define discrete subsets over RDF streams, and at any point in time, a window can be queried as a regular RDF dataset. The approach proposed in this paper extends RSP-QL in two fundamental ways: RDF streams are extended to support RDF$^\star$, and the supported graph patterns in RSP-QL are extended to support those in SPARQL$^\star$. The example in Listing 1.1 shows an RSP-QL$^{\star }\!$ query that illustrates the main features and language constructs.

The registered query is evaluated every 10 seconds. It defines a time-based window with a width of 1 min that slides every 10 s over the heart-rate stream. The query then matches the heart-rate value and confidence of each observation in the window using an RDF$^\star$ pattern [9]. This is the only difference between RSP-QL and RSP-QL$^{\star }\!$ in this query. The results are then filtered based on a threshold, and the heart-rate value and timestamp of the matched observations are reported. There are conceptually no limitations on the complexity of the provided annotations, and they can, e.g., instead be represented as confidence intervals or distributions rather than single values.

5 Data Model

This section defines the concepts that capture the notion of streams considered by our approach. We begin with the basic notions of RDF and RDF$^\star$.

As usual [5, 16], we assume three pairwise disjoint, countably infinite sets $\mathcal {I}$ (IRIs), $\mathcal {B}$ (blank nodes), and $\mathcal {L}$ (literals). Then, an RDF triple is a tuple $(s,p,o) \in (\mathcal {I} \cup \mathcal {B}) \times \mathcal {I} \times (\mathcal {I} \cup \mathcal {B} \cup \mathcal {L})$, and an RDF graph is a set of RDF triples. For such a triple (s, p, o), s is called the subject, p the predicate, and o the object.

RDF$^\star$ extends this notion of triples by allowing the subject or the object to be another triple [9]. This form of nesting of triples, which may be arbitrarily deep, allows for statements to capture metadata about other statements. Formally, an RDF$^*$ triple is defined recursively as follows [9]: (i) any RDF triple is an RDF$^\star$ triple, and (ii) given two RDF$^\star$ triples t and $t'$, and the RDF terms $s \in (\mathcal {I} \cup \mathcal {B})$, $p \in \mathcal {I}$, and $o \in (\mathcal {I} \cup \mathcal {B} \cup \mathcal {L})$, the tuples (t, p, o), (s, p, t), and $(t,p,t')$ are RDF$^\star$ triples. Furthermore, a set of RDF$^\star$ triples is called an RDF$^*$ graph.

The concept of an RDF dataset has been introduced to represent collections of RDF graphs [5]. We extend this concept to cover RDF$^\star$ graphs.

Definition 1

A named RDF$^*$ graph is a pair $(n, G^\star )$ where $n \in (\mathcal {I} \cup \mathcal {B})$, which is called the graph name, and $G^\star$ is an RDF$^\star$ graph. An RDF$^*$ dataset is a set $D=\{ G^\star _{0}, (n_1, G^\star _1), (n_2, G^\star _2), ..., (n_i, G^\star _i) \}$, where $G^\star _0$ is an RDF$^\star$ graph, called the default graph of D, and $(n_k, G^\star _k)$ is a named RDF$^\star$ graph for all $k \in \lbrace 1, 2, ..., i \rbrace$.

While the RDF model is atemporal, the notion of an RDF stream has been introduced to capture the dynamic nature of streaming RDF data [7]. Along the same lines, we define an RDF$^*$ stream as a time-ordered sequence of elements that are captured by a specific form of RDF$^\star$ datasets.

Definition 2

Let p be an IRI that denotes a predicate to capture timestamps for named RDF$^\star$ graphs. Then, an RDF$^*$ stream element E is an RDF$^\star$ dataset that consists of a default graph $G_o^\star$ and exactly one named RDF$^\star$ graph $(n, G^\star )$ such that the default graph $G_o^\star$ contains one RDF triple of the form $(n, p, \tau )$, where $\tau$ is a timestamp. To denote this timestamp $\tau$ in E we write $\tau (E)$.

Definition 3

An RDF$^*$ stream S is a potentially unbounded sequence of RDF$^\star$ stream elements such that for every pair of such elements $E_i$ and $E_j$, where $E_i$ comes before $E_j$ (i.e., $S=( ..., E_i, ..., E_j, ...)$), the following properties hold:

• 1. $\tau (E_i) \le \tau (E_j)$, and

• 2. the names of the single named RDF$^\star$ graph $(n_i, G^\star _i)$ in $E_i$ and of the single named RDF$^\star$ graph $(n_j, G^\star _j)$ in $E_j$ are different (i.e., $n_i \ne n_j$).

A named RDF$^*$ stream is a pair (n, S) where $n \in \mathcal {I}$ and S is an RDF$^\star$ stream.

We also need to define a notion of windows over such streams as a way of referencing discrete portions of potentially infinite data streams [7].

Definition 4

A window W over an RDF$^\star$ stream S is a finite set of RDF$^\star$ stream elements from S.

In this paper, we focus explicitly on temporal window operators (other window operators, such as count-based windows, can be defined in a similar manner). To this end, we define a time-based window of an RDF$^\star$ stream as a contiguous set of elements from the stream whose timestamp is in a given interval.

Definition 5

Given a time interval [l, u), the time-based window over an RDF$^\star$ stream S for [l, u), denoted by $\mathcal {W}(S, l, u)$, is a window over S that is defined as follows: $\mathcal {W}(S, l, u) = \lbrace E \mid E \text { is in } S \text { and } l \le \tau (E) < u \rbrace .$

Finally, we shall need a function that represents any window as an RDF$^\star$ dataset. Informally, this dataset consists of all the named RDF$^\star$ graphs of all RDF$^\star$ stream elements within the window, and the default graph of this dataset is constructed from the default graphs in all these RDF$^\star$ stream elements.

Definition 6

Let $\mathcal {W} = \lbrace E_1, E_2, ..., E_n \rbrace$ be a window over some RDF$^\star$ stream. The dataset representation of $\mathcal {W}$, denoted by $DS(\mathcal {W})$, is the RDF$^\star$ dataset that is constructed as follows:

• the default graph of $DS(\mathcal {W})$ is $G_0^\star = \bigcup _{\{G^\star _\text {dflt}, (n,G^\star )\} \in \mathcal {W}} G^\star _\text {dflt}$, and

• the set of named RDF$^\star$ graphs in $DS(\mathcal {W})$ is $\lbrace (n,G^\star ) \mid \{G^\star _\text {dflt}, (n,G^\star )\} \in \mathcal {W} \rbrace$.

6 Syntax and Semantics of RSP-QL$^{\star }\!$

This section defines RSP-QL$^{\star }\!$, which is an RDF$^\star$-aware extension of RSP-QL. RSP-QL, in turn, is an extension of SPARQL. Hence, our definitions in this section extend RSP-QL [7] along the lines of how SPARQL$^\star$ extends SPARQL [9, 10], and by also taking into account the abstract syntax and semantics draft of the W3C RSP community group [2]. For the SPARQL-specific constructs we adopt the algebraic SPARQL syntax introduced by Pérez et al. [16]. Due to space constraints, we limit ourselves to presenting only the core concepts of the language.

6.1 Syntax of RSP-QL$^{\star }\!$ Queries

RSP-QL is an extension of SPARQL [17], and the basic building block is a basic graph pattern (BGP), that is, a finite set of triple patterns. A triple pattern is a tuple $(s,p,o) \in (\mathcal {V} \cup \mathcal {B} \cup \mathcal {I}) \times (\mathcal {V} \cup \mathcal {I}) \times (\mathcal {V} \cup \mathcal {B} \cup \mathcal {I} \cup \mathcal {L})$, where $\mathcal {V}$ is a countably infinite set of query variables that is disjoint from $\mathcal {B}$, $\mathcal {I}$, and $\mathcal {L}$, respectively.

Like SPARQL$^\star$ [9, 10], RSP-QL$^{\star }\!$ extends these notions further by supporting the concept of triple$^*$ patterns, which add the possibility to nest triple patterns (arbitrarily deep), and which are defined recursively as follows [9, 10]:

• any triple pattern is a triple$^\star$ pattern, and

• given two triple$^\star$ patterns tp and $tp'$, and $s \in (\mathcal {I} \cup \mathcal {B} \cup \mathcal {V})$, $p \in (\mathcal {I} \cup \mathcal {V})$, and $o \in (\mathcal {I} \cup \mathcal {B} \cup \mathcal {L} \cup \mathcal {V})$, then (tp, p, o), (s, p, tp), and $(tp,p,tp')$ are triple$^\star$ patterns.

A finite set of triple$^\star$ patterns is referred to as a BGP$^*$.

On top of BGPs, RSP-QL supports all the other forms of graph patterns that have been introduced for SPARQL, and RSP-QL adds a new form to match data within windows of streaming data. We define a corresponding notion of patterns for RSP-QL$^{\star }\!$, but for brevity we here focus only on the core constructs.

Definition 7

An RSP-QL$^*$ pattern is defined recursively as follows:

• 1. Any BGP$^\star$ is an RSP-QL$^{\star }\!$ pattern.

• 2. If $n \in (\mathcal {V} \cup \mathcal {I})$ and P is a RSP-QL$^{\star }\!$ pattern, then (WINDOW n P) and (GRAPH n P) are RSP-QL$^{\star }\!$ patterns.

• 3. If $P_1$ and $P_2$ are RSP-QL$^{\star }\!$ patterns, then ($P_1$ AND $P_2$), ($P_1$ OPT $P_2$), and ($P_1$ UNION $P_2$) are RSP-QL$^{\star }\!$ patterns.

In addition to such patterns, every RSP-QL$^{\star }\!$ query may declare windows over named RDF$^\star$ streams, which we capture by the concept of window declarations.

Definition 8

A window declaration is a tuple $(u_S, \alpha , \beta , \tau _0)$ where $u_S \in \mathcal {I}$ is an IRI (representing the name of a named RDF$^\star$ stream), $\alpha$ is a time duration (representing a window width), $\beta$ is a time duration (representing a slide parameter), and $\tau _{0}$ is a timestamp (representing a start time).

We now have everything required to define RSP-QL$^{\star }\!$ queries, which consist of an RSP-QL$^{\star }\!$ pattern and window declarations that are associated with IRIs to serve as names for the corresponding windows in the query.

Definition 9

An RSP-QL$^*$ query is a pair $(\omega ,P)$ where $\omega$ is a partial function that maps some IRIs in $\mathcal {I}$ to a window declaration, respectively, and P is an RSP-QL$^{\star }\!$ pattern such that for every sub-pattern (WINDOW n $P'$) in P it holds that if $n \in \mathcal {I}$, then $\omega$ is defined for n, i.e., $n \in \mathrm {dom}(\omega )$.

6.2 Semantics of RSP-QL$^{\star }\!$ Queries

We now define the semantics of RSP-QL$^{\star }\!$ queries, for which we have to introduce some concepts used to define the query semantics of SPARQL and of SPARQL$^\star$.

The query semantics of SPARQL is based on the notion of solution mappings [16] that map query variables to blank nodes, IRIs, or literals. For SPARQL$^\star$, this notion has been extended to also be able to map to RDF$^\star$ triples. That is, a RSP-QL$^*$ is a partial function $\eta : \mathcal {V} \rightarrow (\mathcal {T} \cup \mathcal {I} \cup \mathcal {B} \cup \mathcal {L})$ where $\mathcal {T}$ denotes the set of all RDF$^\star$ triples [9, 10]. The standard notions of compatibility, merging and application of solution mappings can then be adapted as follows.

Definition 10

Two solution$^\star$ mappings $\eta$, $\eta '$ are compatible if $\eta (v) = \eta '(v)$ for every variable $v \in dom(\eta ) \cap dom(\eta ')$.

Definition 11

The merge of two compatible solution$^\star$ mappings $\eta$ and $\eta '$, denoted by $\eta \cup \eta '$, is a solution$^\star$ mapping $\eta ''$ with the following three properties:

• $dom(\eta '') = dom(\eta ) \cup dom(\eta ')$,

• $\eta ''(v) = \eta (v)$ for all $v \in dom(\eta )$, and

• $\eta ''(v) = \eta '(v)$ for all $v \in dom(\eta )' \setminus dom(\eta )$.

Definition 12

The application of a solution$^\star$ mapping $\eta$ to an RSP-QL$^{\star }\!$ pattern P, denoted by $\eta [P]$, is the RSP-QL$^{\star }\!$ pattern obtained by replacing all variables in P according to $\eta$.

We now define the corresponding algebra operators join, union, and left join.

Definition 13

Let $\varOmega _1$ and $\varOmega _2$ be sets of solution* mappings.

• $\varOmega _1 \bowtie \varOmega _2 = \{\eta _1 \cup \eta _2 \mid \eta _1 \in \varOmega _1, \eta _2 \in \varOmega _2, \ \eta \ \text {and} \ \eta ' \ \text {are compatible}\}$

• $\varOmega _1 \cup \varOmega _2 = \{\eta \mid \eta \in \varOmega _1\ \text {or}\ \eta \in \varOmega _2\}$

  

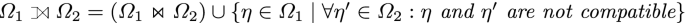
Based on these algebra operators, RSP-QL$^{\star }\!$ patterns are evaluated over a background dataset and a set of named windows at a given timestamp.

Definition 14

Let W be a partial function that maps some IRIs in $\mathcal {I}$ to a window over some RDF$^\star$ stream, respectively, and P be an RSP-QL$^{\star }\!$ pattern such that for every sub-pattern (WINDOW n $P'$) in P with $n \in \mathcal {I}$, it holds that W is defined for n, i.e., $n \in \mathrm {dom}(W)$. Furthermore, let D be an RDF$^\star$ dataset, G be an RDF$^\star$ graph, and $\tau$ be a timestamp. Then, the evaluation of P over D and W at $\tau$ with G, denoted by $[\![P ]\!]^{D,W,\tau }_G$, is defined recursively as follows:

• 1. If P is a triple$^\star$ pattern tp, then $[\![P ]\!]^{D,W,\tau }_G \!= \{ \eta \mid dom(\eta ) = var(tp) \ \text {and} \,\,\eta (tp) \in G\}$ where var(tp) denotes the set of variables occurring in tp.

• 2. If P is (GRAPH u $P'$), then $[\![P ]\!]^{D,W,\tau }_G = [\![P' ]\!]^{D,W,\tau }_{G'}$ where $(u, G') \in D$

• 3. If P is (GRAPH ?x $P'$), then $[\![P ]\!]^{D,W,\tau }_G = \bigcup _{(u,G') \in D}[\![\text {GRAPH} \ u \ P' ]\!]^{D,W,\tau }_{G'}$

• 4. If P is (WINDOW u $P'$), then $[\![P ]\!]^{D,W,\tau }_G = [\![P' ]\!]^{DS(\mathcal {W}),\emptyset {},\tau }_{G'}$ where $\mathcal {W} = W(u)$ and $G'$ is the default graph of the RDF$^\star$ dataset $DS(\mathcal {W})$

• 5. If P is (WINDOW ?x $P'$), then $[\![P ]\!]^{D,W,\tau }_G = \bigcup _{u \in \mathrm {dom}(W)} [\![\text {WINDOW} \ u \ P' ]\!]^{D,W,\tau }_G$

• 6. If P is (P1 AND P2), then $[\![P ]\!]^{D,W,\tau }_G = [\![P1 ]\!]^{D,W,\tau }_G \bowtie [\![P2 ]\!]^{D,W,\tau }_G$

• 7. If P is (P1 UNION P2), then $[\![P ]\!]^{D,W,\tau }_G = [\![P1 ]\!]^{D,W,\tau }_G \cup [\![P2 ]\!]^{D,W,\tau }_G$

• 8. If P is (P1 OPT P2), then  

It remains to define the semantics of RSP-QL$^{\star }\!$ queries, which contain window declarations in addition to an RSP-QL$^{\star }\!$ pattern (cf. Definition 9).

Definition 15

Let $\mathcal {S}$ be a finite set of named RDF$^\star$ streams and $q = (\omega ,P)$ be an RSP-QL$^{\star }\!$ query such that for every IRI $u_S \in \mathrm {dom}(\omega )$ there exists a named RDF$^\star$ stream $(u_S,S) \in \mathcal {S}$. Furthermore, let D be an RDF$^\star$ dataset and $\tau$ be a timestamp. The evaluation of q over D and $\mathcal {S}$ at $\tau$, denoted by $[\![q ]\!]^{D,\mathcal {S},\tau }$, is defined as $[\![q ]\!]^{D,\mathcal {S},\tau } = [\![P ]\!]^{D,W,\tau }_G$ where G is the default graph of D and W is a partial function such that $\mathrm {dom}(W) = \mathrm {dom}(\omega )$ and for every IRI $u \in \mathrm {dom}(W)$, it holds that W(u) is the time-based window $\mathcal {W}(S, x-\alpha , x)$ with $(u_S,S) \in \mathcal {S}$, $(u_S, \alpha , \beta , \tau _0) = \omega (u)$ and $x = \tau _0 + \alpha + \beta \times i$ for the greatest possible $i \in \mathbb {N}$ for which $x < \tau$.

7 Application-Based Evaluation

In this section, we evaluate RSP-QL$^{\star }\!$ based on the application use-case scenario introduced in Sect. 3. To this end, we make three assumptions: First, we assume that all parameters about the patient are provided in separate streams.

Second, the thresholds for the physiological parameters are context dependent, and we assume that the background data contains information about Rut’s expected values with respect to some activity. Third, we assume that all physiological parameters are reported with a confidence value representing some inherent uncertainty of the sample.

Listing 1.2 illustrates a typical query for the application scenario. For the sake of readability, we have simplified the query slightly compared to the actual project application. Additional optimization strategies would also be employed in practice to provide improved scalability.

The inputs to the query are 5 different streams that report data about the patient’s current heart rate, breathing rate, oxygen saturation, location (of both Rut and Rut’s partner), and current activity, respectively. The activity stream might have been created by another reasoning mechanism in the system, which infers activities of daily life based on sensor inputs and the context. For each window, the values are filtered for specific values or a confidence threshold, and then the aggregated data is checked against the threshold values specific to the current context of the patient (e.g., including the type of activity). If these conditions are met, we consider it a low-emergency situation, as described in the scenario outlined in Sect. 3. The resulting event is pushed to another stream upon which the system can act appropriately. In our use-case scenario, the system would first contact Rut’s partner. Similar queries could be set up to deal with other situations that the system should be able to detect.

The application of RSP-QL$^{\star }\!$ to this project use case shows that it is possible to express the queries needed, and that the proposed language thereby fulfills our use-case based requirements. In particular, it is worth noting the compactness and relative readability of the query in Listing 1.2, as compared to the corresponding RDF reification query³ (excluded to space constraints).

8 Performance Evaluation

In this section, we begin by briefly describing a prototype implementation of the proposed approach. We then report on the effects of the proposed RDF stream model with respect to data bandwidth, and compare it with a baseline approach of using RDF reification. Finally, we compare the query execution performance of the prototype when using RDF$^\star$ as opposed to RDF reification, while varying the number of annotated triples per streamed element.

All experiments were run on a MacBook Pro with 16 GB 1600 MHz DDR3 memory, and a 2.8 GHz Intel Core i7. The experiments were run using Java 1.8.0 with 2048 MB allocated for the JVM. All experiments were preceded by warm-up runs and averages for execution times were collected only after memory usage had stabilized.

8.1 Prototype Implementation

We implemented the prototype using Apache Jena⁴ and RDFstarTools⁵, where the latter provides a collection of Java libraries for processing RDF$^\star$ data and SPARQL$^\star$ queries. Additionally, we implemented a separate RSP-QL$^{\star }\!$ query parser and integrated it with the standard Jena architecture, along with an extension of Jena’s query class to support the additional syntax elements defined in RSP-QL$^{\star }\!$.

For the query execution, the implementation provides an extension of Jena’s query engine and query execution, supporting the new query operators. During query execution, all windows over streams are materialized as individual RDF$^\star$ datasets. The execution’s active dataset then changes as needed when a window operation is evaluated. To improve evaluation efficiency, all parsed nodes are encoded as integers in one of two dictionaries: the node dictionary or the reference dictionary. Regular RDF nodes are added to the node dictionary, while triple nodes are added to the reference dictionary, which (recursively) encodes each separate node of the triple. All nodes, regardless of type, are internally represented as an integer, where the most significant bit signals whether the ID represents a regular node or a reference triple. This allows the system to quickly check how a node should be decoded. Encoding and decoding iterators are provided to support moving between ID-based iterators, and Jena’s standard iterator implementations.

The prototype is provided as open-source⁶ under the MIT License. The underlying data structures can easily be changed by providing alternative implementations for the corresponding interfaces.

8.2 Serialization Overhead

One of the side-effects of using RDF reification to annotate triples is that it increases the size of the dataset, since for each reification triple four additional triples have to be added. Thus, one of the benefits of the proposed extension is the reduced overhead involved in transferring statement-level annotations in data streams. To compare the impact on bandwidth requirements, we compared the overhead in terms of bytes for each of the two approaches. The data was serialized using TriG$^\star$, which is an extension of Turtle$^\star$ [9] for supporting named graphs, and compressed⁷.

The amount of metadata per annotated triple impacts the relative overhead of the two approaches. For this evaluation, the TriG$^\star$ serialization of each RDF$^\star$ stream element contains declarations of one prefix, a base IRI, and a single metadata statement per annotated triple. Figure 1 shows the bandwidth required by the approaches as a function of the number of annotated triples per streamed element. The results show that the amount of bytes required when using RDF$^\star$ is around half of what is required when using RDF reification.

8.3 Query Execution Performance

The performance of the approach was evaluated on the prototype implementation. The streamed elements contained a single confidence annotated triple, where the number of additional triples annotated with some other metadata predicate varied between experiments runs. A single evaluation query was used to match and filter all triples annotated with the confidence value. We compared query execution times when representing the metadata using RDF$^\star$ and querying it using RSP-QL$^{\star }\!$ versus representing the metadata using RDF reification and querying it using pure reification-based RSP-QL queries. The prototype applies no specific optimization techniques for the queries; thus, the two approaches differ only with respect to how statement-level metadata is represented internally. The RDF reification approach simply uses regular triple-pattern matching, whereas the RDF$^\star$ approach represents the annotated triples as resources on the physical level. For the RDF reification query, we provided an additional version of the query optimized based on the heuristics described by Tsialiamanis et al. [19], where the order of the matched triple patterns was determined based on selectivity. Figure 2 presents the average query execution times. The results show that the advantage of the proposed approach grows with the number of distinct triples annotated in each streamed element, but that this difference can potentially be reduced by applying established optimization heuristics.

Fig. 1.

Byte size of a serialized RDF$^\star$ stream element as a function of the number of triples in it, where each triple is annotated with exactly one metadata triple.

Fig. 2.

Average query execution times of the prototype implementation when using either RDF$^\star$, reification, or reification with query optimization based on selectivity.

9 Discussion

The proposed approach provides a compact and intuitive way for both representing and querying annotated triples. Other approaches that could be considered for this purpose include single-triple named graphs [12], singleton properties [15], and RDF reification [11], but these approaches come with various drawbacks.

The application of named graphs inhibits the use of the graph name for other purposes, which means it is not compatible with the structure of RDF stream elements. Singleton properties introduce large numbers of unique predicates, which can adversely affect query execution performance. RDF reification, on the other hand, is both part of the RDF standard and can be supported in RSP-QL. However, RDF reification is verbose, both with respect to representing and querying data.

We note that RDF$^\star$ and SPARQL$^\star$ may be understood simply as syntactic sugar on top of RDF and SPARQL [9], and by extension this applies to the approach presented in this paper. However, the evaluation of the prototype implementation illustrates that representing annotated triples as resources on the physical level can have positive effects on the query execution level. When matching a single RDF reification triple, a total of four additional triple patterns have to be evaluated. In fact, due to this inefficiency, many RDF stores implement specific strategies for representing annotated triples [8]. For example, Virtuoso⁸ encodes RDF reification statements as quads, Apache Jena⁹ provides an implementation of a node type with direct access to the statement it reifies, and Blazegraph¹⁰ uses an approach similar to the one implemented in our prototype.

RDF$^\star$ and SPARQL$^\star$, and thus RSP-QL$^{\star }\!$, simplifies the representation of complex scenarios, both from the perspective of modeling and of querying annotated metadata. For example, we may want to treat an RDF statement differently depending on whether the uncertainty associated with it has been automatically generated by a sensor, or if it originates from a physician. Querying this using RSP-QL$^{\star }\!$ simply involves having a triple$^\star$ pattern with two layers of nesting.

As part of future work, we plan on relaxing some of the assumptions made in the semantics, and add support for additional features defined in RSP-QL, such as count-based window operators and output stream operators.

10 Conclusion

In this paper, we have presented a novel way of annotating and querying statement-level metadata in RDF Stream Processing (RSP), and formally defined the new continuous query language RSP-QL$^{\star }\!$. The approach extends RDF streams to allow triples to directly use other triples in the subject and object positions, and similarly extends the current version of RSP-QL to query these, by leveraging and building on the concepts previously proposed for RDF$^\star$ and SPARQL* [9, 10].

The proposed approach was applied in a use case from an e-health research project, where multiple data streams have to be queried in parallel, and over extended periods of time, to detect possibly abnormal situations. The results show that RSP-QL$^{\star }\!$ meets all our use-case requirements, and provides a compact and intuitive way of expressing and querying statement-level metadata, compared with the baseline approach of using RDF reification. Furthermore, the prototype implementation presented in the paper, which is provided as open-source, demonstrates benefits over the baseline approach, both with respect to the bandwidth required for data transfer and with respect to query execution performance over statement-level annotations. RDF$^\star$ is a syntactically more compact way to express metadata annotations, and our experiments show that this difference is large enough to have an impact in deployed real-world systems and applications, where bandwidth may be limited. Although our prototype implementation is not optimized for query performance, we were able to demonstrate that the approach was faster with respect to query execution performance, when compared to using standard RDF reification.

This is the first work on RSP that has focused on supporting annotations on the statement level. We believe that the proposed approach provides an intuitive and compact way for representing and querying statement-level metadata, and that this work provides a good foundation for future research on efficient management of, e.g., uncertainty and provenance, in RDF data streams.