Abstract
Grid-connected battery storage systems on megawatt-scale play an important role for the integration of renewable energies into electricity markets and grids. In reality, these systems consist of several batteries and inverters, which have a lower energy conversion efficiency in partial load operation. In renewable energy sources (RES) applications, however, battery systems are often operated at low power. The modularity of grid-connected battery storage systems thus allows improving system efficiency during operation. This contribution aims at quantifying the effect of segmenting the system into multiple battery-inverter subsystems on reducing operating losses. The analysis is based on a mixed-integer linear program that determines the system operation by minimizing operating losses. The analysis shows that systems with high modularity can meet a given schedule with lower losses. Increasing modularity from one to 32 subsystems can reduce operating losses by almost 40%. As the number of subsystems increases, the benefit of higher efficiency decreases. The resulting state of charge (SOC) pattern of the batteries is similar for the investigated systems, while the average SOC value is higher in highly modular systems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Grid storage systems on megawatt scale play a vital role for the integration of renewable energies into electricity markets and grids. Several investigations focus on the development of optimized battery operation strategies [1,2,3,4,5]. For several reasons, existing grid storage systems usually consist of multiple batteries and inverters. For reasons of economies of scale, hardware manufacturers offer components in limited number of size classes, allowing lower production costs. Furthermore, the use of modular components supports the systems’ scalability. In addition, the size of modular systems can be changed over their lifetime. Moreover, modular systems avoid single points of failure, which leads to higher fault tolerance. Although the modularity of existing grid storage systems is well known, most of the analyses describe the storage system as a single battery combined with a single inverter [1,2,3,4,5,6,7,8,9]. Few studies are known that analyze the modularity of grid-connected battery systems and the related effect on system efficiency during operation and the influence of these energy losses on the operating strategy of the system [10, 11].
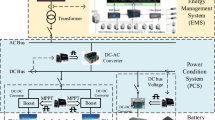
The consideration of this architectural aspect in the model-based analyses of battery operation provides a degree of freedom in optimizing the overall yield of a grid storage system. Figure 1 shows an example for a grid storage system with a high modularity. In this setup, three inverters and batteries are connected to one point of common coupling.
Storage systems operated together with a renewable energy source are most likely not charged and discharged at their nominal power. Figure 2 shows the frequency of the operational inverter power over the course of a year for a large battery that is operated together with a wind farm with the purpose of supporting market integration of wind energy [14].
During 79% of the time, the system is in standby mode. During 5% of the time the system is operated at less than 50% rated power, while during 14% the power rating is between 80% and 100%.
This suggests the importance of energy conversion efficiency not only in full-load operation, but also in standby mode and in partial-load operation. The inverter efficiency, however, is a nonlinear function in terms of power flow (Fig. 3 with N = 1). In partial-load operation, the relative inverter losses are significantly higher in comparison to relative losses at full-load operation. Because of the possibility to use several inverter units, the efficiency is higher in high modularity systems. At low power flows, using one smaller inverter unit can limit the losses. Figure 3 shows the effect of number of inverters on the total efficiency curve. Here, we assume the power rating of the total storage system to be constant. Therefore, the power rating of the inverter and the constant losses scale with \(\frac {1}{N}\). The impact on the efficiency is evident up to a number of inverters of 4. Constant losses become less relevant with the increase from 4 to 8 inverters.
Figure 3 provides an overview of the influence on the efficiency of modular battery systems. For operating a system with higher modularity, with discrete battery-inverter pairs, the operating strategy is more complex. Without an optimization strategy, which combines knowledge about power transfer losses, the SOC of the batteries and requests from the grid, suboptimal operating states can be realized, which increases losses. Hence, the operating strategy has a significant influence on the yield of a grid storage system. In this study we avoid choosing an individual optimization strategy by formulating an optimization problem. This optimization problem is formulated in terms of power flows and minimizes the power losses of the system. So, changes in the operating strategy, caused by increasing the number of inverter-battery pairs, are identified by solving the optimization problem.
The target function optimizing the operating strategy of the system is purely technical driven, i.e. we optimize in terms of power losses. Since most of the business models for grid storage systems rely on the power in and outflows of the system for economic evaluation, an optimization in terms of losses is always of benefit for the system operator.
As there is no direct connection between the batteries on the DC-side the energy management needs to take the state of charge of each battery into account. This increases the complexity of the energy management strategy.
This study addresses the questions to which extent the segmentation of the system into multiple battery-inverter subsystems can reduce operating losses and aims at quantifying this effect. Therefore, we develop a mixed-integer linear program that represents the operational strategy of an energy management system of such a modular system as it could be applied in real applications. The mixed-integer linear program determines the system operation for meeting a given schedule for the whole system at the point of common coupling by minimizing inverter losses. As a result, the required energy to be fed into or stored from the grid is allocated over the different battery-inverter-subsystems. The resulting SOC of the batteries is investigated and ideas for further investigations are derived.
Furthermore, the overall system topology has an influence on the power losses and the operating strategy. This study reduces the complexity by looking for identical battery-inverter pairs, which are coupled on the AC-side. A coupling on the DC-side has not been investigated in this study.
This paper is structured as follows. Section 2 describes the mathematical model and presents the data chosen for the analysis. Section 3 presents the results and compares the efficiencies of systems with different degrees of modularity. Section 4 draws conclusions for the design of grid-connected battery systems.
2 Methodology
2.1 Mathematical Model
2.1.1 Power Flow Model
The grid storage system is described as a set of nodes, representing the discrete time steps t with duration of the time steps d, with transfer of energy from one node to another [12, 13]. In this model, each pair of inverter and battery represents a single storage node. The inverter is only described by its influence on the power transfer from the battery into the grid and vice versa. The SOC represents the battery state of charge and interlinks the periods between each other, adding energy flows, both for energy charged and energy discharged during the previous period. N storage systems S i are connected to one point of common coupling. G t represents an additional connection to the grid. It serves as a backup when power requests to the storage cannot be met and shall avoid infeasibility of the model.
Hereinafter, a power flow from node A to node B is described as A B and the efficiency of this transfer is described as η AB(A B). Per definition, transfer losses are assigned to the sink.
The underlying power model is generic and initially independent of the technical implementation of the storage system. Different technologies might add different boundary conditions and parameters to the power flow. All parameters underlying the assumed technical realization are described in 2.1.3 to 2.1.5.
2.1.2 Consideration of Losses
The power transfer losses can be divided into constant, linear, and quadratic terms. This results in the common representation of the inverter efficiency (1):
In case of battery storage systems, constant losses \(a_{A_{B}} \) have their origin in auxiliary power, e.g. for the battery management system, active cooling and thermal control of the battery cells, and other subsystems. These losses are independent from the status of the inverter. Some systems can reduce the constant losses during standby operation by switching off subsystems. We consequently assume that the systems considered in our analysis can be turned off, avoiding standby losses during operation, as it is shown to be possible in Munzke et al. [14].
Linear losses \(b_{A_{B}} \) are proportional to the rated power. They are mainly heat losses. Furthermore, we consider battery efficiency. This is reflected by losses that are proportional to the charging and discharging power.
Quadratic losses \(c_{A_{B}}\)represent losses caused by nonlinear saturation effects in the inductance. In this work, the quadratic terms are not taken into account because non-linear losses cannot be clearly observed in all inverter systems [14].
Self-discharge of the battery cells, here represented as power loss of the storage path η SS, is usually very low and thus neglected [14,15,16]. Moreover, we do not consider the power supply of the battery management system (BMS).
We furthermore do not take into account losses which are independent of the degree of modularity, such as the power consumption of sensors or the climate control. Moreover, we do not consider transformer losses, neglecting the effect of additional power flows, introduced for ensuring model feasibility, on transformer losses.
Inverter loss data is obtained based on a curve fitting approach of the efficiency curve of SMA’s 250 kVA inverter “Sunny Central” [17]. The battery loss parameters are approximated based on data measured in Munzke et al. [14].
2.1.3 Parameters and Decision Variables
Table 1 shows the exogenously given parameters used in the model. Table 2 lists the decision variables as well as their lower and upper bounds. Power values are always given in Watt. The penalty parameter p and two decision variables for additional, unplanned power flows to and from the grid (\({G}_{L}^{t}\) and \({G}_{C}^{t}\)) are introduced for reducing deviations from the predetermined schedule and at the same time ensuring the model solvability. The same penalty parameter is applied both for charging from and discharging into the grid.
2.1.4 Target Function
The target function minimizes all losses and penalizes additional power flows (2). The solution is obtained by carrying out one optimization for every hour, i.e. four 15-min time steps at a time.
The target function determines the behaviour of the optimized power management strategy. In a modular system, the given power demand can be met by a subset of inverters. Given the example of two inverters in Fig. 3, only one inverter is used if it can provide the requested power, thus limiting constant losses. When power demand exceeds the single inverter’s power rating, the second subsystem is used. In this case, there is no incentive to operate the modules at different power. Therefore, if charge and discharge power requests are sufficiently high, we expect a nearly equal distribution on the SOC.
2.1.5 Constraints
Two binary variables are introduced for charging and discharging \((\gamma _{G_{S_{i}}},\gamma _{S_{i_{G}}} \in \{0;1\})\) in order to ensure that the storage system is not charged and discharged at the same time (3).
The power flow at the point of common coupling is defined by Eq. (4):
Equation (5) describes the energy flow for each storage system. It is solved for each hour independently. Therefore, the SOC t=0 is set as an external parameter. For the subsequent iterations, the SOC-value of the first time step is set as parameter according to the solution of the optimization of the previous optimization.
In addition, Eqs. (6) and (7) assure that battery charging or discharging is only realized if the binary variable is equal to 1.
Equations (8) and (9) set the boundaries for the power demand at the point of common coupling. These boundaries are calculated outside of and prior to the optimization.
2.1.6 Implementation
The model is implemented in MATLAB, using CPLEX as a solver. The solution is obtained on an hourly basis in 15-min resolution with a MIP gap of 0.5%.
2.2 Data
The battery schedule was calculated by Ried et al. [4]. It results from a planned operation of a 50 MW/100 MWh battery which is connected to a 50 MW wind farm. The system participates in the German day-ahead and tertiary control reserve markets. The battery schedule is a time series in 15-min resolution and obtained by a mixed-integer linear program maximizing the contribution margin of the system. For this study, the schedule is scaled to a 2 MW/2 MWh battery system and used as the power demand at the point of common coupling G t. Since it does not account for detailed losses, the battery used for this study is scaled 30% larger. All assumptions are given in Table 3.
Based on this data, the model is applied to six systems with varying degrees of modularity (Table 4).
3 Results and Discussion
In this section, we compare the yearly losses and resulting battery operation for the different systems, and discuss potential implications for the system layout.
3.1 Losses
Figure 4 shows the losses of systems with varying degrees of modularity relative to the losses of the system with N = 1. In accordance with the assumption shown in Fig. 3, the losses scale with the number of inverter-battery subsystems. By increasing the number of inverters to 32, the operating losses can be reduced by 38%. The gradual decrease of operating losses declines as the modularity increases.
This effect can be explained if the distribution of charge and discharge power over the course of one year for one and 32 inverters are compared. In a single inverter system, 50–70% of the charge and discharge power, neglecting standby mode, lies between 70% and 80% of the rated inverter power (Fig. 5). While 91% of the energy is charged at a rated power above 70%, 88% of the energy is discharged above 70% power rating. Power below 50% is requested during 29–31% of the time, corresponding to 5–6% of the energy flow. This is the mode of operation in which the individual inverter is less efficient and losses increase.
As the number of inverters increases, the maximum power of each inverter decreases. Figure 6 shows the resulting distribution of charge and discharge power. As expected, the most likely power is the maximum power of the inverter, which corresponds to \(\frac {1}{N}\) of the maximum power of the single inverter setup. Only very few events occur, where low power is requested.
3.2 Battery Operation
A difference between the systems with one and 32 inverters is a different SOC-level during the course of the year. Figure 7 shows the distribution of the state of charge over the course of a year for systems consisting of one and 32 sub-systems. In the non-modular system, the battery is operated at an average 13% SOC, while in the high-modularity system the average SOC is 27%. While 86% of the SOC-values in the non-modular system range between 10–20%, 57% of the SOC-values are in this range in the system consisting of 32 inverters and batteries. Due to lower operating losses, less energy is wasted and higher SOC-values occur more often.
Due to a larger number of batteries, there are relatively more downtimes of the batteries in high-modularity systems. While the system consisting of one inverter stands still during 79% of all periods, the sub-systems of the high-modularity systems are in standby-mode during 87% of the time. This suggests a higher redundancy of the system consisting of 32 batteries, which could be beneficial in case of failure, especially when power output must be guaranteed.
4 Conclusions
In summary, we have performed a study on the operating losses of grid-connected battery storage systems on megawatt-scale consisting of several battery-inverter subsystems. Therefore, we applied a mixed-integer linear program determining the optimal operation of all sub-systems for a given schedule for the point of common coupling of a case study where a battery is operated together with a wind farm.
The analysis shows that by increasing the system modularity, the frequency of operating points at low power decreases, resulting in a reduction of operating losses. The higher degree of freedom in modular systems thus allows following a given schedule at lower losses. By increasing the modularity from one to 32 sub-systems, operating losses can be reduced by almost 40%. The effect of modularity on efficiency is most evident for systems consisting of few sub-systems. With increasing modularity, the gradual decrease of operating losses declines. The resulting state-of-charge of the batteries shows a similar operation pattern for the investigated systems. The avoidance of losses in high-modularity systems, however, leads to a shift towards higher SOC levels.
We believe that this work motivates a modular layout of grid-connected battery systems. A higher efficiency should translate into lower operating cost. Moreover, the higher redundancy of modular battery systems can be advantageous particularly in applications that must ensure the system’s availability. The related investment cost is another aspect to consider when determining the system design. On the one hand, very large inverter and battery systems might translate into lower investment cost due to less balance of system components. A higher degree of modularity could thus be associated with higher costs. The opposite could also be the case, if the modularity enables the usage of standardized components produced in higher volumes, overcompensating the higher costs for the peripheral components.
Further analyses could address the effect of considering monetary aspects within the target function. Moreover, the penalty parameter ensures model feasibility, but does not fully avoid additional power flows. Both the additional power flows and the choice of the penalty parameter could be further investigated. In order to penalize any deviation from the predetermined schedule, the same penalty parameter was applied both for charging from and for discharging into the grid. However, especially deviations leading to battery discharging might be less critical and sometimes even desirable from energy system perspective, possibly leading to positive revenues. This could be the case if the system participates in additional electricity markets. Consequently, the value of the penalty parameter could be different for positive and negative deviations and should be subject to further research.
Maybe the most interesting potential for further research lies in the operation of the different batteries, the effect on battery ageing and implications on technology choice and system design. Our results show higher average SOC-levels of the batteries in high-modularity systems. The average SOC has an impact on the calendar ageing, so that higher SOC-levels could lead to reduced battery lifetime, at least for most technologies. Another aspect worth investigating is the effect of higher C-rates on battery degradation. Because of allocating the same requested power to fewer batteries with lower capacities, the C-rates might be higher in high-modularity systems. The modular system architecture might thus be more suitable for some battery technologies than for others. The selection of one or more appropriate battery technologies could positively influence battery lifetime.
Lastly, the battery management system determining the operational strategy could be adapted in order to take quadratic losses into account or vary operating patterns, SOC levels, and power requests for different storages. Moreover, asymmetric system topologies would allow for stressing the batteries at different depths of discharge and C-rates, even when running the same schedule. This might be an argument for hybrid storage systems consisting of different battery technologies with different characteristics and furthermore improve cycle ageing of the batteries, another important factor for battery degradation.
References
F. Braeuer, J. Rominger, R. McKenna, W. Fichtner, Battery storage systems: an economic model-based analysis of parallel revenue streams and general implications for industry. Appl. Energy 239, 1424–1440 (2019)
M. Gitizadeh, H. Fakharzadegan, Battery capacity determination with respect to optimized energy dispatch schedule in grid-connected photovoltaic (PV) systems. Energy 65, 665–674 (2014)
A. Parisio, E. Rikos, L. Glielmo, A model predictive control approach to microgrid operation optimization. IEEE Trans. Control Syst. Technol. 22(5), 1813–1827 (2014)
S. Ried, M. Reuter-Oppermann, P. Jochem, W. Fichtner, Dispatch of a wind farm with a battery storage, in Proceedings of the Operations Research Conference, Aachen (2014), pp. 473–479
P. Mokrain, M. Stephan, A stochastic programming framework for the valuation of electricity storage, in Proceeding of the 26th USAEE/IAEE North American Conference, Ann Arbor (2006), pp. 24–27
L. Hannah, D.B. Dunson, Approximate dynamic programming for storage problems, in Proceedings of the 28th International Conference on Machine Learning, Bellevue, Washington (2011)
N. Löhndorf and S. Minner, Optimal day-ahead trading and storage of renewable energies—an approximate dynamic programming approach. Energy Syst. 1(1), 61–77 (2010)
Y. Tang, H. He, Z. Ni, J.Wen, Optimal operation for energy storage with wind power generation using adaptive dynamic programming, in 2015 IEEE Power Energy Society General Meeting, Denver (2015), pp. 1–6
A. Das, Z. Ni, T. M. Hansen, X. Zhong, Energy storage system operation: case studies in deterministic and stochastic environments, in 2016 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis (2016), pp. 1–5
S. König, K. Iliopoulos, M.R. Suriyah, T. Leibfried, How direct marketing of a wind power plant affects optimal design and operation of vanadium redox flow batteries, in Proceeding of the 9th International Renewable Energy Storage (IRES), Düsseldorf (2015)
M. Schreiber, M. Harrer, A. Whitehead, H. Bucsich, M. Dragschitz, E. Seifert, P. Tymciw, Practical and commercial issues in the design and manufacture of vanadium flow batteries. J. Power Sources 206, 483–489 (2012)
A.U. Schmiegel, A. Kleine, Optimized operation strategies for PV storages systems yield limitations, optimized battery configuration and the benefit of a perfect forecast. Energy Proc. 46, 104–113 (2014)
A.U. Schmiegel, A. Kleine, Upper Economical Performance Limits for PV-Storage Systems, in Proceeding of the 28th European Photovoltaic Solar Energy Conference and Exhibition, Paris (2013), pp. 3745–3750
N. Munzke, B. Schwarz, F. Büchle, J. Barry, Lithium-Ionen Heimspeichersysteme: performance auf dem Prüfstand, in Tagungsband des 32. Symposium Photovoltaische Solarenergie, Kloster Banz Bad Staffelstein, vol. 32 (2017)
B.T. Kuhn, G.E. Pitel, P.T. Krein, Electrical properties and equalization of lithium-ion cells in automotive applications, in Vehicle Power and Propulsion, 2005 IEEE Conference (2005)
A.H. Zimmerman, Self-discharge losses in lithium-ion cells. IEEE Aerosp. Electron. Syst. Mag. 19(2), 19–24 (2004)
Solar Electric Supply, Inc. SMA Sunny Central 250-US Inverter (2018), Available at https://www.solarelectricsupply.com/sunny-boy-sunny-central-250-us-inverters-495. Accessed on 23 Jan 2018
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Ried, S., Schmiegel, A.U., Munzke, N. (2020). Efficient Operation of Modular Grid-Connected Battery Inverters for RES Integration. In: Bertsch, V., Ardone, A., Suriyah, M., Fichtner, W., Leibfried, T., Heuveline, V. (eds) Advances in Energy System Optimization. ISESO 2018. Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-32157-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-32157-4_10
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-32156-7
Online ISBN: 978-3-030-32157-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)