A Mechanised Proof of an Adaptive State Counting Algorithm

Abstract

In this paper it is demonstrated that the capabilities of state-of-the-art proof assistant tools are sufficient to present mechanised and, at the same time, human-readable proofs establishing completeness properties of test methods and the correctness of associated test generation algorithms. To this end, the well-known Isabelle/HOL proof assistant is used to mechanically verify a complete test theory elaborated by the second author for checking the reduction conformance relation between a possibly nondeterministic finite state machine (FSM) serving as reference model and an implementation whose behaviour can also be represented by an FSM. The formalisation also helps to clarify an ambiguity in the original test generation algorithm which was specified in natural language and could be misinterpreted in a way leading to insufficient fault coverage.

1 Introduction

Objectives. In this paper, we present a comprehensive mechanised proof for a complete test strategy originally published in [7] by the second author. The strategy allows for verifying the reduction conformance relation between two finite state machines (FSMs); the first serving as reference model, and the second representing the true behaviour of the system under test (SUT). Both FSMs may be nondeterministic. The test strategy uses an adaptive state counting approach to generate finite test suites guaranteeing complete fault coverage under the assumption of an upper bound for the number of states contained in the (unknown) observable, minimised FSM representing the SUT behaviour. In many situations, this results in significantly fewer test cases than the well-known “brute force” strategy based on product FSMs¹, which requires $O(a^{mn})$ test cases² to guarantee full fault coverage.

Motivation. We advocate an approach to systematic testing where fault coverage capabilities of test suites are formally proven, so that no doubt with respect to their test strength and their underlying hypotheses, such as the specification of fault domains, remains. Preferably, the proofs should be mechanically checked by proof assistants, as it cannot be expected that every new strategy and its variants and specialisations will be manually checked for correctness by many members of the testing community. Since complete test strategies are of considerable importance for the verification of safety-critical systems, the correctness of fault coverage claims for a given strategy is crucial from the system certification perspective. In absence of a “social process”, where the scientific community can be expected to re-verify every detail of a completeness argument, the mechanised re-verification and publication of the tool-based proofs is the best alternative from our perspective. Ideally, these proofs could be presented to the certification authorities responsible for authorisation of safety-critical systems becoming operative, to show that the complete testing strategy applied really has the test strength (i.e. the fault detection capabilities) that was claimed for the strategy.

Main Contributions. To our best knowledge, this is the first time that a mechanised proof for the complete reduction testing strategy from [7] is presented. Moreover, a formalised version of the associated test case generation algorithm is presented and proven to be correct as well, while in [7], only a textual description of the algorithm has been given. The formalisation has the advantage of removing an ambiguity in the algorithm’s textual presentation, that could lead to a misinterpretation and, in turn, to the generation of incomplete test suites.

Related Work. The first complete state counting approach to reduction testing has been published in [14]. It specialised on the case of deterministic implementations to be tested for language inclusion against nondeterministic reference models. This work has been optimised later in [13] by using adaptive state counting. The general problem admitting both nondeterministic reference models and implementations has been studied in [7] – this is the article the present paper is based on – and [15], where it is stated that the complete, adaptive strategy elaborated there results in fewer test cases than for the strategy published in [7].

Applying proof assistants to testing has first been advocated in [3]. In [4], the same authors present an integrated testing framework with Isabelle/HOL at its core, which allows for test strategy elaboration (a strategy is called a test theorem in [4]), fault coverage proof, test case and test data generation in the same tool. The authors present several cases of mechanised proofs establishing the completeness of testing theories. They do not, however, prove the theory analysed in the present paper.

Our general approach to model-based testing (MBT) contrasts to the one advocated in [4], since we favour specialised tools for strategy elaboration (Isabelle/HOL), modelling (FSM and SysML modelling tools), and test case and test data generation (RT-Tester [10] with SMT solver [12]). We agree with [2] that the use of SMT solvers in testing requires less specialised expertise than the interactive handling of proof assistants, since SMT solving can often be performed internally, without requiring explicit interactions with the users.

Reference to Comprehensive Online Resources. The Isabelle/HOL files containing the theories and proofs elaborated with the tool are publicly available for download on https://bitbucket.org/RobertSachtleben/formalisation-of-an-adaptive-state-counting-algorithm. The adaptive test algorithm has been implemented and made available in the fsmlib-cpp library, an open source project programmed in C++. The library contains fundamental algorithms for processing Mealy Machine FSMs and a variety of model-based test generation algorithms. Download, contents, and installation of the library is explained in the lecture notes [11, Appendix B] which are also publicly available.

Overview. In Sect. 2, the adaptive state counting test strategy from [7] is explained, in order to make this paper sufficiently self-contained. In Sect. 3, our mechanised proof is presented. First, an informal overview of the proof strategy is given. Then the main features of the theory and proof mechanisation in Isabelle/HOL are explained. Finally, the ambiguity in the informal description of the test generation algorithm in [7] is illustrated by an example, and it is shown that the algorithm’s new formalised version produces a complete test suite for this example. In Sect. 4, we present the conclusions.

2 Adaptive State Counting

The adaptive state counting algorithm re-verified in this paper serves to check the reduction conformance relation between a reference model $M_1$, given as a finite state machine, and an SUT whose behaviour is assumed to correspond to some unknown finite state machine $M_2$.

Finite State Machines. A Finite State Machine (also called a Mealy Machine) is usually defined as a tuple $M = (Q,q_0,\varSigma _I,\varSigma _O,h)$, consisting of a finite set of states Q containing an initial state $q_0$, a finite input alphabet $\varSigma _I$, a finite output alphabet $\varSigma _O$ and a transition relation $h \subseteq Q \times \varSigma _I \times \varSigma _O \times Q$ where $(q_1,x,y,q_2) \in h$ if and only if there exists a transition from $q_1$ to $q_2$ for input x that produces output y. We write ${initial}(M)$ to denote the initial state of M and |M| to denote the number of states of M. The language of state $q \in Q$ of an FSM $M = (Q,q_0,\varSigma _I,\varSigma _O,h)$, denoted L(M, q), is the set of all input-output (IO) sequences $\bar{x}/\bar{y} \in (\varSigma _I \times \varSigma _O)^*$ such that q can react to $\bar{x}$ with outputs $\bar{y}$. The language of M, denoted L(M), is the language of its initial state.

FSM M is said to be observable if for each q in Q, input x and output y there is at most one state $q'$ that is reached from q through a transition with input/output x/y, i.e. there is at most one state $q'$ in Q such that $(q,x,y,q') \in h$. If from any state of M there exists a transition for any input in the input alphabet, then M is said to be completely specified. Finally, M is said to be minimised, if $L(M,q) \not = L(M,q')$ holds for every pair $q \not = q'$ of states of M. If M is observable, then the state reached by an IO-sequence $\bar{x}/\bar{y} \in L(M,q)$ applied to state q, denoted ${io\_target}(M,q,\bar{x}/\bar{y})$ is uniquely determined. In the remainder of this paper, we assume every FSM to be completely specified over the same alphabet, observable and minimised. Recall that this is no restriction, since every FSM can be completed using one of the three methods described in [7] and transformed into a language-equivalent observable minimised machine [8].

A state q of FSM M is deterministically reached (d-reached) by an input sequence $\bar{v}$ if there exists some sequence $\bar{v}/\bar{v}' \in L(M)$ that reaches q and every sequence $\bar{v}/\bar{v}'' \in L(M)$ also reaches q. Such a state is called d-reachable. A deterministic state cover of M is a minimal set of input sequences V containing the empty sequence $\epsilon$ such that every d-reachable state of M is d-reached by some $\bar{v} \in V$. Finally, the product machine of two FSMs $M_1 = (S,s_1,\varSigma _I,\varSigma _O,h_1)$ and $M_2 = (T,t_1,\varSigma _I,\varSigma _O,h_2)$ is an FSM $\text {PM} = (S \times T, (s_1,t_1), \varSigma _I, \varSigma _O, h)$, where h is constructed as follows, ensuring that $L(\text {PM}) = L(M_2) \cap L(M_1)$ holds: $((s,t),x,y,(s',t')) \in h \Longleftrightarrow (s,x,y,s') \in h_1 \wedge (t,x,y,t') \in h_2$.

Adaptive Testing for Reduction. $M_2$ is a reduction of $M_1$, denoted $M_2 \preceq M_1$, if and only if $L(M_2) \subseteq L(M_1)$. Intuitively speaking, $M_2 \preceq M_1$ states that $M_2$ can only behave in ways that are also admissible in $M_1$. Analogously, $M_2$ is a reduction of $M_1$ on a set U of input sequences, denoted $M_2 \preceq _U M_1$, if every reaction of $M_2$ to an input sequence $\bar{x} \in U$ is also a reaction of $M_1$ to $\bar{x}$.

The latter definition is required, as it is generally infeasible to test for reduction by enumerating the languages of both machines. Thus, the algorithm tests for reduction by only applying a finite number of input sequences to both machines and checking whether the reactions of $M_2$ to each input sequence can also be observed in $M_1$. In doing so, some input sequence $\bar{x}$ may produce an output $\bar{y}$ in $M_1$ which is never produced by the implementation $M_2$. In such a situation, it is unnecessary to check whether $M_2$ conforms to the behaviour of $M_1$ after having run through $\bar{x}/\bar{y}$.

An adaptive test case (ATC) serves to apply inputs to $M_2$ depending on previously observed outputs, thus possibly reducing the number of applied inputs by omitting certain inputs if specific outputs are not observed. ATCs are tree-like structures whose nodes are either leaves, denoted null, or pairs (x, f), where x is an input and f maps outputs to ATCs. Applying an ATC $\sigma = (x,f)$ to an FSM M is performed by applying x to M and next applying ATC f(y) where y is the reaction of M to x. Applying null produces just $\epsilon$. The response set of all responses observed when applying an ATC to M in state q is calculated by function IO, defined as follows.

$$\begin{aligned} IO(M,q, {null})&:= \{\epsilon \} \\ IO(M,q,(x,f))&:= \bigcup _{x/y \in L(M,q)} \{x/y\}{.}IO(M,{io\_target}(M, q, {x}/{y}), f(y)) \end{aligned}$$

From this, we define additional functions ($\bar{x}/\bar{y}\in L(M)$, $\varOmega$ a set of ATCs).

$$\begin{aligned} B(M,\bar{x}/\bar{y},\varOmega ):= & {} \bigcup _{\sigma \in \varOmega } IO(M,{io\_target}(M, {initial}(M), \bar{x}/\bar{y}),\sigma ) \\ D(M,U,\varOmega ):= & {} \{ B(M,\bar{x}/\bar{y}, \varOmega ) \ | \ \bar{x} \in U \wedge \bar{x}/\bar{y} \in L(M) \} \end{aligned}$$

Function B maps $(M,\bar{x}/\bar{y},\varOmega )$, to the set of all IO sequences $\bar{x}{.}\bar{x}_1/\bar{y}{.}\bar{y}_1$, where $\bar{x}/\bar{y}$ reaches some q in M, $\bar{x}_1/\bar{y}_1 \in IO(M,q,(x,f))$, and ATC (x, f) is in $\varOmega$. Function D comprises all sets $B(M,\bar{x}/\bar{y},\varOmega )$, such that $\bar{x}$ is an input sequence from U and $\bar{y}$ is a possible response of M, when applying $\bar{x}$ to its initial state.

In testing, sets U of input sequences are followed by ATC sets $\varOmega$ in the sense that $\varOmega$ is applied to every state reached by some sequence in U. We say that $M_2$ is a reduction of $M_1$ on U followed with $\varOmega$, denoted $M_2 \preceq _{U.\varOmega } M_1$, if the following property holds:

$$\begin{aligned} M_2 \preceq _{U} M_1 \wedge \forall \bar{x} \in U . \ \forall \bar{y} . \ \bar{x}/\bar{y} \in L(M_2) \Longrightarrow B(M_2,\bar{x}/\bar{y},\varOmega ) \subseteq B(M_1,\bar{x}/\bar{y},\varOmega ) \end{aligned}$$

This requires $M_2$ to be a reduction of $M_1$ on U, while for any $\bar{x}/\bar{y} \in L(M_2)$ with $\bar{x} \in U$ the responses observed by applying $\varOmega$ to the states reached in $M_2$ by $\bar{x}/\bar{y}$ are also observed by applying $\varOmega$ to all states reached by $\bar{x}/\bar{y}$ in $M_1$.

The idea behind this application of ATCs is to distinguish states: If the same $\varOmega$ applied after two distinct IO sequences produces different response sets, then these sequences must reach distinct states. We say that two states s and $s'$ in $M_1$ are r-distinguishable if there exists an ATC $\sigma \not =\textit{null}$ such that ${IO}(M_1,s,\sigma ) \cap {IO}(M_1,s',\sigma ) = \emptyset$. Then, for some states $t,t'$ of $M_2$, if both ${IO}(M_2,t,\sigma ) \subseteq {IO}(M_1,s,\sigma )$ and ${IO}(M_2,t',\sigma ) \subseteq {IO}(M_1,s',\sigma )$ hold, $\sigma$ is also sufficient to distinguish t from $t'$. To increase the potential to distinguish states of the implementation, the set $\varOmega$ used in the algorithm is thus preferably an adaptive characterising set of $M_1$, which is a set containing for each pair of r-distinguishable states of $M_1$ an ATC that r-distinguishes them.

2.1 Overview of the Adaptive State Counting Algorithm

The adaptive state counting algorithm introduced in [7] describes a procedure to generate a finite set of input sequences TS for completely specified, observable, minimised FSMs $M_1$ and $M_2$ over the same alphabet and for an adaptive characterising $\varOmega$ of $M_1$ such that $M_2 \preceq M_1 \Longleftrightarrow M_2 \preceq _{TS.\varOmega } M_1$ holds. FSM $M_2$ is assumed to have at most m states. Then the application of TS followed with $\varOmega$ is sufficient to test for reduction. Starting from some deterministic state cover V of $M_1$ and iteratively extending this set of input sequences until a termination criterion is met, the test suite $TS{.}\varOmega$ is generated by a breadth-first search for a minimal length input sequence $\bar{x}$ such that, for some $\bar{v} \in V$, $M_2$ reacts to $\bar{v}\bar{x}$ in a way not observed in $M_1$. This criterion is based on state counting in the sense that a lower bound function LB is used to calculate for some IO-sequence $\bar{v}\bar{x}/\bar{v}'\bar{y} \in L(M_2)$ with $\bar{v} \in V$ a lower bound on the number of states that $M_2$ must contain for any extension of $\bar{x}/\bar{y}$ to be a minimal sequence to a failure if applied after $\bar{v}/\bar{v}'$. If this lower bound exceeds m, then no extension of $\bar{x}/\bar{y}$ applied after $\bar{v}/\bar{v}'$ can be minimal. Hence, $\bar{v}\bar{x}/\bar{v}'\bar{y}$ needs not be considered further. Moreover, if no response of $M_2$ to some input sequence $\bar{x}$ needs to be considered further, then $\bar{x}$ does not need to be extended. The search terminates as soon as no sequence needs to be extended further or an examined sequence has uncovered a failure.

Lower Bound Function LB. The calculation of the lower bound by function LB is based on two parts: First, the number of sequences reaching certain states in $M_1$ and second, the number of distinct response sets observed by applying the same set of ATCs after different input sequences to $M_2$, not counting response sets observed by applying the ATCs after the sequences of the first part. The first part is calculated using functions R and RP as defined below. For state s of $M_1$, function R collects all prefixes of $\bar{v}\bar{x}/\bar{v}'\bar{y}$ longer than $\bar{v}/\bar{v}'$ reaching s. Function RP adds to this certain $\bar{w}/\bar{w}' \in V'' \subseteq L(M_2)$ observed while testing $M_2$ that also reach s in $M_1$.

The lower bound function is then defined for arguments $M_1$, $M_2$, IO sequences $\bar{v}/\bar{v}'$ and $\bar{x}/\bar{y}$, a set U of input sequences, a subset $S_1$ of states of $M_1$, a set $\varOmega$ of ATCs, and some $V'' \subseteq L(M_2)$ as follows.

Splitting Sequences. In the algorithm, the $V''$ argument passed to the lower bound function is always contained in the set of all permutations of reactions of $M_2$ to V, denoted ${\textit{Perm}}(M_2,V)$ and defined for $V = \{\bar{v_1}, \ldots , \bar{v}_k \}$ as follows:

$$\begin{aligned} {\textit{Perm}}(M_2,V) := \{\{ \bar{v}_1/\bar{v}_1', \ldots , \bar{v}_k/\bar{v}_k'\} \ | \ \forall \ 1 \le i \le k . \ \bar{v}_i/\bar{v}_i' \in L(M_2) \} \end{aligned}$$

Furthermore, when calculating a lower bound for some IO-sequence $\bar{x}'/\bar{y}'$ and some $V''$, $\bar{x}'/\bar{y}'$ is split into a prefix $\bar{v}/\bar{v}'$ and a suffix $\bar{x}/\bar{y}$ such that $\bar{x}'/\bar{y}' = \bar{v}\bar{x}/\bar{v}'\bar{y}$ and $\bar{v}/\bar{v}'$ is the maximum length prefix of $\bar{x}'/\bar{y}'$ in $V''$. Depending on the $V''$ considered, sequence $\bar{x}'/\bar{y}'$ might thus be split in many different ways. We avoid this ambiguity by introducing function N to further restrict possible choices of $V''$ in such a way that for all remaining $V''$, sequence $\bar{x}'/\bar{y}'$ is split in the same way. This function N is defined as follows, using helper function mcp:

Function N thus for a sequence $\bar{x}/\bar{y}$ narrows the result of ${\textit{Perm}}$ to only those sets of responses $V''$ where the maximal prefix of $\bar{x}$ in V is also the input portion of the maximal prefix of $\bar{x}/\bar{y}$ in $V''$. In Subsect. 3.2 we use this narrowing to avoid an ambiguity in the description of the algorithm given in [7].

Test Suite Generation. Using the LB function as the main termination criterion, we define the test suite generated by the adaptive state counting algorithm using families of sets TS, C, and RM indexed by an iteration counter. $TS_i{.}\varOmega$ then describes the test suite generated up to iteration i. Similarly, $C_i$ contains all sequences considered for further extension and $RM_i \subseteq C_i$ contains those sequences not extended. We say that a sequence $\bar{x} \in RM_i$ is removed in iteration i. The families are defined as follows:

Starting from a deterministic state cover V of $M_1$, the test suite is thus generated by iteratively extending all sequences currently considered and not removed with every element of the input alphabet (see $C_{i+1}$ and $TS_{i+1}$).

Some sequence $\bar{x}'$ is removed only if it uncovers a failure (F) or if for every reaction $\bar{x}'/\bar{y}'$ of $M_2$ to it, $\bar{x}'/\bar{y}'$ can be split into $\bar{v}/\bar{v}'$ and $\bar{x}/\bar{y}$ where $\bar{v}/\bar{v}'$ is the maximum length prefix of $\bar{x}'/\bar{y}'$ also contained in $V'' \in N(\bar{x}'/\bar{y}',M_2,V)$, $\varOmega$ pairwise distinguishes the states reached in $M_2$ via sequences in the RP-sets for distinct states in some subset $S_1$ of the states of $M_1$, and the lower bound calculated by LB for these parameters exceeds m (L). Note here that if $\varOmega$ is an adaptive characterising set of $M_1$, no failure is observed when applying $\varOmega$ after $TS_i \cup V$, and $S_1$ contains a pair of r-distinguishable states s and $s'$ of $M_1$, then, by construction, $\varOmega$ must distinguish the states of $M_2$ reached by sequences in the RP-set for s from those reached by sequences in the RP-set for $s'$.

The presented method of iterative test suite generation can be implemented in a WHILE-language in a straightforward way, for example by Algorithm 1.

3 The Mechanised Proof

Isabelle/HOL. Isabelle is a generic proof assistant featuring an extensive implementation of higher-order logic (Isabelle/HOL). We have based our formalisation of the adaptive state counting algorithm in this logic, as it is highly expressive and already contains many useful definitions and theorems. For an introduction see Nipkow et al. [9]. The Isabelle core libraries are further extended by the Archive of Formal Proofs (see www.isa-afp.org). The Isar (Intelligible Semi-Automated Reasoning) proof language offered in Isabelle distributions allows for proofs to be written in a human-readable style [16]. An example is given in Sect. 3.1. Finally, we make use of Isabelle’s locales [1] facilitating the management of parametric theories, type hierarchies and structured contexts, by reusing the definition of transition systems given in [5] to define finite state machines.

Data Structures. In our Isabelle/HOL formalisation, we define FSMs by the following parametrised record-type:

Our definition thus syntactically deviates from the initial definition by using a successor function succ instead of the transition relation. This is no restriction, as $(q_1,x,y,q_2) \in h \equiv q_2 \in \textit{succ}((x,y), q_1)$. We also omit explicitly enumerating the state set; instead, it is assumed to be the set of all states that can be reached from the initial states by some sequence of transitions. This state set of FSM M is denoted by $nodes (M)$, and its cardinality is denoted by |M|.

Furthermore, this definition of FSMs by itself does neither enforce the finiteness and non-emptiness of the alphabets and the set of reachable states, nor restrict the successor function to allow only transitions over the input and output alphabets. We alleviate this problem by encoding these requirements in a predicate $\mathtt {well\_formed}$, which is then explicitly assumed to hold for relevant FSMs (see the assumptions of the example lemma in Sect. 3.1). Furthermore, we say that a value of type FSM is an OFSM if it is well-formed, observable and completely specified.

We interpret values of type FSM as transition systems with initial states as defined by Brunner in [5]. This interpretation allows us to reuse a large number of theorems, in particular concerning paths and reachability.

Finally, we define ATCs as a data type such that a value of this type is either a Leaf (null) or a Node containing an input and a function from outputs to ATCs:

Fig. 1.

Overview of the main proof steps and their dependencies.

3.1 Proof Strategy

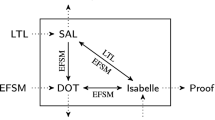
The strategy employed in mechanising and proving the adaptive state counting algorithm correct is given schematically by Fig. 1. In this figure, definitions are given in rectangles with cut corners, whereas rectangles with rounded corners represent lemmata. The corresponding definitions and lemmata in the Isabelle code are given in brackets in the lower half of the corresponding rectangle. The information flow from definitions and lemmata to other lemmata is indicated by arrows. Note that, due to size constraints, the lemmata and deductions do not list all assumptions. Figure 1 makes use of the following abbreviations: (a) $detSC(M_1,V)$ states that V is a deterministic state cover of $M_1$, (b) $\text { mstfe}(V,M_2,M_1,\bar{v}/\bar{v}',\bar{x}/\bar{y})$ states that $\bar{v} \in V$ and $\bar{x}/\bar{y}$ is a minimal sequence to a failure from the state reached by $\bar{v}/\bar{v}'$, and (c) $noRep(\bar{v}\bar{x}/\bar{v}'\bar{y})$ states that $\bar{x}/\bar{y}$ applied to $M_2$ after $\bar{v}/\bar{v}'$ contains no repetitions (as defined below).

Following the depicted strategy, we first prove that it is sufficient to search for minimal sequences to failures extending a deterministic state cover of $M_1$ (1). Next, we show that a value calculated by the LB function in the algorithm is a valid lower bound on $|M_2|$ (2) under certain assumptions, which are proven to be met by minimal sequences to failures (3). Additionally, we show that if an input sequence is not contained in TS, then either $TS{.}\varOmega$ uncovers a failure or the lower bound for any reaction of $M_2$ to that input sequence exceeds m (4). Using these results, we prove that if $TS{.}\varOmega$ does not uncover an existing failure, then $M_2$ must contain more than m states (5), providing a contradiction under the assumption that $|M_2| \le m$ holds (6). Thus, applying TS followed with $\varOmega$ is sufficient to test for reduction (7). Finally, we provide an implementation of the algorithm in a simple WHILE-language (8) and show that it generates and applies $TS{.}\varOmega$ until it has been fully applied or a failure has been observed (9), therefore being able to decide whether $M_2$ is a reduction of $M_1$ (10).

Our Isabelle/HOL code is split into theory files accordingly: First, FSM.thy defines FSMs and proves (1). Next, FSM_Product.thy and ATC.thy introduce product machine and data type ATC, respectively. ASC_LB.thy then defines LB, establishing (2), and ASC_Suite.thy defines TS, C and RM as functions, providing (4). Thereafter, ASC_Sufficiency.thy proves (3) and then (7) via (5,6). Finally, an implementation (8) is proven correct (9,10) in ASC_Hoare.thy.

Sequences to Failures. To provide a concrete example of an Isabelle lemma and its proof, we consider a sequence to a failure. This is an IO-sequence $\bar{v}\bar{x}/\bar{v}'\bar{y} \in L(M_2) \setminus L(M_1)$ extending a deterministic state cover V of $M_1$ such that every proper prefix is contained in $L(M_2) \cap L(M_1)$ and $\bar{v} \in V$. Such a sequence $\bar{v}\bar{x}/\bar{v}'\bar{y}$ is called minimal if furthermore no sequence $\bar{x}'/\bar{y}'$ shorter than $\bar{x}/\bar{y}$ constitutes a sequence to a failure extending V if appended to some $\bar{w}/\bar{w}'$ with $\bar{w} \in V$. If $M_2$ is not a reduction of $M_1$, then some sequences to a failure extending V must exist, since, by definition, a deterministic state cover contains the empty input sequence. Hence, any sequence to a failure extends V. From these, a minimal sequence to a failure extending V can then finally be selected. We express this result and proof in Isabelle as follows, where $[\ ]$ denotes the empty list and @ denotes list concatenation:

Observe the use of the by keyword to apply automatic proof methods (e.g. blast, auto, metis) to mechanically verify each individual proof step. Note that most of these steps are so simple that they would very likely not be proven explicitly in a manual proof “on paper”.

Furthermore, note that a sequence $\bar{v}\bar{x}x/\bar{v}'\bar{y}y$ to a failure extending V is not minimal in the above sense if $\bar{x}/\bar{y}$ applied after $\bar{v}/\bar{v}'$ visits any state of the product machine of $M_1$ and $M_2$ twice: in this case $\bar{x}x/\bar{y}y$ can be shortened by removing the resulting loop. It is also not minimal if $\bar{x}/\bar{y}$ applied after $\bar{v}/\bar{v}'$ visits some state that is reached by some sequence $\bar{w}/\bar{w}' \in L(M_2)$ with $\bar{w} \in V$ and $\bar{w} \not = \bar{v}$, as in this case a proper suffix of $\bar{x}/\bar{y}$ applied after $\bar{w}/\bar{w}'$ is a shorter sequence to a failure extending V. The absence of repetitions of the first and second kind is denoted by predicates $\lnot \texttt {Rep\_Pre}(M_1,M_2,\bar{v}/\bar{v}',\bar{x}/\bar{y})$ and $\lnot \texttt {Rep\_Cov}(M_1,M_2,V'',\bar{v}/\bar{v}',\bar{x}/\bar{y})$, respectively, where $V'' \subseteq L(M_2)$ usually is a set of reactions of $M_2$ to V.

Lemma $\mathtt {mstfe\_no\_repetition}$ then encodes that for a minimal sequence $\bar{v}\bar{x}/\bar{v}'\bar{y}$ to a failure extending V and some $\bar{x}'/\bar{y}' \in {\textit{pref}}(\bar{x}/\bar{y})$, repetition properties $\texttt {Rep\_Pre}(M_1,M_2,\bar{v}/\bar{v}',\bar{x}'/\bar{y}')$ and $\texttt {Rep\_Cov}(M_1,M_2,V'',\bar{v}/\bar{v}',\bar{x}'/\bar{y}')$ do not hold if $V''$ is contained in $N(\bar{v}\bar{x}/\bar{v}'\bar{y}, M_2, V)$.

Validity of the Calculated Lower Bound. Let s be some state of $M_1$. All sequences contained in $R(M,s,\bar{v}/\bar{v}',\bar{x}/\bar{y})$ by definition reach s in $M_1$. If it is assumed that $\texttt {Rep\_Pre}(M_1,M_2,\bar{v}/\bar{v}',\bar{x}/\bar{y})$ does not hold, then each contained sequence must reach a distinct state in $M_2$, as otherwise some state in the product automaton is visited twice. Similarly, if $\texttt {Rep\_Cov}(M_1,M_2,V'',\bar{v}/\bar{v}',\bar{x}/\bar{y})$ is assumed not to hold and $V''$ is an element of $N(\bar{v}\bar{x}/\bar{v}'\bar{y}, M_2, V)$, then the additional sequences of $V''$ contained in $RP(M,s,\bar{v}/\bar{v}',\bar{x}/\bar{y}, V'')$ must also reach distinct states in $M_2$. Hence, $M_2$ contains at least $|RP(M,s,\bar{v}/\bar{v}',\bar{x}/\bar{y}, V'')|$ distinct states.

When this function is applied in the algorithm, it is ensured that $\varOmega$ is sufficient to distinguish states of $M_2$ reached by sequences calculated by RP for distinct states $s,s' \in S_1$. Then no sequence in $RP(M,s,\bar{v}/\bar{v}',\bar{x}/\bar{y}, V'')$ reaches a state in $M_2$ that is also reached by some sequence in $RP(M,s',\bar{v}/\bar{v}',\bar{x}/\bar{y}, V'')$, which guarantees that, under the assumption that no repetitions occur, part (LB1) of LB is a valid lower bound. Adding to this, part (LB2) calculates the number of response sets observed by applying $\varOmega$ to $M_2$ after every input sequence in T, not counting those already observed by applying $\varOmega$ after sequences in the RP-sets. Any such distinct response set indicates the existence of at least one state of $M_2$ not reached via the RP-sets and hence the value calculated by LB is an actual lower bound on the number of states in $M_2$. This result is encoded in lemma $\mathtt {LB\_count}$.

Properties of the Generated Test Suite. Every removed sequence either uncovers a failure directly or, following from $|M_2| \le m$, cannot be prefix of a minimal sequence to a failure extending V (see $\mathtt {mstfe\_no\_repetition}$). Note that by this iterative process of extension, $C_{i+1}$ contains only sequences created by extending V with sequences of length i.

In order to ensure practical applicability of this test suite generation process, we first show that it terminates in the sense that after a finite number of iterations the test suite does not change for any further iteration. We call such an iteration final. Some final iteration must exist: Consider some IO-sequence $\bar{x}'/\bar{y}'$ with $\bar{x}' \in C_{|M_1| * m + 1}$. Then $\bar{x}'/\bar{y}'$ is of the form $\bar{v}\bar{x}/\bar{v}'\bar{y}$ such that $\bar{v} \in V$, $\bar{x}/\bar{y}$ is of length $|M_1| * m$ and $\bar{v}\bar{x}$ has not been removed in some $RM_j$ with $j < |M_1| * m+1$. Then $\bar{x}/\bar{y}$ applied after $\bar{v}/\bar{v}'$ either uncovers a failure, or visits states of the product machine of $M_1$ and $M_2$ a total of $|M_1| * m + 1$ times and must hence visit some state s of $M_1$ at least $m+1$ times, which causes the RP-set for s to contain $m+1$ sequences. By choosing $S_1 = \{s\}$ it is then possible to select parameters such that the lower bound is at least $m+1>m$. By this argument, every sequence in $C_{|M_1| * m + 1}$ is removed and $|M_1| * m + 1$ is a final iteration. In our Isabelle code, this result is given in lemma $\mathtt {final\_iteration\_ex}$.

Finally, let i be a final iteration, implying $C_i = \emptyset$, and note that $TS_i = \bigcup _{j\le i} C_j$ holds by construction. Therefore, $TS_i = \bigcup _{j\le i} RM_j$ follows (i.e., every sequence contained in $TS_i$ has been removed at some point). As the test suite is generated by iteratively extending it with every input in the input alphabet $\varSigma _I$ of $M_1$, if some sequence $\bar{x}$ over $\varSigma _I$ is not contained in $TS_i$, then there must exist some $j \le i$ such that a proper prefix $\bar{x}'$ of $\bar{x}$ is contained in $RM_j$. This constitutes lemma $\mathtt {TS\_non\_containment\_causes\_final}$. Note that the removal of $\bar{x}'$ indicates that it either already uncovers a failure or that the lower bounds calculated for the reactions of $M_2$ to it all exceed m.

Sufficiency for Proving Reduction. We show next that the test suite $TS_i{.}\varOmega$ for some final iteration i is sufficient to test for reduction (i.e., that $M_2 \preceq _{TS_i.\varOmega } M_1$ implies $M_2 \preceq M_1$).

Assume that $M_2 \preceq _{TS_i.\varOmega } M_1$ and hence also $M_2 \preceq _{TS_i} M_1$ holds. For $M_2 \preceq M_1$ not to hold, there must thus exist some minimal sequence to a failure $\bar{v}\bar{x}/\bar{v}'\bar{y}$ extending V such that $\bar{v}\bar{x} \not \in TS$. By lemma $\mathtt {TS\_non\_containment\_causes\_final}$, this is only possible if for a proper prefix $\bar{v}\bar{x}'/\bar{v}'\bar{y}'$ of $\bar{v}\bar{x}/\bar{v}'\bar{y}$ its input portion $\bar{v}\bar{x}'$ has been removed, which, in turn, requires the lower bound calculated for $\bar{v}\bar{x}'/\bar{v}'\bar{y}'$ to exceed m. Following from lemma $\mathtt {mstfe\_no\_repetition}$ applied to $\bar{v}\bar{x}/\bar{v}'\bar{y}$, no repetitions occur for $\bar{x}'/\bar{y}'$ applied after $\bar{v}/\bar{v}'$, and hence this lower bound is valid, implying that $M_2$ has more than m states. Thus, the assumption of $|M_2| \le m$ is contradicted, proving that no minimal sequence to a failure can exist whose input portion is not contained in $TS_i$. This is the proof idea for lemma $\mathtt {asc\_sufficiency}$.

Note that the reverse implication, $M_2 \preceq M_1 \Longrightarrow M_2 \preceq _{TS_i.\varOmega } M_1$, trivially holds by definition. From the above lemma it thus follows directly that $M_2$ is a reduction of $M_1$ if and only if it is a reduction of $M_1$ on $TS_i{.}\varOmega$.

Also observe that the above proofs do not require $\varOmega$ to be an adaptive characterising set of $M_2$. Yet, as described for the calculation of the lower bound, choosing an adaptive characterising set for $\varOmega$ ensures that for pairs of r-distinguishable states in $M_1$, the application of $\varOmega$ either uncovers a failure or successfully distinguishes the states reached by sequences in the corresponding RP-sets, thus possibly enabling earlier removal of sequences.

Correctness of an Implementation. The idea behind Algorithm 1 is to first initialise variables ts, c and rm with ${TS}_0$, $C_1$ and $RM_0$, respectively, and then to loop, calculating the values for the next iterations of those sets, until a failure has been observed or $c = \emptyset$ holds, indicating a final iteration. During this process, the observed reactions of $M_1$ and $M_2$ to the input sequences in c and the response sets to $\varOmega$ applied after c are stored in corresponding obs-variables. Finally, the algorithm is to return true if and only if no failure has been observed. In our Isabelle/HOL code, this algorithm is defined within lemma $\mathtt {asc\_algorithm\_correctness}$.

We prove the correctness of Algorithm 1 (i.e., whether it returns true if and only if $M_2 \preceq M_1$ holds) using Hoare-logic by first establishing a loop-invariant: If variables ts, c and rm contain $TS_{{\textit{iter}}-1}$, $C_{\textit{iter}}$ and $RM_{{\textit{iter}}-1}$, respectively, before executing the body of the loop, then they contain the respective sets for the updated value of ${\textit{iter}}$ after having executed the loop body. As ${\textit{iter}}$ is incremented by 1 during each execution of the body, this shows that each such execution performs a single iteration in the calculation of the test suite. Since the invariant trivially holds before first execution of the loop body, this proves that the algorithm iteratively generates the desired test suite.

By lemma $\mathtt {final\_iteration\_ex}$, a final iteration i must exist. Therefore, the loop terminates with the value of ${\textit{iter}}$ not exceeding $i+1$. Furthermore, from the loop-invariant and the construction of the obs-sets it follows that $(obs_1 \subseteq obs_2 \wedge obs_1^\varOmega \subseteq obs_2^\varOmega )$ holds if and only if $M_2 \preceq _{(ts \cup c).\varOmega } M_1$. Hence, if the loop terminates because $(obs_1 \subseteq obs_2 \wedge obs_1^\varOmega \subseteq obs_2^\varOmega )$ does not hold, then a failure has been observed and the algorithm correctly returns false. Finally, if the loop terminates due to c being empty, then a final iteration has been reached and the truth value of $M_2 \preceq _{ts.\varOmega } M_1 \equiv M_2 \preceq _{TS_i.\varOmega } M_1$ is returned. Thus, by lemma $\mathtt {asc\_sufficiency}$, the algorithm returns true if and only if $M_2 \preceq M_1$ holds.

3.2 Ambiguity

The following example serves to highlight an ambiguity in the original natural language specification of the algorithm, where the ambiguity allows for the generation of a test suite that is not sufficient to uncover an existing failure.

Consider $M_1$ and $M_2$ given in Fig. 2, where $M_2$ is not a reduction of $M_1$ on any input sequence of length at least 3. Let $m = 2$ be the assumed upper bound on the number of states of $M_2$ and let $V = \{\epsilon ,a\}$. Then ${\textit{Perm}}(V,M_2) = \{V''_0,V''_1\}$ where $V''_i = \{\epsilon ,a/i\}$. Furthermore, let $\varOmega = \{(a,f)\}$ with f mapping every output to null. Note that applying (a, f) is equivalent to applying input a and thus sufficient to distinguish states in both FSMs.

Fig. 2.

FSMs $M_1$ (left) and $M_2$ (right)

The first iteration of the algorithm thus applies $C_1{.}\varOmega = V{.}\varOmega$, which is equivalent to applying $\{a,aa\}$, and observes no failure. As the extension of $\epsilon$ by $\varSigma _I = \{a\}$ is $a \in TS_1$ and hence cannot be contained in $C_2$, it remains only to check whether a is contained in $RM_1$. This reduces to checking whether the removal conditions are met for the two responses of $M_2$ to a: a/0 and a/1. Consider first the case of a/0: The original description of the algorithm can be read in a way that allows for $V''$ to be chosen arbitrarily from ${\textit{Perm}}(V,M_2)$, in particular allowing the choice of $V'' = V''_1$. This is not possible in the definition of RM given here, which requires $V''$ to be contained in $N(a/0,M_2,V) = \{V''_0\}$. By choosing $V'' = V''_1$, $S_1 = \{s_1,s_2\}$, $\bar{v}/\bar{v}' = \epsilon$ and $\bar{x}/\bar{y} = a/1$, the RP-set for $s_1$ contains $\epsilon$ and that for $s_2$ contains a/0 and a/1, together containing three sequences. The calculated lower bound then is $3 > m$ and all requirements for the removal of $\bar{a/1}$ are satisfied. Analogously, by choosing $V'' = V''_0$ for case a/1, the removal condition can again be satisfied and hence $a \in RM_1$ holds, $C_2$ is empty and the final iteration is already reached by $TS_1 = V$. Thus, only $TS_1{.}\varOmega = \{a,aa\}$ is applied, which is insufficient to uncover a failure.

In contrast, the algorithm formalised in this paper does not remove a, as restricting the choices of $V''$ to $V''_0$ for a/0 and $V''_1$ for a/1 results in lower bounds not exceeding m. Hence, a is extended to aa, which, followed by $\varOmega$, uncovers the failure $aaa/022 \in L(M_2) \setminus L(M_1)$. Therefore, aa is removed from $C_2 = \{aa\}$ and the complete test suite is $TS_2{.}\varOmega = \{a,aa,aaa\}$.

3.3 Effort, Challenges and Benefits

The implementation in Isabelle of the proof strategy presented in Sect. 3.1 has required a combined effort equivalent to about 6 weeks work of a single person to complete, not including the time the authors required to familiarise themselves with Isabelle/HOL, and some subordinate activities concerning cleanup and reformatting of the theory and proof files created. This work resulted in several theory files with a combined size of about 11,000 lines of code, proving a total of 241 lemmata of various complexities. On a computer running Isabelle2018 on Ubuntu 18.04 and equipped with an Intel Core i7-4700MQ processor, all proofs are verified within 149 s. Details for each theory file are presented in Table 1.

Table 1. Sizes and verification times of the Isabelle theory files

The data structures and functions defined in the Isabelle code closely resemble those used in the manual proof. For finite state machines and adaptive test cases, the Isabelle definitions have already been discussed above. Furthermore, most functions defined in [7] (e.g. function LB) did not require any rephrasing other than finding the corresponding Isabelle functions for the operations performed in their calculation. Functions whose definitions rely on $io\_target(M,q,\bar{x}/\bar{y})$ being uniquely determined (e.g. function B) are slightly rewritten in the Isabelle code so that the resulting definitions do not assume that input FSMs are observable. Instead, the functions operate on all states reached by $\bar{x}/\bar{y}$. Finally, the definitions of functions C, RM, TS and algorithm performAdaptiveStateCounting follow directly from the original textual description of the algorithm and thus constitute only a simple transcription.

Similarly, the overall proof strategy of the mechanised proof follows the strategy used in the manual proof, resulting in closely related intermediate steps. For example, lemma LB_count in the mechanised proof is a specialisation of Lemma 12 of [7]. The proofs performed in Isabelle differ from manual proofs mainly by explicitly stating all assumptions and by the necessity to prove correct all those intermediate properties that are often omitted in manual proofs, because they are considered to be trivial or analogous to previous steps. Proofs of such intermediate properties can usually be found in a fully automated way using the Sledgehammer tool (part of Isabelle). If some intermediate property is used in several proofs, we introduce and prove it as a separate lemma, which can then be reused in different contexts. This method of handling intermediate properties results in a large number of lemmata. This holds in particular for FSMs, as shown in Table 1, where many lemmata describe rather simple properties. For example, lemma language_state_prefix in FSM.thy states that if $\bar{x}/\bar{y} \in L(M,q)$, then any prefix of $\bar{x}/\bar{y}$ is contained in L(M, q).

Thus, the challenges encountered in mechanising the manual proof consisted mainly in the large number of such intermediate properties to prove, caused by the complexity of the algorithm, and in the requirement to provide a formalisation of the algorithm that does not include the ambiguity discussed in Sect. 3.2.

For reasons described above, the mechanised proof presented here is much longer than the manual proof given in [7], but provides also many theorems concerning finite state machines and adaptive test cases, which might be reused in other mechanised proofs. For example, the existence of minimal sequences to failures extending the state cover, proven in Sect. 3.1, is also used in a proof given in [11] about the completeness of test suites generated using the H-Method, originally presented in [6]. More generally, theory file FSM.thy proves various properties about paths and languages of finite state machines (focusing on observable FSMs), which are not specific to the presented adaptive state counting algorithm. This theory file might therefore be used as a starting point to mechanise other algorithms for generating complete test suites based on finite state machines.

4 Conclusions

For the first time, a comprehensive mechanised verification of a complete test strategy and its associated test case generation algorithm previously elaborated by the second author has been presented. The underlying theories and proofs have been developed using the Isabelle/HOL tool. The results presented show that today’s proof assistant tools are powerful enough and do possess adequate usability, so that such an undertaking can be achieved with acceptable effort, provided that some expertise in working with proof assistant tools is available. We advocate mechanised proofs for complete testing theories, since these theories are of considerable value for the verification of safety-critical system. Errors in theories or algorithms, however, may lead to fatal discrepancies between their claimed and actual fault coverage. This could be illustrated by an ambiguity in the original informal description of the test case generation algorithm.