Keywords

1 Introduction

Many products such as medicine, high-tech products, fruits, and blood are exposed to the deterioration process. It means that their usefulness is decreased over time due to loss of utility or loss of original value of the items. For some products, there is a span of maintaining quality or original condition where in that period, there is no deterioration occurring. [1] introduced this kind of product as “non-instantaneous deterioration item”.

In the real world, this type of phenomenon exists commonly such as firsthand vegetables and fruits have a short span of maintaining fresh quality, in which there is almost no spoilage. Afterward, some of the items will start to decay. For this kind of items, the assumption that the deterioration starts from the instant of arrival in stock may cause retailers to make inappropriate replenishment policies due to overvalue the total annual relevant inventory cost. Therefore, in the field of inventory management, it is necessary to consider the inventory problems for non-instantaneous deteriorating items. Some important studies in this area are [2,3,4,5,6].

Furthermore, the companies use marketing policy such as pricing and advertisement efforts to improve their performance. In fact, the marketing policy is a necessary element in controlling the inventory and customer’s demand for all companies. Thus, many studies such as [7,8,9,10,11,12,13,14] combined the inventory control problem of deteriorating products with pricing and advertisement activities.

A pricing and inventory control model for a non-instantaneous deteriorating product subject to advertisement effort is introduced in this paper. The demand is price and time dependent and shortage is allowed and partially backlogged. We simultaneously determine the optimal sale price, replenishment schedule and order quantity to maximize the total profit as the objective function.

The rest of the paper is as follows: Sect. 2 introduces the notations, mathematical modelling and the searching algorithm to solve the proposed model. Section 3 presents the numerical example and discussion based on the sensitivity analysis. Finally, we conclude the paper in Sect. 4 and suggest some future works.

2 Mathematical Modelling

First, we introduce the notations applied throughout the paper.

\( c \) :

Unit purchase cost

\( h \) :

Unit holding cost

\( s \) :

Unit backorder cost

\( o \) :

Unit lost sale cost

\( p \) :

Unit sale price, where \( p > c \)

\( \theta \) :

Deterioration parameter

\( \rho \) :

Advertisement coefficient

\( t_{d} \) :

No-deterioration time length

\( T \) :

Inventory cycle time length

\( t_{1} \) :

No-shortage time length

\( Q \) :

Order quantity

\( I_{1} \left( t \right) \) :

inventory level at time \( t \in \left[ {0,t_{d} } \right] \)

\( I_{2} \left( t \right) \) :

inventory level at time \( t \in \left[ {t_{d} ,t_{1} } \right] \)

\( I_{3} \left( t \right) \) :

inventory level at time \( t \in \left[ {t_{1} ,T} \right] \).

\( I_{0} \) :

maximum inventory level.

\( S \) :

maximum amount of demand backlogged.

\( PE \) :

advertisement cost

\( TP\left( {p,t_{1} ,T} \right) \) :

total profit per unit time of the inventory system.

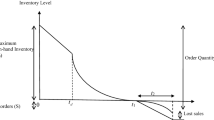
Figure 1 shows the studied inventory model. There are \( I_{0} \) units of products at the beginning of each cycle. The inventory level falls down to zero due to satisfying demand and deterioration in the system. Then, shortage is happened until the end of the order cycle time. We assume that the demand function \( D\left( {p,t} \right) = \left( {a - bp} \right)e^{\lambda t} \) (where \( a > 0,b > 0 \)) depends on price and time where the demand may increase when the sale price decreases, or it may change through time changing. [9] showed that this kind demand function is appropriate for deteriorating products such as high-tech items, fruits and vegetables, and fashion commodities. In the inventory system, shortage is allowed and partially backlogged. We assume that the fraction of shortage backordered is \( \beta \left( t \right) = k_{0} e^{ - \delta t} \), \( \left( {0\,\text{ < }\,k_{0} \, \le \,1,\,\text{ > }\,\delta 0} \right) \) where \( t \) is the waiting time up to the next replenishment and \( \delta \) is a positive constant and \( 0 \le \beta \left( t \right) \le 1,\beta \left( 0 \right) = 1 \). We also adopt the advertisement function from [9] as \( {\text{PE}} = {\text{K}}\left( {\uprho - 1} \right)^{2} \left[ {\mathop \smallint \limits_{0}^{\text{T}} {\text{D}}\left( {{\text{p}},{\text{t}}} \right){\text{dt}}} \right]^{\upalpha} \) where \( {\text{K}} > 0 \) and \( \alpha \) is a constant. Further, we assume that advertisement coefficient \( ace corresponding \) impacts the effort induced demand, i.e. \( \rho D\left( {p,t} \right) \). Finally, it is assumed that the time where the item show no deterioration is greater than or equal to the time with no shortage. i.e. \( t_{1} > t_{d} \).

Fig. 1.
figure 1

Inventory level against time (by author).

Full size image

During the time interval \( \left[ {0,t_{d} } \right] \), the inventory level is only reduced to satisfy the demand. So the following differential equation shows the inventory status:

$$ \begin{array}{*{20}l} {\frac{{dI_{1} (t)}}{dt} = - \rho D(p,t) = - \rho (a - bp)e^{\lambda t} ,} \hfill & {} \hfill & {0 \le t \le t_{d} } \hfill \\ \end{array} $$
(1)

We have \( I_{1} \left( 0 \right) = I_{0} \). solving (1) results:

$$ \begin{array}{*{20}l} {I_{1} (t) = \frac{\rho (a - bp)}{\lambda }\left[ {1 - e^{\lambda t} } \right] + I_{0} ,} \hfill & {} \hfill & {0 \le t \le t_{d} } \hfill \\ \end{array} $$
(2)

In the second interval \( \left[ {t_{d} ,t_{1} } \right] \), demand and deterioration process decrease the inventory level. Therefore, the inventory status is presented by the differential equation as follows:

$$ \begin{array}{*{20}l} {\frac{{dI_{2} (t)}}{dt} + \theta I_{2} (t) = - \rho D(p,t),} \hfill & {} \hfill & {t_{d} \le t \le t_{1} } \hfill \\ \end{array} $$
(3)

With the condition \( I_{2} \left( {t_{1} } \right) = 0 \), Eq. (3) yields:

$$ \begin{array}{*{20}l} {I_{2} (t) = \frac{{\rho (a - bp)e^{ - \theta t} }}{\lambda + \theta }\left[ {e^{{(\lambda + \theta )t_{1} }} - e^{(\lambda + \theta )t} } \right],} \hfill & {} \hfill & {t_{d} \le t \le t_{1} } \hfill \\ \end{array} $$
(4)

From Fig. 1 we conclude \( I_{1} \left( {t_{d} } \right) = I_{2} \left( {t_{d} } \right) \) therefore, the maximum inventory level \( I_{0} \) will be as:

$$ I_{0} = \frac{{\rho (a - bp)e^{{ - \theta t_{d} }} }}{\lambda + \theta }\left[ {e^{{(\lambda + \theta )t_{1} }} - e^{{(\lambda + \theta )t_{d} }} } \right] - \frac{\rho (a - bp)}{\lambda }\left[ {1 - e^{{\lambda t_{d} }} } \right] $$
(5)

Substituting (5) into (2) gives:

$$ \begin{array}{*{20}l} {I_{1} (t) = \frac{\rho (a - bp)}{\lambda }\left[ {1 - e^{\lambda t} } \right] + \frac{{\rho (a - bp)e^{{ - \theta t_{d} }} }}{\lambda + \theta }\left[ {e^{{(\lambda + \theta )t_{1} }} - e^{{(\lambda + \theta )t_{d} }} } \right] - \frac{\rho (a - bp)}{\lambda }\left[ {1 - e^{{\lambda t_{d} }} } \right],\quad } \hfill & {0 \le t \le t_{d} } \hfill \\ \end{array} $$
(6)

During the third interval \( \left[ {t_{1} ,T} \right] \) the inventory system confronts to shortage and the demand is partially backlogged according to the fraction \( \beta \left( {T - t} \right) \). Thus, the inventory level is formulated as Eq. (7):

$$ \begin{array}{*{20}l} {\frac{{dI_{3} (t)}}{dt} = - \rho D(p,t)\beta (T - t) = \frac{ - \rho D(p,t)}{{e^{\delta (T - t)} }},} \hfill & {} \hfill & {t_{1} \le t \le T} \hfill \\ \end{array} $$
(7)

From primitive condition \( I_{3} (t_{1} ) = 0 \), solving Eq. (7) yields:

$$ \begin{array}{*{20}l} {I_{3} (t) = \frac{{\rho (a - bp)e^{ - \delta T} (e^{{(\delta + \lambda )t_{1} }} - e^{(\lambda + \delta )t} )}}{\lambda + \delta },} \hfill & {} \hfill & {t_{1} \le t \le T} \hfill \\ \end{array} $$
(8)

Considering \( t = T \) into (8), the maximum amount of demand backlogging will be:

$$ S = - I_{3} (T) = - \frac{{\rho (a - bp)e^{ - \delta T} (e^{{(\delta + \lambda )t_{1} }} - e^{(\lambda + \delta )T} )}}{\lambda + \delta } $$
(9)

Order quantity per cycle (\( Q \)) equals to summation of \( S \) and \( I_{0} \), i.e.

$$ Q = S + I_{0} = - \frac{{\rho (a - bp)e^{ - \delta T} (e^{{(\delta + \lambda )t_{1} }} - e^{(\lambda + \delta )T} )}}{\lambda + \delta } + \frac{{\rho (a - bp)e^{{ - \theta t_{d} }} }}{\lambda + \theta }\left[ {e^{{(\lambda + \theta )t_{1} }} - e^{{(\lambda + \theta )t_{d} }} } \right] - \frac{\rho (a - bp)}{\lambda }\left[ {1 - e^{{\lambda t_{d} }} } \right] $$
(10)

Now, we can compute the inventory costs and revenue as follows:

$$ \begin{array}{*{20}r} \hfill {HC : {\text{ inventory}}\;{\text{holding}}\;{\text{cost}}} & \hfill {HC = h\left[ {\int_{0}^{{t_{d} }} {I_{1} (t)dt} + \int_{{t_{d} }}^{{t_{1} }} {I_{2} (t)dt} } \right]} \\ \end{array} $$
(11)
$$ \begin{array}{*{20}l} {SC : {\text{ shortage}}\;{\text{cost}}\;{\text{due}}\;{\text{to}}\;{\text{backlog}}} \hfill & {SC = s\int_{{t_{1} }}^{T} {\left[ { - I_{3} (t)} \right]} dt} \hfill \\ \end{array} $$
(12)
$$ \begin{array}{*{20}l} {\text{OC: the opportunity cost due to lost sales}} \hfill & {OP = o\int_{{t_{1} }}^{T} {\rho D(p,t)(1 - \beta (T - t))dt} } \hfill \\ \end{array} $$
(13)
$$ \begin{array}{*{20}r} \hfill {PC : {\text{ the}}\;{\text{purchase}}\;{\text{cost}}} & \hfill {PC = cQ} \\ \end{array} $$
(14)
$$ \begin{array}{*{20}l} {SR : {\text{ the }}\,{\text{sales}}\,{\text{ revenue}}} \hfill & {} \hfill & {SR = p\left[ {\int_{0}^{{t_{1} }} {\rho D(p,t)dt + S} } \right]} \hfill \\ \end{array} $$
(15)
$$ \begin{array}{*{20}l} {PE : {\text{ the }}\,{\text{promotion}}\,{\text{ cost}}} \hfill & {} \hfill & {PE = K(\rho - 1)^{2} \left[ {\int_{0}^{T} {D(p,t)dt} } \right]^{\alpha } } \hfill \\ \end{array} $$
(16)

\( A \): ordering cost

Thus, the total profit per unit time \( TP(p,t_{1} ,T) \) will be as:

$$ \begin{aligned} & TP_{{\left( {p,t_{1} ,T} \right)}} = \frac{SR - A - HC - SC - OC - PC - PE}{T} = - \frac{1}{T}(A + K\left( {\frac{{\left( { - 1 + {\text{e}}^{T\lambda } } \right)\left( {a - bp} \right)}}{\lambda }} \right)^{\alpha } \left( { - 1 + \rho } \right)^{2} \\ & - \,p\left( {a - } \right.\left. {bp} \right)\left( {\frac{{ - 1 + {\text{e}}^{{{\text{t}}1\lambda }} }}{\lambda } + \frac{{{\text{e}}^{T\lambda } - {\text{e}}^{{ - T\delta + {\text{t}}1\left( {\delta + \lambda } \right)}} }}{\delta + \lambda }} \right)\rho + \frac{{o\left( {a - bp} \right)\left( {{\text{e}}^{T\lambda } \delta + {\text{e}}^{{ - T\delta + {\text{t}}1\left( {\delta + \lambda } \right)}} \lambda - {\text{e}}^{{{\text{t}}1\lambda }} \left( {\delta + \lambda } \right)} \right)\rho }}{{\lambda \left( {\delta + \lambda } \right)}} \\ & \left. { + \,c\left( {a - } \right.bp} \right)(\frac{{ - 1 + {\text{e}}^{{{\text{td}}\lambda }} }}{\lambda } + \frac{{{\text{e}}^{ - T\delta } \left( { - {\text{e}}^{{{\text{t}}1\left( {\delta + \lambda } \right)}} + {\text{e}}^{{{\text{td}}\left( {\delta + \lambda } \right)}} } \right)}}{\delta + \lambda } - \frac{{{\text{e}}^{{{\text{td}}\lambda }} - {\text{e}}^{{ - {\text{td}}\theta + {\text{t}}1\left( {\theta + \lambda } \right)}} }}{\theta + \lambda })\rho \\ & + \,\frac{{{\text{e}}^{{ - {\text{td}}\theta }} h\left( {a - bp} \right)\left( {{\text{e}}^{{{\text{t}}1\left( {\theta + \lambda } \right)}} \left( {1 + {\text{td}}\theta } \right)\lambda^{2} + {\text{e}}^{{{\text{td}}\theta }} \theta \left( {\theta + \lambda } \right) - {\text{e}}^{{{\text{td}}\theta + {\text{t}}1\lambda }} \lambda \left( {\theta + \lambda } \right) + {\text{e}}^{{{\text{td}}\left( {\theta + \lambda } \right)}} \theta^{2} \left( { - 1 + {\text{td}}\lambda } \right)} \right)\rho }}{{\theta \lambda^{2} \left( {\theta + \lambda } \right)}} \\ & + \,\frac{{{\text{e}}^{ - T\delta } \left( {a - bp} \right)s\left( {{\text{e}}^{{T\left( {\delta + \lambda } \right)}} + {\text{e}}^{{{\text{t}}1\left( {\delta + \lambda } \right)}} \left( { - 1 - T\left( {\delta + \lambda } \right) + {\text{t}}1\left( {\delta + \lambda } \right)} \right)} \right)\rho }}{{\left( {\delta + \lambda } \right)^{2} }}) \\ \end{aligned} $$
(17)

The decision maker aims to maximize the total profit determining the optimal ordering policies and sale price. On the other hands, we want to maximize \( TP_{{\left( {p,t_{1} ,T} \right)}} \) indicating the optimal value for \( \left( {p,t_{1} ,T} \right) \). We first show that for any given \( p \) the optimal value for \( t_{1} ,T \) exists. Then, for any given value of \( t_{1} ,T \), there exists a unique \( p \) where obtain the maximize value for \( TP_{{\left( {p,t_{1} ,T} \right)}} \).

\( TP_{{\left( {p,t_{1} ,T} \right)}} \) is a function of \( p,t_{1} ,T \). So, for any given \( p \), the necessary condition for the total profit per unit time (17) to be maximized is:

$$ \frac{{\partial TP_{{\left( {p,t_{1} ,T} \right)}} }}{{\partial t_{1} }} = 0 $$
(18)
$$ \frac{{\partial TP_{{\left( {p,t_{1} ,T} \right)}} }}{\partial T} = 0 $$
(19)

It is easy to prove the concavity of \( TP_{{\left( {p,t_{1} ,T} \right)}} \). So for any given price, the point \( \left( {t_{1}^{*} ,T^{*} } \right) \) which maximize the total profit per unit time not only exists but is unique. Next, we study the condition under which the optimal selling price also exists. For any \( \left( {t_{1}^{*} ,T^{*} } \right) \) the first-order necessary condition for \( TP\left( {p,t_{1}^{*} ,T^{*} } \right) \) to be maximize is:

$$ \frac{{\partial TP_{{\left( {p,t_{1}^{*} ,T^{*} } \right)}} }}{\partial p} = 0 $$
(20)

We will numerically show that \( TP\left( {p,t_{1}^{*} ,T^{*} } \right) \) is a concave function of \( p \) for a given \( t_{1}^{*} ,T^{*} \), hence a value of \( p \) that obtain from (20) is unique. As a result, we prove that there is a unique value of \( (p^{*} \)) which maximizes \( TP\left( {p,t_{1}^{*} ,T^{*} } \right) \). \( p^{*} \) can be obtained by solving (20).

2.1 Searching Algorithm

Based on the mathematical formulation, we apply a searching algorithm to obtain \( (p^{*} ,t_{1}^{*} ,T^{*} ) \). This algorithm is an iterative search process starts with an arbitrary initial value, then using the proposed model formulation, finds the optimal solution. The algorithm uses the computations from the model formulation section to find the solutions in steps 2nd and 3rd. As we showed in the model formulation, the algorithm is utilized to solve a non-linear optimization model. The model depends on three variables. So in step 1, the algorithm considers an initial value for one of the variables. Then, applying the taking derivative method computes the other two variables. Next, use the resulted value for two variables to find the next value of the first variable. The algorithm reiterates the entire process till the difference between two consecutive values of the first variable is sufficiently small. The algorithm steps are as follows:

step1: begin with \( j = 0 \) and set \( p_{j} = p_{1} \) as the initial value of \( p_{j} \)

step2: for \( p_{j} \), solve the equations system (18) and (19) and determine the optimal value of \( \left( {t_{1}^{*} ,T^{*} } \right) \)

step3: using result of step 2 and solve Eq. (20) to find the optimal of \( p_{j + 1} \).

Step 4: if \( \left| {p_{j} - p_{j + 1} } \right| \le 0.0001 \), set \( p^{*} = p_{j + 1} \), then \( (p^{*} ,t_{1}^{*} ,T^{*} ) \) is the optimal solution and stop. Otherwise, set \( j = j + 1 \) and go back to step 2.

using above algorithm, we obtain the optimal solution \( (p^{*} ,t_{1}^{*} ,T^{*} ) \).then; we can obtain \( Q^{*} \) by using (10) and \( TP^{*} \) by using (17).

3 Numerical Example

In this section, we rely on a numerical example to show the efficiency of the proposed model and algorithm. The results can be found using Mathematica 9.0. in the subsequent analysis, the following base values are used. \( A = \$ 250, c = \$ 200, h = \$ 40, s = \$ 80, o = \$ 120,\theta = 0.08, \) \( \rho = 2, t_{d} = 0.04, f\left( {t,p} \right) = \left( {500 - 0.5p} \right)e^{ - 0.98t} , \beta \left( t \right) = e^{ - 0.1t} \). We consider initial value for sale price equals to 600, \( p_{1} = 600 \). Using the searching algorithm, after 5 iterations, the optimal solution will be computed as \( p^{*} = 525.948, t_{1}^{*} = 0.128, T^{*} = 0.182, TP^{*} = 204292, Q^{*} = 19.111 \). Table 1 shows the computational results.

Table 1. The computational results
Full size table

Table 1 highlights the main output of this study. Applying the suggested algorithm, we obtained the optimal solution for selling price and replenishment policy for a vendor who sells a non-instantaneous deteriorating product. This optimal solution helps the vendor to achieve the highest total profit in each inventory cycle time. This finding provides a mathematical tool for the vendor to make better decision in a simultaneous manner about two significant decisions in its system; inventory control policy and pricing. As we talked earlier, the total profit is a concave function corresponding to the sale price. Here, we perform the numerical example with various starting value of sale price 460, 480, 500, 520, 540,560, 580, 600 and 620. As shown in Fig. 2, the result reveals that \( TP^{*} \) is strictly concave in \( p \). Hence, we assure that the obtained local maximum from the proposed algorithm is indeed the global maximum solution.

Fig. 2.
figure 2

Optimal total profit associated to \( p \)

Full size image

3.1 Discussion

In this section, we extend some managerial implications based on the sensitivity analysis of parameters. First, we solve the suggested numerical example for distinct values of \( t_{d} \). This sensitivity analysis shows the impact of non-instantaneous phenomena. The computational results for \( t_{d} \in \left\{ {0, 0.08, 0.16, 0.24} \right\} \) are shown in Table 2.

Table 2. Optimal solution for various values of \( t_{d} \)
Full size table

If \( t_{d} \) = 0, the model becomes the instantaneous deterioration items case, and the optimal solution is TP* = 193678. It can be seen that there is an improvement in total profit from the non-instantaneously deteriorating demand model. Moreover, the longer of time where no deterioration occurs, the greater the improvement in total profit from the non-instantaneously deteriorating demand model. This implies that if the retailer can convert the instantaneously to non-instantaneously items by improving stock equipment, then the total profit per unit time will increase. Next, we perform the Example for different values of the promotional effort \( \rho \). The results are shown in Table 3.

Table 3. Optimal solution for various values of \( \rho \)
Full size table

If ρ = 1 (the retailer does not adopt the promotion policy), the optimal solutions is TP* = 101687. This optimal total profit is greatly lower than \( \varvec{TP}^{ *} \) when \( = {\mathbf{2}} \). Moreover, the greater of promotional effort, the greater the improvement in total profit. This implies that if the retailer can increase the effect of promotional activity, then the total profit will increase drastically.

4 Conclusions and Future Works

In this study, we developed an inventory control model with pricing and advertising efforts for a non-instantaneous deterioration product. We assumed price-and-time dependent demand and partially backlogged shortage. The mathematical formulation is presented and a searching algorithm to find the optimal solution is extended. In the last section, we run a numerical example with sensitivity analysis on the main parameters.

The main result of this paper is determining the optimal sale price and replenishment policy for the retailer. We also showed that the total profit is significantly higher in non-instantaneous case rather than instantaneous deterioration case. Furthermore, the total profit for the retailer has improved in the presence of advertisement activity. This research can be extended through some new ways. It would be interesting to examine the proposed model with stochastic demand or deterioration function. Besides, we just consider a retailer. As supply chain includes multiple players, it becomes imperative to examine the inventory model in a supply chain context.