Abstract
In this paper we extend Hughes’ combinatorial proofs to modal logics. The crucial ingredient for modeling the modalities is the use of a self-dual non-commutative operator that has first been observed by Retoré through pomset logic. Consequently, we had to generalize the notion of skew fibration from cographs to Guglielmi’s relation webs.
Our main result is a sound and complete system of combinatorial proofs for all normal and non-normal modal logics in the \(\mathsf {S4}\)-tesseract. The proof of soundness and completeness is based on the sequent calculus with some added features from deep inference.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Note that \(\bot \) is only allowed directly inside a
 or \(\Diamond \). The main purpose of avoiding \(\bot \) as proper formula is to avoid the empty relation web (to be introduced in the next section). However, we do need formulas
or \(\Diamond \). The main purpose of avoiding \(\bot \) as proper formula is to avoid the empty relation web (to be introduced in the next section). However, we do need formulas  and \(\Diamond \bot \) in order to allow weakenings inside a
and \(\Diamond \bot \) in order to allow weakenings inside a  or \(\Diamond \), which is needed to prove the decomposition theorem (stated in Theorem 2.2 below) which in turn is the basis for combinatorial proofs.
or \(\Diamond \), which is needed to prove the decomposition theorem (stated in Theorem 2.2 below) which in turn is the basis for combinatorial proofs. - 2.
The logics defined by these systems can be seen as the “linear logic variants” of the standard modal logics \(\mathsf K\) and \(\mathsf K\mathsf {D}\).
- 3.
Observe that all the logics in the \(\mathsf {S4}\)-tesseract are monotone. In fact, our methods can not be applied in presence of the rule
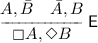 . We therefore have to leave the investigation of combinatorial proofs for non-monotonic non-normal modal logics as an open problem for future research.
. We therefore have to leave the investigation of combinatorial proofs for non-monotonic non-normal modal logics as an open problem for future research.
References
Acclavio, M., Straßburger, L.: From syntactic proofs to combinatorial proofs. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 481–497. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_32
Acclavio, M., Straßburger, L.: On combinatorial proofs for logics of relevance and entailment. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds.) WoLLIC 2019. LNCS, vol. 11541, pp. 1–16. Springer, Heidelberg (2019). https://doi.org/10.1007/978-3-662-59533-6_1
Avron, A.: The method of hypersequents in the proof theory of propositional non-classical logics. In: Logic: From Foundations to Applications, European Logic Colloquium, pp. 1–32. Oxford University Press (1994)
Benjamin, R., Straßburger, L.: Towards a combinatorial proof theory. In: Cerrito, S., Popescu, A., (eds.) TABLEAUX 2019. LNAI, vol. 11714, pp. 259–276 (2019)
Brünnler, K.: Deep sequent systems for modal logic. Arch. Math. Log. 48(6), 551–577 (2009)
Brünnler, K., Tiu, A.F.: A local system for classical logic. In: Nieuwenhuis, R., Voronkov, A. (eds.) LPAR 2001. LNCS (LNAI), vol. 2250, pp. 347–361. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45653-8_24
Chaudhuri, K., Marin, S., Straßburger, L.: Focused and synthetic nested sequents. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 390–407. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_23
Chaudhuri, K., Marin, S., Straßburger, L.: Modular focused proof systems for intuitionistic modal logics. In: Kesner, D., Pientka, B. (eds.) FSCD 2016. LIPIcs, vol. 52, pp. 16:1–16:18. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2016)
Cook, S.A., Reckhow, R.A.: The relative efficiency of propositional proof systems. J. Symb. Logic 44(1), 36–50 (1979)
Goré, R., Postniece, L., Tiu, A.: On the correspondence between display postulates and deep inference in nested sequent calculi for tense logics. Log. Methods Comput. Sci. 7(2), 1–38 (2011)
Goré, R., Ramanayake, R., et al.: Labelled tree sequents, tree hypersequents and nested (deep) sequents. Adv. Modal Log. 9, 279–299 (2012)
Guglielmi, A.: A system of interaction and structure. ACM Trans. Comput. Log. 8(1), 1–64 (2007)
Guglielmi, A., Straßburger, L.: Non-commutativity and MELL in the calculus of structures. In: Fribourg, L. (ed.) CSL 2001. LNCS, vol. 2142, pp. 54–68. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44802-0_5
Hein, R., Stewart, C.: Purity through unravelling. In: Structures and Deduction, pp. 126–143 (2005)
Hughes, D.: Proofs without syntax. Ann. Math. 164(3), 1065–1076 (2006)
Hughes, D.: Towards Hilbert’s 24\({}^{\text{ th }}\) problem: combinatorial proof invariants: (preliminary version). Electr. Notes Theor. Comput. Sci. 165, 37–63 (2006)
Hughes, D.J.D.: First-order proofs without syntax, June 2019
Lellmann, B.: Hypersequent rules with restricted contexts for propositional modal logics. Theor. Comput. Sci. 656, 76–105 (2016)
Lellmann, B., Pimentel, E.: Modularisation of sequent calculi for normal and non-normal modalities. ACM Trans. Comput. Log. (TOCL) 20(2), 7 (2019)
Marin, S., Straßburger, L.: Label-free modular systems for classical and intuitionistic modal logics. In: Advances in Modal Logic 10 (2014)
Möhring, R.H.: Computationally tractable classes of ordered sets. In: Rival, I. (ed.) Algorithms and Order, pp. 105–194. Kluwer, Dordrecht (1989)
Negri, S.: Proof analysis in modal logic. J. Philos. Log. 34(5–6), 507 (2005)
Retoré, C.: Pomset logic: a non-commutative extension of classical linear logic. In: de Groote, P., Roger Hindley, J. (eds.) TLCA 1997. LNCS, vol. 1210, pp. 300–318. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62688-3_43
Retoré, C.: Handsome proof-nets: perfect matchings and cographs. Theor. Comput. Sci. 294(3), 473–488 (2003)
Simpson, A.K.: The proof theory and semantics of intuitionistic modal logic. Ph.D. thesis, University of Edinburgh. College of Science and Engineering (1994)
Stewart, C., Stouppa, P.: A systematic proof theory for several modal logics. Adv. Modal Log. 5, 309–333 (2004)
Straßburger, L.: A characterization of medial as rewriting rule. In: Baader, F. (ed.) RTA 2007. LNCS, vol. 4533, pp. 344–358. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73449-9_26
Straßburger, L.: Cut elimination in nested sequents for intuitionistic modal logics. In: Pfenning, F. (ed.) FoSSaCS 2013. LNCS, vol. 7794, pp. 209–224. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37075-5_14
Straßburger, L.: Combinatorial flows and their normalisation. In: Miller, D. (ed.) FSCD 2017. LIPIcs, vol. 84, pp. 31:1–31:17. Schloss Dagstuhl (2017)
Straßburger, L.: The problem of proof identity, and why computer scientists should care about Hilbert’s 24th problem. Philos. Trans. R. Soc. A 377(2140), 20180038 (2019)
Thiele, R.: Hilbert’s twenty-fourth problem. Am. Math. Mon. 110, 1–24 (2003)
Wansing, H.: Sequent calculi for normal modal propositional logics. J. Log. Comput. 4(2), 125–142 (1994)
Wansing, H.: Sequent systems for modal logics. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic. Handbook of Philosophical Logic, vol. 8, pp. 61–145. Springer, Dordrecht (2002)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Acclavio, M., Straßburger, L. (2019). On Combinatorial Proofs for Modal Logic. In: Cerrito, S., Popescu, A. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2019. Lecture Notes in Computer Science(), vol 11714. Springer, Cham. https://doi.org/10.1007/978-3-030-29026-9_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-29026-9_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29025-2
Online ISBN: 978-3-030-29026-9
eBook Packages: Computer ScienceComputer Science (R0)


 or
or  and
and  or
or 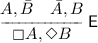 . We therefore have to leave the investigation of combinatorial proofs for non-monotonic non-normal modal logics as an open problem for future research.
. We therefore have to leave the investigation of combinatorial proofs for non-monotonic non-normal modal logics as an open problem for future research.