Abstract
Consider the matrix equation \(\overset {\,\circ }{\gamma } _i\overset {\,\circ }{\gamma } _j + \overset {\,\circ }{\gamma } _j\overset {\,\circ }{\gamma } _i =2\delta _{ij}I, \) in which \(\overset {\,\circ }{\gamma }_i\) are square, generally complex matrices of order 2ν, ν is a positive integer; the indices i, j, determining the numbers of matrices \(\overset {\,\circ }{\boldsymbol \gamma }\), take all integer values from 1 to 2ν; I is the unit matrix of order 2ν; δ ij are the Kronecker delta.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The existence of matrices \(\overset {\,\circ }{\gamma } _i\) satisfying Eq. (1.1) will be shown at the end of the present section.
- 2.
In what follows, the indices i k in \(\overset {\,\circ }{\gamma } \) matrices will be treated as the tensor indices in the Euclidean space with the metric tensor determined in an orthonormal basis by components δ ij. Here, we are so far formally using i k written at different places in order that the equations obtained be tensor equations in an invariant form.
- 3.
- 4.
S is a square matrix of order 2ν with the elements S B A. To simplify the subsequent expressions, as is conventionally done, we will mostly use matrix notations and omit the indices that determine the matrix elements.
- 5.
Evidently, if the set of certain square matrices {S} forms a group, then the corresponding set {±S} also forms a group with respect to the multiplication (1.61) (which is simply the factor group S∕ ± I).
- 6.
Geometrically, such an object determines a non-oriented segment in S N.
- 7.
One could evidently take as a metric spinor the second-rank spinor with covariant components, defined by the matrix \(E\overset {\,\circ }{\gamma } _{2\nu +1}\). If one requires that the metric spinor should be invariant under all transformations of the basis in the Euclidean space \(E_{2\nu }^+\), then, for spinor representations defined by Eqs. (1.70) and (1.76), one should take the spinor E as a metric spinor, while for spinor representations defined by Eqs. (1.75) and (1.77), the spinor \(E\overset {\,\circ }{\gamma } _{2\nu +1}\) should be taken.
- 8.
The space \(E_{2\nu }^q\) may be singled out in the complex Euclidean vector space \(E_{2\nu }^+\) as a linear real shell of a basis of the space \(E_{2\nu }^+\) of the following form:
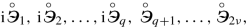
where
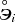 is an orthonormal basis in \(E_{2\nu }^+\).
is an orthonormal basis in \(E_{2\nu }^+\). - 9.
Recall that a connected component of a continuous group is, by definition, such a connected part of the group that its any extension is not connected.
- 10.
The conjugate spinor may also be defined with the aid of the spinor β defined, instead of Eq. (1.127), by the equation
$$\displaystyle \begin{aligned} \dot {\gamma} _i^T=\beta \gamma _i\beta ^{-1}.\end{aligned} $$(*)In physical applications, in the four-dimensional space \(E_4^1\) with the metric signature (+, +, +, −), definition (1.127) is used; in the four-dimensional space \(E_4^3\), with the metric signature (−, −, −, +) (where the matrices γ i are related to the matrices γ i of the space \(E_4^1\) by the factor i) one uses definition (*). It is easy to see that the matrices β, defined in the same space by Eqs. (1.127) and (*), differ by the factor γ 2ν+1.
- 11.
One could express the idea to define the metric spinor in the space \(E_{2\nu -1}^+\) as in the space \(E_{2\nu }^+\), by Eqs. (1.44), in which i = 1, 2, …, 2ν − 1. However, for odd ν, Eq. (1.44) for matrices of order 2ν−1 with i = 1, 2, …, 2ν − 1 has no solution since the matrix E of order 2ν−1 is defined by Eq. (1.44) for i = 1, 2, …, 2(ν − 1) up to a factor and is connected with \(\overset {\,\circ }{\gamma } _{2\nu -1}\) by the equation \(\overset {\,\circ }{\gamma } { }^T_{2\nu -1}= E\overset {\,\circ }{\gamma } _{2\nu -1}E^{-1}\), which is easily obtained by contracting equations (1.54) for k = 2(ν − 1) with components of the Levi-Civita pseudotensor \(\varepsilon ^{i_1i_2\dots i_k} \) with respect to the indices i 1, i 2,…, i k.
- 12.
The equations \( l^j{ }_i\overset {\,\circ }{\gamma } _j= S^{-1}\overset {\,\circ }{\gamma } _iS \) have no solution for S on the full orthogonal group \(O_{2\nu -1}^+\). Indeed, for instance, for the reflection transformation of a single vector from the basis
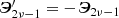 , these equations give $$\displaystyle \begin{aligned} S\overset{\,\circ}{\gamma} _{2\nu -1}=-\overset{\,\circ}{\gamma} _{2\nu -1}S,\qquad S\overset{\,\circ}{\gamma} _{\alpha} =\overset{\,\circ}{\gamma} _{\alpha} S,\qquad \alpha =1,2,\dots ,2(\nu -1).\end{aligned} $$(*)
, these equations give $$\displaystyle \begin{aligned} S\overset{\,\circ}{\gamma} _{2\nu -1}=-\overset{\,\circ}{\gamma} _{2\nu -1}S,\qquad S\overset{\,\circ}{\gamma} _{\alpha} =\overset{\,\circ}{\gamma} _{\alpha} S,\qquad \alpha =1,2,\dots ,2(\nu -1).\end{aligned} $$(*)From the second equation in (*) it follows that S is proportional to the unit matrix S = λI, which, for λ≠0, contradicts the first equation.
- 13.
By definition, the components of the second-rank spinor ψ BA are always defined with a sign, although they can be products of components of first-rank spinors defined up to a common sign.
- 14.
References
Pauli, W.: Contributions mathématicue à la theorie des matrices de Dirac. Ann. Inst. H. Poincaré. 6, 109–136 (1936)
Zhelnorovich, V.A.: Representation of spinors by real and complex tensor aggregates. Theor. Math. Phys. 2, 66–77 (1970)
Zhelnorovich, V.A.: On spinor representations of pseudo-orthogonal groups. Dokl. Math. 22, 337–340 (1980). Maik Nauka/Interperiodica Publishing (Russian Federation)
Zhelnorovich, V.A.: Tensor representation of spinor fields. In: Sedov, L.I. (ed.) Macroscopic Theories of Matter and Fields: A Thermodynamic Approach, pp. 224–261. Mir Publishers, Moscow (1983)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Zhelnorovich, V.A. (2019). Spinors in Finite-Dimensional Euclidean Spaces. In: Theory of Spinors and Its Application in Physics and Mechanics. Springer, Cham. https://doi.org/10.1007/978-3-030-27836-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-27836-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-27835-9
Online ISBN: 978-3-030-27836-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


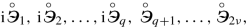
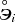 is an orthonormal basis in
is an orthonormal basis in 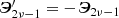 , these equations give
, these equations give