Abstract
We present algorithms and techniques for the repair of timed system models, given as networks of timed automata (NTA). The repair is based on an analysis of timed diagnostic traces (TDTs) that are computed by real-time model checking tools, such as UPPAAL, when they detect the violation of a timed safety property. We present an encoding of TDTs in linear real arithmetic and use the MaxSMT capabilities of the SMT solver Z3 to compute possible repairs to clock bound values that minimize the necessary changes to the automaton. We then present an admissibility criterion, called functional equivalence, that assesses whether a proposed repair is admissible in the overall context of the NTA. We have implemented a proof-of-concept tool called TarTar for the repair and admissibility analysis. To illustrate the method, we have considered a number of case studies taken from the literature and automatically injected changes to clock bounds to generate faulty mutations. Our technique is able to compute a feasible repair for \(91\%\) of the faults detected by UPPAAL in the generated mutants.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The analysis of system design models using model checking technology is an important step in the system design process. It enables the automated verification of system properties against given design models. The automated nature of model checking facilitates the integration of the verification step into the design process since it requires no further intervention of the designer once the model has been formulated and the property has been specified.
Often it is sufficient to abstract from real time aspects when checking system properties, in particular when the focus is on functional aspects of the system. However, when non-functional properties, such as response times or the timing of periodic behavior, play an important role, it is necessary to incorporate real time aspects into the models and the specification, as well as to use specialized real-time model checking tools, such as UPPAAL [6], Kronos [31] or opaal [11] during the verification step.
Next to the automatic nature of model checking, the ability to return counterexamples, in real-time model checking often referred to as timed diagnostic traces (TDT), is a further practical benefit of the use of model checking technology. A TDT describes a timed sequence of steps that lead the design model from the initial state of the system into a state violating a real-time property. A TDT neither constitutes a causal explanation of the property violation, nor does it provide hints as to how to correct the model.
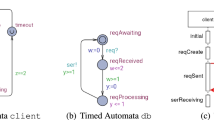
In this paper we describe an automated method that computes proposals for possible repairs of a network of timed automata (NTA) that avoid the violation of a timed safety property. Consider the TDT depicted as a time annotated sequence diagram [5] in Fig. 1. This scenario describes a simple message exchange where the process dbServer sends a message req to process db which, after some processing steps returns a message ser to dbServer. Assume a requirement on the system to be that the time from sending req to receiving ser is not to be more than 4 time units. Assume that the timing interval annotations on the sequence diagram represent the minimum and maximum time for the message transmission and processing steps that the NTA, from which the diagram has been derived, permits. It is then easy to see that it is possible to execute the system in such a way that this property is violated.
Various changes to the underlying NTA model, depicted in Fig. 2, may avoid this property violation. For instance, the maximum time it takes to transmit the req and ser messages can be constrained to be at most 1 time unit, respectively. Alternatively, it may be possible to avoid the property violation by reducing two of the three timings by 0.5 time units. In any case, proposing such changes to the model may either serve to correct clerical mistakes made during the editing of the model, or point to necessary changes in the dimensioning of its time resources, thus contributing to improved design space exploration.
The repair method described in this paper relies on an encoding of a TDT as a constraint system in linear real arithmetic. This encoding provides a symbolic abstract semantics for the TDT by constraining the sojourn time of the NTA in the locations visited along the trace. The constraint system is then augmented by auxiliary model variation variables which represent syntactic changes to the NTA model, for instance the variation of a location invariant condition or a transition guard. We assert that the thus modified constraint system implies the non-reachability of a violation. At the same time, we assert that the model variation variables have a value that implies that no change of the NTA model will occur, for instance by setting a clock bound variation variable to 0. This renders the resulting constraint system unsatisfiable.
In order to compute a repair, we derive a partial MaxSMT instance by turning the constraints that disable any repair into soft constraints. We solve this MaxSMT instance using the SMT solver Z3 [25]. If the MaxSMT instance admits a solution, the resulting model provides values of the model variation variables. These values indicate a repair of the NTA model which entails that along the sequence of locations represented by the TDT, the property violation will no longer be reachable.
In a next step it is necessary to check whether the computed repair is an admissible repair in the context of the full NTA. This is important since the repair was computed locally with respect to only a single given TDT. Thus, it is necessary to define a notion of admissibility that is reasonable and helpful in this setting. To this end, we propose the notion of functional equivalence which states that as a result of the computed repair, neither erstwhile existing functional behavior will be purged, nor will new functional behavior be added. Functional behavior in this sense is represented by languages accepted by the untimed automata of the unrepaired and the repaired NTAs. Functional equivalence is then defined as equivalence of the languages accepted by these automata. We propose a zone-based automaton construction for implementing the functional equivalence test that is efficient in practice.
We have implemented our proposed method in a proof-of-concept tool called TarTarFootnote 1. Our evaluation of TarTar is based on several non-trivial NTA models taken from the literature, including the frequently considered Pacemaker model [19]. For each model, we automatically generate mutants by injecting clock bound variations which we then model check using UPPAAL and repair using TarTar. The evaluation shows that our technique is able to compute an admissible repair for \(91\%\) of the detected faults.
Related Work. There are relatively few results available on a formal treatment of TDTs. The zone based approach to real-time model checking, which relies on a constraint-based abstraction of the state space, is proposed in [14]. The use of constraint solving to perform reachability analysis for NTAs is described in [30]. This approach ultimately leads to the on-the-fly reachability analysis algorithm used in UPPAAL [7]. [12] defines the notion of a time-concrete UPPAAL counterexample. Work documented in [27] describes the computation of concrete delays for symbolic TDTs. The above cited approaches address neither fault analysis nor repair for TDTs. Our use of MaxSMT solvers for computing minimal repairs is inspired by the use MaxSAT solvers for fault localization in C programs, which was first explored in the BugAssist tool [20, 21]. Our approach also shares some similarities with syntax-guided synthesis [2, 28], which has also been deployed in the context of program repair [22]. One key difference is how we determine the admissibility of a repair in the overall system, which takes advantage of the semantic restrictions imposed by timed automata.
Structure of the Paper. We will introduce the automata and real-time concepts needed in our analysis in Sect. 2. In Sect. 3 we present the logical formalization of TDTs. The repair and admissibility analyses are presented in Sects. 4 and 5, respectively. We report on tool development, experimental evaluation and case studies in Sects. 6 and 7 concludes.
2 Preliminaries
The timed automaton model that we use in this paper is adapted from [7]. Given a set of clocks C, we denote by \(\mathcal{B}(C)\) the set of all clock constraints over C, which are conjunctions of atomic clock constraints of the form \(c \sim n\), where \(c \in C\), \(\sim \in \{<,\le , =, \ge , >\}\) and \(n \in \mathbb {N}\). A timed automaton (TA) T is a tuple \(T = (L, l^0, C, \varSigma , \varTheta , I)\) where L is a finite set of locations, \(l^0 \in L\) is an initial location, C is a finite set of clocks, \(\varSigma \) is a set of action labels, \(\varTheta \subseteq _{ fin } L \times \mathcal{B}(C) \times \varSigma \times 2^C \times L\) is a set of actions, and \(I: L \rightarrow \mathcal{B}(C)\) denotes a labeling of locations with clock constraints, referred to as location invariants. For \(\theta \in \varTheta \) with \(\theta = (l, g, a, r, l')\) we refer to g as the guard of \(\theta \) and to r as its clock resets.
The operational semantics of T is given by a timed transition system consisting of states \(s=(l,u)\) where l is a location and \(u: C \rightarrow \mathbb {R}_+\) is a clock valuation. The initial state \(s_0\) is \((\ell , u_0)\) where \(u_0\) maps all clocks to 0. For a clock constraint B we write \(u \models B\) iff B evaluates to true in u. There are two types of transitions. An action transition models the execution of an action whose guard is satisfied. These transitions are instantaneous and reset the specified clocks. The passing of time in a location is modeled by delay transitions. Both types of transitions guarantee that location invariants are satisfied in the pre and post state. Formally, we have \((l, u) {\mathop {\longrightarrow }\limits ^{t}} (l', u')\) iff
-
(action transition) \(t = (l, g, a, r, l') \in \varTheta \), \(u \models I(l) \wedge g\), \(u' \models I(l')\) and for all clocks \(c \in C\), \(u'(c) = 0\) if \(c \in r\) and \(u'(c) = u(c)\) otherwise; or
-
(delay transition) \(t \in \mathbb {R}_+\), \(u \models I(l)\), \(u' \models I(l)\) and \(u' = u + t\).
Definition 1
A symbolic timed trace (STT) of T is a sequence of actions \(S = \theta _0,\dots ,\) \(\theta _{n-1}\). A realization of S is a sequence of delay values \(\delta _0,\dots ,\delta _{n}\) such that there exists states \(s_0,\dots ,s_n,s_{n+1}\) with \(s_i {\mathop {\longrightarrow }\limits ^{\delta _{i}}} {\mathop {\longrightarrow }\limits ^{\theta _{i}}} s_{i+1}\) for all \(i \in [0,n)\) and \(s_n {\mathop {\longrightarrow }\limits ^{\delta _{n}}} s_{n+1}\). We say that a STT is feasible if it has at least one realization.
Property Specification. We focus on the analysis of timed safety properties, which we characterize by an invariant formula that has to hold for all reachable states of a TA. These properties state, for instance, that there are certain locations in which the value of a clock variable is not above, equal to or below a certain (integer) bound. Formally, let \(T = (L, l^0, C, \varSigma , \varTheta , I)\) be a TA. A timed safety property \(\varPi \) is a Boolean combination of atomic clock constraints and location predicates @l where \(l \in L\). A location predicate @l holds in a state \((l', u)\) of T iff \(l'=l\). We say that a STT S witnesses a violation of \(\varPi \) in T if there exists a realization of S whose induced final state does not satisfy \(\varPi \). We refer to such an STT as a timed diagnostic trace of T for \(\varPi \).
T satisfies \(\varPi \) iff all its reachable states satisfy \(\varPi \). This problem can be decided using model checking tools such as Kronos [31] and UPPAAL [6]. UPPAAL in particular computes a finite abstraction of the state space of an NTA using a zone graph construction. Reachability analysis is then performed by an on-the-fly search of the zone graph. If the property is violated, the tool generates a feasible TDT that witnesses the violation. The objective of our work is to analyze TDTs and to propose repairs for the property violation that they represent. We use TDTs generated by the UPPAAL tool in our implementation, but we maintain that our results can be adapted to any other tool producing TDTs.
We further note that UPPAAL takes a network of timed automata (NTA) as input, which is a CCS [24] style parallel composition of timed automata \(T_1 \mid \ldots \mid T_n\). Since our analysis and repair techniques focus on timing-related errors rather than synchronization errors, we use TAs rather than NTAs in our formalization. However, our implementation works on NTAs.
Example 1
The running example that we use throughout the paper consists of an NTA of two timed automata, depicted in Fig. 2. As alluded to in the introduction, the TAs dbServer and db synchronize via the exchange of messages modeled by the pairs of send and receive actions req! and req?, respectively, ser! and ser?. The transmission time of the req message is controlled by the clock variable x and can range between 1 and 2 time units. This is achieved by the location invariant
 on the reqReceived location in db together with the transition guard
on the reqReceived location in db together with the transition guard
 on the transition from reqReceived to reqProcessing. A similar mechanism using clock variable z is used to constrain the timing of the transfer of message ser to be within 1 and 2 time units. The processing time in dbServer is constrained to exactly 1 time unit by the location invariant
on the transition from reqReceived to reqProcessing. A similar mechanism using clock variable z is used to constrain the timing of the transfer of message ser to be within 1 and 2 time units. The processing time in dbServer is constrained to exactly 1 time unit by the location invariant
 and the transition guard
and the transition guard
 . In dbServer, a transition to location timeout can be triggered when the guard z==2 is satisfied in location serReceiving. The clock variable x, which is not reset until the next req message is sent, is recording the time that has elapsed since sending req and is used in location serReceiving in order to verify if more than 4 time units have passed since req was sent. The timed safety property that we will consider for our example is \(\varPi = \lnot \mathtt {@dbServer.serReceiving} \vee (x < 4).\) For the violation of this property, UPPAAL produces the TDT \(S = \theta _0 \ldots \theta _3\) where
. In dbServer, a transition to location timeout can be triggered when the guard z==2 is satisfied in location serReceiving. The clock variable x, which is not reset until the next req message is sent, is recording the time that has elapsed since sending req and is used in location serReceiving in order to verify if more than 4 time units have passed since req was sent. The timed safety property that we will consider for our example is \(\varPi = \lnot \mathtt {@dbServer.serReceiving} \vee (x < 4).\) For the violation of this property, UPPAAL produces the TDT \(S = \theta _0 \ldots \theta _3\) where
3 Logical Encoding of Timed Diagnostic Traces
Our analysis relies on a logical encoding of TDTs in the theory of quantifier-free linear real arithmetic. For the remainder of this paper, we fix a TA \(T = (L, l^0, C, \varSigma , \varTheta , I)\) with a safety property \(\varPi \) and assume that \(S=\theta _0,\dots ,\theta _{n-1}\) is an STT of T. We use the following notation for our logical encoding where \(j \in [0,n+1]\) is a position in a realization of S and \(c \in C\) is a clock:
-
\(l_j\) denotes the location of the pre state of \(\theta _j\) for \(j < n\) and the location of the post state of \(\theta _{j-1}\) for \(j=n\).
-
\(c_{j}\) denotes the value of clock variable c when reaching the state at position j.
-
\(\delta _j\) denotes the delay of the delay transition leaving the state at position \(j \le n\).
-
 denotes the set of clock variables that are being reset by action \(\theta _j\) for \(j < n\).
denotes the set of clock variables that are being reset by action \(\theta _j\) for \(j < n\). -
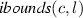 denotes the set of pairs \((\beta , \sim )\) such that the atomic clock constraint \(c \sim \beta \) appears in the location invariant I(l).
denotes the set of pairs \((\beta , \sim )\) such that the atomic clock constraint \(c \sim \beta \) appears in the location invariant I(l). -
 denotes the set of pairs \((\beta , \sim )\) such that the atomic clock constraint \(c \sim \beta \) appears in the guard of action \(\theta \).
denotes the set of pairs \((\beta , \sim )\) such that the atomic clock constraint \(c \sim \beta \) appears in the guard of action \(\theta \).
To illustrate the use of  , assume location l to be labeled with invariants \(x > 2 \wedge x \le 4 \wedge y \le 1\), then
, assume location l to be labeled with invariants \(x > 2 \wedge x \le 4 \wedge y \le 1\), then  The usage of
The usage of  is accordingly.
is accordingly.
Definition 2
The timed diagnostic trace constraint system associated with STT S is the conjunction \(\mathcal {T}\) of the following constraints:

Let further  where \(\varPi [\mathbf {c}_{n+1}/\mathbf {c}]\) is obtained from \(\varPi \) by substituting all occurrences of clocks \(c \in C\) with \(c_{n+1}\). Then the \(\varPi \)-extended TDT constraint system associated with S is defined as \(\mathcal {T}^\varPi = \mathcal {T} \wedge \lnot \varPhi \).
where \(\varPi [\mathbf {c}_{n+1}/\mathbf {c}]\) is obtained from \(\varPi \) by substituting all occurrences of clocks \(c \in C\) with \(c_{n+1}\). Then the \(\varPi \)-extended TDT constraint system associated with S is defined as \(\mathcal {T}^\varPi = \mathcal {T} \wedge \lnot \varPhi \).
To illustrate the encoding consider the transition \(\varTheta _3\) of the TDT in Example 1 corresponding to the transition from state (reqSent, reqProcessing) to state (serReceiving, reqAwaiting) while resetting clock z in the NTA of Fig. 2. The encoding for the constraints on the clocks x, y and z is as following: \(y_3 + d_3 \ge 1\), \(z_4 = 0\), \(x_4 = x_3 + d_3\) and \(y_4 = y_3 + d_3\).
Lemma 1
\(\delta ^c_0,\dots ,\delta ^c_n\) is a realization of an STT S iff there exists a satisfying variable assignment \(\iota \) for \(\mathcal {T}\) such that for all \(j \in [0,n]\), \(\iota (\delta _j) = \delta ^c_j\).
Theorem 1
An STT S witnesses a violation of \(\varPi \) in T iff \(\mathcal {T}^\varPi \) is satisfiable.
4 Repair
We propose a repair technique that analyzes the responsibility of clock bound values occurring in a single TDT for causing the violation of a specification \(\varPi \). The analysis suggests possible syntactic repairs. In a second step we define an admissibility test that assesses the admissibility of the repair in the context of the complete TA model. Throughout this section, we assume that S is a TDT for T and \(\varPi \).
Clock Bound Variation. We introduce bound variation variables \( v \) that stand for correction values that the repair will add to the clock bounds occurring in location invariants and transition guards. The values are chosen such that none of the realizations of S in the modified automaton still witnesses a violation of \(\varPi \). This is done by defining a new constraint system that captures the conditions on the variable \( v \) under which the violation of \(\varPi \) will not occur in the corresponding trace of the modified automaton. Using this constraint system, we then define a maximum satisfiability problem whose solution minimizes the number of changes to T that are needed to achieve the repair.
Recall that the clock bounds occurring in location invariants and in transition guards are represented by the ibounds and gbounds sets defined for the TDT S. Notice that each clock variable c may be associated with \(m_{c,l}\) different clock bounds in the location invariant of l, denoted by the set  Similarly, we enumerate the bounds in
Similarly, we enumerate the bounds in  as \((\beta ^{c,\theta }_k,\sim ^{c,\theta }_k)\). To reduce notational clutter, we let the meta variable r stand for the pairs of the form c, l or \(c,\theta \). We then introduce bound variation variables \( v ^{r}_{k}\) describing the possible static variation in the TA code for the clock bound \(\beta ^{r}_{k}\) and modify the TDT constraint system accordingly. A variation of the bounds only affects the location invariant constraints
as \((\beta ^{c,\theta }_k,\sim ^{c,\theta }_k)\). To reduce notational clutter, we let the meta variable r stand for the pairs of the form c, l or \(c,\theta \). We then introduce bound variation variables \( v ^{r}_{k}\) describing the possible static variation in the TA code for the clock bound \(\beta ^{r}_{k}\) and modify the TDT constraint system accordingly. A variation of the bounds only affects the location invariant constraints  and the transition guard constraints
and the transition guard constraints  . We thus define an appropriate invariant variation constraint
. We thus define an appropriate invariant variation constraint  and guard variation constraint
and guard variation constraint  that capture the clock bound modifications:
that capture the clock bound modifications:

We also need constraints ensuring that the modified clock bounds remain positive:

Putting all of this together we obtain the bound variation TDT constraint system

which captures all realizations of S in TAs  that are obtained from T by modifying the clock bounds \(\beta ^{r}_k\) by some semantically consistent variations \( v ^{r}_k\).
that are obtained from T by modifying the clock bounds \(\beta ^{r}_k\) by some semantically consistent variations \( v ^{r}_k\).
Consider the bound variation for the guard \(y\ge 1\) of transition \(\varTheta _3\) in Example 1. The modified guard constraint, a conjunct in  , is \(y_3 + d_3 \ge 1 + v ^{y}_{3}\). The corresponding non-negativity constraint from
, is \(y_3 + d_3 \ge 1 + v ^{y}_{3}\). The corresponding non-negativity constraint from  is \(1 + v ^{y}_{3} \ge 0\).
is \(1 + v ^{y}_{3} \ge 0\).
Repair by Bound Variation Analysis. The objective of the bound variation analysis is to provide hints to the system designer regarding which minimal syntactic changes to the considered model might prevent the violation of property \(\varPi \). Minimality here is considered with respect to the number of clock bound values in invariants and guards that need to be changed.
We implement this analysis by using the bound variation TDT constraint system  to derive an instance of the partial MaxSMT problem whose solutions yield candidate repairs for the timed automaton T. The partial MaxSMT problem takes as input a finite set of assertion formulas belonging to a fixed first-order theory. These assertions are partitioned into hard and soft assertions. The hard assertions \(\mathcal {F}_H\) are assumed to hold and the goal is to find a maximizing subset \(\mathcal {F}' \subseteq \mathcal {F}_S\) of the soft assertions such that \(\mathcal {F}' \cup \mathcal {F}_H\) is satisfiable in the given theory.
to derive an instance of the partial MaxSMT problem whose solutions yield candidate repairs for the timed automaton T. The partial MaxSMT problem takes as input a finite set of assertion formulas belonging to a fixed first-order theory. These assertions are partitioned into hard and soft assertions. The hard assertions \(\mathcal {F}_H\) are assumed to hold and the goal is to find a maximizing subset \(\mathcal {F}' \subseteq \mathcal {F}_S\) of the soft assertions such that \(\mathcal {F}' \cup \mathcal {F}_H\) is satisfiable in the given theory.
For our analysis, the hard assertions consist of the conjunction

Note that the free variables of  are exactly the bound variation variables \( v ^r_k\). Given a satisfying assignment \(\iota \) for
are exactly the bound variation variables \( v ^r_k\). Given a satisfying assignment \(\iota \) for  , let \(T_\iota \) be the timed automaton obtained from T by adding to each clock bound \(\beta ^r_k\) the according variation value \(\iota ( v ^r_k)\) and let \(S_\iota \) be the TDT corresponding to S in \(T_\iota \). Then
, let \(T_\iota \) be the timed automaton obtained from T by adding to each clock bound \(\beta ^r_k\) the according variation value \(\iota ( v ^r_k)\) and let \(S_\iota \) be the TDT corresponding to S in \(T_\iota \). Then  guarantees that
guarantees that
-
1.
\(S_\iota \) is feasible, and
-
2.
\(S_\iota \) has no realization that witnesses a violation of \(\varPi \) in \(T_\iota \).
We refer to such an assignment \(\iota \) as a local clock bound repair for T and S. To obtain a minimal local clock bound repair, we use the soft assertions given by the conjunction

Clearly  is unsatisfiable because
is unsatisfiable because  is equisatisfiable with \(\mathcal {T}\), and \(\mathcal{{T}} \wedge \lnot \varPhi \) is satisfiable by assumption. However, if there exists at least one local clock bound repair for T and S, then
is equisatisfiable with \(\mathcal {T}\), and \(\mathcal{{T}} \wedge \lnot \varPhi \) is satisfiable by assumption. However, if there exists at least one local clock bound repair for T and S, then  alone is satisfiable. In this case, the MaxSMT instance
alone is satisfiable. In this case, the MaxSMT instance  has at least one solution. Every satisfying assignment of such a solution corresponds to a local repair that minimizes the number of clock bounds that need to be changed in T.
has at least one solution. Every satisfying assignment of such a solution corresponds to a local repair that minimizes the number of clock bounds that need to be changed in T.
Note that hard and soft assertions remain within a decidable logic. Using an SMT solver such as Z3, we can enumerate all the optimal solutions for the partial MaxSMT instance and obtain a minimal local clock bound repair from each of them.
Example 2
We have applied the bound variation repair analysis to the TDT from Example 1, using TarTar, which calls Z3. The following repairs were computed:
-
1.
\( v ^{z,l_5}_{1} = -1\). This corresponds to a variation of the location invariant regarding clock z in location 5 of the TDT, corresponding to location dbServer.serReceiving, to read \(z \le 1\) instead of \(z \le 2\). This indicates that the violation of the bound on the total duration of the transaction, as indicated by a return to the serReceiving location and a value greater than 4 for clock x, can be avoided by ensuring that the time taken for transmitting the ser message to the dbServer is constrained to take exactly 1 time unit.
-
2.
A further computed repair is \( v ^{x,l_2}_{1} = -1\). Interpreting this variation in the context of Example 1 means that location db.reqReceived will be left when the clock x has value 1. In other words, the transmission of the message req to the db takes exactly one time unit, not between 1 and 2 time units as in the unrepaired model.
-
3.
Another possible repair implies the modification of two clock bounds. This is no longer an optimal solution and no further optimal solution exists. Notice that even non-optimal solutions might provide helpful insight for the designer, for instance if optimal repairs turn out not to be implementable, inadmissible or leading to a property violation. It is therefore meaningful to allow a practical tool implementation to compute more than just the optimal repairs.
5 Admissibility of Repair
The synthesized repairs that lead to a TA \(T_\iota \) change the original TA T in fundamental ways, both syntactically and semantically. This brings up the question whether the synthesized repairs are admissible. In fact, one of the key questions is what notion of admissibility is meaningful in this context.
A timed trace [7] is a sequence of timed actions \(\xi = (t_1, a_1), (t_2, a_2), \ldots \) that is generated by a run of a TA, where \(t_i \le t_{i+1}\) for all \(i \ge 1\). The timed language for a TA T is the set of all its timed traces, which we denote by \(\mathcal{L}_T(T)\). The untimed language of T consists of words over T’s alphabet \(\varSigma \) so that there exists at least one timed trace of T forming this word. Formally, for a timed trace \(\xi = (t_1, a_1),(t_2, a_2)\ldots \), the untime operator \(\mu (\xi )\) returns an untimed trace \(\xi _{\mu } = a_1 a_2 ...\). We define the untimed language \(\mathcal{L}_{\mu }(T)\) of the TA T as \(\mathcal{L}_{\mu }(T) = \{ \mu (\xi ) \mid \xi \in \mathcal{L}_T(T) \}\).
Let B be a Büchi automaton (BA) [10] over some alphabet \(\varSigma \). We write \(\mathcal{L}(B) \subseteq \varSigma ^\omega \) for the language accepted by B. Similarly, we denote by \(\mathcal{L}_f(B) \subseteq \varSigma ^*\) the language accepted by B if it is interpreted as a nondeterministic finite automaton (NFA). Further, we write \(\text {pref}(\mathcal{L}(B))\) to denote the set of all finite prefixes of words in \(\mathcal{L}(B)\).
For a given NFA or BA M, the closure \(\texttt {cl}(M)\) denotes the automaton obtained from M by turning all of its states into accepting states. We call M closed iff \(M=\texttt {cl}(M)\). Notice that a Büchi automaton accepts a safety language if and only if it is closed [1].
Admissibility Criteria. From a syntactic point of view the repair obtained from a satisfying assignment \(\iota \) of the MaxSMT instance ensures that \(T_\iota \) is a syntactically valid TA model by, for instance, placing non-negativity constraints on repaired clock bounds. In case repairs alter right hand sides of clock constraints to rational numbers, this can easily be fixed by normalizing all clock constraints in the TA.
From a semantic perspective, the impact of the repairs is more profound. Since the repairs affect time bounds in location invariants and transition guards, as well as clock resets, the behavior of \(T_\iota \) may be fundamentally different from the behavior of T.
-
First, the computed repair for one property \(\varPi \) may render another property \(\varPi '\) violated. To check admissibility of the synthesized repair with respect to the set of all properties \(\widehat{\varPi }\) in the system specification, a full re-checking of \(\widehat{\varPi }\) is necessary.
-
Second, a repair may have introduced zenoness and timelock [4] into \(T_\iota \). As discussed in [4], there exists both an over-approximating static test for zenoness as well as a model checking based precise test for timelocks that can be used to verify whether the repair is admissible in this regard.
-
Third, due to changes in the possible assignment of time values to clocks, reachable locations in the TA T may become unreachable in \(T_\iota \), and vice versa. On the one hand, this means that some functionalities of the system may no longer be provided since part of the actions in T will no longer be executable in \(T_\iota \), and vice versa. Further, a reduction in the set of reachable locations in \(T_\iota \) compared to T may mean that certain locations with property violations in T are no longer reachable in \(T_\iota \), which implies that certain property violations are masked by a repair instead of being fixed. On the other hand, the repair leading to locations becoming reachable in \(T_\iota \) that were unreachable in T may have the effect that previously unobserved property violations become visible and that \(T_\iota \) possesses functionality that T does not have, which may or may not be desirable.
It should be pointed out that we assess admissibility of a repair leading to \(T_\iota \) with respect to a given TA model T, and not with respect to a correct TA model \(T^*\) satisfying \(\varPi \).
Functional Equivalence. While various variants of semantic admissibility may be considered, we are focusing on a notion of admissibility that ensures that a repair does not unduly change the functional behavior of the modeled system while adhering to the timing constraints of the repaired system. We refer to this as functional equivalence. The functional capabilities of a timed system manifest themselves in the sets of action or transition traces that the system can execute. For TAs T and \(T_\iota \) this means that we need to consider the languages over the action or transition alphabets that these TAs define. Considering the timed languages of T and \(T_\iota \), we can state that \(\mathcal{L}_T(T) \ne \mathcal{L}_T(T_\iota )\) since the repair forces at least one timed trace to be purged from \(\mathcal{L}_T(T)\). This means that equivalence of the timed languages cannot be an admissibility criterion ensuring functional equivalence. At the other end of the spectrum we may relate the de-timed languages of T and \(T_\iota \). The de-time operator \(\alpha (T)\) is defined such that it omits all timing constraints and resets from any TA T. Requiring \(\mathcal{L}(\alpha (T)) = \mathcal{L}(\alpha (T_\iota ))\) is tempting since it states that when eliminating all timing related features from T and from the repaired \(T_\iota \), the resulting action languages will be identical.
However, this admissibility criterion would be flawed, since the repair in \(T_\iota \) may imply that unreachable locations in T will be reachable in \(T_\iota \), and vice versa. This may have an impact on the untimed languages, and even though \(\mathcal{L}(\alpha (T)) = \mathcal{L}(\alpha (T_\iota ))\) it may be that \(\mathcal{L}_{\mu }(T) \ne \mathcal{L}_{\mu }(T_\iota )\). To illustrate this point, consider the running example in Fig. 2 and assume the invariant in location dbServer.reqReceiving to be modified from \(z \le 2\) to \(z \le 1\) in the repaired TA \(T_\iota \). Applying the de-time operator to \(T_\iota \) implies that the location dbServer.timeout, which is unreachable in \(T_\iota \), becomes reachable in the de-timed model. Since dbServer.timeout is reachable in T, the TA T and \(T_\iota \) are not functionally equivalent, even though their de-timed languages are identical. Notice that for the untimed languages \(\mathcal{L}_{\mu }(T) \ne \mathcal{L}_{\mu }(T_\iota )\) holds since no timed trace in \(\mathcal{L}_T(T_\iota )\) reaches location timeout, even though such a timed trace exists in \(\mathcal{L}_T(T)\). In detail, \(\mathcal{L}_\mu (T)\) contains the untimed trace \(\varTheta _0\varTheta _1\varTheta _2\varTheta _3\varTheta _4\) that is missing in \(\mathcal{L}_\mu (T_i)\) and where \(\varTheta _4\) is the transition towards the location dbServer.timeout. As consequence, we resort to considering the untimed languages of T and \(T_\iota \) and require \(\mathcal{L}_{\mu }(T) = \mathcal{L}_{\mu }(T_\iota )\). It is easy to see that \(\mathcal{L}_{\mu }(T) = \mathcal{L}_{\mu }(T_\iota ) \Rightarrow \mathcal{L}(\alpha (T)) = \mathcal{L}(\alpha (T_\iota ))\). In other words, the equivalence of the untimed languages ensures functional equivalence.
Admissibility Test. Designing an algorithmic admissibility test for functional equivalence is challenging due to the computational complexity of determining the equivalence of the untimed languages \(\mathcal{L}_{\mu }(T)\) and \(\mathcal{L}_{\mu }(T_\iota )\). While language equivalence is decidable for languages defined by Büchi Automata, it is undecidable for timed languages [3]. For untimed languages, however, this problem is again decidable [3]. The algorithmic implementation of the test for functional equivalence that we propose proceeds in two steps.
-
First, the untimed languages \(\mathcal{L}_\mu (T)\) and \(\mathcal{L}_\mu (T_\iota )\) are constructed. This requires an untime transformation of T and \(T_\iota \) yielding Büchi automata representing \(\mathcal{L}_\mu (T)\) and \(\mathcal{L}_\mu (T_\iota )\). While the standard untime transformation for TAs [3] relies on a region construction, we propose a transformation that relies on a zone construction [14]. This will provide a more succinct representation of the resulting untimed languages and, hence, a more efficient equivalence test.
-
Second, it needs to be determined whether \(\mathcal{L}_\mu (T) = \mathcal{L}_\mu (T_\iota )\). As we shall see, the obtained Büchi automata are closed. Hence, we can reduce the equivalence problem for these \(\omega \)-regular languages to checking equivalence of the regular languages obtained by taking the finite prefixes of the traces in \(\mathcal{L}_\mu (T)\) and \(\mathcal{L}_\mu (T_\iota )\). This allows us to interpret the Büchi automata obtained in the first step as NFAs, for which the language equivalence check is a standard construction [15].
Automata for Untimed Languages. The construction of an automaton representing an untimed language, here referred to as an untime construction, has so far been proposed based on a region abstraction [3]. The region abstraction is known to be relatively inefficient since the number of regions is, among other things, exponential in the number of clocks [4]. We therefore propose an untime construction based on the construction of a zone automaton [14] which in the worst case is of the same complexity as the region automaton, but on the average is more succinct [7].
Definition 3
(Untimed Büchi Automaton). Assume a TA T and the corresponding zone automaton  \(\varTheta _Z)\). We define the untimed Büchi automaton as the closed BA \(B_T = (S, \varSigma ,\rightarrow , S_0,F)\) obtained from
\(\varTheta _Z)\). We define the untimed Büchi automaton as the closed BA \(B_T = (S, \varSigma ,\rightarrow , S_0,F)\) obtained from  such that \(S = S_Z\), \(\varSigma = \varSigma _Z \setminus \{\delta \}\) and \(S_0 = \{s_Z^0\}\). For every transition in \(\varTheta _Z\) with a label \(a \in \varSigma \) we add a transition to \(\rightarrow \) created by the rule
such that \(S = S_Z\), \(\varSigma = \varSigma _Z \setminus \{\delta \}\) and \(S_0 = \{s_Z^0\}\). For every transition in \(\varTheta _Z\) with a label \(a \in \varSigma \) we add a transition to \(\rightarrow \) created by the rule  with \(z^\uparrow = \{ v + d | v \in z, d \in \mathbb {R}_{\ge 0}\}\). In addition, we add self-transitions
with \(z^\uparrow = \{ v + d | v \in z, d \in \mathbb {R}_{\ge 0}\}\). In addition, we add self-transitions  to every state \((l,z) \in S_{B}\).
to every state \((l,z) \in S_{B}\).
The following observations justify this definition:
-
A timed trace of T may remain forever in the same location after a finite number of action transitions. In order to enable B to accept this trace, we add a self-transition labeled with \(\tau \) to \(\rightarrow \) for each state \(s \in S\) in \(B_T\), and later define s as accepting. These \(\tau \)-self-transitions extend every finite timed trace t leading to a state in \(S_\tau \) to an infinite trace \(t.\tau ^\omega \).
-
The construction of the acceptance set F is more intricate. Convergent traces are often excluded from consideration in real-time model checking [4]. As a consequence, in the untime construction proposed in [3], only a subset of the states in S may be included in F. A repair may render a subgraph of the location graph of T that is only reachable by divergent traces, into a subgraph in \(T_\iota \) that is only reachable by convergent traces. However, excluding convergent traces is only meaningful when considering unbounded liveness properties, but not when analyzing timed safety properties, which in effect are safety properties. As argued in [7], unbounded liveness properties appear to be less important than timed safety properties in timed systems. This is due to the observation that divergent traces reflect unrealistic behavior in the limit, but finite prefixes of infinite divergent traces, which only need to be considered for timed safety properties, correspond to realistic behavior. This observation is also reflected in the way in which, e.g., UPPAAL treats reachability by convergent traces. In conclusion, this justifies our choice to define the zone automaton in the untime construction as a closed BA, i.e., \(F = S\).
Theorem 2
(Correctness of Untimed Büchi Automaton Construction). For an untimed Büchi automaton \(B_T\) derived from a TA T according to Definition 3 it holds that \(\mathcal{L}(B_T) = \mathcal{L}_\mu (T)\).
Equivalence Check for Untimed Languages. Given that the zone automaton construction delivers closed BAs we can reduce the admissibility test \(\mathcal{L}_{\mu }(T) = \mathcal{L}_{\mu }(T_\iota )\) defined over infinite languages to an equivalence test over the finite prefixes of these languages, represented by interpreting the zone automata as NFAs. The following theorem justifies this reduction.
Theorem 3
(Language Equivalence of Closed BA). Given closed Büchi automata B and \(B'\), if \(\mathcal{L}_{\text {f}}(B) = \mathcal{L}_{\text {f}}(B')\) then \(\mathcal{L}(B) = \mathcal{L}(B')\).
Discussion. One may want to adapt the admissibility test so that it only considers divergent traces, e.g., in cases where only unbounded liveness properties need to be preserved by a repair. This can be accomplished as follows. First, an overapproximating non-zenoness test [4] can be applied to T and \(T_\iota \). If it shows non-zenoness, then one knows that the respective TA does not include convergent traces. If this test fails, a more expensive test needs to be developed. It requires a construction of the untimed Büchi automata using the approach from [3], and subsequently a language equivalence test of the untimed languages accepted by the untimed BAs using, for instance, the automata-theoretic constructions proposed in [9].
6 Case Studies and Experimental Evaluation
We have implemented the repair computation and admissibility test in a proof-of-concept tool called TarTar. We present the architecture of TarTar and then evaluate the proposed method by applying TarTar to several case studies.
Tool Architecture. The control loop of TarTar, depicted in Fig. 3, computes repairs for a given UPPAAL model and a given property \(\varPi \) using the following steps:
-
1.
Counterexample Creation. TarTar calls UPPAAL with parameters to compute and store a shortest symbolic TDT in XML format, in case \(\varPi \) is violated.
-
2.
Diagnostic Trace Creation. Parsing the model and the TDT, TarTar creates
 as defined in Sect. 4. Z3 can only solve the MaxSMT problem for quantifier-free linear real arithmetic. Hence, TarTar first performs a quantifier elimination on the constraints
as defined in Sect. 4. Z3 can only solve the MaxSMT problem for quantifier-free linear real arithmetic. Hence, TarTar first performs a quantifier elimination on the constraints  of
of 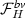 .
. -
3.
Repair Computation. Next, TarTar attempts to compute a repair, by using Z3 to solve the generated quantifier-free MaxSMT instance. In case no solution is found, TarTar terminates. Otherwise, TarTar returns the repair that has been computed from the model of the MaxSMT solution.
-
4.
Admissibility Check. Using adapted routines provided by the opaal model checker [11], TarTar checks the admissibility of the computed repair. To do so, TarTar modifies the constraints of the considered UPPAAL model as indicated by the computed repair. It calls opaal in order to compute the timed transition system (TTS) of the original and the repaired UPPAAL model. TarTar then checks whether the two TTS have equivalent untimed languages, in which case the repair is admissible. This check is implemented using the library AutomataLib included in the package LearnLib [16],
-
5.
Iteration. TarTar is designed to enumerate all repairs, starting with the minimal ones, in an iterative loop. To accomplish this, at the end of each iteration i a new
 is generated by forcing the bound variation variables that were used in the i-th repair to 0. This excludes the repair computed in iteration i from further consideration. Using
is generated by forcing the bound variation variables that were used in the i-th repair to 0. This excludes the repair computed in iteration i from further consideration. Using 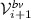 , TarTar iterates back to Step 3 to compute another repair.
, TarTar iterates back to Step 3 to compute another repair.
Evaluation Strategy. The evaluation of our analysis is based on ideas taken from mutation testing [18]. Mutation testing evaluates a test set by systematically modifying the program code to be tested and computing the ratio of modifications that are detected by the test set. Real-time system models that contain violations of timed safety properties are not available in significant numbers. We therefore need to seed faults in existing models and check whether those can be found by our automated repair. An objective of mutation testing is that testing a proportion of the possible modification yields satisfactory results [18]. In order to evaluate repairs for erroneous clock bounds in invariants and transition guards we seed modifications to all bounds of clock constraints by the amount of \(\{ -10, -1, +1, +0.1{\cdot }M, +M\}\), where M is the maximal bound a clock is compared against in a given model. If a thus seeded modification leads to a syntactically invalid UPPAAL model, then UPPAAL returns an exception and we ignore this modification. In analogy to mutation testing, we compute the count of TDTs for which our analysis finds an admissible repair.
Experiments. We have applied this modification seeding strategy to eight UPPAAL models (see Table 1). Not all of the models that we considered have been published with a property that can be violated by mutating a clock constraint. For those models, we suggest a suitable timed safety property specifying an invariant condition. In particular, we add a property to the Bando [29] model which ensures that, for as long as the sender is active, its clock never exceeds the value of 28, 116 time units. In the FDDI token ring protocol [29], the property that we use checks whether the first member of the ring never remains for more than 140 time units in any given state. The Viking model is taken from the set of test models of opaal [26]. For this model we use a property that checks whether one of the Viking processes can only enter a safe state during the first 60 time units. Note that all of these properties are satisfied by the unmodified models.
The results of the clock bound repair computed by TarTar for all considered models are summarized in Table 1. The seeded modifications are characterized quantitatively by the count #Seed of analyzed modified models, the count #TDT of modified models that return a TDT for the considered property, the maximal time \(T_{\textit{UP}}\) UPPAAL needs to create a TDT per analyzed model, and the length Len. of the longest TDT found. For the computation of a repair we give the count #Rep. of all repairs that were computed, the count #Adm. of computed admissible repairs, the count of TDTs #Sol. for which an admissible repair was found, the maximal time \(T_{\textit{QE}}\) that the quantifier elimination required, the average time effort \(T_{\textit{R}}\) to compute a repair, the standard deviation \(\textit{SD}_\textit{R}\) for the computation time of a repair, the time effort \(T_{\textit{Adm}}\) for an admissibility check, the maximal count of variables #Var, and the maximal count of constraints #Con. used in  . The maximal memory consumption was at most 17MB for the repair analysis and 478MB for the admissibility test. We performed all experiments on a computer with an i7-6700K CPU (4.0GHz), 60 GB of RAM and a Linux operating system.
. The maximal memory consumption was at most 17MB for the repair analysis and 478MB for the admissibility test. We performed all experiments on a computer with an i7-6700K CPU (4.0GHz), 60 GB of RAM and a Linux operating system.
We found 60 TDTs by seeding violations of the timed safety property and TarTar returned 204 repairs for these TDTs. TarTar proposed an admissible repair for 55 (\(91\%\)) TDTs and at least one repair for 57 (\(95\%\)) TDTs. For 3 out of the total of 14 TDTs found for the SBR model no repair was computed since the timeout of the quantifier elimination was reached after 2 minutes. For all other models, no timeout occurred.
Space limitations do not permit us to describe all models and computed repairs in detail, we therefore focus on the pacemaker case study. One of the modification increases a location invariant of this model that controls the minimal heart period from 400 to 1, 600. The modification allows the pacemaker to delay an induced ventricular beat for too long so that this violates the property that the time between two ventricular beats of a heart is never longer than the maximal heart period of 1, 000. TarTar finds three repairs. Two repairs reduce the maximal time delay between two ventricular or articular heart beats of the patient. The repairs are classified as inadmissible. In the model context this appears to be reasonable since the repairs would restrict the environment of the pacemaker, and not the pacemaker itself. The third repair is admissible and reduces the bound modified during the seeding of bound modifications by 600.5. The minimal heart period is then below or equal to the maximal heart period of 1, 000.
Result Interpretation. Our repair strategy minimizes the number of repairs but does not optimize the computed value. For instance, in the pacemaker model the computed repair of 600.5 would be a correct and admissible repair even if the value was reduced to 600, which would be the minimal possible repair value.
A comparison of the values \(T_{\textit{QE}}\) and \(T_{\textit{R}}\) reveals that, perhaps unsurprisingly, the quantifier elimination step is computationally almost an order of magnitude more expensive than the repair computation. Overall, the computational cost (\(T_{\textit{QE}}\) + \(T_{\textit{R}}\)) correlates with the number of variables in the constraint system, which depends in turn on the length of the TDT and the number of clocks referenced along the TDT. Consider, for instance, that the pacemaker model has a TDT of maximal length 9 with 116 variables, and the repair requires 0.193 s and 2.070 MB. On the other hand, the Bando model produces a longer maximal TDT of length 279 with 1, 156 variables and requires 6.555 s and 16.650 MB. The impact of the number of clock constraints and clock variables on the computation costs can be seen, for instance, in the data for the pacemaker and FDDI models. While the pacemaker model has a shorter TDT than the Viking model (9 vs. 18), the constraint counts (294 vs. 140) of the pacemaker model are higher than for the Viking model, which coincides with a higher computation time (0.193 s vs. 0.042 s) and a higher memory consumption (2.070 MB vs. 0.910 MB) compared to the Viking model.
We analyzed for every TDT the relationship between the length of the TDT and the computation time for a repair (\(T_r\) = \(T_{\textit{QE}}\) + \(T_{\textit{R}}\)), as well as the relationship between #Var and \(T_r\) by estimating Kendall’s tau [13]. Kendall’s tau is a measurement for the ordinal association between two measured quantities. A correlation is considered significant if the probability p that there is actually no correlation in a larger data set is below a certain threshold. The length of a TDT is significantly related (\(\tau _1=0.673\), \(p<.001\)) to \(T_r\). Also #Var is significantly related (\(\tau _2=0.759\), \(p<.001\)) to \(T_r\). #Var contains clocks for every step of a TDT, hence the combination of trace length and clock count tends to correlate higher than the trace length on its own. This supports our conjecture that the computation time of a repair depends on the trace length and the clock count.
The admissibility test appears to be quite efficient, with a maximum computation time of 34.120 s for the SBR model, which is one of the more complex models that were considered. We observed that most models were action-deterministic, which has a positive influence on the language equivalence test used during admissibility checking.
7 Conclusion
We have presented an approach to derive minimal repairs for timed reachability properties of TA and NTA models from TDTs in order to facilitate fault localization and debugging of such models during the design process. Our approach includes a formalization of TDTs using linear real arithmetic, a repair strategy based on MaxSMT solving, the definition of an admissibility criterion and test for the computed repairs, the development of a prototypical analysis and repair tool, and the application of the proposed method to a number of case studies of realistic complexity. To the best of our knowledge, this is the first rigorous treatment of counterexamples in real-time model checking. We are also not aware of any existing repair approaches for TA or NTA models. This makes a comparative experimental evaluation impossible. We have nonetheless observed that our analysis computes a significant number of admissible repairs within realistic computation time bounds and memory consumption.
Future research will address the development and implementation of repair strategies for further syntactic features in TAs and NTAs, including false comparison operators in invariants and guards, erroneous clock variable references, superfluous or missing resets for clocks, and wrong urgent state choices. We will furthermore address the interplay between different repairs and develop refined strategies to determine their admissibility. Finally, we plan to extend the approach developed in this paper to derive criteria for the actual causation of timing property violations in NTA models based on the counterfactual reasoning paradigm for causation.
Notes
- 1.
TarTar and links to all models used in this paper can be found at URL https://github.com/sen-uni-kn/tartar.
References
Alpern, B., Schneider, F.B.: Recognizing safety and liveness. Distrib. Comput. 2(3), 117–126 (1987)
Alur, R., et al.: Syntax-guided synthesis. In: Dependable Software Systems Engineering, NATO Science for Peace and Security Series, D: Information and Communication Security, vol. 40, pp. 1–25. IOS Press (2015). https://doi.org/10.3233/978-1-61499-495-4-1
Alur, R., Dill, D.L.: A theory of timed automata. Theor. Comput. Sci. 126(2), 183–235 (1994)
Baier, C., Katoen, J.P.: Principles of Model Checking. The MIT Press, Cambridge (2008)
Ben-Abdallah, H., Leue, S.: Timing constraints in message sequence chart specifications. In: FORTE. IFIP Conference Proceedings, vol. 107, pp. 91–106. Chapman & Hall (1997)
Bengtsson, J., Larsen, K., Larsson, F., Pettersson, P., Yi, W.: UPPAAL—a tool suite for automatic verification of real-time systems. In: Alur, R., Henzinger, T.A., Sontag, E.D. (eds.) HS 1995. LNCS, vol. 1066, pp. 232–243. Springer, Heidelberg (1996). https://doi.org/10.1007/BFb0020949
Bengtsson, J., Yi, W.: Timed automata: semantics, algorithms and tools. In: Desel, J., Reisig, W., Rozenberg, G. (eds.) ACPN 2003. LNCS, vol. 3098, pp. 87–124. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27755-2_3
Tiage Brito: Uppaal elevator example (2015). https://github.com/tfbrito/UPPAAL. Accessed 20 Jan 2019
Clarke, E.M., Draghicescu, I.A., Kurshan, R.P.: A unified approach for showing language inclusion and equivalence between various types of omega-automata. Inf. Process. Lett. 46(6), 301–308 (1993)
Clarke, E.M., Henzinger, T.A., Veith, H., Bloem, R. (eds.): Handbook of Model Checking. Springer, Cham (2018)
Dalsgaard, A.E., et al.: A lattice model checker. In: Bobaru, M., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM 2011. LNCS, vol. 6617, pp. 487–493. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20398-5_37
Dierks, H., Kupferschmid, S., Larsen, K.G.: Automatic abstraction refinement for timed automata. In: Raskin, J.-F., Thiagarajan, P.S. (eds.) FORMATS 2007. LNCS, vol. 4763, pp. 114–129. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75454-1_10
Field, A.: Discovering Statistics Using IBM SPSS Statistics: and Sex and Drugs and Rock ‘n’ Roll. Sage, London (2013)
Henzinger, T.A., Nicollin, X., Sifakis, J., Yovine, S.: Symbolic model checking for real-time systems. Inf. Comput. 111(2), 193–244 (1994)
Hopcroft, J.E., Ullman, J.D.: Introduction to Automata Theory, Languages and Computation, 2nd edn. Addison-Wesley, Stanford (2000)
Isberner, M., Howar, F., Steffen, B.: The open-source LearnLib. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 487–495. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21690-4_32
Jensen, H.E., Larsen, K.G., Skou, A.: Modelling and analysis of a collision avoidance protocol using spin and uppaal. In: The Spin Verification System. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 32, pp. 33–50. DIMACS/AMS (1996)
Jia, Y., Harman, M.: An analysis and survey of the development of mutation testing. IEEE Trans. Software Eng. 37(5), 649–678 (2011)
Jiang, Z., Pajic, M., Moarref, S., Alur, R., Mangharam, R.: Modeling and verification of a dual chamber implantable pacemaker. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 188–203. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_14
Jose, M., Majumdar, R.: Bug-assist: assisting fault localization in ANSI-C programs. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 504–509. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_40
Jose, M., Majumdar, R.: Cause clue clauses: error localization using maximum satisfiability. In: PLDI, pp. 437–446. ACM (2011)
Le, X.D., Chu, D., Lo, D., Le Goues, C., Visser, W.: S3: syntax- and semantic-guided repair synthesis via programming by examples. In: Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering, ESEC/FSE 2017, pp. 593–604. ACM (2017). https://doi.org/10.1145/3106237.3106309
Liu, S.: Analysing Timed Traces using SMT Solving. Master’s thesis, University of Konstanz (2018)
Milner, R. (ed.): A Calculus of Communicating Systems. LNCS, vol. 92. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10235-3
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
opaal: opaal test folder (2011). http://opaal-modelchecker.com/opaal-ltsmin/. Accessed 08 Nov 2018
Polsen, D.B., van Vliet, J.: Concrete Delays for Symbolic Traces. Master’s thesis, Department of Computer Science, Aalborg University (2010). https://projekter.aau.dk/projekter/files/32183338/report.pdf
Reynolds, A., Kuncak, V., Tinelli, C., Barrett, C., Deters, M.: Refutation-based synthesis in SMT. Formal Methods in System Design (2017). https://doi.org/10.1007/s10703-017-0270-2
Uppaal: Uppaal benchmarks (2017). http://www.it.uu.se/research/group/darts/uppaal/benchmarks/#benchmarks. Accessed 20 Jan 2019
Yi, W., Pettersson, P., Daniels, M.: Automatic verification of real-time communicating systems by constraint-solving. In: FORTE. IFIP Conference Proceedings, vol. 6, pp. 243–258. Chapman & Hall (1994). http://www.it.uu.se/research/group/darts/papers/texts/wpd-forte94-full.pdf
Yovine, S.: KRONOS: a verification tool for real-time systems. STTT 1(1–2), 123–133 (1997)
Acknowledgments
We wish to thank Nikolaj Bjorner and Zvonimir Pavlinovic for advice on the use of Z3. We are grateful to Sarah Stoll for helping us with the statistical evaluation of the experimental results. This work is in part supported by the National Science Foundation (NSF) under grant CCF-1350574.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Kölbl, M., Leue, S., Wies, T. (2019). Clock Bound Repair for Timed Systems. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11561. Springer, Cham. https://doi.org/10.1007/978-3-030-25540-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-25540-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25539-8
Online ISBN: 978-3-030-25540-4
eBook Packages: Computer ScienceComputer Science (R0)






 denotes the set of clock variables that are being reset by action
denotes the set of clock variables that are being reset by action 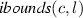 denotes the set of pairs
denotes the set of pairs  denotes the set of pairs
denotes the set of pairs  as defined in Sect.
as defined in Sect.  of
of 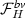 .
. is generated by forcing the bound variation variables that were used in the i-th repair to 0. This excludes the repair computed in iteration i from further consideration. Using
is generated by forcing the bound variation variables that were used in the i-th repair to 0. This excludes the repair computed in iteration i from further consideration. Using 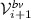 ,
, 