Abstract
Statistical model checking (SMC) is a technique for analysis of probabilistic systems that may be (partially) unknown. We present an SMC algorithm for (unbounded) reachability yielding probably approximately correct (PAC) guarantees on the results. We consider both the setting (i) with no knowledge of the transition function (with the only quantity required a bound on the minimum transition probability) and (ii) with knowledge of the topology of the underlying graph. On the one hand, it is the first algorithm for stochastic games. On the other hand, it is the first practical algorithm even for Markov decision processes. Compared to previous approaches where PAC guarantees require running times longer than the age of universe even for systems with a handful of states, our algorithm often yields reasonably precise results within minutes, not requiring the knowledge of mixing time.
This research was funded in part by TUM IGSSE Grant 10.06 (PARSEC), the Czech Science Foundation grant No. 18-11193S, and the German Research Foundation (DFG) project KR 4890/2-1 “Statistical Unbounded Verification”.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Statistical model checking (SMC) [YS02a] is an analysis technique for probabilistic systems based on
-
1.
simulating finitely many finitely long runs of the system,
-
2.
statistical analysis of the obtained results,
-
3.
yielding a confidence interval/probably approximately correct (PAC) result on the probability of satisfying a given property, i.e., there is a non-zero probability that the bounds are incorrect, but they are correct with probability that can be set arbitrarily close to 1.
One of the advantages is that it can avoid the state-space explosion problem, albeit at the cost of weaker guarantees. Even more importantly, this technique is applicable even when the model is not known (black-box setting) or only qualitatively known (grey-box setting), where the exact transition probabilities are unknown such as in many cyber-physical systems.
In the basic setting of Markov chains [Nor98] with (time- or step-)bounded properties, the technique is very efficient and has been applied to numerous domains, e.g. biological [JCL+09, PGL+13], hybrid [ZPC10, DDL+12, EGF12, Lar12] or cyber-physical [BBB+10, CZ11, DDL+13] systems and a substantial tool support is available [JLS12, BDL+12, BCLS13, BHH12]. In contrast, whenever either (i) infinite time-horizon properties, e.g. reachability, are considered or (ii) non-determinism is present in the system, providing any guarantees becomes significantly harder.
Firstly, for infinite time-horizon properties we need a stopping criterion such that the infinite-horizon property can be reliably evaluated based on a finite prefix of the run yielded by simulation. This can rely on the the complete knowledge of the system (white-box setting) [YCZ10, LP08], the topology of the system (grey box) [YCZ10, HJB+10], or a lower bound \(p_{\min }\) on the minimum transition probability in the system (black box) [DHKP16, BCC+14].
Secondly, for Markov decision processes (MDP) [Put14] with (non-trivial) non-determinism, [HMZ+12] and [LP12] employ reinforcement learning [SB98] in the setting of bounded properties or discounted (and for the purposes of approximation thus also bounded) properties, respectively. The latter also yields PAC guarantees.
Finally, for MDP with unbounded properties, [BFHH11] deals with MDP with spurious non-determinism, where the way it is resolved does not affect the desired property. The general non-deterministic case is treated in [FT14, BCC+14], yielding PAC guarantees. However, the former requires the knowledge of mixing time, which is at least as hard to compute; the algorithm in the latter is purely theoretical since before a single value is updated in the learning process, one has to simulate longer than the age of universe even for a system as simple as a Markov chain with 12 states having at least 4 successors for some state.
Our contribution is an SMC algorithm with PAC guarantees for (i) MDP and unbounded properties, which runs for realistic benchmarks [HKP+19] and confidence intervals in orders of minutes, and (ii) is the first algorithm for stochastic games (SG). It relies on different techniques from literature.
-
1.
The increased practical performance rests on two pillars:
-
extending early detection of bottom strongly connected components in Markov chains by [DHKP16] to end components for MDP and simple end components for SG;
-
improving the underlying PAC Q-learning technique of [SLW+06]:
-
(a)
learning is now model-based with better information reuse instead of model-free, but in realistic settings with the same memory requirements,
-
(b)
better guidance of learning due to interleaving with precise computation, which yields more precise value estimates.
-
(c)
splitting confidence over all relevant transitions, allowing for variable width of confidence intervals on the learnt transition probabilities.
-
(a)
-
-
2.
The transition from algorithms for MDP to SG is possible via extending the over-approximating value iteration from MDP [BCC+14] to SG by [KKKW18].
To summarize, we give an anytime PAC SMC algorithm for (unbounded) reachability. It is the first such algorithm for SG and the first practical one for MDP.
Related work
Most of the previous efforts in SMC have focused on the analysis of properties with bounded horizon [YS02a, SVA04, YKNP06, JCL+09, JLS12, BDL+12].
SMC of unbounded properties was first considered in [HLMP04] and the first approach was proposed in [SVA05], but observed incorrect in [HJB+10]. Notably, in [YCZ10] two approaches are described. The first approach proposes to terminate sampled paths at every step with some probability \(p_{term}\) and re-weight the result accordingly. In order to guarantee the asymptotic convergence of this method, the second eigenvalue \(\lambda \) of the chain and its mixing time must be computed, which is as hard as the verification problem itself and requires the complete knowledge of the system (white box setting). The correctness of [LP08] relies on the knowledge of the second eigenvalue \(\lambda \), too. The second approach of [YCZ10] requires the knowledge of the chain’s topology (grey box), which is used to transform the chain so that all potentially infinite paths are eliminated. In [HJB+10], a similar transformation is performed, again requiring knowledge of the topology. In [DHKP16], only (a lower bound on) the minimum transition probability \(p_{\min }\) is assumed and PAC guarantees are derived. While unbounded properties cannot be analyzed without any information on the system, knowledge of \(p_{\min }\) is a relatively light assumption in many realistic scenarios [DHKP16]. For instance, bounds on the rates for reaction kinetics in chemical reaction systems are typically known; for models in the PRISM language [KNP11], the bounds can be easily inferred without constructing the respective state space. In this paper, we thus adopt this assumption.
In the case with general non-determinism, one approach is to give the non-determinism a probabilistic semantics, e.g., using a uniform distribution instead, as for timed automata in [DLL+11a, DLL+11b, Lar13]. Others [LP12, HMZ+12, BCC+14] aim to quantify over all strategies and produce an \(\epsilon \)-optimal strategy. In [HMZ+12], candidates for optimal strategies are generated and gradually improved, but “at any given point we cannot quantify how close to optimal the candidate scheduler is” (cited from [HMZ+12]) and the algorithm “does not in general converge to the true optimum” (cited from [LST14]). Further, [LST14, DLST15, DHS18] randomly sample compact representation of strategies, resulting in useful lower bounds if \(\varepsilon \)-schedulers are frequent. [HPS+19] gives a convergent model-free algorithm (with no bounds on the current error) and identifies that the previous [SKC+14] “has two faults, the second of which also affects approaches [...] [HAK18, HAK19]”.
Several approaches provide SMC for MDPs and unbounded properties with PAC guarantees. Firstly, similarly to [LP08, YCZ10, FT14] requires (1) the mixing time T of the MDP. The algorithm then yields PAC bounds in time polynomial in T (which in turn can of course be exponential in the size of the MDP). Moreover, the algorithm requires (2) the ability to restart simulations also in non-initial states, (3) it only returns the strategy once all states have been visited (sufficiently many times), and thus (4) requires the size of the state space |S|. Secondly, [BCC+14], based on delayed Q-learning (DQL) [SLW+06], lifts the assumptions (2) and (3) and instead of (1) mixing time requires only (a bound on) the minimum transition probability \(p_{\min }\). Our approach additionally lifts the assumption (4) and allows for running times faster than those given by T, even without the knowledge of T.
Reinforcement learning (without PAC bounds) for stochastic games has been considered already in [LN81, Lit94, BT99]. [WT16] combines the special case of almost-sure satisfaction of a specification with optimizing quantitative objectives. We use techniques of [KKKW18], which however assumes access to the transition probabilities.
2 Preliminaries
2.1 Stochastic Games
A probability distribution on a finite set X is a mapping \(\delta : X \rightarrow [0,1]\), such that \(\sum _{x\in X} \delta (x) = 1\). The set of all probability distributions on X is denoted by \(\mathcal {D}(X)\). Now we define turn-based two-player stochastic games. As opposed to the notation of e.g. [Con92], we do not have special stochastic nodes, but rather a probabilistic transition function.
Definition 1
(SG). A stochastic game (SG) is a tuple  , where
, where  is a finite set of states partitionedFootnote 1 into the sets
is a finite set of states partitionedFootnote 1 into the sets  and
and  of states of the player Maximizer and MinimizerFootnote 2, respectively
of states of the player Maximizer and MinimizerFootnote 2, respectively  is the initial state,
is the initial state,  is a finite set of actions,
is a finite set of actions,  assigns to every state a set of available actions, and
assigns to every state a set of available actions, and  is a transition function that given a state
is a transition function that given a state  and an action
and an action  yields a probability distribution over successor states. Note that for ease of notation we write
yields a probability distribution over successor states. Note that for ease of notation we write  instead of
instead of  .
.
A Markov decision process (MDP) is a special case of \(\text {SG}\) where  . A Markov chain (MC) can be seen as a special case of an MDP, where for all
. A Markov chain (MC) can be seen as a special case of an MDP, where for all  . We assume that \(\text {SG}\) are non-blocking, so for all states
. We assume that \(\text {SG}\) are non-blocking, so for all states  we have
we have  .
.
For a state  and an available action
and an available action  , we denote the set of successors by
, we denote the set of successors by  . We say a state-action pair
. We say a state-action pair  is an exit of a set of states T, written
is an exit of a set of states T, written  , if
, if  , i.e., if with some probability a successor outside of T could be chosen.
, i.e., if with some probability a successor outside of T could be chosen.
We consider algorithms that have a limited information about the SG.
Definition 2
(Black box and grey box). An algorithm inputs an SG as black box if it cannot access the whole tuple, but
-
it knows the initial state,
-
for a given state, an oracle returns its player and available action,
-
given a state
 and action
and action  , it can sample a successor \(\mathsf {t}\) according to
, it can sample a successor \(\mathsf {t}\) according to  ,Footnote 3
,Footnote 3
-
it knows
 , an under-approximation of the minimum transition probability.
, an under-approximation of the minimum transition probability.
When input as grey box it additionally knows the number  of successors for each state
of successors for each state  and action
and action  .Footnote 4
.Footnote 4
The semantics of SG is given in the usual way by means of strategies and the induced Markov chain [BK08] and its respective probability space, as follows. An infinite path  is an infinite sequence
is an infinite sequence  , such that for every \(i \in \mathbb {N}\),
, such that for every \(i \in \mathbb {N}\),  and
and  .
.
A strategy of Maximizer or Minimizer is a function  or
or  , respectively, such that
, respectively, such that  for all
for all  . Note that we restrict to memoryless/positional strategies, as they suffice for reachability in SGs [CH12].
. Note that we restrict to memoryless/positional strategies, as they suffice for reachability in SGs [CH12].
A pair \((\sigma ,\tau )\) of strategies of Maximizer and Minimizer induces a Markov chain  with states
with states  ,
,  being initial, and the transition function
being initial, and the transition function  for states of Maximizer and analogously for states of Minimizer, with \(\sigma \) replaced by \(\tau \). The Markov chain induces a unique probability distribution \(\mathbb P^{\sigma ,\tau }\) over measurable sets of infinite paths [BK08, Ch. 10].
for states of Maximizer and analogously for states of Minimizer, with \(\sigma \) replaced by \(\tau \). The Markov chain induces a unique probability distribution \(\mathbb P^{\sigma ,\tau }\) over measurable sets of infinite paths [BK08, Ch. 10].
2.2 Reachability Objective
For a goal set  , we write
, we write  to denote the (measurable) set of all infinite paths which eventually reach \(\mathsf {Goal}\). For each
to denote the (measurable) set of all infinite paths which eventually reach \(\mathsf {Goal}\). For each  , we define the value in
, we define the value in  as
as

where the equality follows from [Mar75]. We are interested in  , its \(\varepsilon \)-approximation and the corresponding (\(\varepsilon \)-)optimal strategies for both players.
, its \(\varepsilon \)-approximation and the corresponding (\(\varepsilon \)-)optimal strategies for both players.
Let \(\mathsf {Zero}\) be the set of states, from which there is no finite path to any state in \(\mathsf {Goal}\). The value function  satisfies the following system of equations, which is referred to as the Bellman equations:
satisfies the following system of equations, which is referred to as the Bellman equations:

with the abbreviation  . Moreover,
. Moreover,  is the least solution to the Bellman equations, see e.g. [CH08].
is the least solution to the Bellman equations, see e.g. [CH08].
2.3 Bounded and Asynchronous Value Iteration
The well known technique of value iteration, e.g. [Put14, RF91], works by starting from an under-approximation of value function and then applying the Bellman equations. This converges towards the least fixpoint of the Bellman equations, i.e. the value function. Since it is difficult to give a convergence criterion, the approach of bounded value iteration (BVI, also called interval iteration) was developed for MDP [BCC+14, HM17] and SG [KKKW18]. Beside the under-approximation, it also updates an over-approximation according to the Bellman equations. The most conservative over-approximation is to use an upper bound of 1 for every state. For the under-approximation, we can set the lower bound of target states to 1; all other states have a lower bound of 0. We use the function \(\mathsf {INITIALIZE\_BOUNDS}\) in our algorithms to denote that the lower and upper bounds are set as just described; see [AKW19, Algorithm 8] for the pseudocode. Additionally, BVI ensures that the over-approximation converges to the least fixpoint by taking special care of end components, which are the reason for not converging to the true value from above.
Definition 3
(End component (EC)). A non-empty set  of states is an end component (EC) if there is a non-empty set
of states is an end component (EC) if there is a non-empty set  of actions such that (i) for each
of actions such that (i) for each  we do not have
we do not have  and (ii) for each
and (ii) for each  there is a finite path
there is a finite path  , i.e. the path stays inside T and only uses actions in B.
, i.e. the path stays inside T and only uses actions in B.
Intuitively, ECs correspond to bottom strongly connected components of the Markov chains induced by possible strategies, so for some pair of strategies all possible paths starting in the EC remain there. An end component T is a maximal end component (MEC) if there is no other end component \(T'\) such that \(T \subseteq T'\). Given an \(\text {SG}\)  , the set of its MECs is denoted by
, the set of its MECs is denoted by  .
.
Note that, to stay in an EC in an SG, the two players would have to cooperate, since it depends on the pair of strategies. To take into account the adversarial behaviour of the players, it is also relevant to look at a subclass of ECs, the so called simple end components, introduced in [KKKW18].
Definition 4
(Simple end component (SEC) [KKKW18]). An EC T is called simple, if for all  it holds that
it holds that  , where
, where

is called the best exit (of Maximizer) from T according to the function  . To handle the case that there is no exit of Maximizer in T we set \(\max _\emptyset = 0\).
. To handle the case that there is no exit of Maximizer in T we set \(\max _\emptyset = 0\).
Intuitively, SECs are ECs where Minimizer does not want to use any of her exits, as all of them have a greater value than the best exit of Maximizer. Assigning any value between those of the best exits of Maximizer and Minimizer to all states in the EC is a solution to the Bellman equations, because both players prefer remaining and getting that value to using their exits [KKKW18, Lemma 1]. However, this is suboptimal for Maximizer, as the goal is not reached if the game remains in the EC forever. Hence we “deflate” the upper bounds of SECs, i.e. reduce them to depend on the best exit of Maximizer. T is called maximal simple end component (MSEC), if there is no SEC \(T'\) such that \(T \subsetneq T'\). Note that in MDPs, treating all MSECs amounts to treating all MECs.

Algorithm 1 rephrases that of [KKKW18] and describes the general structure of all bounded value iteration algorithms that are relevant for this paper. We discuss it here since all our improvements refer to functions (in capitalized font) in it. In the next section, we design new functions, pinpointing the difference to the other papers. The pseudocode of the functions adapted from the other papers can be found, for the reader’s convenience, in [AKW19, Appendix A]. Note that to improve readability, we omit the parameters  and
and  of the functions in the algorithm.
of the functions in the algorithm.
Bounded Value Iteration: For the standard bounded value iteration algorithm, Line 4 does not run a simulation, but just assigns the whole state space  to XFootnote 5. Then it updates all values according to the Bellman equations. After that it finds all the problematic components, the MSECs, and “deflates” them as described in [KKKW18], i.e. it reduces their values to ensure the convergence to the least fixpoint. This suffices for the bounds to converge and the algorithm to terminate [KKKW18, Theorem 2].
to XFootnote 5. Then it updates all values according to the Bellman equations. After that it finds all the problematic components, the MSECs, and “deflates” them as described in [KKKW18], i.e. it reduces their values to ensure the convergence to the least fixpoint. This suffices for the bounds to converge and the algorithm to terminate [KKKW18, Theorem 2].
Asynchronous Bounded Value Iteration: To tackle the state space explosion problem, asynchronous simulation/learning-based algorithms have been developed [MLG05, BCC+14, KKKW18]. The idea is not to update and deflate all states at once, since there might be too many, or since we only have limited information. Instead of considering the whole state space, a path through the SG is sampled by picking in every state one of the actions that look optimal according to the current over-/under-approximation and then sampling a successor of that action. This is repeated until either a target is found, or until the simulation is looping in an EC; the latter case occurs if the heuristic that picks the actions generates a pair of strategies under which both players only pick staying actions in an EC. After the simulation, only the bounds of the states on the path are updated and deflated. Since we pick actions which look optimal in the simulation, we almost surely find an \(\epsilon \)-optimal strategy and the algorithm terminates [BCC+14, Theorem 3].
3 Algorithm
3.1 Model-Based
Given only limited information, updating cannot be done using  , since the true probabilities are not known. The approach of [BCC+14] is to sample for a high number of steps and accumulate the observed lower and upper bounds on the true value function for each state-action pair. When the number of samples is large enough, the average of the accumulator is used as the new estimate for the state-action pair, and thus the approximations can be improved and the results back-propagated, while giving statistical guarantees that each update was correct. However, this approach has several drawbacks, the biggest of which is that the number of steps before an update can occur is infeasibly large, often larger than the age of the universe, see Table 1 in Sect. 4.
, since the true probabilities are not known. The approach of [BCC+14] is to sample for a high number of steps and accumulate the observed lower and upper bounds on the true value function for each state-action pair. When the number of samples is large enough, the average of the accumulator is used as the new estimate for the state-action pair, and thus the approximations can be improved and the results back-propagated, while giving statistical guarantees that each update was correct. However, this approach has several drawbacks, the biggest of which is that the number of steps before an update can occur is infeasibly large, often larger than the age of the universe, see Table 1 in Sect. 4.
Our improvements to make the algorithm practically usable are linked to constructing a partial model of the given system. That way, we have more information available on which we can base our estimates, and we can be less conservative when giving bounds on the possible errors. The shift from model-free to model-based learning asymptotically increases the memory requirements from  (as in [SLW+06, BCC+14]) to
(as in [SLW+06, BCC+14]) to  . However, for systems where each action has a small constant bound on the number of successors, which is typical for many practical systems, e.g. classical PRISM benchmarks, it is still
. However, for systems where each action has a small constant bound on the number of successors, which is typical for many practical systems, e.g. classical PRISM benchmarks, it is still  with a negligible constant difference.
with a negligible constant difference.
We thus track the number of times some successor \(\mathsf {t}\) has been observed when playing action  from state
from state  in a variable
in a variable  . This implicitly induces the number of times each state-action pair
. This implicitly induces the number of times each state-action pair  has been played
has been played  . Given these numbers we can then calculate probability estimates for every transition as described in the next subsection. They also induce the set of all states visited so far, allowing us to construct a partial model of the game. See [AKW19, Appendix A.2] for the pseudo-code of how to count the occurrences during the simulations.
. Given these numbers we can then calculate probability estimates for every transition as described in the next subsection. They also induce the set of all states visited so far, allowing us to construct a partial model of the game. See [AKW19, Appendix A.2] for the pseudo-code of how to count the occurrences during the simulations.
A running example of an \(\text {SG}\). The dashed part is only relevant for the later examples. For actions with only one successor, we do not depict the transition probability 1 (e.g.  ). For state-action pair \((\mathsf {s_1,b_2})\), the transition probabilities are parameterized and instantiated in the examples where they are used.
). For state-action pair \((\mathsf {s_1,b_2})\), the transition probabilities are parameterized and instantiated in the examples where they are used.
3.2 Safe Updates with Confidence Intervals Using Distributed Error Probability
We use the counters to compute a lower estimate of the transition probability for some error tolerance  as follows: We view sampling \(\mathsf {t}\) from state-action pair
as follows: We view sampling \(\mathsf {t}\) from state-action pair  as a Bernoulli sequence, with success probability
as a Bernoulli sequence, with success probability  , the number of trials
, the number of trials  and the number of successes
and the number of successes  . The tightest lower estimate we can give using the Hoeffding bound (see [AKW19, Appendix D.1]) is
. The tightest lower estimate we can give using the Hoeffding bound (see [AKW19, Appendix D.1]) is

where the confidence width  . Since c could be greater than 1, we limit the lower estimate to be at least 0. Now we can give modified update equations:
. Since c could be greater than 1, we limit the lower estimate to be at least 0. Now we can give modified update equations:

The idea is the same for both upper and lower bound: In contrast to the usual Bellman equation (see Sect. 2.2) we use  instead of
instead of  . But since the sum of all the lower estimates does not add up to one, there is some remaining probability for which we need to under-/over-approximate the value it can achieve. We use the safe approximations 0 and 1 for the lower and upper bound respectively; this is why in
. But since the sum of all the lower estimates does not add up to one, there is some remaining probability for which we need to under-/over-approximate the value it can achieve. We use the safe approximations 0 and 1 for the lower and upper bound respectively; this is why in  there is no second term and in
there is no second term and in  the whole remaining probability is added. Algorithm 2 shows the modified update that uses the lower estimates; the proof of its correctness is in [AKW19, Appendix D.2].
the whole remaining probability is added. Algorithm 2 shows the modified update that uses the lower estimates; the proof of its correctness is in [AKW19, Appendix D.2].
Lemma 1
(\(\mathsf {UPDATE}\) is correct). Given correct under- and over-approximations  of the value function
of the value function  , and correct lower probability estimates
, and correct lower probability estimates  , the under- and over-approximations after an application of \(\mathsf {UPDATE}\) are also correct.
, the under- and over-approximations after an application of \(\mathsf {UPDATE}\) are also correct.

Example 1
We illustrate how the calculation works and its huge advantage over the approach from [BCC+14] on the SG from Fig. 1. For this example, ignore the dashed part and let \(\mathsf {p_1}=\mathsf {p_2}=0.5\), i.e. we have no self loop, and an even chance to go to the target  or a sink \(\mathfrak {0}\). Observe that hence
or a sink \(\mathfrak {0}\). Observe that hence  .
.
Given an error tolerance of \(\delta =0.1\), the algorithm of [BCC+14] would have to sample for more than \(10^{9}\) steps before it could attempt a single update. In contrast, assume we have seen 5 samples of action \(\mathsf b_2\), where 1 of them went to  and 4 of them to \(\mathfrak {0}\). Note that, in a sense, we were unlucky here, as the observed averages are very different from the actual distribution. The confidence width for
and 4 of them to \(\mathfrak {0}\). Note that, in a sense, we were unlucky here, as the observed averages are very different from the actual distribution. The confidence width for  and 5 samples is \(\sqrt{\ln (0.1)/-2 \cdot 5} \approx 0.48\). So given that data, we get
and 5 samples is \(\sqrt{\ln (0.1)/-2 \cdot 5} \approx 0.48\). So given that data, we get  and
and  . Note that both probabilities are in fact lower estimates for their true counterpart.
. Note that both probabilities are in fact lower estimates for their true counterpart.
Assume we already found out that \(\mathfrak {0}\) is a sink with value 0; how we gain this knowledge is explained in the following subsections. Then, after getting only these 5 samples, \(\mathsf {UPDATE}\) already decreases the upper bound of \((\mathsf {s_1,b_2})\) to 0.68, as we know that at least 0.32 of  goes to the sink.
goes to the sink.
Given 500 samples of action \(\mathsf {b_2}\), the confidence width of the probability estimates already has decreased below 0.05. Then, since we have this confidence width for both the upper and the lower bound, we can decrease the total precision for \((\mathsf {s_1,b_2})\) to 0.1, i.e. return an interval in the order of [0.45; 0.55].

Summing up: with the model-based approach we can already start updating after very few steps and get a reasonable level of confidence with a realistic number of samples. In contrast, the state-of-the-art approach of [BCC+14] needs a very large number of samples even for this toy example.
Since for \(\mathsf {UPDATE}\) we need an error tolerance for every transition, we need to distribute the given total error tolerance \(\delta \) over all transitions in the current partial model. For all states in the explored partial model  we know the number of available actions and can over-approximate the number of successors as \(\frac{1}{p_{\min }}\). Thus the error tolerance for each transition can be set to
we know the number of available actions and can over-approximate the number of successors as \(\frac{1}{p_{\min }}\). Thus the error tolerance for each transition can be set to  . This is illustrated in Example 4 in [AKW19, Appendix B].
. This is illustrated in Example 4 in [AKW19, Appendix B].
Note that the fact that the error tolerance  for every transition is the same does not imply that the confidence width for every transition is the same, as the latter becomes smaller with increasing number of samples
for every transition is the same does not imply that the confidence width for every transition is the same, as the latter becomes smaller with increasing number of samples  .
.
3.3 Improved EC Detection
As mentioned in the description of Algorithm 1, we must detect when the simulation is stuck in a bottom EC and looping forever. However, we may also stop simulations that are looping in some EC but still have a possibility to leave it; for a discussion of different heuristics from [BCC+14, KKKW18], see [AKW19, Appendix A.3].
We choose to define \(\mathsf {LOOPING}\) as follows: Given a candidate for a bottom EC, we continue sampling until we are  (i.e. the error probability is smaller than
(i.e. the error probability is smaller than  ) that we cannot leave it. Then we can safely deflate the EC, i.e. decrease all upper bounds to zero.
) that we cannot leave it. Then we can safely deflate the EC, i.e. decrease all upper bounds to zero.
To detect that something is a  EC, we do not sample for the astronomical number of steps as in [BCC+14], but rather extend the approach to detect bottom strongly connected components from [DHKP16]. If in the EC-candidate T there was some state-action pair
EC, we do not sample for the astronomical number of steps as in [BCC+14], but rather extend the approach to detect bottom strongly connected components from [DHKP16]. If in the EC-candidate T there was some state-action pair  that actually has a probability to exit the T, that probability is at least \(p_{\min }\). So after sampling
that actually has a probability to exit the T, that probability is at least \(p_{\min }\). So after sampling  for n times, the probability to overlook such a leaving transition is \((1-p_{\min })^n\) and it should be smaller than
for n times, the probability to overlook such a leaving transition is \((1-p_{\min })^n\) and it should be smaller than  . Solving the inequation for the required number of samples n yields
. Solving the inequation for the required number of samples n yields  .
.
Algorithm 3 checks that we have seen all staying state-action pairs n times, and hence that we are  that T is an EC. Note that we restrict to staying state-action pairs, since the requirement for an EC is only that there exist staying actions, not that all actions stay. We further speed up the EC-detection, because we do not wait for n samples in every simulation, but we use the aggregated counters that are kept over all simulations.
that T is an EC. Note that we restrict to staying state-action pairs, since the requirement for an EC is only that there exist staying actions, not that all actions stay. We further speed up the EC-detection, because we do not wait for n samples in every simulation, but we use the aggregated counters that are kept over all simulations.

We stop a simulation, if \(\mathsf {LOOPING}\) returns true, i.e. under the following three conditions: (i) We have seen the current state before in this simulation ( ), i.e. there is a cycle. (ii) This cycle is explainable by an EC T in our current partial model. (iii) We are
), i.e. there is a cycle. (ii) This cycle is explainable by an EC T in our current partial model. (iii) We are  that T is an EC.
that T is an EC.

Example 2
For this example, we again use the SG from Fig. 1 without the dashed part, but this time with \(\mathsf {p_1}=\mathsf {p_2}=\mathsf {p_3}=\frac{1}{3}\). Assume the path we simulated is \((\mathsf {s_0,a_1,s_1,b_2,s_1})\), i.e. we sampled the self-loop of action \(\mathsf b_2\). Then  is a candidate for an EC, because given our current observation it seems possible that we will continue looping there forever. However, we do not stop the simulation here, because we are not yet
is a candidate for an EC, because given our current observation it seems possible that we will continue looping there forever. However, we do not stop the simulation here, because we are not yet  about this. Given
about this. Given  , the required samples for that are 6, since \(\frac{\ln (0.1)}{\ln (1-\frac{1}{3})} = 5.6\). With high probability (greater than
, the required samples for that are 6, since \(\frac{\ln (0.1)}{\ln (1-\frac{1}{3})} = 5.6\). With high probability (greater than  ), within these 6 steps we will sample one of the other successors of \((\mathsf {s_1,b_2})\) and thus realise that we should not stop the simulation in \(\mathsf {s_1}\). If, on the other hand, we are in state \(\mathfrak {0}\) or if in state \(\mathsf {s_1}\) the guiding heuristic only picks \(\mathsf {b_1}\), then we are in fact looping for more than 6 steps, and hence we stop the simulation.
), within these 6 steps we will sample one of the other successors of \((\mathsf {s_1,b_2})\) and thus realise that we should not stop the simulation in \(\mathsf {s_1}\). If, on the other hand, we are in state \(\mathfrak {0}\) or if in state \(\mathsf {s_1}\) the guiding heuristic only picks \(\mathsf {b_1}\), then we are in fact looping for more than 6 steps, and hence we stop the simulation.

3.4 Adapting to Games: Deflating MSECs
To extend the algorithm of [BCC+14] to SGs, instead of collapsing problematic ECs we deflate them as in [KKKW18], i.e. given an MSEC, we reduce the upper bound of all states in it to the upper bound of the  of Maximizer. In contrast to [KKKW18], we cannot use the upper bound of the
of Maximizer. In contrast to [KKKW18], we cannot use the upper bound of the  based on the true probability, but only based on our estimates. Algorithm 5 shows how to deflate an MSEC and highlights the difference, namely that we use
based on the true probability, but only based on our estimates. Algorithm 5 shows how to deflate an MSEC and highlights the difference, namely that we use  instead of
instead of  .
.

The remaining question is how to find MSECs. The approach of [KKKW18] is to find MSECs by removing the suboptimal actions of Minimizer according to the current lower bound. Since it converges to the true value function, all MSECs are eventually found [KKKW18, Lemma 2]. Since Algorithm 6 can only access the SG as a black box, there are two differences: We can only compare our estimates of the lower bound  to find out which actions are suboptimal. Additionally there is the problem that we might overlook an exit from an EC, and hence deflate to some value that is too small; thus we need to check that any state set \(\mathsf {FIND\_MSECs}\) returns is a
to find out which actions are suboptimal. Additionally there is the problem that we might overlook an exit from an EC, and hence deflate to some value that is too small; thus we need to check that any state set \(\mathsf {FIND\_MSECs}\) returns is a  EC. This is illustrated in Example 3. For a bigger example of how all our functions work together, see Example 5 in [AKW19, Appendix B].
EC. This is illustrated in Example 3. For a bigger example of how all our functions work together, see Example 5 in [AKW19, Appendix B].

Example 3
For this example, we use the full SG from Fig. 1, including the dashed part, with \(\mathsf {p_1,p_2} > 0\). Let  be the path generated by our simulation. Then in our partial view of the model, it seems as if
be the path generated by our simulation. Then in our partial view of the model, it seems as if  is an MSEC, since using \(\mathsf a_2\) is suboptimal for the minimizing state \(\mathsf {s_0}\)Footnote 6 and according to our current knowledge \(\mathsf {a_1,b_1}\) and \(\mathsf b_2\) all stay inside T. If we deflated T now, all states would get an upper bound of 0, which would be incorrect.
is an MSEC, since using \(\mathsf a_2\) is suboptimal for the minimizing state \(\mathsf {s_0}\)Footnote 6 and according to our current knowledge \(\mathsf {a_1,b_1}\) and \(\mathsf b_2\) all stay inside T. If we deflated T now, all states would get an upper bound of 0, which would be incorrect.
Thus in Algorithm 6 we need to require that T is an EC  . This was not satisfied in the example, as the state-action pairs have not been observed the required number of times. Thus we do not deflate T, and our upper bounds stay correct. Having seen \((\mathsf {s_1,b_2})\) the required number of times, we probably know that it is exiting T and hence will not make the mistake.
. This was not satisfied in the example, as the state-action pairs have not been observed the required number of times. Thus we do not deflate T, and our upper bounds stay correct. Having seen \((\mathsf {s_1,b_2})\) the required number of times, we probably know that it is exiting T and hence will not make the mistake.

3.5 Guidance and Statistical Guarantee
It is difficult to give statistical guarantees for the algorithm we have developed so far (i.e. Algorithm 1 calling the new functions from Sects. 3.2, 3.3 and 3.4). Although we can bound the error of each function, applying them repeatedly can add up the error. Algorithm 7 shows our approach to get statistical guarantees: It interleaves a guided simulation phase (Lines 7–10) with a guaranteed standard bounded value iteration (called BVI phase) that uses our new functions (Lines 11–16).
The simulation phase builds the partial model by exploring states and remembering the counters. In the first iteration of the main loop, it chooses actions randomly. In all further iterations, it is guided by the bounds that the last BVI phase computed. After \(\mathcal {N}_k\) simulations (see below for a discussion of how to choose \(\mathcal {N}_k\)), all the gathered information is used to compute one version of the partial model with probability estimates  for a certain error tolerance \(\delta _{k}\). We can continue with the assumption, that these probability estimates are correct, since it is only violated with a probability smaller than our error tolerance (see below for an explanation of the choice of \(\delta _{k}\)). So in our correct partial model, we re-initialize the lower and upper bound (Line 12), and execute a guaranteed standard BVI. If the simulation phase already gathered enough data, i.e. explored the relevant states and sampled the relevant transitions often enough, this BVI achieves a precision smaller than \(\varepsilon \) in the initial state, and the algorithm terminates. Otherwise we start another simulation phase that is guided by the improved bounds.
for a certain error tolerance \(\delta _{k}\). We can continue with the assumption, that these probability estimates are correct, since it is only violated with a probability smaller than our error tolerance (see below for an explanation of the choice of \(\delta _{k}\)). So in our correct partial model, we re-initialize the lower and upper bound (Line 12), and execute a guaranteed standard BVI. If the simulation phase already gathered enough data, i.e. explored the relevant states and sampled the relevant transitions often enough, this BVI achieves a precision smaller than \(\varepsilon \) in the initial state, and the algorithm terminates. Otherwise we start another simulation phase that is guided by the improved bounds.

Choice of \(\delta _{k}\): For each of the full BVI phases, we construct a partial model that is correct with probability \((1-\delta _{k})\). To ensure that the sum of these errors is not larger than the specified error tolerance \(\delta \), we use the variable k, which is initialised to 1 and doubled in every iteration of the main loop. Hence for the i-th BVI, \(k = 2^{i}\). By setting \(\delta _{k}= \frac{\delta }{k}\), we get that \(\displaystyle \sum _{i=1}^{\infty } \delta _{k}= \displaystyle \sum _{i=1}^{\infty } \frac{\delta }{2^{i}} = \delta \), and hence the error of all BVI phases does not exceed the specified error tolerance.
When to Stop Each BVI-Phase: The BVI phase might not converge if the probability estimates are not good enough. We increase the number of iterations for each BVI depending on k, because that way we ensure that it eventually is allowed to run long enough to converge. On the other hand, since we always run for finitely many iterations, we also ensure that, if we do not have enough information yet, BVI is eventually stopped. Other stopping criteria could return arbitrarily imprecise results [HM17]. We also multiply with  to improve the chances of the early BVIs to converge, as that number of iterations ensures that every value has been propagated through the whole model at least once.
to improve the chances of the early BVIs to converge, as that number of iterations ensures that every value has been propagated through the whole model at least once.
Discussion of the Choice of \(\mathcal {N}_k\): The number of simulations between the guaranteed BVI phases can be chosen freely; it can be a constant number every time, or any sequence of natural numbers, possibly parameterised by e.g. k,  , \(\varepsilon \) or any of the parameters of
, \(\varepsilon \) or any of the parameters of  . The design of particularly efficient choices or learning mechanisms that adjust them on the fly is an interesting task left for future work. We conjecture the answer depends on the given SG and “task” that the user has for the algorithm: E.g. if one just needs a quick general estimate of the behaviour of the model, a smaller choice of \(\mathcal {N}_k\) is sensible; if on the other hand a definite precision \(\varepsilon \) certainly needs to be achieved, a larger choice of \(\mathcal {N}_k\) is required.
. The design of particularly efficient choices or learning mechanisms that adjust them on the fly is an interesting task left for future work. We conjecture the answer depends on the given SG and “task” that the user has for the algorithm: E.g. if one just needs a quick general estimate of the behaviour of the model, a smaller choice of \(\mathcal {N}_k\) is sensible; if on the other hand a definite precision \(\varepsilon \) certainly needs to be achieved, a larger choice of \(\mathcal {N}_k\) is required.
Theorem 1
For any choice of sequence for \(\mathcal {N}_k\), Algorithm 7 is an anytime algorithm with the following property: When it is stopped, it returns an interval for  that is PACFootnote 7 for the given error tolerance \(\delta \) and some \(\varepsilon '\), with \(0 \le \varepsilon ' \le ~1\).
that is PACFootnote 7 for the given error tolerance \(\delta \) and some \(\varepsilon '\), with \(0 \le \varepsilon ' \le ~1\).
Theorem 1 is the foundation of the practical usability of our algorithm. Given some time frame and some \(\mathcal {N}_k\), it calculates an approximation for  that is probably correct. Note that the precision \(\varepsilon '\) is independent of the input parameter \(\varepsilon \), and could in the worst case be always 1. However, practically it often is good (i.e. close to 0) as seen in the results in Sect. 4. Moreover, in our modified algorithm, we can also give a convergence guarantee as in [BCC+14]. Although mostly out of theoretical interest, in [AKW19, Appendix D.4] we design such a sequence \(\mathcal {N}_k\), too. Since this a-priori sequence has to work in the worst case, it depends on an infeasibly large number of simulations.
that is probably correct. Note that the precision \(\varepsilon '\) is independent of the input parameter \(\varepsilon \), and could in the worst case be always 1. However, practically it often is good (i.e. close to 0) as seen in the results in Sect. 4. Moreover, in our modified algorithm, we can also give a convergence guarantee as in [BCC+14]. Although mostly out of theoretical interest, in [AKW19, Appendix D.4] we design such a sequence \(\mathcal {N}_k\), too. Since this a-priori sequence has to work in the worst case, it depends on an infeasibly large number of simulations.
Theorem 2
There exists a choice of \(\mathcal {N}_k\), such that Algorithm 7 is PAC for any input parameters \(\varepsilon , \delta \), i.e. it terminates almost surely and returns an interval for  of width smaller than \(\varepsilon \) that is correct with probability at least \(1-\delta \).
of width smaller than \(\varepsilon \) that is correct with probability at least \(1-\delta \).
3.6 Utilizing the Additional Information of Grey Box Input
In this section, we consider the grey box setting, i.e. for every state-action pair  we additionally know the exact number of successors
we additionally know the exact number of successors  . Then we can sample every state-action pair until we have seen all successors, and hence this information amounts to having qualitative information about the transitions, i.e. knowing where the transitions go, but not with which probability.
. Then we can sample every state-action pair until we have seen all successors, and hence this information amounts to having qualitative information about the transitions, i.e. knowing where the transitions go, but not with which probability.
In that setting, we can improve the EC-detection and the estimated bounds in \(\mathsf {UPDATE}\). For EC-detection, note that the whole point of  is to check whether there are further transitions available; in grey box, we know this and need not depend on statistics. For the bounds, note that the equations for
is to check whether there are further transitions available; in grey box, we know this and need not depend on statistics. For the bounds, note that the equations for  and
and  both have two parts: The usual Bellman part and the remaining probability multiplied with the most conservative guess of the bound, i.e. 0 and 1. If we know all successors of a state-action pair, we do not have to be as conservative; then we can use
both have two parts: The usual Bellman part and the remaining probability multiplied with the most conservative guess of the bound, i.e. 0 and 1. If we know all successors of a state-action pair, we do not have to be as conservative; then we can use  respectively
respectively  . Both these improvements have huge impact, as demonstrated in Sect. 4. However, of course, they also assume more knowledge about the model.
. Both these improvements have huge impact, as demonstrated in Sect. 4. However, of course, they also assume more knowledge about the model.
4 Experimental Evaluation
We implemented the approach as an extension of PRISM-Games [CFK+13a]. 11 MDPs with reachability properties were selected from the Quantitative Verification Benchmark Set [HKP+19]. Further, 4 stochastic games benchmarks from [CKJ12, SS12, CFK+13b, CKPS11] were also selected. We ran the experiments on a 40 core Intel Xeon server running at 2.20 GHz per core and having 252 GB of RAM. The tool however utilised only a single core and 1 GB of memory for the model checking. Each benchmark was ran 10 times with a timeout of 30 min. We ran two versions of Algorithm 7, one with the SG as a black box, the other as a grey box (see Definition 2). We chose \(\mathcal {N}_k= 10,000\) for all iterations. The tool stopped either when a precision of \(10^{-8}\) was obtained or after 30 min. In total, 16 different model-property combinations were tried out. The results of the experiment are reported in Table 1.
In the black box setting, we obtained \(\varepsilon < 0.1\) on 6 of the benchmarks. 5 benchmarks were ‘hard’ and the algorithm did not improve the precision below 1. For 4 of them, it did not even finish the first simulation phase. If we decrease \(\mathcal {N}_k\), the BVI phase is entered, but still no progress is made.
In the grey box setting, on 14 of 16 benchmarks, it took only 6 min to achieve \(\varepsilon < 0.1\). For 8 these, the exact value was found within that time. Less than 50% of the state space was explored in the case of pacman, pneuli-zuck-3, rabin-3, zeroconf and cloud_5. A precision of \(\varepsilon < 0.01\) was achieved on 15/16 benchmarks over a period of 30 min.
Figure 2 shows the evolution of the lower and upper bounds in both the grey- and the black box settings for 4 different models. Graphs for the other models as well as more details on the results are in [AKW19, Appendix C].
Performance of our algorithm on various MDP and SG benchmarks in grey and black box settings. Solid lines denote the bounds in the grey box setting while dashed lines denote the bounds in the black box setting. The plotted bounds are obtained after each partial BVI phase, because of which they do not start at [0, 1] and not at time 0. Graphs of the remaining benchmarks may be found in [AKW19, Appendix C].
5 Conclusion
We presented a PAC SMC algorithm for SG (and MDP) with the reachability objective. It is the first one for SG and the first practically applicable one. Nevertheless, there are several possible directions for further improvements. For instance, one can consider different sequences for lengths of the simulation phases, possibly also dependent on the behaviour observed so far. Further, the error tolerance could be distributed in a non-uniform way, allowing for fewer visits in rarely visited parts of end components. Since many systems are strongly connected, but at the same time feature some infrequent behaviour, this is the next bottleneck to be attacked. [KM19]
Notes
- 1.
I.e.,
 ,
, 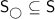 ,
, 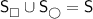 , and
, and  .
. - 2.
The names are chosen, because Maximizer maximizes the probability of reaching a given target state, and Minimizer minimizes it.
- 3.
Up to this point, this definition conforms to black box systems in the sense of [SVA04] with sampling from the initial state, being slightly stricter than [YS02a] or [RP09], where simulations can be run from any desired state. Further, we assume that we can choose actions for the adversarial player or that she plays fairly. Otherwise the adversary could avoid playing her best strategy during the SMC, not giving SMC enough information about her possible behaviours.
- 4.
This requirement is slightly weaker than the knowledge of the whole topology, i.e.
 for each
for each  and
and  .
. - 5.
Since we mainly talk about simulation based algorithms, we included this line to make their structure clearer.
- 6.
For
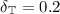 , sampling the path to target once suffices to realize that
, sampling the path to target once suffices to realize that  .
. - 7.
Probably Approximately Correct, i.e. with probability greater than \(1-\delta \), the value lies in the returned interval of width \(\varepsilon '\).
References
Ashok, P., Křetínský, J.: Maximilian Weininger. PAC statistical model checking for markov decision processes and stochastic games. Technical Report arXiv.org/abs/1905.04403 (2019)
Basu, A., Bensalem, S., Bozga, M., Caillaud, B., Delahaye, B., Legay, A.: Statistical abstraction and model-checking of large heterogeneous systems. In: Hatcliff, J., Zucca, E. (eds.) FMOODS/FORTE 2010. LNCS, vol. 6117, pp. 32–46. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13464-7_4
Brázdil, T., et al.: Verification of markov decision processes using learning algorithms. In: Cassez, F., Raskin, J.-F. (eds.) ATVA 2014. LNCS, vol. 8837, pp. 98–114. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11936-6_8
Boyer, B., Corre, K., Legay, A., Sedwards, S.: PLASMA-lab: a flexible, distributable statistical model checking library. In: Joshi, K., Siegle, M., Stoelinga, M., DArgenio, P.R. (eds.) QEST 2013. LNCS, vol. 8054, pp. 160–164. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40196-1_12
Bulychev, P.E., et al.: UPPAAL-SMC: statistical model checking for priced timed automata. In: QAPL (2012)
Bogdoll, J., Ferrer Fioriti, L.M., Hartmanns, A., Hermanns, H.: Partial order methods for statistical model checking and simulation. In: Bruni, R., Dingel, J. (eds.) FMOODS/FORTE 2011. LNCS, vol. 6722, pp. 59–74. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21461-5_4
Bogdoll, J., Hartmanns, A., Hermanns, H.: Simulation and statistical model checking for modestly nondeterministic models. In: Schmitt, J.B. (ed.) MMB&DFT 2012. LNCS, vol. 7201, pp. 249–252. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28540-0_20
Baier, C., Katoen, J.-P.: Principles of Model Checking. MIT Press (2008). ISBN 978-0-262-02649-9
Brafman, R.I., Tennenholtz, M.: A near-optimal poly-time algorithm for learning a class of stochastic games. In: IJCAI, pp. 734–739 (1999)
Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., Simaitis, A.: PRISM-games: a model checker for stochastic multi-player games. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 185–191. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_13
Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., Simaitis, A.: Automatic verification of competitive stochastic systems. Formal Meth. Syst. Des. 43(1), 61–92 (2013)
Chatterjee, K., Henzinger, T.A.: Value iteration. In: Grumberg, O., Veith, H. (eds.) 25 Years of Model Checking. LNCS, vol. 5000, pp. 107–138. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69850-0_7
Chatterjee, K., Henzinger, T.A.: A survey of stochastic \(\omega \)-regular games. J. Comput. Syst. Sci. 78(2), 394–413 (2012)
Calinescu, R., Kikuchi, S., Johnson, K.: Compositional reverification of probabilistic safety properties for large-scale complex IT systems. In: Calinescu, R., Garlan, D. (eds.) Monterey Workshop 2012. LNCS, vol. 7539, pp. 303–329. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34059-8_16
Chen, T., Kwiatkowska, M., Parker, D., Simaitis, A.: Verifying team formation protocols with probabilistic model checking. In: Leite, J., Torroni, P., Ågotnes, T., Boella, G., van der Torre, L. (eds.) CLIMA 2011. LNCS (LNAI), vol. 6814, pp. 190–207. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22359-4_14
Condon, A.: The complexity of stochastic games. Inf. Comput. 96(2), 203–224 (1992)
Clarke, E.M., Zuliani, P.: Statistical model checking for cyber-physical systems. In: ATVA, pp. 1–12 (2011)
David, A., et al.: Statistical model checking for stochastic hybrid systems. In: HSB, pp. 122–136 (2012)
David, A., Du, D., Guldstrand Larsen, K., Legay, A., Mikučionis, M.: Optimizing control strategy using statistical model checking. In: Brat, G., Rungta, N., Venet, A. (eds.) NFM 2013. LNCS, vol. 7871, pp. 352–367. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38088-4_24
Daca, P., Henzinger, T.A., Křetínský, J., Petrov, T.: Faster statistical model checking for unbounded temporal properties. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 112–129. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_7
D’Argenio, P.R., Hartmanns, A., Sedwards, S.: Lightweight statistical model checking in nondeterministic continuous time. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11245, pp. 336–353. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03421-4_22
David, A., et al.: Statistical model checking for networks of priced timed automata. In: Fahrenberg, U., Tripakis, S. (eds.) FORMATS 2011. LNCS, vol. 6919, pp. 80–96. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24310-3_7
David, A., Larsen, K.G., Legay, A., Mikučionis, M., Wang, Z.: Time for statistical model checking of real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 349–355. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_27
D’Argenio, P., Legay, A., Sedwards, S., Traonouez, L.-M.: Smart sampling for lightweight verification of markov decision processes. STTT 17(4), 469–484 (2015)
Ellen, C., Gerwinn, S., Fränzle, M.: Confidence bounds for statistical model checking of probabilistic hybrid systems. In: Jurdziński, M., Ničković, D. (eds.) FORMATS 2012. LNCS, vol. 7595, pp. 123–138. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33365-1_10
Fu, J., Topcu, U.: Probably approximately correct MDP learning and control with temporal logic constraints. In: Robotics: Science and Systems (2014)
Hasanbeig, M., Abate, A., Kroening, D.: Logically-correct reinforcement learning. CoRR, 1801.08099 (2018)
Hasanbeig, M., Abate, A., Kroening, D.: Certified reinforcement learning with logic guidance. CoRR, abs/1902.00778 (2019)
He, R., Jennings, P., Basu, S., Ghosh, A.P., Wu, H.: A bounded statistical approach for model checking of unbounded until properties. In: ASE, pp. 225–234 (2010)
Hartmanns, A., Klauck, M., Parker, D., Quatmann, T., Ruijters, E.: The quantitative verification benchmark set. In: TACAS 2019 (2019, to appear)
Hérault, T., Lassaigne, R., Magniette, F., Peyronnet, S.: Approximate probabilistic model checking. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 73–84. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24622-0_8
Haddad, S., Monmege, B.: Interval iteration algorithm for MDPs and IMDPs. Theor. Comput. Sci. (2017)
Henriques, D., Martins, J., Zuliani, P., Platzer, A., Clarke, E.M.: Statistical model checking for Markov decision processes. In: QEST, pp. 84–93 (2012)
Hahn, E.M., Perez, M., Schewe, S., Somenzi, F., Trivedi, A., Wojtczak, D.: Omega-regular objectives in model-free reinforcement learning. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 395–412. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_27
Jha, S.K., Clarke, E.M., Langmead, C.J., Legay, A., Platzer, A., Zuliani, P.: A bayesian approach to model checking biological systems. In: Degano, P., Gorrieri, R. (eds.) CMSB 2009. LNCS, vol. 5688, pp. 218–234. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03845-7_15
Jegourel, C., Legay, A., Sedwards, S.: A platform for high performance statistical model checking – PLASMA. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 498–503. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_37
Kelmendi, E., Krämer, J., Křetínský, J., Weininger, M.: Value iteration for simple stochastic games: stopping criterion and learning algorithm. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10981, pp. 623–642. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96145-3_36
Křetínský, J., Meggendorfer, T.: Of cores: a partial-exploration framework for Markov decision processes. Submitted 2019
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Larsen, K.G.: Statistical model checking, refinement checking, optimization,. for stochastic hybrid systems. In: Jurdziński, M., Ničković, D. (eds.) FORMATS 2012. LNCS, vol. 7595, pp. 7–10. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33365-1_2
Guldstrand Larsen, K.: Priced timed automata and statistical model checking. In: Johnsen, E.B., Petre, L. (eds.) IFM 2013. LNCS, vol. 7940, pp. 154–161. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38613-8_11
Littman, M.L.: Markov games as a framework for multi-agent reinforcement learning. In: ICML, pp. 157–163 (1994)
Lakshmivarahan, S., Narendra, K.S.: Learning algorithms for two-person zero-sum stochastic games with incomplete information. Math. Oper. Res. 6(3), 379–386 (1981)
Lassaigne, R., Peyronnet, S.: Probabilistic verification and approximation. Ann. Pure Appl. Logic 152(1–3), 122–131 (2008)
Lassaigne, R., Peyronnet, S.: Approximate planning and verification for large Markov decision processes. In: SAC, pp. 1314–1319, (2012)
Legay, A., Sedwards, S., Traonouez, L.-M.: Scalable verification of markov decision processes. In: Canal, C., Idani, A. (eds.) SEFM 2014. LNCS, vol. 8938, pp. 350–362. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-15201-1_23
Martin, D.A.: Borel determinacy. Ann. Math. 102(2), 363–371 (1975)
Mcmahan, H.B., Likhachev, M., Gordon, G.J.: Bounded real-time dynamic programming: RTDP with monotone upper bounds and performance guarantees. In: In ICML 2005, pp. 569–576 (2005)
Norris, J.R.: Markov Chains. Cambridge University Press, Cambridge (1998)
Palaniappan, S.K., Gyori, B.M., Liu, B., Hsu, D., Thiagarajan, P.S.: Statistical model checking based calibration and analysis of bio-pathway models. In: Gupta, A., Henzinger, T.A. (eds.) CMSB 2013. LNCS, vol. 8130, pp. 120–134. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40708-6_10
Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley, Hoboken (2014)
Raghavan, T.E.S., Filar, J.A.: Algorithms for stochastic games – a survey. Z. Oper. Res. 35(6), 437–472 (1991)
El Rabih, D., Pekergin, N.: Statistical model checking using perfect simulation. In: Liu, Z., Ravn, A.P. (eds.) ATVA 2009. LNCS, vol. 5799, pp. 120–134. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04761-9_11
Sutton, R., Barto, A.: Reinforcement Learning: An Introduction. MIT Press, Cambridge (1998)
Sadigh, D., Kim, E.S., Coogan, S., Sastry, S.S.S., Sanjit, A.: A learning based approach to control synthesis of markov decision processes for linear temporal logic specifications. In: CDC, pp. 1091–1096 (2014)
Strehl, A.L., Li, L., Wiewiora, E., Langford, J., Littman, M.L.: PAC model-free reinforcement learning. In: ICML, pp. 881–888 (2006)
Saffre, F., Simaitis, A.: Host selection through collective decision. ACM Trans. Auton. Adapt. Syst. 7(1), 4:1–4:16 (2012)
Sen, K., Viswanathan, M., Agha, G.: Statistical model checking of black-box probabilistic systems. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 202–215. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_16
Sen, K., Viswanathan, M., Agha, G.: On statistical model checking of stochastic systems. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 266–280. Springer, Heidelberg (2005). https://doi.org/10.1007/11513988_26
Wen, M., Topcu, U.: Probably approximately correct learning in stochastic games with temporal logic specifications. In: IJCAI, pp. 3630–3636 (2016)
Younes, H.L.S., Clarke, E.M., Zuliani, P.: Statistical verification of probabilistic properties with unbounded until. In: Davies, J., Silva, L., Simao, A. (eds.) SBMF 2010. LNCS, vol. 6527, pp. 144–160. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19829-8_10
Younes, H.L.S., Kwiatkowska, M.Z., Norman, G., Parker, D.: Numerical vs. statistical probabilistic model checking. STTT 8(3), 216–228 (2006)
Younes, H.L.S., Simmons, R.G.: Probabilistic verification of discrete event systems using acceptance sampling. In: Brinksma, E., Larsen, K.G. (eds.) CAV 2002. LNCS, vol. 2404, pp. 223–235. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45657-0_17
Zuliani, P., Platzer, A., Clarke, E.M.: Bayesian statistical model checking with application to simulink/stateflow verification. In: HSCC, pp. 243–252 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Ashok, P., Křetínský, J., Weininger, M. (2019). PAC Statistical Model Checking for Markov Decision Processes and Stochastic Games. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11561. Springer, Cham. https://doi.org/10.1007/978-3-030-25540-4_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-25540-4_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25539-8
Online ISBN: 978-3-030-25540-4
eBook Packages: Computer ScienceComputer Science (R0)





 and action
and action  , it can sample a successor
, it can sample a successor  ,
, , an under-approximation of the minimum transition probability.
, an under-approximation of the minimum transition probability.

 ,
, 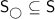 ,
, 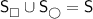 , and
, and  .
. for each
for each  and
and  .
.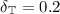 , sampling the path to target once suffices to realize that
, sampling the path to target once suffices to realize that  .
.