Abstract
Stochastic multiplayer games (SMGs) have gained attention in the field of strategy synthesis for multi-agent reactive systems. However, standard SMGs are limited to modeling systems where all agents have full knowledge of the state of the game. In this paper, we introduce delayed-action games (DAGs) formalism that simulates hidden-information games (HIGs) as SMGs, where hidden information is captured by delaying a player’s actions. The elimination of private variables enables the usage of SMG off-the-shelf model checkers to implement HIGs. Furthermore, we demonstrate how a DAG can be decomposed into subgames that can be independently explored, utilizing parallel computation to reduce the model checking time, while alleviating the state space explosion problem that SMGs are notorious for. In addition, we propose a DAG-based framework for strategy synthesis and analysis. Finally, we demonstrate applicability of the DAG-based synthesis framework on a case study of a human-on-the-loop unmanned-aerial vehicle system under stealthy attacks, where the proposed framework is used to formally model, analyze and synthesize security-aware strategies for the system.
This work was supported by the NSF CNS-1652544 grant, as well as the ONR N00014-17-1-2012 and N00014-17-1-2504, and AFOSR FA9550-19-1-0169 awards.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Stochastic multiplayer games (SMGs) are used to model reactive systems where nondeterministic decisions are made by multiple players [4, 13, 23]. SMGs extend probabilistic automata by assigning a player to each choice to be made in the game. This extension enables modeling of complex systems where the behavior of players is unknown at design time. The strategy synthesis problem aims to find a winning strategy, i.e., a strategy that guarantees that a set of objectives (or winning conditions) is satisfied [6, 21]. Algorithms for synthesis include, for instance, value iteration and strategy iteration techniques, where multiple reward-based objectives are satisfied [2, 9, 17]. To tackle the state-space explosion problem, [29] presents an assume-guarantee synthesis framework that relies on synthesizing strategies on the component level first, before composing them into a global winning strategy. Mean-payoffs and ratio rewards are further investigated in [3] to synthesize \(\varepsilon \)-optimal strategies. Formal tools that support strategy synthesis via SMGs include PRISM-games [7, 19] and Uppaal Stratego [10].
SMGs are classified based on the number of players that can make choices at each state. In concurrent games, more than one player is allowed to concurrently make choices at a given state. Conversely, turn-based games assign one player at most to each state. Another classification considers the information available to different players across the game [27]. Complete-information games (also known as perfect-information games [5]) grant all players complete access to the information within the game. In symmetric games, some information is equally hidden from all players. On the contrary, asymmetric games allow some players to have access to more information than the others [27].
This work is motivated by security-aware systems in which stealthy adversarial actions are potentially hidden from the system, where the latter can probabilistically and intermittently gain full knowledge about the current state. While hidden-information games (HIGs) can be used to model such systems by using private variables to capture hidden information [5], standard model checkers can only synthesize strategies for (full-information) SMGs; thus, demanding for alternative representations. The equivalence between turn-based semi-perfect information games and concurrent perfect-information games was shown [5]. Since a player’s strategy mainly rely on full knowledge of the game state [9], using SMGs for synthesis produces strategies that may violate synthesis specifications in cases where required information is hidden from the player. Partially-observable stochastic games (POSGs) allow agents to have different belief states by incorporating uncertainty about both the current state and adversarial plans [15]. Techniques such as active sensing for online replanning [14] and grid-based abstractions of belief spaces [24] were proposed to mitigate synthesis complexity arising from partial observability. The notion of delaying actions has been studied as means for gaining information about a game to improve future strategies [18, 30], but was not deployed as means for hiding information.
To this end, we introduce delayed-action games (DAGs)—a new class of games that simulate HIGs, where information is hidden from one player by delaying the actions of the others. The omission of private variables enables the use of off-the-shelf tools to implement and analyze DAG-based models. We show how DAGs (under some mild and practical assumptions) can be decomposed into subgames that can be independently explored, reducing the time required for synthesis by employing parallel computation. Moreover, we propose a DAG-based framework for strategy synthesis and analysis of security-aware systems. Finally, we demonstrate the framework’s applicability through a case study of security-aware planning for an unmanned-aerial vehicle (UAV) system prone to stealthy cyber attacks, where we develop a DAG-based system model and further synthesize strategies with strong probabilistic security guarantees.
The paper is organized as follows. Section 2 presents SMGs, HIGs, and problem formulation. In Sect. 3, we introduce DAGs and show that they can simulate HIGs. Section 4 proposes a DAG-based synthesis framework, which we use for security-aware planning for UAVs in Sect. 5, before concluding the paper in Sect. 6.
2 Stochastic Games
In this section, we present turn-based stochastic games, which assume that all players have full information about the game state. We then introduce hidden-information games and their private-variable semantics.
Notation. We use \(\mathbb {N}_0\) to denote the set of non-negative integers. \(\mathcal {P}(A)\) denotes the powerset of A (i.e., \(2^A\)). A variable v has a set of valuations \( Ev \left( v\right) \), where \(\eta \left( v\right) \in Ev \left( v\right) \) denotes one. We use \(\varSigma ^*\) to denote the set of all finite words over alphabet \(\varSigma \), including the empty word \(\epsilon \). The mapping  indicates the effect of a finite word on \(\eta \left( v\right) \). Finally, for general indexing, we use \(s_i\) or \(s^{(i)}\), for \(i\in \mathbb {N}_0\), while \(\text{ PL }_\gamma \) denotes Player \(\gamma \).
indicates the effect of a finite word on \(\eta \left( v\right) \). Finally, for general indexing, we use \(s_i\) or \(s^{(i)}\), for \(i\in \mathbb {N}_0\), while \(\text{ PL }_\gamma \) denotes Player \(\gamma \).
Turn-Based Stochastic Games (SMGs). SMGs can be used to model reactive systems that undergo both stochastic and nondeterministic transitions from one state to another. In a turn-based game,Footnote 1 actions can be taken at any state by at most one player. Formally, an SMG can be defined as follows [1, 28, 29].
Definition 1
(Turn-Based Stochastic Game). A turn-based game (SMG) with players \(\varGamma = \{\mathrm{I, II,}\, \bigcirc \}\) is a tuple \(\mathcal {G}= \langle S, (S_\mathrm{I}, S_\mathrm{II}, S_\bigcirc ), A,s_0,\delta \rangle \), where
-
S is a finite set of states, partitioned into \(S_\mathrm{I}\), \(S_\mathrm{II}\) and \(S_\bigcirc \);
-
\(A \!=\!A_\mathrm{I} \cup A_\mathrm{II} \cup \{ \tau \} \) is a finite set of actions where \(\tau \) is an empty action;
-
\(s_0 \in S_\mathrm{II}\) is the initial state; and
-
\(\delta : S \times A \times S \rightarrow [0,1]\) is a transition function, such that \(\delta (s,a,s') \in \{1,0\}\), \(\forall s \in S_\mathrm{I} \cup S_\mathrm{II}, a\in A \) and \(s' \in S\), and \(\delta (s,\tau ,s') \in \left[ 0,1\right] ,~\forall s \in S_\bigcirc \) and \(s' \in S_\mathrm{I} \cup S_\mathrm{II}\), where \(\sum _{s' \in S_\mathrm{I} \cup S_\mathrm{II}}{\delta (s,\tau ,s')} = 1\) holds.
For all \(s \!\in S_\mathrm{I} \cup S_\mathrm{II}\) and \(a \in A_\mathrm{I} \cup A_\mathrm{II} \), we write  if \(\delta (s,a,s') \!=\!1\). Similarly, for all \(s \!\in \! S_{\bigcirc }\) we write
if \(\delta (s,a,s') \!=\!1\). Similarly, for all \(s \!\in \! S_{\bigcirc }\) we write  if \(s^\prime \) is randomly sampled with probability \(p \!=\!\delta (s,\tau ,s')\).
if \(s^\prime \) is randomly sampled with probability \(p \!=\!\delta (s,\tau ,s')\).
Hidden-Information Games. SMGs assume that all players have full knowledge of the current state, and hence provide perfect-information models [5]. In many applications, however, this assumption may not hold. A great example are security-aware models where stealthy adversarial actions can be hidden from the system; e.g., the system may not even be aware that it is under attack. On the other hand, hidden-information games (HIGs) refer to games where one player does not have complete access to (or knowledge of) the current state. The notion of hidden information can be formalized with the use of private variables (PVs) [5]. Specifically, a game state can be encoded using variables \(v_\mathcal {T}\) and \(v_\mathcal {B}\), representing the true information, which is only known to PLI, and PLII belief, respectively.
Definition 2
(Hidden-Information Game). A hidden-information stochastic game (HIG) with players \(\varGamma = \{ \mathrm{I, II,}\, \bigcirc \}\) over a set of variables \(V = \left\{ v_\mathcal {T}, v_\mathcal {B}\right\} \) is a tuple \(\mathcal {G}_{\mathsf {H}}= \langle S, (S_\mathrm{I}, S_\mathrm{II}, S_\bigcirc ), A,s_0, \beta , \delta \rangle \), where
-
set of states \(S \subseteq Ev \left( v_\mathcal {T}\right) \times Ev \left( v_\mathcal {B}\right) \times \mathcal {P} \left( Ev \left( v_\mathcal {T}\right) \right) \times \varGamma \), partitioned in \( S_\mathrm{I}, S_\mathrm{II}\), \( S_\bigcirc \);
-
\(A \!=\!A_\mathrm{I} \cup A_\mathrm{II} \cup \{ \tau , \theta \} \) is a finite set of actions, where \(\tau \) denotes an empty action, and \(\theta \) is the action capturing PLII attempt to reveal the true value \(v_\mathcal {T}\);
-
\(s_0 \in S_\mathrm{II}\) is the initial state;
-
\(\beta :A_\mathrm{II} \!\rightarrow \! \mathcal {P}\! \left( A_I \right) \) is a function that defines the set of available PLI actions, based on PLII action; and
-
\( \delta :S \times A \times S \rightarrow [0,1] \) is a transition function such that \( \delta ( s_\mathrm{I},a, s_\bigcirc )=\) \( \delta ( s_\bigcirc ,a, s_\mathrm{I}) = 0\), and \(\delta (s_\mathrm{II},\theta , s_\bigcirc )\), \( \delta ( s_\mathrm{II},a, s_\mathrm{I})\), \( \delta ( s_\mathrm{I},a, s_\mathrm{II}) \in \left\{ 0, 1 \right\} \) for all \( s_\mathrm{I} \in S_\mathrm{I}\), \( s_\mathrm{II} \in S_\mathrm{II}\), \( s_\bigcirc \in S_\bigcirc \) and \(a \in A\), where \(\sum _{s^\prime \in S_\mathrm{II}}{\delta (s_\bigcirc ,\tau ,s')} \!=\!1\).
In the above definition, \(\delta \) only allows transitions \(s_\mathrm{I}\) to \(s_\mathrm{II}\), \(s_\mathrm{II}\) to \(s_\mathrm{I}\) or \(s_\bigcirc \), with \(s_\mathrm{II}\) to \(s_\bigcirc \) conditioned by action \(\theta \), and probabilistic transitions \(s_\bigcirc \) to \(s_\mathrm{II}\). A game state can be written as \(s = \left( t, u, \varOmega , \gamma \right) \), but to simplify notation we use \(s_{\gamma } \left( t, u, \varOmega \right) \) instead, where \(t \in Ev \left( v_\mathcal {T}\right) \) is the true value of the game, \(u \in Ev \left( v_\mathcal {B}\right) \) is PLII current belief, \(\varOmega \in \mathcal {P}({ Ev \left( v_\mathcal {T}\right) }) \setminus \{ \emptyset \} \) is PLII belief space, and \(\gamma \in \varGamma \) is the current player’s index. When the truth is hidden from PLII, the belief space \(\varOmega \) is the information set [27], capturing PLII knowledge about the possible true values.
Example 1
(Belief vs. True Value). Our motivating example is a system that consists of a UAV and a human operator. For localization, the UAV mainly relies on a GPS sensor that can be compromised to effectively steer the UAV away from its original path. While aggressive attacks can be detected, some may remain stealthy by introducing only bounded errors at each step [16, 20, 22, 26]. For example, Fig. 1 shows a UAV (PLII) occupying zone A and flying north (N). An adversary (PLI) can launch a stealthy attack targeting its GPS, introducing a bounded error (NE, NW) to remain stealthy. The set of stealthy actions available to the attacker depends on the preceding UAV action, which is captured by the function \(\beta \), where \(\beta (\mathsf {N}) \!=\!\lbrace \mathsf {NE}, \mathsf {N}, \mathsf {NW}\rbrace \). Being unaware of the attack, the UAV believes that it is entering zone C, while the true new location is D due to the attack (\(\mathsf {NE}\)). Initially, \(\eta \left( v_{\mathcal {T}}\right) \!=\!\eta \left( v_{\mathcal {B}}\right) \!=\!z_A\), and \(\varOmega \!=\!\{ z_A \}\) as the UAV is certain it is in zone \(z_A\). In \(s_2\), \(\eta \left( v_{\mathcal {B}}\right) \!=\!z_C\), yet \(\eta \left( v_{\mathcal {T}}\right) \!=\!z_D\). Although \(v_{\mathcal {T}}\) is hidden, PLII is aware that \(\eta \left( v_{\mathcal {T}}\right) \) is in \(\varOmega \!=\!\{ z_B, z_C, z_D \}\).
HIG Semantics. \(\mathcal {G}_{\mathsf {H}}\) semantics is described using the rules shown in Fig. 2, where \(\mathsf {H2}\) and \(\mathsf {H3}\) capture PLII and PLI moves, respectively. The rule \(\mathsf {H4}\) specifies that a PLII attempt \(\theta \) to reveal the true value can succeed with probability \(p_i\) where PLII belief is updated (i.e., \(u^\prime = t\)), and remains unchanged otherwise.
Example 2
(HIG Semantics). Continuing Example 1, let us assume that the set of actions \(A_\mathrm{I} = A_\mathrm{II} = \lbrace \mathsf {N},\mathsf {S},\mathsf {E},\mathsf {W},\mathsf {NE},\mathsf {NW},\mathsf {SE},\mathsf {SW} \rbrace \), and that \(\theta \!=\!\mathsf {GT}\) is a geolocation task that attempts to reveal the true value of the game.Footnote 2 Now, consider the scenario illustrated in Fig. 3. At the initial state \(s_0\), the UAV attempts to move north (\(\mathsf {N}\)), progressing the game to the state \(s_1\), where the adversary takes her turn by selecting an action from the set \(\beta (\mathsf {N}) = \lbrace \mathsf {NE}, \mathsf {N}, \mathsf {NW}\rbrace \). The players take turns until the UAV performs a geolocation task \(\mathsf {GT}\), moving from the state \(s_4\) to \(s_5\). With probability \(p = \delta (s_5,\tau ,s_6)\), the UAV detects its true location and updates its belief accordingly (i.e., to \(s_6\)). Otherwise, the belief remains the same (i.e., equal to \(s_4\)).
Problem Formulation. Following the system described in Example 2, we now consider the composed HIG \(\mathcal {G}_{\mathsf {H}}= \mathcal {M}_{\mathrm {adv}} \Vert \mathcal {M}_{\mathrm {uav}} \Vert \mathcal {M}_{\mathrm {as}}\) shown in Fig. 4; the HIG-based model incorporates standard models of a UAV (\(\mathcal {M}_{\mathrm {uav}}\)), an adversary (\(\mathcal {M}_{\mathrm {adv}}\)), and a geolocation-task advisory system (\(\mathcal {M}_{\mathrm {as}}\)) (e.g., as introduced in [11, 12]). Here, the probability of a successful detection \(p(v_\mathcal {T},v_\mathcal {B})\) is a function of both the location the UAV believes to be its current location (\(v_\mathcal {B}\)) as well as the ground truth location that the UAV actually occupies (\(v_\mathcal {T}\)). Reasoning about the flight plan using such model becomes problematic since the ground truth \(v_\mathcal {T}\) is inherently unknown to the UAV (i.e., PLII), and thus so is \(p(v_\mathcal {T},v_\mathcal {B})\). Furthermore, such representation, where some information is hidden, is not supported by off-the-shelf SMG model checkers. Consequently, for such HIGs, our goal is to find an alternative representation that is suitable for strategy synthesis using off-the-shelf SMG model-checkers.
3 Delayed-Action Games
In this section, we provide an alternative representation of HIGs that eliminates the use of private variables—we introduce Delayed-Action Games (DAGs) that exploit the notion of delayed actions. Furthermore, we show that for any HIG, a DAG that simulates the former can be constructed.
Delayed Actions. Informally, a DAG reconstructs an HIG such that actions of PLI (the player with access to perfect information) follow the actions of PLII, i.e., PLI actions are delayed. This rearrangement of the players’ actions provides a means to hide information from PLII without the use of private variables, since in this case, at PLII states, PLI actions have not occurred yet. In this way, PLII can act as though she has complete information at the moment she makes her decision, as the future state has not yet happened and so cannot be known. In essence, the formalism can be seen as a partial ordering of the players’ actions, exploiting the (partial) superposition property that a wide class of physical systems exhibit. To demonstrate this notion, let us consider DAG modeling on our running example.
Example 3
(Delaying Actions). Figure 5 depicts the (HIG-based) scenario from Fig. 3, but in the corresponding DAG, where the UAV actions are performed first (in \(\hat{s}_0,\hat{s}_1,\hat{s}_2\)), followed by the adversary delayed actions (in \(\hat{s}_3,\hat{s}_4\)). Note that, in the DAG model, at the time the UAV executed its actions (\(\hat{s}_0,\hat{s}_1,\hat{s}_2\)) the adversary actions had not occurred (yet). Moreover, \(\hat{s}_0\) and \(\hat{s}_6\) (Fig. 5) share the same belief and true values as \(s_0\) and \(s_6\) (Fig. 3), respectively, though the transient states do not exactly match. This will be used to show the relationship between the games.
The same scenario as in Fig. 3, modeled as a DAG. Solid squares represent UAV belief, while solid diamonds represent the ground truth. The UAV action \(\mathsf {GT}\) denotes performing a geolocation task.
The advantage of this approach is twofold. First, the elimination of private variables enables simulation of an HIG using a full-information game. Thus, the formulation of the strategy synthesis problem using off-the-shelf SMG-based tools becomes feasible. In particular, a PLII synthesized strategy becomes dependent on the knowledge of PLI behavior (possible actions), rather than the specific (hidden) actions. We formalize a DAG as follows.
Definition 3
(Delayed-Action Game). A DAG of an HIG \(\mathcal {G}_{\mathsf {H}}= \langle S, (S_\mathrm{I}, S_\mathrm{II}, S_\bigcirc ), A,s_0, \beta , \delta \rangle \), with players \(\varGamma = \{ \mathrm{I, II,}\,\bigcirc \}\) over a set of variables \(V \!=\!\left\{ v_\mathcal {T}, v_\mathcal {B}\right\} \) is a tuple \(\mathcal {G}_{\mathsf {D}}= \langle \hat{S},(\hat{S}_\mathrm{I}, \hat{S}_\mathrm{II}, \hat{S}_\bigcirc ), A, \hat{s}_0, \beta , \hat{\delta } \rangle \) where
-
\(\hat{S} \subseteq Ev \left( v_\mathcal {T}\right) \times Ev \left( v_\mathcal {B}\right) \times A_\mathrm{II}^* \times \mathbb {N}_0\times \varGamma \) is the set of states, partitioned into \(\hat{S}_\mathrm{I}, \hat{S}_\mathrm{II}\) and \(\hat{S}_\bigcirc \);
-
\(\hat{s}_0 \in \hat{S}_\mathrm{II}\) is the initial state; and
-
\(\hat{\delta } :\hat{S} \times A \times \hat{S} \rightarrow [0,1] \) is a transition function such that \(\hat{\delta } (\hat{s}_\mathrm{II},a,\hat{s}_\bigcirc ) \!=\!\) \(\hat{\delta } (\hat{s}_\mathrm{I},a,\hat{s}_\mathrm{II}) \!=\!\) \(\hat{\delta } (\hat{s}_\bigcirc ,a,\hat{s}_\mathrm{I}) \!=\!0\), and \(\hat{\delta } (\hat{s}_\mathrm{II},a,\hat{s}_\mathrm{II}) \in \left\{ 0, 1 \right\} \), \(\hat{\delta } (\hat{s}_\mathrm{II},\theta ,\hat{s}_\mathrm{I}) \in \left\{ 0, 1 \right\} \), \(\hat{\delta } (\hat{s}_\mathrm{I},a,\hat{s}_\mathrm{I}) \in \left\{ 0, 1 \right\} \), \(\hat{\delta } (\hat{s}_\mathrm{I},a,\hat{s}_\bigcirc ) \in \left\{ 0, 1 \right\} \), for all \(\hat{s}_\mathrm{I} \in \hat{S}_\mathrm{I}\), \(\hat{s}_\mathrm{II} \in \hat{S}_\mathrm{II}\), \(\hat{s}_\bigcirc \in \hat{S}_\bigcirc \) and \(a \in A\), where \(\sum _{\hat{s}^\prime \in \hat{S}_\mathrm{II}}{\delta (\hat{s}_\bigcirc ,a,\hat{s}')} \!=\!1\).
Note that, in contrast to transition function \(\delta \) in HIG \(\mathcal {G}_{\mathsf {H}}\), \(\hat{\delta }\) in DAG \(\mathcal {G}_{\mathsf {D}}\) only allows transitions \(\hat{s}_\mathrm{II}\) to \(\hat{s}_\mathrm{II}\) or \(\hat{s}_\mathrm{I}\), as well as \(\hat{s}_\mathrm{I}\) to \(\hat{s}_\mathrm{I}\) or \(\hat{s}_\bigcirc \), and probabilistic transitions \(\hat{s}_\bigcirc \) to \(\hat{s}_\mathrm{II}\); also note that \(\hat{s}_\mathrm{II}\) to \(\hat{s}_\mathrm{I}\) is conditioned by the action \(\theta \).
DAG Semantics. A DAG state is a tuple \(\hat{s} \!=\!\left( \hat{t}, \hat{u}, w, j, \gamma \right) \), which for simplicity we shorthand as \(\hat{s}_\gamma \left( \hat{t}, \hat{u}, w, j \right) \), where \(\hat{t} \in Ev \left( v_\mathcal {T}\right) \) is the last known true value, \(\hat{u} \in Ev \left( v_\mathcal {B}\right) \) is PLII belief, \(w \in A_\mathrm{II}^*\) captures PLII actions taken since the last known true value, \( j \in \mathbb {N}_0\) is an index on w, and \(\gamma \in \varGamma \) is the current player index. The game transitions are defined using the semantic rules from Fig. 6. Note that PLII can execute multiple moves (i.e., actions) before executing \(\theta \) to attempt to reveal the true value (\(\mathsf {D2}\)), moving to a PLI state where PLI executes all her delayed actions before reaching a ‘revealing’ state \(\hat{s}_\bigcirc \) (\(\mathsf {D3}\)). Finally, the revealing attempt can succeed with probability \(p_i\) where PLII belief is updated (i.e., \(\hat{u}^\prime \!=\!\hat{t}\,\)), or otherwise remains unchanged (\(\mathsf {D4}\)).
In both \(\mathcal {G}_{\mathsf {H}}\) and \(\mathcal {G}_{\mathsf {D}}\), we label states where all players have full knowledge of the current state as proper. We also say that two states are similar if they agree on the belief, and equivalent if they agree on both the belief and ground truth.
Definition 4
(States). Let \(s_\gamma (t,u,\varOmega )\in S\) and \(\hat{s}_{\hat{\gamma }} (\hat{t}, \hat{u}, w,j) \in \hat{S}\). We say:
-
\(s_\gamma \) is proper iff \(\varOmega = \{t\}\), denoted by \(s_\gamma \in \mathrm {Prop}(\mathcal {G}_{\mathsf {H}})\).
-
\(\hat{s}_{\hat{\gamma }}\) is proper iff \(w = \epsilon \), denoted by \(\hat{s}_{\hat{\gamma }} \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}})\).
-
\(s_\gamma \) and \(\hat{s}_{\hat{\gamma }}\) are similar iff \(\hat{u} = u\), \(\hat{t} \in \varOmega \), and \(\gamma =\hat{\gamma }\), denoted by \(s _\gamma \sim \hat{s}_{\hat{\gamma }}\).
-
\(s_\gamma \), \(\hat{s}_{\hat{\gamma }}\) are equivalent iff \(t = \hat{t}\), \(u = \hat{u}\), \(w=\epsilon \), and \(\gamma =\hat{\gamma }\), denoted by \(s_\gamma \simeq \hat{s}_{\hat{\gamma }}\).
From the above definition, we have that \(s \simeq \hat{s} \implies s \in \mathrm {Prop}(\mathcal {G}_{\mathsf {H}}), \hat{s} \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}})\). We now define execution fragments, possible progressions from a state to another.
Definition 5
(Execution Fragment). An execution fragment (of either an SMG, DAG or HIG) is a finite sequence of states, actions and probabilities
\(\varrho = s_0 a_1 p_1 s_1 a_2 p_2 s_2 \ldots a_n p_n s_n \) such that  .Footnote 3
.Footnote 3
We use \( first (\varrho )\) and \( last (\varrho )\) to refer to the first and last states of \(\varrho \), respectively. If both states are proper, we say that \(\varrho \) is proper as well, denoted by \(\varrho \in \mathrm {Prop}(\mathcal {G}_{\mathsf {H}})\).Footnote 4 Moreover, \(\varrho \) is deterministic if no probabilities appear in the sequence.
Definition 6
(Move). A move \(m_\gamma \) of an execution \(\varrho \) from state \(s\in \varrho \), denoted by \( move _\gamma (s,\varrho )\), is a sequence of actions \(a_1 a_2 \ldots a_i \in A_\gamma ^*\) that player \(\gamma \) performs in \(\varrho \) starting from s.
By omitting the player index we refer to the moves of all players. To simplify notation, we use \( move (\varrho )\) as a short notation for \( move ( first (\varrho ),\varrho )\). We write \((m)( first (\varrho )) = last (\varrho )\) to denote that the execution of move m from the \( first (\varrho )\) leads to the \( last (\varrho )\). This allows us to now define the delay operator as follows.
Definition 7
(Delay Operator). For an \(\mathcal {G}_{\mathsf {H}}\), let \(m = move (\varrho ) = a_1 b_1 \ldots a_n b_n \theta \) be a move for some deterministic \(\varrho \in \mathrm {TS}(\mathcal {G}_{\mathsf {H}}) \), where \(a_1 ... a_n \in A_\mathrm{II}^*, b_1 ... b_n \in A_\mathrm{I}^*\). The delay operator, denoted by \(\overline{m}\), is defined by the rule \(\overline{m} = a_1 \ldots a_n \theta b_1 \ldots b_n\).
Intuitively, the delay operator shifts PLI actions to the right of PLII actions up until the next probabilistic state. For example,

Simulation Relation. Given an HIG \(\mathcal {G}_{\mathsf {H}}\), we first define the corresponding DAG \(\mathcal {G}_{\mathsf {D}}\).
Definition 8
(Correspondence). Given an HIG \(\mathcal {G}_{\mathsf {H}}\), a corresponding DAG \(\mathcal {G}_{\mathsf {D}}= \mathfrak {D}[\mathcal {G}_{\mathsf {H}}]\) is a DAG that follows the semantic rules displayed in Fig. 7.
For the rest of this section, we consider \(\mathcal {G}_{\mathsf {D}}= \mathfrak {D} [\mathcal {G}_{\mathsf {H}}]\), and use \(\varrho \in \mathrm {TS}(\mathcal {G}_{\mathsf {H}})\) and \(\hat{\varrho } \in \mathrm {TS}(\mathcal {G}_{\mathsf {D}})\) to denote two execution fragments of the HIG and DAG, respectively. We say that \(\varrho \) and \(\hat{\varrho }\) are similar, denoted by \(\varrho \sim \hat{\varrho }\), iff \( first (\varrho ) \simeq first (\hat{\varrho })\), \( last (\varrho ) \sim last (\hat{\varrho })\), and \(\overline{ move (\varrho )} = move (\hat{\varrho })\).
Definition 9
(Game Proper Simulation). A game \(\mathcal {G}_{\mathsf {D}}\) properly simulates \(\mathcal {G}_{\mathsf {H}}\), denoted by \(\mathcal {G}_{\mathsf {D}}\leadsto \mathcal {G}_{\mathsf {H}}\), iff \(\forall \varrho \in \mathrm {Prop}(\mathcal {G}_{\mathsf {H}})\), \(\exists \hat{\varrho } \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}})\) such that \(\varrho \sim \hat{\varrho }\).
Before proving the existence of the simulation relation, we first show that if a move is executed on two equivalent states, then the terminal states are similar.
Lemma 1
(Terminal States Similarity). For any \(s_0 \!\simeq \! \hat{s}_0\) and a deterministic \(\varrho \!\in \! \mathrm {TS}(\mathcal {G}_{\mathsf {H}})\) where \( first (\varrho ) \!=\!s_0\), \( last (\varrho ) \in S_\mathrm{II}\), then \( last (\varrho ) \!\sim \! \left( \overline{ move (\varrho )}\right) \! \left( \hat{s}_0\right) \) holds.
Proof
Let \( last (\varrho _i) = s^{(i)}_{\gamma _i} (t_i,u_i,\varOmega _i)\) and \(\left( \overline{ move (\varrho _i)}\right) \left( \hat{s}_0\right) = \hat{s}^{(i)}_{\hat{\gamma }_i} (\hat{t}_i,\hat{u}_i,w_i,j_i)\), where \( move (\varrho _i) = a_1 b_1 ... a_i b_i \theta \). We then write \(\overline{ move (\varrho )}=a_1 ... a_i \theta b_1 ... b_i\). We use induction over i as follows:
-
Base \((i \!=\!0)\): \(\varrho _0 \!=\!s_0 \) \(\implies s^{(0)} \simeq \hat{s}^{(0)} \) where \(u_0=\hat{u}_0\) and \(t_0 \!=\!\hat{t}_0\).
-
Induction \((i \!>\! 0)\): Assume that the claim holds for \( move (\varrho _{i-1}) \!=\!a_1 b_1 ... a_{i-1} b_{i-1} \theta \), i.e., \(u_{i-1} \!=\!\hat{u}_{i-1}\) and \(\hat{t}_{i-1} \!\in \! \varOmega _{i-1}\). For \(\varrho _i\) we have that
 and
and  . Also,
. Also, 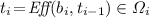 and
and  . Hence, \( u_i \!=\!\hat{u}_i\), \(\hat{t}_i \in \varOmega _i\) and \(\hat{\gamma }_i \!=\!\gamma _i \!=\!\bigcirc \). Thus, \(s^{(i)} \sim \hat{s}^{(i)}\) holds. The same can be shown for \( move (\varrho ) = a_1 b_1 ... a_i b_i \) where no \(\theta \) occurs. \(\square \)
. Hence, \( u_i \!=\!\hat{u}_i\), \(\hat{t}_i \in \varOmega _i\) and \(\hat{\gamma }_i \!=\!\gamma _i \!=\!\bigcirc \). Thus, \(s^{(i)} \sim \hat{s}^{(i)}\) holds. The same can be shown for \( move (\varrho ) = a_1 b_1 ... a_i b_i \) where no \(\theta \) occurs. \(\square \)
Theorem 1
(Probabilistic Simulation). For any \(s_0 \simeq \hat{s}_0\) and \(\varrho \in \mathrm {Prop}(\mathcal {G}_{\mathsf {H}})\) where \( first (\varrho ) = s_0\), it holds that
Proof
We can rewrite \(\varrho \) as  , where \(\varrho _0, \varrho _1,\ldots , \varrho _{n-1}\) are deterministic. Let \( first (\varrho _i) = s_\mathrm{II}^{(i)} (t_i,u_i,\varOmega _i)\), \( last (\varrho _i) = s_\bigcirc ^{(i)} (t_i^\prime ,u_i^\prime ,\varOmega _i^\prime )\), and \(\left( \overline{ move (\varrho )}\right) \! \left( \hat{s}_0 \right) \!=\!\hat{s}^{(n)} (\hat{t}_n, \hat{u}_n, w_n, j_n)\). We use induction over n as follows:
, where \(\varrho _0, \varrho _1,\ldots , \varrho _{n-1}\) are deterministic. Let \( first (\varrho _i) = s_\mathrm{II}^{(i)} (t_i,u_i,\varOmega _i)\), \( last (\varrho _i) = s_\bigcirc ^{(i)} (t_i^\prime ,u_i^\prime ,\varOmega _i^\prime )\), and \(\left( \overline{ move (\varrho )}\right) \! \left( \hat{s}_0 \right) \!=\!\hat{s}^{(n)} (\hat{t}_n, \hat{u}_n, w_n, j_n)\). We use induction over n as follows:
-
Base (\(n \!=\!0\)): for \(\varrho \) to be deterministic and proper, \(\varrho \!=\!\varrho _0 \!=\!s^{(0)} \) holds.
-
Case (\(n \!=\!1\)): \(p_1 = p(t_0^\prime ,u_0^\prime ) \). From Lemma 1, \(\hat{u}_1 \!=\!u_1 \) and \(\hat{t}_1 \!=\!t_1 \). Hence, \( \mathrm {Pr} \left[ last (\varrho ) \!=\!s_\mathrm{II}^{(1)} \right] = \mathrm {Pr} \left[ \left( \overline{ move (\varrho )}\right) \left( \hat{s}_{0}\right) \!=\!\hat{s}_\mathrm{II}^{(1)} \right] \!=\!p(t_0^\prime ,u_0^\prime ) \) and \(s_\mathrm{II}^{(1)} \simeq \hat{s}_\mathrm{II}^{(1)}\).
-
Induction (\(n \!>\! 1\)): It is straightforward to infer that \( p_n \!=\!p\left( t_{n-1}^\prime , u_{n-1}^\prime \right) \), hence \( \mathrm {Pr} \! \left[ last (\varrho ) \!=\!s_\mathrm{II}^{(n)} \right] = \mathrm {Pr} \! \left[ \left( \overline{ move (\varrho )}\right) \! \left( \hat{s}^{(0)}\right) \!=\!\hat{s}^{(n)} \right] = P\), and \(s_\mathrm{II}^{(n)} \simeq \hat{s}_\mathrm{II}^{(n)}\). \(\square \)
Note that in case of multiple \(\theta \) attempts, the above probability P satisfies
where \(m_i\) is the number of \(\theta \) attempts at stage i. Finally, since Theorem 1 imposes no constraints on \( move (\varrho )\), a DAG can simulate all proper executions that exist in the corresponding HIG.
Theorem 2
(DAG-HIG Simulation). For any HIG \(\mathcal {G}_{\mathsf {H}}\) there exists a DAG \(\mathcal {G}_{\mathsf {D}}= \mathfrak {D}[\mathcal {G}_{\mathsf {H}}]\) such that \(\mathcal {G}_{\mathsf {D}}\leadsto \mathcal {G}_{\mathsf {H}}\) (as defined in Definition 9).
4 Properties of DAG and DAG-based Synthesis
We here discuss DAG features, including how it can be decomposed into subgames by restricting the simulation to finite executions, and the preservation of safety properties, before proposing a DAG-based synthesis framework.
Transitions. In DAGs, nondeterministic actions of different players underline different semantics. Specifically, PLI nondeterminism captures what is known about the adversarial behavior, rather than exact actions, where PLI actions are constrained by the earlier PLII action. Conversely, PLII nondeterminism abstracts the player’s decisions. This distinction reflects how DAGs can be used for strategy synthesis under hidden information. To illustrate this, suppose that a strategy \(\pi _\mathrm{II}\) is to be obtained based on a worst-case scenario. In that case, the game is explored for all possible adversarial behaviors. Yet, if a strategy \(\pi _\mathrm{I}\) is known about PLI, a counter strategy \(\pi _\mathrm{II}\) can be found by constructing \(\mathcal {G}_{\mathsf {D}}^{\pi _\mathrm{I}}\).
Probabilistic behaviors in DAGs are captured by \(\mathrm {PL}_{\bigcirc }{}\), which is characterized by the transition function \(\hat{\delta } :\hat{S}_\bigcirc \times \hat{S}_\mathrm{II} \rightarrow [0,1]\). The specific definition of \(\hat{\delta }\) depends on the modeled system. For instance, if the transition function (i.e., the probability) is state-independent, i.e., \( \hat{\delta }(\hat{s}_\bigcirc , \hat{s}_\mathrm{II}) = c , c \in [0,1]\), the obtained model becomes trivial. Yet, with a state-dependent transition function, i.e., \(\hat{\delta }(\hat{s}_\bigcirc ,\hat{s}_\mathrm{II}) = p(\hat{t},\hat{u})\), the probability that PLII successfully reveals the true value depends on both the belief and the true value, and the transition function can then be realized since \(\hat{s}_\bigcirc \) holds both \(\hat{t}\) and \(\hat{u}\).
Decomposition. Consider an execution \(\hat{\varrho }^* \!=\!\hat{s}_0 a_1 \hat{s}_1 a_2 \hat{s}_2 \ldots \) that describes a scenario where PLII performs infinitely many actions with no attempt to reveal the true value. To simulate \(\hat{\varrho }^*\), the word w needs to infinitely grow. Since we are interested in finite executions, we impose stopping criteria on the DAG, such that the game is trapped whenever \(|w| \!=\!h_{\max }\) is true, where \(h_{\max } \in \mathbb {N}\) is an upper horizon. We formalize the stopping criteria as a deterministic finite automaton (DFA) that, when composed with the DAG, traps the game whenever the stopping criteria hold. Note that imposing an upper horizon by itself is not a sufficient criterion for a DAG to be considered a stopping game [8]. Conversely, consider a proper (and hence finite) execution \(\hat{\varrho } \!=\!\hat{s}_0 a_1 \ldots \hat{s}^\prime \), where \(\hat{s}_0, \hat{s}^\prime \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}})\). From Definition 9, it follows that a DAG initial state is strictly proper, i.e., \(\hat{s}_0 \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}})\). Hence, when \(\hat{s}^\prime \) is reached, the game can be seen as if it is repeated with a new initial state \(\hat{s}^\prime \). Consequently, a DAG game (complemented with stopping criteria) can be decomposed into a (possibly infinite) countable set of subgames that have the same structure yet different initial states.
Definition 10
(DAG Subgames). The subgames of a \(\mathcal {G}_{\mathsf {D}}\) are defined by the set  where \( \hat{S} = \bigcup _{i}^{}{\hat{S}^{(i)}} \); \( \hat{S}_{\gamma } = \bigcup _{i}^{}{\hat{S}_{\gamma }^{(i)}} \; \forall \gamma \in \varGamma \); and \( \hat{s}_0^{(i)} = \hat{s}_\mathrm{II}^{(i)} \; \text{ s.t. }\; \hat{s}_\mathrm{II}^{(i)} \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}}^{(i)}) \; , \; \hat{s}_\mathrm{II}^{(i)} \ne \hat{s}_\mathrm{II}^{(j)} \; \forall i,j \in \mathbb {N}_0\).
where \( \hat{S} = \bigcup _{i}^{}{\hat{S}^{(i)}} \); \( \hat{S}_{\gamma } = \bigcup _{i}^{}{\hat{S}_{\gamma }^{(i)}} \; \forall \gamma \in \varGamma \); and \( \hat{s}_0^{(i)} = \hat{s}_\mathrm{II}^{(i)} \; \text{ s.t. }\; \hat{s}_\mathrm{II}^{(i)} \in \mathrm {Prop}(\mathcal {G}_{\mathsf {D}}^{(i)}) \; , \; \hat{s}_\mathrm{II}^{(i)} \ne \hat{s}_\mathrm{II}^{(j)} \; \forall i,j \in \mathbb {N}_0\).
Intuitively, each subgame either reaches a proper state (representing the initial state of another subgame) or terminates by an upper horizon. This decomposition allows for the independent (and parallel) analysis of individual subgames, drastically reducing both the time required for synthesis and the explored state space, and hence improving scalability. An example of this decompositional approach is provided in Sect. 5.
Preservation of Safety Properties. In DAGs, the action \(\theta \) denotes a transition from PLII to PLI states and thus the execution of any delayed actions. While this action can simply describe a revealing attempt, it can also serve as a what-if analysis of how the true value may evolve at stage i of a subgame. We refer to an execution of the second type as a hypothetical branch, where \(\mathrm {Hyp}(\hat{\varrho },h)\) denotes the set of hypothetical branches from \(\hat{\varrho }\) at stage \(h \in \{ 1, \ldots , n \} \). Let \(L_{\mathrm {safe}} (s)\) be a labeling function denoting if a state is safe. The formula  is satisfied by an execution \(\varrho \) in HIG iff all \( s(t,u,\varOmega ) \in \varrho \) are safe.
is satisfied by an execution \(\varrho \) in HIG iff all \( s(t,u,\varOmega ) \in \varrho \) are safe.
Now, consider \(\hat{\varrho }\) of the DAG, with \(\hat{\varrho } \sim \varrho \). We identify the following three cases:
-
(a)
\(L_{\mathrm {safe}} (s)\) depends only on the belief u, then \(\varrho \models \varPhi _{\mathrm {safe}}\) iff all \(\hat{s}_{II} \in \hat{\varrho }\) are safe;
-
(b)
\(L_{\mathrm {safe}} (s)\) depends only on the true value t, then \(\varrho \models \varPhi _{\mathrm {safe}}\) iff all \(\hat{s}_\mathrm{I} \in \mathrm {Hyp}(\hat{\varrho },n)\) are safe; and
-
(c)
\(L_{\mathrm {safe}} (s)\) depends on both the true value t and belief u, then \(\varrho \models \varPhi _{\mathrm {safe}}\) iff \( last (\hat{\varrho }_h)\) is safe for all \( \hat{\varrho }_h \!\in \! \mathrm {Hyp}(\hat{\varrho },h), h \!\in \! \{ 1, ... , n \},\) where n is the number of PLII actions.
Taking into account such relations, both safety (e.g., never encounter a hazard) and distance-based requirements (e.g., never exceed a subgame horizon) can be specified when using DAGs for synthesis, to ensure their satisfaction in the original model. This can be generalized to other reward-based synthesis objectives, which will be part of our future efforts that we discuss in Sect. 6.
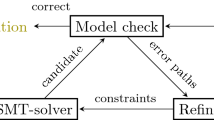
Synthesis Framework. We here propose a framework for strategy synthesis using DAGs, which is summarized in Fig. 8. We start by formulating the automata \(\mathcal {M}_\mathrm{I}\), \(\mathcal {M}_\mathrm{II}\) and \(\mathcal {M}_\bigcirc \), representing PLI, PLII and \(\mathrm {PL}_{\bigcirc }{}\) abstract behaviors, respectively. Next, a FIFO memory stack \((m_i)_{i=1}^{n} \in A_\mathrm{II}^n\) is implemented using two automata \(\mathcal {M}_{\mathrm {mrd}}\) and \(\mathcal {M}_{\mathrm {mwr}}\) to perform reading and writing operations, respectively.Footnote 5 The DAG \(\mathcal {G}_{\mathsf {D}}\) is constructed by following Algorithm 1. The game starts with PLII moves until she executes a revealing attempt \(\theta \), allowing PLI to play her delayed actions. Once an end criterion is met, the game terminates, resembling conditions such as ‘running out of fuel’ or ‘reaching map boundaries’.

Algorithm 2 describes the procedure for strategy synthesis based on the DAG \(\mathcal {G}_{\mathsf {D}}\), and an rPATL [6] synthesis query \(\phi _\mathrm {syn}\) that captures, for example, a safety requirement. Starting with the initial location, the procedure checks whether \(\phi _\mathrm {syn}\) is satisfied if action \(\theta \) is performed at stage h, and updates the set of feasible strategies \(\varPi _{i}\) for subgame \(\hat{\mathcal {G}}_i\) until \(h_{\max }\) is reached or \(\phi _\mathrm {syn}\) is not satisfied.Footnote 6 Next, the set \(\varPi _{i}\) is used to update the list of reachable end locations \(\ell \) with new initial locations of reachable subgames that should be explored. Finally, the composition of both \(\mathcal {G}_{\mathsf {H}}\) and \(\varPi _\mathrm{II}^*\) resolves PLII nondeterminism, where the resulting model \(\mathcal {G}_{\mathsf {H}}^{\varPi _\mathrm{II}^*} \) is a Markov Decision Process (MDP) of complete information that can be easily used for further analysis.
5 Case Study
In this section, we consider a case study where a human operator supervises a UAV prone to stealthy attacks on its GPS sensor. The UAV mission is to visit a number of targets after being airborne from a known base (initial state), while avoiding hazard zones that are known a priori. Moreover, the presence of adversarial stealthy attacks via GPS spoofing is assumed. We use the DAG framework to synthesize strategies for both the UAV and an operator advisory system (AS) that schedules geolocation tasks for the operator.

Modeling. We model the system as a delayed-action game \(\mathcal {G}_{\mathsf {D}}\), where PLI and PLII represent the adversary and the UAV-AS coalition, respectively. Figure 9 shows the model primary and auxiliary components. In the UAV model \(\mathcal {M}_{\mathrm {uav}}\), \(x_\mathcal {B}\!=\!({\texttt {x}}_\mathcal {B}, {\texttt {y}}_\mathcal {B})\) encodes the UAV belief, and \(A_{\mathrm {uav}} \!=\!\{ \mathsf {N}, \mathsf {S}, \mathsf {E}, \mathsf {W}, \mathsf {NE}, \mathsf {NW}, \mathsf {SE}, \mathsf {SW} \}\) is the set of available movements. The AS can trigger the action \( activate \) to initiate a geolocation task, attempting to confirm the current location. The adversary behavior is abstracted by \(\mathcal {M}_{\mathrm {adv}}\) where \(x_\mathcal {T}\!=\!({\texttt {x}}_\mathcal {T}, {\texttt {y}}_\mathcal {T})\) encodes the UAV true location. The adversarial actions are limited to one directional increment at most.Footnote 7 If, for example, the UAV is heading \(\mathsf {N}\), then the adversary set of actions is \(\beta (\mathsf {N}) \!=\!\{\mathsf {N},\mathsf {NE}, \mathsf {NW}\} \). The auxiliary components \(\mathcal {M}_{\mathrm {mwr}}\) and \(\mathcal {M}_{\mathrm {mrd}}\) manage a FIFO memory stack \(({m}_i)_{i=0}^{n-1} \in A_{\mathrm {uav}}^n\). The last UAV movement is saved in \({m}_i\) by synchronizing \(\mathcal {M}_{\mathrm {mwr}}\) with \(\mathcal {M}_\mathrm {uav}\) via \( write \), while \(\mathcal {M}_{\mathrm {mrd}}\) synchronizes with \(\mathcal {M}_\mathrm {adv}\) via \( read \) to read the next UAV action from \({m}_j\). The subgame terminates whenever action \( write \) is attempted and \(\mathcal {M}_{\mathrm {mwr}}\) is at state n (i.e., out of memory).
Primary DAG components: UAV (\(\mathcal {M}_{\mathrm {uav}}\)), adversary (\(\mathcal {M}_{\mathrm {adv}}\)), and AS (\(\mathcal {M}_{\mathrm {as}}\)). Auxiliary DAG components: memory write (\(\mathcal {M}_{\mathrm {mwr}}\)) and memory read (\(\mathcal {M}_{\mathrm {mrd}}\)) models, capturing the DAG representation. At stage i, the next memory location to write/read is \({m}_i\).
The goal is to find strategies for the UAV-AS coalition based on the following:
-
Target reachability. To overcome cases where targets are unreachable due to hazard zones, the label \( reach \) is assigned to the set of states with acceptable checkpoint locations (including the target) to render the objective incrementally feasible. The objective for all encountered subgames is then formalized as \( \mathrm {Pr}_{\max } \left[ \mathsf {F}\; reach \right] \geqslant p_{\min } \) for some bound \(p_{\min }\).
-
Hazard Avoidance. Similar to target reachability, the label \( hazard \) is assigned to states corresponding to hazard zones. The objective \(\mathrm {Pr}_{\max } \left[ \mathsf {G}\; \lnot hazard \right] \geqslant p_{\min }\) is then specified for all encountered subgames.
By refining the aforementioned objectives, synthesis queries are used for both the subgames and the supergame. Specifically, the query

is specified for each encountered subgame \(\hat{\mathcal {G}}_i\), where \( locate \) indicates a successful geolocation task. By following Algorithm 2 for a q number of reachable subgames, the supergame is reduced to an MDP \(\mathcal {G}_{\mathsf {D}}^{ \{ \pi _i \}_{i=1}^{q}}\) (whose states are the reachable subgames), which is checked against the query

to find the bounds on the probability that the target is reached under a maximum number of geolocation tasks n.
Experimental Results. Figure 10(a) shows the map setting used for implementation. The UAV’s ability to actively detect an attack depends on both its belief and the ground truth. Specifically, the probability of success in a geolocation task mainly relies on the disparity between the belief and true locations, captured by \( f _{\mathrm {dis}} : Ev \left( x_\mathcal {B}\right) \times Ev \left( x_\mathcal {T}\right) \rightarrow [0,1]\), obtained by assigning probabilities for each pair of locations according to their features (e.g., landmarks) and smoothed using a Gaussian 2D filter. A thorough experimental analysis where probabilities are extracted from experiments with human operators is described in [11]. The set of hazard zones include the map boundaries to prevent the UAV from reaching boundary values. Also, the adversary is prohibited from launching attacks for at least the first step, a practical assumption to prevent the UAV model from infinitely bouncing around the target location.
We implemented the model in PRISM-games [7, 19] and performed the experiments on an Intel Core i7 4.0 GHz CPU, with 10 GB RAM dedicated to the tool. Figure 10(b) shows the supergame obtained by following the procedure in Algorithm 2. A vertex \(\hat{\mathcal {G}}_{{\texttt {xy}}}\) represents a subgame (composed with its strategy) that starts at location \(({\texttt {x}},{\texttt {y}})\), while the outgoing edges points to subgames reachable from the current one. Note that each edge represents a probabilistic transition. Subgames with more than one outgoing transition imply nondeterminism that is resolved by the adversary actions. Hence, the directed graph depicts an MDP.
The synthesized strategy for \((h_\mathrm {adv}=2,h = 4)\) is demonstrated in Fig. 10(c). For the initial subgame, Fig. 11(a) shows the maximum probability of a successful geolocation task if performed at stage h, and the remaining distance to target. Assuming the adversary can launch attacks after stage \(h_\mathrm {adv}=2\), the detection probability is maximized by performing the geolocation task at step 4, and hazard areas can still be avoided up till \(h=6\). For \(h_\mathrm {adv}=1\), however, \(h=3\) has the highest probability of success, which diminishes at \(h=6\) as no possible flight plan exists without encountering a hazard zone. The effect of the maximum number of geolocation tasks (n) on target reachability is studied by analyzing the supergame against \(\phi _\mathrm {ana}\) as shown in Fig. 11(b). The minimum number of geolocation tasks to guarantee a non-zero probability of reaching the target (regardless of the adversary strategy) is 3 with probability bounds of \((33.7\%,94.4\%)\).
The experimental data obtained for this case study are listed in Table 1. For the same grid size, more complex maps require more time for synthesis while the state space size remains unaffected. The state space grows exponentially with the explored horizon size, i.e., \( \mathcal {O} \left( (|A_{\mathrm {uav}}||A_{\mathrm {adv}}| )^{h} \right) \), and is typically slowed by, e.g., the presence of hazard areas, since the branches of the game transitions are trimmed upon encountering such areas. Interestingly, for \(h=6\) and \(h=7\), while the model construction time (size) for \(h_\mathrm {adv}=1\) is almost twice (quadruple) as those for \(h_\mathrm {adv}=2\), the time for checking \(\phi _\mathrm {syn}\) declines in comparison. This reflects the fact that, in case of \(h_\mathrm {adv}=1\) compared to \(h_\mathrm {adv}=2\), the UAV has higher chances to reach a hazard zone for the same k, leading to a shorter time for model checking.
6 Discussion and Conclusion
In this paper, we introduced DAGs and showed how they can simulate HIGs by delaying players’ actions. We also derived a DAG-based framework for strategy synthesis and analysis using off-the-shelf SMG model checkers. Under some practical assumptions, we showed that DAGs can be decomposed into independent subgames, utilizing parallel computation to reduce the time needed for model analysis, as well as the size of the state space. We further demonstrated the applicability of the proposed framework on a case study focused on synthesis and analysis of active attack detection strategies for UAVs prone to cyber attacks.
DAGs come at the cost of increasing the total state space size as \(\mathcal {M}_\mathrm {mrd}\) and \(\mathcal {M}_\mathrm {mwr}\) are introduced. This does not present a significant limitation due to the compositional approach towards strategy synthesis using subgames. However, the synthesis is still limited to model sizes that off-the-shelf tools can handle.
The concept of delaying actions implicitly assumes that the adversary knows the UAV actions a priori. This does not present a concern in the presented case study as an abstract (i.e., nondeterministic) adversary model is analogous to synthesizing against the worst-case attacking scenario. Nevertheless, strategies synthesized using DAGs (and SMGs in general) are inherently conservative. Depending on the considered system, this can easily lead to no feasible solution.
The proposed synthesis framework ensures preservation of safety properties. Yet, general reward-based strategy synthesis is to be approached with care. For example, rewards dependent on the belief can appear in any state, and exploring hypothetical branches is not required. However, rewards dependent on a state’s true value should only appear in proper states, and all hypothetical branches are to be explored. A detailed investigation of how various properties are preserved by DAGs, along with multi-objective synthesis, is a direction for future work.
Notes
- 1.
The term turn-based indicates that at any state only one player can play an action. It does not necessarily imply that players take fair turns.
- 2.
A geolocation task is an attempt to localize the UAV by examining its camera feed.
- 3.
For deterministic transitions, \(p=1\), hence omitted from \(\varrho \) for readability.
- 4.
An execution fragment lives in the transition system (TS), i.e., \(\varrho \in \mathrm {Prop}(\mathrm {TS}(\mathcal {G}))\). We omit \(\mathrm {TS}\) for readability.
- 5.
Specific implementation details are described in Sect. 5.
- 6.
Failing to find a strategy at stage i implies the same for all horizons of size \(j>i\).
- 7.
References
Baier, C., Brazdil, T., Grosser, M., Kucera, A.: Stochastic game logic. In: Fourth International Conference on the Quantitative Evaluation of Systems, QEST 2007, pp. 227–236. IEEE (2007). https://doi.org/10.1109/QEST.2007.38
Basset, N., Kwiatkowska, M., Topcu, U., Wiltsche, C.: Strategy synthesis for stochastic games with multiple long-run objectives. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 256–271. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_22
Basset, N., Kwiatkowska, M., Wiltsche, C.: Compositional strategy synthesis forstochastic games with multiple objectives. Information and Computation (2017). https://doi.org/10.1016/j.ic.2017.09.010
Brázdil, T., Chatterjee, K., Křetínský, J., Toman, V.: Strategy representation by decision trees in reactive synthesis. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10805, pp. 385–407. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89960-2_21
Chatterjee, K., Henzinger, T.A.: Semiperfect-information games. In: Sarukkai, S., Sen, S. (eds.) FSTTCS 2005. LNCS, vol. 3821, pp. 1–18. Springer, Heidelberg (2005). https://doi.org/10.1007/11590156_1
Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., Simaitis, A.: Automatic verification of competitive stochastic systems. Form. Methods Syst. Des. 43(1), 61–92 (2013). https://doi.org/10.1007/s10703-013-0183-7
Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., Simaitis, A.: PRISM-games: a model checker for stochastic multi-player games. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 185–191. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_13
Chen, T., Forejt, V., Kwiatkowska, M., Simaitis, A., Wiltsche, C.: On stochastic games with multiple objectives. In: Chatterjee, K., Sgall, J. (eds.) MFCS 2013. LNCS, vol. 8087, pp. 266–277. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40313-2_25
Chen, T., Kwiatkowska, M., Simaitis, A., Wiltsche, C.: Synthesis for multi-objective stochastic games: an application to autonomous urban driving. In: Joshi, K., Siegle, M., Stoelinga, M., D’Argenio, P.R. (eds.) QEST 2013. LNCS, vol. 8054, pp. 322–337. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40196-1_28
David, A., Jensen, P.G., Larsen, K.G., Mikučionis, M., Taankvist, J.H.: UPPAAL STRATEGO. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 206–211. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_16
Elfar, M., Zhu, H., Cummings, M.L., Pajic, M.: Security-aware synthesis of human-UAV protocols. In: Proceedings of 2019 IEEE International Conference on Robotics and Automation (ICRA). IEEE (2019)
Feng, L., Wiltsche, C., Humphrey, L., Topcu, U.: Synthesis of human-in-the-loop control protocols for autonomous systems. IEEE Trans. Autom. Sci. Eng. 13(2), 450–462 (2016). https://doi.org/10.1109/TASE.2016.2530623
Fremont, D.J., Seshia, S.A.: Reactive control improvisation. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10981, pp. 307–326. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96145-3_17
Fu, J., Topcu, U.: Integrating active sensing into reactive synthesis with temporal logic constraints under partial observations. In: 2015 American Control Conference (ACC), pp. 2408–2413. IEEE (2015). https://doi.org/10.1109/ACC.2015.7171093
Hansen, E.A., Bernstein, D.S., Zilberstein, S.: Dynamic programming for partially observable stochastic games. AAAI 4, 709–715 (2004)
Jovanov, I., Pajic, M.: Relaxing integrity requirements for attack-resilient cyber-physical systems. IEEE Trans. Autom. Control (2019). https://doi.org/10.1109/TAC.2019.2898510
Kelmendi, E., Krämer, J., Křetínský, J., Weininger, M.: Value iteration for simple stochastic games: stopping criterion and learning algorithm. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10981, pp. 623–642. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96145-3_36
Klein, F., Zimmermann, M.: How much lookahead is needed to win infinite games? In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 452–463. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_36
Kwiatkowska, M., Parker, D., Wiltsche, C.: Prism-games: verification and strategy synthesis for stochastic multi-player games with multiple objectives. Int. J. Softw. Tools Technol. Transf. 20(2), 195–210 (2018)
Lesi, V., Jovanov, I., Pajic, M.: Security-aware scheduling of embedded control tasks. ACM Trans. Embed. Comput. Syst. (TECS) 16(5s), 188:1–188:21 (2017). https://doi.org/10.1145/3126518
Li, W., Sadigh, D., Sastry, S.S., Seshia, S.A.: Synthesis for human-in-the-loop control systems. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 470–484. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_40
Mo, Y., Sinopoli, B.: On the performance degradation of cyber-physical systems under stealthy integrity attacks. IEEE Trans. Autom. Control 61(9), 2618–2624 (2016). https://doi.org/10.1109/TAC.2015.2498708
Neider, D., Topcu, U.: An automaton learning approach to solving safety games over infinite graphs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 204–221. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_12
Norman, G., Parker, D., Zou, X.: Verification and control of partially observable probabilistic real-time systems. In: Sankaranarayanan, S., Vicario, E. (eds.) FORMATS 2015. LNCS, vol. 9268, pp. 240–255. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22975-1_16
Pajic, M., Lee, I., Pappas, G.J.: Attack-resilient state estimation for noisy dynamical systems. IEEE Trans. Control Netw. Syst. 4(1), 82–92 (2017). https://doi.org/10.1109/TCNS.2016.2607420
Pajic, M., Weimer, J., Bezzo, N., Sokolsky, O., Pappas, G.J., Lee, I.: Design and implementation of attack-resilient cyberphysical systems: with a focus on attack-resilient state estimators. IEEE Control Syst. 37(2), 66–81 (2017). https://doi.org/10.1109/MCS.2016.2643239
Rasmusen, E., Blackwell, B.: Games and Information, vol. 15. MIT Press, Cambridge (1994)
Svoreňová, M., Kwiatkowska, M.: Quantitative verification and strategy synthesis for stochastic games. Eur. J. Control 30, 15–30 (2016). https://doi.org/10.1016/j.ejcon.2016.04.009
Wiltsche, C.: Assume-guarantee strategy synthesis for stochastic games. Ph.D. thesis, Ph.D. dissertation, Department of Computer Science, University of Oxford (2015)
Zimmermann, M.: Delay games with WMSO+ U winning conditions. RAIRO Theor. Inform. Appl. 50(2), 145–165 (2016). https://doi.org/10.1051/ita/2016018
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Elfar, M., Wang, Y., Pajic, M. (2019). Security-Aware Synthesis Using Delayed-Action Games. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11561. Springer, Cham. https://doi.org/10.1007/978-3-030-25540-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-25540-4_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25539-8
Online ISBN: 978-3-030-25540-4
eBook Packages: Computer ScienceComputer Science (R0)











 and
and  . Also,
. Also, 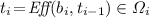 and
and  . Hence,
. Hence, 


