Abstract
Standard modal logic for alethic modalities analyses modalities as ranging over all possible worlds (the Leibnizian universe). This leaves very little room in the space of worlds to entertain impossible things. My proposal is to liberate the Leibnizian universe and reinforce the relative aspect of possibility; worlds are possible with respect to some worlds, and impossible for others. The central idea is to isolate relative possibility (Kripke) from conditionality (Lewis/Stalnaker). To accommodate counterpossibles, I provide a dialetheic conditional modal logic, a theory that is dialetheic at every level, in the logic as well as in the set theory behind it.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
If you’re not familiar with bisimulation, think of the picture as showing that any formula that can be invalidated at \(\texttt {w}\) can also be invalidated at \(\texttt {w}'\) (see Priest 2008, Sect. 3.7.5); anything impossible at \(\texttt {w}\) is also impossible at \(\texttt {w}'\), because \(\texttt {w}\) doesn’t see any more worlds than \(\texttt {w}'\).
- 2.
- 3.
Repetition intended, to stress that dialetheic logic is used in the object and meta levels.
- 4.
I continue to represent models with equivalence classes for \(\texttt {R}\) and Lewis’ systems of spheres \(\texttt {S}\), as I find them more convivial, with apologies if you don’t agree.
- 5.
The proof of soundness and completeness is entirely standard, and I won’t bother you with the details.
- 6.
Williamson formulates pos as the logically equivalent
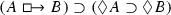 , but this formulation will be better for us.
, but this formulation will be better for us. - 7.
For a thorough criticism of Williamson on counterpossibles, see Berto et al. (2017), who also propose a conditional modal logic similar to mine, but using a distinction between possible and impossible worlds instead of my more general notion of relative possibility. I don’t like the twentieth-century distinction between possible and impossible worlds, or between good and bad worlds in general, as discussed in Girard and Weber (2015).
- 8.
For a counterexample to nec, take a model with two worlds \(\texttt {w}\) and \(\mathtt {v}\) such that \(\mathtt {v}\not \in \texttt {R}(w)\), \(\mathtt {V}(p) =\{\mathtt {v}\}\), \(\mathtt {v}\in \texttt {S}(\texttt {w}, \llbracket p \rrbracket )\) but \(\mathtt {v}\not \in \mathtt {V}(q)\). Then \(\Box (p \rightarrow q)\) is vacuously true at \(\texttt {w}\) whereas
 is false. For a counterexample to pos, take a model with three worlds \(\texttt {w}, \mathtt {u}\) and \(\mathtt {v}\) such that \(\mathtt {V}(p) = \{\mathtt {u}, \mathtt {v}\}\), \(\mathtt {V}(q) = \{\mathtt {v}\}\), \(\mathtt {u}\in \texttt {R}(\texttt {w})\), and \(\mathtt {v}\in \texttt {S}(w, \llbracket p \rrbracket )\).
is false. For a counterexample to pos, take a model with three worlds \(\texttt {w}, \mathtt {u}\) and \(\mathtt {v}\) such that \(\mathtt {V}(p) = \{\mathtt {u}, \mathtt {v}\}\), \(\mathtt {V}(q) = \{\mathtt {v}\}\), \(\mathtt {u}\in \texttt {R}(\texttt {w})\), and \(\mathtt {v}\in \texttt {S}(w, \llbracket p \rrbracket )\). - 9.
From Blackburn et al. (2001, Definition 3.2) A formula \(\varphi \) defines a class of frames K if for all frames \(\mathtt {F}\), \(\mathtt {F}\in \texttt {K}\) iff \(\varphi \) is valid in \(\mathtt {F}\).
- 10.
The proofs of definability are straightforward and left to the reader.
- 11.
A condition that implies but is not equivalent to POS is the converse of NEC: \((\texttt {R}(\texttt {w})\cap \texttt {X}) \subseteq \texttt {S}(\texttt {w}, \texttt {X})\). If we assumed this stronger condition in combination with NEC, we would reduce conditionals to strict implication, which would be a bad idea (cf., David 1973, Sect. 1.2).
- 12.
‘So that is our basic procedure for handling the antecedent of a counterfactual implicated in a case of extra-mathematical explanation: hold as much fixed as you can within mathematics compatible with the twiddle, without inducing a contradiction’, Baron et al. (2017), p.11.
- 13.
VC is Lewis’s favourite counterfactual logic. I choose it here without a strong philosophical commitment. Assume the limit assumption for simplicity. The choice is entirely modular and you can pick your favourite conditional logic if you don’t like VC; no problem.
- 14.
The axiom pos is canonical for POS in a standard Henkin completeness proof adapted from Chellas (1975). Check or proceed without concern.
- 15.
\(\texttt {w}\in \llbracket \Box \lnot \varphi \rrbracket ^{+} \Rightarrow \texttt {R}(\texttt {w}) \subseteq \llbracket \lnot \varphi \rrbracket ^{+} \Rightarrow \texttt {R}(\texttt {w}) \subseteq \llbracket \varphi \rrbracket ^{-}\Rightarrow \texttt {w}\in \llbracket \Diamond \varphi \rrbracket ^{-} \Rightarrow \texttt {w}\in \llbracket \lnot \Diamond \varphi \rrbracket ^{+}\).
- 16.
Since the problem is about the duality of modalities, it arises just the same in a formulation with three truth values.
- 17.
As I want to keep the focus on modalities and conditionals, I won’t go into motivating the propositional logic here, and refer you to (Weber et al. 2016) instead.
- 18.
I add the constant \(\bot \) to be able to identify triviality. Unlike in twentieth-century logic, it cannot be defined by a contradictory formula.
- 19.
With apologies to Kabay (2008).
- 20.
Assume that \(\texttt {w}\in \llbracket \Diamond \bot \rrbracket \), then \(\texttt {R}(\texttt {w}) \cap \llbracket \bot \rrbracket \ne \emptyset \), so there exists a world \(\mathtt {x}\) such that \(\mathtt {x}\in \texttt {R}(\texttt {w}) \wedge \mathtt {x}\in \llbracket \bot \rrbracket \). But \(\mathtt {x}\in \llbracket \bot \rrbracket \) implies that \(\mathtt {x}\in \Box \varphi \) for every \(\varphi \), so \(\texttt {R}(\mathtt {x}) \subseteq \llbracket \varphi \rrbracket \) for every \(\varphi \). Furthermore, \(\mathtt {x}\in \texttt {R}(\texttt {w})\) implies by 5 that \(\texttt {w}\in \texttt {R}(\mathtt {x})\). So there is a world \(\mathtt {x}\) such that \(\texttt {w}\in \texttt {R}(\mathtt {x}) \wedge \texttt {R}(\mathtt {x})\subseteq \llbracket \varphi \rrbracket \) for every \(\varphi \), so \(\texttt {w}\in \llbracket \varphi \rrbracket \) for every \(\varphi \). Therefore \(\texttt {w}\in \llbracket \bot \rrbracket \).
References
Baker, A. (2005). Are there genuine mathematical explanations of physical phenomena? Mind, 114(454), 223–238.
Baron, S., Colyvan, M., & Ripley, D. (2017). How mathematics can make a difference. Philosophers Imprint, 17(3). University of Michigan Press.
Berto, F., French, R., Priest, G., & Ripley, D. (2017, August). Williamson on counterpossibles. Journal of Philosophical Logic.
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic. New York: Cambridge University Press.
Chellas, B. F. (1980). Modal logic: An introduction. Cambridge; New York: Cambridge University Press.
Chellas, B. F. (1975). Basic conditional logic. Journal of Philosophical Logic, 4(2), 133–153.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2015, August). Pragmatic interpretations of vague expressions: Strongest meaning and nonmonotonic consequence. Journal of Philosophical Logic, 44(4), 375–393.
Divers, J. (1999). A genuine realist theory of advanced modalizing. Mind, 108(430), 217–240.
Divers, J. (2014). The modal status of the Lewisian analysis of modality. Mind, 123(491), 861–872.
Forrest, P., & Armstrong, M. D. (1984, June). An argument against David Lewis’ theory of possible worlds. Australasian Journal of Philosophy, 62(2), 164–168.
Girard, P., & Weber, Z. (2015) Bad worlds. Thought: A Journal of Philosophy.
Humberstone, L. (2011, January). Variation on a trivialist argument of Paul Kabay. Journal of Logic, Language and Information, 20(1), 115–132.
Jago, M. (2016, July). Advanced modalizing problems. Mind, 125(499), 627–642.
Kabay, P. D. (2008). A defense of trivialism.
Kant, I. (2004). Prolegomena to any future metaphysics that will be able to come forward as science: With selections from the critique of pure reason. Cambridge texts in the history of philosophy (rev. ed.). Cambridge, UK; New York: Cambridge University Press.
Kripke, S. A. (1959). A completeness theorem in modal logic. The Journal of Symbolic Logic, 24(1), 1–14.
Kripke, S. A. (1980). Naming and necessity. Library of philosophy and logic (revised and enlarged ed.). Oxford: Blackwell.
Lewis, D. K. (1973). Counterfactuals. Library of philosophy and logic. Oxford: Blackwell.
Martin, B. (2014, September). Dialetheism and the impossibility of the world. Australasian Journal of Philosophy, 1–15.
Nolan, D. (1996). Recombination unbound. Philosophical Studies, 84(2–3), 239–262.
Nolan, D. (1997). Impossible worlds: A modest approach. Notre Dame Journal of Formal Logic, 38(4), 535–572.
Priest, G. (2002). Beyond the limits of thought. Oxford: Oxford University Press.
Priest, G. (2006). In contradiction. Oxford Scholarship Online, Oxford University Press.
Priest, G. (2008). An introduction to non-classical logic: From if to is. Cambridge introductions to philosophy (2nd ed.). Cambridge; New York: Cambridge University Press.
Priest, G. (2010, January). Inclosures, vagueness, and self-reference. Notre Dame Journal of Formal Logic, 51(1), 69–84.
Priest, G. (2016). Thinking the impossible. Philosophical Studies, 173(10), 2649–2662.
Pruss, A. R. (2001). The cardinality objection to David Lewis’s modal realism. Philosophical Studies, 104(2), 169–178.
Ripley, D. (2011). Contradictions at the borders. In R. Nouwen, R. van Rooij, U. Sauerland, & H.-C. Schmitz (Eds.), Vagueness in communication (pp. 169–188). Springer.
Stalnaker, R. C. (1968). A theory of conditionals. In W. L. Harper, R. Stalnaker, & G. Pearce (Eds.), IFS, number 15 in The University of Western Ontario Series in Philosophy of Science (pp. 41–55). The Netherlands: Springer. https://doi.org/10.1007/978-94-009-9117-0_2.
Weber, Z. (2010, October). A paraconsistent model of vagueness. Mind, 119(476), 1025–1045.
Weber, Z., Badia, G., & Girard, P. (2016). What is an inconsistent truth table? Australasian Journal of Philosophy, 94(3), 533–548.
Williamson, T. (2010, March). Modal logic within counterfactual logic. In B. Hale & A. Hoffmann (Eds.), Modality: metaphysics, logic, and epistemology. Oxford University Press.
Acknowledgements
Graham, you’ve been a source of inspiration for several scholars that have known or read you, and you are a model of perseverance against adversity. Above all, you are a good friend, and I’m very pleased to be able to contribute this paper in your honour. I would like to thank Zach Weber, Fred Kroon, Joy Britten and Michael Hillas for valuable comments on a previous draft of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Girard, P. (2019). Dialetheic Conditional Modal Logic. In: Başkent, C., Ferguson, T. (eds) Graham Priest on Dialetheism and Paraconsistency. Outstanding Contributions to Logic, vol 18. Springer, Cham. https://doi.org/10.1007/978-3-030-25365-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-25365-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25364-6
Online ISBN: 978-3-030-25365-3
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)



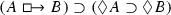 , but this formulation will be better for us.
, but this formulation will be better for us. is false. For a counterexample to
is false. For a counterexample to