Introductory Survey of Multiplicative Ideal Theory

Abstract

This chapter provides an overview, without proofs, of multiplicative ideal theory. All of the information presented in this chapter is restated and proved in Chapters 2 and 3 in greater generality. The first section is a survey of the theory of integral domains, introducing some of the theory’s most central concepts and results. The reader may at any time wish to consult the various figures and tables at the end of Section 1.1, which summarize the characterizations of and interrelationships among the various classes of integral domains discussed here. The second section provides many examples and counterexamples. The third section provides a brief preview of the generalizations of Sections 1.1 and 1.2 to rings with zerodivisors that are discussed in Chapters 2 and 3.

Exercises

Section 1.1

• 1. Let D be an integral domain with quotient field K. Show that K is a fractional ideal of D if and only if $K = D$.

• 2. Let D be an integral domain. Prove the following.

  • a) $((I^{-1})^{-1})^{-1} = I^{-1}$ for any nonzero fractional ideal I of D.

  • b) $v = ((-)^{-1})^{-1}$ is a star operation on D.

  • c) v is the largest star operation on D.

• 3. Show that a domain D is a TD domain (that is, $t = d$ on $\mathbf {F}^{{{\text {reg}}}}(D)$) if and only if every nonzero finitely generated ideal of D is divisorial.

• 4. Let D be an integral domain with quotient field K. Show the following.

  • a) t and w are star operations on D.

  • b) $I^t = \{x \in K: (x/a_1) \cap \cdots \cap (x/a_n) \subseteq D \text{ for } \text{ some } \text{ nonzero } a_1, \ldots , a_n \in I\}$ for any fractional ideal I of D.

• 5. Show by example and direct computation that not every ideal of ${\mathbb Z}[X]$ is v-closed.

• 6. Let D be an integral domain with quotient field K.

  • a) Let $*$ be a star operation on D. Show that $(IJ)^* = IJ^*$ for all $I,J \in \mathbf {F}^{{{\text {reg}}}}(D)$ with I invertible.

  • b) Let $*$ be a self-map of $\mathbf {F}^{{{\text {reg}}}}(D)$. Consider the following axioms.

    ($4'$):

    $(aI)^* = aI^*$ for all $I \in \mathbf {F}^{{{\text {reg}}}}(D)$ and all nonzero $a \in K$.

    ($4''$):

    $(I^*J^*)^* = (IJ)^*$ for all $I,J \in \mathbf {F}^{{{\text {reg}}}}(D)$.

    Show that, assuming axioms (1)–(3) for star operations, axiom (4) for star operations and axioms $(4')$ and $(4'')$ are all equivalent. In the existing literature, the star operation axioms are usually taken to be (1)–(3), $(4')$, and (5).

• 7. Let D be an integral domain, and let $*$ be a self-map of $\mathbf {F}^{{{\text {reg}}}}(D)$. Show that $*$ is a star operation on D if and only if $D^* = D$ and $(I^* :_K J) = (I^* :_K J^*)$ for all $I,J \in \mathbf {F}^{{{\text {reg}}}}(D)$.

• 8. Let I and J be fractional ideals of an integral domain D. Prove the following.

  • a) If $IJ = D$, then $J = I^{-1}$.

  • b) If $*$ is a star operation on D and $(IJ)^* = D$, then $J^* = I^{-1}$.

• 9. Let D be an integral domain with quotient field K. Let $\{D_\lambda : \lambda \in \Lambda \}$ be a collection of rings lying between D and K whose intersection is D. Show that $I \longmapsto \bigcap \{ID_\lambda : \lambda \in \Lambda \}$ is a star operation on D.

• 10.

  • a) Show that, if ${\mathfrak p}$ is a prime ideal of a Noetherian integral domain D, then one need not have $I^v (D/{\mathfrak p}) \subseteq (I (D/{\mathfrak p}))^v$ for every ideal I of D.

  • b) Let $D = {\mathbb Z}[X]$ and $D' = {\mathbb Z}[X/2]$, and let $I = (2,X)D$. Show that $I^v = D$ and $(ID')^v = 2D'$ and therefore $I^v D' \nsubseteq (ID')^v$. Conclude that, if $D'$ is a Noetherian overring of a Noetherian integral domain D, then one need not have $I^v D' \subseteq (ID')^v$ for every ideal I of D.

• 11. Find an example of a Noetherian domain that is not of finite character.

• 12. Complete the following implication diagram to a full implication lattice.

  

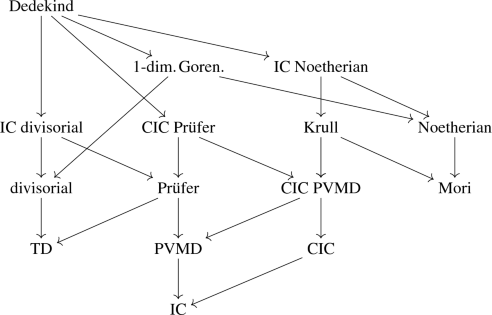
• 13. Draw the smallest full and complete implication lattice that includes the PID, Dedekind, Bézout, Prüfer, UFD, Krull, GCD, PVMD, v-Noetherian, and v-coherent conditions.

• 14. In the following implication diagram, try to find as many pairs of classes as possible whose supremum in the lattice is not the intersection of the two classes. As a challenge, try to complete the diagram to a full implication lattice.

Section 1.2

• 1. Using Theorems 1.2.2 and 1.2.4, verify the examples in Example 1.2.5.

• 2. Using Theorems 1.2.2 and 1.2.6, verify the examples in Example 1.2.8.

• 3. Using Theorems 1.2.2 and 1.2.6, verify the examples in Example 1.2.12.

• 4. Using Theorem 1.2.14, verify the examples in Example 1.2.15.

• 5. Using Theorem 1.2.16, verify the examples in Example 1.2.17.

• 6. In Proposition 1.2.3, verify that $(4) \Leftrightarrow (5) \Rightarrow (6) \Rightarrow (7) \Rightarrow (8)$.

• 7. Using Exercise 1.1.1.3, show that the overring ${\mathbb Z}[X/2]$ of ${\mathbb Z}[X]$ is not t-linked.

• 8. Prove the following using results from the section.

  • a) If D is a Dedekind domain that is not a PID, then $D+XK[X]$ is an H Prüfer domain that is not TV, Bézout, Dedekind, or completely integrally closed.

  • b) If D is a Prüfer domain that is neither Bézout nor Dedekind, then D[X] is a PVMD that is not Krull, GCD, or Prüfer.

  • c) If D is a Dedekind domain that is not a PID, then both $(D+XK[X])[Y]$ and $D[Y]+XK(Y)[X]$ are H PVMDs that are not TV, Krull, GCD, Prüfer, or completely integrally closed.

• 9. Let D be an integral domain with quotient field K, and let $R = D+XK[X]$. Let I be an ideal of R. Show that the following conditions are equivalent.

  • 1) $I \cap D \ne (0)$.

  • 2) $XK[X] \subsetneq I$.

  • 3) $IK[X] = K[X]$.

• 10. Let D be an integral domain with quotient field K, and let $R = D+XK[X]$. Prove the following.

  • a) Every ideal of R is of the form $f IR = f(I+XK[X])$, where $f \in K[X]$ and I is a nonzero D-submodule of K such that $f(0) I \subseteq D$.

  • b) The finitely generated ideals of R are the ideals fJR, where $f \in R$ and J is a finitely generated ideal of D.

• 11. Let D be an integral domain with quotient field K, and let $R = D+XK[X]$. Using the results of the previous exercise, prove that R is a Bézout domain (resp., Prüfer domain) if and only if D is.

• 12. Let D be an integral domain with quotient field K, and let $R = D+XK[X]$. Prove the following.

  • a) The nonzero prime ideals of R are the ideals ${\mathfrak p}+XK[X]$, where ${\mathfrak p}$ is a prime ideal of D, along with the principal ideals fR, where $f \in K[X]$ is irreducible in K[X] and $f(0) = 1$.

  • b) The maximal ideals of R are the ideals ${\mathfrak p}+XK[X]$, where ${\mathfrak p}$ is a maximal ideal of D, along with the principal ideals fR, where $f \in K[X]$ is irreducible in K[X] and $f(0) = 1$.

• 13. Let D be an integral domain with quotient field K. Let $I[X] = ID[X]$ for all ideals I of D. Prove the following.

  • a) $I[X] \cap D = I$ for all ideals I of D.

  • b) $(J :_K I)[X] = (J[X] :_{K(X)} I[X])$ for all nonzero ideals I, J of D. In particular, $I^v[X] = I[X]^v$.

  • c) $I^t[X] = I[X]^t$ for all nonzero ideals I of D.

  • d) The map $I \longmapsto I[X]$ is an inclusion preserving injection from the set of t-closed ideals of D to the set of t-closed ideals of D[X], and its left inverse is the map $J \longmapsto J\cap D$.

  • e) I is t-invertible in D if and only if I[X] is t-invertible in D[X].

• 14. $(**)$ A domain D is essential if $D = \bigcap _{{\mathfrak p}\in {\text {Ess}}(D)} D_{\mathfrak p}$, where ${\text {Ess}}(D)$ is the set of all essential primes of D. Extend Tables 1.5, 1.6, and 1.7 to include any or all of the following properties: essential, Noetherian, Mori, H, of finite character, of finite t-character, coherent, and v-coherent.