Abstract
At the microscale, experiments show that in the vicinity of a moving boundary, rarefied fluid flows exhibit a velocity slip (i.e., the fluid and wall velocities are not equal), as well as a temperature jump (i.e., the fluid temperature is not equal to the wall temperature). Such effects can be captured within the framework of the Boltzmann equation by employing kinetic boundary conditions (i.e., diffuse reflection). In our contribution, we present the systematic construction of lattice Boltzmann (LB) models based on Gauss quadratures, which allows one to simulate gas flows between diffuse reflecting boundaries from the hydrodynamic limit to the ballistic regime. Key to the success of this approach is the use of half-range Gauss–Hermite quadratures, which are essential in order to capture the discontinuity of the distribution function induced by the boundaries. Since the resulting models are off-lattice, an overview of the appropriate numerical schemes for these models is also provided.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
9.1 Introduction
At non-negligible values of the Knudsen number Kn (defined as the ratio between the mean free path of the fluid particles in a gas and the characteristic length of the domain), the Navier–Stokes equations lose applicability [1, 2]. Such rarefied gas flows can be approached within the framework of the Boltzmann equation [3,4,5]. This equation describes the six-dimensional phase-space evolution of the distribution function f, where f(t, x, p)d 3 xd 3 p gives the number of particles at time t which are contained in an infinitesimal volume d 3 x centred on x, having momenta in an infinitesimal range d 3 p about p. Because of its complexity, the Boltzmann equation can be solved analytically only in a very limited number of cases. Alternatively, numerous well-established approaches to the numerical solutions of the Boltzmann equation are now currently used for academic or engineering purposes, of which we only mention the direct simulation Monte Carlo (DSMC) technique [6], the discrete velocity models (DVMs) [7,8,9], the discrete unified gas-kinetic scheme (DUGKS) [10,11,12] and the lattice Boltzmann (LB) models [13,14,15,16,17,18,19,20].
The LB models are a particular type of DVMs and are derived from the Boltzmann equation using a simplified version of the collision operator, as well as an appropriate discretisation of the momentum space, which ensure the recovery of the moments of the distribution function f up to a certain order N. Originally derived nearly 30 years ago from the lattice gas automata [17, 19, 20], the LB models were primarily designed to recover the hydrodynamics of fluid systems at the Navier–Stokes level. The LB models inherited the collision-streaming concept from their ancestors, according to which the velocities of the fluid particles are aligned along the lattice links such that after one time step δt, each particle arrives at a neighbouring node [13, 14, 17, 19, 21, 22].
One disadvantage of the collision-streaming paradigm is the increasing difficulty to approach fluid systems far from equilibrium (e.g., rarefied gases or micro/nano-scale flowing fluids) using suitable LB models. In this case, the accurate recovery of specific effects in channel flow at large values of Kn, such as the velocity slip and the temperature jump at the channel walls [1, 2], requires that higher order moments of the single particle distribution function f are ensured. Since the moments of f are derived by integration in the momentum space, their numerical computation involves the use of convenient quadrature methods. When using a quadrature method, the moments of the single particle distribution f (up to a certain order N) are exactly recovered by sums over a finite set of momentum vectors p k, 1 ≤ k ≤ K [13, 14, 17,18,19, 21,22,23,24,25,26]. As the fluid system is farther from the equilibrium and the characteristic value of the Knudsen number increases, the number K of the momentum vectors (i.e., the quadrature points) should also be increased, as it will be shown later. This task becomes more and more elaborated if one wants to keep the particles hopping from a lattice node to another one during a single time step [27,28,29,30].
An alternative to the collision-streaming paradigm is provided by the off-lattice LB models, where the distribution functions are evolved in the lattice nodes using finite-difference, finite-volume or interpolation schemes [31,32,33,34]. A fourth-order, off-lattice LB model for the simulation of thermal flows in the continuum regime (small values of the Knudsen number), where the fluid density, velocity and temperature fields are derived from a single set of distribution functions, was proposed by Watari and Tsutahara [35] for 2D flows and subsequently extended to the 3D case [36,37,38]. Off-lattice LB models of any order N can be easily constructed using the Gauss quadrature method in the velocity space [18, 23, 25, 26, 39, 40].
Another challenge for microfluidics simulations is due to the implementation of boundary conditions. In general, the particle–wall interaction governs the distribution of particles emerging from the wall back into the fluid. Since the distribution of particles travelling from the fluid towards the wall is essentially arbitrary, the distribution function becomes discontinuous near the wall [41, 42]. Examples of boundary conditions include the diffuse-spectral [9] and Cercignani–Lampis [43] particle–wall interaction models; however, for simplicity, we restrict the analysis to the simpler diffuse reflection model, which is a limiting case of both models mentioned above. According to the diffuse reflection paradigm, the reflected particles follow a Maxwell–Boltzmann distribution corresponding to the wall temperature and velocity. In order to accurately compute the incident and emergent fluxes required to impose diffuse reflection (kinetic) boundary conditions, it is convenient to discretise the velocity set based on half-range Gauss quadrature methods. Such techniques were also used in the frame of DVMs [44, 45] and more recently, they were adapted for the LB method [24, 26, 46, 47].
9.2 Generalities
The Boltzmann equation for a force-driven flow reads:
where on the right-hand side we have used the Bhatnagar–Gross–Krook (BGK) single-relaxation time approximation of the collision term [48]. The distribution function f ≡ f(x, p, t) represents the density of particles at position x and time t, having momentum p, while
is the Maxwell–Boltzmann equilibrium distribution function corresponding to local thermal equilibrium. The force F ≡F(x) in Eq. (9.1) encapsulates all external forces acting on these particles.
The local quantities describing the gas flow at the macroscopic level, namely the particle number density n, the velocity u, the stress tensor T αβ (α, β = 1, 2, 3) and the heat flux q, can be obtained as moments of f:

where ξ α = p α − mu α is the peculiar momentum and ρ = mn is the mass density. The pressure P is defined through:
while the temperature is obtained via T = P∕nk B, which represents the equation of state for an ideal gas (k B is the Boltzmann constant). More generally, it is convenient to introduce the following notation for the moments of f and f eq:

Since mass m, momentum p and energy p 2∕2m are collision invariant quantities, we have:

The basic steps for the construction of an off-lattice LB model are [49]:
-
1.
discretising the momentum space;
-
2.
replacing the equilibrium distribution function f eq in the collision term of Eq. (9.1) by a truncated polynomial with respect to the particle velocity ;
-
3.
replacing the momentum derivative of the distribution function f in Eq. (9.1) using a suitable expression [see Eq. (9.23)];
-
4.
choosing a numerical method for the time evolution and spatial advection;
-
5.
implementation of the boundary conditions.
A common feature of all LB models is that the conservation equations for the particle number density n, macroscopic momentum density ρ u and temperature T (for thermal models) are exactly recovered. Regardless of the chosen discretisation of the momentum space, the Boltzmann–BGK equation (9.1) is replaced by a set of K equations:
where f k (k = 1, 2, …K) represents the distribution function corresponding to the discrete momentum p k. The total number K of discrete momenta are chosen such that the moments Eq. (9.6) are exactly recovered:

The order N of a given LB model is related to the maximum value of the exponents s x, s y, s z for which the above equality holds.
9.3 One-Dimensional Quadrature-Based LB Models
In this section, the procedure for implementing the full-range and half-range Gauss–Hermite quadratures on a single axis of the momentum space will be discussed in Sects. 9.3.1 and 9.3.2, respectively. For convenience, in this section we will refer to the one-dimensional (1D) equivalent of the Boltzmann–BGK equation (9.1):
After discretisation, this equation is replaced by a set of \(K = {\mathcal {Q}}\) equations, where \({\mathcal {Q}}\) is the number of quadrature points on the entire axis:
The general expression of the total number K of discrete momenta employed by a D-dimensional LB model will be introduced in Sect. 9.4.
9.3.1 Full-Range Gauss–Hermite Quadrature
Let us consider integrals of f and f eq along the axis of the 1D momentum space:

For the purpose of this section, we can consider f eq = ng, where g is expressed as in Eq. (9.3), but without using the subscript α. The function g can be expanded with respect to the full-range Hermite polynomials \(\{H_\ell (\overline {p}), \ell = 0, 1, \dots \}\) as follows [25, 26]:

where ⌊⋅⌋ is the floor function, \(\mathcal {G}_\ell \) is the ℓ-th expansion coefficient and \(\overline {p} = p / p_0\) is the particle momentum expressed with respect to some arbitrary momentum scale p 0. The full-range Hermite polynomials [18, 26, 39, 40] satisfy the following orthogonality relation with respect to the weight function \(\omega (\overline {p})\):
The expansion coefficients \(\mathcal {G}_\ell \) given in Eq. (9.15) were obtained according to:
Substituting Eq. (9.15) into Eq. (9.14) gives:
At finite values of s and ℓ, the Gauss–Hermite quadrature can be applied to recover the integral over \(\overline {p}\) on the entire momentum axis, using the following prescription:
where \(P_s(\overline {p})\) is a polynomial of order s in \(\overline {p}\) and the Q quadrature points \(\overline {p}_k\) (k = 1, 2, …, Q) are the roots of the Hermite polynomial of order Q, i.e., \(H_Q(\overline {p}_k) = 0\). Note that \(K = {\mathcal {Q}} = Q\) holds only in a one-dimensional LB model based on full-range Gauss–Hermite quadratures.
Since these roots correspond to the integration over the full momentum space axis, in the case of the full-range Gauss–Hermite quadrature, the number of quadrature points on the entire axis \(\mathcal {Q}\) is equal to the quadrature order Q. The quadrature weights \(w_k^H\) are given by:
The equality in Eq. (9.19) is exact if 2Q > s. In an LB simulation, Q is fixed at runtime. Thus, in order to ensure the exact recovery of \(M^{\mathrm {(eq)}}_s\) in Eq. (9.18), the sum over ℓ in Eq. (9.15) must be truncated at a finite value ℓ = N. Setting Q > N ensures the exact recovery of the first N + 1 moments (i.e., s = 0, 1, …N) of f eq, since the terms of higher order in the expansion of g are orthogonal to all polynomials \(P_s(\overline {p})\) of orders 0 ≤ s ≤ N, by virtue of the orthogonality relation given by Eq. (9.16). This allows \(M^{\mathrm {(eq)}}_s\) to be obtained as:
where \(p_k = p_0 \overline {p}_k\) are the discrete momenta and the notation g H, (N)(p) indicates that the polynomial expansion in Eq. (9.15) of g(p) is truncated at order ℓ = N with respect to the full-range Hermite polynomials. For definiteness, we list below the expression for \(g^H_k\) [25, 26]:
The momentum derivative ∂ p f can be written as:
where the kernel \(\mathcal {K}_{k,k'}\) has the following components [49, 50]:
9.3.2 Half-Range Gauss–Hermite Quadrature
The half-range paradigm is inspired from the discontinuous nature of the distribution function due to the interaction with the channel walls. Such discontinuities naturally induce a split of the momentum space integration domain in two hemispheres, corresponding to particles travelling towards and away from the wall. In order to encompass the discontinuous nature of the distribution function in a one-dimensional LB model for confined fluid flow, it is convenient to introduce the half-range moments \(M_s^\pm \) and \(M_s^{{\mathrm{(eq)}}, \pm }\) (s = 0, 1, 2, …) of f and f (eq) through:

The recovery of the half-range integrals in Eq. (9.25) can be achieved using the half-range Gauss–Hermite quadrature, defined with respect to the weight function \(\omega (\overline {p})\):
where the equality is exact if the number of quadrature points Q satisfies 2Q > s. The quadrature points \(\overline {p}_k\) (k = 1, 2, …Q) are the Q (positive) roots of the half-range Hermite polynomial \({\mathfrak {h}}_Q(\overline {p})\), while the quadrature weights w k are given by [25, 26, 39, 40]:
where \(a_Q = {\mathfrak {h}}_{Q+1,Q+1} / {\mathfrak {h}}_{Q,Q}\) and \({\mathfrak {h}}_{\ell ,s}\) represents the coefficient of \(\overline {p}^s\) in \({\mathfrak {h}}_\ell (\overline {p})\), i.e.,
In our convention, the half-range Hermite polynomials are normalised according to:
In order to apply the half-range Gauss–Hermite quadrature prescription, Eq. (9.26), f and f eq must be expanded with respect to the half-range Hermite polynomials. Since the half-range Hermite polynomials are defined only on half of the momentum axis, f can be split with the help of the Heaviside step function \(\theta (\overline {p})\) as follows [49]:
The functions f +(p) and f −(p) are defined only on the positive and negative momentum semiaxis, respectively, such that they can be expanded with respect to the half-range Hermite polynomials as follows:
where the coefficients \(\mathcal {F}^\pm \) can be obtained using the orthogonality given in Eq. (9.29) of the half-range Hermite polynomials:
The expansion in Eq. (9.31) with respect to the half-range Hermite polynomials \({\mathfrak {h}}_\ell \) can be substituted in Eq. (9.25), yielding:

Truncating the expansion in Eq. (9.31) at ℓ = Q − 1 ensures that a quadrature of order Q can recover the moments in Eq. (9.33) for 0 ≤ s ≤ Q. Since Q quadrature points are required on each semiaxis of the momentum space, the discrete momentum set of the 1D half-range Gauss–Hermite LB model has \(K = \mathcal {Q} = 2Q\) elements (twice as in the full-range model of the same order), which are defined as:
Thus, the half-range moments in Eq. (9.25) are recovered as:
where
Let us now consider the expansion of f eq with respect to the half-range Hermite polynomials, by writing g(p) = θ(p)g +(p) + θ(−p)g −(p), where
The expansion coefficients \(\mathcal {G}^\pm _\ell \) can be obtained in analogy to Eq. (9.32).
Following the convention of Eq. (9.34), the momentum space is discretised using \(\mathcal {Q} = 2Q\) elements with p k > 0 (for the positive semiaxis) and p k+Q = −p k (for the negative semiaxis), where 1 ≤ k ≤ Q. The corresponding equilibrium distributions \({f^{\mathrm {eq}}}_k = n g^{{\mathfrak {h}},(N)}_k\) are constructed using
where the expansion order 0 ≤ N < Q is a free parameter of the model which represents the order up to which the half-range moments of f eq can be exactly recovered. The coefficients \(\mathcal {G}^\pm _\ell \) can be found using the orthogonality relation in Eq. (9.29):
The integrals above can be performed analytically, such that \(g^{{\mathfrak {h}},(N)}_k\) and \(g^{{\mathfrak {h}},(N)}_{k+Q}\) become [25, 26]:
where \(\zeta = u \sqrt {m/2 K_B T}\), \({\mathrm {erf}}\, \zeta = \frac {2}{\sqrt {\pi }} \int _0^\zeta dz\, e^{-z^2}\) is the error function, \(\Phi _s^N(\overline {p}_k)\) is defined as:
where \({\mathfrak {h}}_{\ell ,s}\) is defined in Eq. (9.28), while \(P_s^+(\zeta )\) and \(P_s^*(\zeta )\) represent polynomials of orders s and s − 1, respectively, defined through:
The momentum derivative of f can be projected on the space of the half-range Hermite polynomials as discussed in Sect. 9.3.1. Since this projection is not relevant for the further development of this chapter, we refer the reader to Refs. [49, 50] for further details.
9.4 LB Models in the Three-Dimensional Momentum Space
In the three-dimensional (3D) momentum space, the discretisation procedure can be conducted using a direct product rule. On each Cartesian axis α ∈{x, y, z}, one can choose a specific Gauss–Hermite (full-range or half-range) quadrature of order Q α, depending on the characteristics of the flow (e.g., the existence of a noticeable wall-induced discontinuity of the distribution function along the α axis). Let \(p_{\alpha ,k_{\alpha }}\), \(1\leq k_{\alpha } \leq \mathcal {Q}_{\alpha }\), be the quadrature points on the Cartesian axis α (note that \(\mathcal {Q}_{\alpha } \in \{Q_{\alpha }, 2Q_{\alpha }\}\) as mentioned in Sect. 9.3). These quadrature points are the components of the 3D vectors p k, \(k = (k_{z}-1){\mathcal {Q}_{x}}{\mathcal {Q}_{y}} + (k_{y}-1){\mathcal {Q}_{x}} + k_{x}\), \(1\leq k \leq K = {\mathcal {Q}_{x}}{\mathcal {Q}_{y}}{\mathcal {Q}_{z}} \). Following Refs. [25, 26], we generally refer to the resulting models as mixed quadrature LB models. The numerical solution of the discretised form Eq. (9.10) of the Boltzmann equation can be obtained following the steps described in Sect. 9.3, which will be detailed further.
In this contribution we restrict ourselves to the LB simulation of Couette and force-driven Poiseuille flows of rarefied gases between parallel plates. In these cases, the flow is homogeneous along the z axis and the computational effort can be significantly decreased by taking advantage of the reduced distribution functions introduced in Sect. 9.4.1. Section 9.4.2 discusses the construction of the mixed quadrature LB models for the investigation of rarefied Couette and force-driven Poiseuille flows using the reduced distribution functions and the resulting evolution equations are presented in Sect. 9.4.3. The section ends with a discussion of our non-dimensionalisation convention, presented in Sect. 9.4.4.
9.4.1 Reduced Distributions
In this chapter, we only consider the planar Couette and the force-driven Poiseuille flows between parallel plates. Considering that the walls are perpendicular to the x axis, these flows can be considered homogeneous with respect to the y and z axes, such that the Boltzmann equation (9.1) reduces to:
The force term is present only in the case of the Poiseuille flow. Assuming that the fluid flows along the y direction, the only non-vanishing component of the force is along the y axis (see Sect. 9.5.2 for more details).
Since the flows considered in this chapter are trivial with respect to the z axis, the p z degree of freedom can be eliminated from Eq. (9.43) [44, 51]. This helps to reduce the computational costs, especially when dealing with LB models involving high order quadratures. Defining:
the following two equations are obtained:

where χ eq = k B Tϕ eq and ϕ eq can be factorised using the functions g α Eq. (9.3) as follows:
Note that the reduction procedure introduced above can be used also for the 3D pressure-driven Poiseuille flow between parallel plates, provided that there are no variations along the z axis.
9.4.2 Mixed Quadrature LB Models with Reduced Distribution Functions
In the mixed quadrature LB models, the momentum space is constructed using a direct product rule. This allows the quadrature on each axis to be constructed independently by taking into account the characteristics of the flow. When the gas flow is homogeneous along the z axis, the reduced distribution functions evolve in a two-dimensional space and thus, the elements of the discrete set of momentum vectors can be written as p ij = (p x,i, p y,j). The indices i and j run from 1 to \(\mathcal {Q}_{\alpha }\) (α ∈{x, y}), where \(\mathcal {Q}_\alpha = Q_\alpha \) or \(\mathcal {Q}_{\alpha } = 2Q_\alpha \) when a full-range or a half-range quadrature of order Q α is employed on the α axis. As shown in Refs. [25, 26], a full-range Gauss–Hermite quadrature of order Q y = 4 is sufficient on the y axis in order to capture exactly the evolution of the velocity, temperature and of heat flux fields. For low Mach flows, the quadrature order Q x can be taken to be Q x = 4 in the Navier–Stokes regime, where the full-range Gauss–Hermite quadrature is efficient. As Kn is increased, Q x must also be increased in order to retain the accuracy of the simulation results. In the case of the channel flows considered in this chapter, the discontinuity in the distribution functions ϕ and χ induced by the diffuse-reflective walls becomes significant for sufficiently large Kn. Hence, the full-range Gauss–Hermite quadrature on the x axis becomes inefficient compared to the half-range Gauss–Hermite quadrature, as demonstrated in Refs. [25, 26]. In this chapter, we only consider the half-range Gauss–Hermite quadrature of order Q x on the x axis. The resulting models are denoted HHLB(Q x) ×HLB(4) following the convention in Ref. [26], employing 8Q x velocities and 16Q x distinct populations (ϕ ij and χ ij), as discussed below.
9.4.3 The Lattice Boltzmann Equation
The reduced distribution functions ϕ ij and χ ij corresponding to the momentum vector p ij = (p x,i, p y,j) are linked to ϕ and χ through the direct extension of Eq. (9.36):

The weights \(w_i^x\) and \(w_j^y\) are given by Eqs. (9.27) and (9.20), respectively. After the discretisation of the momentum space, Eq. (9.45) becomes:

where the kernel \(\mathcal {K}_{j,j'}\) is given in Eq. (9.24). In particular, for the case Q y = 4 considered in this chapter, \(\mathcal {K}_{j,j'}\) has the following elements:
Numerically, the above expression reduces to:

The equilibrium distribution \({\phi ^{\mathrm {eq}}}_{ij} = n g_i^{{\mathfrak {h}},(N_x)} g_j^{H,(N_y)}\) is obtained as the product between the expansions \(g_i^{{\mathfrak {h}},(N_x)}\) from Eq. (9.40) and \(g_j^{H,(N_y)}\) from Eq. (9.22), performed with respect to the half-range and full-range Hermite polynomials, respectively. For this particular case, the orders of the expansions are N x = 3 and N y = 3. For definiteness, we list below the exact expression for \(g_j^{H,(3)}\):
where \(\mathfrak {U}_y\) and \(\mathfrak {T}_y\) are defined as [26]:
Similarly, \(g_i^{{\mathfrak {h}},(3)}\) is given by Ambruș and Sofonea [25]:
where \(\zeta _{x,i} = u_x \sigma _{x,i} \sqrt {m/ 2K_B T}\), σ x,i is the sign of p x,i and \(\mathcal {T}_x = \sqrt {m K_B T / 2 p_{0,x}^2}\), while the functions \(\Phi ^{3}_s(z)\) are given below:
Finally, the macroscopic moments Eq. (9.4) can be written in terms of ϕ ij and χ ij as follows:
It can be seen that χ ij appears only in the definition of the temperature field. It is essential to track the evolution of ϕ ij and χ ij simultaneously in order to correctly compute the temperature field appearing in the definition of ϕ eq given in Eq. (9.46), as well as in the definition of χ eq.
9.4.4 Non-Dimensionalisation Procedure
In order to perform numerical simulations, we non-dimensionalise all quantities with respect to the following parameters:
-
The wall temperature, such that T w = 1.
-
The particle mass, such that m = 1.
-
The reference speed \(c_{\mathrm {ref}} = \sqrt {k_B T_w / m}\).
-
The channel width, such that L = 1.
-
The average particle number density, such that the total number of particles obeys:
$$\displaystyle \begin{aligned} N_{\mathrm{tot}} = \int_{-1/2}^{1/2} dx\, n(x) = 1. \end{aligned} $$(9.56)
The reference time is t ref = L∕c ref and we set p 0,x = p 0,y = 1 for the rest of this chapter. With the above conventions, the relaxation time τ is set to
which ensures that the viscosity μ = τnT = Kn is constant throughout the simulation domain.
9.5 Simulation Results
The advantage of the quadrature-based approach to LB modelling quickly becomes apparent when considering rarefied flows. An excellent arena for this type of tests is represented by channel flows. In particular, we will restrict the discussion to the Couette and the force-driven Poiseuille flows between parallel plates, which have become canonical benchmark problems in the microfluidics community. In the context of these flows, the distribution function becomes discontinuous due to the diffuse reflection interaction with the boundary. Thus, at large values of Kn, half-range quadratures are much more efficient than the more traditional full-range ones [25, 26, 52, 53]. More complex flows, where the application of half-range Gauss–Hermite quadrature is essential are investigated in Refs. [50, 54, 55].
9.5.1 Couette Flow Between Parallel Plates
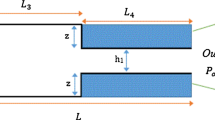
In this section, we consider the Couette flow between parallel plates. The geometry of this flow can be seen in Fig. 9.1. The system consists of two parallel plates at rest located at x = ±1∕2.Footnote 1 The gas between these plates is initially in thermal equilibrium at the wall temperature T w = 1. At t = 0, the left and right plates are set into motion with velocities −u w = (0, −u w, 0) and u w = (0, u w, 0), respectively, as shown in Fig. 9.1 (left). The evolution of the fluid is simulated using the LB algorithm described in Sect. 9.4, until the stationary state is reached. The analysis presented in this section is restricted to the stationary state.
Left: Setup for the Couette flow problem, highlighting the slip velocity u slip = u w − u(1∕2). Right: Boundary conditions and grid characteristics. The fine dotted lines show a grid comprised of S = 8 cells, stretched according to Eq. (9.58) with A = 0.95. Only one cell is used along the y direction
In the stationary state of Couette flow, rarefied gases exhibit a non-linear velocity profile in the proximity of the moving walls. This nonlinearity originates from the wall-induced discontinuity of the particle distribution function and its spatial extension (i.e., the width of the so-called Knudsen layer, where the discontinuity induced through interparticle collisions) is of the order of the mean free path of the fluid particles [1, 2]. Diffuse reflection boundary conditions are used to capture this wall-induced discontinuity [24,25,26], as shown in Fig. 9.1 (right).
Mathematically, diffuse reflection boundary conditions entail that the distribution functions for the particles emerging from the walls back into the fluid satisfy f(x = ±L∕2, p, t) = f eq(p;±u w), which is valid for ± p x < 0, respectively. Noting that f eq(−p;u) = f eq(p;−u), it can be seen that the solution of the Boltzmann equation (9.12) possesses the symmetry f(−x, p, t) = f(x, −p, t). This symmetry allows only the right half of the channel to be considered, provided that bounce back boundary conditions are implemented at the channel centre-line [i.e., f(0, −p, t) = f(0, p, t)]. This simplification effectively halves all computation times. Moreover, since the system is homogeneous along the y axis, no advection is performed in this direction and a discretisation using a single node is sufficient. In fact, this corresponds to implementing periodic boundary conditions along the y axis. The p z degree of freedom is integrated out, as explained in Sect. 9.4.1, and no advection is performed along the z direction. The right panel of Fig. 9.1 presents schematically the implementation of the Couette flow geometry.
In order to capture the Knudsen layer, it is convenient to use a grid which is more refined in the vicinity of the wall. This can be achieved by employing a standard grid-stretching procedure [56, 57]. In this chapter, we follow Refs. [50, 54, 55] and perform an equidistant grid discretisation with respect to the non-dimensional parameter η, defined through:
where 0 ≤ η ≤arctanh(A) and 0 < A < 1 controls the stretching such that when A → 0, the grid becomes equidistant with respect to x, while as A → 1, the grid points accumulate towards the right boundary. For a discretisation employing S points, we have:
where the points with 1 ≤ s ≤ S lie within the flow domain. For the simulations presented in this section, we found that S = 16 points with A = 0.98 are sufficient to yield accurate results. The stretching procedure is illustrated in Fig. 9.1 (right) for a grid with S = 8 cells, when A = 0.95.
In order to employ the finite-difference scheme described in the Appendix, three ghost nodes are required on either side of the simulation domain. The bounce back boundary conditions [17, 19, 20] employed on the left side of the domain can be written as:
and similarly for χ s;ij. The notation \(\widetilde {\imath }\) (\(\widetilde {\jmath }\)) refers to the component \(p_{x,\widetilde {\imath }}\) (\(p_{y,\widetilde {\jmath }}\)) defined through:
On the right boundary, the diffuse reflection concept [24,25,26] is imposed. This requires that the flux of particles coming from the boundary cell at \(s = S + \frac {1}{2}\) towards the first fluid node at s = S is Maxwellian:

where ϕw;ijeq is the reduced equilibrium distribution Eq. (9.46) corresponding to the wall parameters n w, u w and T w = 1 and χw;ijeq = ϕw;ijeq. In the above, the notations \(\Phi _{S + \frac {1}{2};ij}\) and \(X_{S+\frac {1}{2};ij}\) represent the fluxes corresponding to the reduced distributions ϕ ij and χ ij, which can be computed using Eq. (9.76) by replacing p x with p x,i and F s with ϕ ij;s and χ ij;s, as required. Equation (9.62) can be achieved in the frame of the WENO-5 scheme [50] described in the Appendix, when
Similar relations hold also for χ s;ij. The distributions of the particles travelling from the fluid towards the wall are obtained by quadratic extrapolation with respect to the equidistant η coordinate from the fluid towards the wall:
The same relations are valid for χ s;ij. The wall density n w can be obtained by imposing mass conservation:
It can be seen that the accurate computation of n w requires the recovery of half-space quadrature sums, which is the reason why we choose the half-range Gauss–Hermite quadrature on the x axis.
We illustrate the capabilities of our models by considering the velocity profile for a low Mach number flow (u w = 0.1) and perform simulations at various values of Kn. While the Navier–Stokes equations predict a straight-line velocity profile u y = 2xu w∕L [60, 61], the kinetic analysis shows that in the vicinity of the boundary, there is always a Knudsen layer, having an extension of the order of the particle mean free path, where the velocity profile curves along the wall [42]. Figure 9.2 (left) shows the excellent agreement between our LB results and the benchmark linearised Boltzmann–BGK results reported in Ref. [58]. These results are also presented in Ref. [53], but with less accuracy and for a smaller range of values of Kn. The dependence of the slip velocity with respect to Kn is shown in Fig. 9.2 (right), where our results are compared with the linearised Boltzmann–BGK results reported in Refs. [58, 59]. Excellent agreement is found in both cases. In order to compare our simulation results with those reported in Ref. [58], we employed the relation \(\mathrm {Kn} = k / \sqrt {2}\) between the Knudsen number defined in Eq. (9.57) and the parameter k employed in Ref. [58]. The quadrature orders used in these simulations were Q x = 4 (k ≤ 0.1), 5 (k = 0.3), 10 (k = 1), 11 (k = 2), 20 (k = 5) and 40 (k = 30). As k is increased, the fluid velocity at the wall approaches 0 (its free-streaming value). Since the slip velocity can be recovered accurately even if the velocity profile presents visible deviations with respect to the benchmark data, the results presented in the right panel of Fig. 9.2 were obtained using a quadrature order Q x = 21 for all values of Kn.
Validation of the LB results (lines) in the context of the Couette flow. Left: Comparison of the velocity profile in the half-channel 0 ≤ x ≤ 1∕2 with the benchmark results reported in Ref. [58] at various values of \(k = \mathrm {Kn} \sqrt {2}\) (points). Right: Comparison of the slip velocity as a function of Kn with the linearised Boltzmann–BGK results reported in Refs. [58] (circles) and [59] (squares)
9.5.2 Force-Driven Poiseuille Flow Between Parallel Plates
In this section, we consider the force-driven Poiseuille flow between parallel plates. The geometry of this flow can be seen in Fig. 9.3 (left). The system consists of two parallel plates at rest which are taken to be perpendicular to the x axis. The gas between these plates is initially in thermal equilibrium at the wall temperature T w = 1. At t = 0, a constant force F = (0, ma, 0) is applied throughout the fluid domain. According to the non-dimensionalisation discussed in Sect. 9.4.4, the acceleration a is expressed in units of \(c_{\mathrm {ref}}^2 / L\) and m = 1. The evolution of the fluid is simulated using the LB algorithm presented in Sect. 9.4.
Left: Setup for the force-driven Poiseuille flow problem, highlighting the slip velocity u slip = u(1∕2). The mass flow rate is shown in the shaded area. Right: Boundary conditions and grid characteristics. The fine dotted lines show a grid comprised of S = 8 cells, stretched according to Eq. (9.58) with A = 0.95. Only one cell is used along the y direction
The flow geometry, the boundary conditions and the Boltzmann equation (9.12), possess the symmetry property f(−x, p x, p y, t) = f(x, −p x, p y, t). As was the case for the Couette flow, this symmetry allows only half of the channel to be simulated (\(0 \le x \le \frac {1}{2}\)), while the symmetry f(0, p x, p y, t) = f(0, −p x, p y, t) is ensured using specular boundary conditions [17, 19, 20], as shown in Fig. 9.3 (right). In order to implement specular boundary conditions, the distribution functions in the nodes to the left of the flow domain, having indices s = 0, −1, −2, are populated according to:
where only the x component of the momentum is reversed in the right-hand side of the above equations, as shown in Eq. (9.61). On the right boundary, the diffuse reflection concept is imposed, as discussed in Sect. 9.5.1. Furthermore, the grid is stretched using Eq. (9.58), with A = 0.98. In order to accurately capture the main features of the flow, we employed S = 32 nodes along the x axis, distributed in the right half of the channel.
In the case of the force-driven Poiseuille flow, we discuss two features which manifest at non-negligible values of Kn. The first one refers to the Knudsen paradox, according to which the flow rate through the channel decreases with Kn from its value in the Navier–Stokes limit down to a minimum, after which it increases towards infinity as the ballistic regime settles in. The non-dimensionalised mass flow rate Q flow can be computed as follows:
For small values of Kn, Cercignani [62] derived the following approximation for Q flow:
where s = 1.01615 and \(\widetilde {\mathrm {Kn}}\) is defined as:
While accurate at small values of Kn, Eq. (9.68) predicts a linear increase of Q flow with \(\widetilde {\mathrm {Kn}}\), which is not confirmed by experiments or numerical simulations.
An empirical fitting formula was given by Sharipov in Eq. (11.136) of Ref. [9]:
In this formula, which extends the asymptotic term \(-\ln \delta / \sqrt {\pi }\) derived by Cercignani [62], the rarefaction parameter δ and \(G_P^*\) are related to Kn and Q flow through:
Our numerical results for Q flow, together with the approximations Eq. (9.68) and Eq. (9.71), as well as various other semi-analytical or numerical results are shown in Fig. 9.4 (left). These results were obtained using the mixed LB model described in Sect. 9.4.2 with the order of the half-range Gauss–Hermite quadrature set to Q x = 21. Since the velocity profile, and hence the mass flow rate, do not scale linearly with a at large values of a, we used a = 0.01 throughout the simulations in order to ensure good agreement with the validation data.
Validation of the LB results in the context of the force-driven Poiseuille flow. Left: Comparison between the LB results (continuous line) for the flow rate Q flow, defined in Eq. (9.67), and the asymptotic formulae in Eqs. (9.67) and (9.68) due to Cercignani [62] and Sharipov [9] (dashed lines), the results of Cercignani, Lampis and Lorenzani (CLL) [63] (dashed line with filled squares), the DVM results from Ref. [64] (hollow circles), as well as the DSMC results reported by Feuchter and Scheifenbaum in Ref. [52] (filled circles). The results are represented with respect to \(\widetilde {\mathrm {Kn}}\), defined in Eq. (9.69). Right: Illustration of the dip in the temperature profile at various values of Kn. The lines represent the best fits of the analytic expression, Eq. (9.72) to the LB results (points), as described in Sect. 9.5.2 and in Table 9.1
The second remarkable microfluidics specific effect occurring in the force-driven Poiseuille flow refers to the development of a dip (local minimum) in the temperature profile T(x) at the centre x = 0 of the channel. The dip occurrence was predicted by the kinetic theory at the super-Burnett level and observed by DSMC simulations [1, 65,66,67,68,69,70,71].
Using a moments method approach, Mansour et al. [67, 68] derived analytically the following dependence of the temperature profile on the distance x from the centre of the channel:
Using a numerical fit, we found an excellent match between the above functional form and our simulation results. For clarity, Fig. 9.4 (right) shows the half-channel profile of [T(x) − 1]∕(T 0 − 1), where T w = 1 is the wall temperature and T 0 represents the temperature at the centre of the channel, as determined by fitting Eq. (9.72) to the numerical data. The values of the parameters T 0, α and β for the values of Kn considered in Fig. 9.4 (right) are given in Table 9.1. In these simulations we used a = 0.05 in order to enhance the development of the temperature dip. We employed the mixed quadrature LB model described in Sect. 9.4.2 where we set Q x = 4 for Kn ∈ {0.032, 0.05, 0.1}, while at Kn = 0.2, we used Q x = 7.
9.6 Conclusions
In this chapter, we presented a systematic procedure for the construction of high order mixed quadrature LB models based on the full-range and half-range Gauss–Hermite quadratures. A particular attention was given to the case when the flow is homogeneous along the z axis, when reduced distribution functions can be used in order to minimise the computational effort. The capabilities of these models are demonstrated in the context of the Couette and force-driven Poiseuille flows between parallel plates at various values of Kn. Excellent agreement is found between our results and benchmark data available in the literature from the Navier–Stokes level up to the transition regime.
The success of our models relies on the accurate recovery of half-range integrals required for the implementation of diffuse reflection. Such integrals are exactly recovered by employing the half-range Gauss–Hermite quadrature.
Our numerical method for solving the LB evolution equations employs finite-difference techniques. In particular, we implemented the advection using the fifth-order weighted essentially non-oscillatory (WENO-5) scheme and the time-stepping was performed using the third-order Runge–Kutta (RK-3) method. This allowed us to obtain accurate results using a small number of nodes (16 for the Couette flow and 32 for the force-driven Poiseuille flow).
Taking advantage of the homogeneity of the flows studied in this chapter with respect to the z axis, we eliminated the z axis degree of freedom by integrating the Boltzmann–BGK equation with respect to p z. In order to correctly track the evolution of the temperature and heat flux fields, we employed two reduced distribution functions, ϕ and χ, obtained by integrating with respect to p z the Boltzmann distribution f multiplied by 1 and \(p_z^2 / m\), respectively. The extension of the methodology presented in this chapter to more complex flow domains is straightforward since the mixed quadrature paradigm allows the type of quadrature and the quadrature orders to be adjusted for each axis separately. The treatment of complex boundaries can be performed by using the standard staircase approximation [72, 73] or the more recent vielbein approach [50]. Finally, more complex relaxation time models, such as the Shakhov model [74, 75], can be implemented as described in, e.g., Refs. [54, 55].
We conclude that the models described in this chapter can be used to obtain numerical solutions of the Boltzmann–BGK equation for channel flows at arbitrary values of the Knudsen number.
Notes
- 1.
All quantities presented in this section are non-dimensionalised according to the conventions presented in Sect. 9.4.4.
References
G. Karniadakis, A. Beskok, N. Aluru, Microflows and Nanoflows: Fundamentals and Simulation (Springer, Berlin, 2005)
Y. Sone, Molecular Gas Dynamics: Theory, Techniques and Applications (Birkhäuser, Boston, 2007)
C. Cercignani, The Boltzmann Equation and Its Applications (Springer, New York, 1988)
S. Harris, An Introduction to the Theory of the Boltzmann Equation (Holt, Rinehart and Winston, New York, 1971)
R.L. Liboff, Kinetic Theory: Classical, Quantum and Relativistic Descriptions, 3rd edn. (Springer, New York, 2003)
G.A. Bird, Molecular Gas Dynamics and the Direct Simulation of Gas Flows (Oxford University Press, Oxford, 1994)
J.E. Broadwell, Study of rarefied shear flow by the discrete velocity method. J. Fluid Mech. 19, 401 (1964)
M.T. Ho, I. Graur, Heat transfer through rarefied gas confined between two concentric spheres. Int. J. Heat Mass Transf. 90, 58 (2015)
F. Sharipov, Rarefied Gas Dynamics: Fundamentals for Research and Practice (Wiley, Weinheim, 2016)
W. Peng, M.T. Ho, Z.L. Guo, Y.H. Zhang, A comparative study of discrete velocity methods for low-speed rarefied gas flows. Comput. Fluids 161, 33 (2018)
L.H. Zhu, Z.L. Guo, K. Xu, Discrete unified gas kinetic scheme on unstructured meshes. Comput. Fluids 127, 211 (2016)
L.H. Zhu, S.Z. Chen, Z.L. Guo, dugksFoam: an open source OpenFOAM solver for the Boltzmann model equation. Comput. Phys. Commun. 213, 155 (2017)
C.K. Aidun, J.R. Clausen, Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439 (2010)
S. Chen, G.D. Doolen, Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329 (1998)
Z. Guo, C. Shu, The Lattice Boltzmann Method and its Applications in Engineering (World Scientific, Singapore, 2013)
H. Huang, M.C. Sukop, X.Y. Lu, Multiphase Lattice Boltzmann Methods: Theory and Application (Wiley Blackwell, Chichester, 2005)
T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen, The Lattice Boltzmann Method, Principles and Practice (Springer, Oxford, 2017)
X.W. Shan, X.F. Yuan, H.D. Chen, Kinetic theory representation of hydrodynamics: a way beyond the Navier–Stokes equation. J. Fluid Mech. 550, 413 (2006)
S. Succi, The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Clarendon Press, Oxford, 2001)
D.A. Wolf-Gladrow, Lattice-Gas Cellular Automata and Lattice Boltzmann Models (Springer, Berlin, 2000)
X. He, L.S. Luo, A priori derivation of the lattice Boltzmann equation. Phys. Rev. E 55, R6333 (1997)
X. He, L.S. Luo, Theory of the lattice Boltzmann method: from the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 56, 6811 (1997)
V.E. Ambruș, V. Sofonea, High-order thermal lattice Boltzmann models derived by means of Gauss quadrature in the spherical coordinate system. Phys. Rev. E 86, 16708 (2012)
V.E. Ambruș, V. Sofonea, Implementation of diffuse-reflection boundary conditions using lattice Boltzmann models based on half-space Gauss–Laguerre quadratures. Phys. Rev. E 89, 041301(R) (2014)
V.E. Ambruș, V. Sofonea, Application of mixed quadrature lattice Boltzmann models for the simulation of Poiseuille flow at non-negligible values of the Knudsen number. J. Comput. Sci. 17, 403 (2016)
V.E. Ambruș, V. Sofonea, Lattice Boltzmann models based on half-range Gauss–Hermite quadratures. J. Comput. Phys. 316, 760 (2016)
S.S. Chikatamarla, I.V. Karlin, Lattices for the lattice Boltzmann method. Phys. Rev. E 79, 46701 (2009)
M. Namburi, S. Krithivasan, S. Ansumali, Crystallographic lattice Boltzmann method. Nat. Sci. Rep. 6, 27172 (2016)
P.C. Philippi, J. L. A. Hegele, L.O.E.d. Santos, R. Surmas, From the continuous to the lattice Boltzmann equation: the discretization problem and thermal models. Phys. Rev. E 73, 56702 (2006)
M. Sbragaglia, R. Benzi, L. Biferale, S. Succi, K. Sugiyama, F. Toschi, Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 75, 26702 (2007)
N.Z. Cao, S.Y. Shen, S. Jin, D. Martinez, Physical symmetry and lattice symmetry in the lattice Boltzmann method. Phys. Rev. E 55, R21 (1997)
H. Chen, Volumetric formulation of the lattice Boltzmann method for fluid dynamics: basic concept. Phys. Rev. E 58, 3955 (1998)
X.Y. He, Error analysis for the interpolation-supplemented lattice-Boltzmann equation scheme. Int. J. Mod. Phys. C 8, 737 (1997)
R.W. Mei, W. Shyy, On the finite difference-based lattice Boltzmann method in curvilinear coordinates. J. Comput. Phys. 143, 426 (1998)
M. Watari, M. Tsutahara, Two-dimensional thermal model of the finite-difference lattice Boltzmann method with high spatial isotropy. Phys. Rev. E 67, 36306 (2003)
M. Watari, M. Tsutahara, Possibility of constructing a multispeed Bhatnagar–Gross–Krook thermal model of the lattice Boltzmann method. Phys. Rev. E 70, 16703 (2004)
M. Watari, M. Tsutahara, Supersonic flow simulations by a three-dimensional multispeed thermal model of the finite difference lattice Boltzmann method. Phys. A 364, 129 (2006)
M. Watari, Velocity slip and temperature jump simulations by the three-dimensional thermal finite-difference lattice Boltzmann method. Phys. Rev. E 79, 66706 (2009)
F.B. Hildebrand, Introduction to Numerical Analysis, 2nd edn. (Dover, New York, 1987)
B. Shizgal, Spectral Methods in Chemistry and Physics: Applications to Kinetic Theory and Quantum Mechanics (Springer, Berlin, 2015)
E.P. Gross, E.A. Jackson, S. Ziering, Boundary value problems in kinetic theory of gases. Ann. Phys. 1, 141 (1957)
S. Takata, H. Funagane, Singular behaviour of a rarefied gas on a planar boundary. J. Fluid Mech. 717, 30 (2013)
C. Cercignani, M. Lampis, Kinetic models for gas-surface interactions. Transp. Theory Stat. Phys. 1, 101 (1971)
Z.H. Li, H.X. Zhang, Study on gas kinetic unified algorithm for flows from rarefied transition to continuum. J. Comput. Phys. 193, 708 (2004)
M.T. Ho, L. Zhu, L. Wu, P. Wang, Z. Guo, Z.H. Li, Y. Zhang, A multi-level parallel solver for rarefied gas flows in porous media. Comput. Phys. Commun. 234, 14 (2019)
A. Frezzotti, L. Gibelli, B. Franzelli, A moment method for low speed microflows. Contin. Mech. Thermodyn. 21, 495 (2009)
Y. Shi, Y.W. Yap, J.E. Sader, Linearized lattice Boltzmann method for micro- and nanoscale flow and heat transfer. Phys. Rev. E 92, 13307 (2015)
P.L. Bhatnagar, E.P. Gross, M. Krook, A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511 (1954)
V.E. Ambrus, V. Sofonea, R. Fournier, S. Blanco, Implementation of the force term in half-range lattice Boltzmann models. arXiv preprint arXiv:1708.03249 (2017)
S. Busuioc, V.E. Ambruș, Lattice Boltzmann models based on the vielbein formalism for the simulation of flows in curvilinear geometries. Phys. Rev. E. 99(3), 033304 (2019)
J. Meng, L. Wu, J.M. Reese, Y. Zhang, Assessment of the ellipsoidal-statistical Bhatnagar–Gross–Krook model for force-driven Poiseuille flow. J. Comput. Phys. 251, 383 (2013)
C. Feuchter, W. Schleifenbaum, High-order lattice Boltzmann models for wall-bounded flows at finite Knudsen numbers. Phys. Rev. E 94, 13304 (2016)
Y.W. Yap, J.E. Sader, High accuracy numerical solutions of the Boltzmann Bhatnagar–Gross–Krook equation for steady and oscillatory Couette flows. Phys. Fluids 24, 32004 (2012)
V.E. Ambruș, V. Sofonea, Half-range lattice Boltzmann models for the simulation of Couette flow using the Shakhov collision term. Phys. Rev. E 98(6), 063311 (2018)
V.E. Ambruș, F. Sharipov, V. Sofonea, Lattice Boltzmann approach to rarefied gas flows using half-range Gauss–Hermite quadratures: comparison to DSMC results based on ab initio potentials. arXiv preprint arXiv:1810.07803 (2018)
Z. Guo, T.S. Zhao, Explicit finite-difference lattice Boltzmann method for curvilinear coordinates. Phys. Rev. E 67, 66709 (2003)
R. Mei, W. Shyy, On the finite difference-based lattice Boltzmann method in curvilinear coordinates. J. Comput. Phys. 143, 426 (1998)
S. Jiang, L.S. Luo, Analysis and accurate numerical solutions of the integral equation derived from the linearized BGKW equation for the steady Couette flow. J. Comput. Phys 316, 416 (2016)
S.H. Kim, H. Pitsch, I.D. Boyd, Accuracy of higher-order lattice Boltzmann methods for microscale flows with finite Knudsen numbers. J. Comput. Phys. 227, 8655 (2008)
P.K. Kundu, I.M. Cohen, D.R. Dowling, Fluid Mechanics, 6th edn. (Academic Press, New York, 2015)
M. Rieutord, Fluid Mechanics: An Introduction (Springer, Berlin, 2015)
C. Cercignani, Theory and Application of the Boltzmann Equation (Scottish Academic Press, Edinburgh, 1975)
C. Cercignani, M. Lampis, S. Lorenzani, Variational approach to gas flows in microchannels. Phys. Fluids 16, 3426 (2004)
K. Aoki, S. Takata, T. Nakanishi, Poiseuille-type flow of a rarefied gas between two parallel plates driven by a uniform external force. Phys. Rev. E 65, 26315 (2002)
M. Tij, A. Santos, Perturbation analysis of a stationary nonequilibrium flow generated by an external force. J. Stat. Phys. 76, 1399 (1994)
M. Tij, M. Sabbane, A. Santos, Nonlinear Poiseuille flow in a gas. Phys. Fluids 10, 1021 (1998)
M.M. Mansour, F. Baras, A.L. Garcia, On the validity of hydrodynamics in plane Poiseuille flow. Phys. A 240, 255 (1997)
S. Hess, M.M. Mansour, Temperature profile of a dilute gas undergoing a plane Poiseuille flow. Phys. A 272, 481 (1999)
K. Aoki, S. Takata, T. Nakanishi, Poiseuille-type flow of a rarefied gas between two parallel plates driven by a uniform external force. Phys. Rev. E 65, 26315 (2002)
Y. Zheng, A.L. Garcia, B.J. Alder, Comparison of kinetic theory and hydrodynamics for Poiseuille flow. J. Stat. Phys. 109(3/4), 495 (2002)
K. Xu, Super-Burnett solutions for Poiseuille flow. Phys. Fluids 15(7), 2077 (2003)
X. Yin, J. Zhang, An improved bounce-back scheme for complex boundary conditions in lattice Boltzmann method. J. Comput. Phys. 231, 4295 (2012)
L. Li, R. Mei, J.F. Klausner, Boundary conditions for thermal lattice Boltzmann equation method. J. Comput. Phys. 237, 366 (2013)
E.M. Shakhov, Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3, 95 (1968)
E.M. Shakhov, Approximate kinetic equations in rarefied gas theory. Fluid Dyn. 3, 112 (1968)
S. Gottlieb, C.W. Shu, Total variation diminishing Runge–Kutta schemes. Math. Comput. 67, 73 (1998)
A.K. Henrick, T.D. Aslam, J.M. Powers, Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys 207, 542 (2005)
C.W. Shu, S. Osher, Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439 (1988)
J.A. Trangenstein, Numerical Solution of Hyperbolic Partial Differential Equations (Cambridge University Press, New York, 2007)
Y. Gan, A. Xu, G. Zhang, Y. Li, Lattice Boltzmann study on Kelvin–Helmholtz instability: roles of velocity and density gradients. Phys. Rev. E 83, 56704 (2011)
G.S. Jiang, C.W. Shu, Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202 (1996)
J.C. Butcher, Numerical Methods for Ordinary Differential Equations, 2nd edn. (Wiley, Chichester, 2008)
V.E. Ambruș, R. Blaga, High-order quadrature-based lattice Boltzmann models for the flow of ultrarelativistic rarefied gases. Phys. Rev. C 98, 035201 (2018)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Appendix: Numerical Scheme
Appendix: Numerical Scheme
The simulation results presented in this chapter were obtained using an explicit third-order total variation diminishing (TVD) Runge–Kutta (RK-3) time marching procedure [76,77,78,79], together with the fifth-order weighted essentially non-oscillatory (WENO-5) scheme [80, 81] for computing the advection.
In order to implement the time-stepping algorithm, it is convenient to cast the Boltzmann–BGK equation (9.1) in the following form:
Following the discretisation of the time variable using equal time steps δt, the distribution function at time step l is f l ≡ f(t l), when the time coordinate has the value t l = lδt, taken with respect to the initial time t 0 = 0. For simplicity, the dependence of the distribution function on the spatial coordinates and on the momentum degrees of freedom was omitted. The third-order Runge–Kutta TVD integrator described using the Butcher tableau summarised in Table 9.2 gives the following algorithm for computing the value f l+1 of the distribution function at time t l+1:
For more information regarding the Butcher tableaux representation, we refer the reader to Ref. [82].
The advection term is computed, as follows:
Since the flows considered in this chapter are effectively one-dimensional (being homogeneous with respect to the y and z axes), the discussion on the implementation of the WENO-5 scheme for the computation of the above derivatives will cover only the derivative with respect to the x coordinate. Considering that the spatial domain is discretised equidistantly with respect to the η coordinate Eq. (9.59), the derivative with respect to x can be written as:
The flux \(\mathcal {F}_{s+1/2}\) corresponding to the interface between the cells centred on x s ≡ x(η s) and x s+1 is computed in an upwind-biased approach using the WENO-5 algorithm [50, 80, 83], which we summarise below for the case when the advection velocity p x∕m > 0:
The interpolating functions \(\mathcal {F}^q_{s + 1/2}\) (q = 1, 2, 3) are given by:
while the weighting factors \(\overline {\omega }_q\) are defined as:
The ideal weights δ q are:
while the indicators of smoothness σ q are given by:
In the case when one, two or all three of the σ q indicators vanish, the computation of the functions \(\widetilde {\omega }_q\) using Eq. (9.79) implies illegal division by zero operations. In this case, the weighting factors \(\overline {\omega }_q\) can be computed directly as shown in Table 9.3. Alternatively, a small quantity ε ≃ 10−6 can be added to the σ q functions. A more thorough discussion on the side effects of this approach can be found in Ref. [77].
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Ambruș, V.E., Sofonea, V. (2019). Quadrature-Based Lattice Boltzmann Models for Rarefied Gas Flow. In: Toschi, F., Sega, M. (eds) Flowing Matter. Soft and Biological Matter. Springer, Cham. https://doi.org/10.1007/978-3-030-23370-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-23370-9_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23369-3
Online ISBN: 978-3-030-23370-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)