Keywords

1 Introduction

The identification of communities within a network is a typical task that has been widely applied in different contexts. In particular, dense subgraphs (i.e., cohesive communities) have perceived the attention of the scientific literature oriented to the analysis of social [1, 15, 17, 18] and biological networks [3, 19]. A standard approach to compute dense subgraphs is focused on the identification of structures known as cliques: complete subgraphs whose vertices are pairwise connected by edges. However, the use of a clique is too binding for specific applications. For example, a critical issue arises when missing data are persistent in the considered analysis. In this case, the missing information does not allow to represent all links of a dense community, thus requiring to search alternative notions of dense subgraphs. For this reason, different definitions of community have been introduced in literature “by relaxing” to some extent the concept of clique (see, e.g., [13] for the concept of relaxed clique).

Fig. 1.
figure 1

The figure shows a 2-club of 5 vertices. Notice that, each subgraph of 4 vertices is not a 2-club.

Full size image

In this paper, we focus on a distance-based relaxation of the clique model. In other words, instead of seeking structures where distances between pairs of vertices are equal to 1 (i.e., cliques), we will consider dense subgraphs where the distance between vertices can be at most s. Such a structure is generally known as s-club. In particular, due to the importance of this problem for social [1, 15, 17, 18] and biological networks [3, 19], we will consider the case of \(s=2\).

From the computational point of view, the literature concerning s-clubs has mainly focused on the identification of s-clubs of maximum size (a problem known as Max-s-club), and its complexity has been extensively studied. Although the results have shown the NP-hardness of the problem for each \(s\ge 1\) [5], polynomial-time approximation algorithms, with factor \(|V|^{1/2}\), are available for every \(s\ge 2\) [2]. Recently, the problem has been investigated for restricted graph classes  [11, 12], and even for its parameterized complexity. The problem has been shown to be fixed-parameter tractable, when the parameter is the size of the sought s-club [6, 14, 20].

In many real applications, the objective is to find a set of cohesive subgraphs of the original input graph (rather than a single subgraph covering the input). Following the approach proposed in [10], this paper considers the problem of computing the set of largest k 2-clubs, with \(k \ge 1\). We will denote this problem as Top k-2-clubs. Notice that other problems that seek for 2-clubs have been considered recently. In [9], it is considered the problem of finding a maximum set of disjoint s-clubs of at least a given size, while in [7] it is considered the problem of finding a minimum set of s-clubs that covers the input graph.

The identification of Top-k-2-clubs turns to be NP-hard (as Max-2-clubs is NP-hard), for this reason we design a genetic algorithm based heuristic by defining: first, a specific set of search operators for obtaining GA’s approximate solutions, then a greedy approach to extrapolate the k top different approximations. While GA optimization is not new in literature, the interest on designing new heuristics and special operators for the applied models is still required to deal with the intractability of computational problems, with new applications in different contexts [8, 22].

The paper is organized as follows. In Sect. 2 we provide the definitions and we introduce the problem we are interested in. In Sect. 3, we discuss the GA-based approach to seek approximate solutions for the Top-k-2-clubs. In Sect. 4, we report numerical evaluations based on Erdös-Rényi random graphs. Section 5 discusses the preliminary results and the future development of our research.

2 Preliminaries

Let \(G=(V,E)\) be a graph, and \(V' \subseteq V\) a subset of the input vertices V. Denote by \(G[V']\) the subgraph of G induced by \(V'\), and \(d_G(u,v)\) the distance (i.e., length of a shortest path) between two vertices u, v. The diameter of \(G=(V,E)\) is defined as \(\max _{u,v \in V} d_G(u,v)\), i.e., the maximum distance between any two vertices in V.

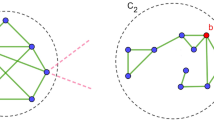
Given a graph \(G=(V,E)\), a 2-club in G is a subgraph G[W], with \(W \subseteq V\), that has diameter of at most 2. The property of being a 2-club is not hereditaryFootnote 1. This means that if a graph G is a 2-club, then a subgraph of G is not necessarily a 2-club (see Fig. 1).

We introduce now the formal definition of the problem, denoted as Top-k-2-clubs. The Top-k-2-clubs maximizes an objective function that considers the size of the 2-clubs in the solution (since we want to compute large 2-clubs) and a distance function dist to provide graphs that are significantly different. The parameter \(\uplambda \) allows us to define how much relevance has the distance with respect to the size of the 2-clubs.

Problem 1

Top-k-2-club

Input: a graph \(G=(V,E)\), a value \(\uplambda > 0\).

Output: a set \(\mathcal {W} = \{ G[W_1], \dots , G[W_k] \}\) of k 2-clubs, with \(1 \le k <|V|\) and \(W_i \subseteq V\), that maximizes the following value

$$ r(\mathcal {W})= \sum _{i=1}^k |W_i| + \uplambda \sum _{i=1}^{k-1} \sum _{j=i+1}^k dist(G[W_i],G[W_j]) $$

where

$$\begin{aligned} dist(G[W_i],G[W_j]) = \left\{ \begin{array}{ll} 2-\frac{|W_i \cap W_j|^2}{|W_i||W_j|} &{} \text {if } W_i \ne W_j,\\ 0 &{} \text {else}. \end{array} \right. \end{aligned}$$

Notice that Top-k-2-clubs, when \(k=1\), is exactly Max-2-club. Since Max-2-club on an input graph \(G=(V,E)\) is NP-hard [3] and not approximable within factor \(|V|^{1/2 - \upvarepsilon }\), for each \(\upvarepsilon >0\) [2], the same properties hold for Top-k-2-clubs.

3 A Genetic Algorithm for the Top-k-s-club Problem

As reported above, the Top-k-2-clubs is NP-hard, thus making optimization potentially impracticable. Our approach here is to provide approximate solutions by designing dedicated genetic operators. Let \(G[V']\) be a 2-club of the input graph \(G=(V,E)\), for some set of vertices \(V' \subseteq V\). We represent GA’s solutions as binary chromosomes c, of size |V|, such that for each \(v_i \in V'\), \(c[i] = 1\) (\(c[i] = 0\) if \(v_i \in V \setminus V'\)). With a slight abuse of notation, we denote by G[c] the subgraph of G induced by the representation of chromosome c. Furthermore, V[c] and E[c] represent the set of vertices, \(V'\), and edges of \(G[c] = G[V']\). With the given representation, a set of k chromosomes, which are involved in the offspring generation, is interpreted as a set of hypothesis of feasible solutions (i.e., hypotheses of potential 2-clubs). To quantify the validity of such (assertions) hypothesis, chromosomes will be then evaluated by the fitness function.

3.1 Fitness Function

We design the fitness function to promote new offspring in such a way that “feasible” chromosomes, able to properly express 2-clubs (i.e., with a correct diameter value \(\le 2\)) will gradually adapt through specific mutation and crossover operators.

Consider a chromosome c, and the graph \(G=(V,E)\). In order to apply a fitness function which promotes the representation of large subgraphs G[c], when \(0 \le \mathrm {diam}\le 2\), we consider the following.

$$\begin{aligned} f(n_v,\mathrm{diam};S)={\left\{ \begin{array}{ll} n_v &{} \text {if } 0 \le \text {diam}\le 2 ; \\ \frac{1}{n_v} &{} \text {if }2 <\text {diam} , \end{array}\right. } \end{aligned}$$
(1)

where \(n_v\) is the number of vertices of G[c].

Notice that, when \(\mathrm {diam} > 2\) (i.e., unfeasible solutions) we obtain fitness values which decrease asymptotically for large subgraphs with size \(n_v\), thus penalizing the corresponding chromosomes.

3.2 Mutation

The following types of mutations are considered with equal probability.

  • Mutation 1. In this case, mutation is applied to correct hypotheses sparingly and consistently. For this, consider the set \(V_{+} = \{v_ i: c[i] = 1\}\) and the associated graph \(G[V_{+}] \), which should correspond to some feasible 2-club. In order to check such a feasibility, we randomly sample a vertex \(v' \in V_{+}\), and for each pair \((v_i,v'), v_i \in V_{+} \setminus \{v'\} \) we verify whether the minimum length between \(v_i\) and \(v'\) is of at most 2. If this is not the case, c[i] is flipped to 0.

  • Mutation 2. Similarly to the previous case this operator has the objective to sparingly increment the size of a solution. We consider now \(V_{-} = \{v_j: c[j]=0 \}\) and the current subgraph \(G[V_{+}]\) induced by c. In order to consistently add vertices to \(V_{+}\), we sample some \(v'\) from \(V_{-}\) (equivalently, we will have some \(j'\) such that \(v' = v_{j'} \in V_{-}: c[j']=0\)) to check whether the shortest distance of \(v'\) from vertices in \(V_{+}\) is not larger than 2. In this case, the corresponding bit \(c[j']\) is flipped to 1.

  • Standard Mutation. This is a standard mutation procedure where bits of the selected chromosome are randomly switched on or off.

3.3 Cross-Over

The cross-over operations operations are selected with equal probability.

  • Standard cross-over. Parts of parents’ chromosomes are copied and mixed in new offspring with standard one-point crossover.

  • Logical AND/OR cross-over. New offspring are generated by applying logical AND and logical OR operations between parents.

Table 1. Performances: Models; Av. Fitness (Fit); Av. Inp. Diameter (InD); Av. Out. Diameter (OutD); Av. Jaccard (AvJ); Av. Covering (AvC); Av. User (T1) and System Time (T2)
Full size table

3.4 Selection of Top k 2-Clubs

The final step of the algorithm selects k 2-clubs (chromosomes) from the population. Denote by \(\mathcal {W}\) the solution of Top-k-2-clubs we are computing. We apply a greedy procedure consisting of k iterations. In the first iteration, a 2-club of the population (denoted by \(G[W_1]\)) having maximum cardinality is added to \(\mathcal {W}\).

Consider iteration t, with \(2 \le t \le k\), of the greedy procedure. Assume that \(\mathcal {W} = \{ G[W_1], \dots , G[W_{t-1}]\}\), iteration t adds to \(\mathcal {W}\) a 2-club \(G[W_t]\) of the population that maximizes the following value

$$ |W_t| + \uplambda \sum _{i=1}^{t-1} \sum _{j=i+1}^t dist(G[W_i],G[W_j]). $$

4 Numerical Experiments

The goal of our experiments was to check the capability of GAs to provide feasible solutions in reasonable computational time. The whole procedure described above was coded in R using the “GA” package [21]. In this work we use synthetic data by sampling Erdos-Renyi (ER) random graphs, \(ER(n,p=0.1)\), with different number of vertices, n [4].

To ensure both the correctness of the Genetic Algorithm and the computational tractability of our approach, we followed a standard practice of the evolutionary methods; that is, maintaining the tractability of genetic operators while promoting, at the same time, new evaluable offspring, which in our case provide feasible diameter values for the obtained solutions.

Similarly, the termination of the genetic algorithm is guaranteed by standard criteria. We have set both the revaluation number of the fitness with respect to new populations (equivalently, the number of GA iterations) and the number of new consecutive generation without fitness improvement. Finally, to get a more robust performance evaluation, each Erdos graph was repeatedly sampled 3 times. Performances are reported in Table 1. The following comments summarize our results.

  1. 1.

    All models are correct, being (2-clubs) with diameter \(\le 2\).

  2. 2.

    Since the considered problem is computationally intractable, it is not possible to compare the optimal solution with those provided by the described approach. In order to give, at least, a qualitative idea of the validity of the obtained approximations, we considered both the average covering (output / input vertices) of the input graph (obtained through the returned solutions, i.e., 10 largest solutions) and a measure of how such solutions differ from each other. In this way, the higher the number of covering ratio (and the more dissimilar are the solutions), the more input graph cover is qualitatively effective. To this aim, the Jaccard index was applied. Specifically, we remind that the smaller this index, the more dissimilar are the solutions. Observing Table 1 more convincing solutions seem to be those obtained for a small number of input vertices. Moreover, the coverage performances do not decrease in an “obvious” way in the considered models.

  3. 3.

    Covering performances are reported. In this case, we get, on average, a covering value at least of 10\(\%\).

  4. 4.

    A reasonable system time is observed after execution (T2 \(\le 4\) s).

5 Conclusion

Identifying cohesive subgraphs within a network is a typical task with many applications in different important fields. In this paper, we reported our work in progress by considering the case where a collection of Top-k-2-clubs (i.e., largest different cohesive subgraphs) is maximized, providing large communities of a network covering. The computational hardness of the problem makes it impracticable to get optimal solutions. Here, we designed a set of dedicated GA operators to return approximate solutions at reasonable costs.

The preliminary results reported in this paper show we can get correct solutions in a reasonable time. Although compelling solutions seem to be provided for small graphs only (\(n \le 150\)), the 10\(\%\) of the input graph size is covered.

Some aspects of this research can certainly be considered in a future extension. For example, a detailed analysis should be applied to optimize the parameters of the applied models. Although different igraph (R package) default values (i.e., probabilities of the search operators) have been used, accurate tuning should be properly considered to evaluate performance improvement. In this case, for example, the irace R package [16] can be easily applied for this purpose. Furthermore, only s–clubs with \(s = 2\) were considered. Our approach can further be scaled up to any value \(s \ge 2 \) and k (number of 2-clubs). Finally, real case analysis cannot be neglected in this research, and this will be another extension for a future version of the work.