Recognizing 3-colorable Basic Patterns on Planar Graphs

Abstract

We recognize the wheel graphs with different kinds of centers or axle faces as the basic pattern forming a planar graph. We focus on the analysis of the vertex-coloring for these graphic patterns, and identify cases for the 3 or 4 colorability of the wheels. We also consider different compositions among wheels and analyze its colorability process.

If a valid 3-coloring exists for the union of wheels G, then our proposal determines the constraints that a set of symbolic variables must hold. These constraints are expressed by a conjunctive normal form $F_G$. We show that the satisfiability of $F_G$ implies the existence of a valid 3-coloring for G. Otherwise, it is necessary to use 4 colors in order to properly color G. The revision of the satisfiability of $F_G$ can be done in polynomial time by applying unit resolution and general properties from equalities and inequalities between symbolic variables.

1 Introduction

By a proper coloring (o just a coloring) of a graph G, we refer to an assignment of colors (elements of a set) to the vertices of G, one color to each vertex, such that adjacent vertices are colored differently. The smallest number of colors in any coloring of G is called the chromatic number of G and is denoted by $\chi (G)$. When it is possible to color G from a set of k colors, then G is said to be k-colorable, while such coloring is called a k-coloring. If $\chi (G)=k$, then G is said to be k-chromatic, and every k-coloring is a minimum coloring of G.

The computation of the chromatic number $\chi (G)$ is polynomial computable if G is k-colorable with $k \le 2$, but in other case the problem becomes NP-complete [4]. As a consequence, there are many unanswered questions related to the colouring of a graph.

Graph vertex colouring problem is an active field of research with many interesting subproblems and applications in areas like frequency allocation,planning, computer vision,scheduling, image processing, etc [2, 7]. In this context, planar graphs play an important role in the graph theory area and complexity theory since it involves the frontier between efficient and intractable computational procedures. In fact, planar graphs have several interesting properties: are four-colorables, scattered, and their inner structure is described elegantly and succinctly [1].

In the case of the vertex coloring problem, the 2-colorability is solvable in polynomial time. It has also been solved in polynomial time the 3-colorability for some graph topologies such as AT-free graphs and perfect graphs. Also the determination of $\chi (G)$ for some classes of graphs, for example: comparability graphs [10], chordal graphs, and interval graphs has been solved efficiently. In all those cases, special structures (patterns) have been found to characterize the classes of graphs that are colorable in polynomial time complexity.

In this article, we introduce for the first time what we believe are the basic graph patterns, that we have called polyhedral wheels, to form any planar graph. We have determined logical specification written as constraints that a set of symbolic variables must hold in order to recognize a valid 3-coloring for a polyhedral wheel. We consider different compositions among polyhedral wheels and analyze its chromatic number, in order to design a novel method for the recognition between 3 or 4-colorable polyhedral wheels.

2 Preliminaries

Let $G=(V,E)$ be an undirected simple graph (i.e. finite, loop-less and without multiple edges) with vertex set V (or V(G)) and set of edges E(orE(G)). We assume the reader is familiar with standar terminology and notation concerning graph theory and planar graphs in particular, see e.g. [8] for standard concepts in graph theory. Here we present only some notations that we will use.

If there is an edge $\{v,w\}\in E$ joining two different vertices then we say that v and w are adjacents. The Neighborhood of $x \in V$ is $N(x) = \{y \in V : \{x,y\}\in E\}$ and its closed neighborhood, denoted by N[x], is $N(x)\cup \{x\}$. The cardinality of a set A is denoted by |A|. The degree of a vertex $x \in V$ is |N(x)|, and it will be denoted by $\delta (x)$,

We say that $G'= (V', E')$ is a subgraph of $G = (V, E)$ if $V' \subset V$ and $E' \subset E$. If $V' = V$ then $G'$ is called a spanning subgraph of G. If $G'$ contains all the edges of G that join two vertices in $V'$ then $G'$ is said to be induced by $V'$. In this way, $G - V'$ is the induced subgraph from $V - V'$. Similarly if $E' \subset E$ then $G - E' = (V, E - E')$. If $V' = \{v \}$ and $e = \{u, v\}$ then this notation is simplified to $G - v$ and $G - e$, respectively.

Given a graph $G=(V,E)$, $S \subseteq V$ is an independent set in G if for whatever two vertices $v_1$, $v_2$ in S, $\{v_1,v_2\} \notin E$. Let I(G) be the set of all independent sets of G. An independent set $S \in I(G)$ is maximal, abbreviated as MIS, if it is not a subset of any larger independent set and, it is maximum if it has the largest size among all independent sets in I(G).

A graph in which every pair of distinct vertices are adjacent is called a complete graph. The complete graph on n vertices is denoted by $K_n$.

By a proper coloring (o just a coloring) of a graph G, we refer to an assignment of colors (elements of a set) to the vertices of G, one color to each vertex, such that adjacent vertices are colored differently. The smallest number of colors in any coloring of G is called the chromatic number of G and is denoted by $\chi (G)$. When it is possible to color G from a set of k colors, then G is said to be k-colorable, while such coloring is called a k-coloring. Thus, every k-coloring is a minimum coloring of G.

If the vertices V of a graph $G=(V,E)$ can be partitioned into two disjoint sets $U_{1}$ and $U_{2}$ (called partite sets), which makes every edge of G join a vertex of $U_{1}$ to a vertex of $U_{2}$, then G is said to be a bipartite graph. If G is a k-chromatic graph, then it is possible to partition V into k independent sets $V_{1},V_{2},...,V_{k}$ (the color classes), but it is not possible to partition V into $k-1$ independent sets.

3 Planar Graphs

A drawing $\varGamma$ of a graph G maps each vertex v to a distinct point $\varGamma (v)$ of the plane and each edge $\{u,v\}$ to a simple open Jordan curve $\varGamma (u,v)$, with endpoints $\varGamma (u)$ and $\varGamma (v)$. A drawing is planar if it can be embedded (or it has an embedding) in the space in a way that no two edges intersect except at an endvertex in common. A graph G is planar if G admits an embedding in the plane. A planar drawing partitions the plane into connected regions called faces. The unbounded face is usually called outer face or external face.

In general, a planar graph has many embeddings in the plane. Two embeddings of a planar graph are equivalent when the boundary of a face in one embedding always corresponds to the boundary of a face in the other. A planar embedding is an equivalent class of planar drawings and it is described by the clockwise circular order of the edges incident to each vertex. A maximal planar graph is one to which no edge can be added without losing planarity. Thus, in any embedding of a maximal planar graph G with $n \ge 3$, the boundary of every face of G is a triangle.

One of the most outstanding results is Kuratowski’s theorem [5], which gives a criterion for a graph to be planar in the case that it contains no subgraph that is a subdivision of $K_{5}$ or $K_{3,3}$, where $K_{5}$ is the complete graph of order 5 and $K_{3,3}$ is the complete bipartite graph with 3 vertices in each of the sets of the partition, then the graph is planar. Similarly, the theorem of Wagner [11] states that a graph G is planar if and only if it does not have $K_{5}$ or $K_{3,3}$ as minor. However, both characterizations are different since a graph may admit $K_{5}$ as minor without having a subgraph that is a subdivision of $K_{5}$.

The famous Four-Color Theorem (4CT) says that every planar graph is vertex 4-colorable. Robertson et al. [9] describes an $O(n^2)$ 4-coloring algorithm. This seems to be very hard to improve, since it would probably require a new proof of the 4CT. On the other hand, to decide if a planar graph requires only three colors is a NP-hard problem. However, the Grötzsch theorem [3] guarantees that every triangle-free planar graph is 3-colorable. Then, the hard part in the coloring of planar graphs is to decide if an unrestricted planar graph is 3 or 4 colorable.

Not all graphs are planar. However planar graphs arise quite naturally in real-world applications, such as road or railway maps, electric printed circuits, chemical molecules, etc. Planar graphs play an important role in these problems, partly due to the fact that some practical problems can be efficiently solved for planar graphs even if they are intractable for general graphs [8]. In recent years, planar graphs have attracted computer scientists’ interest, and a lot of interesting algorithms and complexity results have been obtained from planar graphs.

3.1 The Internal-Face Graph of a Planar Graph

A planar graph G has a set of closed non-intersected regions $F(G) = \{f_1, \ldots ,f_k\}$ called faces. Each face $f_i \in F(G)$ is represented by the set of edges that bound its inside area. All edge $\{u,v\}$ in G, that is not the border of some face from G, is called an acyclic edge.

Two faces $f_i, f_j \in F(G)$ are adjacent if they have common edges, this is, $(E(f_i) \cap E(f_j)) \ne \emptyset$. Otherwise, they are independent faces. Notice that two independent faces can have common vertices but they do not have common edges. A set of faces is independent if each pair of them are independent.

An acyclic edge is adjacent to a face if they have just one common vertex. Two acyclic edges are adjacent if they share a common endpoint. We build an internal-face graph $G_f=(X,E(G_f))$ from G, in the following way:

• 1. Each face $f_i$ has attached a node $x \in V(G_f)$.

• 2. Each acyclic edge from G has attached a vertex of $G_f$ labeled by the label of its vertices.

• 3. There is an edge $\{u,v\} \in E(G_f)$ joining two adjacent vertices of $G_f$, when its corresponding faces (or acyclic edges) are adjacent in G.

$G_f$ is the internal-face graph of a planar graph G. We must emphasize that $G_f$ is not the dual graph of G since in the construction of $G_f$ the external face is not considered. Notice that $G_f$ is also a planar graph with vertices representing faces or edges from G (as we can see in Fig. 2). The internal-face graph $G_f$ of G provides a mapping of the relation among the faces of G that is useful in the search for the 3-coloring pattern graphs.

A basic pattern in planar graphs is a wheel graph that is a single vertex (called the center vertex of the wheel) adjacent to vertices forming a cycle. Each face (called an axle of the wheel) is a triangle. There are two classes of vertices in a wheel; the center vertex and the vertices forming the cycle. Note that a wheel of a planar graph G is represented as a cycle in its internal-face $G_f$. Wheels with a number of even triangles are 3-colorable. Meanwhile any planar graph, containing $K_{4}$ or odd wheels, will request four colors in order to properly color those graphs. However, those topologies are not the unique 4-colorable cases.

We extend the class of wheels by considering any polygon as an axle face of the wheel. Such type of wheel is called a polyhedral wheel. This means that there are vertices in the cycle surrounding the center vertex which are not adjacent to the center. The center vertex is a common vertex to all axle face of the polyhedral wheel.

Fig. 1.

Graph G with faces identified

Fig. 2.

The internal-face graph $G_{f}$ of G

We differentiate the cycle’s vertices in a polyhedral wheel as axle vertices if they are adjacent to the center vertex; and as extra-axle, when they are not adjacent to the center. In the case of the edges in a polyhedral wheel, we have the edges of the cycle and the edges incident to the center, which are called spoke edges. For example, in Fig. 1, a polyhedral wheel is formed by the edges: 10-6-7-8-9-10, whose center vertex is 11. All axle of this wheel is triangular with the exception of the face 1. The spoke edges are: $\{6,11\}, \{10,11\}, \{9,11\}, \{8,11\}$.

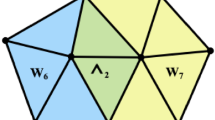
A polyhedral wheel of a planar graph G is represented as a cycle in its internal-face graph $G_f$. However, a cycle in $G_f$ can also codify other kind of wheel of G. A wheel of G where the center is a polygon instead of a single vertex is called a polyhedral subgraph. For example, in Fig. 2 there are 5 polyhedral wheels whose centers are labeled by the single center vertex of the wheel. There is also a polyhedral subgraph whose center is the polygon formed by the set of vertices $\{6,7,8,9,10\}$. Any of these wheels is an odd wheel if it has an odd number of axle faces, otherwise, it is an even wheel.

4 Coloring Planar Graphs

It is easy (in linear-time on the size of the graph) to recognize if an input graph is 2-colorable, since it involves the recognition of only even cycles in the graph. Similarly, it is known by Grotszch’s theorem [3] that any planar graph triangle-free is 3-colorable. However, the recognition of the 3-coloring of a planar graph is a classical NP-Complete problem [4]. It becomes difficult to recognize between the three or four coloring of a planar graph when it contains triangles, because there is not (at least until now) a sufficient condition to recognize the 3-colorability of a planar graph.

Let $Three = \{1,2,3\}$ be the set that contains three different colors. Given a planar graph G, let $x_{v,c}$ be the logical variable denoting that the vertex v has the color $c \in \{1,2,3,4\}$. For each vertex $v \in V(G)$ a Tabu(v) set is associated. Tabu(v) indicates the prohibited colors for the vertex v. In fact, Tabu(v) contains the variables associated to the vertices in N(v) that have been already colored, i.e. $Tabu(v)= \{c : (x_{u,c})$, and $\{u,v\} \in E(G) \}$.

We introduce a typical coloring for a wheel, where its center vertex is assigned the first color. The colors 2,3 are assigned in alternating way to the cycle’s vertices. This coloring begins in any triangle face of the wheel, and follows an opposite clockwise direction from the cycle’s vertices. Only when the last vertex of the cycle is visted, it is determined if a fourth color is necessary.

In this section, we start our analysis for searching basic graphic patterns, and analyzing if it is possible to determine if they are 3 or 4 colorable. We start considering the coloring of simple wheels, because the wheels are basic pattern to form planar graphs,

Lemma 1

The union of even simple wheels, where its center vertices are independent, is 3-colorable.

Proof

When all center vertices of the wheels form an independent set on the graph then the first color can be assigned to those vertices. Common edges between wheels are only given by the cycle’s edges of the wheels. If the center vertices are removed of the graph, since they were already colored, the remaining subgraph is bipartite because it has only the cycle’s edges. As only even cycles remain in the subgraph, then the subgraph is 2-colorable. We obtain a 3-coloring for this kind of planar graphs by using different colors between the center vertices and the cycle’s vertices.

The lemmas to be developed in the next section guarantee the correctness of our proposal. We denote the function Color(v) that assigns a unique color from Three to the vertex v.

Lemma 2

An acyclic component is 3-colorable if all of its vertices have at most one color as a restriction.

Proof

The acyclic component is considered as a tree rooted in $v_r$. A pre-order coloring is made from $v_r$, where $Color(v_r) = MIN\{Three - Tabu(v_r)\}$. If we advance in pre-order for each new level to be colored, all vertex y in the new level will have at most two restricted colors from its parent node and the color that could exist in Tabu(y). Thus, a color has always been available of the three possible from Three. When all nodes of the tree had been visited in pre-order, our proposal has already colored all vertex.

Lemma 3

Let $A = \{f_1, f_2, \ldots ,f_n \}$ be a set of n non-adjacent faces where each face has at least one vertex that does not restrict color 3, then A is 3-colorable.

Proof

As $A = \{f_1, f_2, \ldots ,f_n \}$ is a set of non-adjacent faces, then some faces in A could share a common vertex at the most. The proof is developed by induction on the number of faces in A.

• 1. A single face is 3-colorable, since every cycle with at least one unrestricted vertex is 3-colorable.

• 2. Suppose that the hypothesis on the sets up to $n-1$ faces is held.

• 3. Let A be a set of n faces where each face has at least one vertex that does not restrict color 3. If there is a face $f_a \in A$ that is independent (without common edges nor common vertices) from all other faces of A, then $f_a$ is 3-colorable (as in the case 1), and it can be removed from A. The remaining set in A has $n-1$ faces, and the inductive hypothesis is held.

  Otherwise, the n faces in A share a common vertex. Let $x \in f_i: \forall f_i \in A$ be the common vertex. If $3 \notin Tabu(x)$, then by assigning the color 3 to x and removing it from the graph, all the faces in A become open and they form an acyclic graph, which is 3-colorable by Lemma 2.

  Assuming $Tabu(x) =3$, but $\forall f_i \in A$, there is $y_i \in V(f_i)$ such that $Tabu(y_i) = \emptyset$, by hyphotesis. By assigning color 3 to each one of these $y_i's$, and eliminating them from each $V(f_i)$, an acyclic component is formed and this component is 3-colorable by Lemma 2.

When $G_f$ is a tree, we say that G (its corresponding planar graph) is a polygonal tree [6]. This means that, although G has cycles, all those cycles can be arranged as a tree whose nodes are polygons instead of single vertices of G. The following theorem show that it is enough an order to visit all faces from the planar graph in order to obtain an efficient procedure for the 3-coloring of G.

Theorem 1

If the internal-face graph of a planar graph G has a tree topology, then G is 3-colorable.

Proof

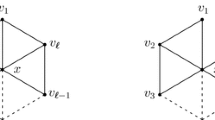
Let $G_f$ be the internal-face graph of a planar graph G. As a face of G is a simple cycle then it is 3-colorable. Also, all acyclic edge of G is also 3-colorable, because all acyclic graph is 2-colorable. A 3-coloring procedure for G can be done by traversing the nodes of $G_f$ in pre-order. The face of the father node of $G_f$ is colored first and after, the faces of its children nodes. In each current level, the two adjacent faces (father and children in G) are considered. Both regions have two common extremal vertices x, y in its common boundaries.

Those common vertices are colored first, and then, the remaining vertices in both faces have two prohibited colors at the most. Notice that there is not a pair of adjacent vertices u and v in any of the two faces, such that $\{u,v\} \subseteq (N(x) \cap N(y))$. This happens because $\{x,y,u,v\}$ form $K_4$ and this subgraph can not be part of any polygonal tree. Thus, for all remaining vertices in both faces it is available at least one color of the three possible in Three. The 3-coloring process ends when all the nodes of the tree $G_f$ have been visited in pre-order.

If a planar graph G has not a polygonal tree topology, this means that there are cycles in $G_f$ and, therefore, wheels in G. For this kind of planar graphs, it is possible to recognize 3-colorable graphic patterns.

Lemma 4

All polyhedral wheel is 3-colorable.

Proof

If $r_x$ is a polyhedral wheel, then there is an axle face that is not triangular. Therefore, there is at least one vertex $v_e \in V(r_x)$ that is not adjacent to the center vertex $v_x$ of the wheel, otherwise all axle face would be triangular. The graph $R_{-v_e}=(r_x - v_e)$ is a polygonal array, and then it is 3-colorable by Lemma 3 and Theorem 1. Any typical 3-coloring for $R_{-v_e}$ can be extended to a 3-coloring for $r_x$ if $v_e$ has the same color as $v_x$, because in a typical coloring the color of the center vertex is not used in the cycle’s vertices. Therefore, the center’s color has not been used for the vertices in $N(v_e)$.

The union of 3-colorable wheels is not necessarily 3-colorable. For example, each individual wheel in the graph of the Fig. 4 is 3-colorable, when the common face is assumed as part of each wheel. Therefore, each one of them is 3-colorable by Lemma 4. However, the final graph (union of the wheels) is 4-colorable as we will see in the following section.

4.1 Method for Determining the 3 or 4 Colorability of a Sequence of Wheels

We propose a logical method for recognizing between three or four colors for the colorabilty of the union of the wheels. Let G be a graph formed by the union of simple wheels sharing common faces. Our proposal is based on the construction of a propositional formula $F_G$ expressed in conjunctive normal form, and whose satisfiability codify the three colorability of G. Otherwise, G would be 4-colorable.

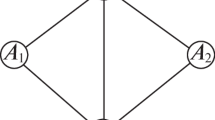
In order to present our proposal, let us consider first a pair of simple wheels $r_x$ and $r_y$ sharing a common face that is denoted as $(r_x \cup _f r_y)$, where $f = (F(r_x) \cap F(r_y))$. The center vertices of the wheels are labeled by x for $r_x$, and a for $r_y$, as it is illustrated in Fig. 3. A triplet of symbolic variables $\{x,y,z\}$ is associated to $V(r_x)$, while the triplet of symbolic variables $\{a,b,c\}$ is associated to $V(r_y)$ in the following way.

• 1. The variable x is associated to the center vertex of $r_x$, while the variable a is associated to the center vertex of $r_y$.

• 2. The cycle’s vertices of $r_x$ are associated with the variables y and z in an alternating way. It begins with a triangular face adjacent to the common face f and follows the other triangular faces in $r_x$ until all cycle’s vertices are covered.

• 3. The cycle’s vertices of $r_y$ are associated with the variables b and c in an alternating way. It begins with a triangular face adjacent to the common face f and follows the other triangular faces in $r_y$ until all cycle’s vertices are covered.

The topology of $(r_x \cup _{f} r_y)$ defines the type of constrainsts forming $F_G$, in the following way.

• (I) The vertices V(f), that are common vertices between $V(r_x) \cap V(r_y)$, determine equality constraints among its corresponding variables: $(y \oplus z) = (a \oplus b)$, where $(\oplus )$ denotes the logical xor operator. This means that the vertices in $V(r_x) \cap V(r_y)$ define equal colors (variables with same values).

• (II) An edge $e \in E(G)$, with endpoints in $V(r_x)$ and $V(r_y)$, define an inequality constraint between its corresponding variables: $(y \oplus z) \ne (a \oplus b)$. This means that adjacent vertices in V(f) define different colors (variables with different values).

• (III) $F_G$ also considers that any pair of adjacent vertices must have different colors. This is codified as: $(x \ne y) \wedge (x \ne z) \wedge (z \ne y) \wedge (a \ne b) \wedge (b \ne c) \wedge (c \ne a)$.

• (IV) In $F_G$ is also added the constraints defining that all vertice in $(V(r_x) \cup V(r_y))$ has to have one of the three possible colors, and this is codified as: $( (x = a) \vee (x = b) \vee (x=c)) \wedge ( (y = a) \vee (y=b) \vee (y=c)) \wedge ((z=a) \vee (z=b) \vee (z=c))$.

Notice that constraints type I and II are unitary clauses, and that any inequality can be considered as the negation of an equality constraint. Furthermore, a pair of contradictory unitary clauses implies the unsatisfiability of $F_G$. The satisfiability of $F_G$ determines that $(r_x \cup _f r_y)$ is 3-colorable. Otherwise, $(r_x \cup _f r_y)$ is 4-colorable. When $F_G$ is satisfiable, then a bijective function $f_R : \{x,y,z\} \rightarrow \{a,b,c\}$ exists. This determines the existence of a valid 3-coloring for the vertices in the pair of wheels.

The Figs. 3 and 4 illustrate the two different cases for the values of $F_G$. For the graph in Fig. 3, the constraints type II define that $(b \ne y) \wedge (a \ne y)$, and then $(c = y)$ is inferred due to the constraints type IV, as it is validated by the unique constraint type I. Since there are no more constraints type II, then the formula $F_G$ can be satisfied by the assignments $((a = x) \wedge (b = z))$, or $( (a=z) \wedge (b =x))$. Thus, the graph is Fig. 3 is 3-colorable. A valid 3-coloring is, for example, $(c = y) \wedge (a = x) \wedge (b = z)$, where $\{a,b,c\}$ represents any permutation of the values $\{1,2,3\}$.

Our proposal for reviewing the 3-colorabilty of a sequence of wheels works even when the centers of the wheels are not independent, or when the graph is formed by the union of two or more wheels.

Fig. 3.

A 3-colorable union of wheels

Fig. 4.

A 4-colorable union of wheels

For example, let us consider the graph in Fig. 4. In this case, we recognize three wheels and, therefore, the triplets $\{x_1,y_1,z_1\}, \{x_2,y_2,z_2\}, \{x_3,y_3,z_3\}$ are associated to $V(r_1), V(r_2),$ and $V(r_3)$, respectively. The constraints type I determine the equalities: $(y_3 = z_1) \wedge (z_3 = y_2) \wedge (z_3 = y_1)$. Meanwhile, the constraints type II determine the inequality: $(y_1 \ne y_2)$. It is not hard to infer $(y_1 = y_2)$ from the conditions: $(z_3 = y_2) \wedge (z_3 = y_1)$. However, this inferred equality contradicts the inequality type II: $(y_1 \ne y_2)$. Therefore, $F_G$ is unsatisfiable. As $F_G$ is unsatisfiable, then the planar graph is not 3-colorable and thus, it is necessary to use a fourth color to properly color the graph according to 4CT Theorem.

Notice that the revision of the satisfiability of $F_G$ can be done in polynomial-time on the size of the graph G. This is possible, since it consists in the application of unit resolution of the constraints Type I and Type II versus all constraints in $F_G$, as well as the application of the transitivity of the equality constraints. If there is a contradiction in $F_G$, then it will be generated during the process of the unit resolution, implying that it is necessary 4 colors to color G.

5 Conclusion

We recognize the polyhedral wheels as the basic pattern graphs to form planar graphs. We analyze for these polyhedral wheels the possibility of determining its 3 or 4 colorability. We also consider different compositions among wheels, and we analyze its colorability process. We propose an efficient method based on the construction of a conjunctive normal form $F_G$, which is formed by the equalities and inequalities constraints defined by the relations of the vertices in a sequence of wheels of G.

Our method determines the conditions that a set of symbolic variables must hold when a valid 3-coloring exists for G. Thus, we show that the satisfiability of $F_G$ implies the existence of a valid 3-coloring for G. Otherwise, it is necessary to use 4 colors to properly color G.