Generic Properties in Some Classes of Automaton Groups

Abstract

We prove, for various important classes of Mealy automata, that almost all generated groups have an element of infinite order. In certain cases, we also prove that some other properties, such as exponential growth, are generic.

1 Introduction

The class of groups generated by Mealy automata presents a considerable variety of behaviours and has been widely used since the eighties as a powerful source of interesting groups [5, 14, 15, 26]. It seems natural to try to produce new examples of groups to be studied by picking a random Mealy automaton and considering the group it generates, or to try to get an interesting distribution over some class of groups starting from a distribution over some class of Mealy automata [12]. This approach also raises a natural question: “what does a typical automaton group look like?”. In this paper, we tackle this problem and give partial answers for several important and well-studied classes, by proving that automata belonging to the class of reversible, reset, or polynomial activity automata generate with great probability a group having at least one element of infinite order. In particular, it means that these groups are generically infinite and not Burnside.

Another motivation for this paper is that the Order Problem —how to decide whether an element generates an infinite group—was recently proven undecidable among automaton groups [4, 11], while the  Finiteness Problem –how to decide whether the whole group is infinite—is known to be undecidable for automaton semigroups but remains open for automaton groups [7, 10]. On the other hand, some classes of automaton (semi)groups are known to have decidable Order Problem  [3, 6]. Our results provide probabilistic answers for these problems.

Depending on the class, we also get stronger or additional statements, among others, the groups generated by reversible or reset Mealy automata have generically exponential growth.

The proposed proofs vary strongly with the considered class and rely on the structural properties of the automata. In particular, the case of general invertible Mealy automata remains open.

In order to simplify the statements, we will use the informal “let ${\mathcal A}$ be a random automaton in $\mathcal {C}$” instead of the formal “let ${\mathcal A}$ be a random variable uniformly distributed over the set $\mathcal {C}$”. All probabilistic statements should be understood accordingly.

2 Automaton Groups

We recall that the order of an element $g$ of a group $G$ is the least (strictly positive) integer $\alpha$ such that $g^\alpha = {{\,\mathrm{\mathbbm {1}}\,}}$. If such an integer does not exist, we say that $g$ has infinite order. Equivalently, the order of $g$ is the cardinal of the subgroup it generates, hence having an element of infinite order implies the infiniteness of the whole group.

If $X$ is a finite set then $X^k$ denotes the set of words of length $k$, and $X^*$ (resp.  $X^+$) the set of words of arbitrary (resp. positive) length. We take as a convention that elements of $X^\ell , \,\ell >1$ are represented with a bold font.

Fig. 1.

The automaton generating the Grigorchuk group (left) and the adding machine, generating ${\mathbb Z}$ (right). The Grigorchuk automaton has stateset $\left\{ a,b,c,d,{{\,\mathrm{\mathbbm {1}}\,}} \right\}$ and the adding machine $\left\{ p,{{\,\mathrm{\mathbbm {1}}\,}} \right\}$. Both automata have alphabet $\left\{ 0,1 \right\}$

2.1 Mealy Automata and Automaton (Semi)Groups

A Mealy automaton is a 4-tuple ${\mathcal A}= (Q,\varSigma ,\delta ,\rho )$ where $Q$ and $\varSigma$ are finite sets, called the stateset and the alphabet respectively, $\delta = { \left\{ \delta _x : Q\rightarrow Q \right\} }_{x \in \varSigma }$ is a set of functions called transition functions, and $\rho = { \left\{ \rho _q : \varSigma \rightarrow \varSigma \right\} }_{q \in Q}$ is a set of functions called production functions. Examples of such automata are presented on Fig. 1, and we refer the reader to [17] for a more complete introduction.

The map $\rho _q$ extends to a length-preserving map on words $\rho _q:\varSigma ^* \rightarrow \varSigma ^*$ by the recursive definition:

$$\begin{aligned} \forall i \in \varSigma , \ \forall {\mathbf {s}} \in \varSigma ^*, \qquad \rho _q(i{\mathbf {s}}) = \rho _q(i)\rho _{\delta _i(q)}({\mathbf {s}}) \,. \end{aligned}$$

We can also extend the set of maps $\rho$ to words of states ${\mathbf {u}} \in Q^*$ by composing the production functions associated with the letters of ${\mathbf {u}}$:

$$\begin{aligned} \forall q \in Q, \ \forall {\mathbf {u}} \in Q^*, \qquad \rho _{q{\mathbf {u}}} = \rho _{{\mathbf {u}}}\circ \rho _{q}\,. \end{aligned}$$

Likewise, we extend the functions $\delta$ to words of state and words via

$$\forall i \in \varSigma , \ \forall {\mathbf {s}} \in \varSigma ^*, \ \forall q \in Q, \ \forall {\mathbf {u}} \in Q^*, \quad \delta _i(q{\mathbf {u}}) = \delta _i(q)\delta _{\rho _q(i)}({\mathbf {u}}) \text { and } \delta _{i{\mathbf {s}}} = \delta _i \circ \delta _{{\mathbf {s}}}\,.$$

For each automaton transition $q~\xrightarrow {x|\rho _q(x)}~\delta _x(q)$, we associate the cross-transition depicted in (cross):

The production functions $\rho _q : \varSigma ^* \rightarrow \varSigma ^*$ of an automaton ${\mathcal A}$ generate a semigroup $\langle {\mathcal A}\rangle _+= \{\rho _{{\mathbf {u}}} : \varSigma ^* \rightarrow \varSigma ^* | {\mathbf {u}} \in Q^+\}$.

A Mealy automaton is invertible when the functions $\rho$ are permutations of $\varSigma$. When a Mealy automaton is invertible one can define its inverse ${\mathcal A}^{-1}$ by

$$\begin{aligned} p \xrightarrow {x\mid y} q \ \in {\mathcal A}\Leftrightarrow p^{-1} \xrightarrow {y\mid x} q^{-1} \in {\mathcal A}^{-1}\,. \end{aligned}$$

Whenever a Mealy automaton is invertible we can consider the group $\langle {\mathcal A}\rangle$ it generates:

$$\begin{aligned} \langle {\mathcal A}\rangle = \langle \rho _q \ | \ q \in Q\rangle = \left\{ \rho ^{\pm 1}_{{\mathbf {u}}}\mid {\mathbf {u}}\in Q^* \right\} \,. \end{aligned}$$

A group (resp. a semigroup) is an automaton group (resp. semigroup) if it can be generated by some Mealy automaton.

Given a Mealy automaton ${\mathcal A}= (Q,\varSigma ,\delta ,\rho )$, its dual is the Mealy automaton $\mathfrak d{\mathcal A}= \left( \varSigma ,Q,\rho ,\delta \right)$ where the roles of the stateset and of the alphabet are exchanged. Its $\ell$-th power is the automaton $\left( Q^\ell ,\varSigma ,\delta ,\rho \right)$where the production and transition functions have been naturally extended. We define also the automaton  acting on sequences of $\ell$ letters and remark that this operation does not change the generated semigroup, i.e.  .

An automaton is called minimal if each state induces a different element in the generated group. Given an automaton ${\mathcal A}$, one can algorithmically construct its minimization $\mathfrak m{{\mathcal A}}$, which generates the same group [2].

From an algebraic point of view, it is convenient to describe the elements of an automaton group via the so-called wreath recursions. For any $g$ in an automaton group $\langle {\mathcal A}\rangle$ on alphabet $\varSigma = \left\{ 1,\ldots ,k \right\}$ and any word ${\mathbf {s}} \in \varSigma ^*$, let ${g} {\cdot } {{\mathbf {s}}}$ denotes the image of ${\mathbf {s}}$ by $g$, and ${g}_{|{{\mathbf {s}}}}$ the unique $h \in \langle {\mathcal A}\rangle$ satisfying ${g} {\cdot } {({\mathbf {st}})}=({g} {\cdot } {{\mathbf {s}}}){h} {\cdot } {{\mathbf {t}}}$ for all ${\mathbf {t}}\in \varSigma ^*$. The wreath recursion of $g$ is:

$$\begin{aligned} g=({g}_{|{1}},\ldots ,{g}_{|{x_{k}}})\sigma _g, \end{aligned}$$

where $\sigma _g \in S_{k}$ denotes the permutation on $\varSigma$ induced by $g$.

Fig. 2.

A 3-letter 6-state invertible reversible non-bireversible Mealy automaton.

In what follows, ${\mathcal A}$ will denote, if not explicited, an invertible Mealy automaton $(Q,\varSigma ,\delta ,\rho )$.

2.2 Classes of Mealy Automata

We now describe several important classes of (invertible) Mealy automata. Since invertibility is required to generate a group, it will be assumed throughout the paper.

An automaton ${\mathcal A}=(Q,\varSigma ,\delta ,\rho )$ is called reversible when the functions $\delta$ are permutations of $Q$. If an automaton is invertible then its dual is reversible. A Mealy automaton is bireversible if both itself and its inverse are invertible and reversible.

Another, somewhat opposite, restriction on the transition function leads to the class of reset automata, studied e.g. in [7, 24]. An automaton ${\mathcal A}$ is called reset if there exists a function $\phi : \varSigma \rightarrow Q$ such that $\forall x, \forall q, \delta _x(q) = \phi (x)$. In other words, all the arrows labelled by an input letter $x$ lead to the same state $\phi (x)$. Up to renaming the states and pruning the automaton of its vertices without ingoing edges (which does not change the finiteness of the generated group nor the existence of element of infinite order), we may assume that all studied reset automata are unfolded, i.e. that $Q=\varSigma$ and $\phi ={{\,\mathrm{\mathbbm {1}}\,}}$.

Another class of Mealy automata linked to the cycle structure is defined in [23], via the activity. Assume that there is a unique state inducing the identity in the group, denoted ${{\,\mathrm{\mathbbm {1}}\,}}$. The activity of an automorphism $t \in \langle {\mathcal A}\rangle$ is defined as the function

$$\begin{aligned} \alpha _t : \ell \mapsto {\left| \left\{ x \in \varSigma ^\ell , \, {t}_{|{x}}\ne {{\,\mathrm{\mathbbm {1}}\,}} \right\} \right| } \,. \end{aligned}$$

It is known that the activity $\alpha _t$ is polynomial if and only if there is not two nontrivial simple cycles accessible one from another in the automaton ${\mathcal A}$, and that in this case the degree of the polynomial is the maximal number of nontrivial cycles that can be reached along of a simple cycle minus one. For a fixed alphabet $\varSigma$, we denote ${\mathrm {Pol}}$ (resp.  ${\mathrm {Pol}}(d)$) the set of all Mealy automata with polynomial activity (resp. with activity bounded by a polynomial of degree $d$), and in particular we call bounded (resp. finitary) the set ${\mathrm {Pol}}(0)$ (resp.  ${\mathrm {Pol}}(-1) = \left\{ t, \, \alpha _t(\ell ) \rightarrow 0 \right\}$). For instance both automata on Fig. 1 have bounded activity. Notice that every finitary automaton generates a finite group [22].

In [6], a tool is defined to understand the orbits of elements of $\varSigma ^*$ under the action of an automorphism described by a Mealy automaton. Given ${\mathcal A}=(Q,\varSigma ,\delta ,\rho )$, $t \in \langle {\mathcal A}\rangle$ and ${\mathbf {x}} \in \varSigma ^*$ define $\text {Orb}_t({\mathbf {x}}) = \min _{\alpha >0} \left\{ \alpha \,|\, {t^\alpha } {\cdot } {{\mathbf {x}}}={\mathbf {x}} \right\}$ the size of the orbit of ${\mathbf {x}}$ under the action of $t$. The Orbit Signalizer is the graph $\Gamma _t$ whose vertices are the ${t^{\text {Orb}_t({\mathbf {x}}) }}_{|{{\mathbf {x}}}}, \, {\mathbf {x}} \in \varSigma ^*$ and edges from ${t^{\text {Orb}_t({\mathbf {x}})}}_{|{{\mathbf {x}}}}$ to ${t^{\text {Orb}_t({\mathbf {x}}y)}}_{|{{\mathbf {x}}y}}, {\mathbf {x}} \in \varSigma ^*, y \in \varSigma$ with label $\text {Orb}_{{t^{\text {Orb}_t({\mathbf {x}})}}_{|{{\mathbf {x}}}}}(y)$.

The Orbit signalizer is used in [3, 6] to solve the Order Problem . Indeed the order of $t$ is the lowest common multiple of all labels along paths starting from vertex $t$ in $\Gamma _t$. In particular if the orbit signalizer is finite then the Order Problem is decidable for $t$, as it reduces to checking if cycles have labels all $1$.

3 Reversible Mealy Automata

We show that groups generated by invertible reversible Mealy automata have an element of infinite order with high probability. In fact we are going to prove a stronger result by showing that almost all invertible reversible automata are not bireversible, then using known results from [13], we obtain that the generated semigroups are almost surely torsion-free.

Since a Mealy automaton is completely defined by its transition and production functions, an invertible reversible Mealy automaton can be understood as ${\left| Q \right| }$ permutations in $S_{{\left| \varSigma \right| }}$ and ${\left| \varSigma \right| }$ permutations in $S_{{\left| Q \right| }}$, thus the uniform distribution on the set of invertible reversible Mealy automata with stateset $Q$ and alphabet $\varSigma$ is the uniform distribution on $S_{{\left| Q \right| }}^{{\left| \varSigma \right| }}\times S_{{\left| \varSigma \right| }}^{{\left| Q \right| }}$.

An invertible reversible automaton is bireversible if and only if each output letter induces a permutation of the stateset. In particular, for bireversible automata, we have that :

$$\begin{aligned} \forall (p,i), (q,j) \in Q\times \varSigma , (p,i)\ne (q,j), \, \delta _i(p) = \delta _j(q) \Rightarrow \rho _p(i)\ne \rho _q(j)\,. \end{aligned}$$

Define, for $r\in Q$, the set $\mathcal {O}_r= \left\{ j \in \varSigma , \exists (p,i) \in Q\times \varSigma , p \xrightarrow {i|j} r \in {\mathcal A} \right\}$ of output letters that lead to $r$. An invertible reversible automaton is bireversible if and only if, for all states $r$, the set $\mathcal {O}_r$ is the whole alphabet.

Example 3.1

Consider the automaton in Fig. 2. We have $\mathcal {O}_a = \left\{ 1,2,3 \right\} =\mathcal {O}_c$ but $\mathcal {O}_b = \left\{ 1,3 \right\}$, hence the automaton is not bireversible.

Proposition 3.2

The probability that a random invertible reversible automaton with $k$ letters and $n$ states is bireversible is less than

$$\begin{aligned} \max \{{1 \over n^{k-1}} + { 1\over k}, {1 \over k^{n-1}} + { 1\over n} \} \end{aligned}$$

Proof

Let ${\mathcal A}= (Q,\varSigma ,\delta ,\rho )$. For $r \in Q$, we denote $\text {pred}_r=\mid \{p \in Q\mid \,\exists i \in \varSigma , \delta _i(p)=r\}\mid$ the size of the set of predecessor of $r$, and $\text {BIR}$ the set of bireversible automata. Let us fix a state $r$. We have:

$$\begin{aligned} \Pr ({\mathcal A}\in \text {BIR})&= \Pr (\forall q \in Q, \mathcal {O}_q=\varSigma ) \\&\le \Pr (\mathcal {O}_r = \varSigma )\,. \end{aligned}$$

From the law of total probability we get:

$$\begin{aligned} \Pr ({\mathcal A}\in \text {BIR})&\le \Pr (\mathcal {O}_r = \varSigma \mid \text {pred}_r = 1 )\Pr ( \text {pred}_r = 1 ) \quad \\&\qquad \quad + \quad \Pr (\mathcal {O}_r = \varSigma \mid \text {pred}_r \ge 2 )\Pr ( \text {pred}_r \ge 2) \\&\le \Pr ( \text {pred}_r = 1 ) + \Pr (\mathcal {O}_r = \varSigma \mid \text {pred}_r \ge 2) \end{aligned}$$

The probability that $r$ has exactly one predecessor can be seen as fixing $\delta _i^{-1}(r)$ for some reference letter $i \in \varSigma$ and requiring that the $k-1$ other $\delta _j^{-1}(r), \, j \in \varSigma \setminus \lbrace i\rbrace$ are equal to $\delta _i^{-1}(r)$, hence:

$$\begin{aligned} \Pr ({\mathcal A}\in \text {BIR})&\le {1 \over n^{k-1}} + \Pr (\mathcal {O}_r = \varSigma \mid \text {pred}_r \ge 2) \end{aligned}$$

For the second term, let us consider a predecessor $p$ of $r$ and let $\lambda$ be the number of input letters leading from $p$ to $r$. We have $1\le \lambda \le {k-1}$. To enforce bireversibility, we have to avoid that $p$ outputs a letter that is already leading to $r$ ($\rho _p(i) \ne \rho _q(j)$ for $\delta _p(i)=\delta _q(j)=r$). Assume that the set $\mathcal {O}_r^{(p)}= \left\{ j \in \varSigma \mid \, \exists q \ne p \in Q, q \xrightarrow {i|j} r \in {\mathcal A} \right\}$ of output letters leading to $r$ from a state $q$ different from $p$ is of maximal size $k-\lambda$. Since $\rho _p$ is random and independent from the others $\rho _q$ we can bound this probability from above: having the letters leading from $p$ to $r$ produce the $\lambda$ out of $k$ required letters is ${k \atopwithdelims ()\lambda }^{-1}$. Hence:

$$\begin{aligned} \Pr ({\mathcal A}\in \text {BIR})&\le {1 \over n^{k-1}} + {k \atopwithdelims ()\lambda }^{-1}\\&\le {1 \over n^{k-1}} + {1 \over k} \,. \end{aligned}$$

Now, by applying the same reasoning to the dual automaton, which is invertible and reversible on $k$ states and $n$ letters, we get the symmetric upper bound

$$\begin{aligned} \Pr ({\mathcal A}\in \text {BIR})&\le {1 \over k^{n-1}} + {1 \over n} \,. \end{aligned}$$

   $\square$

It is proven in [13] that an invertible reversible Mealy automaton without bireversible component generates a torsion-free semigroup¹. Whence our theorem:

Theorem 3.3

The probability that an invertible reversible Mealy automaton taken uniformly at random generates a torsion-free semigroup goes to $1$ as the size of the alphabet grows. Moreover, the probability for the group to have an element of infinite order also goes to $1$ as the stateset or the alphabet grows.

Proof

It is known that, with great probability, two random permutations on a large set generate a transitive group [8]: more precisely, he proved that two random permutations of $S_k$ generate a transitive group with probability $1-1/k +O(1/k^2)$ . In terms of a graph, it means that a typical reversible Mealy automaton on a large alphabet is (strongly) connected, and is not bireversible by Proposition 3.2 whence the first part of the result. The second part is from Proposition 3.2 and [13].   $\square$

From [9], where it is shown that having an element of infinite order implies exponential growth among groups generated by invertible reversible automata, we obtain:

Theorem 3.4

The probability that an invertible reversible Mealy automaton taken uniformly at random generates a group with exponential growth goes to $1$ as the size of the stateset or of the alphabet grows.

Remark 3.5

Notice that Theorem 3.3 is not a priori a consequence of Theorem 3.4: there exists infinite Burnside group with exponential growth ([1]). However, no example of such a group is known within the class of automaton groups.

It is worthwhile noting that it is unknown whether the Order Problem is decidable within the class of (semi)groups generated by reversible Mealy automata.

4 Reset Mealy Automata

The class of reset automata is of particular interest since it is linked to one-way cellular automata, and was used by Gillibert to prove the undecidability of the Order Problem for automaton semigroups [10]. For groups generated by (invertible) reset Mealy automata the Order Problem remains open [7].

As the transition function is trivial in a (unfolded) reset Mealy automaton, the uniform distribution on the set of unfolded invertible reset Mealy automata with stateset $Q$ and alphabet $\varSigma$ is the uniform distribution on $S_{{\left| \varSigma \right| }}^{{\left| Q \right| }}$.

We are going to use a result from [20]:

Theorem 4.1

([20, Theorem 1.20]). Let ${\mathcal A}$ be a reset automaton and $\pi _{\mathcal A}$ be the transformation defined by $\pi _{\mathcal A}: q \mapsto \rho _q^{-1}(q)$ for all $q \in Q$.. If $\pi _{\mathcal A}$ is not a permutation then the group generated by ${\mathcal A}$ has an element of infinite order.

We give the proof for the sake of completeness.

Proof

If $\pi _{\mathcal A}$ is not a permutation, then there exists $x_0$ which does not belong to any cycle of $\pi _{\mathcal A}$ and such that $\pi _{\mathcal A}(x_0)=x_1$ belongs to a cycle $x_1 \xrightarrow {} \cdots \xrightarrow {} x_\ell \xrightarrow {} x_1$ of $\pi _{\mathcal A}$. Computing the orbit of $x_0(x_1\cdots x_\ell )^\alpha$ under the action of any given state $q \in Q$ gives:

Since $x_1=\rho _{x_0}^{-1}(x_0) = \rho _{x_\ell }^{-1}(x_\ell )$. So ${q^{\alpha i}} {\cdot } {x_0(x_1\cdots x_\ell )^\alpha } = {\mathbf {u}}{x_0(x_1\cdots x_\ell )^{(\alpha -i)}}$, for some ${\mathbf {u}} \in Q^{i\alpha }$, hence $q$ has infinite order.    $\square$

Theorem 4.2

The probability that a random (unfolded) reset automaton on $k$ letters has an element of infinite order is at least $1-e\sqrt{k}e^{-k}$.

Proof

Since the $\rho _q ,\; q\in \varSigma$ are random permutations, the function $q \mapsto \rho _q^{-1}(q)$ can be considered as a random mapping from $\varSigma$ to $\varSigma$, and the number of permutations among mappings is ${k! }\over {k^k}$. We conclude using Stirling’s approximation and more precisely [21]:  $k!< \sqrt{2\pi k} ({k\over e})^ke^{1\over 12k} < e\sqrt{k} k^k e^{-k}$ as soon as $k>1$.    $\square$

Using [19], where Olukoya proves that groups generated by reset automata are either finite or have exponential growth, we get (see also Remark 3.5):

Theorem 4.3

The probability that a random (unfolded) reset automaton on $k$ letters has exponential growth is at least $1-e\sqrt{k}e^{-k}$.

From Delacourt and Ollinger [7, Proposition 1], our result also means that permutive one-way cellular automata are generically aperiodic.

Remark 4.4

An unfolded reset automaton is minimal ([2]) if and only if each state induces a different permutation on letters. By the birthday problem, we can extend our result a bit: a random minimal unfolded reset automaton generically generates a group with exponential growth and elements of infinite order.

Fig. 3.

The normal form  of the (invertible) automaton ${\mathcal G}$ of bounded activity generating the Grigorchuk group. A simple path contains at most one nontrivial loop.

5 Mealy Automata with Polynomial Activity

The class of Mealy automata with polynomial activity is interesting as the Order Problem is decidable for (semi)groups generated by automata with bounded activity but remains open for the higher levels of the hierarchy [6].

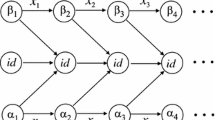
Recall that ${{\,\mathrm{\mathbbm {1}}\,}}$ denotes the identity state in the automaton, which is supposed to be unique. We are going to define a normal form: let ${\mathcal A}= (Q,\varSigma ,\delta ,\rho )$ be an automaton with polynomial activity and let $\ell$ be the lowest common multiple of the sizes of the (simple) cycles. Since an automaton with polynomial growth has no entangled cycles, we have that  has all cycles of length one. Now put $d$ the maximal length of an (oriented) path between a state and a self-loop in . Then the normal form of the automaton ${\mathcal A}$ is the automaton  and it looks as follows: it is a directed acyclic graph whose leaf induces the identity ${{\,\mathrm{\mathbbm {1}}\,}}$, and where each state either has a self-loop or leads to a state with a self-loop. For instance the normal form  of the (invertible) Grigorchuk automaton ${\mathcal G}$ (which has bounded activity) Fig. 1 (left) is depicted Fig. 3.

To the best of our knowledge, and even among automata under normal form, there is no easy description of the uniform distribution on the set of (invertible) Mealy automata with polynomial activity, even if one fixes the degree of the activity. To bypass this difficulty, we show that automata with finitary activity are rare even among automata with bounded activity, and use the fact that once the transition functions are fixed, the choice of production functions does not change the activity.

The next proposition is a simple yet useful observation:

Fig. 4.

Computation of the orbit of $1^j$ under the action of $t$ in a bounded automaton.

Proposition 5.1

Let ${\mathcal A}=(Q,\varSigma ,\delta ,\rho )$ be a Mealy automaton with bounded activity under normal form. If there is some $t \in Q$ with $\delta _{i}{(t)} = t$ and $\rho _{t}{(i)} \ne i$, then $\rho _{t}$ has infinite order.

Proof

Up to renaming, we can assume that $i=1$ and $\rho _{t}{(1)} =2$. We use the orbit signalizer of $t$ to prove that $\rho _{t}$ has infinite order (see Fig. 4): put $\alpha _j ={\left| \text {Orb}_t(1^j) \right| }$. Since the activity is bounded, the set $\left\{ {t^{{\left| \text {Orb}_t(1^j) \right| }}}_{|{1^j}} \right\} _j$ is finite, so there is a self-loop ${t^{\alpha _i}}_{|{1^i}} = {t^{\alpha _{i+j}}}_{|{1^{i+j}}}$. By putting ${t^{\alpha _i}}_{|{1^i}} = ts_\alpha$ we get that ${(ts_i)^\beta }_{|{1^j}} = ts_i$ for some integer $\beta ={\left| \text {Orb}_{ts_i}(1^{j}) \right| }$. Suppose that the size of the orbit is 1. We obtain:

Hence $2=1$, contradiction. The size of the orbit of $\rho _t$ increases strictly through the cycle $1^\beta$, whence the order of $\rho _t$–the lowest common multiple of the paths in the orbit signalizer of $t$ ([6])–is infinite.    $\square$

From this result, we get:

Theorem 5.2

The probability that the group generated by an automaton with polynomial activity has an element of infinite order goes to $1$ as the size of the alphabet goes to infinity.

Proof

We first prove that groups generated by automata with polynomial non finitary activity generically have an element of infinite order: let ${\mathcal A}=(Q,\varSigma ,\delta ,\rho )$ be an automaton in ${\mathrm {Pol}}(d)\setminus {\mathrm {Pol}}(-1)$ and let $t$ be a state with bounded activity on a nontrivial cycle. Since the activity does not depend on the choice of the production functions (except for the trivial state), we can consider the set $\mathcal {C}_{\mathcal A}$ of automata in ${\mathrm {Pol}}(d)\setminus {\mathrm {Pol}}(-1)$ with same transition functions and trivial state. Among $\mathcal {C}_{\mathcal A}$, we have $\rho _t(i)\ne i$ with probability $1-1/k$, so, in the normal form, $t$ is on a cycle labelled by $i{\mathbf {x}} \in \varSigma ^\ell$ with $\rho _t(i{\mathbf {x}})\ne i{\mathbf {x}}$. We can apply Proposition 5.1.

Now we show that the set ${\mathrm {Pol}}(-1)$ has measure 0 in the set ${\mathrm {Pol}}(d), \, d \ge 0$. If an automaton ${\mathcal A}$ has polynomial activity, then there is at least one state $t$ satisfying $\delta _i(t) = {{\,\mathrm{\mathbbm {1}}\,}}$ for all $i$. Given ${\mathcal A}\in {\mathrm {Pol}}(-1)$, we can build $k$ automata ${\mathcal A}_i$ with bounded but not finitary activity by changing for exactly one letter $\delta _i(t) = {{\,\mathrm{\mathbbm {1}}\,}}$ to $\delta _i(t) = t$. If we consistently chose $t$ to be, e.g. , the minimal among acceptable states, we can uniquely reconstruct ${\mathcal A}$ from these ${\mathcal A}_i$, whence the result.

We conclude using the law of total probability: the probability that an automaton in ${\mathrm {Pol}}(d)$ has an element of infinite order is equal to the probability that it has an element of infinite order given it belongs to ${\mathrm {Pol}}(d)\setminus {\mathrm {Pol}}(-1)$ times the probability of the later; we showed that both go to one, the result follows.    $\square$

From the proof we extract the following:

Proposition 5.3

The probability that the group generated by an automaton in ${\mathrm {Pol}}(0)$ on an alphabet of size $k$ has an element of infinite order is at least ${k-1}\over {k+1}$.

6 Conclusion and Future Work

In this work, we proved, for various important classes of Mealy automata, that the generated groups have generically an element of infinite order, thus are infinite. It is natural to wonder whether other properties, such as non-amenability, are generic and to extend these results to the full class of automaton groups.

One interesting direction is to determine if generating a free or an infinitely presented group is generic in a class. These properties are mutually exclusive. Automata with polynomial activity cannot generate free groups [18], while reversible ones can [25]; infinitely presented groups can be found in both classes. It would be striking to find two classes and a group property which is nontrivial in both classes yet generically true in one and generically false in the other.