Abstract
Despite the great success of Weierstrass, Dedekind and Cantor in constructing the continuum from arithmetical materials, a number of thinkers of the late nineteenth and early twentieth centuries remained opposed, in varying degrees, to the idea of explicating the continuum concept entirely in discrete terms. These include the mathematicians du Bois-Reymond , Veronese , Poincaré , Brouwer and Weyl , and the philosophers Brentano and Peirce.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Quoted in Ehrlich (1994), p. x
- 2.
This echoes his older brother Emile’s famous ignorabimus decaration in 1880 concerning “world riddles,” certain of which, such as the ultimate nature of matter and force, and the origin of sensations, would always elude explanation.
- 3.
Fisher(1981), p. 102.
- 4.
The term is Hardy’s: see Hardy (1910).
- 5.
Quoted in Fisher (1981), p. 104.
- 6.
Quoted ibid., p. 105.
- 7.
Ibid., p. 106.
- 8.
Ibid., pp. 107–8.
- 9.
Quoted ibid., p. 107
- 10.
Quoted ibid., p. 107.
- 11.
ibid., p. 108.
- 12.
Quoted ibid., p. 108.
- 13.
Ibid., p. 108.
- 14.
This view of irrational numbers is evidently in direct opposition to Cantor ’s.
- 15.
Quoted ibid., pp. 108–9.
- 16.
Ibid., p.109.
- 17.
Quoted ibid., p. 109.
- 18.
Quoted ibid., p. 109.
- 19.
Quoted ibid., p. 109.
- 20.
Ibid., p. 110.
- 21.
Ibid.,p. 114.
- 22.
Quoted ibid., p. 114.
- 23.
Quoted ibid., p. 115.
- 24.
Quoted ibid., p. 115. Du Bois-Reymond took a dim view of the conception of infinitesimals as being ordinary magnitudes continually in a state of flux towards zero, remarking sarcastically
As long as the book is closed there is perfect repose, but as soon as I open it there commences a race of all the magnitudes which are provided with the letter d towards the zero limit. (Quoted in Ehrlich (1994), pp. 9–10.)
- 25.
Quoted ibid., p. 115.
- 26.
Quoted ibid., p. 115.
- 27.
Ibid., p. 116.
- 28.
Ibid., p. 116.
- 29.
Quoted ibid., p. 116.
- 30.
Quoted in Fisher (1994), p. 135.
- 31.
Quoted ibid., pp. 136–137. In a footnote Veronese observes:
In order to establish the mathematical concepts, we can very well fall back on empirically obtained knowledge without therefore having to make any use of it later in the definitions themselves and in the proof.
- 32.
Quoted ibid., p. 138.
- 33.
Quoted ibid., p. 138.
- 34.
Quoted ibid., p. 139
- 35.
Ibid.
- 36.
Ibid., pp. 139–40.
- 37.
Quoted ibid., p. 140.
- 38.
Ibid., pp. 121–2.
- 39.
Quoted ibid., p. 123. Here A ∞ is an element outside the scale generated by (AA1).
- 40.
Ibid., p. 123.
- 41.
Quoted ibid., p. 142.
- 42.
Quoted ibid., p. 144.
- 43.
Quoted ibid., pp. 142–3.
- 44.
Quoted ibid., pp. 144.
- 45.
Brentano (1988), p. 6.
- 46.
Ibid., p. 21 f. Brentano’s distinction of primary and secondary continua can be neatly represented within category theory: to put it succinctly, a primary continuum is a domain , a secondary continuum a codomain . We form a category
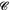 —the category of continua—by taking continua as objects and correlations between continua as arrows. Then, given any arrow f: A→ B in
—the category of continua—by taking continua as objects and correlations between continua as arrows. Then, given any arrow f: A→ B in 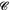 , the domain
A of f may be taken as a “primary” continuum and its codomain
B as a “secondary” continuum. In Brentano
’s example of a coloured surface, for instance, the primary continuum A is the given spatial surface, the secondary continuum B is the colour spectrum, and the correlation f assigns to each place in A its colour as a position in B. In the case of a corporeal point moving in space
, the primary continuum A is an interval of time, the secondary continuum B a region of space
, and the correlation f assigns to each instant in A the position in B occupied by the corporeal point. Finally, in the case of the varying direction of a curve the primary continuum A is the curve itself, the secondary continuum is the continuum of measures of angles, and the correlation f assigns to each point on the curve the slope of the tangent there: thus f is nothing other than the first derivative of the function associated with the curve.
, the domain
A of f may be taken as a “primary” continuum and its codomain
B as a “secondary” continuum. In Brentano
’s example of a coloured surface, for instance, the primary continuum A is the given spatial surface, the secondary continuum B is the colour spectrum, and the correlation f assigns to each place in A its colour as a position in B. In the case of a corporeal point moving in space
, the primary continuum A is an interval of time, the secondary continuum B a region of space
, and the correlation f assigns to each instant in A the position in B occupied by the corporeal point. Finally, in the case of the varying direction of a curve the primary continuum A is the curve itself, the secondary continuum is the continuum of measures of angles, and the correlation f assigns to each point on the curve the slope of the tangent there: thus f is nothing other than the first derivative of the function associated with the curve. - 47.
Quoted ibid., p. xvii.
- 48.
Brentano (1974), p. 357.
- 49.
In a letter to Husserl drafted in 1905, Brentano asserts that “I regard it as absurd to interpret a continuum as a set of points.”
- 50.
Brentano (1974), p. 354.
- 51.
See below.
- 52.
Brentano (1988), p. 39.
- 53.
Here Brentano appears to be saying that when one divides a closed interval [a, b] at an intermediate point c, one necessarily obtains the closed intervals [a, c], [c, b], with the common point c (in half plerosis ). In that case, Brentano have probably have regarded a continuous line as indecomposable, into disjoint intervals at least: see Appendix A.
- 54.
- 55.
Brentano (1988), pp. 4–5.
- 56.
Peirce (1976), p. 925.
- 57.
See below.
- 58.
Peirce (1976), p. xvi: the quotation is from a note written in 1903.
- 59.
In their Introduction to Peirce (1992), Ketner and Putnam characterize Peirce’s conception of the continuum as “a possibility of repeated division which can never be exhausted in any possible world, not even in a possible world in which one can complete [nondenumerably] infinite processes.” There is some resemblance between this conception and John Conway’s system of surreal numbers (see Ehrlich 1994a). Conway’s system may be characterized as being an ηα-field for every ordinal α, that is, a real-closed ordered field S which satisfies the condition that, for any pair of subsets X, Y for which every member of X is less than every member of Y, there is an element of S strictly between X and Y. (In their Introduction to Peirce [1992], Ketner and Putnam characterize Peirce’s conception of the continuum as “a possibility of repeated division which can never be exhausted in any possible world, not even in a possible world in which one can complete [nondenumerably] infinite processes. This description would seem to apply equally well to Conway’s conception.) It is not hard to show that, between any pair of members of S there is a proper class of members of S—in Peirce’s terminology, a supermultitudinous collection. Nevertheless, S is still discrete: its elements, while supermultitudinous, remain distinct and unfused (were it not for this fact, Conway would scarcely be justified in calling the members of S “numbers”). On the face of it the discreteness of S would seem to imply that the presence of superabundant quantity in Peirce’s sense is not enough to ensure continuity. Of course, Brentano would have dismissed this idea altogether, in view of his critical attitude towards any construction of the continuum by repeated insertion of points.
- 60.
Peirce assumed what amounts to the generalized continuum hypothesis in supposing that each possible infinite set has one of the cardinalities \( {\aleph}_0,{2}^{\aleph_0},{2}^{2^{\aleph_0}},\dots \). These he termed denumerable , primipostnumeral, secundipostnumeral, etc.
- 61.
Peirce (1976), p. 95.
- 62.
I do not know whether Peirce was acquainted with their work.
- 63.
Peirce (1976), p. 123. In this connection it is worth quoting from a letter addressed by Peirce in 1900 to the editor of Science in which he defends his views on infinitesimals against the strictures of Josiah Royce:
Professor Royce remarks that my opinion that differentials may quite logically be considered as true infinitesimals, if we like, is shared by no mathematician “outside of Italy”. As a logician, I am more comforted by corroboration in the clear mental atmosphere of Italy than I could be by any seconding from a tobacco-clouded and bemused land (if any such there be) where no philosophical eccentricity misses its champion, but where sane logic has not found favor.
- 64.
Ibid., p. 124.
- 65.
Ibid., p. 925.
- 66.
Impredicativity is a form of circularity: a definition of a term is impredicative if it contains a reference to a totality to which the term under definition belongs. See, e.g., Fraenkel et al. (1973), pp. 193–200.
- 67.
Folina (1992), p. xv.
- 68.
Ibid., p. 113. And yet Poincaré also remarks, in connection with the continuous nowhere differentiable functions of analysis:
Instead of seeking to reconcile intuition with analysis, we have been content to sacrifice one of the two, and as analysis must remain impeccable, we have decided against intuition (1946, p. 52).
- 69.
Folina (1992), p. xvi.
- 70.
Poincaré (1946), pp. 43–44.
- 71.
Ibid., pp. 45–6.
- 72.
This formula ceases to be contradictory if the identity relation = is replaced by a symmetric, reflexive, but nontransitive relation ≈: here x ≈ y is taken to assert that the sensations or perceptions x and y are indistinguishable. See Appendix C below.
- 73.
Ibid., p. 49.
- 74.
Ibid., p. 52.
- 75.
Ibid.
- 76.
Ibid., p. 53.
- 77.
Ibid.
- 78.
Ibid., pp. 50–1.
- 79.
Quoted in Kneebone (1963),p. 246.
- 80.
This is not to say that Brouwer was primarily interested in logic, far from it: indeed, his distaste for formalization caused him to be quite dismissive of subsequent codifications of intuitionistic logic .
- 81.
Brouwer , Intuitionism and Formalism, in Benacerraf and Putnam (1977), p. 80.
- 82.
Brouwer , Mathematics Science and Language. In Mancosu (1998), p.45
- 83.
Brouwer (1975), p. 17.
- 84.
Ibid. p. 45.
- 85.
For an illuminating informal account of choice sequences , see Fraenkel et al. (1973), pp. 255–261.
- 86.
The failure of these important results of classical analysis caused most mathematicians of the day to shun intuitionistic, and even constructive mathematics. It was not until the 1960s that adequate constructive versions were worked out. See Chap. 9 below.
- 87.
Weyl (1949), p. 52.
- 88.
Ibid., p. 54.
- 89.
One might be inclined to regard this claim as impossible: is not a counterexample provided by, for example, the function f given by f(0) = 0, f(x) = |x|/x otherwise? No, because from the intuitionistic standpoint this function is not everywhere defined on the interval [1, 1], being undefined at those arguments x for which it is unknown whether x = 0 or x ≠ 0.
- 90.
See Chap. 9 and Appendix A below.
- 91.
The others, in order , are: understanding and expression; thinking the possible; and finally, in science, the construction of symbols or measuring devices.
- 92.
Weyl (1954), p. 629.
- 93.
Weyl (1987), p. 119.
- 94.
Ibid., p. 17.
- 95.
Weyl (1932), p. 82.
- 96.
Weyl (1929), p. 249.
- 97.
Weyl (1987), p. 23.
- 98.
Weyl (1932), p. 83.
- 99.
Weyl (1949), p. 41.
- 100.
Ibid., p. 42
- 101.
But in this connection see the remarks on the Constancy Principle in Chap. 10.
- 102.
Ibid., pp. 37–8.
- 103.
Ibid., p. 38.
- 104.
Ibid., p. 46.
- 105.
Ibid., p. 50.
- 106.
Weyl (1987), p. 108.
- 107.
Ibid., p. 24.
- 108.
Ibid., p. 94.
- 109.
Ibid., p. 93.
- 110.
The connection between mathematics and physics was of paramount importance for Weyl . His seminal work on relativity theory, Space -Time-Matter, was published in the same year (1918) as Das Kontinuum; the two works show subtle affinities.
- 111.
In this connection it is of interest to note that on 9 February 1918 Weyl and George Pólya made a bet in Zürich in the presence of twelve witnesses (all of whom were mathematicians) that “within 20 years, Pólya, or a majority of leading mathematicians, will come to recognize the falsity of the least upper bound property.” When the bet was eventually called, everyone—with the single exception of Gödel—agreed that Pólya had won.
- 112.
This fact would seem to indicate that in Weyl’s theory the domain of definition of a function is not unambiguously determined by the function, so that the continuity of such a “function” may vary with its domain of definition. (This would be a natural consequence of Weyl’s definition of a function as a certain kind of relation.) A simple but striking example of this phenomenon is provided in classical analysis by the function f which takes value 1 at each rational number, and 0 at each irrational number. Considered as a function defined on the rational numbers, f is constant and so continuous; as a function defined on the real numbers , f fails to be continuous anywhere.
- 113.
Weyl (1987), p. 88.
- 114.
Ibid.
- 115.
Ibid., p. 89.
- 116.
Ibid., p. 90.
- 117.
Ibid., p. 91–92.
- 118.
Ibid., p. 92.
- 119.
E.g. in Weyl (1950), 8 and (1949), p. 123.
- 120.
Many years later, in Insight and Reflection, Weyl expanded the metaphor into a full-fledged analogy: In Weyl (1969), objects, subjects (or egos), and the appearance of an object to a subject are correlated respectively with points on a plane, (barycentric) coordinate systems in the plane, and coordinates of a point with respect to a such a coordinate system. In Weyl’s analogy, a coordinate system S consists of the vertices of a fixed nondegenerate triangle T; each point p in the plane determined by T is assigned a triple of numbers summing to 1—its barycentric coordinates relative to S—representing the magnitudes of masses of total weight 1 which, placed at the vertices of T, have centre of gravity at p. Thus objects, i.e. points, and subjects i.e., coordinate systems or triples of points belong to the same “sphere of reality.” On the other hand, the appearances of an object to a subject, i.e., triples of numbers, lie, Weyl asserts, in a different sphere, that of numbers. These number-appearances, as Weyl calls them, correspond to the experiences of a subject, or of pure consciousness.
From the standpoint of naïv realism the points (objects) simply exist as such, but Weyl indicates the possibility of constructing geometry (which under the analogy corresponds to external reality) solely in terms of number-appearances, so representing the world in terms of the experiences of pure consciousness, that is, from the standpoint of idealism. Thus suppose that we are given a coordinate system S. Regarded as a subject or “consciousness”, from its point of view a point or object now corresponds to what was originally an appearance of an object, that is, a triple of numbers summing to 1; and, analogously, any coordinate system S′ (that is, another subject or “consciousness”) corresponds to three such triples determined by the vertices of a nondegenerate triangle. Each point or object p may now be identified with its coordinates relative to S. The coordinates of p relative to any other coordinate system S′ can be determined by a straightforward algebraic transformation: these coordinates represent the appearance of the object corresponding to p to the subject represented by S′. Now these coordinates will, in general, differ from those assigned to p by our given coordinate system S, and will in fact coincide for all p if and only if S′ is what is termed by Weyl the absolute coordinate system consisting of the three triples (1,0,0), (0,1,0), (0,0,1), that is, the coordinate system which corresponds to S itself. Thus, for this coordinate system, “object” and “appearance” coincide, which leads Weyl to term it the Absolute I. (This term Weyl borrows from Fichte, whom he quotes as follows: “The I demands that it comprise all reality and fill up infinity. This demand is based, as a matter of necessity, on the idea of the infinite I; this is the absolute I—which is not the I given in real awareness.”)
Weyl points out that this argument takes place entirely within the realm of numbers, that is, for the purposes of the analogy, the immanent consciousness. In order to do justice to the claim of objectivity that all “I”s are equivalent, he suggests that only such numerical relations are to be declared of interest as remain unchanged under passage from an “absolute” to an arbitrary coordinate system, that is, those which are invariant under arbitrary linear coordinate transformations. When this scheme is given a purely axiomatic formulation, Weyl sees a third viewpoint emerging in addition to that of realism and idealism, namely, a transcendentalism which “postulates a transcendental reality but is satisfied with modelling it in symbols.”
Interestingly, by the time this was written, Weyl seems to have moved away somewhat from the phenomenology that originally suggested the geometric analogy. For he asserts that a number of Husserl’s theses become “demonstratively false” when translated into the context of the analogy, “something which,” he opines, “gives serious cause for suspecting them.” Unfortunately, he does not specify which of Husserl’s theses he has in mind.
Weyl goes on to emphasize:
Beyond this, it is expected of me that I recognize the other I—the you—not only by observing in my thought the abstract norm of invariance or objectivity, but absolutely: you are for you, once again, what I am for myself: not just an existing but a conscious carrier of the world of appearances.
This recognition of the Thou, according to Weyl , can be presented within his geometric analogy only if it is furnished with a purely axiomatic formulation. In taking this step Weyl sees a third viewpoint emerging in addition to that of realism and idealism, namely, a transcendentalism which “postulates a transcendental reality but is satisfied with modelling it in symbols.”
But Weyl, ever-sensitive to the claims of subjectivity, hastens to point out that this scheme by no means resolves the enigma of selfhood. In this connection he refers to Leibniz’s attempt to resolve the conflict between human freedom and divine predestination by having God select for existence, on the grounds of sufficient reason, certain beings, such as Judas and St. Peter, whose nature thereafter determines their entire history. Concerning this solution Weyl remarks characteristically:
it] may be objectively adequate, but it is shattered by the desperate cry of Judas: Why did I have to be Judas! The impossibility of an objective formulation to this question strikes home, and no answer in the form of an objective insight can be given. Knowledge cannot bring the light that is I into coincidence with the murky, erring human being that is cast out into an individual fate.
For further discussion of Weyl’s philosophical views see Bell (2003).
- 121.
Weyl described Brouwer ’s system of mathematics as refraining from making the “leap into the beyond” required by classical set theory (Weyl 1949, p. 50).
- 122.
- 123.
- 124.
Ibid., p. 97.
- 125.
Ibid., p. 98.
- 126.
See Chap. 9 below.
- 127.
See Appendix A.
- 128.
Weyl (1921), p. 111.
- 129.
See Chap. 1 above.
- 130.
Brouwer established the continuity of functions fully defined on a continuum in 1904 but did not publish a definitive account until 1927. In that account he also considers the possibility of partially defined functions.
- 131.
Weyl (1949), p. 54.
- 132.
Weyl (1985), p. 17.
Bibliography
Bell, J.L. 2003. Hermann Weyl’s later philosophical views: His divergence from Husserl. In Husserl and the Sciences, ed. R. Feist. Ottawa: University of Ottawa Press.
Benacerraf, P., and H. Putnam. 1977. Philosophy of Mathematics: Selected Readings. 2nd ed. Cambridge: Cambridge University Press.
Brentano, F. 1974. Psychology from an Empirical Standpoint. New York: Humanities Press.
———. 1988. Philosophical Investigations on Space, Time and the Continuum. Trans. Smith, B. Croom Helm.
Brouwer, L.E.J. 1975. In Collected Works, 1, ed. A. Heyting. New York: North-Holland.
Ehrlich, P., ed. 1994. Real Numbers, Generalizations of the Reals, and Theories of Continua. Dordrecht: Kluwer.
———. 1994a. All numbers great and small. In , ed. Ehrlich, 239–258. Dordrecht: Kluwer Academic Publishers.
Fisher, G. 1981. The infinite and infinitesimal quantities of du Bois-Reymond and their reception. Archive for History of Exact Sciences 24 (2): 101–163.
———. 1994. Veronese’s non-Archimedean linear continuum. In Ehrlich 1994: 107–146.
Folina, J. 1992. Poincaré and the Philosophy of Mathematics. New York: St. Martin’s Press.
Fraenkel, A., Y. Bar-Hillel, and A. Levy. 1973. Foundations of Set Theory. 2nd ed. Amsterdam: North-Holland.
Hardy, G.H. 1910. Orders of Infinity. Cambridge: Cambridge University Press.
Mancosu, P. 1998. From Brouwer to Hilbert: The Debate on the Foundations of Mathematics in the1920s. Oxford: Clarendon Press.
Peirce, C.S. 1976. In The New Elements of Mathematics, ed. Carolyn Eisele, vol. III. Atlantic Highlands: Mouton Publishers and Humanities Press.
———. 1992. In Reasoning and the Logic of Things, ed. Kenneth Laine Ketner. Cambridge: Harvard University Press.
Poincaré, H. 1946. Foundations of Science. Trans. Halstead. Science Press.
Weyl, H. 1921. On the new foundational crisis in mathematics. (English translation of ‘Über der neue Grundslagenkrise der Mathematik,’ Mathematische Zeitschrift 10, 1921, 37–79.) In Mancosu (1998), pp. 86–122.
———. 1929. Consistency in Mathematics. Rice Institute Pamphlet 16, 245–265. Reprinted in Weyl (1968) II, pp. 150–170.
———. 1932. The Open World: Three Lectures on the Metaphysical Implications of Science. New Haven: Yale University Press.
———. 1949. Philosophy of Mathematics and Natural Science. Princeton: Princeton University Press. (An expanded Engish version of Philosophie der Mathematik und Naturwissenschaft, Leibniz Verlag, 1927.).
———. 1950. Space-Time-Matter. Trans. Brose, H. Dover. (English translation of Raum, Zeit, Materie, Springer, 1918.)
———. 1954. Address on the unity of knowledge. Columbia University Bicentennial Celebration. Reprinted in Weyl (1968) IV, pp. 623–630.
———. 1969. Insight and reflection. (Lecture delivered at the University of Lausanne, Switzerland, May 1954. Translated from German original in Studia Philosophica, 15, 1955.) In T.L. Saaty and F.J. Weyl, eds., The Spirit and Uses of the Mathematical Sciences, pp. 281–301. McGraw-Hill, 1969.
———. 1985. Axiomatic versus constructive procedures in mathematics., ed. T. Tonietti. Mathematical Intelligencer 7, no. 4, pp. 10–17, 38.
———. 1987. The Continuum: A Critical Examination of the Foundation of Analysis, Trans. S. Pollard and T. Bole. Thomas Jefferson University Press. (English translation of Das Kontinuum, Leipzig: Veit, 1918.)
———. 1998a. On the New Foundational Crisis in Mathematics. (English translation of ‘Über der neue Grundslagenkrise der Mathematik,’ Mathematische Zeitschrift 10, 1921, pp. 37–79.) In Mancosu (1998), pp. 86–122.
———. 1998b. On the Current Epistemological Situation in Mathematics. English translation of ‘Die Heutige Erkenntnislage in der Mathematik, Symposion 1, 1925–27, pp. 1–32.) In Mancosu (1998), pp. 123–142.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bell, J.L. (2019). Dissenting Voices: Divergent Conceptions of the Continuum in the Nineteenth and Early Twentieth Centuries. In: The Continuous, the Discrete and the Infinitesimal in Philosophy and Mathematics. The Western Ontario Series in Philosophy of Science, vol 82. Springer, Cham. https://doi.org/10.1007/978-3-030-18707-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-18707-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18706-4
Online ISBN: 978-3-030-18707-1
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


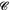 —the category of continua—by taking continua as objects and correlations between continua as arrows. Then, given any arrow f: A→ B in
—the category of continua—by taking continua as objects and correlations between continua as arrows. Then, given any arrow f: A→ B in