Abstract
Mathematicians have developed two methods of deriving the theorems of geometry: the analytic and the synthetic. While the analytical method is based on the introduction of numerical coordinates, and so on the theory of real numbers, the (much older) idea behind the synthetic approach is to furnish the subject of geometry with an autonomous foundation within which the theorems become deducible by logical means from an initial body of postulates.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Busemann (1955).
- 2.
An Incredible Shrinking Man(ifold), no less.
- 3.
It is this deficiency that makes the construction of the tangent bundle in Man something of a headache: see Spivak (1975).
- 4.
That is, differentiable arbitrarily many times
- 5.
See Chap. 7.
- 6.
Also known as the Kock-Lawvere axiom after its formulators, Anders Kock and F. W. Lawvere .
- 7.
This feature of SIA brings to mind Protagoras’s claim (as reported by Aristotle (in Metaphysics III, 2) that “the circle touches the ruler not at a point, but along a line.”
- 8.
See Chap. 2. It should be pointed out, however, that Nieuwentijdt’s infinitesimals differ from those of SIA in that that the product of any two of the former vanishes, while this is not the case for the latter.
- 9.
We shall use letters ε, η, ζ to denote arbitrary microquantities.
- 10.
This can be seen by noting that for any f ∈ R 0, the Mcroaffineness Axiom ensures that there is a unique b ∈ R for which f(ε) = bε for all ε, and conversely each b ∈ R yields the map ε ↦ bε in R 0.
- 11.
A monoid is a multiplicative system (not necessarily commutative) with an identity element.
- 12.
See Chap. 3.
- 13.
Lawvere (2011).
- 14.
This would seem to be consonant with Hermann Cohen’s conception of the infinitesimal as mentioned at the end of Chap. 4.
- 15.
See Chap. 1.
- 16.
See Chap. 5.
- 17.
Note that, with the appropriate choice of maps , each of these constitute the objects of a further topos, the topos of first-order differential structures over objects in S.
- 18.
And closed curves can be treated as infinilateral polygons , as they were by Galileo and Leibniz .
- 19.
What follows is surely the prettiest demonstration of the product rule ever devised. Leibniz would have found it delightful.
- 20.
▼ is in fact the characteristic triangle of seventeenth century analysis (see Chap. 2). As will be seen, in SIA its area reduces to zero.
- 21.
See Chap. 2.
- 22.
See Bell (1998).
- 23.
Weyl (1949) 44–5. Yet we also recall Weyl’s observation:
The principle of gaining knowledge of the external world from the behaviour of its infinitesimal parts is the mainspring of the theory of knowledge in infinitesimal physics as in Riemann’s geometry, and, indeed, the mainspring of all the eminent work of Riemann (Weyl 1950, p. 92).
- 24.
We givde another refutation of (∗) below.
- 25.
See Chap. 5.
- 26.
To be precise, this condition can be shown to hold in a number of models of SIA , See McLarty (1988).
- 27.
See Chap. 9.
- 28.
A set is said to be inhabited if it can be constructively shown to have a member. In intuitionistic logic this is a stronger condition than the assertion that the set be nonempty.
- 29.
See Wagon (1993).
- 30.
See Chap. 4.
- 31.
Moerdijk and Reyes (1991), Remark VII.2.14.
- 32.
Moerdijk and Reyes (1991)
- 33.
Here a ≠ b stands for ¬a = b.
- 34.
- 35.
Here, T, ⊥ are symbols denoting, respectively, the true and the false.
- 36.
It should be noted that, while Δ does not reduce to {0}, nevertheless 0 is the only explicitly nameable element of Δ. For it is easily seen to be inconsistent to assert that Δ actually contains an element ≠ 0.
- 37.
See Chap. 9.
- 38.
In CA , the stability of < can be shown to entail, for certain predicates A, the corresponding instance of Markov’s Principle, namely
$$ \forall x\left(A(x)\vee \neg A(x)\right)\wedge \neg \forall x\neg A(x)\to \exists xA(x). $$Markov’s principle is not generally accepted in constructive analysis . See Dummett (1977) and Bridges and Richman (1987).
- 39.
See Appendix A.
- 40.
Bell (2001).
- 41.
Chap. 9.
- 42.
It should be emphasized that this phenomenon is a consequence of axiom O6: it cannot necessarily be affirmed in versions of SIA not including this axiom.
- 43.
Notice that in CA all of these infinitesimal objects are degenerate. This makes it difficult to formulate a satisfactory theory of infinitesimals in any extension of CA , in particular, in intuitionistic analysis .
- 44.
Here
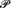 A is the power
set of a set A.
A is the power
set of a set A.
- 45.
See Johnstone (1977). In the topos Shv(X) of sheaves over a topological space X, R d is the sheaf of continuous real-valued functions on open subsets of X.
- 46.
The failure of this law in SIA follows immediately from the cohesiveness of R by considering the predicate x ≠ 0. As originally shown by Johnstone, conditional completeness of R d is actually equivalent to this logical law ¬p ∨ ¬¬p: in Shv(X), the law holds iff X is extremally disconnected, that is, the closure of every open set is open.
- 47.
L. Stout, Topological properties of the real numbers object in a topos. Cahiers Topologie Géom. Différentielle 17, no. 3, (1976), pp. 295-326.
- 48.
It is easily shown that a subset X of a set A is detachable if and only if the property of being a member of X is decidable , that is, if ∀x∈A(x ∈ X or x ∉ X).
- 49.
See Moerdijk and Reyes (1991).
- 50.
IN may accordingly be seen as accommodating both the invertible infinitesimals of Leibniz and the noninvertible nilsquare infinitesimals of Nieuwentijdt .
- 51.
Recall that a set is A is inhabited if it is nonempty in the strong sense of actually possessing an element, as opposed to the constructively weaker sense of the assertion that it is empty being refutable.
- 52.
On the other hand it follows from the nondegeneracy of Δ that it is also inconsistent to assert that Θ reduces to {0}.
- 53.
It should be pointed out, however, that constructive versions of NSA have been developed. See Palmgren (1998).
- 54.
In this connection we recall, for the last time, the words of Hermann Weyl :
The principle of gaining knowledge of the external world from the behaviour of its infinitesimal parts is the mainspring of the theory of knowledge in infinitesimal physics as in Riemann’s geometry and, indeed, the mainspring of all the eminent work of Riemann (1922, p. 92).
Hilbert declared set theory to be “Cantor’s Paradise”; In the same spirit, SIA could be dubbed “Riemann’s Paradise”. The one, the Paradise of the Discrete; the other, the Paradise of the Continuous.
- 55.
A number of these are derived in Bell (1998).
- 56.
Reprinted in English translation in Einstein et al. (1952). It should be noted, however, that in subsequent presentations of special relativity Einstein avoided the use of infinitesimals
- 57.
Here x’ is simply a symbol for the x-coordinate of the moving frame, not to be confused with the derivative of x.
- 58.
See, for example Box 2.1 of Misner et al. (1972).
- 59.
See footnote immediately above.
- 60.
Op. cit., p. 205.
- 61.
Ress (2001).
- 62.
My account here is based on McLarty’s illuminating paper (1988).
- 63.
In this spirit, we may take the microobjects in Space to represent the diverse theories of infinitesimals that were still in place before set theory swept them away.
- 64.
As mentioned in McLarty (1988), it can be shown that, in the presence of the axioms for SIA augmented by the two additional axioms introduced below, discrete spaces together with the maps between them form a category which satisfies the system of axioms characterizing the category Set . In this sense Set may be seen as the result of “imposing” the law of excluded middle on the objects of Space , or more precisely, of discarding those objects of Space which fail to satisfy that law. McLarty mentions another method of obtaining Set from Space, that of passing to double-negation sheaves.
- 65.
McLarty (1988), p. 83.
- 66.
Op. cit., p. 84
- 67.
Ibid.
- 68.
Op. cit., p. 85.
- 69.
Ibid.
- 70.
Boyer (1968), p. 600.
- 71.
For example, Dirichlet’s function r: R → R defined by r(x) =1 for x rational and r(x) = 0 for x irrational.
- 72.
In the passage from Space to Set , nonzero infinitesimals sink without trace, since the application of Γ reduces microobjects such as Δ to singletons such as {0}.
- 73.
McLarty (1988), p. 87.
Bibliography
Bell, J.L. 1998. A Primer of Infinitesimal Analysis. Cambridge: Cambridge University Press. Second edition 2oo8.
———. 2001. In The Continuum in Smooth Infinitesimal Analysis, ed. Peter Schuster, Ulrich Berger, and Horst Osswald, 19–24. Dordrecht: Kluwer Academic Publishers.
Boyer, C. 1968. A History of Mathematics. Hoboken: Wiley.
Bridges, D., and F. Richman. 1987. Varieties of Constructive Mathematics. Cambridge: Cambridge University Press.
Busemann, H. 1955. The Geometry of Geodesics. New York: Academic.
Dummett, M. 1977. Elements of Intuitionism. Oxford: Clarendon Press.
Einstein, A., et al. 1952. The Principle of Relativity : a Collection of Original Memoirs on the Special and General Theory of Relativity. Trans. Perrett and Jeffrey. Dover. Reprint of 1923 Methuen edition.
Johnstone, P.T. 1977. Topos Theory. London: Academic.
Kock, A. 1981. Synthetic Differential Geometry. Cambridge: Cambridge University Press.
Lawvere, F.W. 2011. Euler’s continuum functorially vindicated. In Vintage Enthusiasms: Essays in Honour of John L. Bell, ed. D. Devidi, P. Clark, and M. Hallett. Dordrecht: Springer.
McLarty, C. 1988. Defining sets as sets of points of spaces. Journal of Philosophical Logic 17: 75–90.
———. 1992. Elementary Categories, Elementary Toposes. Oxford: Oxford University Press.
Misner, C., K. Thorne, and J. Wheeler. 1972. Gravitation. San Francisco: Freeman.
Moerdijk, I., and G.E. Reyes. 1991. Models for Smooth Infinitesimal Analysis. New York: Springer.
Palmgren, E. 1998. Developments in constructive nonstandard analysis. The Bulletin of Symbolic Logic 4: 233–272.
Rees, M. 2001. Just Six Numbers: The Deep Forces that Shape the Universe. New York: Basic Books.
Spivak, M. 1975. A Comprehensive Introduction to Differential Geometry. Houston: Publish or Perish Press.
Wagon, S. 1993. The Banach-Tarski Paradox. Cambridge: Cambridge University Press.
Weyl, H. 1949. Philosophy of Mathematics and Natural Science. Princeton: Princeton University Press. (An expanded Engish version of Philosophie der Mathematik und Naturwissenschaft, Leibniz Verlag, 1927.).
———. 1950. Space-Time-Matter. Trans. Brose, H. Dover. (English translation of Raum, Zeit, Materie, Springer, 1918.)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bell, J.L. (2019). Smooth Infinitesimal Analysis/Synthetic Differential Geometry. In: The Continuous, the Discrete and the Infinitesimal in Philosophy and Mathematics. The Western Ontario Series in Philosophy of Science, vol 82. Springer, Cham. https://doi.org/10.1007/978-3-030-18707-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-18707-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18706-4
Online ISBN: 978-3-030-18707-1
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


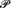 A is the power
set of a set A.
A is the power
set of a set A.