Reinforcement Learning Applied to Adaptive Classification Testing

Abstract

This study investigates how computerized adaptive classification testing task can be considered as a sequential decision process and made accessible to Reinforcement Learning. The proposed method performs a sequential item selection that learns which items are most informative, choosing the next item depending on the already administered items and the internal belief of the classifier. A simulation study shows its efficiency for tests which require to make a confident classification decision with as few items as possible. Solutions for a variety of practical problems using the proposed method are considered in this study.

1 Introduction

The key component of a computerized classification testing (CCT)/adaptive testing (CAT) program is the “adaptive” item selection algorithm, which should find the best suited items for each test taker based on his or her estimated ability.

Several item selection methods have been proposed based on item response theory, including the maximization of item information at the current θ estimate (Reckase 1983), the cut-score (Spray and Reckase 1994, 1996), maximization of item information across a region for θ (Eggen 1999), a log-odds ratio (Lin and Spray 2000), and maximization of item information across θ (Weissman 2004).

In addition to correct classification, several other concerns have to be taken into account when selecting the next item in an operational CAT program. Various non-statistical constraints need to be considered, such as content balancing and exposure control. Several heuristics are proposed for this purpose, including the weighted deviation modelling (WDM) method (Stocking and Swanson 1993), the normalized weighted absolute deviation heuristic (NWADH; Luecht 1998), the maximum priority index (MPI) method (Cheng and Chang 2009); randomization strategies, e.g. randomesque strategy (Kingsbury and Zara 1989); conditional selection strategies, e.g. targeted exposure control strategy (Thompson 2002), shadow test approach (van der Linden and Veldkamp 2005); combined strategies (Eggen 2001), e.g. combined application of Sympson-Hetter strategy (Sympson and Hetter 1985) and Progressive strategy (Revuelta and Ponsoda 1998); maximum information with content control and exposure control (Eggen and Straetmans 2000).

Differences in item selection methods may lead to different choices of items for the same test takers and, consequently, to different classification decisions. The choice of the item selection method is therefore one of the most important parts of computerized adaptive testing.

Test content balancing and item exposure control are separate steps that are generally integrated in the item selection heuristics by limiting the items available for selection or by adding small probability experiments to limit over- or underexposure of items. This study applies a new adaptive item selection method. It explores the possibility to solve problems, such as exposure control and content balancing, that may occur in computerized adaptive classification testing (CACT), and simultaneously attempts to optimize item selection.

2 Method

Fisher information is commonly used for item selection, but this information measure is based on an estimate of the ability parameter, and the ability estimate is not very stable, particularly in the beginning of a CAT administration. Therefore, when the estimate is not close to the true value, using the Fisher information criterion might result in inefficient item selection. The observation that item selection procedures may favor items with optimal properties at wrong ability values is generally known as the attenuation paradox (Lord and Novick 1968, Sect. 16.5).

The foundation of new methodology for incorporating expert test development practices in the construction of adaptive classification tests is the application of reinforcement learning. It has been applied successfully to various selection problems, including robotics, elevator scheduling, telecommunications, a few games, such as backgammon, checkers and go (see Sutton and Barto 1998). Reinforcement learning refers to goal-oriented algorithms, which learn how to attain a complex objective or maximize along over a particular dimension over many steps.

There are two major factors that make reinforcement learning powerful: the use of samples to optimize performance and the use of function approximation to deal with large environments. Reinforcement learning can solve the difficult problem of correlating immediate actions with the delayed returns they produce. Reinforcement learning can be used in the situation, where there is no information about the environment and the only way to collect it is to interact with it. This could be considered to be a genuine learning problem, which is fit to adaptive classification testing, for example to get information about a test taker’s state (classification state) it is needed to give him/her an item (action) and get a response.

In short, an improved approach of item selection is presented, which not only optimally spans the item pool (input space), but also optimizes with respect to data consumption, that is, minimizes the test length needed to classify respondents. Going beyond traditional item selection methods in the computerized adaptive testing, in this paper, we lay out and demonstrate an approach of selecting items in sequence, making the decision which item to select next dependent on previously selected features and the current internal state of the supervised method that it interacts with. In particular, our sequential item selection (SIS) algorithm will embed Reinforcement Learning (RL) into classification tasks, with the objective to reduce data consumption and associated costs of item selection during classification. The main question of this chapter is: “Where do I have to look next, in order to keep data consumption and costs low while maintaining high classification results?” or “Which item should I deliver to the test taker next, in order to keep test constraints satisfied while maintaining high classification results?”

The Framework is mapped out in the following section. After introducing the general idea, the formal definition of sequential classifiers and rephrasing the problem as a Partially Observed Markov Decision Process (POMDP) is represented (see Astrom 1965). In addition, an algorithm to take exposure and content control into consideration is introduced.

3 Framework

3.1 General Idea

Machine learning is often applied to classification problems: mapping an input x to one of a finite set of class labels C. Regarding classification testing, the formulation of the initial problem remains the same: based on a series of item responses of the test takers (vector x), class C is estimated.

In classification testing, item selection is needed as key option for good classification results: filtering out less informative items, while paying attention to exposure and content control. Reformulating this to classic machine learning: item selection is a combinatorial optimization problem that tries to identify those items, which will minimize the generalization error, with different constraints. In particular, item selection can be seen as a process that tries to reduce the amount of redundant data.

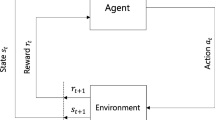
Turning classification into a sequential decision process results in item selection and classification becoming an adaptive and intertwined process: deciding which item to select next depends on the previously-selected items and the behavior of the classifier on them. This will be achieved by using a fully trained classifier as an environment for a Reinforcement Learning agent, that learns which item to select next, receiving the reward on successful classification of the partially uncovered input response pattern. The general schema of reinforcement learning is described below (Fig. 17.1).

Fig. 17.1

Typical framing of reinforcement learning scenario

Figure 17.1 represents how reinforcement learning works in general: an agent interacts with an environment by taking actions, which is translated into a reward and a representation of the state, which are fed back to the agent. Typical framing of RL can be mapped to CACT as follows:

Agent. An agent takes actions. In CACT, the algorithm which select items or terminate a test is an agent.

Action. Action is the set of all possible moves the agent can make. An action is almost self-explanatory, but it should be noted that agents choose among a list of possible actions. In CACT, the list includes all the items and the action which refers to termination of the test.

Environment. The environment is the world through which the agent moves. The environment takes an agent’s current state and action as input, and returns as output the agent’s reward and its next state. In CACT, the environment could be the rules of our classification process, such as, the metric used for making decisions, the maximum number of items in the test, the exposure rate, etc.

State. A state is a concrete and immediate situation in which an agent finds itself; i.e. a specific moment, an instantaneous configuration that puts an agent into relation to other significant things. In CACT, it can be the number of items that have already been administered, the probabilities of selecting next items, etc.

Reward. A reward is the feedback by which we measure the success or failure of the agent’s actions. Rewards can be immediate or delayed. In CACT, rewards can be granted after an agent terminates the test. The reward is delayed, when it is granted after the test has ended. An immediate reward in CACT can be provided as a penalty for the agent, when an agent chooses an item that has already been administered, or an item that would bring the exposure rate over the limit.

3.2 Sequential Classification

First of all, it is needed to formulate CACT as a Partially Observed Markov Decision Process (POMDP), making the problem sequential and thus accessible to Reinforcement Learning algorithms. For detailed information about POMDP, the reader is referred to Astrom (1965). For now we focus on the implementation of POMDP. Therefore, some specific notation and some definitions have to be introduced.

Specific notation used in this chapter:

• ( )—ordered sequences,

• { }—unordered sequences,

• a • k—appending an element k to a.

Besides, several concepts have to be defined:

Power sequence. Related to power sets, a power sequence, denoted as powerseq(M), is defined as a set of all permutations of all elements in the power set of M, including empty sequence ( ). As an example, for M = {0,1}, the resulting powerseq(M) = {( ), (0), (1), (0,1),(1,0)}.

Episode. Each test administration is called an episode. During an episode, the item history $h_{t} \in {\text{powerseq}}\left( F \right)$ is the sequence of all previously selected items in an episode up to and including the current item at time t.

Cost. Costs associated with accessing an item f are represented as negative scalars $r_{f}^{ - } \in {\mathbb{R}},r_{f}^{ - } < 0.$

Reward. A non-negative global reward is defined as $r^{ + } \in {\mathbb{R}},r^{ + } \ge 0$ for correctly classifying an input.

Classifier. Classifiers in general are denoted with the symbol K. A sequential classifier is defined by K*, and it is to be a functional mapping from the power sequence of item responses to a set of classes, i.e., $K^{*} :{\text{powerseq}}\left( {\left\{ {f\left( x \right)} \right\}_{f \in F} } \right) \to \varvec{C}$.

A requirement of CACT as POMDP is to process the sequence one input at a time in an online mode, rather than classifying the whole sequence at once. Besides, as output, a class label is added to each input. Therefore, K* requires some sort of memory. Recurrent Neural Networks (RNN) are known to have implicit memory that can store information about inputs seen in the past (see Hopfield 1982; Hochreiter and Schmidhuber 1997). In this chapter RNN and RNN with Gated Recurrent units (GRU) are used (Cho et al. 2014).

Dealing with a POMDP implies that we need to extract an observation from the classifier that summarizes the past into a stationary belief. Most classifiers base their class decision on some internal belief state. A Feed Forward Network (FFN), for example, often uses a softmax output representation, returning a probability p_i in [0,1] for each of the classes with $\sum\nolimits_{i = 1}^{\varvec{C}} {p_{i} = 1}$. If this is not the case (e.g., for purely discriminative functions like a Support Vector Machine), a straightforward belief representation of the current class is a k-dimensional vector with 1-of-k coding.

To finally map the original problem of classification under the objective to minimize the number of items to be administered to POMDP, the elements of the 6-tuple ($S, A,O,{\rm P},\varOmega ,{\mathcal{R}}$) which describes POMDP can be described as follows. The state $s \in S$ at timestep t comprises the current input response pattern x, the classifier K*, and the previous item history h_t-1, so that $s_{t} = \left( {x, K^{*} ,h_{t - 1} } \right)$. This triple suffices to fully describe the decision process at any point of time. Actions $a_{t} \in A$ are chosen from the set of items F\h_t-1, i.e., previously administered items are not available. The observation $o_{t} \in O$ is represented by the classifier’s internal belief of the class after seeing the values of all items in h_t−1, written as $o_{t} = b\left( {x,K^{*} ,h_{t - 1} } \right) = b\left( {s_{t} } \right)$. The probabilities p_i for each class serve as an observation to the agent: $o_{t} = b\left( {x,K^{*} ,h_{t - 1} } \right) = \left( {p_{1} , p_{2} , \ldots ,p_{{\left| \varvec{C} \right|}} } \right)$.

Assuming a fixed x and a deterministic, pretrained, classifier K*, the state and observation transition probabilities ${\text{\rm P}}\;{\text{and}}\;\Omega$ collapse and can be described by a deterministic transition function T, resulting next state $s_{t + 1} = T_{x} \left( {s_{t} ,a_{t} } \right) = \left( {x, K^{*} , h_{t - 1} \cdot a_{t} } \right)$ and next observation $o_{t + 1} = b\left( {s_{t + 1} } \right)$. Finally, the reward function ${\mathcal{R}}_{{ss^{\prime}}}^{a}$ returns the reward r_t at timestep t for transitioning from state s_t to s_t+1 with action a_t. Given c as the correct class label, it is defined as:

$$ r^{t} = \left\{\!\!{\begin{array}{*{20}c} {r^{ + } + r_{{a_{t} }}^{ - } if K^{ *} \left( {\left( {h_{\tau } \left( x \right)} \right)_{0 < \tau \le t} } \right) = c} \\ \qquad\;\;\;{r_{{a_{t} }}^{ - } \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\,\, else} \\ \end{array} } \right. $$

3.3 Item Selection

In CACT, one needs to ensure that an item (action) is only chosen at most once per test taker (per episode), i.e., the set of available actions at each given decision step is dependent on the history h_t of all previously selected actions (items) in an episode (for one test taker). Note that this does not violate the Markov assumption of the underlying MDP, because no information about available actions flows back into the state and therefore the decision does not depend on the item history.

Value-based reinforcement learning can solve this problem. The action value V is the expected return for selecting action in a state and following policy. By manually changing all action-values V(o, at) to −∞ after choosing action (item) at, this leads to all actions not previously chosen in the current episode having larger value and be preferred over a_t. A compatible exploration strategy for this action selection without replacement is Boltzmann exploration (Cesa-Bianchi et al. 2017). Here a probability of choosing an action is proportional to its value under the given observation:

$$ p\left( {a_{t} |o_{t} } \right) = \frac{{e^{{V\left( {a_{t} |o_{t} } \right)/\tau }} }}{{\mathop \sum \nolimits_{a} e^{{V\left( {a_{t} |o_{t} } \right)/\tau }} }}, $$

where $\tau$ is a temperature parameter that is slowly reduced during learning process for greedier selection towards the end. Thus, when selecting action a_t+1, all actions in h_t have a probability of $e^{ - \infty } = 0$ of being chosen again. At the end of an episode, the original values are restored.

Having defined the original task of classification as a POMDP and solved the problem of action selection without replacement (item selection), it is possible to use existing algorithms for solving this class of problems. Since the transition function is unknown to the agent, it needs to learn from experience, and a second complication is the continuous observation space.

3.4 Algorithm

In this chapter, the actor-critic algorithm is used (see Mnih et al. 2016). The Actor-critic algorithm maintains a policy $\pi (\left( {t_{t} ,a_{t} } \right)|s_{t} ;\theta )$ and an estimate of the value function $V\left( {s_{t} ;\theta_{\upsilon } } \right)$, where $\theta$—parameters, which are learned by iteratively minimizing a sequence of loss functions, and policy represents how items (actions) are picked from the item pool; t—termination gate—action which represent the termination step of the test. Policy and a value can be briefly described as follows:

Policy. A policy is the strategy that the agent employs to determine the next action based on the current state. It maps states to actions, the actions that promise highest reward.

Value. The expected long-term return, as opposed to the short term reward. Value is defined as the expected long-term return of the current state under the policy.

The actor-critic algorithm operates in a forward view and uses a mix of n-step returns to update both the policy and the value-function. The general schema of the actor-critic algorithm is shown in Fig. 17.2. The policy and the value function are updated after every $t_{max}$ actions or when a terminal state is reached. The update performed by the algorithm can be seen as $\nabla_{{\theta^{\prime}}} { \log }\pi (\left( {t_{t} ,a_{t} } \right)|s_{t} ;\theta^{\prime})A\left( {s_{t} ,a_{t} ;\theta ,\theta^{\prime}} \right)$ where $A\left( {s_{t} ,a_{t} ;\theta ,\theta^{\prime}} \right)$ is an estimate of the advantage function given by $\mathop \sum \nolimits_{i = 0}^{k - 1} \gamma^{i} r_{t + i} + \gamma^{k} V\left( {s_{t + k} ;\theta_{v} } \right) - V\left( {s_{t} ;\theta_{v} } \right)$, where k can vary from state to state and is upper-bounded by $t_{max}$.

Fig. 17.2

Typical framing of actor-critic algorithm

The state sequence s is hidden and dynamic, controlled by an RNN sequence model. The Actor-critic algorithm performs a “classification” action a_T at the T-th step, which implies that the termination gate variables equal t_1:T= (t₁= 0, …, t_T−1= 0, t_T = 1). Basically, at the T-th step, the actor-critic model (ACM) gets enough information to terminate tests and make a classification decision. The ACM learns a stochastic policy $\pi (\left( {t_{t} ,a_{t} } \right)|s_{t} ;\theta )$ with parameters $\theta$ to get a distribution of termination actions, to continue administering items, or to stop, and of a ‘classification’ action, if the model decides to stop at the current step. The termination step T can vary from test taker to test taker. However, it is possible to set the maximum of T, to ensure that a test ends anyway at step T. Then, if T is reached, classification decision is made by existing information from steps 1 to T.

The parameters $\theta$ are trained by maximizing the total expect reward. The expected reward for a test taker is defined as:

$$ J\left( \theta \right) = {\mathbb{E}}_{{\pi \left( {t_{1:T} ,a_{T} ;\theta } \right)}} \left[ {\mathop \sum \limits_{t = 1}^{T} r_{t} } \right] $$

The reward can only be received at the final termination step when a classification action a_T is performed. We define r_T = 1 if t_T = 1 and the classification is correct, and r_T = −1 otherwise. The rewards on intermediate steps are zeros, except for cases when items are repeatedly selected, in that case rewards are also −1. This is done to penalize the agent for picking same items for the same test taker; and cases when selecting an item results in exceeding the limit in exposure rate, in that cases reward −0.5. J can be maximized by directly applying gradient-based optimization methods. The gradient of J is given by:

$$ \nabla_{\theta } J\left( \theta \right) = {\mathbb{E}}_{{\pi \left( {t_{1:T} ,a_{T} ;\theta } \right)}} [\nabla_{\theta } { \log }\pi \left( {\left( {t_{1:T} ,a_{T} ;\theta } \right)r_{T} } \right] $$

Motivated by the REINFORCE algorithm (Williams 1992), the following computation of $\nabla_{\theta } J\left( \theta \right)$ is estimated:

$$ \begin{aligned} & {\mathbb{E}}_{{\pi \left( {t_{1:T} ,a_{T} ;\theta } \right)}} [\nabla_{\theta } { \log }\pi \left( {\left( {t_{1:T} ,a_{T} ;\theta } \right)r_{T} } \right] \\ & \quad = \mathop \sum \limits_{{\left( {t_{1:T} ,a_{T} } \right) \in {\mathbb{A}}^{\dag } }} \pi \left( {t_{1:T} ,a_{T} ;\theta } \right)[\nabla_{\theta } { \log }\pi \left( {\left( {t_{1:T} ,a_{T} ;\theta } \right)r_{T} - b_{T} } \right], \end{aligned} $$

where ${\mathbb{A}}^{\dag }$ represents all the possible episodes, and T, t_1:T, a_T and r_T are the termination step, termination action, classification action, and reward, respectively, for the $\left( {t_{1:T} ,a_{T} } \right)$ episode, while. b_T, which is called the reward baseline in the RL literature is introduced to lower the variance (Sutton 1984). It is common to select $b_{T} = {\mathbb{E}}_{\pi } \left[ {r_{T} } \right]$(Sutton et al. 1999), and this term can be updated via an online moving average approach: $b_{T} = \lambda b_{T} + \left( {1 - \lambda } \right)r_{T} .$ However, this might lead to slow convergence in training the ACM. Intuitively, the average baselines {b_T; T = 1…T_max} are global variables, independent of test takers. It is hard for these baselines to capture the dynamic termination behavior of an ACM. Since an ACM may stop at different time steps (different test length) for different test takers, the adoption of a global variable without considering the dynamic variance for each test taker is inappropriate. To resolve this weakness in traditional methods and to account for the dynamic characteristics of an ACM, an instance-dependent baseline method to calculate $\nabla_{\theta } J\left( \theta \right)$ is proposed. The gradient can be rewritten as:

$$ \nabla_{\theta } J\left( \theta \right) = \mathop \sum \limits_{{\left( {t_{1:T} ,a_{T} } \right) \in {\mathbb{A}}^{\dag } }} \pi \left( {t_{1:T} ,a_{T} ;\theta } \right)[\nabla_{\theta } { \log }\pi \left( {\left( {t_{1:T} ,a_{T} ;\theta } \right)r_{T} - b} \right], $$

where the baseline $b = \sum\nolimits_{{\left( {t_{1:T} ,a_{T} } \right) \in {\mathbb{A}}^{\dag } }} {\pi \left( {t_{1:T} ,a_{T} ;\theta } \right)r_{T} }$ is the average reward on the $|{\mathbb{A}}^{\dag } |$ episodes for the n-th training test taker. It allows different baselines for different training test takers. This can be beneficial since the complexity of training test takers varies significantly.

4 Experiments

In this section, evaluation of performance of the ACM is presented. A simulation study utilized a Monte Carlo simulation methodology, with 1000 test takers multiplied by 100 administrations simulated, to evaluate differences in efficiency and accuracy. The population of test takers was randomly drawn and selected from a N(0,1) distribution. With Monte-Carlo simulation, item responses are generated by comparing a randomly generated number 0.0 < r < 1.0 to the probability of an each possible response for each test taker to each item. The probability is calculated using the Generalized Partial Credit Model (GPCM) (see Muraki 1992) and the true test taker’s θ, which is known.

If items are randomly selected, this means that, after each administration, each item that has not been used has an equal chance of being selected. However, with such a method of selecting items, the contents of the test are not matched to the ability of the candidate, consequently, accuracy of decisions may result as inappropriate, and testing is not efficient. Simulation studies have shown that random selection eliminates out the possible gains of adaptive testing. If items are randomly selected, there is an average gain in item pool utilization and exposure rate, but also a loss of accuracy.

Although, in CACT, the optimum item selection method makes sure that each test taker gets a different test, it still occurs that some items from the item pool are administered very frequently while others are never used or hardly ever used. The gains in efficiency go along with two following characteristics of the utilization of the item pool, which result in the following problems:

• (1) Overexposure. Some items are selected with relatively high frequency, that test security is compromised;

• (2) Underexposure. Some items are rarely selected that one wonders how the expenses of developing them can be justified.

Table 17.1 contains the classification accuracies, maximum exposure rate and item pool utilization for the simulation studies. Table 17.1 also shows that problems, that have been explained above, do not occur with random item selection, where all items are used. However, with random selection there is a loss in accuracy.

Table 17.1 Results of simulation studies

The RL-CACT, selecting items on the basis of ACM with T = 10 (maximum length of the test) and with T = 15, uses 65 and 71% items out of item pool, respectively. This is done by implementation of the ACM reward policy as explained in the previous section of this chapter.

Regarding the accuracies, ACM with both T = 10 and T = 15 performed with 89.8 and 92.1% of correct decisions, respectively. Maximum exposure rates are 33.1 and 34.3%. One can vary these rates by changing the reward for the agent, e.g. if one wants to have maximum exposure rate less than 30%, it can be done by tightening penalty for overexposing items.

5 Discussion

Classification CAT is formulated as a POMDP and thereby it is made accessible to RL methods. In this chapter, the main focus is on minimization the number of items (test length) needed to make a confident classification decision. This is done by training the RL agent to pick items that lead to quick and precise classification. Exposure control is maintained by using the different rewards for action selection, which takes into account the item selection history for each test taker. The proposed reward distribution penalizes the agent during the training process if it picks an item, which already has been administered for a certain test taker. Also, it penalizes the agent if the agent selects an item, for which the exposure rate limit is exceeded.

Another issue that might occur with adaptive testing is the content balancing problem. The presented approach can solve this by implementing a specific mask for the items or by giving different rewards for sequences of items. For example, if it assembles a test from an item pool with n domains and M items for each domain, and there is a constraint that exactly m of items from each domain have to be administered. Then we can define the following reward distribution function: give the reward R for the correct classification, and subtract value d for each unadministered domain, or d/m for each missing item from domain.

Any additional constraints can be taken into account by tuning the reward distribution. For instance, for different types of assessment, a different outcome might be desired, e.g. one wants higher accuracy, or higher precision or recall. This can be done by varying rewards during the training process, e.g., after classifying a small sample of test takers, a (batch) additional reward, depending on the desired outcomes, could be implemented. For instance, if in particular batch the number of type II errors exceed limits, then the reward can be reduced by a specific value.

In summary, the proposed method for adaptive item selection in computerized classification testing is efficient for tests requiring to make a confident classification decision with as few items as possible. Moreover, the proposed method can solve problems, such as overexposure and underexposure, with content-distribution constraints, through the reward allocation. However, the design of CACT with ACM model requires simulation research to ensure that the test is implemented to be as efficient as possible.