Abstract
We report on the 2019 edition of the Confluence Competition, a competition of software tools that aim to prove or disprove confluence and related (undecidable) properties of rewrite systems automatically.
This research is supported by FWF (Austrian Science Fund) project P27528.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Confluence Competition (CoCo)Footnote 1 is an annual competition of software tools that aim to prove or disprove confluence and related (undecidable) properties of a variety of rewrite formalisms automatically. Initiated in 2012, CoCo runs live in a single slot at a conference or workshop and is executed on the cross-community competition platform StarExec [1]. For each category, 100 suitable problems are randomly selected from the online database of confluence problems (COPS). Participating tools must answer YES or NO within 60 s, followed by a justification that is understandable by a human expert; any other output signals that the tool could not determine the status of the problem. CoCo 2019 features new categories on commutation, infeasibility problems, and confluence of string rewrite systems.
Confluence provides a general notion of determinism and has been conceived as one of the central properties of rewriting. A rewrite system \(\mathcal {R}\) is a set of directed equations, so called rewrite rules, which induces a rewrite relation \(\rightarrow _\mathcal {R}\) on terms. We provide a simple example.
Example 1
Consider the rewrite system \(\mathcal {R}\) consisting of the rules
which can be viewed as a specification of addition and multiplication over natural numbers in unary notation. Computing \(2 \times (1 + 2)\) amounts to evaluating the term \(s = \mathsf {s}(\mathsf {s}(\mathsf {0})) \times (\mathsf {s}(\mathsf {0}) + \mathsf {s}(\mathsf {s}(\mathsf {0})))\). This is done by matching a subterm with the left-hand side of a rewrite rule, and if matching succeeds, replacing that subterm by the right-hand side of the rule after applying the matching substitution to its variables. For instance, the subterm \(\mathsf {s}(\mathsf {0}) + \mathsf {s}(\mathsf {s}(\mathsf {0}))\) of s matches the left-hand side of the rule \(\mathsf {s}(x) + y \rightarrow \mathsf {s}(x + y)\), with matching substitution \(\{ x \mapsto \mathsf {0}, y \mapsto \mathsf {s}(\mathsf {s}(\mathsf {0})) \}\). Hence the subterm can be replaced by \(\mathsf {s}(\mathsf {0} + \mathsf {s}(\mathsf {s}(\mathsf {0})))\). It follows that s rewrites (in a single step) to the term \(t = \mathsf {s}(\mathsf {s}(\mathsf {0})) \times \mathsf {s}(\mathsf {0} + \mathsf {s}(\mathsf {s}(\mathsf {0})))\). Continuing this process from t eventually results in the term \(\mathsf {s}(\mathsf {s}(\mathsf {s}(\mathsf {s}(\mathsf {s}(\mathsf {s}(\mathsf {0}))))))\). This term cannot be simplified further. Such terms are called normal forms.
In the above example there are several ways to evaluate the term s. The choice does not matter since all maximal rewrite sequences terminate in the same normal form, which is readily checked. This property not only holds for the term s, but for all terms that can be constructed from the symbols in the rules. Confluence is the property that guarantees this. A rewrite system \(\mathcal {R}\) is confluent if the inclusion  holds. Here \(\rightarrow _\mathcal {R}^*\) denotes the transitive reflexive closure of the one-step rewrite relation \(\rightarrow _\mathcal {R}^{ {*}}\),
holds. Here \(\rightarrow _\mathcal {R}^*\) denotes the transitive reflexive closure of the one-step rewrite relation \(\rightarrow _\mathcal {R}^{ {*}}\),  denotes the inverse of \(\rightarrow _\mathcal {R}^*\), and \(\cdot \) denotes relational composition. A more graphical definition of confluence is presented in Fig. 1. The precise notions of rewrite rules, associated rewrite steps, and terms to be rewritten vary from formalism to formalism.
denotes the inverse of \(\rightarrow _\mathcal {R}^*\), and \(\cdot \) denotes relational composition. A more graphical definition of confluence is presented in Fig. 1. The precise notions of rewrite rules, associated rewrite steps, and terms to be rewritten vary from formalism to formalism.
2 Categories
In recent years the focus in confluence research has shifted towards the development of automatable techniques for confluence proofs. To stimulate these developments the Confluence Competition has been set up in 2012. Since its creation with 4 tools competing in 2 categories, CoCo has grown steadily and will feature the following 12 categories in 2019:
-
TRS/CPF-TRS The two original categories are about confluence of first-order term rewriting. CPF-TRS is a category for certified confluence proofs, where participating tools must generate certificates that are checked by an independent certifier.
-
CTRS/CPF-CTRS These two categories, introduced respectively in 2014 and 2015, are concerned (certified) confluence of conditional term rewriting, a formalism in which rewrite rules come equipped with conditions that are evaluated recursively using the rewrite relation.
-
HRS This category, introduced in 2015, deals with confluence of higher-order rewriting, i.e., rewriting with binders and functional variables.
-
GCR This category is about ground confluence of many-sorted term rewrite systems and was also introduced in 2015.
-
NFP/UNC/UNR These three categories, introduced in 2016, are about properties of first-order term rewrite systems related to unique normal forms, namely, the normal form property (NFP), unique normal forms with respect to conversion (UNC), and unique normal forms with respect to reduction (UNR).
-
COM This new category is about commutation of first-order rewrite systems.
-
INF This new category is about infeasibility problems.
-
SRS This new category is concerned with confluence of string rewriting.
The new categories are described in detail in Sect. 5. Descriptions of the other categories can be found in the CoCo 2015 [2] and 2018 [3] reports, and on the CoCo website (see Footnote 1). The underlying problem format is the topic of the next section.
3 Confluence Problems
Tools participating in CoCo are given problems from the database of confluence problems (COPS)Footnote 2 in a format suitable for the category in which the tools participate. Besides commutation and infeasibility problems, which are described in Sect. 5, four different formats are supported: TRS, CTRS, MSTRS, and HRS. As these formats were simplified recently, we present the official syntax below in four subsections.
In addition to the format, tags are used to determine suitable problems for CoCo categories. For instance, for the CTRS category, selected problems must have the 3_ctrs and oriented tags. Such tags are automatically computed when problems are submitted to COPS. Detailed information on COPS, including a description of the tagging mechanism, can be found in [4].
3.1 TRS Format
The format for first-order rewrite systems comes in two versions: a basic version and an extended version. The latter contains an additional signature declaration which is used to define function symbols that do not appear in the rewrite rules.
The basic format is a simplification of the old TPDB format,Footnote 3 according to the following grammar:

Here
 is any sequence of characters and
is any sequence of characters and
 is any nonempty sequence of characters not containing whitespace, the characters
is any nonempty sequence of characters not containing whitespace, the characters
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 , and the sequences
, and the sequences
 ,
,
 ,
,
 ,
,
 , and
, and
 . In
. In
 the variables of the TRS are declared. If this is missing, the TRS is ground. Symbols (
the variables of the TRS are declared. If this is missing, the TRS is ground. Symbols (
 ) appearing in the
) appearing in the
 declaration that were not declared as variables are function symbols. If they appear multiple times, they must be used with the same number (arity) of arguments. Here is an example of the basic format, COPS #1:
declaration that were not declared as variables are function symbols. If they appear multiple times, they must be used with the same number (arity) of arguments. Here is an example of the basic format, COPS #1:

In the extended format, a signature declaration specifying the set of function symbols and their arities is added. In this format, every symbol appearing in the rules must be declared as a function symbol or a variable. Formally, the
 declaration in the basic format is replaced by
declaration in the basic format is replaced by

where
 is a nonempty sequence of digits. An example of the extended format is provided by COPS #557:
is a nonempty sequence of digits. An example of the extended format is provided by COPS #557:

3.2 CTRS Format
The format for first-order conditional rewrite systems is a simplification of the old TPDB format (see Footnote 3), according to the following grammar:

The restrictions on
 and
and
 are the same as in the TRS format. The
are the same as in the TRS format. The
 declaration specifies the semantics of the conditions in the rewrite rules: conversion (\(\leftrightarrow ^*\)) for semi-equational CTRSs, joinability (\(\downarrow \)) for join CTRSs, and reachability (\(\rightarrow ^*\)) for oriented CTRSs. An example of the CTRS format is provided by COPS #488:
declaration specifies the semantics of the conditions in the rewrite rules: conversion (\(\leftrightarrow ^*\)) for semi-equational CTRSs, joinability (\(\downarrow \)) for join CTRSs, and reachability (\(\rightarrow ^*\)) for oriented CTRSs. An example of the CTRS format is provided by COPS #488:

3.3 MSTRS Format
The format for many-sorted term rewrite systems is a modification of the TRS format, according to the following grammar:

The restriction on
 is the same as in the TRS format. Every term must be a well-typed term according the signature declared in
is the same as in the TRS format. Every term must be a well-typed term according the signature declared in
 . Symbols (
. Symbols (
 ) not declared in
) not declared in
 are variables (which can take any sort). We provide an example (COPS #646):
are variables (which can take any sort). We provide an example (COPS #646):

3.4 HRS Format
This format deals with higher-order rewrite systems (HRSs) described by Mayr and Nipkow [5] with small modifications detailed below the typing rules. The format follows the same style as the first-order formats, adding type declarations to variables and function symbols as well as syntax for abstraction and application according to the following grammar:

In
 the function symbols of the HRS are declared, while
the function symbols of the HRS are declared, while
 declares the types of the variables that are used in the rules. An identifier must not occur in both the
declares the types of the variables that are used in the rules. An identifier must not occur in both the
 and
and
 sections, but all identifiers that occur in the
sections, but all identifiers that occur in the
 section must occur in one of them. To save parentheses the following standard conventions are used: In
section must occur in one of them. To save parentheses the following standard conventions are used: In
 ,
,
 associates to the right. For terms, application associates to the left, while abstraction associates to the right. Moreover abstractions extend as far to the right as possible, i.e., application binds stronger than abstraction. The algebraic notation
associates to the right. For terms, application associates to the left, while abstraction associates to the right. Moreover abstractions extend as far to the right as possible, i.e., application binds stronger than abstraction. The algebraic notation
 is syntactic sugar for nested application, i.e.,
is syntactic sugar for nested application, i.e.,
 is syntactic sugar for
is syntactic sugar for
 ; note that due to left-associativity of application,
; note that due to left-associativity of application,
 \(=\)
\(=\)
 . Finally, the expression
. Finally, the expression
 abbreviates
abbreviates
 . Terms must be typable according to the following rules:
. Terms must be typable according to the following rules:

Terms are modulo \(\alpha \beta \eta \). In the interest of user-friendliness and readability we demand that the rules are given in \(\beta \)-normal form, but do not impose any restrictions concerning \(\eta \). Note that the list of variables declared in
 is not exhaustive, fresh variables of arbitrary type are available to construct terms. Left- and right-hand sides of a rewrite rule must be of the same base type, but we do not demand that free variables appearing on the right also occur on the left. An example of the HRS format is provided by COPS #747:
is not exhaustive, fresh variables of arbitrary type are available to construct terms. Left- and right-hand sides of a rewrite rule must be of the same base type, but we do not demand that free variables appearing on the right also occur on the left. An example of the HRS format is provided by COPS #747:

4 Competition
Since 2012 a total of 17 tools participated in CoCo. Many of the tools participated in multiple categories. The proceedings of the International Workshop on ConfluenceFootnote 4 contain (short) descriptions of the contenders. For each category, 100 problems are randomly selected from COPS. Problem selection for CoCo 2019 is subject to the following constraints. For the TRS, CPF-TRS, NFP, UNC, and UNR categories, problems in TRS format are selected. The problems for the SRS category are further restricted to those having the srs tag. For the CTRS and CPF-CTRS categories, problems must be in CTRS format and have the tags 3_ctrs and oriented, since participating tools handle only oriented CTRSs of type 3. In an oriented CTRS the conditions in the rules are interpreted as reachability and type 3 is a syntactic restriction on the distribution of variables in rewrite rules which ensure that rewriting does not introduce fresh variables [6]. For the GCR category, eligible problems must be in TRS or MSTRS format. Being in HRS format is a prerequisite for problems to be selected for the HRS category. For the new COM and INF categories, problems must have the commutation and infeasibility tags, respectively. The respective formats are described in the next section. New in 2019 is the possibility for tool authors to submit secret problems just before the competition. These will be included in the selected problems.
Earlier editions of CoCo only considered problems stemming from the literature. This restriction was put in place to avoid bias towards one particular tool or technique. Since both COPS and CoCo have grown and diversified considerably since their inception, this restriction has become hard to maintain in a meaningful way, while at the same time losing its importance. Consequently it has been dropped for CoCo 2019. Further selection details are available from the CoCo website.
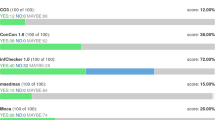
Since 2013 CoCo is executed on the cross-community competition platform StarExec [1]. Each tool has access to a single node and is given 60 s per problem. For a given problem, tools must answer YES or NO, followed by a justification that is understandable by a human expert; any other output signals that the tool could not determine the status of the problem. The possibility in StarExec to reserve a large number of computing nodes allows to complete CoCo within a single slot of a workshop or conference. This live event of CoCo is shared with the audience via the LiveView [4] tool which continuously polls new results from StarExec while the competition is running. A screenshot of the LiveView of CoCo 2018 is shown in Fig. 2. New is the realtime display of YES/NO conflicts. Since all categories deal with undecidable problems, and developing software tools is error-prone, conflicts appear once a while. In the past they were identified after the live competition finished, now action by the SC can be taken before winners are announced. As can be seen from the screenshot, in last year’s competition there was a YES/NO conflict in the HRS category, which led to lively discussion about the semantics of the HRS format. After each competition, the results are made available from the results page.Footnote 5
The certification categories (CPF-TRS and CPF-CTRS) are there to ensure that tools produce correct answers. In these categories tools have to produce certified (non-)confluence proofs with their answers. The predominant approach to achieve this uses a combination of confluence prover and independent certifier. First the confluence prover analyses confluence as usual, restricting itself to criteria supported by the certifier. If it is successful the prover prints its proof in the certification problem format (CPF),Footnote 6 which is then checked by the certifier. To ensure correctness of this check, soundness of the certifier is mechanized in a proof assistant like Isabelle/HOL. So far only one certifier has participated in CoCo:
 .Footnote 7
.Footnote 7
5 New Categories in 2019
5.1 Commutation
TRSs \(\mathcal {R}\) and \(\mathcal {S}\) commute if the inclusion  holds. Commutation is an important generalization of confluence: Apart from direct applications in rewriting, e.g. for confluence,Footnote 8 standardization, normalization, and relative termination, commutation is the basis of many results in computer science, like correctness of program transformations [7], and bisimulation up-to [8].
holds. Commutation is an important generalization of confluence: Apart from direct applications in rewriting, e.g. for confluence,Footnote 8 standardization, normalization, and relative termination, commutation is the basis of many results in computer science, like correctness of program transformations [7], and bisimulation up-to [8].
Currently, commutation is supported by the tools CoLL [9] and FORT [10]. The former supports commutation versions of three established confluence techniques: development closedness [11], rule labeling [12], and an adaption of a confluence modulo result by Jouannaud and Kirchner [13]. The latter is a decision tool for the first-order theory of rewriting based on tree automata techniques, but restricted to left-linear right-ground TRSs.
Commutation problems consist of two TRSs \(\mathcal {R}\) and \(\mathcal {S}\). The question to be answered is whether these commute. To ensure compatibility of the signatures of the involved TRSs, we rename function symbols and variables in \(\mathcal {S}\) on demand. Before we describe this precisely, we give an example of a commutation problem that illustrates the problem.
Consider COPS #82 (consisting of the rewrite rules \(\mathsf {f}(\mathsf {a}) \rightarrow \mathsf {f}(\mathsf {f}(\mathsf {a}))\) and \(\mathsf {f}(x) \rightarrow \mathsf {f}(\mathsf {a})\)) and COPS #80 (consisting of \(\mathsf {a} \rightarrow \mathsf {f}(\mathsf {a},\mathsf {b})\) and \(\mathsf {f}(\mathsf {a},\mathsf {b}) \rightarrow \mathsf {f}(\mathsf {b},\mathsf {a})\)). Since function symbol \(\mathsf {f}\) is unary in COPS #82 and binary in COPS #80, it is renamed to \(\mathsf {f}'\) in COPS #80:

The correct answer of this commutation problem is
 since the critical peak of \(\mathcal {R}\) and \(\mathcal {S}\) makes a decreasing diagram [12]. In COPS this problem is given as
since the critical peak of \(\mathcal {R}\) and \(\mathcal {S}\) makes a decreasing diagram [12]. In COPS this problem is given as

and an inlining tool generates the earlier problem before it is passed to tools participating in the commutation category. In general, commutation problems are incorporated into COPS as follows:

where
 and
and
 refer to existing problems in TRS format. The
refer to existing problems in TRS format. The
 declaration is optional. To ensure that their union is a proper TRS, the inlining tool renames function symbols in COPS #
declaration is optional. To ensure that their union is a proper TRS, the inlining tool renames function symbols in COPS #
 that appear as variable or as function symbol with a different arity in COPS #
that appear as variable or as function symbol with a different arity in COPS #
 by adding a prime (\('\)). The same holds for variables in COPS #
by adding a prime (\('\)). The same holds for variables in COPS #
 that occur as function symbol in COPS #
that occur as function symbol in COPS #
 .
.
5.2 Infeasibility Problems
Infeasibility problems originate from different sources. Critical pairs in a conditional rewrite system are equipped with conditions. If no satisfying substitution for the variables in the conditions exists, the critical pair is harmless and can be ignored when analyzing confluence of the rewrite system in question. In this case the critical pair is said to be infeasible [14, Definition 7.1.8]. Sufficient conditions for infeasibility of conditional critical pairs are reported in [15, 16].
Another source of infeasibility problems is the dependency graph in termination analysis of rewrite systems [17]. An edge from dependency pair \(\ell _1 \rightarrow r_1\) to dependency pair \(\ell _2 \rightarrow r_2\) exists in the dependency graph if two substitutions \(\sigma \) and \(\tau \) can be found such that \(r_1\sigma \) rewrites to \(\ell _2\tau \). (By renaming the variables in the dependency pairs apart, a single substitution suffices.) If no substitutions exists, there is no edge, which may ease the task of proving termination of the underlying rewrite system [18, 19].
We give two examples. The first one stems from the conditional critical pair between the two conditional rewrite rules in COPS #547:

The correct answer of this infeasibility problem is
 since no term in the underlying conditional rewrite system rewrites to both
since no term in the underlying conditional rewrite system rewrites to both
 and
and
 . In COPS this problem is given as
. In COPS this problem is given as

and an inlining tool generates the earlier problem before it is passed to tools participating in the infeasibility category.
The second example is a special case since the condition in the infeasibility problem contains no variables:

has
 as correct answer since the term
as correct answer since the term
 does not rewrite to
does not rewrite to
 . This answer can be used to conclude that the underlying rewrite system is not confluent. Again, in COPS this problem is rendered as
. This answer can be used to conclude that the underlying rewrite system is not confluent. Again, in COPS this problem is rendered as

In general, infeasibility problems are incorporated into COPS as follows:

where

has the same syntax as the conditional part of a conditional rewrite rule and
 refers to an existing problem in CTRS or TRS format. If it is a CTRS then the semantics of
refers to an existing problem in CTRS or TRS format. If it is a CTRS then the semantics of
 is the same as declared in the
is the same as declared in the
 declaration of the CTRS; if it is a TRS then the semantics of
declaration of the CTRS; if it is a TRS then the semantics of
 is
is
 (reachability, \(\rightarrow ^*\)). Variables declared in
(reachability, \(\rightarrow ^*\)). Variables declared in
 are used as variables in
are used as variables in
 . The
. The
 declaration can be omitted if the terms in
declaration can be omitted if the terms in
 are ground. Common function symbols occurring in COPS #
are ground. Common function symbols occurring in COPS #
 and
and
 have the same arity. Moreover, function symbols in COPS #
have the same arity. Moreover, function symbols in COPS #
 do not occur as variables in
do not occur as variables in
 and function symbols in
and function symbols in
 do not occur as variables in COPS #
do not occur as variables in COPS #
 .
.
5.3 String Rewriting
String rewrite systems (SRSs) are special TRSs in which terms are strings. To ensure that the infrastructure developed for TRSs can be reused, we use the TRS format with the restriction that all function symbols are unary. So a string rule \(\mathsf {a}\mathsf {b} \rightarrow \mathsf {b}\mathsf {a}\) is rendered as \(\mathsf {a}(\mathsf {b}(x)) \rightarrow \mathsf {b}(\mathsf {a}(x))\) where x is a variable. A concrete example (COPS #442) is given below:

The correct answer of this problem is
 since the addition of the redundant rules [20]
since the addition of the redundant rules [20]
 and
and
 makes the critical pairs of the SRS development closed [11].
makes the critical pairs of the SRS development closed [11].
The SRS category has been established to stimulate further research on confluence of string rewriting. In the Termination CompetitionFootnote 9 there is an active community developing powerful techniques for (relative) termination of SRSs. We anticipate that these are beneficial when applied to confluence analysis.
6 Outlook
In the near future we plan to merge CoCo with COPS and CoCoWeb,Footnote 10 a convenient web interface to execute the tools that participate in CoCo without local installation, to achieve a single entry point for confluence problems, tools, and competitions. Moreover, the submission interface of COPS will be extended with functionality to support submitters of new problems as well as the CoCo SC. We anticipate that in the years ahead new categories will be added to CoCo. Natural candidates are rewriting modulo AC and nominal rewriting.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
The union of confluent, pairwise commuting rewrite systems is confluent.
- 9.
- 10.
References
Stump, A., Sutcliffe, G., Tinelli, C.: StarExec: a cross-community infrastructure for logic solving. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS, vol. 8562, pp. 367–373. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_28
Aoto, T., Hirokawa, N., Nagele, J., Nishida, N., Zankl, H.: Confluence competition 2015. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS, vol. 9195, pp. 101–104. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_5
Aoto, T., et al.: Confluence competition 2018. In: Proceedings of 3rd International Conference on Formal Structures for Computation and Deduction. LIPIcs, vol. 108, pp. 32:1–32:5 (2018). https://doi.org/10.4230/LIPIcs.FSCD.2018.32
Hirokawa, N., Nagele, J., Middeldorp, A.: Cops and CoCoWeb: infrastructure for confluence tools. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS, vol. 10900, pp. 346–353. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_23
Mayr, R., Nipkow, T.: Higher-order rewrite systems and their confluence. Theor. Comput. Sci. 192(1), 3–29 (1998). https://doi.org/10.1016/S0304-3975(97)00143-6
Middeldorp, A., Hamoen, E.: Completeness results for basic narrowing. Appl. Algebr. Eng. Commun. Comput. 5, 213–253 (1994). https://doi.org/10.1007/BF01190830
Huet, G.: Confluent reductions: abstract properties and applications to term rewriting systems. J. ACM 27(4), 797–821 (1980). https://doi.org/10.1145/322217.322230
Pous, D.: New up-to techniques for weak bisimulation. Theor. Comput. Sci. 380(1), 164–180 (2007). https://doi.org/10.1016/j.tcs.2007.02.060
Shintani, K., Hirokawa, N.: CoLL: a confluence tool for left-linear term rewrite systems. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS, vol. 9195, pp. 127–136. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_8
Rapp, F., Middeldorp, A.: FORT 2.0. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS, vol. 10900, pp. 81–88. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_6
van Oostrom, V.: Developing developments. Theor. Comput. Sci. 175(1), 159–181 (1997). https://doi.org/10.1016/S0304-3975(96)00173-9
Aoto, T.: Automated confluence proof by decreasing diagrams based on rule-labelling. In: Proceedings of 21st RTA. LIPIcs, vol. 6, pp. 7–16 (2010). https://doi.org/10.4230/LIPIcs.RTA.2010.7
Jouannaud, J.P., Kirchner, H.: Completion of a set of rules modulo a set of equations. SIAM J. Comput. 15(4), 1155–1194 (1986). https://doi.org/10.1137/0215084
Ohlebusch, E.: Advanced Topics in Term Rewriting. Springer, New York (2002). https://doi.org/10.1007/978-1-4757-3661-8
Lucas, S., Gutiérrez, R.: Use of logical models for proving infeasibility in term rewriting. Inf. Process. Lett. 136, 90–95 (2018). https://doi.org/10.1016/j.ipl.2018.04.002
Sternagel, T., Middeldorp, A.: Infeasible conditional critical pairs. In: Proceedings of 4th International Workshop on Confluence, pp. 13–17 (2015)
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Comput. Sci. 236, 133–178 (2000). https://doi.org/10.1016/S0304-3975(99)00207-8
Giesl, J., Thiemann, R., Schneider-Kamp, P.: Proving and disproving termination of higher-order functions. In: Gramlich, B. (ed.) FroCoS 2005. LNCS, vol. 3717, pp. 216–231. Springer, Heidelberg (2005). https://doi.org/10.1007/11559306_12
Middeldorp, A.: Approximating dependency graphs using tree automata techniques. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 593–610. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_49
Nagele, J., Felgenhauer, B., Middeldorp, A.: Improving automatic confluence analysis of rewrite systems by redundant rules. In: Proceedings of 26th RTA. LIPIcs, vol. 36, pp. 257–268 (2015)
Acknowledgments
We are grateful to Nao Hirokawa for continuous support for the infrastructure of CoCo. Fabian Mitterwallner contributed to the inlining and renaming tools for the new commutation and infeasibility categories. Raúl Gutiérrez, Naoki Nishida, and Salvador Lucas contributed the initial set of infeasibility problems (COPS #818 – #936). Johannes Waldmann contributed challenging SRS problems (COPS #987 – #1036). Finally, we acknowledge the TOOLympics 2019 initiators for giving us the opportunity to present CoCo 2019.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Middeldorp, A., Nagele, J., Shintani, K. (2019). Confluence Competition 2019. In: Beyer, D., Huisman, M., Kordon, F., Steffen, B. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11429. Springer, Cham. https://doi.org/10.1007/978-3-030-17502-3_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-17502-3_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17501-6
Online ISBN: 978-3-030-17502-3
eBook Packages: Computer ScienceComputer Science (R0)