Abstract
Many transaction systems distribute, partition, and replicate their data for scalability, availability, and fault tolerance. However, observing and maintaining strong consistency of distributed and partially replicated data leads to high transaction latencies. Since different applications require different consistency guarantees, there is a plethora of consistency properties—from weak ones such as read atomicity through various forms of snapshot isolation to stronger serializability properties—and distributed transaction systems (DTSs) guaranteeing such properties. This paper presents a general framework for formally specifying a DTS in Maude, and formalizes in Maude nine common consistency properties for DTSs so defined. Furthermore, we provide a fully automated method for analyzing whether the DTS satisfies the desired property for all initial states up to given bounds on system parameters. This is based on automatically recording relevant history during a Maude run and defining the consistency properties on such histories. To the best of our knowledge, this is the first time that model checking of all these properties in a unified, systematic manner is investigated. We have implemented a tool that automates our method, and use it to model check state-of-the-art DTSs such as P-Store, RAMP, Walter, Jessy, and ROLA.
This work has been partially supported by NRL contract N00173-17-1-G002, and NSFC Project No. 61872146.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Applications handling large amounts of data need to partition their data for scalability and elasticity, and need to replicate their data across widely distributed sites for high availability and fault and disaster tolerance. However, guaranteeing strong consistency properties for transactions over partially replicated distributed data requires lot of costly coordination that results in long transaction delays. Different applications require different consistency guarantees, and balancing well the trade-off between performance and consistency guarantees is key to designing distributed transaction systems (DTSs). There is therefore a plethora of consistency properties for DTSs over partially replicated data—from weak properties such as read atomicity through various forms of snapshot isolation to strong serializability guarantees—and DTSs providing such guarantees.
DTSs and their consistency guarantees are typically specified informally and validated only by testing; there is very little work on their automated formal analysis (see Section 8). We have previously formally modeled and analyzed single state-of-the-art industrial and academic DTSs, such as Google’s Megastore, Apache Cassandra, Walter, P-Store, Jessy, ROLA, and RAMP, in Maude [14].
In this paper we present a generic framework for formalizing both DTSs and their consistency properties in Maude. The modeling framework is very general and should allow us to naturally model most DTSs. We formalize nine popular consistency models in this framework and provide a fully automated method—and a tool which automates this method—for analyzing whether a DTS specified in our framework satisfies the desired consistency property for all initial states with the user-given number of transactions, data items, sites, and so on.
In particular, we show how one can automatically add a monitoring mechanism which records relevant history during a run of a DTS specified in our framework, and we define the consistency properties on such histories so that the DTS can be directly model checked in Maude. We have implemented a tool that uses Maude’s meta-programming features to automatically add the monitoring mechanism, that automatically generates all the desired initial states, and that performs the Maude model checking. We have applied our tool to model check state-of-the-art DTSs such as variants of RAMP, P-Store, ROLA, Walter, and Jessy. To the best of our knowledge, this is the first time that model checking of all these properties in a unified, systematic manner is investigated.
This paper is organized as follows. Section 2 provides background on rewriting and Maude. Section 3 gives an overview of the consistency properties that we formalize. Section 4 presents our framework for modeling DTSs in Maude, and Section 5 explains how to record the history in such models. Section 6 formally defines consistency models as Maude functions on such recorded histories. Section 7 briefly introduces our tool which automates the entire process. Finally, Section 8 discusses related work and Section 9 gives some concluding remarks.
2 Rewriting Logic and Maude
Maude [14] is a rewriting-logic-based executable formal specification language and high-performance analysis tool for object-based distributed systems.
A Maude module specifies a rewrite theory \((\varSigma , E\cup A, R)\), where:
-
\(\varSigma \) is an algebraic signature; i.e., a set of sorts, subsorts, and function symbols.
-
\((\varSigma , E\cup A)\) is a membership equational logic theory [14], with E a set of possibly conditional equations and membership axioms, and A a set of equational axioms such as associativity, commutativity, and identity, so that equational deduction is performed modulo the axioms A. The theory \((\varSigma , E\cup A)\) specifies the system’s states as members of an algebraic data type.
-
R is a collection of labeled conditional rewrite rules \( [l]:\, t\longrightarrow t'\,\, \mathbf{if }\, cond \), specifying the system’s local transitions.
Equations and rewrite rules are introduced with, respectively, keywords eq, or ceq for conditional equations, and rl and crl. The mathematical variables in such statements are declared with the keywords var and vars, or can have the form
 and be introduced on the fly. An equation \(f(t_1, \ldots , t_n) = t\) with the owise (“otherwise”) attribute can be applied to a subterm \(f(\ldots )\) only if no other equation with left-hand side \(f(u_1, \ldots , u_n)\) can be applied. Maude also provides standard parameterized data types (sets, maps, etc.) that can be instantiated (and renamed); for example,
and be introduced on the fly. An equation \(f(t_1, \ldots , t_n) = t\) with the owise (“otherwise”) attribute can be applied to a subterm \(f(\ldots )\) only if no other equation with left-hand side \(f(u_1, \ldots , u_n)\) can be applied. Maude also provides standard parameterized data types (sets, maps, etc.) that can be instantiated (and renamed); for example,
 defines a sort Nats of sets of natural numbers.
defines a sort Nats of sets of natural numbers.
A class declaration
 declares a class C of objects with attributes \(att_1\) to \(att_n\) of sorts \(s_1\) to \(s_n\). An object instance of class C is represented as a term \(\texttt {<}\, O : C \mid att _1: val _1, \dots , att _n: val _n\,\texttt {>}\), where O, of sort Oid, is the object’s identifier, and where \(val_1\) to \(val_n\) are the current values of the attributes \(att_1\) to \(att_n\). A message is a term of sort Msg. A system state is modeled as a term of the sort Configuration, and has the structure of a multiset made up of objects and messages.
declares a class C of objects with attributes \(att_1\) to \(att_n\) of sorts \(s_1\) to \(s_n\). An object instance of class C is represented as a term \(\texttt {<}\, O : C \mid att _1: val _1, \dots , att _n: val _n\,\texttt {>}\), where O, of sort Oid, is the object’s identifier, and where \(val_1\) to \(val_n\) are the current values of the attributes \(att_1\) to \(att_n\). A message is a term of sort Msg. A system state is modeled as a term of the sort Configuration, and has the structure of a multiset made up of objects and messages.
The dynamic behavior of a system is axiomatized by specifying each of its transition patterns by a rewrite rule. For example, the rule (with label l)

defines a family of transitions in which a message m(O, w) is read and consumed by an object O of class C, whose attribute a1 is changed to x + w, and a new message m’(O’,x) is generated. Attributes whose values do not change and do not affect the next state, such as a3 and a2, need not be mentioned in a rule.
Maude also supports metaprogramming in the sense that a Maude specification \( M \) can be represented as a term \(\overline{M}\) (of sort Module), so that a module transformation can be defined as a Maude function \(f: \mathtt {Module} \rightarrow \mathtt {Module}\).
Reachability Analysis in Maude. Maude provides a number of analysis methods, including rewriting for simulation purposes, reachability analysis, and linear temporal logic (LTL) model checking. In this paper, we use reachability analysis. Given an initial state \( init \), a state pattern \( pattern \) and an (optional) condition \( cond \), Maude’s search command searches the reachable state space from \( init \) in a breadth-first manner for states that match \( pattern \) such that \( cond \) holds:

where \( bound \) is an upper bound on the number of solutions to look for. The arrow =>! means that Maude only searches for final states (i.e., states that cannot be further rewritten) that match \( pattern \) and satisfies \( cond \). If the arrow is instead =>* then Maude searches for all reachable states satisfying the search condition.
3 Transactional Consistency
Different applications require different consistency guarantees. There are therefore many consistency properties for DTSs on partially replicated distributed data stores. This paper focuses on the following nine, which span a spectrum from weak consistency such as read committed to strong consistency like serializability:
-
Read committed (RC) [6] disallows a transactionFootnote 1 from seeing any uncommitted or aborted data.
-
Cursor stability (CS) [16], widely implemented by commercial SQL systems (e.g., IBM DB2 [1]) and academic prototypes (e.g., MDCC [21]), guarantees RC and in addition prevents the lost update anomaly.
-
Read atomicity (RA) [5] guarantees that either all or none of a (distributed) transaction’s updates are visible to other transactions. For example, if Alice and Bob become friends on social media, then Charlie should not see that Alice is a friend of Bob’s, and that Bob is not a friend of Alice’s.
-
Update atomicity (UA) [12, 25] guarantees read atomicity and prevents the lost update anomaly.
-
Snapshot isolation (SI) [6] requires a multi-partition transaction to read from a snapshot of a distributed data store that reflects a single commit order of transactions across sites, even if they are independent of each other: Alice sees Charlie’s post before seeing David’s post if and only if Bob sees the two posts in the same order. Charlie and David must therefore coordinate the order of committing their posts even if they do not know each other.
-
Parallel snapshot isolation (PSI) [36] weakens SI by allowing different commit orders at different sites, while guaranteeing that a transaction reads the most recent version committed at the transaction execution site, as of the time when the transaction begins. For example, Alice may see Charlie’s post before seeing David’s post, even though Bob sees David’s post before Charlie’s post, as long as the two posts are independent of each other. Charlie and David can therefore commit their posts without waiting for each other.
-
Non-monotonic snapshot isolation (NMSI) [4] weakens PSI by allowing a transaction to read a version committed after the transaction begins: Alice may see Bob’s post that committed after her transaction started executing.
-
Serializability (SER) [33] ensures that the execution of concurrent transactions is equivalent to one where the transactions are run one at a time.
-
Strict Serializability (SSER) strengthens SER by enforcing the serial order to follow real time.
4 Modeling Distributed Transaction Systems in Maude
This section presents a framework for modeling in Maude DTSs that satisfy the following general assumptions:
-
We can identify and record “when”Footnote 2 a transaction starts executing at its server/proxy and “when” the transaction is committed and aborted at the different sites involved in its validation.
-
The transactions record their read and write sets.
If a such a DTS is modeled in this framework, our tool can automatically model check whether it satisfies the above consistency properties, as long as it can detect the read and write sets and the above events: start of transaction execution, and abort/commit of a transaction at a certain site. This section explains how the system should be modeled so that our tool automatically discovers these events.
We make the following additional assumptions about the DTSs we target:
-
The database is distributed across of a number of sites, or servers or replicas, that communicate by asynchronous message passing. Data are partially replicated across these sites: a data item may be replicated/stored at more than one site. The sites replicating a data item are called that item’s replicas.
-
Systems evolve by message passing or local computations. Servers communicate by asynchronous message passing with arbitrary but finite delays.
-
A client forwards a transaction to be executed to some server (called the transaction’s executing server or proxy), which executes the transaction.
-
Transaction execution should terminate in commit or abort.
4.1 Modeling DTSs in Maude
A DTS is modeled in an object-oriented style, where the state consists of a number of replica objects, each modeling a local database/server/site, and a number of messages traveling between the replica objects. A transaction is modeled as an object which resides inside the replica object executing the transaction.
Basic Data Types. There are user-defined sorts Key for data items (or keys) and Version for versions of data items, with a partial order
 on versions, with \(v\,\texttt {<}\,v'\) denoting that \(v'\) is a later version of v in \(\texttt {<}\). We then define key-version pairs
on versions, with \(v\,\texttt {<}\,v'\) denoting that \(v'\) is a later version of v in \(\texttt {<}\). We then define key-version pairs
 and sets of such pairs, that model a transaction’s read and write sets, as follows:
and sets of such pairs, that model a transaction’s read and write sets, as follows:

To track the status of a transaction (on non-proxies, or remote servers) we define a sort TxnStatus consisting of some transaction’s identifier and its status; this is used to indicate whether a remote transaction (one executed on another server) is committed on this server:

Modeling Replicas. A replica (or site) stores parts of the database, executes the transactions for which it is the proxy, helps validating other transactions, and is formalized as an object instance of a subclass of the following class Replica:

The attributes executing, committed, and aborted contain, respectively, transactions that are being executed, and have been committed or aborted on the executing server; decided is the status of transactions executed on other servers.
To model a system-specific replica a user should specify it as an object instance of a subclass of the class Replica with new attributes.
Example 1
A replica in our Maude model of Walter [26] is modeled as an object instance of the following subclass Walter-Replica of class Replica that adds 14 new attributes (only 4 shown below):

Modeling Transactions. A transaction should be modeled as an object of a subclass of the following class Txn:

where readSet and writeSet denote the key/version pairs read and written by the transaction, respectively.
Example 2
Walter transactions can be modeled as object instances of the subclass Walter-Txn with four new attributes:

Modeling System Dynamics. We describe how the rewrite rules defining the start of a transaction execution and aborts and commits at different sites should be defined so that our tool can detect these events.
-
The start of a transaction execution must be modeled by a rewrite rule where the transaction object appears in the proxy server’s executing attribute in the right-hand side, but not in the left-hand side, of the rewrite rule.
Example 3
A Walter replica starts executing a transaction TID by moving TID in gotTxns (buffering transactions from clients) to executing:Footnote 3

-
When a transaction is committed on the executing server, the transaction object must appear in the committed attribute in the right-hand side—but not in the left-hand side—of the rewrite rule. Furthermore, the readSet and writeSet attributes must be explicitly given in the transaction object.
Example 4
In Walter, when all operations of an executing read-only transaction have been performed, the proxy commits the transaction directly:

-
When a transaction is aborted by the executing server, the transaction object must appear in the aborted attribute in the right-hand side, but not in the left-hand side, of a rewrite rule. Again, the transaction should present its attributes writeSet and readSet (to be able to record relevant history). See our longer report [27] for an example of such a rule.
-
A rewrite rule that models when a transaction’s status is decided remotely (i.e., not on the executing server) must contain in the right-hand side (only) the transaction’s identifier and its status in the replica’s decided attribute.
These requirements are not very strict. The Maude models of the DTSs RAMP [29], Faster [24], Walter [26], ROLA [25], Jessy [28], and P-Store [32] can all be seen as instantiations of our modeling framework, with very small syntactic changes, such as defining transaction and replica objects as subclasses of Txn and Replica, changing the names of the attributes and sorts, etc. The Apache Cassandra NoSQL key-value store can be seen as a transaction system where each transaction is a single operation; the Maude model of Cassandra in [30] can also be easily modified to fit within our modeling framework.
5 Adding Execution Logs
To formalize and analyze consistency properties of distributed transaction systems we add an “execution log” that records the history of relevant events during a system execution. This section explains how this history recording can be added automatically to a model of a DTS that is specified as explained in Section 4.
5.1 Execution Log
To capture the total order of relevant events in a run, we use a “logical global clock” to order all key events (i.e., transaction starts, commits, and aborts). This clock is incremented by one each time such an event takes place.
A transaction in a replicated DTS is typically committed both locally (at its executing server) and remotely at different times. To capture this, we define a “time vector” using Maude’s map data type that maps replica identifiers (of sort Oid) to (typically “logical”) clock values (of sort Time, which here are the natural numbers:
 ):
):

where each element in the mapping has the form
 .
.
An execution log (of sort Log) maps each transaction (identifier) to a record \(\texttt {<} proxy ,\, issueTime ,\) \( finishTime ,\, committed ,\, reads ,\, writes {} \texttt {>}\), with \( proxy \) its proxy server, \( issueTime \) the starting time at its proxy server, \( finishTime \) the commit/abort times at each relevant server, \( committed \) a flag indicating whether the transaction is committed at its proxy, \( reads \) the key-version pairs read by the transaction, and \( writes \) the key-version pairs written:

5.2 Logging Execution History
We show how the relevant history of an execution can be recorded during a run of our Maude model by transforming the original Maude model into one which also records this history.
First, we add to the state a Monitor object that stores the current logical global time in the clock attribute and the current log in the log attribute:

The log is updated each time an interesting event (see Section 4.1) happens. Our tool identifies those events and automatically transforms the corresponding rewrite rules by adding and updating the monitor object.
Executing. A transaction starts executing when the transaction object appears in a Replica’s executing attribute in the right-hand side, but not in the left-hand side, of a rewrite rule. The monitor then adds a record for this transaction, with the proxy and start time, to the log, and increments the logical global clock.
Example 5
The rewrite rule in Example 3 where a Walter replica is served a transaction is modified by adding and updating the monitor object (in blue):

where the monitor O@M adds a new record for the transaction TID in the log, with starting time (i.e., the current logical global time) GT@M at its executing server RID, finish time (empty), flag (false), read set (empty), and write set (empty). The monitor also increments the global clock by one.
Commit. A transaction commits at its proxy when the transaction object appears in the proxy’s committed attribute in the right-hand side, but not in the left-hand side, of a rewrite rule. The record for that transaction is updated with commit status, versions read and written, and commit time, and the global logical clock is incremented.
Example 6
The monitor object is added to the rewrite rule in Example 4 for committing a read-only transaction:

The monitor updates the log for the transaction TID by setting its finish time at the executing server RID to GT@M (insert(RID,GT@M,VTS@M)), setting the committed flag to true, setting the read set to RS and write set to empty (this is a read-only transaction), and increments the global clock.
Abort. Abort is treated as commit, but the commit flag remains false.
Decided. When a transaction’s status is decided remotely, the record for that transaction’s decision time at the remote replica is updated with the current global time. See [27] for an example.
We have formalized/implemented the transformation from a Maude specification of a DTS into one with a monitor as a meta-level function monitorRules : Module -> Module in Maude. See our longer report [27] for details.
6 Formalizing Consistency Models in Maude
This section formalizes the consistency properties in Section 3 as functions on the “history log” of a completed run. The entire Maude specification of these functions is available at https://github.com/siliunobi/cat. Due to space restrictions, we only show the formalization of four of the consistency models, and refer to our report [27] for the formalization of the other properties.
Read Committed (RC). (A transaction cannot read any writes by uncommitted transactions.) Note that standard definitions for single-version databases disallow reading versions that are not committed at the time of the read. We follow the definition for multi-versioned systems by Adya, summarized by Bailis et al. [5], that defines the RC property as follows: (i) a committed transaction cannot read a version that was written by an aborted transaction; and (ii) a transaction cannot read intermediate values: that is, if T writes two versions
 and
and
 with
with
 , then no \(T'\ne T\) can read
, then no \(T'\ne T\) can read
 .
.
The first equation defining the function rc, specifying when RC holds, checks whether some (committed) transaction TID1 read version V of key X (i.e., \(\texttt {<\,X,V\,>}\) is in TID’s read set \(\texttt {<\,X,V\,>\,,\,RS}\), where RS matches the rest of TID’s read set), and this version V was written by some transaction TID2 that was never committed (i.e., TID2’s commit flag is false, and its write set is
 ). The second equation checks whether there was an intermediate read of a version
). The second equation checks whether there was an intermediate read of a version
 that was overwritten by the same transaction TID2 that wrote the version:Footnote 4
that was overwritten by the same transaction TID2 that wrote the version:Footnote 4

Read Atomicity (RA). A system guarantees RA if it prevents fractured reads and prevents transactions from reading uncommitted or aborted data. A transaction \(T_{j}\) exhibits fractured reads if transaction \(T_{i}\) writes versions \(x_{m}\) and \(y_{n}\), \(T_{j}\) reads version \(x_{m}\) and version \(y_{k}\), and \(k<n\) [5]. The function fracRead checks whether there are fractured reads in the log. There is a fractured read if a transaction TID2 reads X and Y, transaction TID1 writes X and Y, TID2 reads the version VX of X written by TID1, and reads a version VY’ of Y written before VY (
 ):
):

We define RA as the combination of RC and no fractured reads:

Parallel snapshot isolation (PSI) is given by three properties [36]:
-
PSI-1 (site snapshot read): All operations read the most recent committed version at the transaction’s site as of time when the transaction began.
-
PSI-2 (no write-write conflicts): The write sets of each pair of committed somewhere-concurrentFootnote 5 transactions must be disjoint.
-
PSI-3 (commit causality across sites): If a transaction \(T_{1}\) commits at a site S before a transaction \(T_{2}\) starts at site S, then \(T_{1}\) cannot commit after \(T_{2}\) at any site.
The function notSiteSnapshotRead checks whether the system log satisfies PSI-1 by returning true if there is a transaction that did not read the most recent committed version at its executing site when it began:

In the first equation, the transaction TID1, hosted at site RID1, has in its read set a version
 written by TID2. Some transaction TID3 wrote version
written by TID2. Some transaction TID3 wrote version
 and was committed at RID1 after TID2 was committed at RID1 (\(\texttt {T3> T2}\)) and before TID1 started executing (\(\texttt {T3 < T}\)). Hence, the version read by TID1 was stale. The second equation checks if TID1 read some version that was committed at RID1 after TID1 started (\(\texttt {T < T2}\)).
and was committed at RID1 after TID2 was committed at RID1 (\(\texttt {T3> T2}\)) and before TID1 started executing (\(\texttt {T3 < T}\)). Hence, the version read by TID1 was stale. The second equation checks if TID1 read some version that was committed at RID1 after TID1 started (\(\texttt {T < T2}\)).
The function someWhereConflict checks whether PSI-2 holds by looking for a write-write conflict between any pair of committed somewhere-concurrent transactions in the system log:

The above function checks whether the transactions with the write conflict are concurrent at the transaction TID1’s proxy RID1. Here, TID2 commits at RID1 at time T2, which is between TID1’s start time T and its commit time T1 at RID1.
The function notCausality analyzes PSI-3 by checking whether there was a “bad situation” in which a transaction TID1 committed at site RID2 before a transaction TID2 started at site RID2 (\(\texttt {T1 < T2}\)), while TID1 committed at site RID after TID2 committed at site RID (\(\texttt {T3 > T4}\)):

PSI can then be defined by combining the above three properties:

Non-monotonic snapshot isolation (NMSI) is the same as PSI except that a transaction may read a version committed even after the transaction begins [3]. NMSI can therefore be defined as the conjunction of PSI-2 and PSI-3:

Serializability (SER) means that the concurrent execution of transactions is equivalent to executing them in some (non-overlapping in time) sequence [33].
A formal definition of SER is based on direct serialization graphs (DSGs): an execution is serializable if and only if the corresponding DSG is acyclic. Each node in a DSG corresponds to a committed transaction, and directed edges in a DSG correspond to the following types of direct dependencies [2]:
-
Read dependency: Transaction \(T_{j}\) directly read-depends on transaction \(T_{i}\) if \(T_{i}\) writes some version \(x_{i}\) and \(T_{j}\) reads that version \(x_{i}\).
-
Write dependency: Transaction \(T_{j}\) directly write-depends on transaction \(T_{i}\) if \(T_{i}\) writes some version \(x_{i}\) and \(T_{j}\) writes x’s next version after \(x_{i}\) in the version order.
-
Antidependency: Transaction \(T_{j}\) directly antidepends on transaction \(T_{i}\) if \(T_{i}\) reads some version \(x_{k}\) and \(T_{j}\) writes x’s next version after \(x_{k}\).
There is a directed edge from a node \(T_{i}\) to another node \(T_{j}\) if transaction \(T_{j}\) directly read-/write-/antidepends on transaction \(T_{i}\).
The dependencies/edges can easily be extracted from the our log as follows:
-
If there is a key-version pair
 both in T2’s read set and in T1’s write set, then T2 read-depends on T1.
both in T2’s read set and in T1’s write set, then T2 read-depends on T1. -
If T1 writes
 and T2 writes
and T2 writes
 , and \(\texttt {V1 < V2}\), and there no version
, and \(\texttt {V1 < V2}\), and there no version
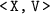 with
with
 , then T2 write-depends on T1.
, then T2 write-depends on T1. -
T2 antidepends on T1 if
 is in T1’s read set,
is in T1’s read set,
 is in T2’s write set with \(\texttt {V1 < V2}\) and there is no version
is in T2’s write set with \(\texttt {V1 < V2}\) and there is no version
 such that \(\texttt {V1< V < V2}\).
such that \(\texttt {V1< V < V2}\).
We have defined a data type Dsg for DSGs, a function dsg : Log -> Dsg that constructs the DSG from a log, and a function cycle : Dsg -> Bool that checks whether a DSG has cycles. We refer to [27] for their definition in Maude.
SER then holds if there is no cycle in the constructed DSG:

7 Formal Analysis of Consistency Properties of DTSs
We have implemented the Consistency Analysis Tool (CAT) that automates the method in this paper. CAT takes as input:
-
A Maude model of the DTS specified as explained in Section 4.
-
The number of each of the following parameters: read-only, write-only, and read-write transactions; operations for each type of transaction; keys; replicas per key; clients; and servers. The tool analyzes the desired property for all initial states with the number of each of these parameters.
-
The consistency property to be analyzed.
Given these inputs, CAT performs the following steps:
-
1.
adds the monitoring mechanism to the user-provided system model;
-
2.
generates all possible initial states with the user-provided number of the different parameters; and
-
3.
executes the following command to search, from all generated initial states, for one reachable final state where the consistency property does not hold:

where the underlined functions are parametric, and are instantiated by the user inputs; e.g.,
 is replaced by the corresponding function rc, psi, nmsi, ..., or ser, depending on which property to analyze.
is replaced by the corresponding function rc, psi, nmsi, ..., or ser, depending on which property to analyze.
CAT outputs either “No solution,” meaning that all runs from all the given initial states satisfy the desired consistency property, or a counterexample (in Maude at the moment) showing a behavior that violates the property.
We have applied our tool to 14 Maude models of state-of-the-art academic DTSs (different variants of RAMP and Walter, ROLA, Jessy, and P-Store) against all nine properties. Table 1 only shows six case studies due to space limitations. All model checking results are as expected. It is worth remarking that our automatic analysis found all the violations of properties that the respective systems should violate. There are also some cases where model checking is not applicable (“-” in Table 1): some system models do not include a mechanism for committing a transaction on remote servers (i.e., no commit time on any remote server is recorded by the monitor). Thus, model checking NMSI or PSI is not applicable.
We have performed our analysis with different initial states, with up to 4 transactions, 4 operations per transaction, 2 clients, 2 servers, 2 keys, and 2 replicas per key. Each analysis command took about 15 minutes (worst case) to execute on a 2.9 GHz Intel 4-Core i7-3520M CPU with 3.6 GB memory.
8 Related Work
Formalizing Consistency Properties in a Single Framework. Adya [2] uses dependencies between reads and writes to define different isolation models in database systems. Bailis et al. [5] adopts this model to define read atomicity. Burckhardt et al. [11] and Cerone et al. [12] propose axiomatic specifications of consistency models for transaction systems using visibility and arbitration relationships. Shapiro et al. [35] propose a classification along three dimensions (total order, visibility, and transaction composition) for transactional consistency models. Crooks et al. [15] formalizes transactional consistency properties in terms of observable states from a client’s perspective. On the non-transactional side, Burckhardt [10] focuses on session and eventual consistency models. Viotti et al. [38] expands his work by covering more than 50 non-transactional consistency properties. Szekeres et al. [37] propose a unified model based on result visibility to formalize both transactional and non-transactional consistency properties.
All of these studies propose semantic models of consistency properties suitable for theoretical analysis. In contrast, we aim at algorithmic methods for automatically verifying consistency properties based on executable specifications of both the systems and their consistency models. Furthermore, none of the studies covered all of the transactional consistency models considered in this paper.
Model Checking Distributed Transaction Systems. There is very little work on model checking state-of-the-art DTSs, maybe because the complexity of these systems requires expressive formalisms. Engineers at Amazon Web Services successfully used TLA+ to model check key algorithms in Amazon’s Simple Storage Systems and DynamoDB database [31]; however, they do not state which consistency properties, if any, were model checked. The designers of the TAPIR transaction protocol have specified and model checked correctness properties of their design using TLA+ [41]. The IronFleet framework [20] combines TLA+ analysis and Floyd-Hoare-style imperative verification to reason about protocol-level concurrency and implementation complexities, respectively. Their methodology requires “considerable assistance from the developer” to perform the proofs.
Distributed model checkers [22, 40] are used to model check implementations of distributed systems such as Cassandra, ZooKeeper, the BerkeleyDB database and a replication protocol implementation.
Our previous work [8, 18, 19, 24,25,26, 28, 29, 32] specifies and model checks single DTSs and consistency properties in different ways, as opposed to in a single framework that, furthermore, automates the “monitoring” and analysis process.
Other Formal Reasoning about Distributed Database Systems. Cerone et al. [13] develop a new characterization of SI and apply it to the static analysis of DTSs. Bernardi et al. [7] propose criteria for checking the robustness of transactional programs against consistency models. Bouajjani et al. [9] propose a formal definition of eventual consistency, and reduce the problem of checking eventual consistency to reachability and model checking problems. Gotsman et al. [17] propose a proof rule for reasoning about non-transactional consistency choices.
There is also work [23, 34, 39] that focuses on specifying, implementing and verifying distributed systems using the Coq proof assistant. Their executable Coq “implementations” can be seen as executable high-level formal specifications, but the theorem proving requires nontrivial user interaction.
9 Concluding Remarks
In this paper we have provided an object-based framework for formally modeling distributed transaction systems (DTSs) in Maude, have explained how such models can be automatically instrumented to record relevant events during a run, and have formally defined a wide range of consistency properties on such histories of events. We have implemented a tool which automates the entire instrumentation and model checking process. Our framework is very general: we could easily adapt previous Maude models of state-of-the-art DTSs such as Apache Cassandra, P-Store, RAMP, Walter, Jessy, and ROLA to our framework.
We then model checked the DTSs w.r.t. all the consistency properties for all initial states with 4 transactions, 2 sites, and so on. This analysis was sufficient to differentiate the DTSs according to which consistency properties they satisfy.
In future work we should formally relate our definitions of the consistency properties to other (non-executable) formalizations of consistency properties. We should also extend our work to formalizing and model checking non-transactional consistency properties for key-value stores such as Cassandra.
Notes
- 1.
A transaction is a user application request, typically consisting of a sequence of read and/or write operations on data items, that is submitted to a (distributed) database.
- 2.
Since we do not necessarily deal with real-time systems, this “when” may not denote the real time, but when the event takes place relative to other events.
- 3.
We do not give variable declarations, but follow the convention that variables are written in (all) capital letters.
- 4.
The configuration union and the union operator ‘,’ for maps and sets are declared associative and commutative. The first equation therefore matches any log where some committed transaction read a key-version pair written by some aborted transaction.
- 5.
Two transactions are somewhere-concurrent if they are concurrent at one of their sites.
References
Adya, A.: Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions. MIT, Cambridge (1999)
Ardekani, M.S., Sutra, P., Preguiça, N.M., Shapiro, M.: Non-monotonic snapshot isolation. CoRR abs/1306.3906 (2013). http://arxiv.org/abs/1306.3906
Ardekani, M.S., Sutra, P., Shapiro, M.: Non-monotonic snapshot isolation: scalable and strong consistency for geo-replicated transactional systems. In: SRDS, pp. 163–172 (2013)
Bailis, P., Fekete, A., Ghodsi, A., Hellerstein, J.M., Stoica, I.: Scalable atomic visibility with RAMP transactions. ACM Trans. Database Syst. 41(3), 15:1–15:45 (2016)
Berenson, H., Bernstein, P.A., Gray, J., Melton, J., O’Neil, E.J., O’Neil, P.E.: A critique of ANSI SQL isolation levels. In: SIGMOD, pp. 1–10. ACM (1995)
Bernardi, G., Gotsman, A.: Robustness against consistency models with atomic visibility. In: CONCUR. LIPIcs, vol. 59, pp. 7:1–7:15. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2016)
Bobba, R., et al.: Survivability: design, formal modeling, and validation of cloud storage systems using Maude. In: Assured Cloud Computing. Wiley/IEEE (2018)
Bouajjani, A., Enea, C., Hamza, J.: Verifying eventual consistency of optimistic replication systems. In: POPL, pp. 285–296. ACM (2014)
Burckhardt, S.: Principles of Eventual Consistency. Foundations and Trends in Programming Languages, vol. 1. Now Publishers, Delft (2014)
Burckhardt, S., Leijen, D., Fähndrich, M., Sagiv, M.: Eventually Consistent Transactions. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 67–86. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_4
Cerone, A., Bernardi, G., Gotsman, A.: A framework for transactional consistency models with atomic visibility. In: CONCUR. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2015)
Cerone, A., Gotsman, A.: Analysing snapshot isolation. In: PODC, pp. 55–64. ACM (2016)
Clavel, M., et al.: All About Maude - A High-Performance Logical Framework. LNCS, vol. 4350. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71999-1
Crooks, N., Pu, Y., Alvisi, L., Clement, A.: Seeing is believing: a client-centric specification of database isolation. In: PODC, pp. 73–82. ACM (2017)
Date, C.: An Introduction to Database Systems, 5th edn. Addison-Wesley, Reading (1990)
Gotsman, A., Yang, H., Ferreira, C., Najafzadeh, M., Shapiro, M.: ’Cause I’m strong enough: reasoning about consistency choices in distributed systems. In: POPL, pp. 371–384. ACM (2016)
Grov, J., Ölveczky, P.C.: Formal modeling and analysis of Google’s Megastore in Real-Time Maude. In: Iida, S., Meseguer, J., Ogata, K. (eds.) Specification, Algebra, and Software. LNCS, vol. 8373, pp. 494–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54624-2_25
Grov, J., Ölveczky, P.C.: Increasing consistency in multi-site data stores: Megastore-CGC and its formal analysis. In: Giannakopoulou, D., Salaün, G. (eds.) SEFM 2014. LNCS, vol. 8702, pp. 159–174. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10431-7_12
Hawblitzel, C., et al.: IronFleet: proving practical distributed systems correct. In: SOSP. ACM (2015)
Kraska, T., Pang, G., Franklin, M.J., Madden, S., Fekete, A.: MDCC: multi-data center consistency. In: EuroSys, pp. 113–126. ACM (2013)
Leesatapornwongsa, T., Hao, M., Joshi, P., Lukman, J.F., Gunawi, H.S.: SAMC: semantic-aware model checking for fast discovery of deep bugs in cloud systems. In: OSDI. USENIX Association (2014)
Lesani, M., Bell, C.J., Chlipala, A.: Chapar: certified causally consistent distributed key-value stores. In: POPL, pp. 357–370. ACM (2016)
Liu, S., Ölveczky, P.C., Ganhotra, J., Gupta, I., Meseguer, J.: Exploring design alternatives for RAMP transactions through statistical model checking. In: Duan, Z., Ong, L. (eds.) ICFEM 2017. LNCS, vol. 10610, pp. 298–314. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68690-5_18
Liu, S., Ölveczky, P.C., Santhanam, K., Wang, Q., Gupta, I., Meseguer, J.: ROLA: a new distributed transaction protocol and its formal analysis. In: Russo, A., Schürr, A. (eds.) FASE 2018. LNCS, vol. 10802, pp. 77–93. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89363-1_5
Liu, S., Ölveczky, P.C., Wang, Q., Meseguer, J.: Formal modeling and analysis of the Walter transactional data store. In: Rusu, V. (ed.) WRLA 2018. LNCS, vol. 11152, pp. 136–152. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99840-4_8
Liu, S., Ölveczky, P., Zhang, M., Wang, Q., Meseguer, J.: Automatic analysis of consistency properties of distributed transaction systems in Maude. Technical report, University of Illinois at Urbana-Champaign (2019). http://hdl.handle.net/2142/102291
Liu, S., Ölveczky, P., Wang, Q., Gupta, I., Meseguer, J.: Read atomic transactions with prevention of lost updates: ROLA and its formal analysis. Technical report, University of Illinois at Urbana-Champaign (2018). http://hdl.handle.net/2142/101836
Liu, S., Ölveczky, P.C., Rahman, M.R., Ganhotra, J., Gupta, I., Meseguer, J.: Formal modeling and analysis of RAMP transaction systems. In: SAC. ACM (2016)
Liu, S., Rahman, M.R., Skeirik, S., Gupta, I., Meseguer, J.: Formal modeling and analysis of Cassandra in Maude. In: Merz, S., Pang, J. (eds.) ICFEM 2014. LNCS, vol. 8829, pp. 332–347. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11737-9_22
Newcombe, C., Rath, T., Zhang, F., Munteanu, B., Brooker, M., Deardeuff, M.: How Amazon Web Services uses formal methods. Commun. ACM 58(4), 66–73 (2015)
Ölveczky, P.C.: Formalizing and validating the P-Store replicated data store in Maude. In: James, P., Roggenbach, M. (eds.) WADT 2016. LNCS, vol. 10644, pp. 189–207. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72044-9_13
Papadimitriou, C.H.: The serializability of concurrent database updates. J. ACM 26(4), 631–653 (1979)
Sergey, I., Wilcox, J.R., Tatlock, Z.: Programming and proving with distributed protocols. Proc. ACM Program. Lang. 2(POPL), 28:1–28:30 (2017)
Shapiro, M., Ardekani, M.S., Petri, G.: Consistency in 3D. In: CONCUR. LIPIcs, vol. 59, pp. 3:1–3:14. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2016)
Sovran, Y., Power, R., Aguilera, M.K., Li, J.: Transactional storage for geo-replicated systems. In: SOSP. ACM (2011)
Szekeres, A., Zhang, I.: Making consistency more consistent: a unified model for coherence, consistency and isolation. In: PaPoC. ACM (2018)
Viotti, P., Vukolić, M.: Consistency in non-transactional distributed storage systems. ACM Comput. Surv. 49(1), 19:1–19:34 (2016)
Wilcox, J.R., et al.: Verdi: a framework for implementing and formally verifying distributed systems. In: PLDI, pp. 357–368. ACM (2015)
Yang, J., et al.: MODIST: transparent model checking of unmodified distributed systems. In: NSDI, pp. 213–228. USENIX Association (2009)
Zhang, I., Sharma, N.K., Szekeres, A., Krishnamurthy, A., Ports, D.R.K.: Building consistent transactions with inconsistent replication. In: SOSP 2015, pp. 263–278. ACM (2015)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Liu, S., Ölveczky, P.C., Zhang, M., Wang, Q., Meseguer, J. (2019). Automatic Analysis of Consistency Properties of Distributed Transaction Systems in Maude. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11428. Springer, Cham. https://doi.org/10.1007/978-3-030-17465-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-17465-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17464-4
Online ISBN: 978-3-030-17465-1
eBook Packages: Computer ScienceComputer Science (R0)





 both in
both in  and
and  , and
, and 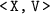 with
with
 , then
, then  is in
is in  is in
is in  such that
such that 
 is replaced by the corresponding function
is replaced by the corresponding function 