Abstract
An effective approach to handling the theory of floating-point is to reduce it to the theory of bit-vectors. Implementing the required encodings is complex, error prone and requires a deep understanding of floating-point hardware. This paper presents SymFPU, a library of encodings that can be included in solvers. It also includes a verification argument for its correctness, and experimental results showing that its use in CVC4 out-performs all previous tools. As well as a significantly improved performance and correctness, it is hoped this will give a simple route to add support for the theory of floating-point.
All of the authors would like to thank ATI project 113099, SECT-AIR; additionally Martin Brain would like to thank DSTL CDE Project 30713 and BTC-ES AG; Florian Schanda was employed at Altran UK when most of the work was done, this paper is not a result of Florian’s work at Zenuity GmbH. Florian would like to thank Elisa Barboni for dealing with a last-minute issue in benchmarking.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords

1 Introduction
From the embedded controllers of cars, aircraft and other “cyber-physical” systems, via JavaScript to the latest graphics, computer vision and machine learning accelerator hardware, floating-point computation is everywhere in modern computing. To reason about contemporary software, we must be able to efficiently reason about floating-point. To derive proofs, counter-examples, test cases or attack vectors we need bit-accurate results.
The vast majority of systems use IEEE-754 [1] floating-point implementations, or slight restrictions or relaxations. This makes unexpected behaviour rare; floating-point numbers behave enough like real numbers that programmers largely do not (need to) think about the difference. This gives a challenge for software verification: finding the rarely considered edge-cases that may result in incorrect, unsafe or insecure behaviour.
Of the many verification tools that can address these challenges, almost all use SMT solvers to find solutions to sets of constraints, or show they are infeasible. So there is a pressing need for SMT solvers to be able to reason about floating-point variables. An extension to the ubiquitous SMT-LIB standard to support floating-point [13] gives a common interface, reducing the wider problem to a question of efficient implementation within SMT solvers.
Most solvers designed for verification support the theory of bit-vectors. As floating-point operations can be implemented with circuits, the “bit-blasting” approach of reducing the floating-point theory to bit-vectors is popular. This method is conceptually simple, makes use of advances in bit-vector theory solvers and allows mixed floating-point/bit-vector problems to be solved efficiently.
Implementing the theory of floating-point should be as simple as adding the relevant circuit designs to the bit-blaster. However, encodings of floating-point operations in terms of bit-vectors, similarly to implementation of floating-point units in hardware, are notoriously complex and detailed. Getting a high degree of assurance in their correctness requires a solid understanding of floating-point operations and significant development effort.
Then there are questions of performance. Floating-point units designed for hardware are generally optimised for low latency, high throughput or low power consumption. Likewise software implementations of floating-point operations tend to focus on latency and features such as arbitrary precision. However, there is nothing to suggest that a design that produces a ‘good’ circuit will also produce a ‘good’ encoding or vice-versa.
To address these challenges this paper presents the following contributions:
-
A comprehensive overview of the literature on automated reasoning for floating-point operations (Section 2).
-
An exploration of the design space for floating-point to bit-vector encodings (Section 3) and the choices made when developing the SymFPU; a library of encodings that can be integrated into SMT solvers that support the theory of bit-vectors (Section 4).
-
A verification case for the correctness of the SymFPU encodings and various other SMT solvers (Section 5).
-
An experimental evaluation five times larger than previous works gives a comprehensive evaluation of existing tools and shows that the SymFPU encodings, even used in a naïve way significantly out-perform all other approaches (Section 6). These experiments subsume the evaluations performed in many previous works, giving a robust replication of their results.
2 The Challenges of Floating-Point Reasoning
Floating-point number systems are based on computing with a fixed number of significant digits. Only the significant digits are stored (the significand), along with their distance from the decimal point (the exponent) as the power of a fixed base. The following are examples of decimals numbers with three significant digits and their floating-point representations.
Arithmetic is performed as normal, but the result may have more than the specified number of digits and need to be rounded to a representable value. This gives the first major challenge for reasoning about floating-point numbers: rounding after each operation means that addition and multiplication are no longer associative, nor are they distributive.
Existence of identities, additive inversesFootnote 1 and symmetry are preserved except for special cases (see below) and in some cases addition even gains an absorptive property (\(a + b = a\) for some non-zero b). However, the resulting structure is not a well studied algebra and does not support many symbolic reasoning algorithms.
Rounding ensures the significand fits in a fixed number of bits, but it does not deal with exponent overflow or underflow. Detecting, and graceful and efficient handling of these edge-cases was a significant challenge for older floating-point systems. To address these challenges, IEEE-754 defines floating-point numbers representing \(\pm \infty \) and \(\pm 0\)Footnote 2 and a class of fixed-point numbers known as denormal or subnormal numbers.
To avoid intrusive branching and testing code in computational hot-spots, all operations have to be defined for these values. This gives troubling questions such as “What is \(\infty + -\infty \)?” or “Is 0 / 0 equal to 1 / 0, \(-1/0\), or neither?”. The standard resolves these with a fifth class of number, not-a-number (NaN).
The proliferation of classes of number is the second source of challenges for automated reasoning. An operation as simple as an addition can result in a 125-way case split if each class of input number and rounding mode is considered individually. Automated reasoning systems for floating-point numbers need an efficient way of controlling the number of side conditions and edge cases.
As well as the two major challenges intrinsic to IEEE-754 floating-point, there are also challenges in how programmers use floating-point numbers. In many systems, floating-point values are used to represent some “real world” quantity – light or volume levels, velocity, distance, etc. Only a small fraction of the range of floating-point numbers are then meaningful. For example, a 64-bit floating-point number can represent the range \([1*10^{-324}, 1*10^{308}]\) which dwarfs the range of likely speeds (in m/s) of any vehicleFootnote 3 \([1*10^{-15}, 3*10^{8}]\). Apart from languages like Ada [35] or Spark [3] that have per-type ranges, the required information on what are meaningful ranges is rarely present in – or can be inferred from – the program alone. This makes it hard to create “reasonable” preconditions or avoid returning laughably infeasible verification failures.
Despite the challenges, there are many use-cases for floating-point reasoning: testing the feasibility of execution paths, preventing the generation of \(\infty \) and NaN, locating absorptive additions and catastrophic cancellation, finding language-level undefined behaviour (such as the much-cited Ariane 5 Flight 501 incident), showing run-time exception freedom, checking hardware and FPGA designs (such as the equally well cited Intel FDIV bug) and proving functional correctness against both float-valued and real-valued specifications.
2.1 Techniques
Current fully automaticFootnote 4 floating-point reasoning tools can be roughly grouped into four categories: bit-blasting, interval techniques, black-box optimisation approaches and axiomatic schemes.
Bit-Blasting. CBMC [17] was one of the first tools to convert from bit-vector formulae to Boolean SAT problems (so called “bit-blasting”). It benefited from the contemporaneous rapid improvement in SAT solver technology and lead to the DPLL(T) [29] style of SMT solver. Later versions of CBMC also converted floating-point constraints directly into Boolean problems [15]. These conversions were based on the circuits given in [44] and served as inspiration for a similar approach in MathSAT [16] and independent development of similar techniques in Z3 [24] and SONOLAR [39]. SoftFloat [34] has been used to simulate floating-point support for integer only tools [48] but is far from a satisfactory approach as the algorithms used for efficient software implementation of floating-point are significantly different from those used for hardware [45] and efficient encodings.
The principle disadvantage of bit-blasting is that the bit-vector formulae generated can be very large and complex. To mitigate this problem, there have been several approaches [15, 56, 57] to approximating the bit-vector formulae. This remains an under-explored and promising area.
Interval Techniques. One of the relational properties preserved by IEEE-754 is a weak form of monotonicity, e.g.: \(0<s \wedge a <b \Rightarrow a + s \leqslant b + s\). These properties allow efficient and tight interval bounds to be computed for common operations. This is used by the numerical methods communities and forms the basis for three independent lineages of automated reasoning tools.
Based on the formal framework of abstract interpretation, a number of techniques that partition abstract domains to compute an exact resultFootnote 5 have been proposed. These include the ACDL framework [26] that generalises the CDCL algorithm used in current SAT solvers. Although this is applicable to a variety of domains, the use of intervals is widespread as an efficient and “precise enough” foundation. CDFPL [27] applied these techniques to programs and [11] implemented them within MathSAT. Absolute [47] uses a different partitioning scheme without learning, but again uses intervals.
From the automated reasoning community similar approaches have been developed. Originally implemented in the nlsat tool [37], mcSAT [25] can be seen as an instantiation of the ACDL framework using a constant abstraction and tying the generalisation step to a particular approach to variable elimination. Application of this technique to floating-point would likely either use intervals or a conversion to bit-vectors [58]. iSAT3 [51] implements an interval partitioning and learning system, which could be seen as another instance of ACDL. Independently, dReal [30] and raSAT [55] have both developed interval partitioning techniques which would be directly applicable to floating-point systems.
A third strand of convergent evolution in the development of interval based techniques comes from the constraint programming community. FPCS [43] uses intervals with sophisticated back-propagation rules [4] and smart partitioning heuristics [59]. Colibri [42] takes a slightly different approach, using a more expressive constraint representation of difference bounded matricesFootnote 6. This favours more powerful inference over a faster search.
These approaches all have compact representations of spaces of possibilities and fast propagation which allow them to efficiently tackle “large but easy” problems. However they tend to struggle as the relations between expressions become more complex, requiring some kind or relational reasoning such as the learning in MathSAT, or the relational abstractions of Colibri. As these advantages and disadvantages fit well with those of bit-blasting, hybrid systems are not uncommon. Both MathSAT and Z3 perform simple interval reasoning during pre-processing and iSAT3 has experimented with using CBMC and SMT solvers for problems that seem to be UNSAT [46, 52].
Optimisation Approaches. It is possible to evaluate many formulae quickly in hardware, particularly those derived from software verification tasks. Combined with a finite search space for floating-point variables, this makes local-search and other “black-box” techniques an attractive proposition. XSat [28] was the first tool to directly make use of this approach (although Ariadne [5] could be seen as a partial precursor), making use of an external optimisation solver. goSAT [38] improved on this by compiling the formulae to an executable form. A similar approach using an external fuzz-testing tool is taken by JFS [40].
These approaches have considerable promise, particularly for SAT problems with relatively dense solution spaces. The obvious limitation is that these techniques are often unable to identify UNSAT problems.
Axiomatic. Although rounding destroys many of the obvious properties, the algebra of floating-point is not without non-trivial results. Gappa [23] was originally created as a support tool for interactive theorem provers, but can be seen a solver in its own right. It instantiates a series of theorems about floating-point numbers until a sufficient error bound is determined. Although its saturation process is naïve, it is fast and effective, especially when directed by a more conventional SMT solver [20]. Why3 [9] uses an axiomatisation of floating-point numbers based on reals when producing verification conditions for provers that only support real arithmetic. Combining these approaches Alt-Ergo [19] ties the instantiation of relevant theorems to its quantifier and non-linear real theory solvers. Finally, KLEE-FP [18] can be seen as a solver in the axiomatic tradition but using rewriting rather than theorem instantiation.
3 Floating-Point Circuits
Floating-point circuits have been the traditional choice for bit-blasting encoding. The ‘classical’ designFootnote 7 for floating-point units is a four stage pipeline [45]: unpacking, operation, rounding, and packing.
Unpacking. IEEE-754 gives an encoding for all five kinds of number. To separate the encoding logic from the operation logic, it is common to unpack; converting arguments from the IEEE-754 format to a larger, redundant format used within the floating-point unit (FPU). The unpacking units and intermediate format are normally the same for all operations within an FPU. A universal feature is splitting the number into three smaller bit-vectors: the sign, exponent and significand. Internal formats may also include some of the following features:
-
Flags to record if the number is an infinity, NaN, zero or subnormal.
-
The leading 1 for normal numbers (the so-called hidden-bit) may be added. Thus the significand may be regarded as a fix-point number in the range [0, 1) or [1, 2). Some designs go further allowing the significand range to be larger, allowing lazy normalisation.
-
The exponent may be biased or unbiasedFootnote 8.
-
Subnormal numbers may be normalised (requiring an extended exponent), flagged, transferred to a different unit or even trapped to software.
Operate. Operations, such as addition or multiplication are performed on unpacked numbers, significantly simplifying the logic required. The result will be another unpacked number, often with an extended significand (two or three extra bits for addition, up to twice the number of bits for multiplication) and extended exponent (typically another one or two bits). For example, using this approach multiplication is relatively straight forward:
-
1.
Multiply the two significands, giving a fixed-point number with twice the precision, in the range [1, 4).
-
2.
Add the exponents (\(2^{e_1} * 2^{e_2} = 2^{e_1 + e_2}\)) and subtract the bias if they are stored in a biased form.
-
3.
Potentially renormalise the exponent into the range [1, 2) (right shift the significand one place and increment the exponent).
-
4.
Use the classification flags to handle special cases (\(\infty \), NaN, etc.).
Addition is more involved as the two significands must be aligned before they can be added or subtracted. In most cases, the location of the leading 1 in the resulting significand is roughly known, meaning that the renormalisation is simple (for example \(s_1 \in [1,2), s_2 \in [1,2) \Rightarrow s_1 + s_2 \in [2,4)\)). However in the case of catastrophic cancellation the location of the leading 1 is non-obvious. Although this case is rare, it has a disproportionate effect on the design of floating-point adders: it is necessary to locate the leading 1 to see how many bits have been cancelled to determine what changes are needed for the exponent.
Round. Given the exact result in extended precision, the next step is to round to the nearest representable number in the target output format. Traditionally, the rounder would have been a common component of the FPU, shared between the functional units and would be independent of the operations. The operation of the rounder is relatively simple but the order of operations is very significant:
-
1.
Split the significand into the representable bits, the first bit after (the guard bit) and the OR of the remaining bits (the sticky bit).
-
2.
The guard bit and sticky bit determine whether the number is less than half way to the previous representable number, exact half way, or over half way. Depending on the rounding mode the significand may be incremented (i.e. rounded up).
-
3.
The exponent is checked to see if it is too large (overflow) or too small (underflow) for the target format, and the output is set to infinity/the largest float or 0/the smallest float depending on the rounding mode.
To work out which bits to convert to the guard and sticky bits, it is critical to know the position of the leading 1, and if the number is subnormal or not.
Pack. The final step is to convert the result back into the packed IEEE-754 format. This is the converse of the unpacking stage, with flags for the type of number being used to set special values. Note that this can result in the carefully calculated and rounded result being ignored in favour of outputting the fixed bit-pattern for \(\infty \) or NaN.
4 SymFPU
SymFPU is a C++ library of bit-vector encodings of floating-point operations. It is available at https://github.com/martin-cs/symfpu. The types used to represent signed and unsigned bit-vectors, Booleans, rounding-modes and floating-point formats are templated so that multiple “back-ends” can be implemented. This allows SymFPU to be used as an executable multi-precision library and to generate symbolic encodings of the operations. As well as the default executable back-end, integrations into CVC4 [6] and CBMC [17] have been developed. These typically require 300–500 effective lines of code, the majority of which is routine interfacing.
Packing Removal. By choosing an unpacked format that is bijective with the packed format, the following property holds: \(pack \circ unpack = id = unpack \circ pack\). The encodings in CBMC do not have this property as the packing phase is used to mask out the significand and exponent when special values are generated. The property allows a key optimisation: the final unpack stage of an operation and the pack of the next can be eliminated. Hence values can be kept in unpacked form and whole chains of operations can be performed without packing. Although this is not necessarily a large saving on its own, it allows the use of unpacked formats which would be too expensive if every operation was packed.
Unpacked Format. Key to SymFPU’s performance is the unpacked format. Flags are used for \(\infty \), NaN and zero. This means that special cases can be handled at the end of the operation, bypassing the need to reason about the actual computation if one of the flags is set. Special cases share the same ‘default’ significand and exponent, so assignment to the flags will propagate values through the rest of the circuit.
The exponent is a signed bit-vector without bias, moving a subtract from the multiplier into the packing and unpacking (avoided as described above) and allowing decision procedures for signed bit-vectors to be used [32].
The significand is represented with the leading one and subnormal numbers are normalised. This adds considerable cost to the packing and unpacking but means that the leading one can be tracked at design time, avoiding the expensive normalisation phase before rounding that CBMC’s encodings have. A normalisation phase is needed in the adder for catastrophic cancellation and the subnormal case of rounding is more expensive but critically both of these cases are rare (see below). Z3’s encodings use a more complex system of lazy normalisation. This works well when operations include packing but is harder to use once packing has been removed. Integrating this approach is a challenge for future work.
Additional Bit-Vector Operations. SymFPU uses a number of non-standard bit-vector operations including add-with-carry (for including the renormalisation bit into exponents during multiply), conditional increment, decrement and left-shift (used for normalisation), max and min, count leading zeros, order encode (output has input number of bits), right sticky shift, and normalise. Work on creating optimal encodings [12] of these operations is on-going.
Invariants. As the significand in the unpacked format always has a leading one, it is possible to give strong invariants on the location of leading ones during the algorithms. Other invariants are general properties of IEEE-754 floating-point, for example the exponent of an effective addition is always \(max(e_a,e_b)\) or \(max(e_a,e_b) + 1\) regardless of rounding. Where possible, bit-vectors operations are used so that no overflows or underflows occur – a frustrating source of bugs in the CBMC encodings. Invariants in SymFPU can be checked with executable back-ends and used as auxiliary constraints in symbolic ones.
Probability Annotations. There are many sub-cases within operations which are unlikely or rare, for example rounding the subnormal result of a multiplication, catastrophic cancellation, or late detection of significand overflow during rounding. These are often more expensive to handle than the common cases. SymFPU contains probability annotations that mark likely and unlikely cases so that these can be handled separately.
5 Correctness
Developing a floating-point implementation, literal and symbolic, is a notoriously detailed and error prone task. For SymFPU we developed a substantial verification process which is summarised in Figure 1. Our verification case is based on system-level testing of SymFPU in CVC4, and double/triple diversity of checks, developers, references and implementations:
-
1.
We use five test suites, four developed specifically for this project. These were developed independently by three different developers using different methodologies and different “ground truth” references. Where hardware was a reference, several different chips from different vendors were used.
-
2.
The results of three different solvers (CVC4 with SymFPU, MathSAT, and Z3) are compared and each test is only regarded as passed when any discrepancy, between solvers or with the reference results, has been resolved. Each solver has its own, independently developed encodings and there is diversity in the algorithms used.
As described above, SymFPU contains a significant number of dynamically-checked invariants. CVC4 also checks the models generated for satisfiable formulae, checking the symbolic back-end against the literal one. The experiments described in Section 6 also acted as system-level tests. This approach uncovered numerous bugs in the SymFPU encodings, the solvers and even our reference libraries. However, as it is a testing based verification argument, it cannot be considered to be complete. [41] used a similar technique successfully in a more limited setting without the emphasis on ground truth.
5.1 PyMPF
Testing-based verification is at best as good as the reference results for the tests – a high-quality test oracle is vital. Various solvers have their own multi-precision libraries, using these would not achieve the required diversity. MPFR [33] was considered but it does not support all of the operations in SMT-LIB, and has an awkward approach to subnormals.
To act as an oracle, we developed PyMPF [49], a Python multi-precision library focused on correctness through simplicity rather than performance. Unlike other multi-precision floating-point libraries it represents numbers as rationals rather than significand and exponent, and explicitly rounds to the nearest representable rational after each operation using a simple binary search. Where possible, all calculations are dynamically checked against a compiled C version of the operation and MPFR, giving triple diversity.
Using PyMPF as an oracle, a test suite was generated covering all combination of classes: \(\pm 0\), subnormal (smallest, random, largest), normal (smallest, random, largest, 1, \(\frac{1}{2}\)), \(\pm \infty \), and NaN along with all combination of five rounding modes. The majority of these require only forwards reasoning, but some require backwards reasoning. Benchmarks are generated for both SAT and UNSAT problems; in addition some benchmarks correctly exploit the unspecified behaviour in the standard. This suite proved particularly effective, finding multiple soundness bugs in all implementations we were able to test.
6 Experimental Results
We had two experimental objectives: (a) compare SymFPU with the state of the art, (b) reproduce, validate, or update results from previous papers.
6.1 Experimental Setup
All benchmarks are available online [50], along with the scripts to run them. Experiments were conducted in the TACAS artefact evaluation virtual machine, hosted on an Intel i7-7820HQ laptop with 32 GiB RAM running Debian Stretch. All experiments were conducted with a one minute timeoutFootnote 9 and 2500 MiB memory limit, set with a custom tool (rather than ulimit) that allowed us to reliably distinguish between tool crashes, timeouts, or memory use limits.
Solver responses were split into six classes: solved (“sat” or “unsat” response), unknown (“unknown” response), timeout, oom (out-of-memory), unsound (“sat” or “unsat” response contradicting the
 annotation), and error (anything else, including “unsupported” messages, parse errors or other tool output).
annotation), and error (anything else, including “unsupported” messages, parse errors or other tool output).
Although one minute is a relatively short limit, it best matches the typical industrial use-cases with Spark; and trial runs with larger time-outs suggest that the additional time does not substantially change the qualitative nature of the results.
6.2 Benchmarks
We have tried to avoid arbitrary choices in benchmark selection as we want to demonstrate that SymFPU’s encodings are a good general-purpose solution. As such we compare with some solvers in their specialised domain. Benchmarks are in logics QF_FP or QF_FPBV except for: Heizmann benchmarks include quantifiers and arrays; SPARK benchmarks (including Industrial_1) include arrays, datatypes, quantifiers, uninterpreted functions, integer and reals, and bitvectors. SAT, UNSAT or unknown here refers to the
 annotations in the benchmarks, not to our results.
annotations in the benchmarks, not to our results.
-
Schanda 200 problems (34.0% SAT, 63.0% UNSAT, 3.0% unknown). Hand-written benchmarks accumulated over the years working on Spark, user-supplied axioms, industrial code and problems, and reviewing papers and the SMT-LIB theory [13, 14].
-
PyMPF 72,925 problems (52.3% SAT, 47.7% UNSAT). A snapshot of benchmarks generated using PyMPF [49] as described above.
-
NyxBrain 52,500 problems (99.5% SAT, 0.5% UNSAT). Hand-written edge-cases, and generated problems based on bugs in existing implementations.
-
Wintersteiger 39,994 problems (50.0% SAT, 50.0% UNSAT). Randomly generated benchmarks that cover many aspects of the floating-point theory.
-
Griggio 214 problems (all unknown). Benchmark set deliberately designed to highlight the limitations of bit-blasting and the advantages of interval techniques. They were the most useful in reproducing other paper’s results.
-
Heizmann 207 problems (1.0% SAT, 99.0% unknown). Taken from the Ultimate Automizer model checker.
-
Industrial_1 388 problems (all UNSAT). Extracted from a large industrial Ada 2005 code base. We used the Spark 2014 tools to produce (identifier obfuscated) verification conditions.
-
Industrial_1 QF 388 problems (all unknown). As above, but with quantifiers and data-types removed.
-
SPARK FP 2950 problems (5.3% UNSAT, 94.7% unknown). The floating-point subset of the verification conditions from the Spark test suiteFootnote 10, generated using a patchedFootnote 11 Spark tool to map the square root function of the Ada Standard library to
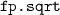 .
. -
SPARK FP QF 2950 problems (all unknown). As above, but with all quantifiers and data-types removed.
-
CBMC 54 problems (7.4% UNSAT, 92.6% unknown). Non-trivial benchmarks from SV-COMP’s floating-point collection [7], fp-bench [21] benchmarks that contained checkable post-conditions, the benchmarks used by [5], and the sample programs from [59]. The benchmarks are provided in SMT-LIB and the original C program for comparing to CBMC’s floating-point solver.
Not all SMT solvers support all features of SMT-LIB, hence we provide alternative encodings in some cases. In particular Alt-Ergo does not parse moden SMT-LIB at all; so Griggio and Wintersteiger have been translated with the
 Footnote 12 tool from [19] and the Spark FP benchmarks have been generated by Spark directly for Alt-Ergo, where possible (since Alt-Ergo does not support the
Footnote 12 tool from [19] and the Spark FP benchmarks have been generated by Spark directly for Alt-Ergo, where possible (since Alt-Ergo does not support the
 contruct, there is a translation step inside Why3 that attempts to remove it, but it sometimes runs out of memory).
contruct, there is a translation step inside Why3 that attempts to remove it, but it sometimes runs out of memory).
6.3 Solvers
We have benchmarked the following solvers in the following configurations on the benchmarks described above: CVC4 [6] (with SymFPU)Footnote 13, Z3 (4.8.1) [24], Z3 Smallfloats (3a3abf82) [57], MathSAT (5.5.2) [16], MathSAT (5.5.2) using ACDCL [11], SONOLAR (2014-12-04) [39], Colibri (r1981) [42], Alt-Ergo (2.2.0) [19], and goSAT (4e475233) [38].
We have also attempted to benchmark XSat [28], but we were unable to reliably use the tools as distributed at the required scale (\(\approx 200\)k benchmarks). However, we understand that goSAT is an evolution of the ideas implemented in XSat, and its results should be representative.
We would have liked to benchmark iSAT3 [51], Coral [53] and Gappa [23], but they do not provide SMT-LIB front-ends and there are no automatic translators we are aware of to their native input language. Binaries for FPCS [43] and Alt-Ergo/Gappa [20] were not available.
6.4 Results
Overall. Table 1 shows the overall summary of how many benchmarks any given solver was able to solve (correct SAT or UNSAT answer). CVC4 using the SymFPU encodings solves the most problems in all but two categories. In the case of the “Griggio” suite this is not surprising, given it’s purpose. A detailed breakdown of that benchmark suite can be found in Table 2.
 indicates that all problems are solved, a blank entry indicates that the solver did not solve any problem for the given benchmark suite. In this table and all subsequent tables a * indicates that at least one benchmark was expressed in a solver-specific dialect, and the best result for each benchmark is typeset in bold.
indicates that all problems are solved, a blank entry indicates that the solver did not solve any problem for the given benchmark suite. In this table and all subsequent tables a * indicates that at least one benchmark was expressed in a solver-specific dialect, and the best result for each benchmark is typeset in bold.Griggio Suite. Table 2 shows the detailed results for the Griggio suite. Since the benchmark suite was designed to be difficult for bit-blasting solvers, it is not surprising that MathSAT (ACDCL) and Colibri do very well here, as they are not bit-blasting solvers. Though it is claimed in [19] that “Bit-blasting based techniques perform better on Griggio benchmarks”, this is evidently not the case.
 in “Unsound” indicates 0 unsound results.
in “Unsound” indicates 0 unsound results.Heizmann Suite. Table 3 shows the detailed results for the benchmarks from the Ultimate Automizer project. These benchmarks were particularly useful to include as they are industrial in nature and are generated independent of all solver developers and the authors of this paper. The errors mainly relate to quantifiers (MathSAT, Colibri, SONOLAR), conversions (MathSAT-ACDCL), sorts (Colibri), and arrays (SONOLAR).
CBMC Suite. Table 4 shows a comparison between CBMC and SMT Solvers when attempting to solve the same problem. The original benchmark in C is given to CBMC, and SMT Solvers attempt to either solve a hand-encoding of the same problem or the encoding of the problem generated by CBMC.
6.5 Replication
As part of our evaluation we have attempted to reproduce, validate or update results from previous papers. We have encountered issues with unclear solver configurations and versions and arbitrary benchmark selections.
The Z3 approximation paper [57] uses the Griggio test suite with a 20 minute timeout. It reported that there is little difference between Z3 and Z3-SmallFloats, and MathSAT outperformed both. Our results in Table 2 confirm this.
The MathSAT ACDCL [11] paper also looks at the Griggio test suite with a 20 minute timeout, our results in Table 2 are roughly ordered as theirs and can be considered to confirm these results.
Although the total number of SAT/UNSAT varied based on algorithm selection (i.e. the tool was clearly unsound) in [38], goSAT has been fixed and the results are broadly reproducible. We discovered some platform dependent behaviour (different SAT/UNSAT answers) between AMD and Intel processors. This can likely be fixed with appropriate compilation flags.
We were unable to reproduce the results of the XSat [28] paper, as we could not get the tools to work reliably. In particular the docker instance cannot be used in our testing infrastructure as the constant-time overhead of running docker ruins performance, and eventually the docker daemon crashes.
We were only able to reproduce small parts from the Alt-Ergo FPA [19] paper. The biggest problem is benchmark selection and generation, which was not repeatable from scratch. Two particular measurements are worth commenting on: while they have roughly equal solved rate for Spark VCs for Alt-Ergo and Z3 (40% and 36% respectively), as can be seen in Table 1 we get (68% and 86%) - although as noted we could not fully replicate their benchmark selection. However even more surprising are their results for the Griggio suite where they report a mere 4% for MathSAT-ACDCL which does not match our results of 69% as seen in Table 2.
7 Conclusion
By careful consideration of the challenges of floating-point reasoning (Section 2) and the fundamentals of circuit design (Section 3) we have designed a library of encodings that reduce the cost of developing a correct and efficient floating-point solver to a few hundred lines of interface code (Section 4). Integration into CVC4 gives a solver that substantially out-performs all previous systems (Section 6) despite using the most direct and naïve approachFootnote 14. The verification process used to develop SymFPU ensures a high-level of quality, as well as locating tens of thousands of incorrect answers from hundreds of bugs across all existing solvers.
At a deeper level our experimental work raises some troubling questions about how developments in solver technology are practically evaluated. It shows that the quality of implementation (even between mature systems) can make a larger difference to performance than the difference between techniques [10]. Likewise the difficulty we had in replicating the trends seen in previous experimental work underscores the need for diverse and substantial benchmark sets.
Notes
- 1.
But not multiplicative ones for subtle reasons.
- 2.
Two distinct zeros are supported so that underflow from above and below can be distinguished, helping handle some branch cuts such as \(\tan \).
- 3.
Based on the optimistic use of the classical electron radius and the speed of light.
- 4.
Machine assisted proof, such as interactive theorem provers are outside the scope of the current discussion. There has been substantial work in Isabelle, HOL, HOL Light, ACL2, PVS, Coq and Meta-Tarski on floating-point.
- 5.
- 6.
In the abstract interpretation view this could be seen as a relational abstraction.
- 7.
Modern high-performance processors often only implement a fused mulitply-add (FMA) unit that computes \(round(x*y + z)\) and then use a mix of table look-ups and Newton-Raphson style iteration to implement divide, square-root, etc.
- 8.
Although the exponent is interpreted as a signed number, it is encoded, in IEEE-754 format using a biased representation, so that the \(000\dots 00\) bit-vector represents the smallest negative number rather than 0 and \(111\dots 11\) represents the largest positive rather than the \(-1\) in 2’s complement encodings. This makes the ordering of bit-vectors and IEEE-754 floating-point numbers compatible.
- 9.
Except for the Wintersteiger suite where we used a 1 s timeout to deal with Alt-Ergo’s behaviour.
- 10.
- 11.
Github: florianschanda/spark_2014 and florianschanda/why3.
- 12.
- 13.
- 14.
SymFPU (as it is used in CVC4) is an eager bit-blasting approach. These were first published in 2006, predating all approaches except some interval techniques.
References
IEEE standard for floating-point arithmetic. IEEE Std 754-2008, pp. 1–70, August 2008. https://doi.org/10.1109/IEEESTD.2008.4610935
AdaCore: CodePeer. https://www.adacore.com/codepeer
Altran, AdaCore: SPARK 2014. https://adacore.com/sparkpro
Bagnara, R., Carlier, M., Gori, R., Gotlieb, A.: Filtering floating-point constraints by maximum ULP (2013). https://arxiv.org/abs/1308.3847v1
Barr, E.T., Vo, T., Le, V., Su, Z.: Automatic detection of floating-point exceptions. In: Proceedings of the 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2013, pp. 549–560. ACM, New York (2013). https://doi.org/10.1145/2429069.2429133
Barrett, C., et al.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_14
Beyer, D.: SV-COMP. https://github.com/sosy-lab/sv-benchmarks
Blanchet, B., et al.: A static analyzer for large safety-critical software. In: Proceedings of the ACM SIGPLAN 2003 Conference on Programming Language Design and Implementation, PLDI 2003, pp. 196–207. ACM, New York (2003). https://doi.org/10.1145/781131.781153
Bobot, F., Filliâtre, J.C., Marché, C., Paskevich, A.: Why3: shepherd your herd of provers. In: Boogie 2011: First International Workshop on Intermediate Verification Languages, pp. 53–64. Wroclaw, Poland (2011). https://hal.inria.fr/hal-00790310
Brain, M., De Vos, M.: The significance of memory costs in answer set solver implementation. J. Logic Comput. 19(4), 615–641 (2008). https://doi.org/10.1093/logcom/exn038
Brain, M., D’Silva, V., Griggio, A., Haller, L., Kroening, D.: Deciding floating-point logic with abstract conflict driven clause learning. Formal Methods Syst. Des. 45(2), 213–245 (2014). https://doi.org/10.1007/s10703-013-0203-7
Brain, M., Hadarean, L., Kroening, D., Martins, R.: Automatic generation of propagation complete SAT encodings. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 536–556. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_26
Brain, M., Tinelli, C.: SMT-LIB floating-point theory, April 2015. http://smtlib.cs.uiowa.edu/theories-FloatingPoint.shtml
Brain, M., Tinelli, C., Rümmer, P., Wahl, T.: An automatable formal semantics for IEEE-754, June 2015. http://smtlib.cs.uiowa.edu/papers/BTRW15.pdf
Brillout, A., Kroening, D., Wahl, T.: Mixed abstractions for floating-point arithmetic. In: FMCAD, pp. 69–76. IEEE (2009). https://doi.org/10.1109/FMCAD.2009.5351141
Cimatti, A., Griggio, A., Schaafsma, B.J., Sebastiani, R.: The MathSAT5 SMT solver. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 93–107. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_7
Clarke, E., Kroening, D., Lerda, F.: A tool for checking ANSI-C programs. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 168–176. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_15
Collingbourne, P., Cadar, C., Kelly, P.H.: Symbolic crosschecking of floating-point and SIMD code. In: Proceedings of the Sixth Conference on Computer Systems, EuroSys 2011, pp. 315–328. ACM, New York (2011). https://doi.org/10.1145/1966445.1966475
Conchon, S., Iguernlala, M., Ji, K., Melquiond, G., Fumex, C.: A three-tier strategy for reasoning about floating-point numbers in SMT. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 419–435. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_22
Conchon, S., Melquiond, G., Roux, C., Iguernelala, M.: Built-in treatment of an axiomatic floating-point theory for SMT solvers. In: Fontaine, P., Goel, A. (eds.) 10th International Workshop on Satisfiability Modulo Theories, pp. 12–21. Manchester, United Kingdom, June 2012. https://hal.inria.fr/hal-01785166
Damouche, N., Martel, M., Panchekha, P., Qiu, C., Sanchez-Stern, A., Tatlock, Z.: Toward a standard benchmark format and suite for floating-point analysis. In: Bogomolov, S., Martel, M., Prabhakar, P. (eds.) NSV 2016. LNCS, vol. 10152, pp. 63–77. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-54292-8_6
Darulova, E., Kuncak, V.: Sound compilation of reals. In: Proceedings of the 41st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2014, pp. 235–248. ACM, New York (2014). https://doi.org/10.1145/2535838.2535874
Daumas, M., Melquiond, G.: Certification of bounds on expressions involving rounded operators. ACM Trans. Math. Softw. 37(1), 2:1–2:20 (2010). https://doi.org/10.1145/1644001.1644003
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
de Moura, L., Jovanović, D.: A model-constructing satisfiability calculus. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 1–12. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35873-9_1
D’Silva, V., Haller, L., Kroening, D.: Abstract conflict driven learning. In: Proceedings of the 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2013, pp. 143–154. ACM, New York (2013). https://doi.org/10.1145/2429069.2429087
D’Silva, V., Haller, L., Kroening, D., Tautschnig, M.: Numeric bounds analysis with conflict-driven learning. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 48–63. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_5
Fu, Z., Su, Z.: XSat: a fast floating-point satisfiability solver. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 187–209. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_11
Ganzinger, H., Hagen, G., Nieuwenhuis, R., Oliveras, A., Tinelli, C.: DPLL(T): fast decision procedures. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 175–188. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_14
Gao, S., Kong, S., Clarke, E.M.: dReal: an SMT solver for nonlinear theories over the reals. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 208–214. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_14
Goubault, E., Putot, S.: Static analysis of numerical algorithms. In: Yi, K. (ed.) SAS 2006. LNCS, vol. 4134, pp. 18–34. Springer, Heidelberg (2006). https://doi.org/10.1007/11823230_3
Hadarean, L., Bansal, K., Jovanović, D., Barrett, C., Tinelli, C.: A tale of two solvers: eager and lazy approaches to bit-vectors. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 680–695. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_45
Hanrot, G., Zimmermann, P., Lefèvre, V., Pèlissier, P., Thèveny, P., et al.: The GNU MPFR Library. http://www.mpfr.org
Hauser, J.R.: SoftFloat. http://www.jhauser.us/arithmetic/SoftFloat.html
ISO/IEC JTC 1/SC 22/WG 9 Ada Rapporteur Group: Ada reference manual. ISO/IEC 8652:2012/Cor.1:2016 (2016). http://www.ada-auth.org/standards/rm12_w_tc1/html/RM-TOC.html
Izycheva, A., Darulova, E.: On sound relative error bounds for floating-point arithmetic. In: Proceedings of the 17th Conference on Formal Methods in Computer-Aided Design, FMCAD 2017, pp. 15–22. FMCAD Inc, Austin, TX (2017). http://dl.acm.org/citation.cfm?id=3168451.3168462
Jovanović, D., de Moura, L.: Solving non-linear arithmetic. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 339–354. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_27
Khadra, M.A.B., Stoffel, D., Kunz, W.: goSAT: floating-point satisfiability as global optimization. In: Formal Methods in Computer Aided Design, FMCAD 2017, pp. 11–14. IEEE (2017). https://doi.org/10.23919/FMCAD.2017.8102235
Lapschies, F.: SONOLAR the solver for non-linear arithmetic (2014). http://www.informatik.uni-bremen.de/agbs/florian/sonolar
Liew, D.: JFS: JIT fuzzing solver. https://github.com/delcypher/jfs
Liew, D., Schemmel, D., Cadar, C., Donaldson, A.F., Zähl, R., Wehrle, K.: Floating-point symbolic execution: a case study in n-version programming, pp. 601–612. IEEE, October 2017. https://doi.org/10.1109/ASE.2017.8115670
Marre, B., Bobot, F., Chihani, Z.: Real behavior of floating point numbers. In: SMT Workshop (2017). http://smt-workshop.cs.uiowa.edu/2017/papers/SMT2017_paper_21.pdf
Michel, C., Rueher, M., Lebbah, Y.: Solving constraints over floating-point numbers. In: Walsh, T. (ed.) CP 2001. LNCS, vol. 2239, pp. 524–538. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45578-7_36
Mueller, S.M., Paul, W.J.: Computer Architecture: Complexity and Correctness. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-662-04267-0
Muller, J.M., et al.: Handbook of Floating-Point Arithmetic. Birkhäuser (2009). https://doi.org/10.1007/978-0-8176-4705-6
Neubauer, F., et al.: Accurate dead code detection in embedded C code by arithmetic constraint solving. In: Ábrahám, E., Davenport, J.H., Fontaine, P. (eds.) Proceedings of the 1st Workshop on Satisfiability Checking and Symbolic Computation. CEUR, vol. 1804, pp. 32–38, September 2016. http://ceur-ws.org/Vol-1804/paper-07.pdf
Pelleau, M., Miné, A., Truchet, C., Benhamou, F.: A constraint solver based on abstract domains. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 434–454. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35873-9_26
Romano, A.: Practical floating-point tests with integer code. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 337–356. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54013-4_19
Schanda, F.: Python arbitrary-precision floating-point library (2017). https://www.github.com/florianschanda/pympf
Schanda, F., Brain, M., Wintersteiger, C., Griggio, A., et al.: SMT-LIB floating-point benchmarks, June 2017. https://github.com/florianschanda/smtlib_schanda
Scheibler, K., Kupferschmid, S., Becker, B.: Recent improvements in the SMT solver iSAT. In: Haubelt, C., Timmermann, D. (eds.) Methoden und Beschreibungssprachen zur Modellierung und Verifikation von Schaltungen und Systemen (MBMV), Warnemünde, Germany, pp. 231–241, 12–14 March 2013. Institut für Angewandte Mikroelektronik und Datentechnik, Fakultät für Informatik und Elektrotechnik, Universität Rostock (2013), http://www.avacs.org/fileadmin/Publikationen/Open/scheibler.mbmv2013.pdf
Scheibler, K., et al.: Accurate ICP-based floating-point reasoning. In: Proceedings of the 16th Conference on Formal Methods in Computer-Aided Design FMCAD 2016, pp. 177–184. FMCAD Inc, Austin, TX (2016). http://dl.acm.org/citation.cfm?id=3077629.3077660
Souza, M., Borges, M., d’Amorim, M., Păsăreanu, C.S.: CORAL: solving complex constraints for symbolic PathFinder. In: Bobaru, M., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM 2011. LNCS, vol. 6617, pp. 359–374. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20398-5_26
The MathWorks Inc: Polyspace. https://www.mathworks.com/polyspace
Tung, V.X., Van Khanh, T., Ogawa, M.: raSAT: an SMT solver for polynomial constraints. Formal Methods Syst. Des. 51(3), 462–499 (2017). https://doi.org/10.1007/s10703-017-0284-9
Zeljic, A., Backeman, P., Wintersteiger, C.M., Rümmer, P.: Exploring approximations for floating-point arithmetic using UppSAT. In: Automated Reasoning - 9th International Joint Conference, IJCAR 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, 14–17 July 2018, Proceedings, pp. 246–262 (2018). https://doi.org/10.1007/978-3-319-94205-6_17
Zeljić, A., Wintersteiger, C.M., Rümmer, P.: Approximations for model construction. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 344–359. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_26
Zeljić, A., Wintersteiger, C.M., Rümmer, P.: Deciding bit-vector formulas with mcSAT. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 249–266. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40970-2_16
Zitoun, H., Michel, C., Rueher, M., Michel, L.: Search strategies for floating point constraint systems. In: Beck, J.C. (ed.) CP 2017. LNCS, vol. 10416, pp. 707–722. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66158-2_45
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Brain, M., Schanda, F., Sun, Y. (2019). Building Better Bit-Blasting for Floating-Point Problems. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11427. Springer, Cham. https://doi.org/10.1007/978-3-030-17462-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-17462-0_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17461-3
Online ISBN: 978-3-030-17462-0
eBook Packages: Computer ScienceComputer Science (R0)






 .
.