Abstract
Symbolic regex matcher is a new open source .NET regular expression matching tool and match generator in the Microsoft Automata framework. It is based on the .NET regex parser in combination with a set based representation of character classes. The main feature of the tool is that the core matching algorithms are based on symbolic derivatives that support extended regular expression operations such as intersection and complement and also support a large set of commonly used features such as bounded loop quantifiers. The particularly useful features of the tool are that it supports full UTF16 encoded strings, the match generation is backtracking free, thread safe, and parallelizes with low overhead in multithreaded applications. We discuss the main design decisions behind the tool, explain the core algorithmic ideas and how the tool works, discuss some practical usage scenarios, and compare it to existing state of the art.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Motivation
We present a new tool called Symbolic Regex Matcher or SRM for fast match generation from extended regular expressions. The development of SRM has been motivated by some concrete industrial use cases and should meet the following expectations. Regarding performance, the overall algorithm complexity of match generation should be linear in the length of the input string. Regarding expressivity, it should handle common types of .NET regexes, including support for bounded quantifiers and Unicode categories; while nonregular features of regexes, such as back-references, are not required. Regarding semantics, the tool should be .NET compliant regarding strings and regexes, and the main type of match generation is: earliest eager nonoverlapping matches in the input string. Moreover, the tool should be safe to use in distributed and multi threaded development environments. Compilation time should be reasonable but it is not a critical factor because the intent is that the regexes are used frequently but updated infrequently. A concrete application of SRM is in an internal tool at Microsoft that scans for credentials and other sensitive content in cloud service software, where the search patterns are stated in form of individual regexes or in certain scenarios as intersections of regexes.
The built-in .NET regex engine uses a backtracking based match search algorithm and does not meet the above expectations; in particular, some patterns may cause exponential search time. While SRM uses the same parser as the .NET regex engine, its back-end is a new engine that is built on the notion of derivatives [1], is developed as a tool in the open source Microsoft Automata framework [5], the framework was originally introduced in [8]. SRM meets all of the above expectations. Derivatives of regular expressions have been studied before in the context of matching of regular expressions, but only in the functional programming world [2, 6] and in related domains [7]. Compared to earlier derivative based matching engines, the new contribution of SRM is that it supports match generation not only match detection, it supports extended features, such as bounded quantifiers, Unicode categories, and case insensitivity, it is .NET compliant, and is implemented in an imperative language. As far as we are aware of, SRM is the first tool that supports derivative based match generation for extended regular expressions. In our evaluation SRM shows significant performance improvements over .NET, with more predictable performance than RE2 [3], a state of the art automata based regex matcher.
In order to use SRM in a .NET application instead of the built-in match generator,
 can be built from [5] on a .NET platform version 4.0 or higher. The library extends the built-in
can be built from [5] on a .NET platform version 4.0 or higher. The library extends the built-in
 class with methods that expose SRM, in particular through the
class with methods that expose SRM, in particular through the
 method.
method.
2 Matching with Derivatives
Here we work with derivatives of symbolic extended regular expressions or regexes for short. Symbolic means that the basic building blocks of single character regexes are predicates as opposed to singleton characters. In the case of standard .NET regexes, these are called character classes, such as the class of digits or
 . In general, such predicates are drawn from a given effective Boolean algebra and are here denoted generally by \(\alpha \) and \(\beta \);
. In general, such predicates are drawn from a given effective Boolean algebra and are here denoted generally by \(\alpha \) and \(\beta \);  denotes the false predicate and
denotes the false predicate and  the true predicate. For example, in .NET
the true predicate. For example, in .NET  can be represented by the empty character class
can be represented by the empty character class
 .Footnote 1 Extended here means that we allow intersection, complement, and bounded quantifiers.
.Footnote 1 Extended here means that we allow intersection, complement, and bounded quantifiers.
The abstract syntax of regexes assumed here is the following, assuming the usual semantics where () denotes the empty sequence \(\epsilon \) and \(\langle \alpha \rangle \) denotes any singleton sequence of character that belongs to the set \([\![\alpha ]\!]_{}\subseteq \varSigma \), where \(\varSigma \) is the alphabet, and n and m are nonnegative integers such that \(n\le m\):
where  ,
,  . The expression \(R*\) is a shorthand for \(R\{0,*\}\). We write
. The expression \(R*\) is a shorthand for \(R\{0,*\}\). We write  also for
also for  . We assume that \([\![R_1 | R_2]\!]_{} = [\![R_1]\!]_{}\cup [\![R_2]\!]_{}\), \( [\![R_1 \& R_2]\!]_{} = [\![R_1]\!]_{}\cap [\![R_2]\!]_{}\), and \([\![\lnot R]\!]_{} =\varSigma ^*\setminus [\![R]\!]_{}\). A less known feature of the .NET regex grammar is that it also supports if-then-else expressions over regexes, so, when combined appropriately with
. We assume that \([\![R_1 | R_2]\!]_{} = [\![R_1]\!]_{}\cup [\![R_2]\!]_{}\), \( [\![R_1 \& R_2]\!]_{} = [\![R_1]\!]_{}\cap [\![R_2]\!]_{}\), and \([\![\lnot R]\!]_{} =\varSigma ^*\setminus [\![R]\!]_{}\). A less known feature of the .NET regex grammar is that it also supports if-then-else expressions over regexes, so, when combined appropriately with  and
and  , it also supports intersection and complement. R is nullable if \(\epsilon \in [\![R]\!]_{}\). Nullability is defined recursively, e.g., \(R\{n,m\}\) is nullable iff R is nullable or \(n=0\).
, it also supports intersection and complement. R is nullable if \(\epsilon \in [\![R]\!]_{}\). Nullability is defined recursively, e.g., \(R\{n,m\}\) is nullable iff R is nullable or \(n=0\).

Given a concrete character x in the underlying alphabet \(\varSigma \), and a regex R, the x-derivative of R, denoted by \(\partial _{x}R\), is defined on the right. Given a language \(L\subseteq \varSigma ^*\), the x-derivative of L,  . It is well-known that \([\![\partial _{x}R]\!]_{} = \varvec{\partial }_{x}[\![R]\!]_{}\). The abstract derivation rules provide a way to decide if an input u matches a regex R as follows. If \(u=\epsilon \) then u matches R iff R is nullable; else, if \(u=xv\) for some \(x\in \varSigma ,v\in \varSigma ^*\) then u matches R iff v matches \(\partial _{x}R\). In other words, the derivation rules can be unfolded lazily to create the transitions of the underlying DFA. In this setting we are considering Brzozowski derivatives [1].
. It is well-known that \([\![\partial _{x}R]\!]_{} = \varvec{\partial }_{x}[\![R]\!]_{}\). The abstract derivation rules provide a way to decide if an input u matches a regex R as follows. If \(u=\epsilon \) then u matches R iff R is nullable; else, if \(u=xv\) for some \(x\in \varSigma ,v\in \varSigma ^*\) then u matches R iff v matches \(\partial _{x}R\). In other words, the derivation rules can be unfolded lazily to create the transitions of the underlying DFA. In this setting we are considering Brzozowski derivatives [1].
Match Generation. The main purpose of the tool is to generate matches. While match generation is a topic that has been studied extensively for classical regular expressions, we are not aware of efforts that have considered the use of derivatives and extended regular expressions in this context, while staying backtracking free in order to guarantee linear complexity in terms of the length of the input. Our matcher implements by default nonoverlapping earliest eager match semantics. An important property in the matcher is that the above set of regular expressions is closed under reversal. The reversal of regex R is denoted \(R^{\mathbf {r}}\). Observe that:

It follows that \([\![R^{\mathbf {r}}]\!]_{} = [\![R]\!]_{}^{\mathbf {r}}\) where \(L^{\mathbf {r}}\) denotes the reversal of \(L\subseteq \varSigma ^*\). The match generation algorithm can now be described at a high level as follows. Given a regex R, find all the (nonoverlapping earliest eager) matches in a given input string u. This procedure uses the three regexes: R, \(R^{\mathbf {r}}\) and  :
:
-
1.
Initially \(i=0\) is the start position of the first symbol \(u_0\) of u.
-
2.
Let \(i_{\text {orig}}=i\). Find the earliest match starting from i and
 : Compute \(q := \partial _{u_i}q\) and \(i := i+1\) until q is nullable. Terminate if no such q exists.
: Compute \(q := \partial _{u_i}q\) and \(i := i+1\) until q is nullable. Terminate if no such q exists. -
3.
Find the start position for the above match closest to \(i_{\text {orig}}\): Let \(p = R^{\mathbf {r}}\). While \(i > i_{\text {orig}}\) let \(p := \partial _{u_i}p\) and \(i := i-1\), if p is nullable let \(i_{\text {start}} := i\).
-
4.
Find the end position for the match: Let \(q= R\) and \(i=i_{\text {start}}\). Compute \(q := \partial _{u_i}q\) and \(i:=i+1\) and let \(i_{\text {end}} := i\) if q is nullable; repeat until
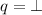 .
. -
5.
Return the match from \(i_{\text {start}}\) to \(i_{\text {end}}\).
-
6.
Repeat step 2 from \(i:=i_{\text {end}}+1\) for the next nonoverlapping start position.
Observe that step 4 guarantees longest match in R from the position \(i_{\text {start}}\) found in step 3 for the earliest match found in step 2. In order for the above procedure to be practical there are several optimizations that are required. We discuss some of the implementation aspects next.
3 Implementation
SRM is implemented in
 . The input to the tool is a .NET regex (or an array of regexes) that is compiled into a serializable object R that implements the main matching interface IMatcher. Initially, this process uses a Binary Decision Diagram (BDD) based representation of predicates in order to efficiently canonicalize various conditions such as case insensitivity and Unicode categories. The use of BDDs as character predicates is explained in [4]. Then all the BDDs that occur in R are collected and their minterms (satisfiable Boolean combinations) are calculated, called the atoms \((\alpha _1,\ldots ,\alpha _k)\) of R, where \(\{{[\![\alpha _i]\!]_{\texttt {BDD}}}\}_{i=1}^k\) forms a partition of \(\varSigma \). Each BDD-predicate \(\alpha \) in R is now translated into a k-bit bit-vector (or BV) value \(\beta \) whose i’th bit is 1 iff \(\alpha \wedge _{\texttt {BDD}}\alpha _i\) is nonempty. Typically k is small (often \(k\le 64\)) and allows BV to be implemented very efficiently (often by ulong), where \(\wedge _{\texttt {BV}}\) is bit-wise-and. All subsequent Boolean operations are performed on this more efficient and thread safe data type. The additional step required during input processing is that each concrete input character c (char value) is now first mapped into an atom id i that determines the bit position in the BV predicate. In other words, \(c\in [\![\beta ]\!]_{\texttt {BV}}\) is implemented by finding the index i such that \(c\in [\![\alpha _i]\!]_{\texttt {BDD}}\) and testing if the i’th bit of \(\beta \) is 1, where the former search is hardcoded into a precomputed lookup table or decision tree.
. The input to the tool is a .NET regex (or an array of regexes) that is compiled into a serializable object R that implements the main matching interface IMatcher. Initially, this process uses a Binary Decision Diagram (BDD) based representation of predicates in order to efficiently canonicalize various conditions such as case insensitivity and Unicode categories. The use of BDDs as character predicates is explained in [4]. Then all the BDDs that occur in R are collected and their minterms (satisfiable Boolean combinations) are calculated, called the atoms \((\alpha _1,\ldots ,\alpha _k)\) of R, where \(\{{[\![\alpha _i]\!]_{\texttt {BDD}}}\}_{i=1}^k\) forms a partition of \(\varSigma \). Each BDD-predicate \(\alpha \) in R is now translated into a k-bit bit-vector (or BV) value \(\beta \) whose i’th bit is 1 iff \(\alpha \wedge _{\texttt {BDD}}\alpha _i\) is nonempty. Typically k is small (often \(k\le 64\)) and allows BV to be implemented very efficiently (often by ulong), where \(\wedge _{\texttt {BV}}\) is bit-wise-and. All subsequent Boolean operations are performed on this more efficient and thread safe data type. The additional step required during input processing is that each concrete input character c (char value) is now first mapped into an atom id i that determines the bit position in the BV predicate. In other words, \(c\in [\![\beta ]\!]_{\texttt {BV}}\) is implemented by finding the index i such that \(c\in [\![\alpha _i]\!]_{\texttt {BDD}}\) and testing if the i’th bit of \(\beta \) is 1, where the former search is hardcoded into a precomputed lookup table or decision tree.
For example let R be constructed for the regex  . Then R has three atoms:
. Then R has three atoms:  ,
,  , and
, and  , since
, since  . For example BV \(110_2\) represents
. For example BV \(110_2\) represents  and \(010_2\) represents
and \(010_2\) represents  .
.
The symbolic regex AST type is treated as a value type and is handled similarly to the case of derivative based matching in the context of functional languages [2, 6]. A key difference though, is that weak equivalence [6] checking is not enough to avoid state-space explosion when bounded quantifiers are allowed. A common situation during derivation is appearance of subexpressions of the form \( (A\{0,k\}B) | (A\{0,k-1\}B) \) that, when kept unchecked, keep reintroducing disjuncts of the same subexpression but with smaller value of the upper bound, potentially causing a substantial blowup. However, we know that \(A\{0,n\}B\) is subsumed by \(A\{0,m\}B\) when \(n\le m\), thus \( (A\{0,m\}B) | (A\{0,n\}B) \) can be simplified to \(A\{0,m\}B\). To this end, a disjunct \(A\{0,k\}B\), where \(k > 0\), is represented internally as a multiset element \(\langle A, B \rangle \mapsto k\) and the expression \( (\langle A, B \rangle \mapsto m)|(\langle A, B \rangle \mapsto n)\) reduces to \((\langle A, B \rangle \mapsto \max (m,n)) \). This is a form of weak subsumption checking that provides a crucial optimization step during derivation. Similarly, when A and B are both singletons, say \(\langle \alpha \rangle \) and \(\langle \beta \rangle \), then \(\langle \alpha \rangle |\langle \beta \rangle \) reduces to \(\langle \alpha \vee _{\texttt {BV}}\beta \rangle \) and \( \langle \alpha \rangle \& \langle \beta \rangle \) reduces to \(\langle \alpha \wedge _{\texttt {BV}}\beta \rangle \). Here thread safety of the Boolean operations is important in a multi threaded application.
Finally, two more key optimizations are worth mentioning. First, during the main match generation loop, symbolic regex nodes are internalized into integer state ids and a DFA is maintained in form of an integer array \(\delta \) indexed by [i, q] where \(1\le i \le k\) is an atom index, and q is a state integer id, such that old state ids are immediately looked up as \(\delta [i,q]\) and not rederived. Second, during step 2, initial search for the relevant initial prefix, when applicable, is performed using string.IndexOf to completely avoid the trivial initial state transition corresponding to the loop  in the case when
in the case when  .
.
4 Evaluation
We have evaluated the performance of SRM on two benchmarks:
-
Twain: 15 regexes matched against a 16 MB file containing the collected works of Mark Twain.
-
Assorted: 735 regexes matched against a synthetic input that includes some matches for each regex concatenated with random strings to produce an input file of 32 MB. The regexes are from the Automata library’s samples and were originally collected from an online database of regular expressions.
We compare the performance of our matcher against the built-in .NET regex engine and Google’s RE2 [3], a state of the art backtracking free regex match generation engine. RE2 is written in
 and internally based on automata. It eliminates bounded quantifiers in a preprocessing step by unwinding them, which may cause the regex to be rejected if the unwinding exceeds a certain limit. RE2 does not support extended operations over regexes such as intersection or complement. We use RE2 through a
and internally based on automata. It eliminates bounded quantifiers in a preprocessing step by unwinding them, which may cause the regex to be rejected if the unwinding exceeds a certain limit. RE2 does not support extended operations over regexes such as intersection or complement. We use RE2 through a
 wrapper library.
wrapper library.
The input to the built-in .NET regex engine and SRM is in UTF16, which is the encoding for NET’s built-in strings, while RE2 is called with UTF8 encoded input. This implies for example that a regex such as
 that tries to locate a single UTF16 surrogate is not meaningful in the context UTF8. All experiments were run on a machine with dual Intel Xeon E5-2620v3 CPUs running Windows 10 with .NET Framework 4.7.1. The reported running times for Twain are averages of 10 samples, while the statistics for Assorted are based on a single sample for each regex.
that tries to locate a single UTF16 surrogate is not meaningful in the context UTF8. All experiments were run on a machine with dual Intel Xeon E5-2620v3 CPUs running Windows 10 with .NET Framework 4.7.1. The reported running times for Twain are averages of 10 samples, while the statistics for Assorted are based on a single sample for each regex.
Figure 1 presents running times for each regex in Twain, while Fig. 2 presents a selection of metrics for the Assorted benchmark.
Both SRM and RE2 are faster than .NET on most regexes. This highlights the advantages of automata based regular expression matching when the richer features of a backtracking matcher are not required.
Compilation of regular expressions into matcher objects takes more time in SRM than RE2 or .NET. The largest contributor to this is finding the minterms of all predicates in the regex. For use cases where initialization time is critical and inputs are known in advance, SRM provides support for pre-compilation and fast deserialization of matchers.
Comparing SRM to RE2 we can see that both matchers have regexes they do better on. While SRM achieves a lower average matching time on Assorted, this is due to the more severe outliers in RE2’s performance profile, as shown by the lower 80th percentile matching time. Overall SRM offers performance that is comparable to RE2 while being implemented in
 without any unsafe code.
without any unsafe code.
Application to Security Leak Scanning. SRM has been adopted in an internal tool at Microsoft that scans for credentials and other sensitive content in cloud service software. With the built-in .NET regex engine the tool was susceptible to catastrophic backtracking on files with long lines, such as minified JavaScript and SQL server seeding files. SRM’s linear matching complexity has helped address these issues, while maintaining compatibility for the large set of .NET regexes used in the application.
Notes
- 1.
The more intuitive syntax [] is unfortunately not allowed.
References
Brzozowski, J.A.: Derivatives of regular expressions. JACM 11, 481–494 (1964)
Fischer, S., Huch, F., Wilke, T.: A play on regular expressions: functional pearl. SIGPLAN Not. 45(9), 357–368 (2010)
Google: RE2. https://github.com/google/re2
Hooimeijer, P., Veanes, M.: An evaluation of automata algorithms for string analysis. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 248–262. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_18
Microsoft: Automata. https://github.com/AutomataDotNet/
Owens, S., Reppy, J., Turon, A.: Regular-expression derivatives re-examined. J. Funct. Program. 19(2), 173–190 (2009)
Traytel, D., Nipkow, T.: Verified decision procedures for MSO on words based on derivatives of regular expressions. SIGPLAN Not. 48(9), 3–12 (2013)
Veanes, M., Bjørner, N.: Symbolic automata: the toolkit. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 472–477. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_33
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Saarikivi, O., Veanes, M., Wan, T., Xu, E. (2019). Symbolic Regex Matcher. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11427. Springer, Cham. https://doi.org/10.1007/978-3-030-17462-0_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-17462-0_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17461-3
Online ISBN: 978-3-030-17462-0
eBook Packages: Computer ScienceComputer Science (R0)





 : Compute
: Compute 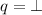 .
.

