Abstract
We address the problem of statically checking safety properties (such as assertions or deadlocks) for parameterized phaser programs. Phasers embody a non-trivial and modern synchronization construct used to orchestrate executions of parallel tasks. This generic construct supports dynamic parallelism with runtime registrations and deregistrations of spawned tasks. It generalizes many synchronization patterns such as collective and point-to-point schemes. For instance, phasers can enforce barriers or producer-consumer synchronization patterns among all or subsets of the running tasks. We consider in this work programs that may generate arbitrarily many tasks and phasers. We propose an exact procedure that is guaranteed to terminate even in the presence of unbounded phases and arbitrarily many spawned tasks. In addition, we prove undecidability results for several problems on which our procedure cannot be guaranteed to terminate.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
We focus on the parameterized verification problem of parallel programs that adopt the phasers construct for synchronization [15]. This coordination construct unifies collective and point-to-point synchronization. Parameterized verification is particularly relevant for mainstream parallel programs as the number of interdependent tasks in many applications, from scientific computing to web services or e-banking, may not be known apriori. Parameterized verification of phaser programs is a challenging problem due to the arbitrary numbers of involved tasks and phasers. In this work, we address this problem and provide an exact symbolic verification procedure. We identify parameterized problems for which our procedure is guaranteed to terminate and prove the undecidability of several variants on which our procedure cannot be guaranteed to terminate in general.
Phasers build on the clock construct from the X10 programming language [5] and are implemented in Habanero Java [4]. They can be added to any parallel programming language with a shared address space. Conceptually, phasers are synchronization entities to which tasks can be registered or unregistered. Registered tasks may act as producers, consumers, or both. Tasks can individually issue signal, wait, and next commands to a phaser they are registered to. Intuitively, a signal command is used to inform other tasks registered to the same phaser that the issuing task is done with its current phase. It increments the signal value associated to the issuing task on the given phaser. The wait command on the other hand checks whether all signal values in the phaser are strictly larger than the number of waits issued by this task, i.e. all registered tasks have passed the issuing task’s wait phase. It then increments the wait value associated to the task on the phaser. As a result, the wait command might block the issuing task until other tasks issue enough signals. The next command consists in a signal followed by a wait. The next command may be associated to a sequence of statements that are to be executed in isolation by one of the registered tasks participating in the command. A program that does not use this feature of the next statement is said to be non-atomic. A task deregisters from a phaser by issuing a drop command on it.
The dynamic synchronization allowed by the construct suits applications that need dynamic load balancing (e.g., for solving non-uniform problems with unpredictable load estimates [17]). Dynamic behavior is enabled by the possible runtime creation of tasks and phasers and their registration/de-registration. Moreover, the spawned tasks can work in different phases, adding flexibility to the synchronization pattern. The generality of the construct makes it also interesting from a theoretical perspective, as many language constructs can be expressed using phasers. For example, synchronization barriers of Single Program Multiple Data programs, the Bulk Synchronous Parallel computation model [16], or promises and futures constructs [3] can be expressed using phasers.
We believe this paper provides general (un)decidability results that will guide verification of other synchronization constructs. We identify combinations of features (e.g., unbounded differences between signal and wait phases, atomic statements) and properties to be checked (e.g., assertions, deadlocks) for which the parameterized verification problem becomes undecidable. These help identify synchronization constructs with enough expressivity to result in undecidable parameterized verification problems. We also provide a symbolic verification procedure that terminates even on fragments with arbitrary phases and numbers of spawned tasks. We get back to possible implications in the conclusion:
-
We show an operational model for phaser programs based on [4, 6, 9, 15].
-
We propose an exact symbolic verification procedure for checking reachability of sets of configurations for non-atomic phaser programs even when arbitrarily many tasks and phasers may be generated.
-
We prove undecidability results for several reachability problems.
-
We show termination of our procedure when checking assertions for non-atomic programs even when arbitrary many tasks may be spawned.
-
We show termination of our procedure when checking deadlock-freedom and assertions for non-atomic programs with bounded gaps between signal and wait values, even when arbitrary many tasks may be spawned.
Related work. The closest work to ours is [9]. It is the only work on automatic and static formal verification of phaser programs. It does not consider the parameterized case. The current work studies decidability of different parameterized reachability problems and proposes a symbolic procedure that, for example, decides program assertions even in the presence of arbitrary many tasks. This is well beyond [9]. The work of [6] considers dynamic deadlock verification of phaser programs and can therefore only detect deadlocks at runtime. The work in [2] uses Java Path Finder [11] to explore all concrete execution paths. A more general description of the phasers mechanism has also been formalized in Coq [7].
Outline. We describe phasers in Sect. 2. The construct is formally introduced in Sect. 3 where we show a general reachability problem to be undecidable. We describe in Sect. 4 our symbolic representation and state some of its non-trivial properties. We use the representation in Sect. 5 to instantiate a verification procedure and establish decidability results. We refine our undecidability results in Sect. 6 and summarize our findings in Sect. 7. Proofs can be found in [10].
An unbounded number of producers and consumers are synchronized using two phasers. In this construction, each consumer requires all producers to be ahead of it (wrt. the p phaser) in order for it to consume their respective products. At the same time, each consumer needs to be ahead of all producers (wrt. the c phaser) in order for the producers to be able to move to the next phase and produce new items.
2 Motivating Example
The program listed in Fig. 1 uses Boolean shared variables \(\mathtt {B}=\left\{ {\mathtt {a},\mathtt {done}}\right\} \). The main task creates two phasers (line 4–5). When creating a phaser, the task gets automatically registered to it. The main task also creates an unbounded number of other task instances (lines 7–8). When a task \(t\) is registered to a phaser \(p\), a pair \((w_{t}^{p},s_{t}^{p})\) in \(\mathbb {N}^2\) can be associated to the couple \((t,p)\). The pair represents the individual wait and signal phases of task \(t\) on phaser \(p\).
Registration of a task to a phaser can occur in one of three modes: \(\mathrm {\textsc {Sig\_Wait}}\), \(\mathrm {\textsc {Wait}}\) and \(\mathrm {\textsc {Sig}}\). In \(\mathrm {\textsc {Sig\_Wait}}\) mode, a task may issue both \(\mathtt {signal}\) and \(\mathtt {wait}\) commands. In \(\mathrm {\textsc {Wait}}\) (resp. \(\mathrm {\textsc {Sig}}\)) mode, a task may only issue \(\mathtt {wait}\) (resp. \(\mathtt {signal}\)) commands on the phaser. Issuing a \(\mathtt {signal}\) command by a task on a phaser results in the task incrementing its signal phase associated to the phaser. This is non-blocking. On the other-hand, issuing a \(\mathtt {wait}\) command by a task on a phaser \(p\) will block until all tasks registered to \(p\) get signal values on \(p\) that are strictly larger than the wait value of the issuing task. The wait phase of the issuing task is then incremented. Intuitively, signals allow issuing tasks to state other tasks need not wait for them. In retrospect, waits allow tasks to make sure all registered tasks have moved past their wait phases.
Upon creation of a phaser, wait and signal phases are initialized to 0 (except in \(\mathrm {\textsc {Wait}}\) mode where no signal phase is associated to the task in order to not block other waiters). The only other way a task may get registered to a phaser is if an already registered task spawns and registers it in the same mode (or in \(\mathrm {\textsc {Wait}}\) or \(\mathrm {\textsc {Sig}}\) if the registrar is registered in \(\mathrm {\textsc {Sig\_Wait}}\)). In this case, wait and signal phases of the newly registered task are initialized to those of the registrar. Tasks are therefore dynamically registered (e.g., lines 7–8). They can also dynamically deregister themselves (e.g., line 10–11).
Here, an unbounded number of producers and consumers synchronize using two phasers. Consumers require producers to be ahead wrt. the phaser they point to with \(\mathtt {p}\). At the same time, consumers need to be ahead of all producers wrt. the phaser pointed to with \(\mathtt {c}\). It should be clear that phasers can be used as barriers for synchronizing dynamic subsets of concurrent tasks. Observe that tasks need not, in general, proceed in a lock step fashion. The difference between the largest signal value and the smallest wait value can be arbitrarily large (several signals before waits catch up). This allows for more flexibility.
We are interested in checking: (a) control reachability as in assertions (e.g., line 20), race conditions (e.g., mutual exclusion of lines 20 and 33) or registration errors (e.g., signaling a dropped phaser), and (b) plain reachability as in deadlocks (e.g., a producer at line 19 and a consumer at line 30 with equal phases waiting for each other). Both problems deal with reachability of sets of configurations. The difference is that control state reachability defines the targets with the states of the tasks (their control locations and whether they are registered to some phasers). Plain reachability can, in addition, constrain values of the phases in the target configurations (e.g., requiring equality between wait and signal values for deadlocks).
3 Phaser Programs and Reachability
We describe syntax and semantics of a core language. We make sure the language is representative of general purpose languages with phasers so that our results have a practical impact. A phaser program \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \) involves a set \(\mathtt {T}\) of tasks including a unique “main” task \(\mathtt {main()\{\mathtt {stmt}\}}\). Arbitrary many instances of each task might be spawned during a program execution. All task instances share a set \( \mathtt {B}\) of Boolean variables and make use of a set \(\mathtt {V}\) of phaser variables that are local to individual task instances. Arbitrary many phasers might also be generated during program execution. Syntax of programs is as follows.

Initially, a unique task instance starts executing the \(\mathtt {main()\{\mathtt {stmt}\}}\) task. A phaser can recall a pair of values (i.e., wait and signal) for each task instance registered to it. A task instance can create a new phaser with \(\mathtt {v}=\mathtt {newPhaser()}\), get registered to it (i.e., gets zero as wait and signal values associated to the new phaser) and refer to the phaser with its local variable \(\mathtt {v}\). We simplify the presentation by assuming all registrations to be in \(\mathrm {\textsc {Sig\_Wait}}\) mode. Including the other modes is a matter of depriving \(\mathrm {\textsc {Wait}}\)-registered tasks of a signal value (to ensure they do not block other registered tasks) and of ensuring issued commands respect registration modes. We use \(\mathtt {V}\) for the union of all local phaser variables. A task \(\mathtt {task}(\mathtt {v}_{1},\ldots ,\mathtt {v}_{k}) \left\{ {\mathtt {stmt}}\right\} \) in \(\mathtt {T}\) takes the phaser variables \(\mathtt {v}_1, \ldots \mathtt {v}_k\) as parameters (write \(\mathtt {paramOf}(\mathtt {task})\) to mean these parameters). A task instance can spawn another task instance with \(\mathtt {asynch(\mathtt {task},\mathtt {v}_1,\ldots ,\mathtt {v}_n)}\). The issuing task instance registers the spawned task to the phasers pointed to by \(\mathtt {v}_1,\ldots ,\mathtt {v}_n\), with its own wait and signal values. Spawner and Spawnee execute concurrently. A task instance can deregister itself from a phaser with \(\mathtt {v}\mathtt {.drop()}\).
A task instance can issue signal or wait commands on a phaser referenced by \(\mathtt {v}\) and on which it is registered. A wait command on a phaser blocks until the wait value of the task instance executing the wait on the phaser is strictly smaller than the signal value of all task instances registered to the phaser. In other words, \(\mathtt {v}.\texttt {wait()}\) blocks if \(\mathtt {v}\) points to a phaser such that at least one of the signal values stored by the phaser is equal to the wait value of the task that tries to perform the wait. A signal command does not block. It only increments the signal value of the task instance executing the signal command on the phaser. \(\mathtt {v}.\mathtt {next()}\) is syntactic sugar for a signal followed by a wait. Moreover, \(\mathtt {v}.\mathtt {next()\{\mathtt {stmt}\}}\) is similar to \(\mathtt {v}.\mathtt {next()}\) but the block of code \(\mathtt {stmt}\) is executed atomically by exactly one of the tasks participating in the synchronization before all tasks continue the execution that follows the barrier. \(\mathtt {v}.\mathtt {next()\{\mathtt {stmt}\}}\) thus requires all tasks to be synchronized on exactly the same statement and is less flexible. Absence of a \(\mathtt {v}.\mathtt {next()\{\mathtt {stmt}\}}\) makes a program non-atomic.
Note that assignment of phaser variables is excluded from the syntax; additionally, we restrict task creation \(\mathtt {asynch(\mathtt {task},\mathtt {v}_1,\ldots ,\mathtt {v}_n)}\) and require that parameter variables \(\mathtt {v}_i\) are all different. This prevents two variables from pointing to the same phaser and avoids the need to deal with aliasing: we can reason on the single variable in a process that points to a phaser. Extending our work to deal with aliasing is easy but would require heavier notations.
We will need the notions of configurations, partial configurations and inclusion in order to define the reachability problems we consider in this work. We introduce them in the following and assume a phaser program \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \).
Configurations. Configurations of a phaser program describe valuations of its variables, control sequences of its tasks and registration details to the phasers.
Control sequences. We define the set \(\mathtt {Suff}\) of control sequences of \(\mathtt {prg}\) to be the set of suffixes of all sequences \(\mathtt {stmt}\) appearing in some statement \(\mathtt {task}(\ldots )\left\{ {\mathtt {stmt}}\right\} \). In addition, we define \(\mathtt {UnrSuff}\) to be the smallest set containing \(\mathtt {Suff}\) in addition to the suffixes of all (i) \(\mathtt {s}_1;\mathtt {while(\mathtt {cond})\left\{ { \mathtt {s}_1 }\right\} };\mathtt {s}_2\) if \(\mathtt {while(\mathtt {cond})\left\{ { \mathtt {s}_1 }\right\} };\mathtt {s}_2\) is in \(\mathtt {UnrSuff}\), and of all (ii) \(\mathtt {s}_1;\mathtt {s}_2\) if \(\mathtt {if(\mathtt {cond}) \left\{ { \mathtt {s}_1 }\right\} };\mathtt {s}_2\) is in \(\mathtt {UnrSuff}\), and of all (iii) \(\mathtt {s}_1;\mathtt {v}.\mathtt {next()\{\}};\mathtt {s}_2\) if \(\mathtt {v}.\mathtt {next()\{\mathtt {s}_1\}};\mathtt {s}_2\) in \(\mathtt {UnrSuff}\), and finally of all (iv) \(\mathtt {v}.\mathtt {signal()};\mathtt {v}.\texttt {wait()}{};\mathtt {s}_2\) if \(\mathtt {v}.\mathtt {next()\{\}};\mathtt {s}_2\) is in \(\mathtt {UnrSuff}\). We write \(\mathtt {hd}(\mathtt {s})\) and \(\mathtt {tl}(\mathtt {s})\) to respectively mean the head and the tail of a sequence \(\mathtt {s}\).
Partial configurations. Partial configurations allow the characterization of sets of configurations by partially stating some of their common characteristics. A partial configuration \(c\) of \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \) is a tuple  where:
where:
-
 is a finite set of task identifiers. We let \(t,u\) range over the values in
is a finite set of task identifiers. We let \(t,u\) range over the values in  .
. -
 is a finite set of phaser identifiers. We let \(p,q\) range over the values in
is a finite set of phaser identifiers. We let \(p,q\) range over the values in 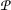 .
. -
 fixes the values of some of the shared variables.Footnote 1
fixes the values of some of the shared variables.Footnote 1
-
 fixes the control sequences of some of the tasks.
fixes the control sequences of some of the tasks. -
 is a mapping that associates to each task \(t\) in
is a mapping that associates to each task \(t\) in  a partial mapping stating which phasers are known by the task and with which registration values.
a partial mapping stating which phasers are known by the task and with which registration values.
Intuitively, partial configurations are used to state some facts about the valuations of variables and the control sequences of tasks and their registrations. Partial configurations leave some details unconstrained using partial mappings or the symbol \(*\). For instance, if  in a partial configuration
in a partial configuration  , then the partial configuration does not constrain the value of the shared variable \(\mathtt {b}\). Moreover, a partial configuration does not constrain the relation between a task \(t\) and a phaser \(p\) when
, then the partial configuration does not constrain the value of the shared variable \(\mathtt {b}\). Moreover, a partial configuration does not constrain the relation between a task \(t\) and a phaser \(p\) when  is undefined. Instead, when the partial mapping
is undefined. Instead, when the partial mapping  is defined on phaser \(p\), it associates a pair
is defined on phaser \(p\), it associates a pair  to \(p\). If \(\mathtt {var}\in {\mathtt {V}}^{\left\{ {-,*}\right\} }\) is a variable \(\mathtt {v}\in \mathtt {V}\) then the task \(t\) in
to \(p\). If \(\mathtt {var}\in {\mathtt {V}}^{\left\{ {-,*}\right\} }\) is a variable \(\mathtt {v}\in \mathtt {V}\) then the task \(t\) in  uses its variable \(\mathtt {v}\) to refer to the phaser \(p\) in
uses its variable \(\mathtt {v}\) to refer to the phaser \(p\) in  Footnote 2. If \(\mathtt {var}\) is the symbol − then the task \(t\) does not refer to \(\mathtt {v}\) with any of its variables in \(\mathtt {V}\). If \(\mathtt {var}\) is the symbol \(*\), then the task might or might not refer to \(p\). The value \(\mathtt {val}\) in
Footnote 2. If \(\mathtt {var}\) is the symbol − then the task \(t\) does not refer to \(\mathtt {v}\) with any of its variables in \(\mathtt {V}\). If \(\mathtt {var}\) is the symbol \(*\), then the task might or might not refer to \(p\). The value \(\mathtt {val}\) in  is either the value \(\mathtt {nreg}\) or a pair \((w_{}^{},s_{}^{})\). The value \(\mathtt {nreg}\) means the task \(t\) is not registered to phaser \(p\). The pair \((w_{}^{},s_{}^{})\) belongs to \((\mathbb {N}\times \mathbb {N})\cup \left\{ {(*,*)}\right\} \). In this case, task \(t\) is registered to phaser \(p\) with a wait phase \(w_{}^{}\) and a signal phase \(s_{}^{}\). The value \(*\) means that the wait phase \(w_{}^{}\) (resp. signal phase \(s_{}^{}\)) can be any value in \(\mathbb {N}\). For instance,
is either the value \(\mathtt {nreg}\) or a pair \((w_{}^{},s_{}^{})\). The value \(\mathtt {nreg}\) means the task \(t\) is not registered to phaser \(p\). The pair \((w_{}^{},s_{}^{})\) belongs to \((\mathbb {N}\times \mathbb {N})\cup \left\{ {(*,*)}\right\} \). In this case, task \(t\) is registered to phaser \(p\) with a wait phase \(w_{}^{}\) and a signal phase \(s_{}^{}\). The value \(*\) means that the wait phase \(w_{}^{}\) (resp. signal phase \(s_{}^{}\)) can be any value in \(\mathbb {N}\). For instance,  means variable \(\mathtt {v}\) of the task \(t\) refers to phaser \(p\) but the task is not registered to \(p\). On the other hand,
means variable \(\mathtt {v}\) of the task \(t\) refers to phaser \(p\) but the task is not registered to \(p\). On the other hand,  means the task \(t\) does not refer to \(p\) but is registered to it with arbitrary wait and signal phases.
means the task \(t\) does not refer to \(p\) but is registered to it with arbitrary wait and signal phases.
Concrete configurations. A concrete configuration (or configuration for short) is a partial configuration  where
where  is total for each
is total for each  and where the symbol \(*\) does not appear in any range. It is a tuple
and where the symbol \(*\) does not appear in any range. It is a tuple  where
where  ,
,  , and
, and  . For a concrete configuration
. For a concrete configuration  , we write
, we write  to mean the predicate
to mean the predicate  . The predicate
. The predicate  captures whether the task \(t\) is registered to phaser \(p\) according to the mapping
captures whether the task \(t\) is registered to phaser \(p\) according to the mapping  .
.
Inclusion of configurations. A configuration  includes a partial configuration
includes a partial configuration  if renaming and deleting tasks and phasers from \(c'\) can give a configuration that “matches” \(c\). More formally, \(c'\) includes \(c\) if
if renaming and deleting tasks and phasers from \(c'\) can give a configuration that “matches” \(c\). More formally, \(c'\) includes \(c\) if  for each \(\mathtt {b}\in \mathtt {B}\) and there are injections
for each \(\mathtt {b}\in \mathtt {B}\) and there are injections  and
and  s.t. for each
s.t. for each  and
and  : (1)
: (1)  , and either (2.a)
, and either (2.a)  is undefined, or (2.b)
is undefined, or (2.b)  and
and  with \(((var\ne var')\implies (var=*))\) and either \((val=val'=\mathtt {nreg})\) or \(val=(w_{}^{},s_{}^{})\) and \(val'=({w'}_{}^{},{s'}_{}^{})\) with \(((w_{}^{}\ne {w'}_{}^{}) \implies (w_{}^{}=*))\) and \(((s_{}^{}\ne {s'}_{}^{}) \implies (s_{}^{}=*))\).
with \(((var\ne var')\implies (var=*))\) and either \((val=val'=\mathtt {nreg})\) or \(val=(w_{}^{},s_{}^{})\) and \(val'=({w'}_{}^{},{s'}_{}^{})\) with \(((w_{}^{}\ne {w'}_{}^{}) \implies (w_{}^{}=*))\) and \(((s_{}^{}\ne {s'}_{}^{}) \implies (s_{}^{}=*))\).
Semantics and reachability. Given a program \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \), the main task \(\mathtt {main()\{\mathtt {stmt}\}}\) starts executing \(\mathtt {stmt}\) from an initial configuration  where
where  is a singleton,
is a singleton,  is empty,
is empty,  sends all shared variables to \(\mathtt {false}\) and
sends all shared variables to \(\mathtt {false}\) and  associates \(\mathtt {stmt}\) to the unique task in
associates \(\mathtt {stmt}\) to the unique task in  . We write \(c\xrightarrow [\mathtt {stmt}]{t} c'\) to mean a task \(t\) in \(c\) can fire statement \(\mathtt {stmt}\) resulting in configuration \(c'\). See Fig. 3 for a description of phaser semantics. We write \(c\xrightarrow [\mathtt {stmt}]{} c'\) if \(c\xrightarrow [\mathtt {stmt}]{t} c'\) for some task \(t\) and \(c\xrightarrow []{} c'\) if \(c\xrightarrow [\mathtt {stmt}]{} c'\) for some \(\mathtt {stmt}\). We write \(\xrightarrow [\mathtt {stmt}]{}^+\) for the transitive closure of \(\xrightarrow [\mathtt {stmt}]{}\) and let \({\xrightarrow []{}}^*\) be the reflexive transitive closure of \(\xrightarrow []{}\). Figure 2 identifies erroneous configurations.
. We write \(c\xrightarrow [\mathtt {stmt}]{t} c'\) to mean a task \(t\) in \(c\) can fire statement \(\mathtt {stmt}\) resulting in configuration \(c'\). See Fig. 3 for a description of phaser semantics. We write \(c\xrightarrow [\mathtt {stmt}]{} c'\) if \(c\xrightarrow [\mathtt {stmt}]{t} c'\) for some task \(t\) and \(c\xrightarrow []{} c'\) if \(c\xrightarrow [\mathtt {stmt}]{} c'\) for some \(\mathtt {stmt}\). We write \(\xrightarrow [\mathtt {stmt}]{}^+\) for the transitive closure of \(\xrightarrow [\mathtt {stmt}]{}\) and let \({\xrightarrow []{}}^*\) be the reflexive transitive closure of \(\xrightarrow []{}\). Figure 2 identifies erroneous configurations.
Operational semantics of phaser statements. Each transition corresponds to a task  executing a statement from a configuration
executing a statement from a configuration  . For instance, the \(\mathtt {drop}\) transition corresponds to a task \(t\) executing \(\mathtt {v}\mathtt {.drop()}\) when registered to phaser
. For instance, the \(\mathtt {drop}\) transition corresponds to a task \(t\) executing \(\mathtt {v}\mathtt {.drop()}\) when registered to phaser  (with phases \((w_{}^{},s_{}^{})\)) and refering to it with variable \(\mathtt {v}\). The result is the same configuration where task \(t\) moves to its next statement without being registered to \(p\).
(with phases \((w_{}^{},s_{}^{})\)) and refering to it with variable \(\mathtt {v}\). The result is the same configuration where task \(t\) moves to its next statement without being registered to \(p\).
We are interested in the reachability of sets of configurations (i.e., checking safety properties). We differentiate between two reachability problems depending on whether the target sets of configurations constrain the registration phases or not. The plain reachability problem may constrains the registration phases of the target configurations. The control reachability problem may not. We will see that decidability of the two problems can be different. The two problems are defined in the following.
Plain reachability. First, we define equivalent configurations. A configuration  is equivalent to configuration
is equivalent to configuration  if
if  and there are bijections
and there are bijections  and
and  such that, for all
such that, for all  ,
,  and \(var\in {\mathtt {V}}^{\left\{ {-}\right\} }\),
and \(var\in {\mathtt {V}}^{\left\{ {-}\right\} }\),  and there are some integers
and there are some integers  such that
such that  iff
iff  . We write \(c\sim c'\) to mean that \(c\) and \(c'\) are equivalent. Intuitively, equivalent configurations simulate each other. We can establish the following:
. We write \(c\sim c'\) to mean that \(c\) and \(c'\) are equivalent. Intuitively, equivalent configurations simulate each other. We can establish the following:
Lemma 1
(Equivalence). Assume two configurations \(c_1\) and \(c_2\). If \(c_1\xrightarrow []{}c_2\) and \(c_1'\sim c_1\) then there is a configuration \(c_2'\) s.t. \(c_2'\sim c_2\) and \(c_1'\xrightarrow []{}c_2'\).
Observe that if the wait value of a task \(t\) on a phaser \(p\) is equal to the signal of a task \(t'\) on the same phaser \(p\) in some configuration \(c\), then this is also the case, up to a renaming of the phasers and tasks, in all equivalent configurations. This is particularly relevant for defining deadlock configurations where a number of tasks are waiting for each other. The plain reachability problem is given a program and a target partial configuration and asks whether a configuration (equivalent to a configuration) that includes the target partial configuration is reachable.
More formally, given a program \(\mathtt {prg}\) and a partial configuration \(c\), let \(c_{init}\) be the initial configuration of \(\mathtt {prg}\), then \(\mathtt {reach}(\mathtt {prg},c)\) if and only if \(c_{init}\xrightarrow []{}^* c_1\) for \(c_1\sim c_2\) and \(c_2\) includes \(c\).
Definition 1
(Plain reachability). For a program \(\mathtt {prg}\) and a partial configuration \(c\), decide whether \(\mathtt {reach}(\mathtt {prg},c)\) holds.
Control reachability. A partial configuration  is said to be a control partial configuration if for all
is said to be a control partial configuration if for all  and
and  , either
, either  is undefined or
is undefined or  . Intuitively, control partial configurations do not constrain phase values. They are enough to characterize, for example, configurations where an assertion is violated (see Fig. 2).
. Intuitively, control partial configurations do not constrain phase values. They are enough to characterize, for example, configurations where an assertion is violated (see Fig. 2).
Definition 2
(Control reachability). For a program \(\mathtt {prg}\) and a control partial configuration \(c\), decide whether \(\mathtt {reach}(\mathtt {prg},c)\) holds.
Observe that plain reachability is at least as hard to answer as control reachability since any control partial configuration is also a partial configuration. It turns out the control reachability problem is undecidable for programs resulting in arbitrarily many tasks and phasers as stated by the theorem below. This is proven by reduction of the state reachability problem for 2-counter Minsky machines. A 2-counter Minsky machine \(\left( {S,\left\{ {x_1,x_2}\right\} ,\varDelta ,s_0,s_F}\right) \) has a finite set S of states, two counters \(\left\{ {x_1,x_2}\right\} \) with values in \(\mathbb {N}\), an initial state \(s_0\) and a final state \(s_F\). Transitions may increment, decrement or test a counter. For example \(\left( {s_0,\text {test}(x_1),s_F}\right) \) takes the machine from \(s_0\) to \(s_F\) if the counter \(x_1\) is zero.
Theorem 1
(Minsky machines [14]). Checking whether \(s_F\) is reachable from configuration \((s_0,0,0)\) for 2-counter machines is undecidable in general.
Theorem 2
Control reachability is undecidable in general.
Proof sketch. State reachability of an arbitrary 2-counters Minsky machine is encoded as the control reachability problem of a phaser program. The phaser program (see [10]) has three tasks \(\mathtt {main}\), \(\mathtt {xUnit}\) and \(\mathtt {yUnit}\). It uses Boolean shared variables to encode the state \(s\in S\) and to pass information between different task instances. The phaser program builds two chains, one with \(\mathtt {xUnit}\) instances for the x-counter, and one with \(\mathtt {yUnit}\) instances for the y-counter. Each chain alternates a phaser and a task and encodes the values of its counter with its length. The idea is to have the phaser program simulate all transitions of the counter machine, i.e., increments, decrements and tests for zero. Answering state reachability of the counter machine amounts to checking whether there are reachable configurations where the boolean variables encoding the counter machine can evaluate to the target machine state \(s_F\).
4 A Gap-Based Symbolic Representation
The symbolic representation we propose builds on the following intuitions. First, observe the language semantics impose, for each phaser, the invariant that signal values are always larger or equal to wait values. We can therefore assume this fact in our symbolic representation. In addition, our reachability problems from Sect. 3 are defined in terms of reachability of equivalence classes, not of individual configurations. This is because configurations violating considered properties (see Fig. 2) are not defined in terms of concrete phase values but rather in terms of relations among them (in addition to the registration status, control sequences and variable values). Finally, we observe that if a wait is enabled with smaller gaps on a given phaser, then it will be enabled with larger ones. We therefore propose to track the gaps of the differences between signal and wait values wrt. to an existentially quantified level (per phaser) that lies between wait and signal values of all tasks registered to the considered phaser.
We formally define our symbolic representation and describe a corresponding entailment relation. We also establish a desirable property (namely being a \(\mathcal {WQO}\), i.e., well-quasi-ordering [1, 8]) on some classes of representations. This is crucial for the decidability of certain reachability problems (see Sect. 5).
Named gaps. A named gap is associated to a task-phaser pair. It consists in a tuple (var, val) in \(\mathbb {G}=\left( {{\mathtt {V}}^{\left\{ {-,*}\right\} } \times \left( \left( \mathbb {N}^4 \cup \left( \mathbb {N}^2\times \left\{ {\infty }\right\} ^2\right) \right) \cup \left\{ {\mathtt {nreg}}\right\} \right) } \right) \). Like for partial configurations in Sect. 3, \(var\in {\mathtt {V}}^{\left\{ {-,*}\right\} }\) constrains variable values. The val value describes task registration to the phaser. If registered, then val is a 4-tuple \((\mathtt {lw},\mathtt {ls},\mathtt {uw},\mathtt {us})\). This intuitively captures, together with some level l common to all tasks registered to the considered phaser, all concrete wait and signal values \((w_{}^{},s_{}^{})\) satisfying \(\mathtt {lw}\le (l-w_{}^{}) \le \mathtt {uw}\) and \(\mathtt {ls}\le (s_{}^{}-l)\le \mathtt {us}\). A named gap \((var,(\mathtt {lw},\mathtt {ls},\mathtt {uw},\mathtt {us}))\) is said to be free if \(\mathtt {uw}=\mathtt {us}=\infty \). It is said to be B-gap-bounded, for \(B\in \mathbb {N}\), if both \(\mathtt {uw}\le B\) and \(\mathtt {us}\le B\) hold. A set  is said to be free (resp. B-gap-bounded) if all its named gaps are free (resp. B-gap-bounded). The set
is said to be free (resp. B-gap-bounded) if all its named gaps are free (resp. B-gap-bounded). The set  is said to be B-good if each one of its named gaps is either free or B-gap-bounded. Finally,
is said to be B-good if each one of its named gaps is either free or B-gap-bounded. Finally,  is said to be good if it is B-good for some \(B\in \mathbb {N}\). Given a set
is said to be good if it is B-good for some \(B\in \mathbb {N}\). Given a set  of named gaps, we define the partial order \(\unlhd \) on
of named gaps, we define the partial order \(\unlhd \) on  , and write \((var,val) \unlhd (var',val')\), to mean (i) \(\left( var\ne var'\Rightarrow var=*\right) \), and (ii) \((val = \mathtt {nreg}) \Longleftrightarrow (val' = \mathtt {nreg})\), and (iii) if \(val=(\mathtt {lw},\mathtt {ls},\mathtt {uw},\mathtt {us})\) and \(val'=(\mathtt {lw}',\mathtt {ls}',\mathtt {uw}',\mathtt {us}')\) then \(\mathtt {lw}\le \mathtt {lw}'\), \(\mathtt {ls}\le \mathtt {ls}'\), \(\mathtt {uw}' \le \mathtt {uw}\) and \(\mathtt {us}' \le \mathtt {us}\). Intuitively, named gaps are used in the definition of constraints to capture relations (i.e., reference, registration and possible phases) of tasks and phasers. The partial order \((var,val) \unlhd (var',val')\) ensures relations allowed by \((var',val')\) are also allowed by (var, val).
, and write \((var,val) \unlhd (var',val')\), to mean (i) \(\left( var\ne var'\Rightarrow var=*\right) \), and (ii) \((val = \mathtt {nreg}) \Longleftrightarrow (val' = \mathtt {nreg})\), and (iii) if \(val=(\mathtt {lw},\mathtt {ls},\mathtt {uw},\mathtt {us})\) and \(val'=(\mathtt {lw}',\mathtt {ls}',\mathtt {uw}',\mathtt {us}')\) then \(\mathtt {lw}\le \mathtt {lw}'\), \(\mathtt {ls}\le \mathtt {ls}'\), \(\mathtt {uw}' \le \mathtt {uw}\) and \(\mathtt {us}' \le \mathtt {us}\). Intuitively, named gaps are used in the definition of constraints to capture relations (i.e., reference, registration and possible phases) of tasks and phasers. The partial order \((var,val) \unlhd (var',val')\) ensures relations allowed by \((var',val')\) are also allowed by (var, val).
Constraints. A constraint \(\phi \) of \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \) is a tuple  that denotes a possibly infinite set of configurations. Intuitively,
that denotes a possibly infinite set of configurations. Intuitively,  and
and  respectively represent a minimal set of tasks and phasers that are required in any configuration denoted by the constraint. In addition:
respectively represent a minimal set of tasks and phasers that are required in any configuration denoted by the constraint. In addition:
-
 and
and  respectively represent, like for partial configurations, a valuation of the shared Boolean variables and a mapping of tasks to their control sequences.
respectively represent, like for partial configurations, a valuation of the shared Boolean variables and a mapping of tasks to their control sequences. -
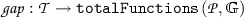 constrains relations between
constrains relations between  -tasks and
-tasks and  -phasers by associating to each task \(t\) a mapping
-phasers by associating to each task \(t\) a mapping  that defines for each phaser \(p\) a named gap \((var,val)\in \mathbb {G}\) capturing the relation of \(t\) and \(p\).
that defines for each phaser \(p\) a named gap \((var,val)\in \mathbb {G}\) capturing the relation of \(t\) and \(p\). -
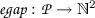 associates lower bounds \((\mathtt {ew},\mathtt {es})\) on gaps of tasks that are registered to
associates lower bounds \((\mathtt {ew},\mathtt {es})\) on gaps of tasks that are registered to  -phasers but which are not explicitly captured by
-phasers but which are not explicitly captured by  . This is described further in the constraints denotations below.
. This is described further in the constraints denotations below.
We write  to mean the task \(t\) is registered to the phaser \(p\), i.e.,
to mean the task \(t\) is registered to the phaser \(p\), i.e.,  . A constraint \(\phi \) is said to be free (resp. B-gap-bounded or B-good) if the set
. A constraint \(\phi \) is said to be free (resp. B-gap-bounded or B-good) if the set  is free (resp. B-gap-bounded or B-good). The dimension of a constraint is the number of phasers it requires (i.e.,
is free (resp. B-gap-bounded or B-good). The dimension of a constraint is the number of phasers it requires (i.e.,  ). A set of constraints \(\varPhi \) is said to be free, B-gap-bounded, B-good or K-dimension-bounded if each of its constraints are.
). A set of constraints \(\varPhi \) is said to be free, B-gap-bounded, B-good or K-dimension-bounded if each of its constraints are.
Denotations. We write  to mean constraint
to mean constraint 
 denotes configuration
denotes configuration  . Intuitively, the configuration \(c\) should have at least as many tasks (captured by a surjection \(\tau \) from a subset
. Intuitively, the configuration \(c\) should have at least as many tasks (captured by a surjection \(\tau \) from a subset  of
of  to
to  ) and phasers (captured by a bijection \(\pi \) from a subset
) and phasers (captured by a bijection \(\pi \) from a subset  of
of  to
to  ). Constraints on the tasks and phasers in
). Constraints on the tasks and phasers in  and
and  ensure target configurations are reachable. Additional constraints on the tasks in
ensure target configurations are reachable. Additional constraints on the tasks in  ensure this reachability is not blocked by tasks not captured by
ensure this reachability is not blocked by tasks not captured by  . More formally:
. More formally:
-
1.
for each \(\mathtt {b}\in \mathtt {B}\),
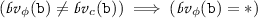 , and
, and -
2.
 and
and  can be written as
can be written as  and
and  , with
, with -
3.
 is a surjection and
is a surjection and  is a bijection, and
is a bijection, and -
4.
for
 with \(t_\phi =\tau (t_c)\),
with \(t_\phi =\tau (t_c)\),  , and
, and -
5.
for each \(p_\phi =\pi (p_c)\), there is a natural level
 such that:
such that:-
(a)
if
 with \(t_\phi =\tau (t_c)\),
with \(t_\phi =\tau (t_c)\),  and
and  , then it is the case that:
, then it is the case that:-
i.
\((var_c\ne var_\phi ) \implies (var_\phi =*)\), and
-
ii.
\((val_c=\mathtt {nreg}) \Longleftrightarrow (val_\phi =\mathtt {nreg})\), and
-
iii.
if \((val_c=(w_{}^{},s_{}^{}))\) and \((val_\phi =(\mathtt {lw},\mathtt {ls},\mathtt {uw},\mathtt {us}))\) then
 and
and  .
.
-
i.
-
(b)
if
 , then for each \(p_\phi =\pi (p_c)\) with
, then for each \(p_\phi =\pi (p_c)\) with  and
and  , we have:
, we have:  and
and 
-
(a)
Intuitively, for each phaser, the bounds given by  constrain the values of the phases belonging to tasks captured by
constrain the values of the phases belonging to tasks captured by  (i.e., those in
(i.e., those in  ) and registered to the given phaser. This is done with respect to some non-negative level, one per phaser. The same level is used to constrain phases of tasks registered to the phaser but not captured by
) and registered to the given phaser. This is done with respect to some non-negative level, one per phaser. The same level is used to constrain phases of tasks registered to the phaser but not captured by  (i.e., those in
(i.e., those in  ). For these tasks, lower bounds are enough as we only want to ensure they do not block executions to target sets of configurations. We write \([\![{\phi }]\!]\) for
). For these tasks, lower bounds are enough as we only want to ensure they do not block executions to target sets of configurations. We write \([\![{\phi }]\!]\) for  .
.
Entailment. We write \(\phi _a\sqsubseteq \phi _b\) to mean  is entailed by
is entailed by  . This will ensure that configurations denoted by \(\phi _b\) are also denoted by \(\phi _a\). Intuitively, \(\phi _b\) should have at least as many tasks (captured by a surjection \(\tau \) from a subset
. This will ensure that configurations denoted by \(\phi _b\) are also denoted by \(\phi _a\). Intuitively, \(\phi _b\) should have at least as many tasks (captured by a surjection \(\tau \) from a subset  of
of  to
to  ) and phasers (captured by a bijection \(\pi \) from a subset
) and phasers (captured by a bijection \(\pi \) from a subset  of
of  to
to  ). Conditions on tasks and phasers in
). Conditions on tasks and phasers in  and
and  ensure the conditions in \(\phi _a\) are met. Additional conditions on the tasks in
ensure the conditions in \(\phi _a\) are met. Additional conditions on the tasks in  ensure at least the
ensure at least the  conditions in \(\phi _a\) are met. More formally:
conditions in \(\phi _a\) are met. More formally:
-
1.
 , for each \(\mathtt {b}\in \mathtt {B}\) and
, for each \(\mathtt {b}\in \mathtt {B}\) and -
2.
 and
and 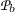 can be written as
can be written as  and
and  with
with -
3.
 is a surjection and
is a surjection and  is a bijection, and
is a bijection, and -
4.
 for each
for each  with \(t_a=\tau (t_b)\), and
with \(t_a=\tau (t_b)\), and -
5.
for each phaser \(p_a=\pi (p_b)\) in
 :
:-
(a)
if
 and
and  then \(\mathtt {ew}_a \le \mathtt {ew}_b\) and \(\mathtt {es}_a\le \mathtt {es}_b\)
then \(\mathtt {ew}_a \le \mathtt {ew}_b\) and \(\mathtt {es}_a\le \mathtt {es}_b\) -
(b)
for each
 with \(t_a=\tau (t_b)\) and
with \(t_a=\tau (t_b)\) and  , and
, and  , it is the case that:
, it is the case that:-
i.
\((var_b \ne var_a) \implies (var_a=*)\), and
-
ii.
\((val_b=\mathtt {nreg}) \Longleftrightarrow (val_a=\mathtt {nreg})\), and
-
iii.
if \(val_a=(\mathtt {lw}_a,\mathtt {ls}_a,\mathtt {uw}_a,\mathtt {us}_a)\) and \(val_b=(\mathtt {lw}_b,\mathtt {ls}_b,\mathtt {uw}_b,\mathtt {us}_b)\), then \((\mathtt {lw}_a \le \mathtt {lw}_b)\), \((\mathtt {ls}_a \le \mathtt {ls}_b)\), \((\mathtt {uw}_b \le \mathtt {uw}_a)\) and \((\mathtt {us}_b \le \mathtt {us}_a)\).
-
i.
-
(c)
for each
 with
with  , with
, with  , both \((\mathtt {ew}_a \le \mathtt {lw}_b)\) and \((\mathtt {es}_a \le \mathtt {ls}_b)\) hold.
, both \((\mathtt {ew}_a \le \mathtt {lw}_b)\) and \((\mathtt {es}_a \le \mathtt {ls}_b)\) hold.
-
(a)
The following lemma shows that it is safe to eliminate entailing constraints in the working list procedure of Sect. 5.
Lemma 2
(Constraint entailment). \(\phi _a\sqsubseteq \phi _b\) implies \([\![{\phi _b}]\!]\subseteq [\![{\phi _a}]\!]\)
A central contribution that allows establishing the positive results of Sect. 5 is to show \(\sqsubseteq \) is actually \(\mathcal {WQO}\) on any K-dimension-bounded and B-good set of constraints. For this, we prove  is \(\mathcal {WQO}\) if
is \(\mathcal {WQO}\) if  is B-good, where
is B-good, where  is the set of multisets over
is the set of multisets over  and \(M{{~}_\exists \!\!\preceq _\forall }\ M'\) requires each \((\mathtt {s}',g'_1,\ldots ,g'_K)\in M'\) may be mapped to some \((\mathtt {s},g_1,\ldots ,g_K)\in M\) for which \(\mathtt {s}=\mathtt {s}'\) and \(g_i \unlhd g_i'\) for each \(i:1\le i \le K\) (written
and \(M{{~}_\exists \!\!\preceq _\forall }\ M'\) requires each \((\mathtt {s}',g'_1,\ldots ,g'_K)\in M'\) may be mapped to some \((\mathtt {s},g_1,\ldots ,g_K)\in M\) for which \(\mathtt {s}=\mathtt {s}'\) and \(g_i \unlhd g_i'\) for each \(i:1\le i \le K\) (written  ). Intuitively, we need to use \({{~}_\exists \!\!\preceq _\forall }\), and not simply \({{~}_\forall \!\!\preceq _\exists }\), in order to “cover all registered tasks” in the larger constraint as otherwise some tasks may block the path to the target configurations. Rado’s structure [12, 13] shows that, in general, \((\mathcal {M}\left( {S}\right) ,{{~}_\exists \!\!\preceq _\forall })\) need not be \(\mathcal {WQO}\) just because \(\preceq \) is \(\mathcal {WQO}\) over S. The proof details can be found in [10].
). Intuitively, we need to use \({{~}_\exists \!\!\preceq _\forall }\), and not simply \({{~}_\forall \!\!\preceq _\exists }\), in order to “cover all registered tasks” in the larger constraint as otherwise some tasks may block the path to the target configurations. Rado’s structure [12, 13] shows that, in general, \((\mathcal {M}\left( {S}\right) ,{{~}_\exists \!\!\preceq _\forall })\) need not be \(\mathcal {WQO}\) just because \(\preceq \) is \(\mathcal {WQO}\) over S. The proof details can be found in [10].
Theorem 3
\((\varPhi ,\sqsubseteq )\) is \(\mathcal {WQO}\) if \(\varPhi \) is K-dimension-bounded and B-good for some pre-defined \(K,B\in \mathbb {N}\).
5 A Symbolic Verification Procedure
We use the constraints defined in Sect. 4 as a symbolic representation in an instantiation of the classical framework of Well-Structured-Transition-Systems [1, 8]. The instantiation (described in [10]) is a working-list procedure that takes as arguments a program \(\mathtt {prg}\) and a \(\sqsubseteq \)-minimal set \(\varPhi \) of constraints denoting the targeted set of configurations. Such constraints can be easily built from the partial configurations described in Fig. 2.
The procedure computes a fixpoint using the entailment relation of Sect. 4 and a predecessor computation that results, for a constraint \(\phi \) and a statement \(\mathtt {stmt}\), in a finite set  . Figure 4 describes part of the computation for the \(\mathtt {v}.\mathtt {signal()}\) instruction (see [10] for other instructions). For all but atomic statements, the set
. Figure 4 describes part of the computation for the \(\mathtt {v}.\mathtt {signal()}\) instruction (see [10] for other instructions). For all but atomic statements, the set  is exact in the sense that \(\left\{ {c' ~|~c\in [\![{\phi }]\!] \text { and } c'\xrightarrow [\mathtt {stmt}]{}{}c }\right\} \subseteq \bigcup _{\phi '\in \mathtt {pre_\mathtt {stmt}}}[\![{\phi '}]\!] \subseteq \left\{ {c' ~|~c\in [\![{\phi }]\!] \text { and } c'\xrightarrow [\mathtt {stmt}]{}^+c }\right\} \). Intuitively, the predecessors calculation for the atomic \(\mathtt {v}.\mathtt {next()\{\mathtt {stmt}\}}\) is only an over-approximation because such an instruction can encode a test-and-set operation. Our representation allows for more tasks, but the additional tasks may not be able to carry the atomic operation. We would therefore obtain a non-exact over-approximation and avoid this issue by only applying the procedure to non-atomic programs. We can show the following theorems.
is exact in the sense that \(\left\{ {c' ~|~c\in [\![{\phi }]\!] \text { and } c'\xrightarrow [\mathtt {stmt}]{}{}c }\right\} \subseteq \bigcup _{\phi '\in \mathtt {pre_\mathtt {stmt}}}[\![{\phi '}]\!] \subseteq \left\{ {c' ~|~c\in [\![{\phi }]\!] \text { and } c'\xrightarrow [\mathtt {stmt}]{}^+c }\right\} \). Intuitively, the predecessors calculation for the atomic \(\mathtt {v}.\mathtt {next()\{\mathtt {stmt}\}}\) is only an over-approximation because such an instruction can encode a test-and-set operation. Our representation allows for more tasks, but the additional tasks may not be able to carry the atomic operation. We would therefore obtain a non-exact over-approximation and avoid this issue by only applying the procedure to non-atomic programs. We can show the following theorems.
Theorem 4
Control reachability is decidable for non-atomic phaser programs generating a finite number of phasers.
The idea is to systematically drop, in the instantiated backward procedure, constraints violating K-dimension-boundedness (as none of the denoted configurations is reachable). Also, the set of target constraints is free (since we are checking control reachability) and this is preserved by the predecessors computation (see [10]). Finally, we use the exactness of the \(\mathtt {pre_\mathtt {stmt}}\) computation, the soundness of the entailment relation and Theorem 3. We can use a similar reasoning for plain reachability of programs generating a finite number of phasers and bounded gap-values for each phaser.
Theorem 5
Plain reachability is decidable for non-atomic phaser programs generating a finite number of phasers with, for each phaser, bounded phase gaps.
6 Limitations of Deciding Reachability
Assume a program \(\mathtt {prg}=\left( {\mathtt {B},\mathtt {V},\mathtt {T}}\right) \) and its initial configuration \(c_{init}\). We show a number of parameterized reachability problems to be undecidable. First, we address checking control reachability when restricting to configurations with at most K task-referenced phasers. We call this K-control-reachability.
Definition 3
(K-control-reachability). Given a partial control configuration \(c\), we write \(\mathtt {reach}_{K}(\mathtt {prg},c)\), and say \(c\) is K-control-reachable, to mean there are \(n+1\) configurations \((c_i)_{i:0\le i\le n}\), each with at most K reachable phasers (i.e., phasers referenced by at least a task variable) s.t. \(c_{init}=c_0\) and \(c_i {\mathop {\longrightarrow }\limits ^{}} c_{i+1}\) for \(i:0 \le i < n - 1\) with \(c_n\) equivalent to a configuration that includes \(c\).
Theorem 6
K-control-reachability is undecidable in general.
Proof sketch. Encode state reachability of an arbitrary Minsky machine with counters x and y using K-control-reachability of a suitable phaser program. The program (see [10]) has five tasks: \(\mathtt {main}\), \(\mathtt {xTask}\), \(\mathtt {yTask}\), \(\mathtt {child1}\) and \(\mathtt {child2}\). Machine states are captured with shared variables and counter values with phasers \(\mathtt {xPh}\) for counter x (resp. \(\mathtt {yPh}\) for counter y). Then, (1) spawn an instance of \(\mathtt {xTask}\) (resp. \(\mathtt {yTask}\)) and register it to \(\mathtt {xPh}\) (resp. \(\mathtt {yPh}\)) for increments, and (2) perform a wait on \(\mathtt {xPh}\) (resp. \(\mathtt {yPh}\)) to test for zero. Decrementing a counter, say x, involves asking an \(\mathtt {xTask}\), via shared variables, to exit (hence, to deregister from \(\mathtt {xPh}\)). However, more than one task might participate in the decrement operation. For this reason, each participating task builds a path from \(\mathtt {xPh}\) to \(\mathtt {child2}\) with two phasers. If more than one \(\mathtt {xTask}\) participates in the decrement, then the number of reachable phasers of an intermediary configuration will be at least five.
Theorem 7
Control reachability is undecidable if atomic statements are allowed even if only a finite number of phasers is generated.
Proof sketch. Encode state reachability of an arbitrary Minsky machine with counters x and y using a phaser program with atomic statements. The phaser program (see [10]) has three tasks: \(\mathtt {main}\), \(\mathtt {xTask}\) and \(\mathtt {yTask}\) and encodes machine states with shared variables. The idea is to associate a phaser \(\mathtt {xPh}\) to counter x (resp. \(\mathtt {yPh}\) to y) and to perform a signal followed by a wait on \(\mathtt {xPh}\) (resp. \(\mathtt {yPh}\)) to test for zero. Incrementing and decrementing is performed by asking spawned tasks to spawn a new instance or to deregister. Atomic-next statements are used to ensure exactly one task is spawned or deregistered.
Finally, even with finite numbers of tasks and phasers, but with arbitrary gap-bounds, we can show [9] the following.
Theorem 8
Plain reachability is undecidable if generated gaps are not bounded even when restricting to non-atomic programs with finite numbers of phasers.
 and undecidable ones with
and undecidable ones with  .
.7 Conclusion
We have studied parameterized plain (e.g., deadlocks) and control (e.g., assertions) reachability problems. We have proposed an exact verification procedure for non-atomic programs. We summarize our findings in Table 1. The procedure is guaranteed to terminate, even for programs that may generate arbitrary many tasks but finitely many phasers, when checking control reachability or when checking plain reachability with bounded gaps. These results were obtained using a non-trivial symbolic representation for which termination had required showing an \({{~}_\exists \!\!\preceq _\forall }\) preorder on multisets on gaps on natural numbers to be a \(\mathcal {WQO}\). We are working on a tool that implements the procedure to verify phaser programs that dynamically spawn tasks. We believe our general decidability results are useful to reason about synchronization constructs other than phasers. For instance, a traditional static barrier can be captured with one phaser and with bounded gaps (in fact one). Similarly, one phaser with one producer and arbitrary many consumers can capture futures where “gets” are modeled with waits. Also, test-and-set operations can model atomic instructions and may result in undecidability of reachability. This suggests more general applications of the work are to be investigated.
Notes
- 1.
For any set S, \({S}^{\left\{ {a,b,...}\right\} }\) denotes \({S}\cup \{a,b,...\}\).
- 2.
The uniqueness of this variable is due to the absence of aliasing discussed above.
References
Abdulla, P.A., Cerans, K., Jonsson, B., Tsay, Y.K.: General decidability theorems for infinite-state systems. In: Proceedings of the Eleventh Annual IEEE Symposium on Logic in Computer Science, LICS 1996, pp. 313–321. IEEE (1996)
Anderson, P., Chase, B., Mercer, E.: JPF verification of Habanero Java programs. SIGSOFT Softw. Eng. Notes 39(1), 1–7 (2014). https://doi.org/10.1145/2557833.2560582. http://doi.acm.org/10.1145/2557833.2560582
de Boer, F.S., Clarke, D., Johnsen, E.B.: A complete guide to the future. In: De Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 316–330. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71316-6_22
Cavé, V., Zhao, J., Shirako, J., Sarkar, V.: Habanero-Java: the new adventures of old x10. In: Proceedings of the 9th International Conference on Principles and Practice of Programming in Java, pp. 51–61. ACM (2011)
Charles, P., et al.: X10: an object-oriented approach to non-uniform cluster computing. SIGPLAN Not. 40(10), 519–538 (2005). https://doi.org/10.1145/1103845.1094852. http://doi.acm.org/10.1145/1103845.1094852
Cogumbreiro, T., Hu, R., Martins, F., Yoshida, N.: Dynamic deadlock verification for general barrier synchronisation. In: 20th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2015, pp. 150–160. ACM, New York (2015). https://doi.org/10.1145/2688500.2688519. http://doi.acm.org/10.1145/2688500.2688519
Cogumbreiro, T., Shirako, J., Sarkar, V.: Formalization of Habanero phasers using Coq. J. Log. Algebraic Methods Program. 90, 50–60 (2017). https://doi.org/10.1016/j.jlamp.2017.02.006. http://www.sciencedirect.com/science/article/pii/S2352220816300839
Finkel, A., Schnoebelen, P.: Well-structured transition systems everywhere!. Theoret. Comput. Sci. 256(1), 63–92 (2001). https://doi.org/10.1016/S0304-3975(00)00102-X. http://www.sciencedirect.com/science/article/pii/S030439750000102X
Ganjei, Z., Rezine, A., Eles, P., Peng, Z.: Safety verification of phaser programs. In: Proceedings of the 17th Conference on Formal Methods in Computer-Aided Design, FMCAD 2017, pp. 68–75. FMCAD Inc., Austin (2017). http://dl.acm.org/citation.cfm?id=3168451.3168471
Ganjei, Z., Rezine, A., Henrio, L., Eles, P., Peng, Z.: On reachability in parameterized phaser programs. arXiv:1811.07142 (2019)
Havelund, K., Pressburger, T.: Model checking Java programs using Java pathfinder. Int. J. Softw. Tools Technol. Transfer (STTT) 2(4), 366–381 (2000)
Jancar, P.: A note on well quasi-orderings for powersets. Inf. Process. Lett. 72(5–6), 155–160 (1999). https://doi.org/10.1016/S0020-0190(99)00149-0
Marcone, A.: Fine analysis of the quasi-orderings on the power set. Order 18(4), 339–347 (2001). https://doi.org/10.1023/A:1013952225669
Minsky, M.L.: Computation: Finite and Infinite Machines. Prentice-Hall Inc., Englewood Cliffs (1967)
Shirako, J., Peixotto, D.M., Sarkar, V., Scherer, W.N.: Phasers: a unified deadlock-free construct for collective and point-to-point synchronization. In: 22nd Annual International Conference on Supercomputing, pp. 277–288. ACM (2008)
Valiant, L.G.: A bridging model for parallel computation. CACM 33(8), 103 (1990)
Willebeek-LeMair, M.H., Reeves, A.P.: Strategies for dynamic load balancing on highly parallel computers. IEEE Trans. Parallel Distrib. Syst. 4(9), 979–993 (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Ganjei, Z., Rezine, A., Henrio, L., Eles, P., Peng, Z. (2019). On Reachability in Parameterized Phaser Programs. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11427. Springer, Cham. https://doi.org/10.1007/978-3-030-17462-0_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-17462-0_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17461-3
Online ISBN: 978-3-030-17462-0
eBook Packages: Computer ScienceComputer Science (R0)






 is a finite set of task identifiers. We let
is a finite set of task identifiers. We let  .
. is a finite set of phaser identifiers. We let
is a finite set of phaser identifiers. We let 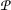 .
. fixes the values of some of the shared variables.
fixes the values of some of the shared variables. fixes the control sequences of some of the tasks.
fixes the control sequences of some of the tasks. is a mapping that associates to each task
is a mapping that associates to each task  a partial mapping stating which phasers are known by the task and with which registration values.
a partial mapping stating which phasers are known by the task and with which registration values.
 if tasks
if tasks  form a cycle where each
form a cycle where each 
 and
and  respectively represent, like for partial configurations, a valuation of the shared Boolean variables and a mapping of tasks to their control sequences.
respectively represent, like for partial configurations, a valuation of the shared Boolean variables and a mapping of tasks to their control sequences.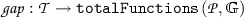 constrains relations between
constrains relations between  -tasks and
-tasks and  -phasers by associating to each task
-phasers by associating to each task  that defines for each phaser
that defines for each phaser 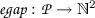 associates lower bounds
associates lower bounds  -phasers but which are not explicitly captured by
-phasers but which are not explicitly captured by  . This is described further in the constraints denotations below.
. This is described further in the constraints denotations below.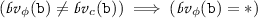 , and
, and and
and  can be written as
can be written as  and
and  , with
, with is a surjection and
is a surjection and  is a bijection, and
is a bijection, and with
with  , and
, and such that:
such that: with
with  and
and  , then it is the case that:
, then it is the case that: and
and  .
. , then for each
, then for each  and
and  , we have:
, we have:  and
and 
 , for each
, for each  and
and  can be written as
can be written as  and
and  with
with is a surjection and
is a surjection and  is a bijection, and
is a bijection, and for each
for each  with
with  :
: and
and  then
then  with
with  , and
, and  , it is the case that:
, it is the case that: with
with  , with
, with  , both
, both 
 is registered to
is registered to  and refers to it with
and refers to it with 