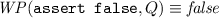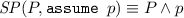Semantic Fault Localization and Suspiciousness Ranking

Abstract

Static program analyzers are increasingly effective in checking correctness properties of programs and reporting any errors found, often in the form of error traces. However, developers still spend a significant amount of time on debugging. This involves processing long error traces in an effort to localize a bug to a relatively small part of the program and to identify its cause. In this paper, we present a technique for automated fault localization that, given a program and an error trace, efficiently narrows down the cause of the error to a few statements. These statements are then ranked in terms of their suspiciousness. Our technique relies only on the semantics of the given program and does not require any test cases or user guidance. In experiments on a set of C benchmarks, we show that our technique is effective in quickly isolating the cause of error while out-performing other state-of-the-art fault-localization techniques.

1 Introduction

In recent years, program analyzers are increasingly applied to detect errors in real-world software. When detecting an error, static (or dynamic) analyzers often present the user with an error trace (or a failing test case), which shows how an assertion can be violated. Specifically, an error trace refers to a sequence of statements through the program that leads to the error. The user then needs to process the error trace, which is often long for large programs, in order to localize the problem to a manageable number of statements and identify its actual cause. Therefore, despite the effectiveness of static program analyzers in detecting errors and generating error traces, users still spend a significant amount of time on debugging.

Our Approach. To alleviate this situation, we present a technique for automated fault localization, which significantly reduces the number of statements that might be responsible for a particular error. Our technique takes as input a program and an error trace, generated by a static analyzer, and determines which statements along the error trace are potential causes of the error. We identify the potential causes of an error by checking, for each statement along the error trace, whether there exists a local fix such that the trace verifies. We call this technique semantic fault localization because it exclusively relies on the semantics of the given program, without for instance requiring any test cases or guidance from the user.

Although there is existing work that also relies on program semantics for fault localization, our technique is the first to semantically rank the possible error causes in terms of suspiciousness. On a high level, we compute a suspiciousness score for a statement by taking into account how much code would become unreachable if we were to apply a local fix to the statement. Specifically, suspiciousness is inversely proportional to the amount of unreachable code. The key insight is that developers do not intend to write unreachable code, and thus the cause of the error is more likely to be a statement that, when fixed, renders fewer parts of the program unreachable.

Our experimental evaluation compares our technique to six fault-localization approaches from the literature on the widely-used TCAS benchmarks (of the Siemens test suite [19]). We show that in 30 out of 40 benchmarks, our technique narrows down the cause of the error more than any of the other approaches and is able to pin-point the faulty statement in 14 benchmarks. In addition, we evaluate our technique on several seeded bugs in SV-COMP benchmarks [5].

Contributions. We make the following contributions:

• We present an automated fault-localization technique that is able to quickly narrow down the error cause to a small number of suspicious statements.

• We describe an effective ranking mechanism for the suspicious statements.

• We implement this technique in a tool architecture for localizing and ranking suspicious statements along error traces reported by the Ultimate Automizer [16] software model checker.

• We evaluate the effectiveness of our technique on 51 benchmarks.

2 Guided Tour

This section uses a motivating example to give an overview of our technique for semantic fault localization and suspiciousness ranking.

Fig. 1.

The running example (left) and its control-flow graph (right).

Example. Let us consider the simple program on the left of Fig. 1. The statement on line 2 denotes that y is assigned a non-deterministic value, denoted by $\star$. The conditional on line 3 has a non-deterministic predicate, but in combination with the assume statements (lines 4 and 7), it is equivalent to a conditional of the following form:

The assertion on line 10 fails when program execution takes the then branch of the if statement, and thus, it cannot be verified by a (sound) static analyzer. The error trace that is generated by a static analyzer for this program is

and we mark it in bold on the control-flow graph of the program, which is shown on the right of Fig. 1. Statement indicates that the error trace takes the failing branch of the assertion on line 10 of the program. The assert false statement denotes that this trace through the program results in an error.

Fault Localization. From such an error trace, our technique is able to determine a set of suspicious assignment statements, which we call trace-aberrant statements. Intuitively, these are statements along the error trace for which there exists a local fix that makes the trace verify. An assignment statement has a local fix if there exists an expression that may replace the right-hand side of the assignment such that the error becomes unreachable along this error trace. (In Sect. 5, we explain how our technique is able to identify other suspicious statements, apart from assignments.)

For example, statement x := 0 of the error trace is trace-aberrant because there exists a value that may be assigned to variable x such that the trace verifies. In particular, when x is assigned a positive value, terminates execution before reaching the error. Statement $\texttt {y := } \star$ is trace-aberrant for similar reasons. These are all the trace-aberrant statements along this error trace. For instance, x := 2 is not trace-aberrant because the value of x is over-written by the second assignment to the variable, thus making the error reachable along this trace, regardless of the initial value of x.

Suspiciousness Ranking. So far, we have seen that, when given the above error trace and the program of Fig. 1, semantic fault localization detects two trace-aberrant statements, $\texttt {y := } \star$ and x := 0. Since for real programs there can be many trace-aberrant statements, our technique computes a semantic suspiciousness score for each of them. Specifically, the computed score is inversely proportional to how much code would become unreachable if we applied a local fix to the statement. This is because developers do not intentionally write unreachable code. Therefore, when they make a mistake, they are more likely to fix a statement that renders fewer parts of the program unreachable relatively to other suspicious statements.

For example, if we were to fix statement x := 0 as discussed above (that is, by assigning a positive value to x), no code would become unreachable. As a result, this statement is assigned the highest suspiciousness score. On the other hand, if we were to fix statement $\texttt {y := } \star$ such that $\texttt {3} \le \texttt {y}$ holds and the trace verifies, the then branch of the if statement would become unreachable. Consequently, $\texttt {y := } \star$ is assigned a lower suspiciousness score than x := 0.

As we show in Sect. 6, this ranking mechanism is very effective at narrowing down the cause of an error to only a few lines in the program.

Fig. 2.

A simple programming language.

3 Semantic Fault Localization

As mentioned in the previous section, our technique consists of two steps, where we determine (trace-)aberrant statements in the first step and compute their suspiciousness ranks in the next one.

3.1 Programming Language

To precisely describe our technique, we introduce a small programming language, shown in Fig. 2. As shown in the figure, a program consists of a statement, and statements include sequencing, assignments, assertions, assumptions, conditionals, and loops. Observe that conditionals and loops have non-deterministic predicates, but note that, in combination with assumptions, they can express any conditional or loop with a predicate p. To simplify the discussion, we do not introduce additional constructs for procedure definitions and calls.

We assume that program execution terminates as soon as an assertion or assumption violation in encountered (that is, when the corresponding predicate evaluates to false). For simplicity, we also assume that our technique is applied to one failing assertion at a time.

3.2 Trace-Aberrant Statements

Recall from the previous section that trace-aberrant statements are assignments along the error trace for which there exists a local fix that makes the trace verify (that is, the error becomes unreachable along this trace):

Definition 1

(Trace aberrance). Let $\tau$ be a feasible error trace and s an assignment statement of the form $v := \star$ or $v := e$ along $\tau$. Statement s is trace-aberrant iff there exists an expression $e'$ that may be assigned to variable v such that the trace verifies.

To determine which assignments along an error trace are trace-aberrant, we first compute, in the post-state of each assignment, the weakest condition that ensures that the trace verifies. We, therefore, define a predicate transformer $WP$ such that, if $WP(S, Q)$ holds in a state along the error trace, then the error is unreachable and Q holds after executing statement S. The definition of this weakest-precondition transformer is standard [9] for all statements that may appear in an error trace:

• $WP (s_1;s_2, Q) \equiv WP(s_1, WP(s_2, Q))$

• $WP (v:=\star , Q) \equiv \forall v'.Q[v:=v'], \text {where } v' \notin freeVars (Q)$

• $WP (v:=e, Q) \equiv Q[v:=e]$

• 
• 

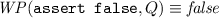
In the weakest precondition of the non-deterministic assignment, $v'$ is fresh in Q and $Q[v:=v']$ denotes the substitution of v by $v'$ in Q.

To illustrate, we compute this condition in the post-state of each assignment along the error trace of Sect. 2. Weakest precondition

should hold in the pre-state of statement , and thus in the post-state of assignment x := 0, for the trace to verify. Similarly, $3 \le \texttt {y}$ and $false$ should hold in the post-state of assignments $\texttt {y = }\star$ and x := 2, respectively. Note that condition $false$ indicates that the error is always reachable after assignment x := 2.

Second, we compute, in the pre-state of each assignment along the error trace, the strongest condition that holds when executing the error trace until that state. We define a predicate transformer $SP$ such that condition $SP(P, S)$ describes the post-state of statement S for an execution of S that starts from an initial state satisfying P. The definition of this strongest-postcondition transformer is also standard [10] for all statements that may appear in an error trace:

• $SP (P, s_1;s_2) \equiv SP(SP(P, s_1), s_2)$

• $SP (P, v:=\star ) \equiv \exists v'.P[v:=v'], \text {where } v' \notin freeVars (P)$

• $SP (P, v:=e) \equiv \exists v'.P[v:=v'] \wedge v=e[v:=v'],$ $\text {where } v' \notin freeVars (P) \cup freeVars (e)$

• 
• 

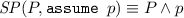
In the strongest postcondition of the assignment statements, $v'$ represents the previous value of v.

For example, strongest postcondition

$$ SP ( true ,\texttt {x := 2}) \equiv \texttt {x} = 2 $$

holds in the post-state of assignment x := 2, and therefore in the pre-state of $\texttt {y := }\star$. Similarly, the strongest such conditions in the pre-state of assignments x := 2 and x := 0 along the error trace are $true$ and $\texttt {x} = 2 \wedge \texttt {y} < 3$, respectively.

Third, our technique determines if an assignment a (of the form $v := \star$ or $v := e$) along the error trace is trace-aberrant by checking whether the Hoare triple [17] $\{\phi \} \; v := \star \; \{\psi \}$ is valid. Here, $\phi$ denotes the strongest postcondition in the pre-state of assignment a, v the left-hand side of a, and $\psi$ the negation of the weakest precondition in the post-state of a. If this Hoare triple is invalid, then assignment statement a is trace-aberrant, otherwise it is not.

Intuitively, the validity of the Hoare triple implies that, when starting from the pre-state of a, the error is always reachable no matter which value is assigned to v. In other words, there is no local fix for statement a that would make the trace verify. Consequently, assignment a is not trace-aberrant since it cannot possibly be the cause of the error. As an example, consider statement x := 2. For this assignment, our technique checks the validity of the Hoare triple $\{ true \} \; \texttt {x := } \star \; \{ true \}$. Since any value for x satisfies the true postcondition, assignment x := 2 is not trace-aberrant.

If, however, the Hoare triple is invalid, there exists a value for variable v such that the weakest precondition in the post-state of a holds. This means that there is a local fix for a that makes the error unreachable. As a result, statement a is found to be trace-aberrant. For instance, for statement x := 0, we construct the following Hoare triple: $\{\texttt {x} = 2 \wedge \texttt {y} < 3\} \; \texttt {x := } \star \; \{\texttt {x} \le 0\}$. This Hoare triple is invalid because there are values that may be assigned to x such that $\texttt {x} \le 0$ does not hold in the post-state. Assignment x := 0 is, therefore, trace-aberrant. Similarly, for $\texttt {y := }\star$, the Hoare triple $\{\texttt {x} = 2\} \; \texttt {y := } \star \; \{\texttt {y} < 3\}$ is invalid.

3.3 Program-Aberrant Statements

We now define program-aberrant statements; these are assignments for which there exists a local fix that makes every trace through them verify:

Definition 2

(Program aberrance). Let $\tau$ be a feasible error trace and s an assignment statement of the form $v := \star$ or $v := e$ along $\tau$. Statement s is program-aberrant iff there exists an expression $e'$ that may be assigned to variable v such that all traces through s verify.

Based on the above definition, the trace-aberrant assignments in the program of Fig. 1 are also program-aberrant. This is because there is only one error trace through these statements.

As another example, let us replace the assignment on line 8 of the program by x := -1. In this modified program, the assertion on line 10 fails when program execution takes either branch of the if statement. Now, assume that a static analyzer, which clearly fails to verify the assertion, generates the same error trace that we described in Sect. 2 (for the then branch of the if statement). Like before, our technique determines that statements $\texttt {y := }\star$ and x := 0 along this error trace are trace-aberrant. However, although there is still a single error trace through statement x := 0, there are now two error traces through $\texttt {y := }\star$, one for each branch of the conditional. We, therefore, know that x := 0 is program-aberrant, but it is unclear whether assignment $\texttt {y := }\star$ is.

To determine which trace-aberrant assignments along an error trace are also program-aberrant, one would need to check if there exists a local fix for these statements such that all traces through them verify. Recall that there exists a fix for a trace-aberrant assignment if there exists a right-hand side that satisfies the weakest precondition in the post-state of the assignment along the error trace. Therefore, checking the existence of a local fix for a program-aberrant statement involves computing the weakest precondition in the post-state of the statement in the program, which amounts to program verification and is undecidable.

Identifying which trace-aberrant statements are also program-aberrant is desirable since these are precisely the statements that can be fixed for the program to verify. However, determining these statements is difficult for the reasons indicated above. Instead, our technique uses the previously-computed weakest preconditions to decide which trace-aberrant assignments must also be program-aberrant, in other words, it can under-approximate the set of program-aberrant statements. In our experiments, we find that many trace-aberrant statements are must-program-aberrant.

To compute the must-program-aberrant statements, our technique first identifies the trace-aberrant ones, for instance, $\texttt {y := }\star$ and x := 0 for the modified program. In the following, we refer to the corresponding error trace as $\epsilon$.

As a second step, our technique checks whether all traces through the trace-aberrant assignments verify with the most permissive local fix that makes $\epsilon$ verify. To achieve this, we instrument the faulty program as follows. We replace a trace-aberrant statement $a_i$ of the form $v := e$ by a non-deterministic assignment $v := \star$ with the same left-hand side v. Our technique then introduces an assume statement right after the non-deterministic assignment. The predicate of the assumption corresponds to the weakest precondition that is computed in the post-state of the assignment along error trace $\epsilon$¹. We apply this instrumentation separately for each trace-aberrant statement $a_i$, where $i = 0, \dots , n$, and we refer to the instrumented program that corresponds to trace-aberrant statement $a_i$ as $P_{a_i}$. (Note that our technique uses this instrumentation for ranking aberrant statements in terms of suspiciousness, as we explain in Sect. 4.) Once we obtain a program $P_{a_i}$, we instrument it further to add a flag that allows the error to manifest itself only for traces through statement $a_i$ (as per Definition 2). We denote each of these programs by $P_{a_i}^\dag$.

For example, the light gray boxes on the right show the instrumentation for checking whether statement x := 0 of the modified program is program-aberrant (the darker boxes should be ignored). Lines 8–9 constitute the instrumentation that generates program $P_{\texttt {x := 0}}$. As explained in Sect. 3.2, when the computed weakest precondition holds on line 9, it implies that trace $\epsilon$ verifies. Consequently, this instrumentation represents a hypothetical local fix for assignment x := 0. Lines 1, 10, and 15 block any program execution that does not go through statement x := 0. As a result, the assertion may fail only due to failing executions through this statement. Similarly, when considering the dark gray boxes in addition to lines 1 and 15 (and ignoring all other light boxes), we obtain $P_{\texttt {y := }\star }^\dag$. Line 4 alone constitutes the instrumentation that generates program $P_{\texttt {y := }\star }$.

Third, our technique runs the static analyzer on each of the n instrumented programs $P_{a_i}^\dag$. If the analyzer does not generate a new error trace, then statement $a_i$ must be program-aberrant, otherwise we do not know. For instance, when running the static analyzer on $P_{\texttt {x := 0}}^\dag$ from above, no error is detected. Statement x := 0 is, therefore, program-aberrant. However, an error trace is reported for program $P_{\texttt {y := }\star }^\dag$ (through the else branch of the conditional). As a result, our technique cannot determine whether $\texttt {y := }\star$ is program-aberrant. Notice, however, that this statement is, in fact, not program-aberrant because there is no fix that we can apply to it such that both traces verify.

3.4 k-Aberrance

So far, we have focused on (trace- or program-) aberrant statements that may be fixed to single-handedly make one or more error traces verify. The notion of aberrance, however, may be generalized to sets of statements that make the corresponding error traces verify only when fixed together:

Definition 3

(k-Trace aberrance). Let $\tau$ be a feasible error trace and $\bar{s}$ a set of assignment statements of the form $v := \star$ or $v := e$ along $\tau$. Statements $\bar{s}$ are $|\bar{s}|$-trace-aberrant, where $|\bar{s}|$ is the cardinality of $\bar{s}$, iff there exist local fixes for all statements in $\bar{s}$ such that trace $\tau$ verifies.

Definition 4

(k-Program aberrance). Let $\bar{\tau }$ be the set of all feasible error traces through any assignment statement s in a set $\bar{s}$. Each statement s is of the form $v := \star$ or $v := e$ along an error trace $\tau$ in $\bar{\tau }$. Statements $\bar{s}$ are $|\bar{s}|$-program-aberrant, where $|\bar{s}|$ is the cardinality of $\bar{s}$, iff there exist local fixes for all statements in $\bar{s}$ such that all traces $\bar{\tau }$ verify.

For example, consider the modified version of the program in Fig. 1 that we discussed above. Assignments x := 0 and x := -1 are 2-program-aberrant because their right-hand side may be replaced by a positive value such that both traces through these statements verify.

Our technique may be adjusted to compute k-aberrant statements by exploring all combinations of k assignments along one or more error traces.

4 Semantic Suspiciousness Ranking

In this section, we present how aberrant statements are ranked in terms of their suspiciousness. As mentioned earlier, the suspiciousness score of an aberrant statement is inversely proportional to how much code would become unreachable if we applied a local fix to the statement.

First, for each aberrant statement $a_i$, where $i = 0, \dots , n$, our technique generates the instrumented program $P_{a_i}$ (see Sect. 3.3 for the details). Recall that the trace-aberrant statements for the program of Fig. 1 are $\texttt {y := }\star$ and x := 0.

Second, we check reachability of the code in each of these n instrumented programs $P_{a_i}$. Reachability may be simply checked by converting all existing assertions into assumptions and introducing an assert false at various locations in the program. An instrumentation for checking reachability in $P_{\texttt {x := 0}}$ is shown on the right; all changes are highlighted. In particular, we detect whether the injected assertion on line 7 is reachable by passing the above program (without the dark gray box) to an off-the-shelf analyzer. We can similarly check reachability of the other assertion. In the above program, both assertions are reachable, whereas in the corresponding program for assignment $\texttt {y := }\star$, only one of them is. The number of reachable assertions in a program $P_{a_i}$ constitutes the suspiciousness score of statement $a_i$.

As a final step, our technique ranks the aberrant statements in order of decreasing suspiciousness. Intuitively, this means that, by applying a local fix to the higher-ranked statements, less code would become unreachable in comparison to the statements that are ranked lower. Since developers do not typically intend to write unreachable code, the cause of the error in P is more likely to be a higher-ranked aberrant statement. For our running example, trace-aberrant statement x := 0 is ranked higher than $\texttt {y := }\star$.

As previously discussed, when modifying the program of Fig. 1 to replace assignment x := 1 by x := -1, our technique determines that only x := 0 must be program-aberrant. For the error trace through the other branch of the conditional, we would similarly identify statement x := -1 as must-program-aberrant. Note that, for this example, must program aberrance does not miss any program-aberrant statements. In fact, in our experiments, must program aberrance does not miss any error causes, despite its under-approximation.

5 Implementation

We have implemented our technique in a toolchain for localizing and ranking suspicious statements in C programs. We used UAutomizer in the Ultimate analysis framework to obtain error traces (version 0.1.23). UAutomizer is a software model checker that translates C programs to Boogie [4] and then employs an automata-based verification approach [16]. Our implementation extends UAutomizer to identify (trace- or program-) aberrant statements along the generated error traces, as we describe in Sect. 3. Note that, due to abstraction (for instance, of library calls), UAutomizer may generate spurious error traces. This is an orthogonal issue that we do not address in this work.

To also identify aberrant expressions, for instance, predicates of conditionals or call arguments, we pre-process the program by first assigning these expressions to temporary variables, which are then used instead. This allows us to detect error causes relating to statements other than assignments.

Once the aberrant statements have been determined, we instrument the Boogie code to rank them (see Sect. 4). Specifically, our implementation inlines procedures and injects an assert false statement at the end of each basic block (one at a time). Instead of extending the existing support for “smoke checking” in Boogie, we implemented our own reachability checker in order to have more control over where the assertions are injected. While this might not be as efficient due to the larger number of Boogie queries (each including the time for parsing, pre-processing, and SMT solving), one could easily optimize or replace this component.

6 Experimental Evaluation

We evaluate the effectiveness of our technique in localizing and ranking suspicious statements by applying our toolchain to several faulty C programs. In the following, we introduce our set of benchmarks (Sect. 6.1), present the experimental setup (Sect. 6.2), and investigate four research questions (Sect. 6.3).

6.1 Benchmark Selection

For our evaluation, we used 51 faulty C programs from two independent sources. On the one hand, we used the faulty versions of the TCAS task from the Siemens test suite [19]. The authors of the test suite manually introduced faults in several tasks while aiming to make these bugs as realistic as possible. In general, the Siemens test suite is widely used in the literature (e.g., [14, 20, 22, 25,26,27,28]) for evaluating and comparing fault-localization techniques.

The TCAS task implements an aircraft-collision avoidance system and consists of 173 lines of C code; there are no specifications. This task also comes with 1608 test cases, which we used to introduce assertions in the faulty program versions. In particular, in each faulty version, we specified the correct behavior as this was observed by running the tests against the original, correct version of the code. This methodology is commonly used in empirical studies with the Siemens test suite, and it was necessary for obtaining an error trace from UAutomizer.

On the other hand, we randomly selected 4 correct programs (with over 250 lines of code) from the SV-COMP software-verification competition [5], which includes standard benchmarks for evaluating program analyzers. We automatically injected faults in each of these programs by randomly mutating statements within the program. All SV-COMP benchmarks are already annotated with assertions, so faults manifest themselves by violating the existing assertions.

6.2 Experimental Setup

We ran all experiments on an Intel® Core i7 CPU @ 2.67 GHz machine with 16 GB of memory, running Linux. Per analyzed program, we imposed a timeout of 120 s and a memory limit of 6 GB to UAutomizer.

To inject faults in the SV-COMP benchmarks, we developed a mutator that randomly selects an assignment statement, mutates the right-hand side, and checks whether the assertion in the program is violated. If it is, the mutator emits a faulty program version. Otherwise, it generates up to two additional mutations for the same assignment before moving on to another.

6.3 Experimental Results

To evaluate our technique, we consider the following research questions:

• RQ1: How effective is our technique in narrowing down the cause of an error to a small number of suspicious statements?

• RQ2: How efficient is our technique?

• RQ3: How does under-approximating program-aberrant statements affect fault localization?

• RQ4: How does our technique compare against state-of-the-art approaches for fault localization in terms of effectiveness and efficiency?

Table 1. Our experimental results for the TCAS benchmarks.

RQ1 (Effectiveness). Tables 1 and 2 summarize our experimental results on the TCAS and SV-COMP benchmarks, respectively. The first column of Table 1 shows the faulty versions of the program, and the second column the number of trace-aberrant statements that were detected for every version. Similarly, in Table 2, the first column shows the program version², the second column the lines of source code in every version, and the third column the number of trace-aberrant statements. For all benchmarks, the actual cause of each error is always included in the statements that our technique identifies as trace-aberrant. This is to be expected since the weakest-precondition and strongest-postcondition transformers that we use for determining trace aberrance are known to be sound.

The fourth column of Table 1 and the fifth column of Table 2 show the suspiciousness rank that our technique assigns to the actual cause of each error. For both sets of benchmarks, the average rank of the faulty statement is 3, and all faulty statements are ranked in the top 6. A suspiciousness rank of 3 means that users need to examine at least three statements to identify the problem; they might have to consider more in case multiple statements have the same rank.

To provide a better indication of how much code users have to examine to identify the bug, the eighth column of Table 1 and the seventh column of Table 2 show the percentage reduction in the program size. On average, our technique reduces the code size down to 5% for TCAS and less than 1% for SV-COMP.

RQ2 (Efficiency). The sixth column of Table 1 shows the time that our technique requires for identifying the trace-aberrant statements in a given error trace as well as for ranking them in terms of suspiciousness. This time does not include the generation of the error trace by UAutomizer. As shown in the table, our technique takes only a little over 2 min on average to reduce a faulty program to about 5% of its original size.

Table 2. Our experimental results for the SV-COMP benchmarks.

Note that most of this time (98.5% on average) is spent on the suspiciousness ranking. The average time for determining the trace-aberrant statements in an error trace is only 1.7 s. Recall from Sect. 5 that our reachability analysis, which is responsible for computing the suspiciousness score of each aberrant statement, is not implemented as efficiently as possible (see Sect. 5 for possible improvements).

RQ3 (Program aberrance). In Sect. 3.3, we discussed that our technique can under-approximate the set of program-aberrant statements along an error trace. The third, fifth, seventh, and ninth columns of Table 1 as well as the fourth, sixth, and eighth columns of Table 2 show the effect of this under-approximation.

There are several observations to be made here, especially in comparison to the experimental results for trace aberrance. First, there are fewer aberrant statements, which is to be expected since (must-)program-aberrant statements may only be a subset of trace-aberrant statements. Perhaps a bit surprisingly, the actual cause of each error is always included in the must-program-aberrant statements. In other words, the under-approximation of program-aberrant statements does not miss any error causes in our benchmarks. Second, the suspiciousness rank assigned to the actual cause of each error is slightly higher, and all faulty statements are ranked in the top 5. Third, our technique requires about 1.5 min for fault localization and ranking, which is faster due to the smaller number of aberrant statements. Fourth, the code is reduced even more, down to 4.3 for TCAS and 0.3% for SV-COMP.

RQ4 (Comparison). To compare our technique against state-of-the-art fault-localization approaches, we evaluated how five of the most popular [35] spectrum-based fault-localization (SBFL) techniques [20, 24, 34] perform on our benchmarks. In general, SBFL is the most well-studied and evaluated fault-localization technique in the literature [26]. SBFL techniques essentially compute suspiciousness scores based on statement-execution frequencies. Specifically, the more frequently a statement is executed by failing test cases and the less frequently it is executed by successful tests, the higher its suspiciousness score. We also compare against an approach that reduces fault localization to the maximal satisfiability problem (MAX-SAT) and performs similarly to SBFL.

The last eight columns of Table 1 show the comparison in code reduction across different fault-localization techniques. Columns A, B, C, D, and E refer to the SBFL techniques, and in particular, to Tarantula [20], Ochiai [2], Op2 [24], Barinel [1], and DStar [34], respectively. The last column (F) corresponds to BugAssist [21, 22], which uses MAX-SAT. To obtain these results, we implemented all SBFL techniques and evaluated them on TCAS using the existing test suite. For BugAssist, we used the published percentages of code reduction for these benchmarks [22]. Note that we omit version 38 in Table 1 as is common in experiments with TCAS. The fault is in a non-executable statement (array declaration) and its frequency cannot be computed by SBFL.

The dark gray boxes in the table show which technique is most effective with respect to code reduction for each version. Our technique for must program aberrance is the most effective for 30 out of 40 versions. The light gray boxes in the trace-aberrance column denote when this technique is the most effective in comparison with columns A–F (that is, without considering program aberrance). As shown in the table, our technique for trace aberrance outperforms approaches A–F in 28 out of 40 versions. In terms of lines of code, users need to inspect 7–9 statements when using our technique, whereas they would need to look at 13–15 statements when using other approaches. This is a reduction of 4–8 statements, and every statement that users may safely ignore saves them valuable time.

Regarding efficiency, our technique is comparable to SBFL (A–E); we were not able to run BugAssist (F), but it should be very lightweight for TCAS. SBFL techniques need to run the test suite for every faulty program. For the TCAS tests, this takes 1 min 11 s on average on our machine. Parsing the statement-execution frequencies and computing the suspiciousness scores takes about 5 more seconds. Therefore, the average difference with our technique ranges from a few seconds (for program aberrance) to a little less than a minute (for trace aberrance). There is definitely room for improving the efficiency of our technique, but despite it being slightly slower than SBFL for these benchmarks, it saves the user the effort of inspecting non-suspicious statements. Moreover, note that the larger the test suite, the higher the effectiveness of SBFL, and the longer its running time. Thus, to be as effective as our technique, SBFL would require more test cases, and the test suite would take longer to run. We do not consider the time for test case generation just like we do not consider the running time of the static analysis that generates the error traces.

7 Related Work

Among the many fault-localization techniques [35], SBFL [20, 24, 34] is the most well-studied and evaluated. Mutation-based fault localization (MBFL) [23, 25] is almost as effective as SBFL but significantly more inefficient [26]. In general, MBFL extends SBFL by considering, not only how frequently a statement is executed in tests, but also whether a mutation to the statement affects the test outcomes. So, MBFL generates many mutants per statement, which requires running the test suite per mutant, and not per faulty program as in SBFL. Our local fixes resemble mutations, but they are performed symbolically and can be seen as applying program-level abductive reasoning [6, 11, 12] or angelic verification [8] for fault localization.

The use of error invariants [7, 13, 18, 29] is a closely-related fault-localization technique. Error invariants are computed from Craig interpolants along an error trace and capture which states will produce the error from that point on. They are used for slicing traces by only preserving statements whose error invariants before and after the statement differ. Similarly, Wang et al. [32] use a syntactic-level weakest-precondition computation for a given error trace to produce a minimal set of word-level predicates, which explain why the program fails. In contrast, we use the novel notion of trace aberrance for this purpose and compute a suspiciousness ranking to narrow down the error cause further.

Griesmayer et al. [14] use an error trace from a bounded model checker to instrument the program with “abnormal predicates”. These predicates allow expressions in the program to take arbitrary values, similarly to how our technique replaces a statement $v := e$ by a non-deterministic one. Unlike our technique, their approach may generate a prohibitively large instrumentation, requires multiple calls to the model checker, and does not rank suspicious statements.

Several fault-localization algorithms leverage the differences between faulty and successful traces [3, 15, 27, 36]. For instance, Ball et al. [3] make several calls to a model checker and compare any generated counterexamples with successful traces. In contrast, we do not require successful traces for comparisons.

Zeller [36] uses delta-debugging, which identifies suspicious parts of the input by running the program multiple times. Slicing [31, 33] removes statements that are definitely not responsible for the error based on data and control dependencies. Shen et al. [30] use unsatisfiable cores for minimizing counterexamples. Our technique is generally orthogonal to these approaches, which could be run as a pre-processing step to reduce the search space.

8 Conclusion

We have presented a novel technique for fault localization and suspiciousness ranking of statements along an error trace. We demonstrated its effectiveness in narrowing down the error cause to a small fraction of the entire program.

As future work, we plan to evaluate the need for k-aberrance by analyzing software patches and to combine our technique with existing approaches for program repair to improve their effectiveness.