Abstract
Research into C verification often ignores that the C standard leaves the evaluation order of expressions unspecified, and assigns undefined behavior to write-write or read-write conflicts in subexpressions—so called “sequence point violations”. These aspects should be accounted for in verification because C compilers exploit them.
We present a verification condition generator (vcgen) that enables one to semi-automatically prove the absence of undefined behavior in a given C program for any evaluation order. The key novelty of our approach is a symbolic execution algorithm that computes a frame at the same time as a postcondition. The frame is used to automatically determine how resources should be distributed among subexpressions.
We prove correctness of our vcgen with respect to a new monadic definitional semantics of a subset of C. This semantics is modular and gives a concise account of non-determinism in C.
We have implemented our vcgen as a tactic in the Coq interactive theorem prover, and have proved correctness of it using a separation logic for the new monadic definitional semantics of a subset of C.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The ISO C standard [22]—the official specification of the C language—leaves many parts of the language semantics either unspecified (e.g., the order of evaluation of expressions), or undefined (e.g., dereferencing a NULL pointer or integer overflow). In case of undefined behavior a program may do literally anything, e.g., it may crash, or it may produce an arbitrary result and side-effects. Therefore, to establish the correctness of a C program, one needs to ensure that the program has no undefined behavior for all possible choices of non-determinism due to unspecified behavior.
In this paper we focus on the undefined and unspecified behaviors related to C ’s expression semantics, which have been ignored by most existing verification tools, but are crucial for establishing the correctness of realistic C programs. The C standard does not require subexpressions to be evaluated in a specific order (e.g., from left to right), but rather allows them to be evaluated in any order. Moreover, an expression has undefined behavior when there is a conflicting write-write or read-write access to the same location between two sequence points [22, 6.5p2] (so called “sequence point violation”). Sequence points occur e.g., at the end of a full expression (
 ), before and after each function call, and after the first operand of a conditional expression (
), before and after each function call, and after the first operand of a conditional expression (
 ) has been evaluated [22, Annex C]. Let us illustrate this by means of the following example:
) has been evaluated [22, Annex C]. Let us illustrate this by means of the following example:

Due to the unspecified evaluation order, one would naively expect this program to print either “
 ” or “
” or “
 ”, depending on which assignment to
”, depending on which assignment to
 was evaluated first. But this program exhibits undefined behavior due to a sequence point violation: there are two conflicting writes to the variable
was evaluated first. But this program exhibits undefined behavior due to a sequence point violation: there are two conflicting writes to the variable
 . Indeed, when compiled with GCC (version 8.2.0), the program in fact prints “
. Indeed, when compiled with GCC (version 8.2.0), the program in fact prints “
 ”, which does not correspond to the expected results of any of the evaluation orders.
”, which does not correspond to the expected results of any of the evaluation orders.
One may expect that these programs can be easily ruled out statically using some form of static analysis, but this is not the case. Contrary to the simple program above, one can access the values of arbitrary pointers, making it impossible to statically establish the absence of write-write or read-write conflicts. Besides, one should not merely establish the absence of undefined behavior due to conflicting accesses to the same locations, but one should also establish that there are no other forms of undefined behavior (e.g., that no NULL pointers are dereferenced) for any evaluation order.
To deal with this issue, Krebbers [29, 30] developed a program logic based on Concurrent Separation Logic (CSL) [46] for establishing the absence of undefined behavior in C programs in the presence of non-determinism. To get an impression of how his logic works, let us consider the rule for the addition operator:

This rule is much like the rule for parallel composition in CSL—the precondition should be separated into two parts \(P_1\) and \(P_2\) describing the resources needed for proving the Hoare triples of both operands. Crucially, since \(P_1\) and \(P_2\) describe disjoint resources as expressed by the separating conjunction \(*\), it is guaranteed that  and
and  do not interfere with each other, and hence cannot cause sequence point violations. The purpose of the rule’s last premise is to ensure that for all possible return values
do not interfere with each other, and hence cannot cause sequence point violations. The purpose of the rule’s last premise is to ensure that for all possible return values  and
and  , the postconditions
, the postconditions  and
and  of both operands can be combined into the postcondition
of both operands can be combined into the postcondition  of the whole expression.
of the whole expression.
Krebbers’s logic [29, 30] has some limitations that impact its usability:
-
The rules are not algorithmic, and hence it is not clear how they could be implemented as part of an automated or interactive tool.
-
It is difficult to extend the logic with new features. Soundness was proven with respect to a monolithic and ad-hoc model of separation logic.
In this paper we address both of these problems.
We present a new algorithm for symbolic execution in separation logic. Contrary to ordinary symbolic execution in separation logic [5], our symbolic executor takes an expression and a precondition as its input, and computes not only the postcondition, but also simultaneously computes a frame that describes the resources that have not been used to prove the postcondition. The frame is used to infer the pre- and postconditions of adjacent subexpressions. For example, in  , we use the frame of
, we use the frame of  to symbolically execute
to symbolically execute  .
.
In order to enable semi-automated reasoning about C programs, we integrate our symbolic executor into a verification condition generator (vcgen). Our vcgen does not merely turn programs into proof goals, but constructs the proof goals only as long as it can discharge goals automatically using our symbolic executor. When an attempt to use the symbolic executor fails, our vcgen will return a new goal, from which the vcgen can be called back again after the user helped out. This approach is useful when integrated into an interactive theorem prover.
We prove soundness of the symbolic executor and verification condition generator with respect to a refined version of the separation logic by Krebbers [29, 30]. Our new logic has been developed on top of the Iris framework [24,25,26, 33], and thereby inherits all advanced features of Iris (like its expressive support for ghost state and invariants), without having to model these explicitly. To make our new logic better suited for proving the correctness of the symbolic executor and verification condition generator, our new logic comes with a weakest precondition connective instead of Hoare triples as in Krebbers’s original logic.
To streamline the soundness proof of our new program logic, we give a new monadic definitional translation of a subset of C relevant for non-determinism and sequence points into an ML-style functional language with concurrency. Contrary to the direct style operational semantics for a subset of C by Krebbers [29, 30], our approach leads to a semantics that is both easier to understand, and easier to extend with additional language features.
We have mechanized our whole development in the Coq interactive theorem prover. The symbolic executor and verification condition generator are defined as computable functions in Coq, and have been integrated into tactics in the Iris Proof Mode/MoSeL framework [32, 34]. To obtain end-to-end correctness, we mechanized the proofs of soundness of our symbolic executor and verification condition generator with respect to our new separation logic and new monadic definitional semantics for a subset of C. The Coq development is available at [18].
Contributions. We describe an approach to semi-automatically prove the absence of undefined behavior in a given C program for any evaluation order. While doing so, we make the following contributions:
-
We define \(\lambda \mathsf {MC} \): a small C-style language with a semantics by a monadic translation into an ML-style functional language with concurrency (Sect. 2);
-
We present a separation logic with weakest preconditions for \(\lambda \mathsf {MC} \) based on the separation logic for non-determinism in C by Krebbers [29, 30] (Sect. 3);
-
We prove soundness of our separation logic with weakest preconditions by giving a modular model using the Iris framework [24,25,26, 33] (Sect. 4);
-
We present a new symbolic executor that not only computes the postcondition of a C expression, but also a frame, used to determine how resources should be distributed among subexpressions (Sect. 5);
-
On top of our symbolic executor, we define a verification condition generator that enables semi-automated proofs using an interactive theorem prover (Sect. 6);
-
We demonstrate that our approach can be implemented and proved sound using Coq for a superset of the \(\lambda \mathsf {MC} \) language considered in this paper (Sect. 7).
2 \(\lambda \mathsf {MC} \): A Monadic Definitional Semantics of C
In this section we describe a small C-style language called \(\lambda \mathsf {MC} \), which features non-determinism in expressions. We define its semantics by translation into a ML-style functional language with concurrency called HeapLang.
We briefly describe the \(\lambda \mathsf {MC} \) source language (Sect. 2.1) and the HeapLang target language (Sect. 2.2) of the translation. Then we describe the translation scheme itself (Sect. 2.3). We explain in several steps how to exploit concurrency and monadic programming to give a concise and clear definitional semantics.
2.1 The Source Language \(\lambda \mathsf {MC} \)
The syntax of our source language called \(\lambda \mathsf {MC} \) is as follows:

The values include integers, \(\mathtt {NULL}\) pointers, concrete locations \(\mathtt {l}\), function pointers \(\mathtt {f}\), structs with two fields (tuples), and the unit value \(\texttt {()}\) (for functions without return value). There is a global list of function definitions, where each definition is of the form  . Most of the expression constructs resemble standard C notation, with some exceptions. We do not differentiate between expressions and statements to keep our language uniform. As such, if-then-else and sequencing constructs are not duplicated for both expressions and statements. Moreover, we do not differentiate between lvalues and rvalues [22, 6.3.2.1]. Hence, there is no address operator
. Most of the expression constructs resemble standard C notation, with some exceptions. We do not differentiate between expressions and statements to keep our language uniform. As such, if-then-else and sequencing constructs are not duplicated for both expressions and statements. Moreover, we do not differentiate between lvalues and rvalues [22, 6.3.2.1]. Hence, there is no address operator
 , and, similarly to ML, the load (
, and, similarly to ML, the load ( ) and assignment (
) and assignment ( ) operators take a reference as their first argument.
) operators take a reference as their first argument.
The sequenced bind operator  generalizes the normal sequencing operator
generalizes the normal sequencing operator  of C by binding the result of
of C by binding the result of  to the variable \(\mathtt {x}\) in
to the variable \(\mathtt {x}\) in  . As such,
. As such,  can be thought of as the declaration of an immutable local variable \(\mathtt {x}\). We omit mutable local variables for now, but these can be easily added as an extension to our method, as shown in Sect. 7. We write
can be thought of as the declaration of an immutable local variable \(\mathtt {x}\). We omit mutable local variables for now, but these can be easily added as an extension to our method, as shown in Sect. 7. We write  for a sequenced bind
for a sequenced bind  in which we do not care about the return value of
in which we do not care about the return value of  .
.
To focus on the key topics of the paper—non-determinism and the sequence point restriction—we take a minimalistic approach and omit most other features of C. Notably, we omit non-local control (return, break, continue, and goto). Our memory model is simplified; it only supports structs with two fields (tuples), but no arrays, unions, or machine integers. In Sect. 7 we show that some of these features (arrays, pointer arithmetic, and mutable local variables) can be incorporated.
2.2 The Target Language HeapLang
The target language of our definitional semantics of \(\lambda \mathsf {MC} \) is an \(\textsf {ML} \)-style functional language with concurrency primitives and a call-by-value semantics. This language, called HeapLang, is included as part of the Iris Coq development [21]. The syntax is as follows:

The language contains some concurrency primitives that we will use to model non-determinism in \(\lambda \mathsf {MC} \). Those primitives are  ,
,  ,
,  , and
, and  . The first primitive is the parallel composition operator, which executes expressions
. The first primitive is the parallel composition operator, which executes expressions  and
and  in parallel, and returns a tuple of their results. The expression
in parallel, and returns a tuple of their results. The expression  creates a new mutex. If \({\textit{lk}}\) is a mutex that was created this way, then
creates a new mutex. If \({\textit{lk}}\) is a mutex that was created this way, then  tries to acquire it and blocks until no other thread is using \({\textit{lk}}\). An acquired mutex can be released using
tries to acquire it and blocks until no other thread is using \({\textit{lk}}\). An acquired mutex can be released using  .
.
2.3 The Monadic Definitional Semantics of \(\lambda \mathsf {MC} \)
We now give the semantics of \(\lambda \mathsf {MC} \) by translation into HeapLang. The translation is carried out in several stages, each iteration implementing and illustrating a specific aspect of C. First, we model non-determinism in expressions by concurrency, parallelizing execution of subexpressions (step 1). After that, we add checks for sequence point violations in the translation of the assignment and dereferencing operations (step 2). Finally, we add function calls and demonstrate how the translation can be simplified using a monadic notation (step 3).
Step 1: Non-determinism via Parallel Composition. We model the unspecified evaluation order in binary expressions like  and
and  by executing the subexpressions in parallel using the \((\mathbin {||_{\textsf {\tiny HL}}})\) operator:
by executing the subexpressions in parallel using the \((\mathbin {||_{\textsf {\tiny HL}}})\) operator:

Since our memory model is simple, the value interpretation is straightforward:

The only interesting case is the translation of locations. Since there is no concept of a \(\mathtt {NULL}\) pointer in HeapLang, we use the option type to distinguish \(\mathtt {NULL}\) pointers from concrete locations (\(\mathtt {l}\)). The interpretation of assignments thus contains a pattern match to check that no \(\mathtt {NULL}\) pointers are dereferenced. A similar check is performed in the interpretation of the load operation ( ). Moreover, each location contains an option to distinguish freed from active locations.
). Moreover, each location contains an option to distinguish freed from active locations.
Step 2: Sequence Points. So far we have not accounted for undefined behavior due to sequence point violations. For instance, the program
 gets translated into a HeapLang expression that updates the value of the location
gets translated into a HeapLang expression that updates the value of the location
 non-deterministically to either 3 or 4, and returns 7. However, in C, the behavior of this program is undefined, as it exhibits a sequence point violation: there is a write conflict for the location
non-deterministically to either 3 or 4, and returns 7. However, in C, the behavior of this program is undefined, as it exhibits a sequence point violation: there is a write conflict for the location
 .
.
To give a semantics for sequence point violations, we follow the approach by Norrish [44], Ellison and Rosu [17], and Krebbers [29, 30]. We keep track of a set of locations that have been written to since the last sequence point. We refer to this set as the environment of our translation, and represent it using a global variable env of the type  . Because our target language HeapLang is concurrent, all updates to the environment \({\textit{env}}\) must be executed atomically, i.e., inside a critical section, which we enforce by employing a global mutex \({\textit{lk}}\). The interpretation of assignments
. Because our target language HeapLang is concurrent, all updates to the environment \({\textit{env}}\) must be executed atomically, i.e., inside a critical section, which we enforce by employing a global mutex \({\textit{lk}}\). The interpretation of assignments  now becomes:
now becomes:

Whenever we assign to (or read from) a location l, we check if the location l is not already present in the environment \({\textit{env}}\). If the location l is present, then it was already written to since the last sequence point. Hence, accessing the location constitutes undefined behavior (see the  in the interpretation of assignments above). In the interpretation of assignments, we furthermore insert the location l into the environment \({\textit{env}}\).
in the interpretation of assignments above). In the interpretation of assignments, we furthermore insert the location l into the environment \({\textit{env}}\).
In order to make sure that one can access a variable again after a sequence point, we define the sequenced bind operator  as follows:
as follows:

After we finished executing the expression  , we clear the environment \({\textit{env}}\), so that all locations are accessible in
, we clear the environment \({\textit{env}}\), so that all locations are accessible in  again.
again.
Step 3: Non-interleaved Function Calls. As the final step, we present the correct translation scheme for function calls. Unlike the other expressions, function calls are not interleaved during the execution of subexpressions [22, 6.5.2.2p10]. For instance, in the program  the possible orders of execution are: either all the instructions in
the possible orders of execution are: either all the instructions in  followed by all the instructions in
followed by all the instructions in  , or all the instructions in
, or all the instructions in  followed by all the instructions in
followed by all the instructions in  .
.
To model this, we execute each function call atomically. In the previous step we used a global mutex for guarding the access to the environment. We could use that mutex for function calls too. However, reusing a single mutex for entering each critical section would not work because a body of a function may contain invocations of other functions. To that extent, we use multiple mutexes to reflect the hierarchical structure of function calls.
To handle multiple mutexes, each C expression is interpreted as a HeapLang function that receives a mutex and returns its result. That is, each C expression is modeled by a monadic expression in the reader monad  . For consistency’s sake, we now also use the monad to thread through the reference to the environment (
. For consistency’s sake, we now also use the monad to thread through the reference to the environment ( ), instead of using a global variable
), instead of using a global variable  as we did in the previous step.
as we did in the previous step.
We use a small set of monadic combinators, shown in Fig. 1, to build the translation in a more abstract way. The return and bind operators are standard for the reader monad. The parallel operator runs two monadic expressions concurrently, propagating the environment and the mutex. The \(\mathtt {atomic}\, \) combinator invokes a monadic expression with a fresh mutex. The \(\mathtt {atomic\_env}\, \) combinator atomically executes its body with the current environment as an argument. The \(\mathtt {run}{}\) function executes the monadic computation by instantiating it with a fresh mutex and a new environment. Selected clauses for the translation are presented in Fig. 2. The translation of the binary operations remains virtually unchanged, except for the usage of monadic parallel composition instead of the standard one. The translation for the assignment and the sequenced bind uses the \(\mathtt {atomic\_env}\, \) combinator for querying and updating the environment. We also have to adapt our translation of values, by wrapping it in \(\mathtt {ret}\, \):  .
.
A global function definition  is translated as a top level let-binding. A function call is then just an atomically executed function invocation in HeapLang, modulo the fact that the function pointer and the arguments are computed in parallel. In addition, sequence points occur at the beginning of each function call and at the end of each function body [22, Annex C], and we reflect that in our translation by clearing the environment at appropriate places.
is translated as a top level let-binding. A function call is then just an atomically executed function invocation in HeapLang, modulo the fact that the function pointer and the arguments are computed in parallel. In addition, sequence points occur at the beginning of each function call and at the end of each function body [22, Annex C], and we reflect that in our translation by clearing the environment at appropriate places.
Our semantics by translation can easily be extended to cover other features of C, e.g., a more advanced memory model (see Sect. 7). However the fragment presented here already illustrates the challenges that non-determinism and sequence point violations pose for verification. In the next section we describe a logic for reasoning about the semantics by translation given in this section.
3 Separation Logic with Weakest Preconditions for \(\lambda \mathsf {MC} \)
In this section we present a separation logic with weakest precondition propositions for reasoning about \(\lambda \mathsf {MC} \) programs. The logic tackles the main features of our semantics—non-determinism in expressions evaluation and sequence point violations. We will discuss the high-level rules of the logic pertaining to C connectives by going through a series of small examples.
The logic presented here is similar to the separation logic by Krebbers [29], but it is given in a weakest precondition style, and moreover, it is constructed synthetically on top of the separation logic framework Iris [24,25,26, 33], whereas the logic by Krebbers [29] is interpreted directly in a bespoke model.
The following grammar defines the formulas of the logic:

Most of the connectives are commonplace in separation logic, with the exception of the modified points-to connective, which we describe in this section.
As is common, Hoare triples  are syntactic sugar for
are syntactic sugar for  . The weakest precondition connective
. The weakest precondition connective  states that the program
states that the program  is safe (the program has defined behavior), and if
is safe (the program has defined behavior), and if  terminates to a value \(\mathtt {\mathtt {v}}\), then \(\mathtt {\mathtt {v}}\) satisfies the predicate
terminates to a value \(\mathtt {\mathtt {v}}\), then \(\mathtt {\mathtt {v}}\) satisfies the predicate  . We write
. We write  for
for  .
.
Contrary to the paper by Krebbers [29], we use weakest preconditions instead of Hoare triples throughout this paper. There are several reasons for doing so:
-
1.
We do not have to manipulate the preconditions explicitly, e.g., by applying the consequence rule to the precondition.
-
2.
The soundness of our symbolic executor (Theorem 5.1) can be stated more concisely using weakest precondition propositions.
-
3.
It is more convenient to integrate weakest preconditions into the Iris Proof Mode/MoSeL framework in Coq that we use for our implementation (Sect. 7).
A selection of rules is presented in Fig. 3. Each inference rule  in this paper should be read as the entailment
in this paper should be read as the entailment  . We now explain and motivate the rules of our logic.
. We now explain and motivate the rules of our logic.
Non-determinism. In the introduction (Sect. 1) we have already shown the rule for addition from Krebbers’s logic [29], which was written using Hoare triples. Using weakest preconditions, the corresponding rule ( wp-bin-op ) is:

This rule closely resembles the usual rule for parallel composition in ordinary concurrent separation logic [46]. This should not be surprising, as we have given a definitional semantics to binary operators using the parallel composition operator. It is important to note that the premises
wp-bin-op
are combined using the separating conjunction \(*\). This ensures that the weakest preconditions  and
and  for the subexpressions
for the subexpressions  and
and  are verified with respect to disjoint resources. As such they do not interfere with each other, and can be evaluated in parallel without causing sequence point violations.
are verified with respect to disjoint resources. As such they do not interfere with each other, and can be evaluated in parallel without causing sequence point violations.
To see how one can use the rule
wp-bin-op
, let us verify  . That is, we want to show that
. That is, we want to show that  satisfies the postcondition
satisfies the postcondition  assuming the precondition P. This goal can be proven by separating the precondition P into disjoint parts
assuming the precondition P. This goal can be proven by separating the precondition P into disjoint parts  . Then using
wp-bin-op
the goal can be reduced to proving
. Then using
wp-bin-op
the goal can be reduced to proving  for \(i \in \{0,1\}\), and
for \(i \in \{0,1\}\), and  for any return values
for any return values  of the expressions
of the expressions  .
.
Fractional Permissions. Separation logic includes the points-to connective \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\), which asserts unique ownership of a location \(\mathtt {l}\) with value \(\mathtt {\mathtt {v}}\). This connective is used to specify the behavior of stateful operations, which becomes apparent in the following proposed rule for load:

In order to verify  we first make sure that
we first make sure that  evaluates to a location \(\mathtt {l}\), and then we need to provide the points-to connective
evaluates to a location \(\mathtt {l}\), and then we need to provide the points-to connective  for some value stored at the location. This rule, together with
wp-value
, allows for verification of simple programs like
for some value stored at the location. This rule, together with
wp-value
, allows for verification of simple programs like  .
.
However, the rule above is too weak. Suppose that we wish to verify the program  from the precondition \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\). According to
wp-bin-op
, we have to separate the proposition \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\) into two disjoint parts, each used to verify the load operation. In order to enable sharing of points-to connectives we use fractional permissions [7, 8]. In separation logic with fractional permissions each points-to connective is annotated with a fraction \(q \in (0,1]\), and the resources can be split in accordance with those fractions:
from the precondition \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\). According to
wp-bin-op
, we have to separate the proposition \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\) into two disjoint parts, each used to verify the load operation. In order to enable sharing of points-to connectives we use fractional permissions [7, 8]. In separation logic with fractional permissions each points-to connective is annotated with a fraction \(q \in (0,1]\), and the resources can be split in accordance with those fractions:

A connective  provides a unique ownership of the location, and we refer to it as a write permission. A points-to connective with \(q \le 1\) provides shared ownership of the location, referred to as a read permission. By convention, we write \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\) to denote the write permission
provides a unique ownership of the location, and we refer to it as a write permission. A points-to connective with \(q \le 1\) provides shared ownership of the location, referred to as a read permission. By convention, we write \(\mathtt {l}\mapsto \mathtt {\mathtt {v}}\) to denote the write permission  .
.
With fractional permissions at hand, we can relax the proposed load rule, by allowing to dereference a location even if we only have a read permission:

This corresponds to the intuition that multiple subexpressions can safely dereference the same location, but not write to them.
Using the rule above we can verify  by splitting the assumption into
by splitting the assumption into  and first applying
wp-bin-op
with
and first applying
wp-bin-op
with  and
and  being
being  . Then we apply
wp-load
on both subgoals. After that, we can use
mapsto-split
to prove the remaining formula:
. Then we apply
wp-load
on both subgoals. After that, we can use
mapsto-split
to prove the remaining formula:

The Assignment Operator. The second main operation that accesses the heap is the assignment operator  . The arguments on the both sides of the assignment are evaluated in parallel, and a points-to connective is required to perform an update to the heap. A naive version of the assignment rule can be obtained by combining the binary operation rule and the load rule:
. The arguments on the both sides of the assignment are evaluated in parallel, and a points-to connective is required to perform an update to the heap. A naive version of the assignment rule can be obtained by combining the binary operation rule and the load rule:

The write permission  can be obtained by combining the resources of both sides of the assignment. This allows us to verify programs like
can be obtained by combining the resources of both sides of the assignment. This allows us to verify programs like  .
.
However, the rule above is unsound, because it fails to account for sequence point violations. We could use the rule above to prove safety of undefined programs, e.g., the program  .
.
To account for sequence point violations we decorate the points-to connectives  with access levels \(\xi \in \{L, U\}\). These have the following semantics: we can read from and write to a location that is unlocked (\(U\)), and the location becomes locked (\(L\)) once someone writes to it. Proposition
with access levels \(\xi \in \{L, U\}\). These have the following semantics: we can read from and write to a location that is unlocked (\(U\)), and the location becomes locked (\(L\)) once someone writes to it. Proposition  (resp.
(resp.  ) asserts ownership of the unlocked (resp. locked) location
) asserts ownership of the unlocked (resp. locked) location  . We refer to such propositions as lockable points-to connectives. Using lockable points-to connectives we can formulate the correct assignment rule:
. We refer to such propositions as lockable points-to connectives. Using lockable points-to connectives we can formulate the correct assignment rule:

The set \(\{ L, U\}\) has a lattice structure with \(L\le U\), and the levels can be combined with a join operation, see
mapsto-split
. By convention,  denotes
denotes  .
.
The Unlocking Modality. As locations become locked after using the assignment rule, we wish to unlock them in order to perform further heap operations. For instance, in the expression  the location
the location  becomes unlocked after the sequence point “\(\mathtt {;}\)” between the store and the dereferencing operations. To reflect this in the logic, we use the rule
wp-seq
which features the unlocking modality \(\mathbb {U}\) (which is called the unlocking assertion in [29, Definition 5.6]):
becomes unlocked after the sequence point “\(\mathtt {;}\)” between the store and the dereferencing operations. To reflect this in the logic, we use the rule
wp-seq
which features the unlocking modality \(\mathbb {U}\) (which is called the unlocking assertion in [29, Definition 5.6]):

Intuitively, \(\mathbb {U}P\) states that P holds, after unlocking all locations. The rules of \(\mathbb {U}\) in Fig. 3 allow one to turn  into
into  . This is done by applying either
U-unlock
or
U-intro
to each premise; then collecting all premises into one formula under \(\mathbb {U}\) by
U-sep
; and finally, applying
U-mono
to the whole sequent.
. This is done by applying either
U-unlock
or
U-intro
to each premise; then collecting all premises into one formula under \(\mathbb {U}\) by
U-sep
; and finally, applying
U-mono
to the whole sequent.
4 Soundness of Weakest Preconditions for \(\lambda \mathsf {MC} \)
In this section we prove adequacy of the separation logic with weakest preconditions for \(\lambda \mathsf {MC} \) as presented in Sect. 3. We do this by giving a model using the Iris framework that is structured in a similar way as the translation that we gave in Sect. 2. This translation consisted of three layers: the target HeapLang language, the monadic combinators, and the \(\lambda \mathsf {MC}\) operations themselves. In the model, each corresponding layer abstracts from the details of the previous layer, in such a way that we never have to break the abstraction of a layer. At the end, putting all of this together, we get the following adequacy statement:
Theorem 4.1
(Adequacy of Weakest Preconditions). If  is derivable, then
is derivable, then  has no undefined behavior for any evaluation order. In other words,
has no undefined behavior for any evaluation order. In other words,  does not assert false.
does not assert false.
The proof of the adequacy theorem closely follows the layered structure, by combining the correctness of the monadic \(\mathtt {run}\) combinator with adequacy of HeapLang in Iris [25, Theorem 6]. The rest of this section is organized as:
-
1.
Because our translation targets HeapLang, we start by recalling the separation logic with weakest preconditions, for HeapLang part of Iris (Sect. 4.1).
-
2.
On top of the logic for HeapLang, we define a notion of weakest preconditions
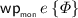 for expressions
for expressions  built from our monadic combinators (Sect. 4.2).
built from our monadic combinators (Sect. 4.2). -
3.
Next, we define the lockable points-to connective
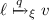 using Iris’s machinery for custom ghost state (Sect. 4.3).
using Iris’s machinery for custom ghost state (Sect. 4.3). -
4.
Finally, we define weakest preconditions for \(\lambda \mathsf {MC} \) by combining the weakest preconditions for monadic expressions with our translation scheme (Sect. 4.4).
4.1 Weakest Preconditions for HeapLang
We recall the most essential Iris connectives for reasoning about HeapLang programs:  and
and  , which are the HeapLang weakest precondition proposition and the HeapLang points-to connective, respectively. Other Iris connectives are described in [6, Section 8.1] or [25, 33]. An example rule is the store rule for HeapLang, shown in Fig. 4. The rule requires a points-to connective
, which are the HeapLang weakest precondition proposition and the HeapLang points-to connective, respectively. Other Iris connectives are described in [6, Section 8.1] or [25, 33]. An example rule is the store rule for HeapLang, shown in Fig. 4. The rule requires a points-to connective  , and the user receives the updated points-to connective
, and the user receives the updated points-to connective  back for proving
back for proving  . Note that the rule is formulated for a concrete location \(\ell \) and a value
. Note that the rule is formulated for a concrete location \(\ell \) and a value  , instead of arbitrary expressions. This does not limit the expressive power; since the evaluation order in HeapLang is deterministicFootnote 1, arbitrary expressions can be handled using the
wp
hl
-bind
rule. Using this rule, one can bind an expression
, instead of arbitrary expressions. This does not limit the expressive power; since the evaluation order in HeapLang is deterministicFootnote 1, arbitrary expressions can be handled using the
wp
hl
-bind
rule. Using this rule, one can bind an expression  in an arbitrary evaluation context
in an arbitrary evaluation context  . We can thus use the
wp
hl
-bind
rule twice to derive a more general store rule for HeapLang:
. We can thus use the
wp
hl
-bind
rule twice to derive a more general store rule for HeapLang:

To verify the monadic combinators and the translation of \(\lambda \mathsf {MC}\) operations in the upcoming Sects. 4.2 and 4.4, we need the specifications for all the functions that we use, including those on mutable sets and mutexes. The rules for mutable sets are standard, and thus omitted. They involve the usual abstract predicate \(\mathsf {is\_mset}({\textit{s}},X)\) stating that the reference \({\textit{s}}\) represents a set with contents X. The rules for mutexes are presented in Fig. 4. When a new mutex is created, a user gets access to a proposition  , which states that the value \({\textit{lk}}\) is a mutex containing the resources R. This proposition can be duplicated freely (
ismutex-dupl
). A thread can acquire the mutex and receive the resources contained in it. In addition, the thread receives a token
, which states that the value \({\textit{lk}}\) is a mutex containing the resources R. This proposition can be duplicated freely (
ismutex-dupl
). A thread can acquire the mutex and receive the resources contained in it. In addition, the thread receives a token  meaning that it has entered the critical section. When a thread leaves the critical section and releases the mutex, it has to give up both the token and the resources R.
meaning that it has entered the critical section. When a thread leaves the critical section and releases the mutex, it has to give up both the token and the resources R.
4.2 Weakest Preconditions for Monadic Expressions
As a next step, we define a weakest precondition proposition  for a monadic expression
for a monadic expression  . The definition is constructed in the ambient logic, and it encapsulates the monadic operations in a separate layer. Due to that, we are able to carry out proofs of high-level specifications without breaking the abstraction (Sect. 4.4). The specifications for selected monadic operations in terms of
. The definition is constructed in the ambient logic, and it encapsulates the monadic operations in a separate layer. Due to that, we are able to carry out proofs of high-level specifications without breaking the abstraction (Sect. 4.4). The specifications for selected monadic operations in terms of  are presented in Fig. 5. We define the weakest precondition for a monadic expression
are presented in Fig. 5. We define the weakest precondition for a monadic expression  as follows:
as follows:

The idea is that we first reduce  to a monadic value \({\textit{g}}\). To perform this reduction we have the outermost
to a monadic value \({\textit{g}}\). To perform this reduction we have the outermost  connective in the definition of
connective in the definition of  . This monadic value is then evaluated with an arbitrary environment and an arbitrary mutex. Note that we universally quantify over any mutex \({\textit{lk}}\) to support nested locking in \(\mathtt {atomic}\, \). This definition is parameterized by an environment invariant \(\mathsf {env\_inv}({\textit{env}})\), which describes the resources accessible in the critical sections. We show how to define \(\mathsf {env\_inv}\) in the next subsection.
. This monadic value is then evaluated with an arbitrary environment and an arbitrary mutex. Note that we universally quantify over any mutex \({\textit{lk}}\) to support nested locking in \(\mathtt {atomic}\, \). This definition is parameterized by an environment invariant \(\mathsf {env\_inv}({\textit{env}})\), which describes the resources accessible in the critical sections. We show how to define \(\mathsf {env\_inv}\) in the next subsection.
Using this definition we derive the monadic rules in Fig. 5. In a monad, the expression evaluation order is made explicit via the bind operation  . To that extent, contrary to HeapLang, we no longer have a rule like
wp
hl
-bind
, which allows to bind an expression in a general evaluation context. Instead, we have the rule
wp-bind
, which reflects that the only evaluation context we have is the monadic bind
. To that extent, contrary to HeapLang, we no longer have a rule like
wp
hl
-bind
, which allows to bind an expression in a general evaluation context. Instead, we have the rule
wp-bind
, which reflects that the only evaluation context we have is the monadic bind  .
.
4.3 Modeling the Heap
The monadic rules in Fig. 5 are expressive enough to derive some of the \(\lambda \mathsf {MC} \)-level rules, but we are still missing one crucial part: handling of the heap. In order to do that, we need to define lockable points-to connectives  in such a way that they are linked to the HeapLang points-to connectives
in such a way that they are linked to the HeapLang points-to connectives  .
.
The key idea is the following. The environment invariant \(\mathsf {env\_inv}\) of monadic weakest preconditions will track all HeapLang points-to connectives  that have ever been allocated at the \(\lambda \mathsf {MC}\) level. Via Iris ghost state, we then connect this knowledge to the lockable points-to connectives
that have ever been allocated at the \(\lambda \mathsf {MC}\) level. Via Iris ghost state, we then connect this knowledge to the lockable points-to connectives  . We refer to the construction that allows us to carry this out as the lockable heap. Note that the description of lockable heap is fairly technical and requires an understanding of the ghost state mechanism in Iris.
. We refer to the construction that allows us to carry this out as the lockable heap. Note that the description of lockable heap is fairly technical and requires an understanding of the ghost state mechanism in Iris.
A lockable heap is a map  that keeps track of the access levels and values associated with the locations. The connective
that keeps track of the access levels and values associated with the locations. The connective  asserts the ownership of all the locations present in the domain of \(\sigma \). Specifically, it asserts
asserts the ownership of all the locations present in the domain of \(\sigma \). Specifically, it asserts  for each
for each  . The connective
. The connective  then states that
then states that  is part of the global lockable heap, and it asserts this with the fractional permission q. We treat the lockable heap as an opaque abstraction, whose exact implementation via Iris ghost state is described in the Coq formalization [18]. The main interface for the locking heap are the rules in Fig. 6. The rule
heap-alloc
states that we can turn a HeapLang points-to connective
is part of the global lockable heap, and it asserts this with the fractional permission q. We treat the lockable heap as an opaque abstraction, whose exact implementation via Iris ghost state is described in the Coq formalization [18]. The main interface for the locking heap are the rules in Fig. 6. The rule
heap-alloc
states that we can turn a HeapLang points-to connective  into
into  by changing the lockable heap \(\sigma \) accordingly. The rule
heap-upd
states that given
by changing the lockable heap \(\sigma \) accordingly. The rule
heap-upd
states that given  , we can temporarily get a HeapLang points-to connective
, we can temporarily get a HeapLang points-to connective  out of the locking heap and update its value.
out of the locking heap and update its value.
The environment invariant \(\mathsf {env\_inv}({\textit{env}})\) in the definition of  ties the contents of the lockable heap to the contents of the environment \({\textit{env}}\):
ties the contents of the lockable heap to the contents of the environment \({\textit{env}}\):

The first conjunct states that  is a set of locked locations, according to the environment \({\textit{env}}\). The second conjunct asserts ownership of the global lockable heap \(\sigma \). Finally, the last conjunct states that the contents of \({\textit{env}}\) agrees with the lockable heap: every location that is in X is locked according to \(\sigma \).
is a set of locked locations, according to the environment \({\textit{env}}\). The second conjunct asserts ownership of the global lockable heap \(\sigma \). Finally, the last conjunct states that the contents of \({\textit{env}}\) agrees with the lockable heap: every location that is in X is locked according to \(\sigma \).
The Unlocking Modality. The unlocking modality is defined in the logic as:

Here S is a finite multiset of tuples containing locations, values, and fractions. The update modality accumulates the locked locations, waiting for them to be unlocked at a sequence point.
4.4 Deriving the \(\lambda \mathsf {MC} \) Rules
To model weakest preconditions for \(\lambda \mathsf {MC}\) (Fig. 3) we compose the construction we have just defined with the translation of Sect. 2  Here,
Here,  is the obvious lifting of
is the obvious lifting of  from \(\lambda \mathsf {MC} \) values to HeapLang values. Using the rules from Figs. 5 and 6 we derive the high-level \(\lambda \mathsf {MC} \) rules without unfolding the definition of the monadic
from \(\lambda \mathsf {MC} \) values to HeapLang values. Using the rules from Figs. 5 and 6 we derive the high-level \(\lambda \mathsf {MC} \) rules without unfolding the definition of the monadic  .
.
Example 4.2
Consider the rule
wp-store
for assignments  . Using
wp-bind
and
wp-par
, the soundness of
wp-store
can be reduced to verifying the assignment with
. Using
wp-bind
and
wp-par
, the soundness of
wp-store
can be reduced to verifying the assignment with  being \(\mathtt {l}\),
being \(\mathtt {l}\),  being \(\mathtt {\mathtt {v}}'\), under the assumption
being \(\mathtt {\mathtt {v}}'\), under the assumption  . We use
wp-atomic-env
to turn our goal into a HeapLang weakest precondition proposition and to gain access an environment \({\textit{env}}\), and to the proposition \(\mathsf {env\_inv}({\textit{env}})\), from which we extract the lockable heap \(\sigma \). We then use
heap-upd
to get access to the underlying HeapLang location and obtain that
. We use
wp-atomic-env
to turn our goal into a HeapLang weakest precondition proposition and to gain access an environment \({\textit{env}}\), and to the proposition \(\mathsf {env\_inv}({\textit{env}})\), from which we extract the lockable heap \(\sigma \). We then use
heap-upd
to get access to the underlying HeapLang location and obtain that  is not locked according to \(\sigma \). Due to the environment invariant, we obtain that
is not locked according to \(\sigma \). Due to the environment invariant, we obtain that  is not in \({\textit{env}}\), which allows us to prove the
is not in \({\textit{env}}\), which allows us to prove the  for sequence point violation in the interpretation of the assignment. Finally, we perform the physical update of the location.
for sequence point violation in the interpretation of the assignment. Finally, we perform the physical update of the location.
5 A Symbolic Executor for \(\lambda \mathsf {MC} \)
In order to turn our program logic into an automated procedure, it is important to have rules for weakest preconditions that have an algorithmic form. However, the rules for binary operators in our separation logic for \(\lambda \mathsf {MC} \) do not have such a form. Take for example the rule
wp-bin-op
for binary operators  . This rule cannot be applied in an algorithmic manner. To use the rule one should supply the postconditions for
. This rule cannot be applied in an algorithmic manner. To use the rule one should supply the postconditions for  and
and  , and frame the resources from the context into two disjoint parts. This is generally impossible to do automatically.
, and frame the resources from the context into two disjoint parts. This is generally impossible to do automatically.
To address this problem, we first describe how the rules for binary operators can be transformed into algorithmic rules by exploiting the notion of symbolic execution [5] (Sect. 5.1). We then show how to implement these algorithmic rules as part of an automated symbolic execution procedure (Sect. 5.2).
5.1 Rules for Symbolic Execution
We say that we can symbolically execute an expression  using a precondition P, if we can find a symbolic execution tuple
using a precondition P, if we can find a symbolic execution tuple  consisting of a return value
consisting of a return value  , a postcondition Q, and a frame R satisfying:
, a postcondition Q, and a frame R satisfying:

This specification is much like that of ordinary symbolic execution in separation logic [5], but there is important difference. Apart from computing the postcondition Q and the return value  , there is also the frame R, which describes the resources that are not used for proving
, there is also the frame R, which describes the resources that are not used for proving  . For instance, if the precondition P is
. For instance, if the precondition P is  and
and  is a load operation
is a load operation  , then we can symbolically execute
, then we can symbolically execute  with the postcondition Q being
with the postcondition Q being  , and the frame R being
, and the frame R being  . Clearly, \(P'\) is not needed for proving the load, so it can be moved into the frame. More interestingly, since loading the contents of
. Clearly, \(P'\) is not needed for proving the load, so it can be moved into the frame. More interestingly, since loading the contents of  requires a read permission
requires a read permission  , with \(p \in (0,1]\), we can split the hypothesis
, with \(p \in (0,1]\), we can split the hypothesis  into two halves and move one into the frame. Below we will see why that matters.
into two halves and move one into the frame. Below we will see why that matters.
If we can symbolically execute one of the operands of a binary expression  , say
, say  in P, and find a symbolic execution tuple
in P, and find a symbolic execution tuple  , then we can use the following admissible rule:
, then we can use the following admissible rule:

This rule has a much more algorithmic flavor than the rule
wp-bin-op
. Applying the above rule now boils down to finding such a tuple  , instead of having to infer postconditions for both operands, as we need to do to apply
wp-bin-op
.
, instead of having to infer postconditions for both operands, as we need to do to apply
wp-bin-op
.
For instance, given an expression  and a precondition
and a precondition  , we can derive the following rule:
, we can derive the following rule:

This rule matches the intuition that only a fraction of the permission  is needed to prove a load
is needed to prove a load  , so that the remaining half of the permission can be used to prove the correctness of
, so that the remaining half of the permission can be used to prove the correctness of  (which may contain other loads of
(which may contain other loads of  ).
).
5.2 An Algorithm for Symbolic Execution
For an arbitrary expression  and a proposition P, it is unlikely that one can find such a symbolic execution tuple
and a proposition P, it is unlikely that one can find such a symbolic execution tuple  automatically. However, for a certain class of C expressions that appear in actual programs we can compute a choice of such a tuple. To illustrate our approach, we will define such an algorithm for a small subset
automatically. However, for a certain class of C expressions that appear in actual programs we can compute a choice of such a tuple. To illustrate our approach, we will define such an algorithm for a small subset  of C expressions described by the following grammar:
of C expressions described by the following grammar:

We keep this subset small to ease presentation. In Sect. 7 we explain how to extend the algorithm to cover the sequenced bind operator  .
.
Moreover, to implement symbolic execution, we cannot manipulate arbitrary separation logic propositions. We thus restrict to symbolic heaps (\(m\in \mathsf {sheap}\)), which are defined as finite partial functions  representing a collection of points-to propositions:
representing a collection of points-to propositions:

We use the following operations on symbolic heaps:
-
 sets the entry
sets the entry  to
to 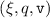 ;
; -
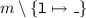 removes the entry
removes the entry  from
from 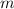 ;
; -
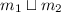 merges the symbolic heaps
merges the symbolic heaps  and
and 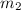 in such a way that for each
in such a way that for each  , we have:
, we have: 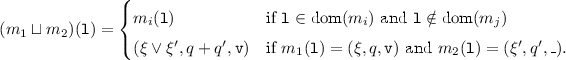
With this representation of propositions, we define the symbolic execution algorithm as a partial function  , which satisfies the specification stated in Sect. 5.1, i.e., for which the following holds:
, which satisfies the specification stated in Sect. 5.1, i.e., for which the following holds:
Theorem 5.1
Given an expression  and an symbolic heap
and an symbolic heap  , if
, if  returns a tuple
returns a tuple  , then
, then 
The definition of the algorithm is shown in Fig. 7. Given a tuple  , a call to
, a call to  either returns a tuple
either returns a tuple  or fails, which either happens when
or fails, which either happens when  or when one of intermediate steps of computation fails. In the latter cases, we write
or when one of intermediate steps of computation fails. In the latter cases, we write  .
.
The algorithm proceeds by case analysis on the expression  . In each case, the expected output is described by the equation
. In each case, the expected output is described by the equation  . The results of the intermediate computations appear on separate lines under the clause “
. The results of the intermediate computations appear on separate lines under the clause “ ”. If one of the corresponding equations does not hold, e.g., a recursive call fails, then the failure is propagated. Let us now explain the case for the assignment operator.
”. If one of the corresponding equations does not hold, e.g., a recursive call fails, then the failure is propagated. Let us now explain the case for the assignment operator.
If  is an assignment operator
is an assignment operator  , we first evaluate
, we first evaluate  and then
and then  . Fixing the order of symbolic execution from left to right does not compromise the non-determinism underlying the C semantics of binary operators. Indeed, when
. Fixing the order of symbolic execution from left to right does not compromise the non-determinism underlying the C semantics of binary operators. Indeed, when  , we evaluate the expression
, we evaluate the expression  , using the frame \(m_1\), i.e., only the resources of \(m\) that remain after the execution of
, using the frame \(m_1\), i.e., only the resources of \(m\) that remain after the execution of  . When
. When  , with
, with 
 , and
, and  , the function
, the function  checks whether
checks whether  contains the write permission
contains the write permission  . If this holds, it removes the location
. If this holds, it removes the location  , so that the write permission is now consumed. Finally, we merge
, so that the write permission is now consumed. Finally, we merge  with the output heap \(m_3^o\), so that after assignment, the write permission
with the output heap \(m_3^o\), so that after assignment, the write permission  is given back in a locked state.
is given back in a locked state.
6 A Verification Condition Generator for \(\lambda \mathsf {MC} \)
To establish correctness of programs, we need to prove goals  . To prove such a goal, one has to repeatedly apply the rules for weakest preconditions, intertwined with logical reasoning. In this section we will automate this process for \(\lambda \mathsf {MC} \) by means of a verification condition generator (vcgen).
. To prove such a goal, one has to repeatedly apply the rules for weakest preconditions, intertwined with logical reasoning. In this section we will automate this process for \(\lambda \mathsf {MC} \) by means of a verification condition generator (vcgen).
As a first attempt to define a vcgen, one could try to recurse over the expression  and apply the rules in Fig. 3 eagerly. This would turn the goal into a separation logic proposition that subsequently should be solved. However, as we pointed out in Sect. 5.1, the resulting separation logic proposition will be very difficult to prove—either interactively or automatically—due to the existentially quantified postconditions that appear because of uses of the rules for binary operators (e.g.,
wp-bin-op
). We then proposed alternative rules that avoid the need for existential quantifiers. These rules look like:
and apply the rules in Fig. 3 eagerly. This would turn the goal into a separation logic proposition that subsequently should be solved. However, as we pointed out in Sect. 5.1, the resulting separation logic proposition will be very difficult to prove—either interactively or automatically—due to the existentially quantified postconditions that appear because of uses of the rules for binary operators (e.g.,
wp-bin-op
). We then proposed alternative rules that avoid the need for existential quantifiers. These rules look like:

To use this rule, the crux is to symbolically execute  with precondition P into a symbolic execution triple \((\mathtt {\mathtt {v}}_1,Q,R)\), which we alluded could be automatically computed by means of the symbolic executor if
with precondition P into a symbolic execution triple \((\mathtt {\mathtt {v}}_1,Q,R)\), which we alluded could be automatically computed by means of the symbolic executor if  (Sect. 5.2).
(Sect. 5.2).
We can only use the symbolic executor if P is of the shape \(\llbracket m \rrbracket \) for a symbolic heap \(m\). However, in actual program verification, the precondition P is hardly ever of that shape. In addition to a series of points-to connectives (as described by a symbolic heap), we may have arbitrary propositions of separation logic, such as pure facts, abstract predicates, nested Hoare triples, Iris ghost state, etc. These propositions may be needed to prove intermediate verification conditions, e.g., for function calls. As such, to effectively apply the above rule, we need to separate our precondition P into two parts: a symbolic heap \(\llbracket m \rrbracket \) and a remainder \(P'\). Assuming  , we may then use the following rule:
, we may then use the following rule:

It is important to notice that by applying this rule, the remainder \(P'\) remains in our precondition as is, but the symbolic heap is changed from \(\llbracket m \rrbracket \) into \(\llbracket m_1 \rrbracket \), i.e., into the frame that we obtained by symbolically executing  .
.
It should come as no surprise that we can automate this process, by applying rules, such as the one we have given above, recursively, and threading through symbolic heaps. Formally, we do this by defining the vcgen as a total function:  where
where  is the type of propositions of our logic. The definition of \(\mathsf {vcg} \) is given in Fig. 8. Before explaining the details, let us state its correctness theorem:
is the type of propositions of our logic. The definition of \(\mathsf {vcg} \) is given in Fig. 8. Before explaining the details, let us state its correctness theorem:
Theorem 6.1
Given an expression  , a symbolic heap \(m\), and a postcondition
, a symbolic heap \(m\), and a postcondition  , the following statement holds:
, the following statement holds:

This theorem reflects the general shape of the rules we previously described. We start off with a goal  , and after using the vcgen, we should prove that the generated goal follows from \(P'\). It is important to note that the continuation in the vcgen is not only parameterized by the return value, but also by a symbolic heap corresponding to the resources that remain. To get these resources back, the vcgen is initiated with the continuation
, and after using the vcgen, we should prove that the generated goal follows from \(P'\). It is important to note that the continuation in the vcgen is not only parameterized by the return value, but also by a symbolic heap corresponding to the resources that remain. To get these resources back, the vcgen is initiated with the continuation  .
.
Most clauses of the definition of the vcgen (Fig. 8) follow the approach we described so far. For unary expressions like load we generate a condition that corresponds to the weakest precondition rule. For binary expressions, we symbolically execute either operand, and proceed recursively in the other. There are a number of important bells and whistles that we will discuss now.
Sequencing. In the case of sequenced binds  , we recursively compute the verification condition for
, we recursively compute the verification condition for  with the continuation:
with the continuation:

Due to a sequence point, all locations modified by  will be in the unlocked state after it is finished executing. Therefore, in the recursive call to
will be in the unlocked state after it is finished executing. Therefore, in the recursive call to  we unlock all locations in the symbolic heap (c.f. \(\mathsf {unlock}\texttt {(}m'\texttt {)}\)), and we include a \(\mathbb {U}\) modality in the continuation. The \(\mathbb {U}\) modality is crucial so that the resources that are not given to the vcgen (the remainder \(P'\) in Theorem 6.1) can also be unlocked.
we unlock all locations in the symbolic heap (c.f. \(\mathsf {unlock}\texttt {(}m'\texttt {)}\)), and we include a \(\mathbb {U}\) modality in the continuation. The \(\mathbb {U}\) modality is crucial so that the resources that are not given to the vcgen (the remainder \(P'\) in Theorem 6.1) can also be unlocked.
Handling Failure. In the case of binary operators  , it could be that the symbolic executor fails on both
, it could be that the symbolic executor fails on both  and
and  , because neither of the arguments were of the right shape (i.e., not an element of \(\overline{\mathsf {expr}}\)), or the required resources were not present in the symbolic heap. In this case the vcgen generates the goal of the form
, because neither of the arguments were of the right shape (i.e., not an element of \(\overline{\mathsf {expr}}\)), or the required resources were not present in the symbolic heap. In this case the vcgen generates the goal of the form  where
where  . What appears here is that the current symbolic heap
. What appears here is that the current symbolic heap  is given back to the user, which they can use to prove the weakest precondition of
is given back to the user, which they can use to prove the weakest precondition of  by hand. Through the postcondition
by hand. Through the postcondition  the user can resume the vcgen, by choosing a new symbolic heap \(m'\) and invoking the continuation
the user can resume the vcgen, by choosing a new symbolic heap \(m'\) and invoking the continuation  .
.
For assignments  we have a similar situation. Symbolic execution of both
we have a similar situation. Symbolic execution of both  and
and  may fail, and then we generate a goal similar to the one for binary operators. If the location
may fail, and then we generate a goal similar to the one for binary operators. If the location  that we wish to assign to is not in the symbolic heap, we use the continuation
that we wish to assign to is not in the symbolic heap, we use the continuation  As before, the user gets back the current symbolic heap \(\llbracket m \rrbracket \), and could resume the vcgen through the postcondition
As before, the user gets back the current symbolic heap \(\llbracket m \rrbracket \), and could resume the vcgen through the postcondition  by picking a new symbolic heap.
by picking a new symbolic heap.
7 Discussion
Extensions of the Language. The memory model that we have presented in this paper was purposely oversimplified. In Coq, the memory model for \(\lambda \mathsf {MC} \) additionally supports mutable local variables, arrays, and pointer arithmetic. Adding support for these features was relatively easy and required only local changes to the definitional semantics and the separation logic.
For implementing mutable local variables, we tag each location with a Boolean that keeps track of whether it is an allocated or a local variable. That way, we can forbid deallocating local variables using the \(\mathtt {free}\texttt {(} \mathtt {-}\texttt {)}\) operator.
Our extended memory model is block/offset-based like CompCert’s memory model [38]. Pointers are not simply represented as locations, but as pairs \((\ell , i)\), where \(\ell \) is a HeapLang reference to a memory block containing a list of values, and i is an offset into that block. The points-to connectives of our separation logic then correspondingly range over block/offset-based pointers.
Symbolic Execution of Sequence Points. We adapt our \(\mathsf {forward} \) algorithm to handle sequenced bind operators  . The subtlety lies in supporting nested sequenced binds. For example, in an expression
. The subtlety lies in supporting nested sequenced binds. For example, in an expression  the postcondition of
the postcondition of  can be used (along with the frame) for the symbolic execution of
can be used (along with the frame) for the symbolic execution of  , but it cannot be used for the symbolic execution of
, but it cannot be used for the symbolic execution of  . In order to solve this, our \(\mathsf {forward} \) algorithm takes a stack of symbolic heaps as an input, and returns a stack of symbolic heaps (of the same length) as a frame. All the cases shown in Fig. 7 are easily adapted w.r.t. this modification, and the following definition captures the case for the sequence point bind:
. In order to solve this, our \(\mathsf {forward} \) algorithm takes a stack of symbolic heaps as an input, and returns a stack of symbolic heaps (of the same length) as a frame. All the cases shown in Fig. 7 are easily adapted w.r.t. this modification, and the following definition captures the case for the sequence point bind:

Shared Resource Invariants. As in Krebbers’s logic [29], the rules for binary operators in Fig. 3 require the resources to be separated into disjoint parts for the subexpressions. If both sides of a binary operator are function calls, then they can only share read permissions despite that both function calls are executed atomically. Following Krebbers, we address this limitation by adding a shared resource invariant R to our weakest preconditions and add the following rules:

To temporarily transfer resources into the invariant, one can use the first rule. Because function calls are not interleaved, one can use the last rule to gain access to the shared resource invariant for the duration of the function call.
Our handling of shared resource invariants generalizes the treatment by Krebbers: using custom ghost state in Iris we can endow the resource invariant with a protocol. This allows us to verify examples that were previously impossible [29]:

Krebbers could only prove that
 returns 0, 3 or 4, whereas we can prove it returns 3 or 4 by combining resource invariants with Iris’s ghost state.
returns 0, 3 or 4, whereas we can prove it returns 3 or 4 by combining resource invariants with Iris’s ghost state.
Implementation in Coq. In the Coq development [18] we have:
-
Defined \(\lambda \mathsf {MC} \) with the extensions described above, as well as the monadic combinators, as a shallow embedding on top of Iris’s HeapLang [21, 25].
-
Modeled the separation logic for \(\lambda \mathsf {MC} \) and the monadic combinators as a shallow embedding on top of the Iris’s program logic for HeapLang.
-
Implemented the symbolic executor and vcgen as computable Coq functions, and proved their soundness w.r.t. our separation logic.
-
Turned the verification condition generator into a tactic that integrates into the Iris Proof Mode/MoSeL framework [32, 34].
This last point allowed us to leverage the existing machinery for separation logic proofs in Coq. Firstly, we get basic building blocks for implementing the vcgen tactic for free. Secondly, when the vcgen is unable to solve the goal, one can use the Iris Proof Mode/MoSeL tactics to help out in a convenient manner.
To implement the symbolic executor and vcgen, we had to reify the terms and values of \(\lambda \mathsf {MC} \). To see why reification is needed, consider the data type for symbolic heaps, which uses locations as keys. In proofs, those locations appear as universally quantified variables. To compute using these, we need to reify them into some symbolic representation. We have implemented the reification mechanism using type classes, following Spitters and van der Weegen [47].
With all the mechanics in place, our vcgen is able to significantly aid us. Consider the following program that copies the contents of one array into another:

We proved  in 11 lines of Coq code. The vcgen can automatically process the program up until the while loop. At that point, the user has to manually perform an induction on the array, providing a suitable induction hypothesis. The vcgen is then able to discharge the base case automatically. In the inductive case, it will automatically process the program until the next iteration of the while loop, where the user has to apply the induction hypothesis.
in 11 lines of Coq code. The vcgen can automatically process the program up until the while loop. At that point, the user has to manually perform an induction on the array, providing a suitable induction hypothesis. The vcgen is then able to discharge the base case automatically. In the inductive case, it will automatically process the program until the next iteration of the while loop, where the user has to apply the induction hypothesis.
8 Related Work
C Semantics. There has been a considerable body of work on formal semantics for the C language, including several large projects that aimed to formalize substantial subsets of C [17, 20, 30, 37, 41, 44], and projects that focused on specific aspects like its memory model [10, 13, 27, 28, 31, 38, 40, 41], weak memory concurrency [4, 36, 43], non-local control flow [35], verified compilation [37, 48], etc.
The focus of this paper—non-determinism in C expressions—has been treated formally a number of times, notably by Norrish [44], Ellison and Rosu [17], Krebbers [31], and Memarian et al. [41]. The first three have in common that they model the sequence point restriction by keeping track of the locations that have been written to. The treatment of sequence points in our definitional semantics is closely inspired by the work of Ellison and Rosu [17], which resembles closely what is in the C standard. Krebbers [31] used a more restrictive version of the semantics by Ellison and Rosu—he assigned undefined behavior in some corner cases to ease the soundness theorem of his logic. We directly proved soundness of the logic w.r.t. the more faithful model by Ellison and Rosu.
Memarian et al. [41] give a semantics to C by elaboration into a language they call Core. Unspecified evaluation order in Core is modeled using an unseq operation, which is similar to our \(\mathbin {||_{\textsf {\tiny HL}}}\) operation. Compared to our translation, Core is much closer to C (it has function calls, memory operations, etc. as primitives, while we model them with monadic combinators), and supports concurrency.
Reasoning Tools and Program Logics for C. Apart from formalizing the semantics of C, there have been many efforts to create reasoning tools for the C language in one way or another. There are standalone tools, like VeriFast [23], VCC [12], and the Jessie plugin of Frama-C [42], and there are tools built on top of general purpose proof assistants like VST [1, 10] in Coq, or AutoCorres [19] in Isabelle/HOL. Although, admittedly, all of these tools cover larger subsets of C than we do, as far as we know, they all ignore non-determinism in expressions.
There are a few exceptions. Norrish proved confluence for a certain class of C expressions [45]. Such a confluence result may be used to justify proofs in a tool that does not have an underlying non-deterministic semantics.
Another exception is the separation logic for non-determinism in C by Krebbers [29]. Our work is inspired by his, but there are several notable differences:
-
We have proved soundness with respect to a definitional semantics for a subset of C. We believe that this approach is more modular, since the semantics can be specified at a higher level of abstraction.
-
We have built our logic on top of the Iris framework. This makes the development more modular (since we can use all the features as well as the Coq infrastructure of Iris) and more expressive (as shown in Sect. 7).
-
There was no automation like our vcgen, so one had to subdivide resources between subexpressions manually all the time. Also, there was not even tactical support for carrying out proofs manually. Our logic is redesigned to get such support from the Iris Proof Mode/MoSeL framework.
To handle missing features of C as part of our vcgen, we plan to explore approaches by other verification projects in proof assistants. A notable example of such a project is VST, which supports machine arithmetic [16] and data types like structs and unions [10] as part of its tactics for symbolic execution.
Separation Logic and Symbolic Execution. In their seminal work, Berdine et al. [5] demonstrate the application of symbolic execution to automated reasoning in separation logic. In their setting, frame inference is used to perform symbolic execution of function calls. The frame has to be computed when the call site has more resources than needed to invoke a function. In our setting we compute frames for subexpressions, which, unlike functions, do not have predefined specifications. Due to that, we have to perform frame inference simultaneously with symbolic execution. The symbolic execution algorithm of Berdine et al. can handle inductive predicates, and can be extended with shape analysis [15]. We do not support such features, and leave them to future work.
Caper [14] is a tool for automated reasoning in concurrent separation logic, and it also deals with non-determinism, although the nature of non-determinism in Caper is different. Non-determinism in Caper arises due to branching on unknown conditionals and due to multiple possible ways to apply ghost state related rules (rules pertaining to abstract regions and guards). The former cause is tackled by considering sets of symbolic execution traces, and the latter is resolved by employing heuristics based on bi-abduction [9]. Applications of abductive reasoning to our approach to symbolic execution are left for future work.
Recently, Bannister et al. [2, 3] proposed a new separation logic connective for performing forwards reasoning whilst avoiding frame inference. This approach, however, is aimed at sequential deterministic programs, focusing on a notion of partial correctness that allows for failed executions. Another approach to verification of sequential stateful programs is based on characteristic formulae [11]. A stateful program is transformed into a higher-order logic predicate, implicitly encoding the frame rule. The resulting formula is then proved by a user in Coq.
When implementing a vcgen in a proof assistant (see e.g., [10, 39]) it is common to let the vcgen return a new goal when it gets stuck, from which the user can help out and call back the vcgen. The novelty of our work is that this approach is applied to operations that are called in parallel.
Notes
- 1.
And right-to-left, although our monadic translation does not rely on that.
References
Appel, A.W. (ed.): Program Logics for Certified Compilers. Cambridge University Press, New York (2014)
Bannister, C., Höfner, P.: False failure: creating failure models for separation logic. In: Desharnais, J., Guttmann, W., Joosten, S. (eds.) RAMiCS 2018. LNCS, vol. 11194, pp. 263–279. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-02149-8_16
Bannister, C., Höfner, P., Klein, G.: Backwards and forwards with separation logic. In: Avigad, J., Mahboubi, A. (eds.) ITP 2018. LNCS, vol. 10895, pp. 68–87. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94821-8_5
Batty, M., Owens, S., Sarkar, S., Sewell, P., Weber, T.: Mathematizing C++ concurrency. In: POPL, pp. 55–66 (2011)
Berdine, J., Calcagno, C., O’Hearn, P.W.: Symbolic execution with separation logic. In: Yi, K. (ed.) APLAS 2005. LNCS, vol. 3780, pp. 52–68. Springer, Heidelberg (2005). https://doi.org/10.1007/11575467_5
Birkedal, L., Bizjak, A.: Lecture Notes on Iris: Higher-Order Concurrent Separation Logic, August 2018. https://iris-project.org/tutorial-material.html
Bornat, R., Calcagno, C., O’Hearn, P.W., Parkinson, M.J.: Permission accounting in separation logic. In: POPL, pp. 259–270 (2005)
Boyland, J.: Checking interference with fractional permissions. In: Cousot, R. (ed.) SAS 2003. LNCS, vol. 2694, pp. 55–72. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44898-5_4
Calcagno, C., Distefano, D., O’Hearn, P.W., Yang, H.: Compositional shape analysis by means of bi-abduction. J. ACM 58(6), 26:1–26:66 (2011)
Cao, Q., Beringer, L., Gruetter, S., Dodds, J., Appel, A.W.: VST-Floyd: a separation logic tool to verify correctness of C programs. JAR 61(1–4), 367–422 (2018)
Charguéraud, A.: Characteristic formulae for the verification of imperative programs. SIGPLAN Not. 46(9), 418–430 (2011)
Cohen, E., et al.: VCC: a practical system for verifying concurrent C. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 23–42. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_2
Cohen, E., Moskal, M., Tobies, S., Schulte, W.: A precise yet efficient memory model for C. ENTCS 254, 85–103 (2009)
Dinsdale-Young, T., da Rocha Pinto, P., Andersen, K.J., Birkedal, L.: Caper - automatic verification for fine-grained concurrency. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 420–447. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_16
Distefano, D., O’Hearn, P.W., Yang, H.: A local shape analysis based on separation logic. In: Hermanns, H., Palsberg, J. (eds.) TACAS 2006. LNCS, vol. 3920, pp. 287–302. Springer, Heidelberg (2006). https://doi.org/10.1007/11691372_19
Dodds, J., Appel, A.W.: Mostly sound type system improves a foundational program verifier. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 17–32. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03545-1_2
Ellison, C., Rosu, G.: An executable formal semantics of C with applications. In: POPL, pp. 533–544 (2012)
Frumin, D., Gondelman, L., Krebbers, R.: Semi-automated reasoning about non-determinism in C expressions: Coq development, February 2019. https://cs.ru.nl/~dfrumin/wpc/
Greenaway, D., Lim, J., Andronick, J., Klein, G.: Don’t sweat the small stuff: formal verification of C code without the pain. In: PLDI, pp. 429–439 (2014)
Hathhorn, C., Ellison, C., Roşu, G.: Defining the undefinedness of C. In: PLDI, pp. 336–345 (2015)
Iris: Iris Project, November 2018. https://iris-project.org/
ISO: ISO/IEC 9899–2011: Programming Languages - C. ISO Working Group 14 (2012)
Jacobs, B., Smans, J., Piessens, F.: A quick tour of the VeriFast program verifier. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 304–311. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17164-2_21
Jung, R., Krebbers, R., Birkedal, L., Dreyer, D.: Higher-order ghost state. In: ICFP, pp. 256–269 (2016)
Jung, R., Krebbers, R., Jourdan, J.H., Bizjak, A., Birkedal, L., Dreyer, D.: Iris from the ground up: a modular foundation for higher-order concurrent separation logic. J. Funct. Program. 28, e20 (2018). https://doi.org/10.1017/S0956796818000151
Jung, R., et al.: Iris: monoids and invariants as an orthogonal basis for concurrent reasoning. In: POPL, pp. 637–650 (2015)
Kang, J., Hur, C., Mansky, W., Garbuzov, D., Zdancewic, S., Vafeiadis, V.: A formal C memory model supporting integer-pointer casts. In: POPL, pp. 326–335 (2015)
Krebbers, R.: Aliasing restrictions of C11 formalized in Coq. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 50–65. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03545-1_4
Krebbers, R.: An operational and axiomatic semantics for non-determinism and sequence points in C. In: POPL, pp. 101–112 (2014)
Krebbers, R.: The C standard formalized in Coq. Ph.D. thesis, Radboud University Nijmegen (2015)
Krebbers, R.: A formal C memory model for separation logic. JAR 57(4), 319–387 (2016)
Krebbers, R., et al.: MoSeL: a general, extensible modal framework for interactive proofs in separation logic. PACMPL 2(ICFP), 77:1–77:30 (2018)
Krebbers, R., Jung, R., Bizjak, A., Jourdan, J.-H., Dreyer, D., Birkedal, L.: The Essence of higher-order concurrent separation logic. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 696–723. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_26
Krebbers, R., Timany, A., Birkedal, L.: Interactive proofs in higher-order concurrent separation logic. In: POPL, pp. 205–217 (2017)
Krebbers, R., Wiedijk, F.: Separation logic for non-local control flow and block scope variables. In: Pfenning, F. (ed.) FoSSaCS 2013. LNCS, vol. 7794, pp. 257–272. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37075-5_17
Lahav, O., Vafeiadis, V., Kang, J., Hur, C., Dreyer, D.: Repairing Sequential Consistency in C/C++11. In: PLDI, pp. 618–632 (2017)
Leroy, X.: Formal verification of a realistic compiler. CACM 52(7), 107–115 (2009)
Leroy, X., Blazy, S.: Formal verification of a C-like memory model and its uses for verifying program transformations. JAR 41(1), 1–31 (2008)
Malecha, G.: Extensible proof engineering in intensional type theory. Ph.D. thesis, Harvard University (2014)
Memarian, K., et al.: Exploring C semantics and pointer provenance. PACMPL 3(POPL), 67:1–67:32 (2019)
Memarian, K., et al.: Into the depths of C: elaborating the De Facto Standards. In: PLDI, pp. 1–15 (2016)
Moy, Y., Marché, C.: The Jessie Plugin for Deduction Verification in Frama-C, Tutorial and Reference Manual (2011)
Nienhuis, K., Memarian, K., Sewell, P.: An operational semantics for C/C++11 concurrency. In: OOPSLA, pp. 111–128 (2016)
Norrish, M.: C Formalised in HOL. Ph.D. thesis, University of Cambridge (1998)
Norrish, M.: Deterministic expressions in C. In: Swierstra, S.D. (ed.) ESOP 1999. LNCS, vol. 1576, pp. 147–161. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49099-X_10
O’Hearn, P.W.: Resources, concurrency, and local reasoning. Theor. Comput. Sci. 375(1), 271–307 (2007). Festschrift for John C. Reynolds’s 70th birthday
Spitters, B., Van der Weegen, E.: Type classes for mathematics in type theory. Math. Struct. Comput. Sci. 21(4), 795–825 (2011)
Stewart, G., Beringer, L., Cuellar, S., Appel, A.W.: Compositional CompCert. In: POPL, pp. 275–287 (2015)
Acknowledgments
We are grateful to Gregory Malecha and the anonymous reviewers and for their comments and suggestions. This work was supported by the Netherlands Organisation for Scientific Research (NWO), project numbers STW.14319 (first and second author) and 016.Veni.192.259 (third author).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Frumin, D., Gondelman, L., Krebbers, R. (2019). Semi-automated Reasoning About Non-determinism in C Expressions. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)








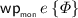 for expressions
for expressions  built from our monadic combinators (Sect.
built from our monadic combinators (Sect. 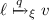 using Iris’s machinery for custom ghost state (Sect.
using Iris’s machinery for custom ghost state (Sect. 
 rules.
rules.
 rules.
rules.
 sets the entry
sets the entry  to
to 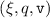 ;
;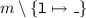 removes the entry
removes the entry  from
from 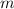 ;
;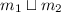 merges the symbolic heaps
merges the symbolic heaps  and
and 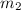 in such a way that for each
in such a way that for each  , we have:
, we have: