Abstract
We present an abstract domain able to infer invariants on programs manipulating trees. Trees considered in the article are defined over a finite alphabet and can contain unbounded numeric values at their leaves. Our domain can infer the possible shapes of the tree values of each variable and find numeric relations between: the values at the leaves as well as the size and depth of the tree values of different variables. The abstract domain is described as a product of (1) a symbolic domain based on a tree automata representation and (2) a numerical domain lifted, for the occasion, to describe numerical maps with potentially infinite and heterogeneous definition set. In addition to abstract set operations and widening we define concrete and abstract transformers on these environments. We present possible applications, such as the ability to describe memory zones, or track symbolic equalities between program variables. We implemented our domain in a static analysis platform and present preliminary results analyzing a tree-manipulating toy-language.
This work is supported by the European Research Council under Consolidator Grant Agreement 681393 – MOPSA.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The abstract interpretation framework [5] enables the development of sound static analyzers by inferring and proving invariants on reachable states of programs. Invariants in the scope of abstract interpretation are elements of a lattice called an abstract domain. Most domains focus on numeric or pointer variables. By contrast, we propose an abstract domain for variables whose values are tree data-structures. Tree values appear natively in some languages (such as OCaml) and applications (such as the DOM in web programming) or can be encoded through pointer manipulations (as in C). Trees can abstract terms in logic programming. A tree domain can also be useful to collect symbolic expressions appearing in a program.

Used Memory Zones. Program 1 describes an append function defined in the C language, this function adds an integer at the end of a linked list. The infinite set of unbounded terms of the form \(\texttt {*(*( \dots *(head + 4) \dots + 4) + 4)}\) represents memory zones that are used by the append function. Our analyzer is able to infer and represent such sets of terms. This provides the information that Program 1 does not use any of the data field of the linked list. Such a function would be fairly commonly called in a real-life project. In a classical top-down static analysis by abstract interpretation, function calls are inlined at each call site. A way to improve scalability is to design modular analyzers able to reuse previous analysis results (as emphasized in [7]). In order to be able to successfully reuse function body analysis, input states must be unified. Moreover the cost of performing the analysis of the body of functions grows with the number of variables that need to be tracked. A common way to deal with both problems is to use framing on the inputs of the functions (as in separation logic [25]). This improves (1) precision: as we know that they are not modified by the function call, (2) body analysis efficiency: as the input state is reduced and finally (3) modularity: as constraints on the usage of the first analysis are relaxed by the removal of constraints.
Symbolic Relations. Program 2 is a C function computing an approximation of the golden ration (as it is the limit of the sequence \(r_0 = 1\), \(r_{n+1}=1+\frac{1}{r_n}\)). As classical numerical domains can not represent such numerical relations, methods were proposed to track symbolic equality between expressions (see [23]). However such methods can not handle the unbounded iteration of Program 2. The set of reachable states at the end of Program 2 can be expressed by \(\texttt {r} = 1 + 1 / (1 + 1 / \dots 1 \dots )\) with depth \(\texttt {n}\). Please note that to infer such results we need to express numerical relations between the size of trees and the numeric variables from the program.
Numerical Environment. Consider now the OCaml Program 3, we want to prove that the assert false expression is never reached. This program builds a list of size \(2* \texttt {n}\) with alternating values \(\texttt {x} + 1\) and \(\texttt {x} -1\). The assertion states that the head of the list is \(\texttt {x} + 1\). After the definition of \(\texttt {t}\) there are two types of reachable states. (1) Those that have not gone through the loop \((\texttt {t} \mapsto \texttt {[]}, \texttt {x} \mapsto \mathbb Z, \texttt {n} \mapsto 0)\), and (2) those that have gone through at least one iteration of the loop: \((\texttt {t} \mapsto \texttt {[}a_1\texttt {;} a_2\texttt {;}a_3\texttt {; \dots ]}, x \mapsto \alpha , \texttt {n} > 0, a_1 \mapsto \alpha +1, a_2 \mapsto \alpha -1, a_3 \mapsto \alpha +1)\), where \(\alpha \in \mathbb Z\). Therefore we need to be able to keep numerical relations between the parametric and unbounded number of numeric values appearing in t and numeric variables from the program. Classical numeric domains do not provide out-of-the-box abstractions for sets of partially defined numerical functions, therefore we define such an abstraction. As an example of analysis result, the memory representation obtained by our analysis for t describes the set of trees of the form: Cons( a , Cons( b , Cons( a , ..., Nil) ...)) where \(a = \texttt {x}+1\) and \(b=\texttt {x}-1\). Therefore we are able to prove that the assert false expression is never reached.
Contributions. The main contributions of the article are threefold: (1) The extension of results on tree automata to the abstract interpretation framework by definition of a widening operator, in order to represent the set of tree shapes that a variable can contain. (2) The definition of a numerical domain built upon classical abstract domains able to represent sets of partial numerical maps with heterogeneous and unbounded definition sets. This is necessary to represent the numeric values at the leaves of a set of trees, as trees are unbounded and can contain a different number of leaves. (3) The definition of a novel abstraction for trees that can contain numerical values at their leaves. This last domain combines the abstractions (1) and (2). Moreover it is relational as it can express relations between numerical values found in trees and in the rest of the program, and relations between trees. Finally all results were implemented in an existing framework and experimented on a toy-language.
Limitations. At this point, analyses can only be performed on the toy language presented thereinafter, not on real life code, therefore we do not present any benchmark results, even though examples of analysis results will be put forth. Indeed Programs 1, 2 and 3 were precisely analyzed once encoded into our toy-language (see Programs 4 and 5).
Outline. We start, in Sect. 2, by presenting the concrete semantic we want to abstract. In Sect. 3 we build a first abstraction which forgets numerical values and focuses on abstracting tree shapes. Section 4 presents a novel numerical abstract domain required for the definition of the abstract domain of Sect. 5, which aims at precisely representing numerical constraints between trees and program variables. In Sect. 6 we provide remarks on the implementation and results of the analyzer. Finally Sect. 7 mentions related works while Sect. 8 concludes.
Notations. Classical Galois connections (see [5]) are denoted  . When no best abstraction can be defined, we use the representation framework (as defined by Bourdoncle in [3], also known as concretization only framework), representations are denoted by \((A,\subseteq _A) \xleftarrow {\gamma }{} (B, \subseteq _B)\). \(A \nrightarrow B\) denotes the set of partial maps from A to B, and \(\lambda _{\mid A}x.f(x) \in B\) denotes the map in \(A \rightarrow B\) that associates f(x) to x. Finally when \(f\in A \rightarrow C\) and \(g \in B \rightarrow C\), with \(A \cap B = \emptyset \), \(f \uplus g\) is the function defined on \(A \cup B\), that associates f(x) (resp. g(x)) to x whenever \(x \in A\) (resp. \(x \in B\)).
. When no best abstraction can be defined, we use the representation framework (as defined by Bourdoncle in [3], also known as concretization only framework), representations are denoted by \((A,\subseteq _A) \xleftarrow {\gamma }{} (B, \subseteq _B)\). \(A \nrightarrow B\) denotes the set of partial maps from A to B, and \(\lambda _{\mid A}x.f(x) \in B\) denotes the map in \(A \rightarrow B\) that associates f(x) to x. Finally when \(f\in A \rightarrow C\) and \(g \in B \rightarrow C\), with \(A \cap B = \emptyset \), \(f \uplus g\) is the function defined on \(A \cup B\), that associates f(x) (resp. g(x)) to x whenever \(x \in A\) (resp. \(x \in B\)).
2 Syntax and Concrete Semantics
Definition 1
An alphabet \(\mathcal {F}\) is a finite set, a ranked alphabet is a pair \(\mathcal {R}=(\mathcal {F}, a)\) where \(\mathcal {F}\) is an alphabet and \(a\in \mathcal {F}\rightarrow \mathbb N\). For \(f \in \mathcal {F}\), we call arity of f the value \(a(f)\). We assume that \(\mathbb Z\) and \(\mathcal {F}\) are disjoint and we define the set of natural terms over \(\mathcal {R}\) (denoted \(T_{\mathbb Z}(\mathcal {R})\)) to be the smallest set defined by:
-
\(\mathbb Z \subseteq T_{\mathbb Z}(\mathcal {R})\)
-
\(\forall p \ge 0,\ f \in \mathcal {F}, t_1,\ \dots , t_p \in T_{\mathbb Z}(\mathcal {R}),\ a(f) = p \Rightarrow f(t_1, \dots , t_p) \in T_{\mathbb Z}(\mathcal {R})\)
Moreover when \(\mathcal {R}\) contains at least one symbol of arity 0, we define terms over \(\mathcal {R}\) (denoted \(T(\mathcal {R})\)) to be the smallest set defined by:
-
\(\forall p \ge 0,\ f \in \mathcal {F}, t_1,\ \dots , t_p \in T(\mathcal {R}),\ a(f) = p \Rightarrow f(t_1, \dots , t_p) \in T(\mathcal {R})\)
In the following, \(\mathcal {F}_n\) denotes the subset of \(\mathcal {F}\) of arity n. Moreover given a term \(t \in T(\mathcal {R})\) we denote \(f=\mathbf {head}(t) \in \mathcal {F}\) and \(\mathbf {sons}(t)\) a possibly empty tuple \((t_1,\dots ,t_n)\) of elements of \(T(\mathcal {R})\) such that \(t = f(t_1,\dots ,t_n)\).
Remark 1
Numerical leaves are defined to contain integers, however this could be modified to rationals, real numbers or floats. We are parametric in the type of numeric values, as they are delegated to an underlying numerical domain.
Example 1
Consider the ranked alphabet  , u(n) means that symbol u has arity n. Then
, u(n) means that symbol u has arity n. Then  , but
, but  , and
, and  . Using this alphabet we can model C pointer arithmetic.
. Using this alphabet we can model C pointer arithmetic.
Example 2
\(U=\{+(x,y)\mid x \le y\}\) and \(V = \{+(x,+(z,y))\mid x \le y \wedge z \le y\}\) are two sets of natural terms over \(\mathcal {R}= \{+(2)\}\) which we use as running examples.

Syntax of the Language and Concrete Operations. We assume already defined a small imperative language and extend it (in Fig. 1) with statements, tree expressions ( ) which are expressions that are evaluated to trees, and simple symbol expressions (
) which are expressions that are evaluated to trees, and simple symbol expressions ( ) which enable the manipulation of symbols. We add the ability to build a tree which contains only a numerical leaf: \(\texttt {make\_integer}(e)\), the ability to read the i-th son of a tree t: \(\texttt {get\_son}(t, i)\), .... Figure 2 defines concrete operations over the set \(\wp (T_{\mathbb Z}(\mathcal {R}))\). Figure 2 assumes given a set of program numerical variables \(\mathcal V\), a set of numerical expressions (over \(\mathcal V\)) denoted
) which enable the manipulation of symbols. We add the ability to build a tree which contains only a numerical leaf: \(\texttt {make\_integer}(e)\), the ability to read the i-th son of a tree t: \(\texttt {get\_son}(t, i)\), .... Figure 2 defines concrete operations over the set \(\wp (T_{\mathbb Z}(\mathcal {R}))\). Figure 2 assumes given a set of program numerical variables \(\mathcal V\), a set of numerical expressions (over \(\mathcal V\)) denoted  , a set of statements
, a set of statements  , a notion of numerical environment \(E \in \mathfrak E = \mathcal V \rightarrow \mathbb Z\), a set of tree program variables \(\mathcal T\), a notion of tree environment \(F \in \mathfrak F = \mathcal T \rightarrow \wp (T_{\mathbb Z}(\mathcal {R}))\), \(D = E \times F\) is our concrete domain. Finally we assume already partially defined on numerical expressions an evaluation function
, a notion of numerical environment \(E \in \mathfrak E = \mathcal V \rightarrow \mathbb Z\), a set of tree program variables \(\mathcal T\), a notion of tree environment \(F \in \mathfrak F = \mathcal T \rightarrow \wp (T_{\mathbb Z}(\mathcal {R}))\), \(D = E \times F\) is our concrete domain. Finally we assume already partially defined on numerical expressions an evaluation function  . Using this operator we are able to define Program 4 which computes the memory zones used by append from Program 1, and Program 5 that simulates the behavior of Program 3.
. Using this operator we are able to define Program 4 which computes the memory zones used by append from Program 1, and Program 5 that simulates the behavior of Program 3.
3 Natural Term Abstraction by Tree Automata
In this section we start by defining a value abstraction for tree sets (in Sect. 3.1), which is then lifted to an environment abstraction (in Sect. 3.2).
3.1 Value Abstraction
As a first abstraction for natural terms, we put aside numerical values and define an abstraction able to describe sets of tree shapes. Tree automata enable the description of set of terms built upon a finite ranked alphabet. The ranked alphabet of the language we want to analyze is extend with the \(\square \) symbol to denote potential positions of numerical values.
Definition 2 (Finite tree automata)
A finite tree automaton (FTA) over a ranked alphabet \(\mathcal {R}\) is a tuple \((Q, \mathcal {R}, Q_f, \delta )\), where \(Q\) is a (finite) set of states, \(Q_f\subseteq Q\) is the set of final states, and \(\delta \in \wp (\bigcup _{n \in \mathbb N} \mathcal {F}_n \times Q^n \times Q)\) is the set of transitions. We define \(\overline{\delta }: (\bigcup _{n \in \mathbb N} \mathcal {F}_n \times Q^n) \rightarrow \wp (Q)\) by: \(\overline{\delta }(f,\overrightarrow{q}) = \{q' \mid (f, \overrightarrow{q}, q') \in \delta \}\). When \(\overline{\delta }\) is such that, \(\forall n\in \mathbb N,\ f \in \mathcal {F}_n,\ \overrightarrow{q} \in Q^n,\ |\overline{\delta }(f,\overrightarrow{q})| = 1\), we say that the automaton is complete and deterministic (CDFTA). We then abuse notations and denote by \(\delta (f,\overrightarrow{q})\) the unique element in the set \(\overline{\delta }(f,\overrightarrow{q})\).
Definition 3 (Reachability)
Given a FTA \(\mathcal A= (Q, \mathcal {R}, Q_f, \delta )\) we define, a reachability function \(\textsc {reach}_{\mathcal A}: T(\mathcal {R}) \rightarrow \wp (Q)\)

If \(\mathbf {sons}(t)\) is the empty tuple (which is the case when t is a constant a), the union is made over a unique element (which is the empty tuple), which then boils down to: \(\overline{\delta }(a,())\). If \(\mathbf {sons}(t)\) is not the empty tuple and for some i, \(\textsc {Reach}_{\mathcal A}(t_i)\) is empty, then \(\textsc {Reach}_{\mathcal A}(t)\) is also empty.
Example 3
Consider the ranked alphabet \(\mathcal {R}=\{f(2), a(0)\}\), and the automaton \(\mathcal A= (\{u,v\},\mathcal {R},\{v\},\{a() \rightarrow u, f(v,v)\rightarrow v, f(u,u) \rightarrow u, f(u,u) \rightarrow v\})\). Then \(\textsc {reach}_{\mathcal A}(a) = \{u\}\), \(\textsc {reach}_{\mathcal A}(f(a,a)) = \{u,v\}\), \(\textsc {reach}_{\mathcal A}(f(f(a,a),a)) = \{u,v\}\).
Definition 4 (Acceptance)
Given a FTA \(\mathcal A= (Q, \mathcal {R}, Q_f, \delta )\), a term t, we say that t is accepted by the automaton if \(\textsc {reach}_{\mathcal A}(t) \cap Q_f\ne \emptyset \). \(\mathcal L(\mathcal A)\) denotes the set of terms accepted by automaton \(\mathcal A\).
Example 4
With the definition of Example 3, \(\mathcal L(\mathcal A)\) is the set of terms over \(\mathcal {R}\) that contain at least one f.
Definition 5 (Tree regular languages)
A set of terms \(\mathcal T\) over a ranked alphabet \(\mathcal {R}\) is called tree regular if there exists a FTA \(\mathcal A\) over \(\mathcal {R}\) such that \(\mathcal L(\mathcal A)=\mathcal T\). The set of such languages is denoted \(\text {TReg}(\mathcal {R})\).
Remark 2
As for regular languages, for all \(\mathcal A\in \text {FTA}\) there exists \(\mathcal A' \in \text {CDFTA}\) such that \(\mathcal L(\mathcal A)=\mathcal L(\mathcal A')\), moreover \(\mathcal A'\) is computable (see [4]).
Example 5
-
As proved in Example 4 the set of all terms over \(\{f(2), a(0)\}\) that contain at least one f is tree regular.
-
Consider now the ranked alphabet \(\{a(1), b(1), \epsilon (0)\}\) and the set of terms \(\mathcal T=\{\epsilon , a(b(\epsilon )), a(a(b(b(\epsilon )))),\dots \}\). We can prove (in a similar way as for \(a^n b^n\) in regular languages) that \(\mathcal T\) is not tree regular.
-
On every ranked alphabet \(\mathcal {R}\): every finite language, the empty language and \(T(\mathcal {R})\) are tree regular.
Proposition 1
\((\text {TReg}(\mathcal {R}), \subseteq , \cap , \cup , .^c, \emptyset , T(\mathcal {R}))\) is a complemented lattice with infinite height, moreover it is not complete. \(\subseteq , \cap , \cup \) and complementation (\(.^c\)) are computable operations on tree automata [4].
We denote by \(\mathcal {R}^{\square }\) the ranked alphabet \(\mathcal {R}\) after adding the symbol \(\square \) of arity 0 (we assume that \( \square \not \in \mathcal {R}\)). Given a natural term t, we define \(t^{\square }\) to be the term obtained by replacing every integer with the \(\square \) symbol.
Proposition 2
\((\wp (T_{\mathbb Z}(\mathcal {R})),\subseteq ) \xleftarrow {\gamma }{} (\text {TReg}(\mathcal {R}^{\square }), \subseteq )\) where \(\gamma (\mathcal A) = \{t \mid t^{\square } \in \mathcal L(\mathcal A)\}\) is a representation. Moreover with such a \(\gamma \) definition, \(\cup \), \(\cap \) soundly represent the union and the intersection.
Remark 3
We only have a representation and not a Galois connection as language \(\mathcal T\) of Example 5 does not have a best tree regular over approximation.
Example 6
Let \(\mathcal {R}=\{+(2)\}\) and \(\mathcal A=(\{0,1\},\mathcal {R}^{\square },\{0,1\},\{(\square () \rightarrow 0, +(0,0)\rightarrow 1, +(0,1)\rightarrow 1)\})\). Examples of terms recognized by \(\mathcal A\) are shown on Fig. 3. Natural terms from our running example U and V (defined in Example 2) are also contained in \(\gamma (\mathcal A)\). Moreover as we do not provide numerical constraints: \(1+(3+4)\), 23, \(1+(2+(3+4))\) are also elements in \(\gamma (\mathcal A)\).
Due to the infinite height of the lattice, a widening operator is required. In the following, we assume given a constant \(w \in \mathbb N\), this constant will be used to stabilize increasing chains, the greater the constant, the more precise our widening operator will be.
Definition 6
Let \(\mathcal A= (Q, \mathcal {R}, Q_f, \delta ) \in \text {FTA}\), and \(\sim \) be an equivalence relation on \(Q\), such that \(p\sim q \wedge p \in Q_f\Rightarrow q \in Q_f\). We define \(\mathcal A/\sim = (Q/\sim , \mathcal {R}, Q_f/\sim , \bigcup _{(f,q_1,\dots ,q_n,q) \in \delta } \{(f,q_1^{\sim },\dots ,q_n^{\sim },q^{\sim }) \})\) where \(q^{\sim }\) is the equivalence class of q in \(\sim \).
Proposition 3
For every \(\mathcal A\in \text {FTA}\) and every \(\sim \) equivalence relation on its states, \(\mathcal L(\mathcal A) \subseteq \mathcal L(\mathcal A/\sim )\).
Therefore following the idea from [9] and in [11], we define a widening operation by quotienting states of automata by an equivalence relation of finite index. We define by induction a special sequence of equivalence relations on states of tree automata: \(\sim _1 = \{Q_f, Q\setminus Q_f\}\) and \(\sim _{k+1}\) is \(\sim _{k}\) where we split equivalence classes not satisfying the following condition: \(\forall f \in \mathcal {F}_n,\ \forall p_1,\dots ,p_n \in Q,\ \forall q_1,\dots ,q_n \in Q, (\bigwedge _{i=1}^n p_i \sim _k q_i) \Rightarrow \delta (f,p_1,\dots ,p_n) \sim _k \delta (f,q_1,\dots ,q_n)\) and \(\forall q\in Q_f,\ q^{\sim _k} \subseteq Q_f\). This sequence of equivalence relations is the Myhill-Nerode sequence (see [4]). This sequence is of length at most the number of states of the automaton (before stabilization). Let \(\phi (w)=\text {max}\{i \le |Q| \mid \text {index of }\sim _i \le w\}\) (given an integer w, \(\phi \) yields the index of the most precise of the equivalence relationships in the Myhill-Nerode sequence, that contains at most w equivalence classes) and \([\mathcal A]_w = \mathcal A/\sim _{\phi (w)}\). \([\mathcal A]_w\) is therefore a FTA with at most w states such that \(\mathcal L(\mathcal A) \subseteq \mathcal L([\mathcal A]_w)\). As for regular languages, for every CDFTA a equivalent minimal CDFTA (in the sense of the number of states, and unique modulo state renaming) can be obtained by quotienting the automaton by \(\sim _{|Q|}\). Therefore we define a widening operator on CDFTAs, which is then lifted to tree regular languages.
Definition 7
(Widening operator \(\triangledown \)). \(\mathcal A\triangledown \mathcal A' = [\mathcal A\cup \mathcal A']_w\).
Proposition 4
This widening is sound and stabilizes infinite sequences.
Remark 4
Consider the two following complete and deterministic tree automata: \(\mathcal A = (\{a, b, h\}, \{+(2)\}, \{a\}, \{\square () \rightarrow b, +(b, b) \rightarrow a\} )\) and \(\mathcal B = (\{a, b, c, h\}, \{+(2)\}, \{a\}, \{\square () \rightarrow b, +(b, b) \rightarrow c, +(b,c) \rightarrow a\} )\) (unmentioned transitions go to h). \(\mathcal A\) (resp. \(\mathcal B\)) recognizes the tree \(+(\square , \square )\) (resp. \(+(\square ,+(\square ,\square ))\)), it over-approximates U (resp. V) from our running example. \(\mathcal A \cup \mathcal B\) is recognized by the following complete and deterministic tree automaton: \(\mathcal C = (\{a, b, c, h\}, \{+(2)\}, \{a, c\}, \{\square () \rightarrow b, +(b, b) \rightarrow c, +(b,c) \rightarrow a\} )\). If we want to widen \(\mathcal A\) and \(\mathcal B\) with parameter 3, the following equivalence relation is computed: \(\{\{h\}, \{b\}, \{a, c\}\}\). Merging equivalent states produces \((\{a, b, h\}, \{+(2)\}, \{a \}, \{\square () \rightarrow b, +(b, b) \rightarrow a, +(b, a) \rightarrow a\} )\), which contains a loop and over-approximates the union.
Example of accepted trees from Example 6
3.2 Environment Abstraction
Now that we are given an abstraction for natural term sets, let us show how this is lifted to a notion of abstract natural term environments mapping variables to natural terms. Given a set of natural term variables \(\mathcal T\), consider \(\mathfrak {F}^{\sharp } = (\mathcal T \rightarrow \text {TReg}(\mathcal {R}^{\square })) \cup \{\bot \}\) and the set operators defined by the point-wise lifting of operators on \(\text {TReg}(\mathcal {R}^{\square })\). We also lift the concretization function \(\wp (T_{\mathbb Z}(\mathcal {R})) \leftarrow \text {TReg}(\mathcal {R}^{\square })\) to \( \mathfrak F \leftarrow \mathfrak F^{\sharp }\). We assume given an abstract numerical environment \(E^{\sharp }\) and an abstract evaluator \(\mathbb E [\![e ]\!]^{\sharp }\). Abstract transformers \([\![\texttt {make\_symbolic} ]\!]^{\sharp }\), \([\![\texttt {is\_symbol} ]\!]^{\sharp }\), \([\![\texttt {get\_son}(e) ]\!]^{\sharp }\), \([\![\texttt {get\_sym\_head} ]\!]^{\sharp }\) and \([\![\texttt {get\_num\_head} ]\!]^{\sharp }\) are simple tree automata operations. For concision Fig. 4 only provides definitions of two of these operators. Please note that these definitions require all states of the automata to be reachable. An example of use of the is_symbol operator can be found in Example 7. Other abstract operators are similar.
Example 7
Consider the tree automaton \(\mathcal A\) of Example 6, (Fig. 3), with \(F^{\sharp }=(x \mapsto \mathcal A)\): \([\![\texttt {get\_sym\_head}(x) ]\!]^{\sharp }(E^{\sharp }, F^{\sharp }) = \{+\}\) and \([\![\texttt {get\_num\_head}(x) ]\!]^{\sharp }(E^{\sharp }, F^{\sharp }) = \top \).
4 Numerical Abstractions
As emphasized in the introductory example, we rely on numerical domains to introduce constraints on numerical variables found in trees. In a classical numeric abstraction (e.g. intervals [6], octagons [22], polyhedra [8], ...), each abstract element represents a set of maps \(\mathcal V \rightarrow \mathbb R\) for a fixed, finite set of variables \(\mathcal V\). In contrast, our numeric variables are leaves of a possibly infinite set of trees of unbounded size. Hence before starting the presentation of the numerical abstraction for natural terms, we show how to extend in a generic way an abstract element in two steps. Firstly we want to be able to represent a set of maps, where each map is defined over a (possibly different) finite subset of an infinite set of variables (this is done in Sect. 4.1). Secondly, we use summarization variables to relax the finiteness constraint, so as to represent sets of maps over heterogeneous maps over infinitely many variables (done in Sect. 4.2).
4.1 Heterogeneous Support
We define  , the set of partial maps from \(\mathcal V\), to \(\mathbb R\). \(\mathfrak M\) is ordered by the inclusion relation \(\subseteq \). In the following \(\mathbf {def}(f)\) denotes the definition set of f. We assume defined a representation \((\wp (\mathcal S \rightarrow \mathbb R), \subseteq ) \xleftarrow {\gamma _0^{\mathcal S}}{} (N_\mathcal S, \sqsubseteq ^{\mathcal S}_0)\), for every finite set \(\mathcal S \subseteq \mathcal V\) (such as octagons in |S| dimensions). \(N_{\mathcal S}\) comes with the usual abstract set operator \(\sqcap _0^{\mathcal S}\), \(\sqcup _{0}^{\mathcal S}\). Moreover if \(x\in \mathcal S\), \(y \notin \mathcal S\), \(\mathcal S'\) is another finite set and \(N^{\sharp }\in N_{\mathcal S}\) then \(N^{\sharp }[x\mapsto y] \in N_{\mathcal S \cup \{y\} \setminus \{x\}}\) is the abstract element obtained by renaming x into y, \(N^{\sharp }_{\mid \mathcal S'} \in N_{\mathcal S'}\) is obtained by existentially quantifying dimensions associated to elements in \(\mathcal S\) and not in \(\mathcal S'\) and adding unconstrained dimensions for elements in \(\mathcal S'\) and not in \(\mathcal S\). From now on we assume that this last operator is exact (as for intervals, octagons, polyhedra over \(\mathbb R\)). However results from this section can be extended to numerical domains that are able, given \(N^{\sharp }\in N_{\mathcal S}\), \(N^{\sharp \prime }\in N_{\mathcal S'}\), to check if \(\gamma _0^{\mathcal S}(N^{\sharp }) \subseteq \gamma _0^{\mathcal S'}(N^{\sharp \prime })_{\mid \mathcal S}\). The precision of the extension defined in this subsection would then depend upon the precision of this test in the underlying domain. Finally \([\![. ]\!]_0^{\mathcal S}\) (resp. \([\![. ]\!]_0^{\sharp , \mathcal S}\)) refers to the classical concrete (resp. abstract) semantic of operators on sets of numerical maps (resp. abstract elements). A classical method for the abstraction of heterogeneous maps is the use of a partitioning of the concrete element according to the definition set of its represented maps. However partitioning induces an increase in numerical operation cost (exponential in the number of variable) which we would like to avoid. Therefore in order to abstract sets of maps with heterogeneous definition sets, we start by abstracting the potential definition set. We choose a simple lower-bound/upper-bound abstraction (l and u in the following definition). Moreover we need to abstract the potential mappings given a definition set: this is done using a classical numerical domain. Contrary to partitioning, we will use only one numerical abstract element, defined on the upper-bound u, to represent all environments (instead of one abstract element by definition set). We also add a \(\top \) element, used in the case where the upper bound u is infinite.
, the set of partial maps from \(\mathcal V\), to \(\mathbb R\). \(\mathfrak M\) is ordered by the inclusion relation \(\subseteq \). In the following \(\mathbf {def}(f)\) denotes the definition set of f. We assume defined a representation \((\wp (\mathcal S \rightarrow \mathbb R), \subseteq ) \xleftarrow {\gamma _0^{\mathcal S}}{} (N_\mathcal S, \sqsubseteq ^{\mathcal S}_0)\), for every finite set \(\mathcal S \subseteq \mathcal V\) (such as octagons in |S| dimensions). \(N_{\mathcal S}\) comes with the usual abstract set operator \(\sqcap _0^{\mathcal S}\), \(\sqcup _{0}^{\mathcal S}\). Moreover if \(x\in \mathcal S\), \(y \notin \mathcal S\), \(\mathcal S'\) is another finite set and \(N^{\sharp }\in N_{\mathcal S}\) then \(N^{\sharp }[x\mapsto y] \in N_{\mathcal S \cup \{y\} \setminus \{x\}}\) is the abstract element obtained by renaming x into y, \(N^{\sharp }_{\mid \mathcal S'} \in N_{\mathcal S'}\) is obtained by existentially quantifying dimensions associated to elements in \(\mathcal S\) and not in \(\mathcal S'\) and adding unconstrained dimensions for elements in \(\mathcal S'\) and not in \(\mathcal S\). From now on we assume that this last operator is exact (as for intervals, octagons, polyhedra over \(\mathbb R\)). However results from this section can be extended to numerical domains that are able, given \(N^{\sharp }\in N_{\mathcal S}\), \(N^{\sharp \prime }\in N_{\mathcal S'}\), to check if \(\gamma _0^{\mathcal S}(N^{\sharp }) \subseteq \gamma _0^{\mathcal S'}(N^{\sharp \prime })_{\mid \mathcal S}\). The precision of the extension defined in this subsection would then depend upon the precision of this test in the underlying domain. Finally \([\![. ]\!]_0^{\mathcal S}\) (resp. \([\![. ]\!]_0^{\sharp , \mathcal S}\)) refers to the classical concrete (resp. abstract) semantic of operators on sets of numerical maps (resp. abstract elements). A classical method for the abstraction of heterogeneous maps is the use of a partitioning of the concrete element according to the definition set of its represented maps. However partitioning induces an increase in numerical operation cost (exponential in the number of variable) which we would like to avoid. Therefore in order to abstract sets of maps with heterogeneous definition sets, we start by abstracting the potential definition set. We choose a simple lower-bound/upper-bound abstraction (l and u in the following definition). Moreover we need to abstract the potential mappings given a definition set: this is done using a classical numerical domain. Contrary to partitioning, we will use only one numerical abstract element, defined on the upper-bound u, to represent all environments (instead of one abstract element by definition set). We also add a \(\top \) element, used in the case where the upper bound u is infinite.
Definition 8 (Numerical abstraction)
Let us define the following set: 
 . An element of \(\mathfrak M^{\sharp }\) is therefore: either \(\top \), \(\bot \) or a triple \(\langle N^{\sharp }, l, u \rangle \) where l and u are finite sets of variables such that \(N^{\sharp }\) is defined over u.
. An element of \(\mathfrak M^{\sharp }\) is therefore: either \(\top \), \(\bot \) or a triple \(\langle N^{\sharp }, l, u \rangle \) where l and u are finite sets of variables such that \(N^{\sharp }\) is defined over u.
Definition 9 (Concretization function)
Abstract elements from \(\mathfrak M^{\sharp }\) are mapped to \(\mathfrak M\) thanks to the following concretization function: \(\gamma (\bot ) = \emptyset \), \(\gamma (\top ) = \mathfrak M\) and \(\gamma (\langle N^{\sharp }, l, u \rangle ) = \{\rho \in \mathcal S \rightarrow \mathbb Z \mid l \subseteq \mathcal S \subseteq u \wedge \rho \in \gamma _0^{\mathcal S}(N^{\sharp })_{\mid \mathcal S})\}\).
Example 8
As an example consider \(\gamma (\langle \{x = y, x \le 3, z = 0\}, \{x\}, \{x, y, z\} \rangle ) = \{(x \mapsto a) \mid a \le 3\} \cup \{(x \mapsto a, y \mapsto a) \mid a \le 3\} \cup \{(x \mapsto a, z \mapsto 0) \mid a \le 3\} \cup \{(x \mapsto a, y \mapsto a, z \mapsto 0) \mid a \le 3\}\). As intended, the resulting set of maps contains maps with different definition sets.
Definition 10 (Order)
On \(\mathfrak M^{\sharp }\) we define the following comparison operator: \(\langle N^{\sharp }, l, u \rangle \sqsubseteq \langle N^{\sharp \prime }, l', u' \rangle \Leftrightarrow l' \subseteq l \subseteq u \subseteq u' \wedge N^{\sharp }\sqsubseteq _0^u N^{\sharp \prime }_{\mid u}\), this comparison is trivially extended to \(\top \) (resp. \(\bot \)) as being the biggest (resp. smallest) element in \(\mathfrak M^{\sharp }\). In the following \(\mathfrak M^{\sharp }_\mathfrak p\) denotes the subset of \(\mathfrak M^{\sharp }\) where \(u=\mathfrak p\) extended with \(\top \) and \(\bot \).
Proposition 5
\(\gamma \) is monotonic for \(\sqsubseteq \).
Figure 5 provides the definition of the concrete and abstract semantics of the classical numerical statements, \(\texttt {Assume}\) and \(\texttt {Assign}\) (denoted \(x \leftarrow e\)). We denote \(\mathbf {vars}(e)\) the set of variables appearing in e. We recall that \([\![\texttt {Assume}(c) ]\!]_0^{\mathcal S}(E \in \wp (\mathcal S \rightarrow \mathbb R)) = \{f \in E \mid \texttt {true} \in \mathbb E [\![c ]\!](f)\}\) and \([\![x \leftarrow e ]\!]_0^{\mathcal S}(E \in \wp (\mathcal S \rightarrow \mathbb R)) = \{f[x \mapsto e'] \mid f \in E \wedge e' \in \mathbb E [\![e ]\!](f)\}\). In order to ease the lifting of these classical operators we define  , for every statement stmt. Moreover we assume the existence of the following abstract operators: \([\![\texttt {Assume}(c) ]\!]_0^{\sharp ,u}(N^{\sharp })\) and \([\![x \leftarrow e ]\!]_0^{\sharp ,u}{N^{\sharp }}\) abstracting soundly their respective concrete transformers. Note that the concrete semantic of \(\texttt {Assume}(c)\) (resp. \(x \leftarrow e\)) enforces that maps are defined at least on the variables appearing in c (resp. in e and on x). Abstract operators from Fig. 5 are sound with respect to \(\gamma \) and their concrete operators.
, for every statement stmt. Moreover we assume the existence of the following abstract operators: \([\![\texttt {Assume}(c) ]\!]_0^{\sharp ,u}(N^{\sharp })\) and \([\![x \leftarrow e ]\!]_0^{\sharp ,u}{N^{\sharp }}\) abstracting soundly their respective concrete transformers. Note that the concrete semantic of \(\texttt {Assume}(c)\) (resp. \(x \leftarrow e\)) enforces that maps are defined at least on the variables appearing in c (resp. in e and on x). Abstract operators from Fig. 5 are sound with respect to \(\gamma \) and their concrete operators.
We now need to define \(\sqcup \) that abstracts the classic set operator \(\cup \). We can not directly apply the corresponding abstract operator on the numerical component of the abstractions as they might have different definition sets. A first naive solution would be to extend their respective definition set and to perform the abstract operation on the resulting elements: \(N^{\sharp }_{\mid u \cup u'} \sqcup _0^{u \cup u'} N^{\sharp \prime }_{\mid u \cup u'}\). However consider \(M = \langle \{x = y\} (= U^{\sharp }), \{x,y\} , \{x,y\} \rangle \) and \(N = \langle \{x = z\} (= V^{\sharp }), \{x,z\} , \{x,z\} \rangle \), where the underlying domain is the octagon domain where elements are represented as a set of linear constraints (e.g. \(\{x=y\}\)). We have \(U^{\sharp }_{\mid \{x, y, z\}} = \{x = y\}\) and \(V^{\sharp }_{\mid \{x, y, z\}} = \{x = z\}\), hence \(U^{\sharp }_{\mid \{x, y, z\}} \sqcup _0^{\{x, y, z\}}V^{\sharp }_{\mid \{x, y, z\}} = \top \). Consider now the abstract element in \(\mathfrak M^{\sharp }\): \(R = \langle \{ x = y , x = z \}(= W^{\sharp }) , \{x\} , \{x , y , z\} \rangle \). The concretization of R over-approximates the union of the concretization of M and N, and its numerical component is more precise than \(\top \). We note that the numerical constraints appearing in \(W^{\sharp }\) could be found in \(U^{\sharp }\) or \(V^{\sharp }\), therefore in order to remove the aforementioned imprecision we define a refined abstract union operator, denoted as  , that uses constraints found in the inputs in order to refine its result. This is done using the \(\mathbf {strenghtening}\) operator of Algorithm 1 which adds constraints from C that do not make the projection of \(X^{\sharp }\) to u (resp. v) lower than the threshold \(U^{\sharp }\) (resp. \(V^{\sharp }\)). We assume that, given an abstract element \(U^{\sharp }\), we can extract a finite set of constraints satisfied by \(U^{\sharp }\), those are denoted \(\mathbf {constraints}(U^{\sharp })\) (the more constraints can be extracted, the more precise the result will be). For example if the numerical domain is the interval domain, constraints have the form \(\pm x \ge a\). If the numerical domain is the octagon domain the \(\mathbf {constraints}\) operator yields all the linear relations among variables that define the octagon.
, that uses constraints found in the inputs in order to refine its result. This is done using the \(\mathbf {strenghtening}\) operator of Algorithm 1 which adds constraints from C that do not make the projection of \(X^{\sharp }\) to u (resp. v) lower than the threshold \(U^{\sharp }\) (resp. \(V^{\sharp }\)). We assume that, given an abstract element \(U^{\sharp }\), we can extract a finite set of constraints satisfied by \(U^{\sharp }\), those are denoted \(\mathbf {constraints}(U^{\sharp })\) (the more constraints can be extracted, the more precise the result will be). For example if the numerical domain is the interval domain, constraints have the form \(\pm x \ge a\). If the numerical domain is the octagon domain the \(\mathbf {constraints}\) operator yields all the linear relations among variables that define the octagon.

Definition 11
(  operator). Let \(U^{\sharp }\in N_u\), \(V^{\sharp }\in N_v\) be two numerical environments, let \(X^{\sharp }\in N_{u \cup v}\), let C be a sequence of numerical constraints over \(u \cup v\), let \(\mathfrak c= u \cap v\) we define:
operator). Let \(U^{\sharp }\in N_u\), \(V^{\sharp }\in N_v\) be two numerical environments, let \(X^{\sharp }\in N_{u \cup v}\), let C be a sequence of numerical constraints over \(u \cup v\), let \(\mathfrak c= u \cap v\) we define:

Remark 5
-
The precision of
 depends upon the order of iteration over constraints \(c \in C\) in Algorithm 1. Our implementation currently iterates in the order in which constraints are returned from the abstract domains. More clever heuristics will be considered in future work.
depends upon the order of iteration over constraints \(c \in C\) in Algorithm 1. Our implementation currently iterates in the order in which constraints are returned from the abstract domains. More clever heuristics will be considered in future work. -
 starts by performing the join over the domain \(\mathfrak c\), the result is then strengthened. Other \(\mathbf {strenghtening}(X^{\sharp }, U^{\sharp }\in N_u, V^{\sharp }\in N_v)\) operator could be defined, however in order to ensure soundness of
starts by performing the join over the domain \(\mathfrak c\), the result is then strengthened. Other \(\mathbf {strenghtening}(X^{\sharp }, U^{\sharp }\in N_u, V^{\sharp }\in N_v)\) operator could be defined, however in order to ensure soundness of  , it must satisfy the following constraints: \(U^{\sharp }\sqsubseteq _0^u \mathbf {strenghtening}(X^{\sharp }, U^{\sharp }, V^{\sharp })\) and \(V^{\sharp }\sqsubseteq _0^v \mathbf {strenghtening}(X^{\sharp }, U^{\sharp }, V^{\sharp })\).
, it must satisfy the following constraints: \(U^{\sharp }\sqsubseteq _0^u \mathbf {strenghtening}(X^{\sharp }, U^{\sharp }, V^{\sharp })\) and \(V^{\sharp }\sqsubseteq _0^v \mathbf {strenghtening}(X^{\sharp }, U^{\sharp }, V^{\sharp })\).
Example 9
Let us now consider the example introduced thereinbefore  . Indeed using the notations of Definition 11:
. Indeed using the notations of Definition 11:  , \(C=\{x=y,y=z\}\), moreover
, \(C=\{x=y,y=z\}\), moreover  , \( U^{\sharp }\sqsubseteq _0^{\{x,y\}} \{x=y\} = T^{\sharp }_{\mid \{x,y\}}\) and \(V^{\sharp }\sqsubseteq _0^{\{x,z\}} \top = T^{\sharp }_{\mid \{x,z\}}\). Therefore constraint \(x = y\) is added to \(Z^{\sharp }\). At the next loop iteration:
, \( U^{\sharp }\sqsubseteq _0^{\{x,y\}} \{x=y\} = T^{\sharp }_{\mid \{x,y\}}\) and \(V^{\sharp }\sqsubseteq _0^{\{x,z\}} \top = T^{\sharp }_{\mid \{x,z\}}\). Therefore constraint \(x = y\) is added to \(Z^{\sharp }\). At the next loop iteration:  , \(U^{\sharp }\sqsubseteq _0^{\{x,y\}} \{x = y\} = T^{\sharp }_{\mid \{x,y\}}\) and \(V^{\sharp }\sqsubseteq _0^{\{x,z\}} \{x = z\} = T^{\sharp }_{\mid \{x,z\}}\). Therefore constraint \(x = z\) is added to \(Z^{\sharp }\).
, \(U^{\sharp }\sqsubseteq _0^{\{x,y\}} \{x = y\} = T^{\sharp }_{\mid \{x,y\}}\) and \(V^{\sharp }\sqsubseteq _0^{\{x,z\}} \{x = z\} = T^{\sharp }_{\mid \{x,z\}}\). Therefore constraint \(x = z\) is added to \(Z^{\sharp }\).
Proposition 6
(Soundness of  ). let \(U^{\sharp }\in N_u\) and \(V^{\sharp }\in N_v\), then
). let \(U^{\sharp }\in N_u\) and \(V^{\sharp }\in N_v\), then  and
and  .
.
Definition 12 (Union abstract operators)
We define the following abstract set operator:  . This operator soundly abstracts the union. Moreover in order to ensure the stabilization of infinitely increasing chains in \(\mathfrak M^{\sharp }\) we define the following widening operator:
. This operator soundly abstracts the union. Moreover in order to ensure the stabilization of infinitely increasing chains in \(\mathfrak M^{\sharp }\) we define the following widening operator:

Remark 6
This widening operator over-approximates to \(\top \) whenever the upper-bound on the definition set is growing. This yields a huge loss of information however this numerical domain is designed as a tool domain used by a higher level abstraction in charge of stabilizing the environment before applying the widening, so that this case will not be used in practice.
Subsequent tree abstractions require the definition of the following operators:
-
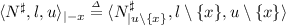 and
and  which respectively removes (adds) a variable to the numerical environment.
which respectively removes (adds) a variable to the numerical environment. -
\(\langle N^{\sharp }, l , u \rangle _{\mid \mathcal S}\) is computed by adding variables in \(\mathcal S\) and not in u and removing variables in u that are not in \(\mathcal S\).
4.2 Representation of Maps over Potentially Unbounded Sets
In this subsection we focus on the problem of defining abstract numerical environments on potentially infinite environments. A classical method we use here is variable summarization (see [13]). This is based on the folding of several concrete objects (a potentially infinite number) to an abstract element which summarizes all concrete objects. The folding is encoded in a function f mapping summarized variables to the set of concrete variables they abstract. Given an abstract numerical environment \(N^{\sharp }\) and a mapping from summary variables: \(\mathcal V'\) to sets of concrete variables \(f \in \mathcal V' \rightarrow \wp (\mathcal V)\) where \(f(v_1) \cap f(v_2) \ne \emptyset \Rightarrow v_1 = v_2\), we define the collapsing of a partial map \(\rho \in \mathcal V \nrightarrow \mathbb Z\) under a summarizing function f:
Example 10
Consider \(\mathcal V' = \{x, y, z, t\}\) and \(\mathcal V = \{a, b, c, d, g, h\}\), the environment \(\rho =(a\mapsto 0, b \mapsto 1, c \mapsto 2, d\mapsto 3)\) and finally the summarizing function \(f = (x \mapsto \{a\}, y \mapsto \{b, c\}, z \mapsto \{d\}, t \mapsto \{g\})\). Collapsing environment \(\rho \) under f yields the set of environments: \((x \mapsto 0, y \mapsto 1, z \mapsto 3)\) and \((x \mapsto 0, y \mapsto 2, z \mapsto 3)\).
Given a summarizing function f we can now define an extension of the concretization function \(\gamma \) of the previous subsection in the following manner:
Example 11
Going back to Example 10 and considering the numerical abstract element: \(N^{\sharp }= \langle \{x \le y\}, \{x\} , \{x, y\}\rangle \), we have: \(\gamma (N^{\sharp }) = \{(x \mapsto \alpha ) \mid \alpha \in \mathbb Z\}~\cup ~\{(x \mapsto \alpha , y \mapsto \beta ) \mid \alpha \le \beta \}\). We have: \(m \in \gamma [f](N^{\sharp }) \Leftrightarrow \downarrow _f(m) \subseteq \gamma (N^{\sharp }) \Rightarrow \{x\} \subseteq \mathbf {def}(\downarrow _f(m)) \subseteq \{x, y\}\). Therefore if we assume m defined on d then \(f(z)~\cap ~\mathbf {def}(m) \ne \emptyset \) hence there would be an element in \(\downarrow _f(m)\) defined on z. Hence m is not defined on d, similarly for g. Moreover \(\{x\} \subseteq \mathbf {def}(\downarrow _f(m))\) implies that m is defined on a. Finally: defining \(S = \{(a \mapsto \alpha ) \mid \alpha \in \mathbb Z\} \cup \{(a \mapsto \alpha , b \mapsto \beta ) \mid \alpha \le \beta \} \cup \{(a \mapsto \alpha , c \mapsto \beta ) \mid \alpha \le \beta \} \cup \{(a \mapsto \alpha , b \mapsto \beta , c \mapsto \gamma ) \mid \alpha \le \beta \wedge \alpha \le \gamma \}\). We have: \(\gamma [f](N^{\sharp }) = S \cup (\bigcup _{f \in S} \{f \uplus (h \mapsto \delta ) \mid \delta \in \mathbb Z\})\).
The abstract domains we will define in the following sections will employ this summarization framework. The manipulation of summarized variables requires the definition of a \(\mathbf {fold}(E, x , \mathcal S)\) (resp. \(\mathbf {expand}(E, x, \mathcal S)\)) operator yielding a new environment where x is used as a summary variable for \(\mathcal S\) (resp. where a summary variable x is desummarized into a set of variables \(\mathcal S\)). Let \(\mathcal S\) and \(\mathcal S'\) be two finite sets of elements such that \(\mathcal S' \cap \mathcal S \subseteq \{x\}\), we define: \(\mathbf {expand}_0(N^{\sharp },x,\mathcal S'')=\bigsqcap _{v \in \mathcal S''} N^{\sharp }[x \mapsto v]_{\mid (\mathcal S \setminus \{x\}) \cup \mathcal S''}\) and \( \mathbf {fold}_0(N^{\sharp }, x, \mathcal S'') = \bigsqcup _{v \in \mathcal S''} N^{\sharp }[v \mapsto x]_{\mid (\mathcal S \setminus \mathcal S'') \cup \{x\} }\) (which generalize the one introduced in [13]). These operations are lifted as operators on elements of \(\mathfrak M^{\sharp }\):

5 Natural Term Abstraction by Numerical Constraints
We are now able to represent sets of maps with heterogeneous supports and to lift their concretization (modulo a summarization function) to sets of maps with infinite and heterogeneous supports. Given a tree shape (in the sense of Sect. 3), we can associate a numeric variable to each numeric leaf, and use a numeric abstract element to represent the possible values of these leaves. We will name the variable of each leaf as the path from the root to the leaf, i.e., \(\mathcal V\) is a set of words in \(\{0,...,n-1\}\) where n is the maximum arity of the considered ranked alphabet. In order to avoid confusion such paths will be denoted  for the word (0, 1, 1). A summarized variable then represents a set of such paths. We will abstract such sets as regular expressions. Using the summarization extended to heterogeneous supports presented in the previous section, it will be possible to represent, using a single numeric abstract element, a set of contraints over the numeric leaves of an infinite set of unbounded trees of arbitrary shape.
for the word (0, 1, 1). A summarized variable then represents a set of such paths. We will abstract such sets as regular expressions. Using the summarization extended to heterogeneous supports presented in the previous section, it will be possible to represent, using a single numeric abstract element, a set of contraints over the numeric leaves of an infinite set of unbounded trees of arbitrary shape.
5.1 Hole Positions and Numerical Constraints
The presentation of our computable abstraction able to represent numerical values in trees is broken down (for presentation purposes) into two consecutive abstractions. The first one is not computable, as natural terms are abstracted as partial environments over tree paths to numerical values. This abstraction looses most of the tree shapes but focuses on their numerical environment. A second abstraction will show how partial environments over paths are abstracted into numerical abstract elements defined over a regular expression environment.
In the following, when \(\mathcal {R}\) is a ranked alphabet of maximum arity n, we call words sequences of integers, \(w= (w_0, \dots , w_{p-1})\in \{0,\dots ,(n-1)\}^p\) will be called a word of length p (denoted \(|w|\)), \(w_i\) denotes the i-th integer of the sequence, \(\overline{w}= (w_1,\dots ,w_{p-1})\) is the tail of word \(w\), \(\mathcal W(\mathcal {R}) = \{0, \dots , (n-1)\}^{\star }\) is the set of all words over \(\{0, \dots , n-1\}\) of arbitrary size.
Definition 13 (Position in a term)
Given a natural term \(t\) and a word \(w\) we inductively define the subterm of t at position w (denoted \(t_{\mid w}\)) to be:
Moreover we denote by \(\mathbf {numeric}(t) = \{w\in \mathbb N^{\star } \mid t_{\mid w} \in \mathbb Z\}\).
Definition 14 (Positioning lattice with exact numerical constraints)
We define  , an element of \(\mathcal C(\mathcal R)\) is therefore a set of partial maps that are acceptable bindings of positions to integers.
, an element of \(\mathcal C(\mathcal R)\) is therefore a set of partial maps that are acceptable bindings of positions to integers.
Proposition 7 (Galois connection with natural terms)
When \(t\) is a natural term, \(t_{\mathbb Z}\) is the partial map:  . We have the following Galois connection:
. We have the following Galois connection:  , with:
, with:

Example 12
Consider our running example (introduced in Example 2), \(V = \{+(x,+(z, y)) \mid x \le y \wedge z \le y\}\), we have  . The concretization of which is exactly V.
. The concretization of which is exactly V.
Example 13
Consider however the ranked alphabet \(\{f(2), g(2), a(0)\}\), and the tree a. Its abstraction contains only the empty map, the concretization of which is the set of all terms that do not contain any numerical value. For example: \(f(g(a,a),a), g(a,a),\dots \). This emphasizes that we loose information on:
-
the labels in the natural terms: we only have the path from the root of the term to leaves with numerical labels, not the actual symbols along the path.
-
the shape of the natural terms: we do not keep any information on subterms that do not contain numerical values.
Now that we have abstracted away the shape of the terms, we are left with numerical environments with potentially infinite dimensions (that are words over the alphabet \(\{0,\dots , n-1\}\)) and different definition sets. Therefore following the idea of Sect. 4 we want to define a summarization for sets of words over the alphabet \(\{0,\dots , n-1\}\). A summarization of such a language can be expressed as a partition into sub-languages. The set of regular languages over the alphabet \(\{0,\dots , n-1\}\) is a subset of the set of languages over this alphabet, that is closed under common set operations. Hence given a set \(\{r_1,\dots , r_m\}\) of regular expressions (with respective recognized language \(\{L_1,\dots ,L_m\}\)), we summarize all words in \(L_i\) inside a common variable \(r_i\) and therefore \(\uparrow \{r_1,\dots , r_m\}\) denotes the summarization function: \(\lambda r_i. L_i\). In the following, \(\text {Reg}_n\) denotes the set of regular expressions over the alphabet \(A_n=\{0,\dots ,n-1\}\). As for tree regular expressions, \((\text {Reg}_n, \subset , \cap , \cup , .^c ,\emptyset , A_n^{\star })\) is a (non complete) complemented lattice of infinite height, upon which we can define a widening operator \(\triangledown \) (see [10]) in a similar manner as for tree regular expressions (this widening is also parameterized by an integer constant). We recall moreover that operators \(\subset , \cap , \cup \) and complementation (\(.^c\)) are computable, and that every finite set of words is regular. Moreover we have the following representation: \((A_n^{\star },\sqsubseteq ) \xleftarrow {\gamma _{\text {Reg}_n}=Id}{} (\text {Reg}_n,\sqsubseteq )\). Finally in order to disambiguate regular expressions from integers we will typeset them within \(\lfloor .\rfloor \) in a bold font as in: \(\lfloor \mathbf {0}+ \mathbf {0}.\mathbf {1}^{\star } \rfloor \).
Example 14
Using notations from Sect. 4.2, \(\mathcal V'=\text {Reg}_n\) and \(\mathcal V=\mathcal W(\mathcal {R})\). Consider our running example (introduced in Example 2), natural terms from \(V=\{+(x, +(z , y )) \mid x \le y \wedge z \le y\}\) contain three paths to numerical values:  ,
,  and
and  . Numerical constraints on
. Numerical constraints on  and
and  are similar, therefore the two paths are summarized into one regular expression: \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \),
are similar, therefore the two paths are summarized into one regular expression: \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \),  is left alone in its regular expression: \(\lfloor \mathbf {1}.\mathbf {1} \rfloor \). The two constraints \(x \le y \wedge z \le y\) can now be expressed as one: \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \).
is left alone in its regular expression: \(\lfloor \mathbf {1}.\mathbf {1} \rfloor \). The two constraints \(x \le y \wedge z \le y\) can now be expressed as one: \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \).
In Example 14, we saw that tree paths with similar numerical constraints can be summarized in one regular expression. However, for precision purposes, we do not want to summarize all tree paths into one regular expression. Hence, we will keep several disjoint regular expressions, which we call a subpartitioning.
Definition 15 (Subpartitioning)
Given a regular expression s, a subpartitioning of s is a set \(\{s_1, \dots , s_n\}\) of regular expressions such that \(\forall i \ne j,\ s_i \cap s_j = \emptyset \) and \(\bigcup _{i=1}^n s_i \subseteq s\). We note P(s) the set of all subpartitioning of s. Moreover if \(S=\{s_1,\dots ,s_n\}\) is a set of regular expressions, \([S]_{\emptyset }=S\setminus \{\emptyset \}\).
Remark 7
Contrary to a partitioning of s, we do not require that the set of partitions covers s. Indeed when a set of tree paths is unconstrained we can just remove it from the partitioning, therefore no dimension in the numerical abstract environment will be allocated for this path.
Definition 16 (Positioning lattice with numerical abstraction)
Given a ranked alphabet \(\mathcal {R}\), where the maximum arity of symbols is n, we define \(\mathcal C^{\sharp }(\mathcal R)= \{\langle s, \mathfrak p, R^{\sharp }\rangle \mid s \in \text {Reg}_n, \mathfrak p\in P(s), R^{\sharp }\in \mathfrak M^{\sharp }_\mathfrak p\}\). Therefore \(\mathcal C^{\sharp }(\mathcal R)\) are triples containing:
-
s: (called support) a regular expression coding for positions at which numerical values can be located.
-
\(\mathfrak p\): a subpartitioning of s. Elements of the same partition are subject to the same numerical constraints. Note that these partitions are regular.
-
\(R^{\sharp }\): an abstract numeric element where a dimension is associated to each partition, this dimension plays the role of a summary dimension.

Remark 8
In the following, numerical abstract elements described in the form \(\{c\}\), where c is a set of constraints, refer to \(\langle c, \mathbf {vars}(c), \mathbf {vars}(c) \rangle \in \mathfrak M^{\sharp }\).
Unification. The previous definition shows that two elements \(U^{\sharp }= \langle s , \mathfrak p, R^{\sharp }\rangle \) and \(V^{\sharp }= \langle s' , \mathfrak p', R^{\sharp \prime }\rangle \) can have different subpartitionings (\(\mathfrak p\) and \(\mathfrak p'\)). However the partitions in \(\mathfrak p\) and in \(\mathfrak p'\) might overlap, thus giving constraints to similar tree paths. Therefore in order to define the classical operators: \(\sqsubseteq , \sqcup \) and \(\triangledown \), we need to unify the two abstract elements (\(U^{\sharp }\) and \(V^{\sharp }\)) so that given a tree path and the partition in which it is contained in \(U^{\sharp }\), it is contained in the same partition in \(V^{\sharp }\). This will enable us to rely on abstract operators on the numerical domain. In order to perform unification, we rely on the \(\mathbf {expand}\) and \(\mathbf {fold}\) operators. Indeed consider our running example, \(U^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \} , \{\lfloor \mathbf {0} \rfloor \le \lfloor \mathbf {1} \rfloor \}\rangle \) and \(V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1}.(\mathbf {0}+ \mathbf {1}) \rfloor , \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor , \lfloor \mathbf {1}.\mathbf {1} \rfloor \}, \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \} \rangle \). We see that constraints on tree path  is given: in \(U^{\sharp }\) by partition \(\lfloor \mathbf {0} \rfloor \) and in \(V^{\sharp }\) by partition \(\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \). However we can split the partition \(\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \) into two partitions: \(\lfloor \mathbf {0} \rfloor \) and \(\lfloor \mathbf {1}.\mathbf {0} \rfloor \), and expand variable \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \) into the two variables \(\lfloor \mathbf {0} \rfloor \) and \(\lfloor \mathbf {1}.\mathbf {0} \rfloor \) in the numeric component: \(\mathbf {expand}(\{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \}, \lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor , \{\lfloor \mathbf {0} \rfloor ,\lfloor \mathbf {1}.\mathbf {0} \rfloor \}) = \{\lfloor \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor , \lfloor \mathbf {1}.\mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \}\). Once \(U^{\sharp }\) and \(V^{\sharp }\) are unified we can rely on the numerical join to soundly abstract the union. Note that splitting partitions is more precise than merging them. Indeed, consider the example where: in \(U^{\sharp }\) we have \(\lfloor \mathbf {0} \rfloor \ge 0\) and \(\lfloor \mathbf {1} \rfloor \le 0\) and in \(V^{\sharp }\) we have \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor = 0\). Splitting partition in \(V^{\sharp }\) yields: \(\lfloor \mathbf {0} \rfloor = 0, \lfloor \mathbf {1} \rfloor = 0\), after joining we get \(\lfloor \mathbf {0} \rfloor \ge 0, \lfloor \mathbf {1} \rfloor \le 0\). Whereas merging partitions in \(U^{\sharp }\) yields \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor \) unconstrained, after joining we also get that \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor \) is unconstrained. However unifying by splitting or merging partitions in both abstract elements might result in an over-approximation of the initial elements. This does not pose a threat to the soundness of the join operator, but it does for the inclusion test. Unifying by splitting partitions induces an increase in the number of partitions which we want to avoid when trying to stabilize abstract elements in the widening. Hence, we define three unification operators:
is given: in \(U^{\sharp }\) by partition \(\lfloor \mathbf {0} \rfloor \) and in \(V^{\sharp }\) by partition \(\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \). However we can split the partition \(\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \) into two partitions: \(\lfloor \mathbf {0} \rfloor \) and \(\lfloor \mathbf {1}.\mathbf {0} \rfloor \), and expand variable \(\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor \) into the two variables \(\lfloor \mathbf {0} \rfloor \) and \(\lfloor \mathbf {1}.\mathbf {0} \rfloor \) in the numeric component: \(\mathbf {expand}(\{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \}, \lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor , \{\lfloor \mathbf {0} \rfloor ,\lfloor \mathbf {1}.\mathbf {0} \rfloor \}) = \{\lfloor \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor , \lfloor \mathbf {1}.\mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \}\). Once \(U^{\sharp }\) and \(V^{\sharp }\) are unified we can rely on the numerical join to soundly abstract the union. Note that splitting partitions is more precise than merging them. Indeed, consider the example where: in \(U^{\sharp }\) we have \(\lfloor \mathbf {0} \rfloor \ge 0\) and \(\lfloor \mathbf {1} \rfloor \le 0\) and in \(V^{\sharp }\) we have \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor = 0\). Splitting partition in \(V^{\sharp }\) yields: \(\lfloor \mathbf {0} \rfloor = 0, \lfloor \mathbf {1} \rfloor = 0\), after joining we get \(\lfloor \mathbf {0} \rfloor \ge 0, \lfloor \mathbf {1} \rfloor \le 0\). Whereas merging partitions in \(U^{\sharp }\) yields \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor \) unconstrained, after joining we also get that \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor \) is unconstrained. However unifying by splitting or merging partitions in both abstract elements might result in an over-approximation of the initial elements. This does not pose a threat to the soundness of the join operator, but it does for the inclusion test. Unifying by splitting partitions induces an increase in the number of partitions which we want to avoid when trying to stabilize abstract elements in the widening. Hence, we define three unification operators:
-
An operator \(\mathbf {unify\_join}\) that splits partitions from \(U^{\sharp }\) and \(V^{\sharp }\), this operator might induce an over-approximation for both \(U^{\sharp }\) and \(V^{\sharp }\) and is used in the join operation. This operator is presented in Algorithm 2, and illustrated in Fig. 6.
-
An operator \(\mathbf {unify\_subset}\) that does not modify \(V^{\sharp }\) (in order to avoid over-approximated it), we only split and merge (using the \(\mathbf {fold}\) operator) partitions from \(U^{\sharp }\) as, if the over-approximated \(U^{\sharp }\) is smaller than \(V^{\sharp }\), then so is the original \(U^{\sharp }\).
-
An operator \(\mathbf {unify\_widen}\) that unifies \(U^{\sharp }\) and \(V^{\sharp }\) by only merging partitions so that the number of partitions does not increase. This operator is used in the widening definition.
Operators \(\mathbf {unify\_subset}\) and \(\mathbf {unify\_widen}\) are very similar to \(\mathbf {unify\_join}\).
Definition 17
(Comparison \(\sqsubseteq _{\mathcal C^{\sharp }(\mathcal R)}\)). Using \(\mathbf {unify\_subset}\) we define a relation on \(\mathcal C^{\sharp }(\mathcal R)\): \(\sqsubseteq _{\mathcal C^{\sharp }(\mathcal R)}=\{(U^{\sharp }, V^{\sharp }) \mid (\langle s, \mathfrak p, N^{\sharp }\rangle , \langle s', \mathfrak p', N^{\sharp \prime }\rangle ) = \mathbf {unify\_subset}(U^{\sharp },V^{\sharp }) \Rightarrow s \subseteq s' \wedge \forall b \in \mathfrak p', (b \subseteq s^c \vee \exists ! a \in \mathfrak p,\, b \cap s = a) \wedge N^{\sharp }\sqsubseteq N^{\sharp \prime }[\phi ]\}\) where \(\phi \) is the renaming from \(\mathfrak p'\) into \(\mathfrak p\) that renames b to a when such an a exists.
Example 15
Going back to our running example: \(U^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \} , \{\lfloor \mathbf {0} \rfloor \le \lfloor \mathbf {1} \rfloor \} (=A^{\sharp }) \rangle \) and \(V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1}.(\mathbf {0}+ \mathbf {1}) \rfloor , \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor , \lfloor \mathbf {1}.\mathbf {1} \rfloor \}, \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \} \rangle \). We have \(s \not \subseteq s'\) hence \(U^{\sharp }\not \sqsubseteq V^{\sharp }\). However if we now consider \(W^{\sharp }\): \(\langle \lfloor (\epsilon + \mathbf {1}).(\mathbf {0}+ \mathbf {1}) \rfloor , \{\lfloor (\epsilon + \mathbf {1}) .\mathbf {0} \rfloor , \lfloor (\epsilon + \mathbf {1}) . \mathbf {1} \rfloor \}, \{\lfloor (\epsilon + \mathbf {1}) .\mathbf {0} \rfloor \le \lfloor (\epsilon + \mathbf {1}) .\mathbf {1} \rfloor \} (=B^{\sharp }) \rangle \). \(W^{\sharp }\) is already unified with \(U^{\sharp }\), we have \(s \subseteq s'\) and \(\phi : (\lfloor (\epsilon + \mathbf {1}).\mathbf {0} \rfloor \mapsto {\mathbf {0}}, \lfloor (\epsilon + \mathbf {1}).\mathbf {1} \rfloor \mapsto \lfloor \mathbf {1} \rfloor )\). Moreover \(A^{\sharp } \sqsubseteq B^{\sharp }[\phi ] = \{\lfloor \mathbf {0} \rfloor \le \lfloor \mathbf {1} \rfloor \}\). Hence \(U^{\sharp } \sqsubseteq W^{\sharp }\).
Proposition 8
We have: \((\mathcal C(\mathcal R), \sqsubseteq _{\mathcal C(\mathcal R)}) \xleftarrow {\gamma _1}{} (\mathcal C^{\sharp }(\mathcal R), \sqsubseteq _{\mathcal C^{\sharp }(\mathcal R)})\), where: \( \gamma _1 (\langle s, \mathfrak p, R^{\sharp }\rangle ) = \{f \mid \mathbf {def}(f) \subseteq \gamma _{\text {Reg}_n}(s) \wedge f \in \gamma [\uparrow \mathfrak p](R^{\sharp }) \}\). By composition we get: \((\wp (T_{\mathbb Z}(\mathcal {R})), \subseteq ) \xleftarrow {\gamma _2}{} (\mathcal C^{\sharp }(\mathcal R), \sqsubseteq _{\mathcal C^{\sharp }{\mathcal R}})\), with \(\gamma _2 = \gamma _{\mathcal C(\mathcal R)} \circ \gamma _1\).
Example 16
Going back to our running example: \(V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1}.(\mathbf {0}+ \mathbf {1}) \rfloor , \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor , \lfloor \mathbf {1}.\mathbf {1} \rfloor \}, \{\lfloor \mathbf {0}+ \mathbf {1}. \mathbf {0} \rfloor \le \lfloor \mathbf {1}.\mathbf {1} \rfloor \} \rangle \). We have:  . Hence,
. Hence, 
 . The product with tree automata refines this result so that only the last set is left.
. The product with tree automata refines this result so that only the last set is left.
We now define the \(\sqcup \) operator that relies on the \(\mathbf {unify\_join}\) operator of Algorithm 2. Once elements are unified we can distinguish three kinds of partitions: (1) Partitions found in both abstract elements (e.g.
 in Fig. 6). (2) Partitions found in only one of the two, which do not overlap over the support of the other abstract element (denoted \(u^o\)), these are outer-partitions. Information on such partitions can be soundly kept when joining two abstract elements (e.g. partition a in Fig. 6). (3) Partitions found in only one of the two, which overlap over the support of the other abstract element, these are inner-partitions. Information on such partitions can not be soundly kept when joining two abstract elements. (e.g. partition b in Fig. 6). Therefore in the following definition of the join operator, we compute (once elements are unified) the common partitions and both outer-partitions and merge them to form the resulting subpartitioning.
in Fig. 6). (2) Partitions found in only one of the two, which do not overlap over the support of the other abstract element (denoted \(u^o\)), these are outer-partitions. Information on such partitions can be soundly kept when joining two abstract elements (e.g. partition a in Fig. 6). (3) Partitions found in only one of the two, which overlap over the support of the other abstract element, these are inner-partitions. Information on such partitions can not be soundly kept when joining two abstract elements. (e.g. partition b in Fig. 6). Therefore in the following definition of the join operator, we compute (once elements are unified) the common partitions and both outer-partitions and merge them to form the resulting subpartitioning.
Definition 18 (Union abstract operator)
Given \(U^{\sharp }, V^{\sharp }\in \mathcal C^{\sharp }(\mathcal R)\), if \((\langle s, \mathfrak p, R^{\sharp }\rangle , \langle s', \mathfrak p', R^{\sharp \prime }\rangle ) = \mathbf {unify\_join}(U^{\sharp },V^{\sharp })\), let \(\mathfrak c\) be \(\mathfrak p\cup \mathfrak p'\), let \(u^o\) (\(U^{\sharp }\) outer-partition) be \(\{e \in \mathfrak p\mid e \subseteq s^{\prime c}\}\), let \(v^o\) (\(V^{\sharp }\) outer-partition) be \(\{e \in \mathfrak p' \mid e \subseteq s^{c}\}\), we then define:
Proposition 9
We have: \( \gamma _1 (U^{\sharp }) \cup \gamma _1 (V^{\sharp }) \subseteq \gamma _1(U^{\sharp }\sqcup _{\mathcal C^{\sharp }(\mathcal R)} V^{\sharp })\).
Example 17
Consider the two following abstract elements (this is the particular case of our running example where all numerical values are equal): \(V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1}.(\mathbf {0}+ \mathbf {1}) \rfloor (=s), \{\lfloor \mathbf {0}+ \mathbf {1}.\mathbf {0} \rfloor (=a), \lfloor \mathbf {1}.\mathbf {1} \rfloor (=b), \{a=b\}\} \rangle \), and \(U^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor (=s'), \{\lfloor \mathbf {0} \rfloor (=c), \lfloor \mathbf {1} \rfloor (=d)\}, \{c=d\} \rangle \). Intuitively \(U^{\sharp }\) could encode the term \((x + x)\) and \(V^{\sharp }\) the term \((x + (x + x))\). The unification of those two elements is: \(V^{\sharp }_1= \langle s, \{c, b, \lfloor \mathbf {1}.\mathbf {0} \rfloor (=e) \}, R^{\sharp }\rangle \) where \(R^{\sharp }= \langle \{c = b, e = b\}, \{b\}, \{c,b,e\} \rangle \) and \(U^{\sharp }_1= U^{\sharp }\), moreover the common environment (\(\mathfrak c\) in previous definition) is: \(\{c\}\), \(V^{\sharp }\) outer-partitioning is \(\{e, f\}\), \(U^{\sharp }\) outer-partitioning is \(\{d\}\). Hence: the numerical component resulting of the join is: \(\langle \{c = d\} , \{c, d\}, \{c,d\} \rangle \sqcup \langle \{c = b, e = b\}, \{b\}, \{c,b,e\} \rangle \) which is: \(\langle \{c = b, e = b, c = d\} , \emptyset , \{c, d, e, b\}\rangle \). We see here that using a naive numerical join operator, we would not have been able to get such a precise result (the numerical join would have yielded \(\top \)).
\(\mathbf {unify\_widen}\) \(\mathcal C^{\sharp }(\mathcal {R})\) contains infinite increasing chains, therefore, we need to provide a widening operator. As for the other operators, widening is computed on unified abstract elements. A \(\mathbf {unify\_widen}\) operator is defined: it produces \(U^{\sharp }\) and \(V^{\sharp }\), over-approximations of its inputs with the same number of partitions. Moreover it ensures that each partition of \(U^{\sharp }\) intersects exactly one partition of \(V^{\sharp }\). This can be obtained by iterative merging partitions that overlap in both arguments until the abstract elements have the exact same partitions. Therefore from the result of \(\mathbf {unify\_widen}\) we can extract a list of pairs (a, b) where a is a partition from \(U^{\sharp }\), b is a partition from \(V^{\sharp }\) and \(a \cap b \ne \emptyset \). This defines a bijection from partitions of \(U^{\sharp }\) onto partitions of \(V^{\sharp }\).
\(\mathbf {compose}\). In order to ensure stabilization we first need to stabilize the supports on which abstract elements are defined. This is easily done using the automaton widening (\(s_1 \triangledown s_2\) in Algorithm 3). Figure 7 illustrates the following simple example: \(U^{\sharp }\) is an abstract element with support \(\lfloor \mathbf {0}+\mathbf {1} \rfloor \), two partitions \(u = \lfloor \mathbf {0} \rfloor \) and \(u' = \lfloor \mathbf {1} \rfloor \), and numerical constraints \(u'=1\) and \(u= 0\). \(V^{\sharp }\) is an abstract element with support \(\lfloor (\epsilon + \mathbf {1}).( \mathbf {0}+ \mathbf {1}) \rfloor \), two partitions \(v=\lfloor (\epsilon + \mathbf {1}). \mathbf {0} \rfloor \) and \(v'=\lfloor (\epsilon + \mathbf {1}). \mathbf {1} \rfloor \) with the numerical constraints that \(v = 0\) and \(v' = 1\). Supports are unstable, therefore we start by widening them, which yields a new support: \(\lfloor \mathbf {1}^{\star }.(\mathbf {0}+\mathbf {1}) \rfloor \). The unification of \(U^{\sharp }\) and \(V^{\sharp }\) leaves subpartitionings unchanged and yields the bijection \((u \mapsto v, u' \mapsto v')\). Given this information we now need to provide a new subpartitioning for the result of the widening. We see in this example that we could soundly use the subpartitioning from \(V^{\sharp }\), this would produce the abstract element \(Z^{\sharp }_1\) depicted in Fig. 7. However due to the widening of the support, paths of the form  are in the support of the result but are left unconstrained as they are not in any of the partitions. Therefore we need to use the opportunity of the extension of the support to place constraints on the newly added paths. In order to do so we would like to force the extension of the existing partitions from \(U^{\sharp }\) and \(V^{\sharp }\) into the new support. Therefore we need to define a \(\mathbf {compose}\) operator that produces a sound new partition, given: (1) a pair a, b of partitions (such as the one produced by \(\mathbf {unify\_widen}\)), (2) the support \(s_1\) (resp \(s_2\)) in which a (resp. b) lives and (3) a space to occupy r. The following criteria must be verified by the resulting partition p in order to be sound and to terminate: \(p \cap s_1 = a\), \(p \cap s_2 = b\) and \(p \setminus (s_1 \cup s_2) \subseteq r\). A variety of \(\mathbf {compose}\) operators could be defined, we chose: \(\mathbf {compose}(a, b, s_1, s_2, r)=a \cup (b \cap (s_2 \setminus s_1)) \cup ((a \triangledown (a \cup b)) \cap r)\). The idea is the following: we keep a (as it is always sound thanks to the definition of the \(\mathbf {unify\_widen}\) operator), we keep the part from b that satisfies the soundness condition, and we extend into the space left to occupy according to the automata widening of a and \(a \cup b\). In our example, considering the pair (u, v), this would translate as: \(a = \mathbf {0}\), \(b \cap (s_2 \setminus s_1) = \lfloor \mathbf {1}.\mathbf {0} \rfloor \) and \((a \triangledown (a \cup b)) \cap r= \lfloor \mathbf {0} \rfloor \triangledown \lfloor (\epsilon + 1).\mathbf {0} \rfloor \cap \lfloor \mathbf {1}^{\ge 2}(\mathbf {0}+ \mathbf {1}) \rfloor = \lfloor \mathbf {1}^{\ge 2}.\mathbf {0} \rfloor \). We get the new partition: \(\lfloor \mathbf {1}^{\star }.\mathbf {0} \rfloor \). Doing the same with the pair \((v, v')\) yields \(\lfloor \mathbf {1}^{\star }.\mathbf {1} \rfloor \). Finally we get the abstract element \(Z^{\sharp }_2\) from Fig. 7, which is more precise than \(Z^{\sharp }_1\).
are in the support of the result but are left unconstrained as they are not in any of the partitions. Therefore we need to use the opportunity of the extension of the support to place constraints on the newly added paths. In order to do so we would like to force the extension of the existing partitions from \(U^{\sharp }\) and \(V^{\sharp }\) into the new support. Therefore we need to define a \(\mathbf {compose}\) operator that produces a sound new partition, given: (1) a pair a, b of partitions (such as the one produced by \(\mathbf {unify\_widen}\)), (2) the support \(s_1\) (resp \(s_2\)) in which a (resp. b) lives and (3) a space to occupy r. The following criteria must be verified by the resulting partition p in order to be sound and to terminate: \(p \cap s_1 = a\), \(p \cap s_2 = b\) and \(p \setminus (s_1 \cup s_2) \subseteq r\). A variety of \(\mathbf {compose}\) operators could be defined, we chose: \(\mathbf {compose}(a, b, s_1, s_2, r)=a \cup (b \cap (s_2 \setminus s_1)) \cup ((a \triangledown (a \cup b)) \cap r)\). The idea is the following: we keep a (as it is always sound thanks to the definition of the \(\mathbf {unify\_widen}\) operator), we keep the part from b that satisfies the soundness condition, and we extend into the space left to occupy according to the automata widening of a and \(a \cup b\). In our example, considering the pair (u, v), this would translate as: \(a = \mathbf {0}\), \(b \cap (s_2 \setminus s_1) = \lfloor \mathbf {1}.\mathbf {0} \rfloor \) and \((a \triangledown (a \cup b)) \cap r= \lfloor \mathbf {0} \rfloor \triangledown \lfloor (\epsilon + 1).\mathbf {0} \rfloor \cap \lfloor \mathbf {1}^{\ge 2}(\mathbf {0}+ \mathbf {1}) \rfloor = \lfloor \mathbf {1}^{\ge 2}.\mathbf {0} \rfloor \). We get the new partition: \(\lfloor \mathbf {1}^{\star }.\mathbf {0} \rfloor \). Doing the same with the pair \((v, v')\) yields \(\lfloor \mathbf {1}^{\star }.\mathbf {1} \rfloor \). Finally we get the abstract element \(Z^{\sharp }_2\) from Fig. 7, which is more precise than \(Z^{\sharp }_1\).
Definition 19 (Widening)
Algorithm 3 provides the definition of a widening operator using the \(\mathbf {unify\_widen}\) operator and parameterized by a \(\mathbf {compose}\) function.

Widening Stabilization. Our abstraction contains three components: (1) a support that describes the set of paths (2) a subpartitioning of this support and (3) a numerical component giving constraints on partitions in the subpartitioning. We show how the widening operator stabilizes all three components.
-
Regular expression widening is used on supports when widening is called. Therefore ensuring support stabilization.
-
Once supports are stable (this means \(s_2 \subseteq s_1\)), we have \(p=a\) for every pair (a, b) of partitions. Meaning that once shapes stabilize, the only modifications allowed on the subpartitionings are those made by the \(\mathbf {unify\_widen}\) operator. Each partition resulting from the operator is the union of input partitions, hence the subpartitioning will stabilize.
-
Once subpartitionings are stable (\(\mathfrak p_1 = \mathfrak p\) in Algorithm 3) numerical widening is applied on the numerical component in order to ensure stabilization.
Example 18 (Numerical example)
Consider the simple example where: \(\mathcal R = \{f(2)\}\), \(U^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \}, \{\lfloor \mathbf {1} \rfloor = \lfloor \mathbf {0} \rfloor \}\rangle \) and \(V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \}, \{\lfloor \mathbf {1} \rfloor \ge \lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \le \lfloor \mathbf {0} \rfloor +1 \}\rangle \). \(U^{\sharp }\) and \(V^{\sharp }\) have the same shape, therefore widening will be performed on the numerical component of the abstraction, therefore: \(U^{\sharp }\triangledown V^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \}, \{\lfloor \mathbf {1} \rfloor \ge \lfloor \mathbf {0} \rfloor \}\rangle \).
Reducing Dimensionality and Improving Precision. As emphasized by the previous examples, definitions and illustrations, the numerical component of an abstract state is used as a container for constraints on regular expressions, every node in a regular expression must then satisfy all numerical constraints on the underlying regular expression. Therefore when two nodes of a tree satisfy the same constraints, they should be stored in the same partition so as to reduce the dimension of the numerical domain (thus improving efficiency). Moreover the widening operator provided in Algorithm 3 relies (for precision) on the fact that partitions are built by similarity of constraints, therefore partition merging, when it does not result in an over-approximation, also leads to a precision gain. The unification operator defined in Algorithm 2 tends to split partitions whereas the widening operator defined in Algorithm 3 tends to merge them. In order to reduce dimensionality, we would like to define a \(\mathbf {reduce}: \mathcal C^{\sharp }(\mathcal R) \rightarrow \mathcal C^{\sharp }(\mathcal R)\) operator, that folds variables with similar constraints into one. Please note that \(\forall S \cap S' \subseteq \{x\}\), \(x \in S\) and \(R^{\sharp }\in N_S\), we have that \(R^{\sharp }\sqsubseteq _{N_S} \mathbf {expand}(\mathbf {fold}(R^{\sharp }, x, S'), x, S')\). This means that when variables are folded into one, expanding them afterwards would yield a bigger abstract element. For example, consider the octagon \(R^{\sharp }= \{ x \ge 2, y \ge 2, x = y \}\) then  and \(\mathbf {expand}(R^{\sharp \prime }, z, \{x, y\}) = \{x \ge 2, y \ge 2\}\). However if we consider \(R^{\sharp }= \{ x \ge 2, y \ge 2\}\) then \(\mathbf {fold}(\mathbf {expand}(R^{\sharp }, z ,\{x,y\}), z, \{x,y\}) = R^{\sharp }\). Therefore if we assume given a score function \(\mathbf {score}(R^{\sharp }, x, S')\) ranging in [0, 1] such that \(\mathbf {score}(R^{\sharp }, x, S') = 1 \Leftrightarrow R^{\sharp }= \mathbf {expand}(\mathbf {fold}(R^{\sharp }, x, S'), x, S')\), we are able to define a generic \(\mathbf {reduce}\) operator parameterized by a value \(\alpha \). This \(\mathbf {reduce}\) operator merges partitions until no more set of partitions has a high enough score according to the \(\mathbf {score}\) function. Finding a good \(\mathbf {score}\) function is a work in progress. As a first approximation we used the following trivial one: \(\mathbf {score}_0(R^{\sharp }, S) = 1 \text { when } \mathbf {expand}(\mathbf {fold}(R^{\sharp }, x, S), x , S) = R^{\sharp }\text { and } 0 \text { otherwise}\). This \(\mathbf {score}_0\) guarantees there is no loss of precision, but can miss opportunities for simplification.
and \(\mathbf {expand}(R^{\sharp \prime }, z, \{x, y\}) = \{x \ge 2, y \ge 2\}\). However if we consider \(R^{\sharp }= \{ x \ge 2, y \ge 2\}\) then \(\mathbf {fold}(\mathbf {expand}(R^{\sharp }, z ,\{x,y\}), z, \{x,y\}) = R^{\sharp }\). Therefore if we assume given a score function \(\mathbf {score}(R^{\sharp }, x, S')\) ranging in [0, 1] such that \(\mathbf {score}(R^{\sharp }, x, S') = 1 \Leftrightarrow R^{\sharp }= \mathbf {expand}(\mathbf {fold}(R^{\sharp }, x, S'), x, S')\), we are able to define a generic \(\mathbf {reduce}\) operator parameterized by a value \(\alpha \). This \(\mathbf {reduce}\) operator merges partitions until no more set of partitions has a high enough score according to the \(\mathbf {score}\) function. Finding a good \(\mathbf {score}\) function is a work in progress. As a first approximation we used the following trivial one: \(\mathbf {score}_0(R^{\sharp }, S) = 1 \text { when } \mathbf {expand}(\mathbf {fold}(R^{\sharp }, x, S), x , S) = R^{\sharp }\text { and } 0 \text { otherwise}\). This \(\mathbf {score}_0\) guarantees there is no loss of precision, but can miss opportunities for simplification.
Example 19
Consider the following example: \(U^{\sharp }= \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{ \lfloor \mathbf {0} \rfloor , \lfloor \mathbf {1} \rfloor \}, \{\lfloor \mathbf {0} \rfloor = 0, \lfloor \mathbf {1} \rfloor = 0\} \rangle \). Relations on \(\lfloor \mathbf {0} \rfloor \) and \(\lfloor \mathbf {1} \rfloor \) can be expressed in one relation using the summarizing variable \(\lfloor \mathbf {0}+ \mathbf {1} \rfloor \). This yields: \(\mathbf {reduce}(U^{\sharp }) = \langle \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {0}+ \mathbf {1} \rfloor \}, \{\lfloor \mathbf {0}+ \mathbf {1} \rfloor = 0 \}\rangle \). Note that \(\mathbf {expand}(\{\lfloor \mathbf {0}+ \mathbf {1} \rfloor = 0 \}, \lfloor \mathbf {0}+ \mathbf {1} \rfloor , \{\lfloor \mathbf {1} \rfloor , \lfloor \mathbf {0} \rfloor \}) = \{\lfloor \mathbf {0} \rfloor = 0, \lfloor \mathbf {1} \rfloor = 0\}\). Therefore no information is lost.
Abstract Semantic of Operators. As for tree automata, abstract semantic of operators defined in Sect. 2 can be defined as simple transformations on regular automata. Indeed the \(\texttt {make\_symbolic}(s \in \mathcal {R})\) (resp. \(\texttt {get\_son}\)) operator, amounts to adding (resp. removing) an integer letter to: (1) the partitions in the subpartitioning and (2) the support.  amounts to building an abstract element with support \(\lfloor \epsilon \rfloor \) and a subpartitioning containing only \(\{\lfloor \epsilon \rfloor \}\), on which we put the constraint that it is equal to e. is_symbol needs only split the support and each partition, in the two language \(L = \{\epsilon \}\) and \(A_n^{\star } \setminus L\). Indeed in order to restrict to terms having only an integer as root, the support must be reduced to \(\epsilon \). The get_sym_head operator always yields the whole ranked alphabet (as this was abstracted away and will be refined by the automaton abstraction). Finally for get_num_head: (1) if the empty path
amounts to building an abstract element with support \(\lfloor \epsilon \rfloor \) and a subpartitioning containing only \(\{\lfloor \epsilon \rfloor \}\), on which we put the constraint that it is equal to e. is_symbol needs only split the support and each partition, in the two language \(L = \{\epsilon \}\) and \(A_n^{\star } \setminus L\). Indeed in order to restrict to terms having only an integer as root, the support must be reduced to \(\epsilon \). The get_sym_head operator always yields the whole ranked alphabet (as this was abstracted away and will be refined by the automaton abstraction). Finally for get_num_head: (1) if the empty path  is in the support we produce the set of integers satisfying the numerical constraints on the partition containing \(\epsilon \), and \(\top \) in case no such partition could be found, and (2) otherwise we know that no numerical value is produced.
is in the support we produce the set of integers satisfying the numerical constraints on the partition containing \(\epsilon \), and \(\top \) in case no such partition could be found, and (2) otherwise we know that no numerical value is produced.
5.2 Product of Tree Automata and Numerical Constraints
The abstraction by tree automata defined in Sect. 3 and the abstraction by numerical constraints on tree paths defined in Sect. 5.1 provide non comparable information on the set of terms they abstract. Indeed the former describes precisely the shape of the term but can not express numerical constraints whereas the latter abstracts away most of the shape and focuses on numerical constraints. To benefit from both kinds of information, we use a reduced product between the two domains. Both abstractions in the product contain information on potential integer positions. The position of the \(\square \) symbol in the tree automaton abstraction and the support in the numerical constraints abstractions both yield this information. We remove the support component from the product as the information can be retrieved from the tree abstraction. The definitions of the abstract operators in Sect. 5.1 require the support to be a regular language. We show in this subsection how to retrieve the support of a tree automaton with holes and that it is regular.
Given a FTA\((Q, \mathcal {R}, Q_f, \delta )\) over a ranked alphabet \(\mathcal {R}\) with maximum arity n. We assume that every node in \(Q\) is reachable. Consider the following system over variables \(v_p\) for \(p\in Q\) with values in the set of languages over the alphabet \(A_n\) (. designates the classical concatenation operator lifted to languages):
Every language \(\{i\}\) for \(i \in \mathbb N\) is regular and does not contain \(\epsilon \), moreover \(\emptyset \) and \(\{\epsilon \}\) are regular languages. By application of Arden’s rule (see [18]) and Gauss elimination we can compute the unique solution of this system, moreover every \(v_p\) is regular. Variable \(v_p\) is defined so that: \(w\in v_p\) if and only if there exists a tree t recognized by the automaton such that \(p \in \textsc {reach}(t_{\mid w})\). If \(\square \in \mathcal R\) we have that the regular language: \(\cup _{(\square ,(),p) \in \delta } v_p\) represents exactly the potential positions of integers in trees accepted by the tree automaton.
Height and Size. The product is enriched with a simple height and size abstraction: numerical variables (encoding heights and sizes) are added to the numerical component of the abstraction.
5.3 Environment Abstraction
In the previous section, we designed abstractions for sets of trees. However in order to be able to tackle the examples from the introductory section (Sect. 1) we need to design an abstraction able to represent maps from a set of variables to natural terms. In Sect. 3 we have shown how to lift abstractions on natural terms to abstractions of environments over a given finite set of finite term variables \(\mathcal T\). We apply the same mechanism here to lift the product presented in Sect. 5.2. However lifting the product would result in abstract environments being maps from natural term variables to abstractions containing a numerical environment. In order to be able to express numerical relations between two sets of natural terms or even between numerical program variables and numerical values of natural terms we factor away the numerical environment so that it is shared by all natural term abstractions in the term environment and by the program variables in the numerical environment. Therefore the final abstraction is a pair \((m, R^{\sharp })\) where: (1) m is a map from \(\mathcal T\) to an abstract element that is a product of the automaton abstraction and the hole positioning abstraction. Moreover as all the numerical constraints are stored in a common numerical environment the product abstraction amounts to a pair \((\mathcal A, \mathfrak p)\) where \(\mathcal A\) is an element of the automaton abstraction and \(\mathfrak p\) is a partitioning of its support. (2) \(R^{\sharp }\) is an element of \(\mathfrak M^{\sharp }\) binding in the same numerical element: numerical program variables and all partitions found in the mapping m.
6 Implementation and Example
6.1 Implementation
The analyzer was implemented in OCaml (\(\sim \)5000 loc) in the novel and still in development Mopsa framework (see [21]). Mopsa enables a modular development of static analyzers defined by abstract interpretation. An analyzer is built by choosing abstract domains, and combining them according to the user specification. Mopsa comes with pre-existing iterators and domains (e.g. inter-procedural analysis, loop iterators, numerical domains, ...), and new ones can be added (e.g. tree abstract domain). A key feature of Mopsa is the ability of an abstract domain to use the abstract knowledge it maintains to transform dynamically expressions into other expressions that can be manipulated more easily by further domains, providing a flexible way to combine relational domains. For instance, assume that a domain abstracts arrays by associating a scalar variable \(a_0\), \(a_1\), ..., to each element a[0], a[1], ..., of an array a, and delegating the abstraction of the array contents to a numeric domain for scalars. It can then evaluate \(\mathbb E^{\sharp } [\![2*a[i]+i ]\!](i \mapsto [0,1])\) into the disjunction \((2*a_0+i,i \mapsto [0,0]) \vee (2*a_1+i,i \mapsto [1,1])\), indicating that \(2*a[i]+i\) is equivalent to \(2*a_0+i\) in the sub-environment where \(i=0\) and to \(2*a_1+i\) in the sub-environment where \(i=1\). Each term of the disjunction contains an array-free expression that can be handled by the scalar domain in the corresponding sub-environment. In the abstract, expressions can be evaluated by induction on the syntax into symbolic expressions to retain the full power of relational domains and disjunctive reasoning (see [21] for more details). We exploit this feature in our implementation to combine our tree abstractions. We implemented (in the Mopsa framework) libraries for regular and tree regular languages that offer the usual lattice interface enriched with a widening operator. These libraries can be reused for the definition of other abstract domains. The overall complexity of the analysis is driven by the complexity of the lattice operations in the regular and tree regular libraries. These are exponential in the number of states of the considered automata, which is bounded by the widening parameter.
6.2 Examples of Analysis
Numerical variables of the form \(\texttt {t}.x\), where \(\texttt {t}\) is a natural term variable, represent a variable allocated for tree \(\texttt {t}\). For example: \(\texttt {t}.r\) where r is a regular expression is the variable allocated for partition r in tree \(\texttt {t}\).
C Introductory Example. Let us consider the introductory example Program 4. The loop invariant inferred with our analysis is the following abstract element: \(U^{\sharp }= (\texttt {y} \mapsto (\mathcal A, \{\lfloor \mathbf {0}.(\mathbf {0}.\mathbf {0})^{\star }.\mathbf {1} \rfloor (=r)\}), R^{\sharp })\), with \(\mathcal A= \langle \{a,b,c,d\}, \{*(1),+(2),\square (0),(p,0)\}, \{c\}, \{*(d) \rightarrow c, +(c,a)\rightarrow d, \square () \rightarrow a, p \rightarrow c\} \rangle \), and \(R^{\sharp }\) satisfies the constraints: \(\{\texttt {i} \ge 0, \texttt {i} \le \texttt {n}, \texttt {y}.r = 4\}\). This describes precisely the set of terms of the form: p, \(*(p+4)\), \(*(*(p+4)+4)\), .... As mentioned in Sect. 6.1 evaluations of tree expressions yield pairs containing an expression and an abstract environment. Tree expressions are pairs \((\mathcal A, \mathfrak p)\), partitions in \(\mathfrak p\) are bound by the adjoined environment. Let us now present the result of the evaluation of the make_integer(4) expression in the abstract environment \(U^{\sharp }\). Here we get the expression \((\mathcal A', \{\lfloor \epsilon \rfloor \})\) (where \(\mathcal A'\) recognizes only \(\square \)) in the environment: \((\texttt {y} \mapsto (\mathcal A, \{r\}), R^{\sharp \prime })\) where \(R^{\sharp \prime }=R^{\sharp }\cup \{\lfloor \epsilon \rfloor = 4\}\). This emphasizes how the environment is used to give constraints on the adjoined expression. This transports numerical relations from the leafs of the expression up to the assigned variable t.
OCaml Introductory Example. Let us now consider the introductory example Program 5. The inferred loop invariant is the following (\(r= \lfloor (\mathbf {1}.\mathbf {1})^{\star }.\mathbf {0} \rfloor \) and \(r'= \lfloor (\mathbf {1}.\mathbf {1})^{\star }.\mathbf {1}.\mathbf {0} \rfloor \)): \((\texttt {t} \mapsto (\mathcal A, \{r, r'\}), R^{\sharp })\) and \(R^{\sharp }\) satisfies the constraints: \(\{\texttt {t}.r' = \texttt {x}-1, \texttt {t}.r = \texttt {t}.r'+2, i \ge 0, i \le \texttt {n}\}\) and \(\mathcal A=(\{a,b,c,d\}, \{\texttt {Cons}(2), \texttt {Nil}(0), \square (0)\}, \{a\}, \{\texttt {Cons}(c,a)\rightarrow d, \texttt {Cons}(c,d) \rightarrow a, \texttt {Nil} \rightarrow a, \square \rightarrow c\})\). Please note that at the end of the while loops the two numerical environments that need to be joined are not defined over the same set of variables (in the environments that have not gone through the loop, variables \(\texttt {t}.r'\) and \(\texttt {t}.r\) are not present). However thanks to the  operator, we do not have to loose the numerical relations between these variables and \(\texttt {x}\). Hence we are able to prove that the assertion holds.
operator, we do not have to loose the numerical relations between these variables and \(\texttt {x}\). Hence we are able to prove that the assertion holds.
The analyzer was able to successfully analyze and infer the expected invariants for both examples.
7 Related Works
Previous works on sets of trees abstractions [20] were able to recognize larger classes of tree languages than tree automata. However we focused here on the abstraction of trees labeled with numerical values, therefore the work closest to ours would be [12]. Indeed it defines tree automata where leaves can be elements of a lattice (for example an interval). They are therefore able to represent sets of natural terms, but can not express numerical relations between the leaves of trees. Moreover they rely on a partitioning of the leaf lattice for tree automata operations. In [1] (and [2]) tree automata and regular automata are used for the model checking of programs manipulating C pointers and structures. Other uses have been made of tree automata in verification: shape analysis of C programs as in [15], computation of an over-approximation of terms computable by attackers of cryptographic protocols as in [24]. Widening regular languages by the computation of an equivalence relation of bounded index is also done in [9] and in [11]. As mentioned, variable summarization is often used to represent unbounded memory locations as in [17] or [14]. Moreover numerical abstract domains able to handle optional variables have been defined such as [19]. Finally termination analyses have been proposed for the analysis of programs manipulating tree structures (AVL, red-black trees) see [16].
8 Conclusion
In this article we presented a relational abstract environment for sets of trees over a finite algebra, with numerically labeled leaves. We emphasized the potential applications of being able to describe such trees: description of reachable memory zones, tracking symbolic equalities between program variables, description of tree like structures. In order to improve the precision of the analysis while not blowing up its cost we defined a novel abstraction for sets of maps with heterogeneous supports. This numeric abstraction is able to represent optional dimensions in numerical domains without losing relations with optional variables. All domains presented in the article were implemented as a library in the Mopsa framework.
References
Bouajjani, A., Habermehl, P., Rogalewicz, A., Vojnar, T.: Abstract regular tree model checking of complex dynamic data structures. In: Yi, K. (ed.) SAS 2006. LNCS, vol. 4134, pp. 52–70. Springer, Heidelberg (2006). https://doi.org/10.1007/11823230_5
Bouajjani, A., Habermehl, P., Vojnar, T.: Abstract regular model checking. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 372–386. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_29
Bourdoncle, F.: Sémantiques des Langages Impératifs d’Ordre Supérieur et Interprétation Abstraite. Ph.D. thesis, Ecole polytechnique (1992)
Comon, H., et al.: Tree automata techniques and applications (2007). Release October, 12th 2007
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Proceedings of POPL, pp. 238–252. ACM (1977)
Cousot, P., Cousot, R.: Static determination of dynamic properties of generalized type unions. In: Language Design for Reliable Software, pp. 77–94 (1977)
Cousot, P., Cousot, R.: Modular static program analysis. In: Horspool, R.N. (ed.) CC 2002. LNCS, vol. 2304, pp. 159–179. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45937-5_13
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: Proceedings of POPL, pp. 84–96. ACM Press (1978)
Feret, J.: Abstract interpretation-based static analysis of mobile ambients. In: Cousot, P. (ed.) SAS 2001. LNCS, vol. 2126, pp. 412–430. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47764-0_24
Le Gall, T.: Abstract lattices for the verification of systèmes with stacks and queues. Ph.D. thesis, University of Rennes 1, France (2008)
Le Gall, T., Jeannet, B., Jéron, T.: Verification of communication protocols using abstract interpretation of FIFO queues. In: Johnson, M., Vene, V. (eds.) AMAST 2006. LNCS, vol. 4019, pp. 204–219. Springer, Heidelberg (2006). https://doi.org/10.1007/11784180_17
Genet, T., Le Gall, T., Legay, A., Murat, V.: Tree regular model checking for lattice-based automata. CoRR, abs/1203.1495 (2012)
Gopan, D., DiMaio, F., Dor, N., Reps, T., Sagiv, M.: Numeric domains with summarized dimensions. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 512–529. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_38
Gopan, D., Reps, T.W., Sagiv, S.: A framework for numeric analysis of array operations. In: Proceedings of POPL, pp. 338–350. ACM (2005)
Habermehl, P., Holík, L., Rogalewicz, A., Šimáček, J., Vojnar, T.: Forest automata for verification of heap manipulation. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 424–440. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_34
Habermehl, P., Iosif, R., Rogalewicz, A., Vojnar, T.: Proving termination of tree manipulating programs. In: Namjoshi, K.S., Yoneda, T., Higashino, T., Okamura, Y. (eds.) ATVA 2007. LNCS, vol. 4762, pp. 145–161. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75596-8_12
Halbwachs, N., Péron, M.: Discovering properties about arrays in simple programs. In: Proceedings of PLDI, pp. 339–348. ACM (2008)
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation, 3rd edn. Addison-Wesley Longman Publishing Co., Inc, Boston (2006)
Liu, J., Rival, X.: Abstraction of optional numerical values. In: Feng, X., Park, S. (eds.) APLAS 2015. LNCS, vol. 9458, pp. 146–166. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26529-2_9
Mauborgne, L.: Representation of sets of trees for abstract interpretation. Ph.D. thesis, Ecole polytechnique (1999)
Miné, A., Ouadjaout, A., Journault, M.: Design of a modular platform for static analysis. In: The Ninth Workshop on Tools for Automatic Program Analysis (TAPAS 2018), Fribourg-en-Brisgau, Germany, August 2018. https://hal.sorbonne-universite.fr/hal-01870001/file/mine-al-tapas18.pdf
Miné, A.: The octagon abstract domain. In: Proceedings of WCRE, p. 310. IEEE Computer Society (2001)
Miné, A.: Symbolic methods to enhance the precision of numerical abstract domains. In: Emerson, E.A., Namjoshi, K.S. (eds.) VMCAI 2006. LNCS, vol. 3855, pp. 348–363. Springer, Heidelberg (2005). https://doi.org/10.1007/11609773_23
Monniaux, D.: Abstracting cryptographic protocols with tree automata. In: Cortesi, A., Filé, G. (eds.) SAS 1999. LNCS, vol. 1694, pp. 149–163. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48294-6_10
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Proceedings of 17th IEEE (LICS 2002), pp. 55–74. IEEE Computer Society (2002)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Journault, M., Miné, A., Ouadjaout, A. (2019). An Abstract Domain for Trees with Numeric Relations. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)










 depends upon the order of iteration over constraints
depends upon the order of iteration over constraints  starts by performing the join over the domain
starts by performing the join over the domain  , it must satisfy the following constraints:
, it must satisfy the following constraints: 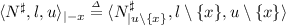 and
and  which respectively removes (adds) a variable to the numerical environment.
which respectively removes (adds) a variable to the numerical environment.

