Abstract
Incremental computation has recently been studied using the concepts of change structures and derivatives of programs, where the derivative of a function allows updating the output of the function based on a change to its input. We generalise change structures to change actions, and study their algebraic properties. We develop change actions for common structures in computer science, including directed-complete partial orders and Boolean algebras. We then show how to compute derivatives of fixpoints. This allows us to perform incremental evaluation and maintenance of recursively defined functions with particular application generalised Datalog programs. Moreover, unlike previous results, our techniques are modular in that they are easy to apply both to variants of Datalog and to other programming languages.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Consider the following classic Datalog programFootnote 1, which computes the transitive closure of an edge relation e:
The semantics of Datalog tells us that the denotation of this program is the least fixpoint of the rule tc. Kleene’s fixpoint Theorem tells us that we can compute this fixpoint by repeatedly applying the rule until the output stops changing, starting from the empty relation. For example, supposing that \(e = \{ (1, 2), (2, 3), (3, 4) \}\), we get the following evaluation trace:

At this point we have reached a fixpoint, and so we are done.
However, this process is quite wasteful. We deduced the fact (1, 2) at every iteration, even though we had already deduced it in the first iteration. Indeed, for a chain of n such edges we will deduce \(O(n^2)\) facts along the way.
The standard improvement to this evaluation strategy is known as “semi-naive” evaluation (see [1, section 13.1]), where we transform the program into a delta program with two parts:
-
A delta rule that computes the new facts at each iteration.
-
An accumulator rule that accumulates the delta at each iteration to compute the final result.
In this case our delta rule is simple: we only get new transitive edges at iteration \(n+1\) if we can deduce them from transitive edges we deduced at iteration n.

This is much better—we have turned a quadratic computation into a linear one. The delta transformation is a kind of incremental computation: at each stage we compute the changes in the rule given the previous changes to its inputs.
But the delta rule translation works only for traditional Datalog. It is common to liberalise the formula syntax with additional features, such as disjunction, existential quantification, negation, and aggregation.Footnote 2 This allows us to write programs like the following, where we compute whether all the nodes in a subtree given by child have some property p:

The body of this predicate amounts to recursion through an universal quantifier (encoded as \(\lnot \exists \lnot \)). We would like to be able to use semi-naive evaluation for this rule too, but the standard definition of semi-naive transformation is not well defined for the extended program syntax, and it is unclear how to extend it (and the correctness proof) to handle such cases.
It is possible, however, to write a delta program for treeP by hand; indeed, here is a definition for the delta predicate (the accumulator is as before):Footnote 3

This is a correct delta program (in that using it to iteratively compute treeP gives the right answer), but it is not precise because it derives some facts repeatedly. We will show how to construct correct delta programs generally using a program transformation, and show how we have some freedom to optimize within a range of possible alternatives to improve precision or ease evaluation.
Handling extended Datalog is of more than theoretical interest—the research in this paper was carried out at Semmle, which makes heavy use of a commercial Datalog implementation to implement large-scale static program analysis [7, 37, 39, 40]. Semmle’s implementation includes parity-stratified negationFootnote 4, recursive aggregates [34], and other non-standard features, so we are faced with a dilemma: either abandon the new language features, or abandon incremental computation.
We can tell a similar story about maintenance of Datalog programs. Maintenance means updating the results of the program when its inputs change, for example, updating the value of tc given a change to e. Again, this is a kind of incremental computation, and there are known solutions for traditional Datalog [25], but these break down when the language is extended.
There is a piece of folkloric knowledge in the Datalog community that hints at a solution: the semi-naive translation of a rule corresponds to the derivative of that rule [8, 9, section 3.2.2]. The idea of performing incremental computation using derivatives has been studied recently by Cai et al. [14], who give an account using change structures. They use this to provide a framework for incrementally evaluating lambda calculus programs.
However, Cai et al.’s work isn’t directly applicable to Datalog: the tricky part of Datalog’s semantics are recursive definitions and the need for the fixpoints, so we need some additional theory to tell us how to handle incremental evaluation and maintenance of fixpoint computations.
This paper aims to bridge that gap by providing a solid semantic foundation for the incremental computation of Datalog, and other recursive programs, in terms of changes and differentiable functions.
Contributions. We start by generalizing change structures to change actions (Sect. 2). Change actions are simpler and weaker than change structures, while still providing enough structure to handle incremental computation, and have fruitful interactions with a variety of structures (Sects. 3 and 6.1).
We then show how change actions can be used to perform incremental evaluation and maintenance of non-recursive program semantics, using the formula semantics of generalized Datalog as our primary example (Sect. 4). Moreover, the structure of the approach is modular, and can accommodate arbitrary additional formula constructs (Sect. 4.3).
We also provide a method of incrementally computing and maintaining fixpoints (Sect. 6.2). We use this to perform incremental evaluation and maintenance of recursive program semantics, including generalized recursive Datalog (Sect. 7). This provides, to the best of our knowledge, the world’s first incremental evaluation and maintenance mechanism for Datalog that can handle negation, disjunction, and existential quantification.
We have omitted the proofs from this paper. Most of the results have routine proofs, but the proofs of the more substantial results (especially those in Sect. 6.2) are included in an extended report [3], along with some extended worked examples, and additional material on the precision of derivatives.
2 Change Actions and Derivatives
Incremental computation requires understanding how values change. For example, we can change an integer by adding a natural to it. Abstractly, we have a set of values (the integers), and a set of changes (the naturals) which we can “apply” to a value (by addition) to get a new value.
This kind of structure is well-known—it is a set action. It is also very natural to want to combine changes sequentially, and if we do this then we find ourselves with a monoid action.
Using monoid actions for changes gives us a reason to think that change actions are an adequate representation of changes: any subset of \(A \rightarrow A\) which is closed under composition can be represented as a monoid action on A, so we are able to capture all of these as change actions.
2.1 Change Actions
Definition 1
A change action is a tuple:

where A is a set, \(\varDelta A\) is a monoid, and \(\oplus _A : A \times \varDelta A \rightarrow A\) is a monoid action on A.Footnote 5
We will call A the base set, and \(\varDelta A\) the change set of the change action. We will use \(\cdot \) for the monoid operation of \(\varDelta A\), and \(\mathbf {0}\) for its identity element. When there is no risk of confusion, we will simply write \(\oplus \) for \(\oplus _A\).
Examples. A typical example of a change action is  where \(A^*\) is the set of finite words (or lists) of A. Here we represent changes to a word made by concatenating another word onto it. The changes themselves can be combined using
where \(A^*\) is the set of finite words (or lists) of A. Here we represent changes to a word made by concatenating another word onto it. The changes themselves can be combined using  as the monoid operation with the empty word as the identity, and this is a monoid action:
as the monoid operation with the empty word as the identity, and this is a monoid action:  .
.
This is a very common case: any monoid \((A, \cdot , \mathbf {0})\) can be seen as a change action \((A,(A, \cdot , \mathbf {0}),\cdot )\). Many practical change actions can be constructed in this way. In particular, for any change action \((A,\varDelta A,\oplus )\), \((\varDelta A,\varDelta A,\cdot )\) is also a change action. This means that we do not have to do any extra work to talk about changes to changes—we can always take \(\varDelta \varDelta A = \varDelta A\) (although there may be other change actions available).
Three examples of change actions are of particular interest to us. First, whenever L is a Boolean algebra, we can give it the change actions \((L, L, \vee )\) and \((L, L, \wedge )\), as well as a combination of these (see Sect. 3.2). Second, the natural numbers with addition have a change action  , which will prove useful during inductive proofs.
, which will prove useful during inductive proofs.
Another interesting example of change actions is semiautomata. A semiautomaton is a triple \((Q, \varSigma , T)\), where Q is a set of states, \(\varSigma \) is a (non-empty) finite input alphabet and \(T : Q \times \varSigma \rightarrow Q\) is a transition function. Every semiautomaton corresponds to a change action \((Q, \varSigma ^*, T^*)\) on the free monoid over \(\varSigma ^*\), with \(T^*\) being the free extension of T. Conversely, every change action \(\hat{A}\) whose change set \(\varDelta A\) is freely generated by a finite set corresponds to a semiautomaton.
Other recurring examples of change actions are:
-
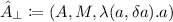 , where M is any monoid, which we call the empty change action on any base set, since it induces no changes at all.
, where M is any monoid, which we call the empty change action on any base set, since it induces no changes at all. -
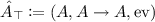 , where A is an arbitrary set, \(A \rightarrow A\) denotes the set of all functions from A into itself, considered as a monoid under composition and \({\text {ev}}\) is the usual evaluation map. We will call this the “full” change action on A since it contains every possible non-redundant change.
, where A is an arbitrary set, \(A \rightarrow A\) denotes the set of all functions from A into itself, considered as a monoid under composition and \({\text {ev}}\) is the usual evaluation map. We will call this the “full” change action on A since it contains every possible non-redundant change.
These are particularly relevant because they are, in a sense, the “smallest” and “largest” change actions that can be imposed on an arbitrary set A.
Many other notions in computer science can be understood naturally in terms of change actions, e.g. databases and database updates, files and diffs, Git repositories and commits, even video compression algorithms that encode a frame as a series of changes to the previous frame.
2.2 Derivatives
When we do incremental computation we are usually trying to save ourselves some work. We have an expensive function \(f: A \rightarrow B\), which we’ve evaluated at some point a. Now we are interested in evaluating f after some change \(\delta a\) to a, but ideally we want to avoid actually computing \(f(a \oplus \delta a)\) directly.
A solution to this problem is a function \(f': A \times \varDelta A \rightarrow \varDelta B\), which given a and \(\delta a\) tells us how to change f(a) to \(f(a \oplus \delta a)\). We call this a derivative of a function.
Definition 2
Let \(\hat{A}\) and \(\hat{B}\) be change actions. A derivative of a function \(f: A \rightarrow B\) is a function \(f': A \times \varDelta A \rightarrow \varDelta B\) such that
A function which has a derivative is differentiable, and we will write \(\hat{A} \rightarrow \hat{B}\) for the set of differentiable functions between A and B.Footnote 6
Derivatives need not be unique in general, so we will speak of “a” derivative. Functions into “thin” change actions—where \(a \oplus \delta a = a \oplus \delta b\) implies \(\delta a = \delta b\)—have unique derivatives, but many change actions are not thin. For example, \((\mathcal {P}(\mathbb {N}),\mathcal {P}(\mathbb {N}),\cap )\) is not thin because \(\{0\} \cap \{1\} = \{0\} \cap \{2\}\).
Derivatives capture the structure of incremental computation, but there are important operational considerations that affect whether using them for computation actually saves us any work. As we will see in a moment (Proposition 1), for many change actions we will have the option of picking the “worst” derivative, which merely computes \(f(a \oplus \delta a)\) directly and then works out the change that maps f(a) to this new value. While this is formally a derivative, using it certainly does not save us any work! We will be concerned with both the possibility of constructing correct derivatives (Sects. 3.2 and 6.2 in particular), and also in giving ourselves a range of derivatives to choose from so that we can soundly optimize for operational value.
For our Datalog case study, we aim to cash out the folkloric idea that incremental computation functions via a derivative. We will construct a derivative of the semantics of Datalog in stages: first the non-recursive formula semantics (Sect. 4); and later the full, recursive, semantics (Sect. 7).
2.3 Useful Facts About Change Actions and Derivatives
The Chain Rule. The derivative of a function can be computed compositionally, because derivatives satisfy the standard chain rule.
Theorem 1
(The Chain Rule). Let \(f: \hat{A} \rightarrow \hat{B}\), \(g: \hat{B} \rightarrow \hat{C}\) be differentiable functions. Then \(g \circ f\) is also differentiable, with a derivative given by
or, in curried form
Complete change actions and minus operators. Complete change actions are an important class of change actions, because they have changes between any two values in the base set.
Definition 3
A change action is complete if for any \(a, b \in A\), there is a change \(\delta a \in \varDelta A\) such that \(a \oplus \delta a = b\).
Complete change actions have convenient “minus operators” that allow us to compute the difference between two values.
Definition 4
A minus operator is a function \(\ominus : A \times A \rightarrow \varDelta A\) such that \(a \oplus (b \ominus a) = b\) for all \(a, b \in A\).
Proposition 1
Given a minus operator \(\ominus \), and a function f, let

Then \(f'_\ominus \) is a derivative for f.
Proposition 2
Let \(\hat{A}\) be a change action. Then the following are equivalent:
-
\(\hat{A}\) is complete.
-
There is a minus operator on \(\hat{A}\).
-
For any change action \(\hat{B}\) all functions \(f: {B} \rightarrow {A}\) are differentiable.
This last property is of the utmost importance, since we are often concerned with the differentiability of functions.
Products and sums. Given change actions on sets A and B, the question immediately arises of whether there are change actions on their Cartesian product \(A \times B\) or disjoint union \(A + B\). While there are many candidates, there is a clear “natural” choice for both.
Proposition 3
(Products). Let \(\hat{A} = (A,\varDelta A,\oplus _A)\) and \(\hat{B} = (B,\varDelta B,\oplus _B)\) be change actions.
Then  is a change action, where \(\oplus _{\times }\) is defined by:
is a change action, where \(\oplus _{\times }\) is defined by:

The projection maps \(\pi _1\),\(\pi _2\) are differentiable with respect to it. Furthermore, a function \(f : A \times B \rightarrow C\) is differentiable from \(\hat{A} \times \hat{B}\) into \(\hat{C}\) if and only if, for every fixed \(a \in A\) and \(b \in B\), the partially applied functions
are differentiable.
Whenever \(f : A \times B \rightarrow C\) is differentiable, we will sometimes use \(\partial _1 f\) and \(\partial _2 f\) to refer to derivatives of the partially applied versions, i.e. if \(f'_a : B \times \varDelta B \rightarrow \varDelta C\) and \(f'_b : A \times \varDelta A \rightarrow \varDelta C\) refer to derivatives for \(f(a, \cdot ), f(\cdot , b)\) respectively, then

Proposition 4
(Disjoint unions). Let \(\hat{A} = (A,\varDelta A,\oplus _A)\) and \(\hat{B} = (B,\varDelta B,\oplus _B)\) be change actions.
Then  is a change action, where \(\oplus _{+}\) is defined as:
is a change action, where \(\oplus _{+}\) is defined as:

The injection maps \(\iota _1, \iota _2\) are differentiable with respect to \(\hat{A} + \hat{B}\). Furthermore, whenever \(\hat{C}\) is a change action and \(f : A \rightarrow C, g: B \rightarrow C\) are differentiable, then so is \(\left[ f, g \right] \).
2.4 Comparing Change Actions
Much like topological spaces, we can compare change actions on the same base set according to coarseness. This is useful since differentiability of functions between change actions is characterized entirely by the coarseness of the actions.
Definition 5
Let \(\hat{A}_1\) and \( \hat{A}_2\) be change actions on A. We say that \(\hat{A}_1\) is coarser than \(\hat{A}_2\) (or that \(\hat{A}_2\) is finer than \(\hat{A}_1\)) whenever for every \(x \in A\) and change \(\delta a_1 \in \varDelta A_1\), there is a change \(\delta a_2 \in \varDelta A_2\) such that \(x \oplus _{A_1} \delta a_1 = x \oplus _{A_2} \delta a_2\).
We will write \(\hat{A}_1 \le \hat{A}_2\) whenever \(\hat{A}_1\) is coarser than \(\hat{A}_2\). If \(\hat{A}_1\) is both finer and coarser than \(\hat{A}_2\), we will say that \(\hat{A}_1\) and \(\hat{A}_2\) are equivalent.
The relation \(\le \) defines a preorder (but not a partial order) on the set of all change actions over a fixed set A. Least and greatest elements do exist up to equivalence, and correspond respectively to the empty change action \(\hat{A}_\bot \) and any complete change action, such as the full change action \(\hat{A}_\top \), defined in Sect. 2.1.
Proposition 5
Let \(\hat{A}_2 \le \hat{A}_1\), \(\hat{B}_1 \le \hat{B}_2\) be change actions, and suppose the function \(f : A \rightarrow B\) is differentiable as a function from \(\hat{A}_1\) into \(\hat{B}_1\). Then f is differentiable as a function from \(\hat{A}_2\) into \(\hat{B}_2\).
A consequence of this fact is that whenever two change actions are equivalent they can be used interchangeably without affecting which functions are differentiable. One last parallel with topology is the following result, which establishes a simple criterion for when a change action is coarser than another:
Proposition 6
Let \(\hat{A}_1, \hat{A}_2\) be change actions on A. Then \(\hat{A}_1\) is coarser than \(\hat{A}_2\) if and only if the identity function \({\text {id}}: A \rightarrow A\) is differentiable from \(\hat{A}_1\) to \(\hat{A}_2\).
3 Posets and Boolean Algebras
The semantic domain of Datalog is a complete Boolean algebra, and so our next step is to construct a good change action for Boolean algebras. Along the way, we will consider change actions over posets, which give us the ability to approximate derivatives, which will turn out to be very important in practice.
3.1 Posets
Ordered sets give us a constrained class of functions: monotone functions. We can define ordered change actions, which are those that are well-behaved with respect to the order on the underlying set.Footnote 7
Definition 6
A change action \(\hat{A}\) is ordered if
-
A and \(\varDelta A\) are posets.
-
\(\oplus \) is monotone as a map from \(A \times \varDelta A \rightarrow A\)
-
\(\cdot \) is monotone as a map from \(\varDelta A \times \varDelta A \rightarrow \varDelta A\)
In fact, any change action whose base set is a poset induces a partial order on the corresponding change set:
Definition 7
\(\delta a \le _\varDelta \delta b\) iff for all \(a \in A\) it is the case that \(a \oplus \delta a \le a \oplus \delta b\).
Proposition 7
Let \(\hat{A}\) be a change action on a set A equipped with a partial order \(\le \) such that \(\oplus \) is monotone in its first argument. Then \(\hat{A}\) is an ordered change action when \(\varDelta A\) is equipped with the partial order \(\le _\varDelta \).
In what follows, we will extend the partial order \(\le _\varDelta \) on some change set \(\varDelta B\) pointwise to functions from some A into \(\varDelta B\). This pointwise order interacts nicely with derivatives, in that it gives us the following lemma:
Theorem 2
(Sandwich lemma). Let \(\hat{A}\) be a change action, and \(\hat{B}\) be an ordered change action, and let \(f: {A} \rightarrow {B}\) and \(g: A \times \varDelta A \rightarrow \varDelta B\) be function. If \(f_\uparrow \) and \(f_\downarrow \) are derivatives for f such that
then g is a derivative for f.
If unique minimal and maximal derivatives exist, then this gives us a characterisation of all the derivatives for a function.
Theorem 3
Let \(\hat{A}\) and \(\hat{B}\) be change actions, with \(\hat{B}\) ordered, and let \(f: {A} \rightarrow {B}\) be a function. If there exist \(f_{\downarrow \downarrow }\) and \(f_{\uparrow \uparrow }\) which are unique minimal and maximal derivatives of f, respectively, then the derivatives of f are precisely the functions \(f'\) such that
This theorem gives us the leeway that we need when trying to pick a derivative: we can pick out the bounds, and that tells us how much “wiggle room” we have above and below.
3.2 Boolean Algebras
Complete Boolean algebras are a particularly nice domain for change actions because they have a negation operator. This is very helpful for computing differences, and indeed Boolean algebras have a complete change action.
Proposition 8
(Boolean algebra change actions). Let L be a complete Boolean algebra. Define

where


with identity element \((\bot , \bot )\).
Then \(\hat{L}_{\bowtie }\) is a complete change action on L.
We can think of \(\hat{L}_{\bowtie }\) as tracking changes as pairs of “upwards” and “downwards” changes, where the monoid action simply applies one after the other, with an adjustment to make sure that the components remain disjoint.Footnote 8 For example, in the powerset Boolean algebra \(\mathcal {P}(\mathbb {N})\), a change to \(\{ 1, 2 \}\) might consist of adding \(\{ 3 \}\) and removing \(\{ 1 \}\), producing \(\{ 2, 3 \}\). In \(\mathcal {P}(\mathbb {N})_{\bowtie }\) this would be represented as \((\{ 1, 2 \}) \oplus (\{ 3 \}, \{ 1 \}) = \{ 2, 3 \}\).
Boolean algebras also have unique maximal and minimal derivatives, under the usual partial order based on implication. The change set is, as usual, given the change partial order, which in this case corresponds to the natural order on \(L \times L^{\text {op}}\).
Proposition 9
Let L be a complete Boolean algebra with the \(\hat{L}_{\bowtie }\) change action, and \(f: A \rightarrow L\) be a function. Then, the following are minus operators:
Additionally, \(f'_{\ominus _{\bot }}\) and \(f'_{\ominus _{\top }}\) define unique least and greatest derivatives for f.
Theorem 3 then gives us bounds for all the derivatives on Boolean algebras:
Corollary 1
Let L be a complete Boolean algebra with the corresponding change action \(\hat{L}_{\bowtie }\), \(\hat{A}\) be an arbitrary change action, and \(f: A \rightarrow L\) be a function. Then the derivatives of f are precisely those functions \(f': A \times \varDelta A \rightarrow \varDelta A\) such that
This makes Theorem 3 actually usable in practice, since we have concrete definitions for our bounds (which we will make use of in Sect. 4.2).
4 Derivatives for Non-recursive Datalog
We now want to apply the theory we have developed to the specific case of the semantics of Datalog. Giving a differentiable semantics for Datalog will lead us to a strategy for performing incremental evaluation and maintenance of Datalog programs. To begin with, we will restrict ourselves to the non-recursive fragment of the language—the formulae that make up the right hand sides of Datalog rules. We will tackle the full program semantics in a later section, once we know how to handle fixpoints.
Although the techniques we are using should work for any language, Datalog provides a non-trivial case study where the need for incremental computation is real and pressing, as we saw in Sect. 1.
4.1 Semantics of Datalog Formulae
Datalog is usually given a logical semantics where formulae are interpreted as first-order logic predicates and the semantics of a program is the set of models of its constituent predicates. We will instead give a simple denotational semantics (as is typical when working with fixpoints, see e.g. [17]) that treats a Datalog formula as directly denoting a relation, i.e. a set of named tuples, with variables ranging over a finite schema.
Definition 8
A schema \(\varGamma \) is a finite set of names. A named tuple over \(\varGamma \) is an assignment of a value \(v_i\) for each name \(x_i\) in \(\varGamma \). Given disjoint schemata \(\varGamma = \{ x_1, \ldots , x_n \}\) and \(\varSigma = \{ y_1, \ldots , y_m \}\), the selection function \(\sigma _\varGamma \) is defined as

i.e. \(\sigma _\varGamma \) restricts a named tuple over \(\varGamma \cup \varSigma \) into a tuple over \(\varGamma \) with the same values for the names in \(\varGamma \). We denote the elementwise extension of \(\sigma _\varGamma \) to sets of tuples also as \(\sigma _\varGamma \).
We will adopt the usual closed-world assumption to give a denotation to negation.
Definition 9
For any schema \(\varGamma \), there exists a universal relation \(\mathcal {U}_\varGamma \). Negation on relations can then be defined as

This makes \(\mathbf {Rel}_\varGamma \), the set of all subsets of \(\mathcal {U}_\varGamma \), a complete Boolean algebra.
Definition 10
A Datalog formula T whose free term variables are contained in \(\varGamma \) denotes a function from \(\mathbf {Rel}_\varGamma ^n\) to \(\mathbf {Rel}_\varGamma \).
If \(\mathcal {R}= (\mathcal {R}_1, \ldots , \mathcal {R}_n)\) is a choice of a relation \(\mathcal {R}_i\) for each of the variables \(R_i\), \(\llbracket T \rrbracket (\mathcal {R})\) is inductively defined according to the rules in Fig. 1.
Since \(\mathbf {Rel}_\varGamma \) is a complete Boolean algebra, and so is \(\mathbf {Rel}_\varGamma ^n\), \(\llbracket T \rrbracket _\varGamma \) is a function between complete Boolean algebras. For brevity, we will often leave the schema implicit, as it is clear from the context.
4.2 Differentiability of Datalog Formula Semantics
In order to actually perform our incremental computation, we first need to provide a concrete derivative for the semantics of Datalog formulae. Of course, since \(\llbracket T \rrbracket _\varGamma \) is a function between the complete Boolean algebras \(\mathbf {Rel}_\varGamma ^n\) and \(\mathbf {Rel}_\varGamma \), and we know that the corresponding change actions \(\widehat{\mathbf {Rel}_\varGamma ^n}_{\bowtie }\) and \(\widehat{\mathbf {Rel}_\varGamma }_{\bowtie }\) are complete, this guarantees the existence of a derivative for \(\llbracket T \rrbracket \).
Unfortunately, this does not necessarily provide us with an efficient derivative for \(\llbracket T \rrbracket \). The derivatives that we know how to compute (Corollary 1) rely on computing \(f(a \oplus \delta a)\) itself, which is the very thing we were trying to avoid computing!
Of course, given a concrete definition of a derivative we can simplify this expression and hopefully make it easier to compute. But we also know from Corollary 1 that any function bounded by \(f'_{\ominus _\bot }\) and \(f'_{\ominus _\top }\) is a valid derivative, and we can therefore optimize anywhere within that range to make a trade-off between ease of computation and precision.Footnote 9
There is also the question of how to compute the derivative. Since the change set for \(\widehat{\mathbf {Rel}}_{\bowtie }\) is a subset of \(\mathbf {Rel}\times \mathbf {Rel}\), it is possible and indeed very natural to compute the two components via a pair of Datalog formulae, which allows us to reuse an existing Datalog formula evaluator. Indeed, if this process is occurring in an optimizing compiler, the derivative formulae can themselves be optimized. This is very beneficial in practice, since the initial formulae may be quite complex.
This does give us additional constraints that the derivative formulae must satisfy: for example, we need to be able to evaluate them; and we may wish to pick formulae that will be easy or cheap for our evaluation engine to compute, even if they compute a less precise derivative.
The upshot of these considerations is that the optimal choice of derivatives is likely to be quite dependent on the precise variant of Datalog being evaluated, and the specifics of the evaluation engine. Here is one possibility, which is the one used at Semmle.
A concrete Datalog formula derivative. In Fig. 2, we define a “symbolic” derivative operator as a pair of mutually recursive functions, \(\varDelta \) and \(\nabla \), which turn a Datalog formula T into new formulae that compute the upwards and downwards parts of the derivative, respectively. Our definition uses an auxiliary function, \({\mathsf X}\), which computes the “neXt” value of a term by applying the upwards and downwards derivatives. As is typical for a derivative, the new formulae will have additional free relation variables for the upwards and downwards derivatives of the free relation variables of T, denoted as \(\varDelta R\) and \(\nabla R\) respectively. Evaluating the formula as a derivative means evaluating it as a normal Datalog formula with the new relation variables set to the input relation changes.
While the definitions mostly exhibit the dualities we would expect between corresponding operators, there are a few asymmetries to explain.
The asymmetry between the cases for \(\varDelta (T \vee U)\) and \(\nabla (T \wedge U)\) is for operational reasons. The symmetrical version of \(\varDelta (T \vee U)\) is \((\varDelta (T) \wedge \lnot U) \vee (\varDelta (U) \wedge \lnot T)\) (which is also precise). The reason we omit the negated conjuncts is simply that they are costly to compute and not especially helpful to our evaluation engine.
The asymmetry between the cases for \(\exists \) is because our dialect of Datalog does not have a primitive universal quantifier. If we did have one, the cases for \(\exists \) would be dual to the corresponding cases for \(\forall \).
Theorem 4
(Concrete Datalog formula derivatives). Let \(\varDelta \), \(\nabla \), \({\mathsf X}: \mathrm {Formula}\rightarrow \mathrm {Formula}\) be mutually recursive functions defined by structural induction as in Fig. 2.
Then \(\varDelta (T)\) and \(\nabla (T)\) are disjoint, and for any schema \(\varGamma \) and any Datalog formula T whose free term variables are contained in \(\varGamma \),  is a derivative for \(\llbracket T \rrbracket _\varGamma \).
is a derivative for \(\llbracket T \rrbracket _\varGamma \).
We can give a derivative for our treeP predicate by mechanically applying the recursive functions defined in Fig. 2.
The upwards difference in particular is not especially easy to compute. If we naively compute it, the third conjunct requires us to recompute the whole of the recursive part. However, the second conjunct gives us a guard: if it is empty we then the whole formula will be, so we only need to evaluate the third conjunct if the second conjunct is non-empty, i.e if there is some change in the body of the existential.
This shows that our derivatives aren’t a panacea: it is simply hard to compute downwards differences for \(\exists \) (and, equivalently, upwards differences for \(\forall \)) because we must check that there is no other way of deriving the same facts.Footnote 10 However, we can still avoid the re-evaluation in many cases, and the inefficiency is local to this subformula.
4.3 Extensions to Datalog
Our formulation of Datalog formula semantics and derivatives is generic and modular, so it is easy to extend the language with new formula constructs: all we need to do is add cases for \(\varDelta \) and \(\nabla \).
In fact, because we are using a complete change action, we can always do this by using the maximal or minimal derivative. This justifies our claim that we can support arbitrary additional formula constructs: although the maximal and minimal derivatives are likely to be impractical, having them available as options means that we will never be completely stymied.
This is important in practice: here is a real example from Semmle’s variant of Datalog. This includes a kind of aggregates which have well-defined recursive semantics. Aggregates have the form
where \(\mathrm {agg}\) refers to an aggregation function (such as “sum” or “min”), vs is a sequence of variables, p and r are variables, T is a formula possibly mentioning vs, and U is a formula possibly mentioning vs and p. The full details can been found in Moor and Baars [34], but for example this allows us to write
which recursively computes the height of a node in a tree.
Here is an upwards derivative for an aggregate formula:

While this isn’t a precise derivative, it is still substantially cheaper than re-evaluating the whole subformula, as the first conjunct acts as a guard, allowing us to skip the second conjunct when U has not changed.
5 Changes on Functions
So far we have defined change actions for the kinds of things that typically make up data, but we would also like to have change actions on functions. This would allow us to define derivatives for higher-order languages (where functions are first-class); and for semantic operators like fixpoint operators \(\mathbf {fix}: (A \rightarrow A) \rightarrow A\), which also operate on functions.
Function spaces, however, differ from products and disjoint unions in that there is no obvious “best” change action on \(A \rightarrow B\). Therefore instead of trying to define a single choice of change action, we will instead pick out subsets of function spaces which have “well-behaved” change actions.
Definition 11
(Functional Change Action). Given change actions \(\hat{A}\) and \(\hat{B}\) and a set \(U \subseteq A \rightarrow B\), a change action \(\hat{U} = (U, \varDelta U, \oplus _U)\) is functional whenever the evaluation map \({\text {ev}}: U \times A \rightarrow B\) is differentiable, that is to say, whenever there exists a function \({\text {ev}}' : (U \times A) \times (\varDelta U \times \varDelta A) \rightarrow \varDelta B\) such that:
We will write \(\hat{U} \subseteq \hat{A} \Rightarrow \hat{B}\) whenever \(U \subseteq A \rightarrow B\) and \(\hat{U}\) is functional.
There are two reasons why functional change actions are usually associated with a subset of \(U \subseteq A \rightarrow B\). Firstly, it allows us to restrict ourselves to spaces of monotone or continuous functions. But more importantly, functional change actions are necessarily made up of differentiable functions, and thus a functional change action may not exist for the entire function space \(A \rightarrow B\).
Proposition 10
Let \(\hat{U} \subseteq \hat{A} \Rightarrow \hat{B}\) be a functional change action. Then every \(f \in U\) is differentiable, with a derivative \(f'\) given by:
5.1 Pointwise Functional Change Actions
Even if we restrict ourselves to the differentiable functions between \(\hat{A}\) and \(\hat{B}\) it is hard to find a concrete functional change action for this set. Fortunately, in many important cases there is a simple change action on the set of differentiable functions.
Definition 12
(Pointwise functional change action). Let \(\hat{A}\) and \(\hat{B}\) be change actions. The pointwise functional change action \(\hat{A} \Rightarrow _{pt}\hat{B}\), when it is defined, is given by \((\hat{A} \rightarrow \hat{B}, A \rightarrow \varDelta B, \oplus _\rightarrow )\), with the monoid structure \((A \rightarrow \varDelta B, \cdot _\rightarrow , \mathbf {0}_\rightarrow )\) and the action \(\oplus _\rightarrow \) defined by:

That is, a change is given pointwise, mapping each point in the domain to a change in the codomain.
The above definition is not always well-typed, since given \(f : \hat{A} \rightarrow \hat{B}\) and \(\delta f : A \rightarrow \varDelta B\) there is no guarantee that \(f \oplus _\rightarrow \delta f\) is differentiable. We present two sufficient criteria that guarantee this.
Theorem 5
Let \(\hat{A}\) and \(\hat{B}\) be change actions, and suppose that \(\hat{B}\) satisfies one of the following conditions:
-
\(\hat{B}\) is a complete change action.
-
The change action
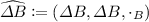 is complete and \(\oplus _B : B \times \varDelta B \rightarrow B\) is differentiable.
is complete and \(\oplus _B : B \times \varDelta B \rightarrow B\) is differentiable.
Then the pointwise functional change action \((\hat{A} \rightarrow \hat{B}, A \rightarrow \varDelta B, \oplus _\rightarrow )\) is well defined.Footnote 11
As a direct consequence of this, it follows that whenever L is a Boolean algebra (and hence has a complete change action), the pointwise functional change action \(\hat{A} \Rightarrow _{pt}\hat{L}_{\bowtie }\) is well-defined.
Pointwise functional change actions are functional in the sense of Definition 11. Moreover, the derivative of the evaluation map is quite easy to compute.
Proposition 11
(Derivatives of the evaluation map). Let \(\hat{A}\) and \(\hat{B}\) be change actions such that the pointwise functional change action \(\hat{A} \Rightarrow _{pt}\hat{B}\) is well defined, and let \(f: \hat{A} \rightarrow \hat{B}\), \(a \in A\), \(\delta a \in \varDelta A\), \(\delta f \in A \rightarrow \varDelta B\).
Then the following are both derivatives of the evaluation map:

A functional change action merely tells us that a derivative of the evaluation map exists—a pointwise change action actually gives us a definition of it. In practice, this means that we will only be able to use the results in Sect. 6.2 (incremental computation and derivatives of fixpoints) when we have pointwise change actions, or where we have some other way of computing a derivative of the evaluation map.
6 Directed-Complete Partial Orders and Fixpoints
Directed-complete partial orders (dcpos) equipped with a least element, are an important class of posets. They allow us to take fixpoints of (Scott-)continuous maps, which is important for interpreting recursion in program semantics.
6.1 Dcpos
As before, we can define change actions on dcpos, rather than sets, as change actions whose base and change sets are endowed with a dcpo structure, and where the monoid operation and action are (Scott-)continuous.
Definition 13
A change action \(\hat{A}\) is continuous if
-
A and \(\varDelta A\) are dcpos.
-
\(\oplus \) is Scott-continuous as a map from \(A \times \varDelta A \rightarrow A\).
-
\(\cdot \) is Scott-continuous as a map from \(\varDelta A \times \varDelta A \rightarrow \varDelta A\).
Unlike posets, the change order \(\le _\varDelta \) does not, in general, induce a dcpo on \(\varDelta A\). As a counterexample, consider the change action \((\overline{\mathbb {N}}, \mathbb {N}, +)\), where \(\overline{\mathbb {N}}\) denotes the dcpo of natural numbers extended with positive infinity.
A key example of a continuous change action is the \(\hat{L}_{\bowtie }\) change action on Boolean algebras.
Proposition 12
(Boolean algebra continuity). Let L be a Boolean algebra. Then \(\hat{L}_{\bowtie }\) is a continuous change action.
For a general overview of results in domain theory and dcpos, we refer the reader to an introductory work such as [2], but we state here some specific results that we shall be using, such as the following, whose proof can be found in [2, Lemma 3.2.6]:
Proposition 13
A function \(f : A \times B \rightarrow C\) is continuous iff it is continuous in each variable separately.
It is a well-known result in standard calculus that the limit of an absolutely convergent sequence of differentiable functions \(\{f_i\}\) is itself differentiable, and its derivative is equal to the limit of the derivatives of the \(f_i\). A consequence of Proposition 13 is the following analogous result:
Corollary 2
Let \(\hat{A}\) and \(\hat{B}\) be change actions, with \(\hat{B}\) continuous and let \(\{f_i\}\) and \(\{f_i'\}\) be I-indexed directed sets of functions in \(A \rightarrow B\) and \(A \times \varDelta A \rightarrow \varDelta B\) respectively.
Then, if for every \(i \in I\) it is the case that \(f_i'\) is a derivative of \(f_i\), then \(\bigsqcup _{i \in I} f_i'\) is a derivative of \(\bigsqcup _{i \in I} f_i \).
6.2 Fixpoints
Fixpoints appear frequently in the semantics of languages with recursion. If we can give a generic account of how to compute fixpoints using change actions, then this gives us a compositional way of extending a derivative for the non-recursive semantics of a language to a derivative that can also handle recursion. We will later apply this technique to create a derivative for the semantics of full recursive Datalog (Sect. 7.2).
Iteration functions. Over directed-complete partial orders we can define a least fixpoint operator \(\mathbf {lfp}\) in terms of the iteration function \(\mathbf {iter}\):

The iteration function is the basis for all the results in this section: we can take a partial derivative with respect to n, and this will give us a way to get to the next iteration incrementally; and we can take the partial derivative with respect to f, and this will give us a way to get from iterating f to iterating \(f \oplus \delta f\).
Incremental computation of fixpoints. The following theorems provide a generalization of semi-naive evaluation to any differentiable function over a continuous change action. Throughout this section we will assume that we have a continuous change action \(\hat{A}\), and any reference to the change action \(\hat{\mathbb {N}}\) will refer to the monoidal change action on the naturals defined in Sect. 2.1.
Since we are trying to incrementalize the iterative step, we start by taking the partial derivative of \(\mathbf {iter}\) with respect to n.
Proposition 14
(Derivative of the iteration map with respect to n). Let \(\hat{A}\) be a complete change action and let \(f: A \rightarrow A\) be a differentiable function. Then \(\mathbf {iter}\) is differentiable with respect to its second argument, and a partial derivative is given by:

By using the following recurrence relation, we can then compute \(\partial _2{\mathbf {iter}}\) along with \(\mathbf {iter}\) simultaneously:

Which has the property that
This gives us a way to compute a fixpoint incrementally, by adding successive changes to an accumulator until we reach it. This is exactly how semi-naive evaluation works: you compute the delta relation and the accumulator simultaneously, adding the delta into the accumulator at each stage until it becomes the final output.
Theorem 6
(Incremental computation of least fixpoints). Let \(\hat{A}\) be a complete, continuous change action, \(f: \hat{A} \rightarrow \hat{A}\) be continuous and differentiable.
Then \(\mathbf {lfp}(f) = \bigsqcup _{n \in \mathbb {N}}(\pi _1(\mathbf {recur}_f^n(\bot , \bot )))\).Footnote 12
Derivatives of fixpoints. In the previous section we have shown how to use derivatives to compute fixpoints more efficiently, but we also want to take the derivative of the fixpoint operator itself. A typical use case for this is where we have calculated some fixpoint

then update the parameter E with some change \(\delta E\) and wish to compute the new value of the fixpoint, i.e.

This can be seen as applying a change to the function whose fixpoint we are taking. We go from computing the fixpoint of \(F(E, \_)\) to computing the fixpoint of \(F(E \oplus \delta E, \_)\). If we have a pointwise functional change action then we can express this change as a function giving the change at each point, that is:
In Datalog this would allow us to update a recursively defined relation given an update to one of its non-recursive dependencies, or the extensional database. For example, we might want to take the transitive closure relation and update it by changing the edge relation e.
However, to compute these examples would requires us to provide a derivative for the fixpoint operator \(\mathbf {fix}\): we want to know how the resulting fixpoint changes given a change to its input function.
Definition 14
(Derivatives of fixpoints). Let \(\hat{A}\) be a change action, let \(\hat{U} \subseteq \hat{A} \Rightarrow \hat{A}\) be a functional change action (not necessarily pointwise) and suppose \(\mathbf {fix}_U\) and \(\mathbf {fix}_{\varDelta A}\) are fixpoint operators for endofunctions on U and \(\varDelta A\) respectively.
Then we define

The suggestively named \(\mathbf {fix}_U'\) will in fact turn out to be a derivative—for least fixpoints. The appearance of \({\text {ev}}'\), a derivative of the evaluation map, in the definition of \(\mathbf {adjust}\) is also no coincidence: as evaluating a fixpoint consists of many steps of applying the evaluation map, so computing the derivative of a fixpoint consists of many steps of applying the derivative of the evaluation map.Footnote 13
Since \(\mathbf {lfp}\) is characterized as the limit of a chain of functions, Corollary 2 suggests a way to compute its derivative. It suffices to find a derivative \(\mathbf {iter}_n'\) of each iteration map such that the resulting set \(\{ \mathbf {iter}_n' \mid n \in \mathbb {N}\}\) is directed, which will entail that \(\bigsqcup _{n \in \mathbb {N}}\mathbf {iter}_n'\) is a derivative of \(\mathbf {lfp}\).
These correspond to the first partial derivative of \(\mathbf {iter}\)—this time with respect to f. While we are differentiating with respect to f, we are still going to need to define our derivatives inductively in terms of n.
Proposition 15
(Derivative of the iteration map with respect to f). \(\mathbf {iter}\) is differentiable with respect to its first argument and a derivative is given by:

As before, we can now compute \(\partial _1{\mathbf {iter}}\) together with \(\mathbf {iter}\) by mutual recursion.Footnote 14

Which has the property that
This indeed provides us with a function whose limit we can take. If we do so we will discover that it is exactly \(\mathbf {lfp}'\) (defined as in Definition 14), showing that \(\mathbf {lfp}'\) is a true derivative.
Theorem 7
(Derivatives of least fixpoint operators). Let
-
\(\hat{A}\) be a continuous change action
-
U be the set of continuous functions \(f : A \rightarrow A\), with a functional change action \(\hat{U} \subseteq \hat{A} \Rightarrow \hat{A}\)
-
\(f \in U\) be a continuous, differentiable function
-
\(\delta f \in \varDelta U\) be a function change
-
\({\text {ev}}'\) be a derivative of the evaluation map which is continuous with respect to a and \(\delta a\).
Then \(\mathbf {lfp}'\) is a derivative of \(\mathbf {lfp}\).
Computing this derivative still requires computing a fixpoint—over the change lattice—but this may still be significantly less expensive than recomputing the full new fixpoint.
7 Derivatives for Recursive Datalog
Given the non-recursive semantics for a language, we can extend it to handle recursive definitions using fixpoints. Section 6.2 lets us extend our derivative for the non-recursive semantics to a derivative for the recursive semantics, as well as letting us compute the fixpoints themselves incrementally.
Again, we will demonstrate the technique with Datalog, although the approach is generic.
7.1 Semantics of Datalog Programs
First of all, we define the usual “immediate consequence operator” which computes “one step” of our program semantics.
Definition 15
Given a program \(\mathbb {P} = (P_1, \dots , P_n)\), where \(P_i\) is a predicate, with schema \(\varGamma _i\), the immediate consequence operator \(\mathcal {I}: \mathbf {Rel}^n \rightarrow \mathbf {Rel}^n\) is defined as follows:
That is, given a value for the program, we pass in all the relations to the denotation of each predicate, to get a new tuple of relations.
Definition 16
The semantics of a program \(\mathbb {P}\) is defined to be

and may be calculated by iterative application of \(\mathcal {I}\) to \(\bot \) until fixpoint is reached.
Whether or not this program semantics exists will depend on whether the fixpoint exists. Typically this is ensured by constraining the program such that \(\mathcal {I}\) is monotone (or, in the context of a dcpo, continuous). We do not require monotonicity to apply Theorem 6 (and hence we can incrementally compute fixpoints that happen to exist even though the generating function is not monotonic), but it is required to apply Theorem 7.
7.2 Incremental Evaluation of Datalog
We can easily extend a derivative for the formula semantics to a derivative for the immediate consequence operator \(\mathcal {I}\). Putting this together with the results from Sect. 6.2, we have now created modular proofs for the two main results, which allows us to preserve them in the face of changes to the underlying language.
Corollary 3
Datalog program semantics can be evaluated incrementally.
Corollary 4
Datalog program semantics can be incrementally maintained with changes to relations.
Note that our approach makes no particular distinction between changes to the extensional relations (adding or removing facts), and changes to the intensional relations (changing the definition). The latter simply amounts to a change to the denotation of that relation, which can be incrementally propagated in exactly the same way as we would propagate a change to the extensional relations.
8 Related Work
8.1 Change Actions and Incremental Computation
Change structures. The seminal paper in this area is Cai et al. [14]. We deviate from that excellent paper in three regards: the inclusion of minus operators, the nature of function changes, and the use of dependent types.
We have omitted minus operators from our definition because there are many interesting change actions that are not complete and so cannot have a minus operator. Where we can find a change structure with a minus operator, often we are forced to use unwieldy representations for change sets, and Cai et al. cite this as their reason for using a dependent type of changes. For example, the monoidal change actions on sets and lists are clearly useful for incremental computation on streams, yet they do not admit minus operators—instead, one would be forced to work with e.g. multisets admitting negative arities, as Cai et al. do.
Our function changes (when well behaved) correspond to what Cai et al. call pointwise differences (see [14, section 2.2]). As they point out, you can reconstruct their function changes from pointwise changes and derivatives, so the two formulations are equivalent.
The equivalence of our presentations means that our work should be compatible with their Incremental Lambda Calculus (see [14, section 3]). The derivatives we give in Sect. 4.2 are more or less a “change semantics” for Datalog (see [14, section 3.5]).
S-acts. S-acts (i.e the category of monoid actions on sets) and their categorical structure have received a fair amount of attention over the years (Kilp, Knauer, and Mikhalev [30] is a good overview). However, there is a key difference between change actions considered as a category (\(\mathbf {CAct}\)) and the category of S-acts (\(\mathbf {SAct}\)): the objects of \(\mathbf {SAct}\) all maintain the same monoid structure, whereas we are interested in changing both the base set and the structure of the action.
Derivatives of fixpoints. Arntzenius [5] gives a derivative operator for fixpoints based on the framework in Cai et al. [14]. However, since we have different notions of function changes, the result is inapplicable as stated. In addition, we require a somewhat different set of conditions; in particular, we do not require our changes to always be increasing.
8.2 Datalog
Incremental evaluation. The earliest interpretation of semi-naive evaluation as a derivative appears in Bancilhon [8]. The idea of using an approximate derivative and the requisite soundness condition appears as a throwaway comment in Bancilhon and Ramakrishnan [9, section 3.2.2], and it would appear that nobody has since developed that approach.
As far as we know, traditional semi-naive is the state of the art in incremental, bottom-up, Datalog evaluation, and there are no strategies that accommodate additional language features such as parity-stratified negation and aggregates.
Incremental maintenance. There is existing literature on incremental maintenance of relational algebra expressions.
Griffin, Libkin, and Trickey [24] following Qian and Wiederhold [35] compute differences with both an “upwards” and a “downwards” component, and produce a set of rules that look quite similar to those we derive in Theorem 4. However, our presentation is significantly more generic, handles recursive expressions, and works on set semantics rather than bag semantics.Footnote 15
Several approaches [25, 27]—most notably DReD—remove facts until one can start applying the rules again to reach the new fixpoint. Given a good way of deciding what facts to remove this can be quite efficient. However, such techniques tend to be tightly coupled to the domain. Although we know of no theoretical reason why either approach should give superior performance when both are applicable, an empirical investigation of this could prove interesting.
Other approaches [19, 43] consider only restricted subsets of Datalog, or incur other substantial constraints.
Embedding Datalog. Datafun (Arntzenius and Krishnaswami [6]) is a functional programming language that embeds Datalog, allowing significant improvements in genericity, such as the use of higher-order functions. Since we have directly defined a change action and derivative operator for Datalog, our work could be used as a “plugin” in the sense of Cai et al., allowing Datafun to compute its internal fixpoints incrementally, but also allowing Datafun expressions to be fully incrementally maintained.
In a different direction, Cathcart Burn, Ong, and Ramsay [15] have proposed higher-order constrained Horn clauses (HoCHC), a new class of constraints for the automatic verification of higher-order programs. HoCHC may be viewed as a higher-order extension of Datalog. Change actions can be readily applied to organise an efficient semi-naive method for solving HoCHC systems.
8.3 Differential \(\lambda \)-calculus
Another setting where derivatives of arbitrary higher-order programs have been studied is the differential \(\lambda \)-calculus [20, 21]. This is a higher-order, simply-typed \(\lambda \)-calculus which allows for computing the derivative of a function, in a similar way to the notion of derivative in Cai’s work and the present paper.
While there are clear similarities between the two systems, the most important difference is the properties of the derivatives themselves: in the differential \(\lambda \)-calculus, derivatives are guaranteed to be linear in their second argument, whereas in our approach derivatives do not have this restriction but are instead required to satisfy a strong relation to the function that is being differentiated (see Definition 2).
Families of denotational models for the differential \(\lambda \)-calculus have been studied in depth [12, 13, 16, 29], and the relationship between these and change actions is the subject of ongoing work.
8.4 Higher-Order Automatic Differentiation
Automatic differentiation [23] is a technique that allows for efficiently computing the derivative of arbitrary programs, with applications in probabilistic modeling [31] and machine learning [10] among other areas. In recent times, this technique has been successfully applied to higher-order languages [11, 41]. While some approaches have been suggested [28, 33], a general theoretical framework for this technique is still a matter of open research.
To this purpose, some authors have proposed the incremental \(\lambda \)-calculus as a foundational framework on which models of automatic differentiation can be based [28]. We believe our change actions are better suited to this purpose than the incremental \(\lambda \)-calculus, since one can easily give them a synthetic differential geometric reading (by interpreting \(\hat{A}\) as an Euclidean module and \(\varDelta A\) as its corresponding spectrum, for example).
9 Conclusions and Future Work
We have presented change actions and their properties, and used them to provide novel, compositional, strategies for incrementally evaluating and maintaining recursive functions, in particular the semantics of Datalog.
The main avenue for future theoretical work is the categorical structure of change actions. This has begun to be explored by the authors in [4], where change actions are generalized to arbitrary Cartesian base categories and a construction is provided to obtain “canonical” Cartesian closed categories of change actions and differentiable maps.
We hope that these generalizations would allow us to extend the theory of change actions towards other classes of models, such as synthetic differential geometry and domain theory. Some early results in [4] also indicate a connection between 2-categories and change actions which has yet to be fully mapped.
The compositional nature of these techniques suggest that an approach like that used in [22] could be used for an even more generic approach to automatic differentiation.
In addition, there is plenty of scope for practical application of the techniques given here to languages other than Datalog.
Notes
- 1.
See [1, part D] for an introduction to Datalog.
- 2.
See, for example, LogiQL [26, 32], Datomic [18], Souffle [38, 42], and DES [36], which between them have all of these features and more. We do not here explore supporting extensions to the syntax of rule heads, although as long as this can be given a denotational semantics in a similar style our techniques should be applicable.
- 3.
This rule should be read as: we can newly deduce that x is in treeP if x satisfies the predicate, and we have newly deduced that one of its children is in treeP, and we currently believe that all of its children are in treeP.
- 4.
Parity-stratified negation means that recursive calls must appear under an even number of negations. This ensures that the rule remains monotone, so the least fixpoint still exists.
- 5.
Why not just work with monoid actions? The reason is that while the category of monoid actions and the category of change actions have the same objects, they have different morphisms. See Sect. 8.1 for further discussion.
- 6.
Note that we do not require that \(f'(a, \delta a \cdot \delta b) = f'(a, \delta a) \cdot f'(a \oplus \delta a, \delta b)\) nor that \(f'(a, \mathbf {0}) = \mathbf {0}\). These are natural conditions, and all the derivatives we have studied also satisfy them, but none of the results on this paper require them to hold.
- 7.
If we were giving a presentation that was generic in the base category, then this would simply be the definition of being a change action in the category of posets and monotone maps.
- 8.
The intuition that \(\hat{L}_{\bowtie }\) is made up of an “upwards” and a “downwards” change action glued together can in fact be made precise, but the specifics are outside the scope of this paper.
- 9.
The idea of using an approximation to the precise derivative, and a soundness condition, appears in Bancilhon [9].
- 10.
The “support” data structures introduced by [25] are an attempt to avoid this issue by tracking the number of derivations of each tuple.
- 11.
Either of these conditions is enough to guarantee that the pointwise functional change action is well defined, but it can be the case that \(\hat{B}\) satisfies neither and yet pointwise change actions into \(\hat{B}\) do exist. A precise account of when pointwise functional change actions exist is outside the scope of this paper.
- 12.
Note that we have not taken the fixpoint of \(\mathbf {recur}_f\), since it is not continuous.
- 13.
Perhaps surprisingly, the authors first discovered an expanded version of this formula, and it was only later that we realised the remarkable connection to \({\text {ev}}'\).
- 14.
In fact, the recursion here is not mutual: the first component does not depend on the second. However, writing it in this way makes it amenable to computation by fixpoint, and we will in fact be able to avoid the recomputation of \(\mathbf {iter}_n\) when we show that it is equivalent to \(\mathbf {lfp}'\).
- 15.
The same approach of finding derivatives would work with bag semantics, although unfortunately the Boolean algebra structure is missing.
References
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases: The Logical Level. Addison-Wesley Longman Publishing Co., Inc., Boston (1995)
Abramsky, S., Jung, A.: Domain theory. In: Handbook of Logic in Computer Science. Oxford University Press, New York (1994)
Alvarez-Picallo, M., Eyers-Taylor, A., Jones, M.P., Ong, C.L.: Fixing incremental computation: derivatives of fixpoints, and the recursive semantics of datalog. CoRR abs/1811.06069 (2018). http://arxiv.org/abs/1811.06069
Alvarez-Picallo, M., Ong, C.H.L.: Change actions: models of generalised differentiation. In: International Conference on Foundations of Software Science and Computation Structures. Springer (2019, in press)
Arntzenius, M.: Static differentiation of monotone fixpoints (2017). http://www.rntz.net/files/fixderiv.pdf
Arntzenius, M., Krishnaswami, N.R.: Datafun: a functional datalog. In: Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, pp. 214–227. ACM (2016)
Avgustinov, P., de Moor, O., Jones, M.P., Schäfer, M.: QL: object-oriented queries on relational data. In: LIPIcs-Leibniz International Proceedings in Informatics, vol. 56. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2016)
Bancilhon, F.: Naive evaluation of recursively defined relations. In: Brodie, M.L., Mylopoulos, J. (eds.) On Knowledge Base Management Systems. TINF, pp. 165–178. Springer, New York (1986). https://doi.org/10.1007/978-1-4612-4980-1_17
Bancilhon, F., Ramakrishnan, R.: An amateur’s introduction to recursive query processing strategies, vol. 15. ACM (1986)
Baydin, A.G., Pearlmutter, B.A.: Automatic differentiation of algorithms for machine learning. arXiv preprint arXiv:1404.7456 (2014)
Baydin, A.G., Pearlmutter, B.A., Siskind, J.M.: DiffSharp: an AD library for .NET languages. arXiv preprint arXiv:1611.03423 (2016)
Blute, R., Ehrhard, T., Tasson, C.: A convenient differential category. arXiv preprint arXiv:1006.3140 (2010)
Bucciarelli, A., Ehrhard, T., Manzonetto, G.: Categorical models for simply typed resource calculi. Electron. Notes Theor. Comput. Sci. 265, 213–230 (2010)
Cai, Y., Giarrusso, P.G., Rendel, T., Ostermann, K.: A theory of changes for higher-order languages: incrementalizing \(\lambda \)-calculi by static differentiation. In: ACM SIGPLAN Notices, vol. 49, pp. 145–155. ACM (2014)
Cathcart Burn, T., Ong, C.L., Ramsay, S.J.: Higher-order constrained horn clauses for verification. PACMPL 2(POPL), 11:1–11:28 (2018). https://doi.org/10.1145/3158099
Cockett, J.R.B., Gallagher, J.: Categorical models of the differential \(\lambda \)-calculus revisited. Electron. Notes Theor. Comput. Sci. 325, 63–83 (2016)
Compton, K.J.: Stratified least fixpoint logic. Theor. Comput. Sci. 131(1), 95–120 (1994)
Datomic website (2018). https://www.datomic.com. Accessed 01 Jan 2018
Dong, G., Su, J.: Incremental maintenance of recursive views using relational calculus/SQL. ACM SIGMOD Rec. 29(1), 44–51 (2000)
Ehrhard, T.: An introduction to differential linear logic: proof-nets, models and antiderivatives. Math. Struct. Comput. Sci. 1–66 (2017)
Ehrhard, T., Regnier, L.: The differential lambda-calculus. Theor. Comput. Sci. 309(1–3), 1–41 (2003)
Elliott, C.: The simple essence of automatic differentiation. Proc. ACM Program. Lang. 2(ICFP), 70 (2018)
Griewank, A., Walther, A.: Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, vol. 105. SIAM, Philadelphia (2008)
Griffin, T., Libkin, L., Trickey, H.: An improved algorithm for the incremental recomputation of active relational expressions. IEEE Trans. Knowl. Data Eng. 3, 508–511 (1997)
Gupta, A., Mumick, I.S., Subrahmanian, V.S.: Maintaining views incrementally. ACM SIGMOD Rec. 22(2), 157–166 (1993)
Halpin, T., Rugaber, S.: LogiQL: A Query Language for Smart Databases. CRC Press, Boca Raton (2014)
Harrison, J.V., Dietrich, S.W.: Maintenance of materialized views in a deductive database: an update propagation approach. In: Workshop on Deductive Databases, JICSLP, pp. 56–65 (1992)
Kelly, R., Pearlmutter, B.A., Siskind, J.M.: Evolving the incremental \(\lambda \) calculus into a model of forward automatic differentiation (AD). arXiv preprint arXiv:1611.03429 (2016)
Kerjean, M., Tasson, C.: Mackey-complete spaces and power series-a topological model of differential linear logic. Math. Struct. Comput. Sci. 1–36 (2016)
Kilp, M., Knauer, U., Mikhalev, A.V.: Monoids, Acts and Categories: With Applications to Wreath Products and Graphs. A Handbook for Students and Researchers, vol. 29. Walter de Gruyter, Berlin (2000)
Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., Blei, D.M.: Automatic differentiation variational inference. J. Mach. Learn. Res. 18(1), 430–474 (2017)
LogicBlox Inc. website (2018). http://www.logicblox.com. Accessed 01 Jan 2018
Manzyuk, O.: A simply typed \(\lambda \)-calculus of forward automatic differentiation. Electron. Notes Theor. Comput. Sci. 286, 257–272 (2012)
de Moor, O., Baars, A.: Doing a doaitse: simple recursive aggregates in datalog. In: Liber Amicorum for Doaitse Swierstra, pp. 207–216 (2013). http://www.staff.science.uu.nl/~hage0101/liberdoaitseswierstra.pdf. Accessed 01 Jan 2018
Qian, X., Wiederhold, G.: Incremental recomputation of active relational expressions. IEEE Trans. Knowl. Data Eng. 3(3), 337–341 (1991)
Sáenz-Pérez, F.: DES: a deductive database system. Electron. Notes Theor. Comput. Sci. 271, 63–78 (2011)
Schäfer, M., de Moor, O.: Type inference for datalog with complex type hierarchies. In: ACM SIGPLAN Notices, vol. 45, pp. 145–156. ACM (2010)
Scholz, B., Jordan, H., Subotić, P., Westmann, T.: On fast large-scale program analysis in datalog. In: Proceedings of the 25th International Conference on Compiler Construction, pp. 196–206. ACM (2016)
Semmle Ltd. website (2018). https://semmle.com. Accessed 01 Jan 2018
Sereni, D., Avgustinov, P., de Moor, O.: Adding magic to an optimising datalog compiler. In: Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, pp. 553–566. ACM (2008)
Siskind, J.M., Pearlmutter, B.A.: Nesting forward-mode AD in a functional framework. High.-Order Symb. Comput. 21(4), 361–376 (2008)
Souffle language website (2018). http://souffle-lang.org. Accessed 01 Jan 2018
Urpi, T., Olive, A.: A method for change computation in deductive databases. In: VLDB, vol. 92, pp. 225–237 (1992)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Alvarez-Picallo, M., Eyers-Taylor, A., Peyton Jones, M., Ong, CH.L. (2019). Fixing Incremental Computation. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)





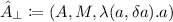 , where M is any monoid, which we call the empty change action on any base set, since it induces no changes at all.
, where M is any monoid, which we call the empty change action on any base set, since it induces no changes at all.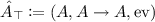 , where A is an arbitrary set,
, where A is an arbitrary set, 

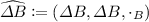 is complete and
is complete and 