Abstract
Secure compilers generate compiled code that withstands many target-level attacks such as alteration of control flow, data leaks or memory corruption. Many existing secure compilers are proven to be fully abstract, meaning that they reflect and preserve observational equivalence. Fully abstract compilation is strong and useful but, in certain cases, comes at the cost of requiring expensive runtime constructs in compiled code. These constructs may have no relevance for security, but are needed to accommodate differences between the source and target languages that fully abstract compilation necessarily needs.
As an alternative to fully abstract compilation, this paper explores a different criterion for secure compilation called robustly safe compilation or RSC. Briefly, this criterion means that the compiled code preserves relevant safety properties of the source program against all adversarial contexts interacting with the compiled program. We show that RSC can be proved more easily than fully abstract compilation and also often results in more efficient code. We also develop two illustrative robustly-safe compilers and, through them, illustrate two different proof techniques for establishing that a compiler attains RSC. Based on these, we argue that proving RSC can be simpler than proving fully abstraction.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
To better explain and clarify notions, this paper uses colours. For a better experience, please print or view this paper in colours. Footnote 1
1 Introduction
Low-level adversaries, such as those written in C or assembly can attack co-linked code written in a high-level language in ways that may not be feasible in the high-level language itself. For example, such an adversary may manipulate or hijack control flow, cause buffer overflows, or directly access private memory, all in contravention to the abstractions of the high-level language. Specific countermeasures such as Control Flow Integrity [3] or Code Pointer Integrity [41] have been devised to address some of these attacks individually. An alternative approach is to devise a secure compiler, which seeks to defend against entire classes of such attacks. Secure compilers often achieve security by relying on different protection mechanisms, e.g., cryptographic primitives [4, 5, 22, 26], types [10, 11], address space layout randomisation [6, 37], protected module architectures [9, 53, 57, 59] (also know as enclaves [46]), tagged architectures [7, 39], etc. Once designed, the question researchers face is how to formalise that such a compiler is indeed secure, and how to prove this. Basically, we want a criterion that specifies secure compilation. A widely-used criterion for compiler security is fully abstract compilation (FAC) [2, 35, 52], which has been shown to preserve many interesting security properties like confidentiality, integrity, invariant definitions, well-bracketed control flow and hiding of local state [9, 37, 53, 54].
Informally, a compiler is fully abstract if it preserves and reflects observational equivalence of source-level components (i.e., partial programs) in their compiled counterparts. Most existing work instantiates observational equivalence with contextual equivalence: co-divergence of two components in any larger context they interact with. Fully abstract compilation is a very strong property, which preserves all source-level abstractions.
Unfortunately, preserving all source-level abstractions also has downsides. In fact, while FAC preserves many relevant security properties, it also preserves a plethora of other non-security ones, and the latter may force inefficient checks in the compiled code. For example, when the target is assembly, two observationally equivalent components must compile to code of the same size [9, 53], else full abstraction is trivially violated. This requirement is security-irrelevant in most cases. Additionally, FAC is not well-suited for source languages with undefined behaviour (e.g., \({\texttt {C}}\) and \({\texttt {LLVM}}\)) [39] and, if used naïvely, it can fail to preserve even simple safety properties [60] (though, fortunately, no existing work falls prey to this naïvety).
Motivated by this, recent work started investigating alternative secure compilation criteria that overcome these limitations. These security-focussed criteria take the form of preservation of hyperproperties or classes of hyperproperties, such as hypersafety properties or safety properties [8, 33]. This paper investigates one of these criteria, namely, Robustly Safe Compilation (RSC) which has clear security guarantees and can often be attained more efficiently than FAC.
Informally, a compiler attains RSC if it is correct and it preserves robust safety of source components in the target components it produces. Robust safety is an important security notion that has been widely adopted to formalize security, e.g., of communication protocols [14, 17, 34]. Before explaining RSC, we explain robust safety as a language property.
Robust Safety as a Language Property. Informally, a program property is a safety property if it encodes that “bad” sequences of events do not happen when the program executes [13, 63]. A program is robustly safe if it has relevant (specified) safety properties despite active attacks from adversaries. As the name suggests, robust safety relies on the notions of safety and robustness which we now explain.
Safety. As mentioned, safety asserts that “no bad sequence of events happens”, so we can specify a safety property by the set of finite observations which characterise all bad sequences of events. A whole program has a safety property if its behaviours exclude these bad observations. Many security properties can be encoded as safety, including integrity, weak secrecy and functional correctness.
Example 1
(Integrity). Integrity ensures that an attacker does not tamper with code invariants on state. For example, consider the function \({\texttt {charge\_account(n)}}\) which deducts amount \({\texttt {n}}\) from an account as part of an electronic card payment. A card PIN is required if \({\texttt {n}}\) is larger than 10 euros. So the function checks whether \({\texttt {n}}\) \(>10\), requests the PIN if this is the case, and then changes the account balance. We expect this function to have a safety (integrity) property in the account balance: A reduction of more than 10 euros in the account balance must be preceded by a call to \({\texttt {request\_pin()}}\). Here, the relevant observation is a trace (sequence) of account balances and calls to \({\texttt {request\_pin()}}\). Bad observations for this safety property are those where an account balance is at least 10 euros less than the previous one, without a call to \({\texttt {request\_pin()}}\) in between. Note that this function seems to have this safety property, but it may not have the safety property robustly: a target-level adversary may transfer control directly to the “else” branch of the check \({\texttt {n}}\) \(>10\) after setting \({\texttt {n}}\) to more than 10, to violate the safety property.\(\boxdot \)
Example 2
(Weak Secrecy). Weak secrecy asserts that a program secret never flows explicitly to the attacker. For example, consider code that manages \({\texttt {network\_h}}\), a handler (socket descriptor) for a sensitive network interface. This code does not expose \({\texttt {network\_h}}\) directly to external code but it provides an API to use it. This API makes some security checks internally. If the handler is directly accessible to outer code, then it can be misused in insecure ways (since the security checks may not be made). If the code has weak secrecy wrt \({\texttt {network\_h}}\) then we know that the handler is never passed to an attacker. In this case we can define bad observations as those where \({\texttt {network\_h}}\) is passed to external code (e.g., as a parameter, as a return value on or on the heap).\(\boxdot \)
Example 3
(Correctness). Program correctness can also be formalized as a safety property. Consider a program that computes the \({\texttt {n}}\)th Fibonacci number. The program reads \({\texttt {n}}\) from an input source and writes its output to an output source. Correctness of this program is a safety property. Our observations are pairs of an input (read by the program) and the corresponding output. A bad observation is one where the input is \({\texttt {n}}\) (for some \({\texttt {n}}\)) but the output is different from the \({\texttt {n}}\)th Fibonacci number.\(\boxdot \)
These examples not only illustrate the expressiveness of safety properties, but also show that safety properties are quite coarse-grained: they are only concerned with (sequences of) relevant events like calls to specific functions, changes to specific heap variables, inputs, and outputs. They do not specify or constrain how the program computes between these events, leaving the programmer and the compiler considerable flexibility in optimizations. However, safety properties are not a panacea for security, and there are security properties that are not safety. For example, noninterference [70, 72], the standard information flow property, is not safety. Nonetheless, many interesting security properties are safety. In fact, many non-safety properties including noninterference can be conservatively approximated as safety properties [20]. Hence, safety properties are a meaningful goal to pursue for secure compilation.
Robustness. We often want to reason about properties of a component of interest that hold irrespective of any other components the component interacts with. These other components may be the libraries the component is linked against, or the language runtime. Often, these surrounding components are modelled as the program context whose hole the component of interest fills. From a security perspective the context represents the attacker in the threat model. When the component of interest links to a context, we have a whole program that can run. A property holds robustly for a component if it holds in any context that the component of interest can be linked to.
Robust Safety Preservation as a Compiler Property. A compiler attains robustly safe compilation or RSC if it maps any source component that has a safety property robustly to a compiled component that has the same safety property robustly. Thus, safety has to hold robustly in the target language, which often does not have the powerful abstractions (e.g., typing) that the source language has. Hence, the compiler must insert enough defensive runtime checks into the compiled code to prevent the more powerful target contexts from launching attacks (violations of safety properties) that source contexts could not launch. This is unlike correct compilation, which either considers only those target contexts that behave like source contexts [40, 49, 65] or considers only whole programs [43].
As mentioned, safety properties are usually quite coarse-grained. This means that RSC still allows the compiler to optimise code internally, as long as the sequence of observable events is not affected. For example, when compiling the \({\texttt {fibonacci}}\) function of Example 3, the compiler can do any internal optimisation such as caching intermediate results, as long as the end result is correct. Crucially, however, these intermediate results must be protected from tampering by a (target-level) attacker, else the output can be incorrect, breaking RSC.
A RSC-attaining compiler focuses only on preserving security (as captured by robust safety) instead of contextual equivalence (typically captured by full abstraction). So, such a compiler can produce code that is more efficient than code compiled with a fully abstract compiler as it does not have to preserve all source abstractions (we illustrate this later).
Finally, robust safety scales naturally to thread-based concurrency [1, 34, 58]. Thus RSC also scales naturally to thread-based concurrency (we demonstrate this too). This is unlike FAC, where thread-based concurrency can introduce additional undesired abstractions that also need to be preserved.
RSC is a very recently proposed criterion for secure compilers. Recent work [8, 33] define RSC abstractly in terms of preservation of program behaviours, but their development is limited to the definition only. Our goal in this paper is to examine how RSC can be realized and established, and to show that in certain cases it leads to compiled code that is more efficient than what FAC leads to. To this end, we consider a specific setting where observations are values in specific (sensitive) heap locations at cross-component calls. We define robust safety and RSC for this specific setting (Sect. 2). Unlike previous work [8, 33] which assumed that the domain of traces (behaviours) is the same in the source and target languages, our RSC definition allows for different trace domains in the source and target languages, as long as they can be suitably related. The second contribution of our paper is two proof techniques to establish RSC.
-
The first technique is an adaption of trace-based backtranslation, an existing technique for proving FAC [7, 9, 59]. To illustrate this technique, we build a compiler from an untyped source language to an untyped target language with support for fine-grained memory protection via so-called capabilities [23, 71] (Sect. 3). Here, we guarantee that if a source program is robustly safe, then so is its compilation.
-
The second proof technique shows that if source programs are verified for robust safety, then one can simplify the proof of RSC so that no backtranslation is needed. In this case, we develop a compiler from a typed source language where the types already enforce robust safety, to a target language similar to that of the first compiler (Sect. 4). In this instance, both languages also support shared-memory concurrency. Here, we guarantee that all compiled target programs are robustly safe.
To argue that RSC is general and is not limited to compilation targets based on capabilities, we also develop a third compiler. This compiler starts from the same source language as our second compiler but targets an untyped concurrent language with support for coarse-grained memory isolation, modelling recent hardware extensions such as Intel’s SGX [46]. Due to space constraints, we report this result only in the companion technical report [61].
The final contribution of this paper is a comparison between RSC and FAC. For this, we describe changes that would be needed to attain FAC for the first compiler and argue that these changes make generated code inefficient and also complicate the backtranslation proof significantly (Sect. 5).
Due to space constraints, we elide some technical details and limit proofs to sketches. These are fully resolved in the companion technical report [61].
2 Robustly Safe Compilation
This section first discusses robust safety as a language (not a compiler) property (Sect. 2.1) and then presents RSC as a compiler property along with an informal discussion of techniques to prove it (Sect. 2.2).
2.1 Safety and Robust Safety
To explain robust safety, we first describe a general imperative programming model that we use. Programmers write components on which they want to enforce safety properties robustly. A component is a list of function definitions that can be linked with other components (the context) in order to have a runnable whole program (functions in “other” components are like \({\texttt {extern}}\) functions in C). Additionally, every component declares a set of “sensitive” locations that contain all the data that is safety-relevant. For instance, in Example 1 this set may contain the account balance and in Example 3 it may contain the I/O buffers. We explain the relevance of this set after we define safety properties.
We want safety properties to specify that a component never executes a “bad” sequence of events. For this, we first need to fix a notion of events. We have several choices here, e.g., our events could be inputs and outputs, all syscalls, all changes to the heap (as in CompCert [44]), etc. Here, we make a specific choice motivated by our interest in robustness: We define events as calls/returns that cross a component boundary, together with the state of the heap at that point. Consequently, our safety properties can constrain the contents of the heap at component boundaries. This choice of component boundaries as the point of observation is meaningful because, in our programming model, control transfers to/from an adversary happen only at component boundaries (more precisely, they happen at cross-component function call and returns). This allows the compiler complete flexibility in optimizing code within a component, while not reducing the ability of safety properties to constrain observations of the adversary.
Concretely, a component behaviour is a trace, i.e., a sequence of actions recording component boundary interactions and, in particular, the heap at these points. Actions, the items on a trace, have the following grammar:

These actions respectively capture call and callback to a function f with parameter v when the heap is H as well as return and returnback with a certain heap H.Footnote 2 We use ? and ! decorations to indicate whether the control flow of the action goes from the context to the component (?) or from the component to the context (!). Well-formed traces have alternations of  and
and  decorated actions, starting with
decorated actions, starting with  since execution starts in the context. For a sequence of actions \(\overline{\alpha }\),
since execution starts in the context. For a sequence of actions \(\overline{\alpha }\),  is the list of heaps \(\overline{H}\) mentioned in the actions of \(\overline{\alpha }\).
is the list of heaps \(\overline{H}\) mentioned in the actions of \(\overline{\alpha }\).
Next, we need a representation of safety properties. Generally, properties are sets of traces, but safety properties specifically can be specified as automata (or monitors in the sequel) [63]. We choose this representation since monitors are less abstract than sets of traces and they are closer to enforcement mechanisms used for safety properties, e.g., runtime monitors. Briefly, a safety property is a monitor that transitions states in response to events of the program trace. At any point, the monitor may refuse to transition (it gets stuck), which encodes property violation. While a monitor can transition, the property has not been violated. Schneider [63] argues that all properties codable this way are safety properties and that all enforceable safety properties can be coded this way.
Formally, a monitor  in our setting consists of a set of abstract states
in our setting consists of a set of abstract states  , the transition relation
, the transition relation  , an initial state
, an initial state  , the set of heap locations that matter for the monitor,
, the set of heap locations that matter for the monitor,  , and the current state
, and the current state  (we indicate a set of elements of class e as \(\left\{ e\cdots \right\} \)). The transition relation
(we indicate a set of elements of class e as \(\left\{ e\cdots \right\} \)). The transition relation  is a set of triples of the form
is a set of triples of the form  consisting of a starting state
consisting of a starting state  , a final state
, a final state  and a heap
and a heap  . The transition
. The transition  is interpreted as “state
is interpreted as “state  transitions to
transitions to  when the heap is
when the heap is  ”. When determining the monitor transition in response to a program action, we restrict the program’s heap to the location set
”. When determining the monitor transition in response to a program action, we restrict the program’s heap to the location set  , i.e., to the set of locations the monitor cares about. This heap restriction is written \(H\big |_{\left\{ l\cdots \right\} }\). We assume determinism of the transition relation: for any
, i.e., to the set of locations the monitor cares about. This heap restriction is written \(H\big |_{\left\{ l\cdots \right\} }\). We assume determinism of the transition relation: for any  and (restricted heap)
and (restricted heap)  , there is at most one
, there is at most one  such that
such that  .
.
Given the behaviour of a program as a trace \(\overline{\alpha }\) and a monitor  specifying a safety property,
specifying a safety property,  denotes that the trace satisfies the safety property. Intuitively, to satisfy a safety property, the sequence of heaps in the actions of a trace must never get the monitor stuck (Rule Valid trace). Every single heap must allow the monitor to step according to its transition relation (Rule Monitor Step). Note that we overload the
denotes that the trace satisfies the safety property. Intuitively, to satisfy a safety property, the sequence of heaps in the actions of a trace must never get the monitor stuck (Rule Valid trace). Every single heap must allow the monitor to step according to its transition relation (Rule Monitor Step). Note that we overload the  notation here to also denote an auxiliary relation, the monitor small-step semantics (Rule Monitor Step-base and Rule Monitor Step-ind).
notation here to also denote an auxiliary relation, the monitor small-step semantics (Rule Monitor Step-base and Rule Monitor Step-ind).

With this setup in place, we can formalise safety, attackers and robust safety. In defining (robust) safety for a component, we only admit monitors (safety properties) whose  agrees with the sensitive locations declared by the component. Making the set of safety-relevant locations explicit in the component and the monitor gives the compiler more flexibility by telling it precisely which locations need to be protected against target-level attacks (the compiler may choose to not protect the rest). At the same time, it allows for expressive modelling. For instance, in Example 3 the safety-relevant locations could be the I/O buffers from which the program performs inputs and outputs, and the safety property can constrain the input and output buffers at corresponding call and return actions involving the Fibonacci function.
agrees with the sensitive locations declared by the component. Making the set of safety-relevant locations explicit in the component and the monitor gives the compiler more flexibility by telling it precisely which locations need to be protected against target-level attacks (the compiler may choose to not protect the rest). At the same time, it allows for expressive modelling. For instance, in Example 3 the safety-relevant locations could be the I/O buffers from which the program performs inputs and outputs, and the safety property can constrain the input and output buffers at corresponding call and return actions involving the Fibonacci function.
Definition 1
(Safety, attacker and robust safety).

A whole program  is safe for a monitor
is safe for a monitor  , written
, written  , if the monitor accepts any trace the program generates from its initial state (\({\varOmega _0}\left( {C}\right) \)).
, if the monitor accepts any trace the program generates from its initial state (\({\varOmega _0}\left( {C}\right) \)).
An attacker  is valid for a component
is valid for a component  , written
, written  , if
, if  ’s free names (denoted
’s free names (denoted  ) do not refer to the locations that the component cares about. This is a basic sanity check: if we allow an attacker to mention heap locations that the component cares about, the attacker will be able to modify those locations, causing all but trivial safety properties to not hold robustly.
) do not refer to the locations that the component cares about. This is a basic sanity check: if we allow an attacker to mention heap locations that the component cares about, the attacker will be able to modify those locations, causing all but trivial safety properties to not hold robustly.
A component  is robustly safe wrt monitor
is robustly safe wrt monitor  , written
, written  , if
, if  composed with any attacker is safe wrt
composed with any attacker is safe wrt  . As mentioned, for this setup to make sense, the monitor and the component must agree on the locations that are safety-relevant. This agreement is denoted
. As mentioned, for this setup to make sense, the monitor and the component must agree on the locations that are safety-relevant. This agreement is denoted  .
.
2.2 Robustly Safe Compilation
Robustly-safe compilation ensures that robust safety properties and their meanings are preserved across compilation. But what does it means to preserve meanings across languages? If a source safety property says 




 , and we compile to an assembly language by mapping numbers to binary, the corresponding target property should say
, and we compile to an assembly language by mapping numbers to binary, the corresponding target property should say 




 .
.
In order to relate properties across languages, we assume a relation  between source and target values that is total, so it maps any source value
between source and target values that is total, so it maps any source value  to a target value
to a target value  . This value relation is used to define a relation between heaps:
. This value relation is used to define a relation between heaps:  , which intuitively holds when related locations point to related values. This is then used to define a relation between actions:
, which intuitively holds when related locations point to related values. This is then used to define a relation between actions:  , which holds when the two actions are the “same” modulo this relation, i.e.,
, which holds when the two actions are the “same” modulo this relation, i.e.,  only relates to
only relates to  and the arguments of the action (values and heap) are related. Next, we require a relation
and the arguments of the action (values and heap) are related. Next, we require a relation  between source and target monitors, which means that the source monitor
between source and target monitors, which means that the source monitor  and the target monitor
and the target monitor  code the same safety property, modulo the relation
code the same safety property, modulo the relation  on values assumed above. The precise definition of this relation depends on the source and target languages; specific instances are shown in Sects. 3.3 and 4.3.Footnote 3
on values assumed above. The precise definition of this relation depends on the source and target languages; specific instances are shown in Sects. 3.3 and 4.3.Footnote 3
We denote a compiler from language  to language
to language  by
by
 . A compiler
. A compiler
 attains RSC, if it maps any component
attains RSC, if it maps any component  that is robustly safe wrt
that is robustly safe wrt  to a component
to a component  that is robustly safe wrt
that is robustly safe wrt  , provided that
, provided that  .
.
Definition 2
(Robustly Safe Compilation).

A consequence of the universal quantification over monitors here is that the compiler cannot be property-sensitive. A robustly-safe compiler preserves all robust safety properties, not just a specific one, e.g., it does not just enforce that \({\texttt {fibonacci}}\) is correct. This seemingly strong goal is sensible as compiler writers will likely not know what safety properties individual programmers will want to preserve.
Remark. Some readers may wonder why we do not follow existing work and specify safety as “programmer-written assertions never fail” [31, 34, 45, 68]. Unfortunately, this approach does not yield a meaningful criterion for specifying a compiler, since assertions in the compiled program (if any) are generated by the compiler itself. Thus a compiler could just erase all assertions and the compiled code it generates would be trivially (robustly) safe – no assertion can fail if there are no assertions in the first place!
Proving RSC. Proving that a compiler attains RSC can be done either by proving that a compiler satisfies Definition 2 or by proving something equivalent. To this end, Definition 3 below presents an alternative, equivalent formulation of RSC. We call this characterisation property-free as it does not mention monitors explicitly (it mentions the  function for reasons we explain below).
function for reasons we explain below).
Definition 3
(Property-Free RSC ).

Specifically,  states that the compiled code produces behaviours that refine source level behaviours robustly (taking contexts into account).
states that the compiled code produces behaviours that refine source level behaviours robustly (taking contexts into account).
 and RSC should, in general, be equivalent (Proposition 1).
and RSC should, in general, be equivalent (Proposition 1).
Proposition 1
(
 and
RSC
are equivalent).
and
RSC
are equivalent).

Informally, a property is safety if and only if it implies programs not having any trace prefix from a given set of bad prefixes (i.e., finite traces). Hence, not having a safety property robustly amounts to some context being able to induce a bad prefix. Consequently, preserving all robust safety properties (RSC) amounts to ensuring that all target prefixes can be generated (by some context) in the source too ( ). Formally, since Definition 2 relies on the monitor relation, we can prove Proposition 1 only after such a relation is finalised. We give such a monitor relation and proof in Sect. 3.3 (see Theorem 3). However, in general this result should hold for any cross-language monitor relation that correctly relates safety properties. If the proposition does not hold, then the relation does not capture how safety in one language is represented in the other.
). Formally, since Definition 2 relies on the monitor relation, we can prove Proposition 1 only after such a relation is finalised. We give such a monitor relation and proof in Sect. 3.3 (see Theorem 3). However, in general this result should hold for any cross-language monitor relation that correctly relates safety properties. If the proposition does not hold, then the relation does not capture how safety in one language is represented in the other.
Assuming Proposition 1, we can prove  for a compiler in place of RSC.
for a compiler in place of RSC.  can be proved with a backtranslation technique. This technique has been often used to prove full abstraction [7,8,9, 33, 39, 50, 53, 54, 59] and it aims at building a source context starting from a target one. In fact
can be proved with a backtranslation technique. This technique has been often used to prove full abstraction [7,8,9, 33, 39, 50, 53, 54, 59] and it aims at building a source context starting from a target one. In fact  , leads directly to a backtranslation-based proof technique since it can be rewritten (eliding irrelevant details) as:
, leads directly to a backtranslation-based proof technique since it can be rewritten (eliding irrelevant details) as:
-
If

-
then
 and
and 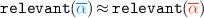
Essentially, given a target context  , a compiled program
, a compiled program  and a target trace
and a target trace  that
that  causes
causes  to have, we need to construct, or backtranslate to, a source context
to have, we need to construct, or backtranslate to, a source context  that will cause the source program
that will cause the source program  to simulate
to simulate  . Such backtranslation based proofs can be quite difficult, depending on the features of the languages and the compiler. However, backtranslation for RSC (as we show in Sect. 3.3) is not as complex as backtranslation for FAC (Sect. 5.2).
. Such backtranslation based proofs can be quite difficult, depending on the features of the languages and the compiler. However, backtranslation for RSC (as we show in Sect. 3.3) is not as complex as backtranslation for FAC (Sect. 5.2).
A simpler proof strategy is also viable for RSC when we compile only those source programs that have been verified to be robustly safe (e.g., using a type system). The idea is this: from the verification of the source program, we can find an invariant which is always maintained by the target code, and which, in turn, implies the robust safety of the target code. For example, if the safety property is that values in the heap always have their expected types, then the invariant can simply be that values in the target heap are always related to the source ones (which have their expected types). This is tantamount to proving type preservation in the target in the presence of an active adversary. This is harder than standard type preservation (because of the active adversary) but is still much easier than backtranslation as there is no need to map target constructs to source contexts syntactically. We illustrate this proof technique in Sect. 4.
RSC Implies Compiler Correctness. As stated in Sect. 1, RSC implies (a form of) compiler correctness. While this may not be apparent from Definition 2, it is more apparent from its equivalent characterization in Definition 3. We elaborate this here.
Whether concerned with whole programs or partial programs, compiler correctness states that the behaviour of compiled programs refines the behaviour of source programs [18, 36, 40, 44, 49, 65]. So, if  and
and  are the sets of compiled and source behaviours, then a compiler should force
are the sets of compiled and source behaviours, then a compiler should force  , where
, where  is the composition of \(\subseteq \) and of the relation
is the composition of \(\subseteq \) and of the relation  .
.
If we consider a source component  that is whole, then it can only link against empty contexts, both in the source and in the target. Hence, in this special case,
that is whole, then it can only link against empty contexts, both in the source and in the target. Hence, in this special case,  simplifies to standard refinement of traces, i.e., whole program compiler correctness. Hence, assuming that the correctness criterion for a compiler is concerned with the same observations as safety properties (values in safety-relevant heap locations at component crossings in our illustrative setting),
simplifies to standard refinement of traces, i.e., whole program compiler correctness. Hence, assuming that the correctness criterion for a compiler is concerned with the same observations as safety properties (values in safety-relevant heap locations at component crossings in our illustrative setting),  implies whole program compiler correctness.
implies whole program compiler correctness.
However,  (or, equivalently, RSC) does not imply, nor is implied by, any form of compositional compiler correctness (CCC) [40, 49, 65]. CCC requires that the behaviours produced by a compiled component linked against a target context that is related (in behaviour) to a source context can also be produced by the source component linked against the related source context. In contrast,
(or, equivalently, RSC) does not imply, nor is implied by, any form of compositional compiler correctness (CCC) [40, 49, 65]. CCC requires that the behaviours produced by a compiled component linked against a target context that is related (in behaviour) to a source context can also be produced by the source component linked against the related source context. In contrast,  allows picking any source context to simulate the behaviours. Hence,
allows picking any source context to simulate the behaviours. Hence,  does not imply CCC. On the other hand,
does not imply CCC. On the other hand,  universally quantifies over all target contexts, while CCC only quantifies over target contexts related to a source context, so CCC does not imply
universally quantifies over all target contexts, while CCC only quantifies over target contexts related to a source context, so CCC does not imply  either. Hence, compositional compiler correctness, if desirable, must be imposed in addition to
either. Hence, compositional compiler correctness, if desirable, must be imposed in addition to  . Note that this lack of implications is unsurprising:
. Note that this lack of implications is unsurprising:  and CCC capture two very different aspects of compilation: security (against all contexts) and compositional preservation of behaviour (against well-behaved contexts).
and CCC capture two very different aspects of compilation: security (against all contexts) and compositional preservation of behaviour (against well-behaved contexts).
3 RSC via Trace-Based Backtranslation
This section illustrates how to prove that a compiler attains RSC by means of a trace-based backtranslation technique [7, 53, 59]. To present such a proof, we first introduce our source language  , an untyped, first-order imperative language with abstract references and hidden local state (Sect. 3.1). Then, we present our target language
, an untyped, first-order imperative language with abstract references and hidden local state (Sect. 3.1). Then, we present our target language  , an untyped imperative target language with a concrete heap, whose locations are natural numbers that the context can compute.
, an untyped imperative target language with a concrete heap, whose locations are natural numbers that the context can compute.  provides hidden local state via a fine-grained capability mechanism on heap accesses (Sect. 3.2). Finally, we present the compiler
provides hidden local state via a fine-grained capability mechanism on heap accesses (Sect. 3.2). Finally, we present the compiler  and prove that it attains RSC (Sect. 3.3) by means of a trace-based backtranslation. The section conclude with an example detailing why RSC preserves security (Example 4).
and prove that it attains RSC (Sect. 3.3) by means of a trace-based backtranslation. The section conclude with an example detailing why RSC preserves security (Example 4).
To avoid focussing on mundane details, we deliberately use source and target languages that are fairly similar. However, they differ substantially in one key point: the heap model. This affords the target-level adversary attacks like guessing private locations and writing to them that do not obviously exist in the source (and makes our proofs nontrivial). We believe that (with due effort) the ideas here will generalize to languages with larger gaps and more features.
3.1 The Source Language 
 is an untyped imperative while language [51]. Components
is an untyped imperative while language [51]. Components  are triples of function definitions, interfaces and a special location written
are triples of function definitions, interfaces and a special location written  , so
, so  . Each function definition maps a function name and a formal argument to a body
. Each function definition maps a function name and a formal argument to a body  :
:  . An interface is a list of functions that the component relies on the context to provide (similar to C’s extern declarations). The special location
. An interface is a list of functions that the component relies on the context to provide (similar to C’s extern declarations). The special location  defines the locations that are monitored for safety, as explained below. Attackers
defines the locations that are monitored for safety, as explained below. Attackers  (program contexts) are function definitions that represent untrusted code that a component interacts with. A function’s body is a statement,
(program contexts) are function definitions that represent untrusted code that a component interacts with. A function’s body is a statement,  . Statements are rather standard, so we omit a formal syntax. Briefly, they can manipulate the heap (location creation
. Statements are rather standard, so we omit a formal syntax. Briefly, they can manipulate the heap (location creation  , assignment
, assignment  ), do recursive function calls (
), do recursive function calls ( ), condition (if-then-else), define local variables (let-in) and loop. Statements use effect-free expressions,
), condition (if-then-else), define local variables (let-in) and loop. Statements use effect-free expressions,  , which contain standard boolean expressions (
, which contain standard boolean expressions ( ), arithmetic expressions (
), arithmetic expressions ( ), pairing (
), pairing ( ) and projections, and location dereference (
) and projections, and location dereference ( ). Heaps
). Heaps  are maps from abstract locations
are maps from abstract locations  to values
to values  .
.
As explained in Sect. 2.1, safety properties are specified by monitors.  ’s monitors have the form:
’s monitors have the form:  . Note that in place of the set
. Note that in place of the set  of safety-relevant locations, the description of a monitor here (as well as a component above) contains a single location
of safety-relevant locations, the description of a monitor here (as well as a component above) contains a single location  . The interpretation is that any location reachable in the heap starting from
. The interpretation is that any location reachable in the heap starting from
 is relevant for safety. This set of locations can change as the program executes, and hence this is more flexible than statically specifying all of
is relevant for safety. This set of locations can change as the program executes, and hence this is more flexible than statically specifying all of
 upfront. This representation of the set by a single location is made explicit in the following monitor rule:
upfront. This representation of the set by a single location is made explicit in the following monitor rule:

Other than this small point, monitors, safety, robust safety and RSC are defined as in Sect. 2. In particular, a monitor and a component agree if they mention the same  :
: 
A program state  (denoted with
(denoted with  ) includes the function bodies
) includes the function bodies  , the heap
, the heap  , a statement
, a statement  being executed and a stack of function calls
being executed and a stack of function calls  (often omitted in the rules for simplicity). The latter is used to populate judgements of the form
(often omitted in the rules for simplicity). The latter is used to populate judgements of the form  . These determine whether calls and returns are
. These determine whether calls and returns are  (within the attacker or within the component), directed from the attacker to the component (
(within the attacker or within the component), directed from the attacker to the component ( ) or directed from the component to the attacker (
) or directed from the component to the attacker ( ). This information is used to determine whether the semantics should generate a label, as in Rules
). This information is used to determine whether the semantics should generate a label, as in Rules
 to
to
 , or no label, as in Rules
, or no label, as in Rules
 and
and
 since internal calls should not be observable.
since internal calls should not be observable.  has a big-step semantics for expressions (
has a big-step semantics for expressions ( ) that relies on evaluation contexts, a small-step semantics for statements (
) that relies on evaluation contexts, a small-step semantics for statements ( ) that has labels
) that has labels  and a semantics that accumulates labels in traces (
and a semantics that accumulates labels in traces (
 ) by omitting silent actions
) by omitting silent actions  and concatenating the rest. Unlike existing work on compositional compiler correctness which only rely on having the component [40], the semantics relies on having both the component and the context.
and concatenating the rest. Unlike existing work on compositional compiler correctness which only rely on having the component [40], the semantics relies on having both the component and the context.

3.2 The Target Language 
 is an untyped, imperative language that follows the structure of
is an untyped, imperative language that follows the structure of  and it has similar expressions and statements. However, there are critical differences (that make the compiler interesting). The main difference is that heap locations in
and it has similar expressions and statements. However, there are critical differences (that make the compiler interesting). The main difference is that heap locations in  are concrete natural numbers. Upfront, an adversarial context can guess locations used as private state by a component and clobber them. To support hidden local state, a location can be “hidden” explicitly via the statement
are concrete natural numbers. Upfront, an adversarial context can guess locations used as private state by a component and clobber them. To support hidden local state, a location can be “hidden” explicitly via the statement  , which allocates a new capability
, which allocates a new capability  , an abstract token that grants access to the location
, an abstract token that grants access to the location  to which
to which  points [64]. Subsequently, all reads and writes to
points [64]. Subsequently, all reads and writes to  must be authenticated with the capability, so reading and writing a location take another parameter as follows:
must be authenticated with the capability, so reading and writing a location take another parameter as follows:  and
and  . In both cases, the
. In both cases, the  after the
after the  is the capability. Unlike locations, capabilities cannot be guessed. To make a location private, the compiler can make the capability of the location private. To bootstrap this hiding process, we assume that a component has one location that can only be accessed by it, a priori in the semantics (in our formalization, we always focus on only one component and we assume that, for this component, this special location is at address
is the capability. Unlike locations, capabilities cannot be guessed. To make a location private, the compiler can make the capability of the location private. To bootstrap this hiding process, we assume that a component has one location that can only be accessed by it, a priori in the semantics (in our formalization, we always focus on only one component and we assume that, for this component, this special location is at address  ).
).
In detail,  heaps
heaps  are maps from natural numbers (locations)
are maps from natural numbers (locations)  to values
to values  and a tag
and a tag  as well as capabilities, so
as well as capabilities, so  . The tag
. The tag  can be
can be  , which means that
, which means that  is globally available (not protected) or a capability
is globally available (not protected) or a capability  , which protects
, which protects  . A globally available location can be freely read and written but one that is protected by a capability requires the capability to be supplied at the time of read/write (Rule
. A globally available location can be freely read and written but one that is protected by a capability requires the capability to be supplied at the time of read/write (Rule
 , Rule
, Rule
 ).
).
 also has a big-step semantics for expressions, a labelled small-step semantics and a semantics that accumulates traces analogous to that of
also has a big-step semantics for expressions, a labelled small-step semantics and a semantics that accumulates traces analogous to that of  .
.

A second difference between  and
and  is that
is that  has no booleans, while
has no booleans, while  has them. This makes the compiler and the related proofs interesting, as discussed in the proof of Theorem 1.
has them. This makes the compiler and the related proofs interesting, as discussed in the proof of Theorem 1.
In  , the locations of interest to a monitor are all those that can be reached from the address
, the locations of interest to a monitor are all those that can be reached from the address  .
.  itself is protected with a capability
itself is protected with a capability  that is assumed to occur only in the code of the component in focus, so a component is defined as
that is assumed to occur only in the code of the component in focus, so a component is defined as  . We can now give a precise definition of component-monitor agreement for
. We can now give a precise definition of component-monitor agreement for  as well as a precise definition of attacker, which must care about the
as well as a precise definition of attacker, which must care about the  capability.
capability.

3.3 Compiler from  to
to 
We now present  , the compiler from
, the compiler from  to
to  , detailing how it uses the capabilities of
, detailing how it uses the capabilities of  to achieve RSC. Then, we prove that
to achieve RSC. Then, we prove that  attains RSC.
attains RSC.
Compiler  takes as input a
takes as input a  component
component  and returns a
and returns a  component (excerpts of the translation are shown below). The compiler performs a simple pass on the structure of functions, expressions and statements. Each
component (excerpts of the translation are shown below). The compiler performs a simple pass on the structure of functions, expressions and statements. Each  location is encoded as a pair of a
location is encoded as a pair of a  location and the capability to access the location; location update and dereference are compiled accordingly. The compiler codes source booleans
location and the capability to access the location; location update and dereference are compiled accordingly. The compiler codes source booleans  to
to  and
and  to
to  , and the source number
, and the source number  to the target counterpart
to the target counterpart  .
.

This compiler solely relies on the capability abstraction of the target language as a defence mechanism to attain RSC. Unlike existing secure compilers,  needs neither dynamic checks nor other constructs that introduce runtime overhead to attain RSC [9, 32, 39, 53, 59].
needs neither dynamic checks nor other constructs that introduce runtime overhead to attain RSC [9, 32, 39, 53, 59].
Proof of RSC . Compiler  attains RSC (Theorem 1). In order to set up this theorem, we need to instantiate the cross-language relation for values, which we write as
attains RSC (Theorem 1). In order to set up this theorem, we need to instantiate the cross-language relation for values, which we write as  here. The relation is parametrised by a partial bijection
here. The relation is parametrised by a partial bijection  from source heap locations to target heap locations which determines when a source location and a target location (and its capability) are related. On values,
from source heap locations to target heap locations which determines when a source location and a target location (and its capability) are related. On values,  is defined as follows:
is defined as follows:  ;
;  when
when  ;
;  ;
;  if
if  ;
;  if
if  ;
;  if
if  and
and  . This relation is then used to define the heap, monitor state and action relations. Heaps are related, written
. This relation is then used to define the heap, monitor state and action relations. Heaps are related, written  , when locations related in \(\beta \) point to related values. States are related, written
, when locations related in \(\beta \) point to related values. States are related, written  , when they have related heaps. The action relation (
, when they have related heaps. The action relation ( ) is defined as in Sect. 2.2.
) is defined as in Sect. 2.2.
Monitor Relation. In Sect. 2.2, we left the monitor relation abstract. Here, we define it for our two languages. Two monitors are related when they can simulate each other on related heaps. Given a monitor-specific relation  on monitor states, we say that a relation \(\mathcal {R}\) on source and target monitors is a bisimulation if the following hold whenever
on monitor states, we say that a relation \(\mathcal {R}\) on source and target monitors is a bisimulation if the following hold whenever  and
and  are related by \(\mathcal {R}\):
are related by \(\mathcal {R}\):
-
1.
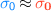 , and
, and 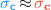 , and
, and -
2.
For all \(\beta \) containing
 and all
and all  with
with 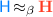 :
:-
(a)
 iff
iff 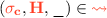 , and
, and -
(b)
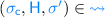 and
and  imply
imply  .
.
-
(a)
In words, \(\mathcal {R}\) is a bisimulation only if  implies that
implies that  and
and  simulate each other on heaps related by any \(\beta \) that relates
simulate each other on heaps related by any \(\beta \) that relates  to
to  . In particular, this means that neither
. In particular, this means that neither  nor
nor  can be sensitive to the specific addresses allocated during the run of the program. However, they can be sensitive to the “shape” of the heap or the values stored in the heap. Note that the union of any two bisimulations is a bisimulation. Hence, there is a largest bisimulation, which we denote as
can be sensitive to the specific addresses allocated during the run of the program. However, they can be sensitive to the “shape” of the heap or the values stored in the heap. Note that the union of any two bisimulations is a bisimulation. Hence, there is a largest bisimulation, which we denote as  . Intuitively,
. Intuitively,  implies that
implies that  and
and  encode the same safety property (up to the aforementioned relation on values
encode the same safety property (up to the aforementioned relation on values  ). With all the boilerplate for RSC in place, we state our main theorem.
). With all the boilerplate for RSC in place, we state our main theorem.
Theorem 1
(
 attains
RSC
).
attains
RSC
).

We outline our proof of Theorem 1, which relies on a backtranslation
 . Intuitively,
. Intuitively,
 takes a target trace
takes a target trace  and builds a set of source contexts such that one of them when linked with
and builds a set of source contexts such that one of them when linked with  , produces a related trace
, produces a related trace  in the source (Theorem 2). In prior work, backtranslations return a single context [10, 11, 21, 28, 50, 53, 59]. This is because they all, explicitly or implicitly, assume that
in the source (Theorem 2). In prior work, backtranslations return a single context [10, 11, 21, 28, 50, 53, 59]. This is because they all, explicitly or implicitly, assume that  is injective from source to target. Under this assumption, the backtranslation is unique: a target value
is injective from source to target. Under this assumption, the backtranslation is unique: a target value  will be related to at most one source value
will be related to at most one source value  . We do away with this assumption (e.g., the target value
. We do away with this assumption (e.g., the target value  is related to both source values
is related to both source values  and
and  ) and thus there can be multiple source values related to any given target value. This results in a set of backtranslated contexts, of which at least one will reproduce the trace as we need it.
) and thus there can be multiple source values related to any given target value. This results in a set of backtranslated contexts, of which at least one will reproduce the trace as we need it.
We bypass the lengthy technical setup for this proof and provide an informal description of why the backtranslation achieves what it is supposed to. As an example, Fig. 1 contains a trace  and the the output of
and the the output of  .
.
 first generates empty method bodies for all context methods called by the compiled component. Then it backtranslates each action on the given trace, generating code blocks that mimic that action and places that code inside the appropriate method body. Figure 1 shows the code blocks generated for each action. Backtranslated code maintains a support data structure at runtime, a list of locations denoted
first generates empty method bodies for all context methods called by the compiled component. Then it backtranslates each action on the given trace, generating code blocks that mimic that action and places that code inside the appropriate method body. Figure 1 shows the code blocks generated for each action. Backtranslated code maintains a support data structure at runtime, a list of locations denoted  where locations are added (
where locations are added ( ) and they are looked up (
) and they are looked up ( ) based on their second field
) based on their second field  , which is their target-level address. In order to backtranslate the first call, we need to set up the heap with the right values and then perform the call. In the diagram, dotted lines describe which source statement generates which part of the heap. The return only generates code that will update the list
, which is their target-level address. In order to backtranslate the first call, we need to set up the heap with the right values and then perform the call. In the diagram, dotted lines describe which source statement generates which part of the heap. The return only generates code that will update the list  to ensure that the context has access to all the locations it knows in the target too. In order to backtranslate the last call we lookup the locations to be updated in
to ensure that the context has access to all the locations it knows in the target too. In order to backtranslate the last call we lookup the locations to be updated in  so we can ensure that when the
so we can ensure that when the  statement is executed, the heap is in the right state.
statement is executed, the heap is in the right state.
For the backtranslation to be used in the proof we need to prove its correctness, i.e., that  generates a context
generates a context  that, together with
that, together with  , generates a trace
, generates a trace  related to the given target trace
related to the given target trace  .
.
Theorem 2
(
 is correct)
is correct)

This theorem immediately implies that  , which, by Theorem 3 below, implies that
, which, by Theorem 3 below, implies that  .
.
Theorem 3
(
 and
RSC
are equivalent for
and
RSC
are equivalent for
 ).
).

Example 4
(Compiling a secure program). To illustrate RSC at work, let us consider the following source component  , which manages an account whose balance is security-relevant. Accordingly, the balance is stored in a location (
, which manages an account whose balance is security-relevant. Accordingly, the balance is stored in a location ( that is tracked by the monitor.
that is tracked by the monitor.  provides functions to deposit to the account as well as to print the account balance.
provides functions to deposit to the account as well as to print the account balance.

 never leaks any sensitive location (
never leaks any sensitive location ( ) to an attacker. Additionally, an attacker has no way to decrement the amount of the balance since deposit only adds the absolute value
) to an attacker. Additionally, an attacker has no way to decrement the amount of the balance since deposit only adds the absolute value  of its input
of its input  to the existing balance.
to the existing balance.
By compiling  with
with  , we obtain the following target program.
, we obtain the following target program.

Recall that location  is mapped to location
is mapped to location  and protected by the
and protected by the  capability. In the compiled code, while location
capability. In the compiled code, while location  is freely computable by a target attacker, capability
is freely computable by a target attacker, capability  is not. Since that capability is not leaked to an attacker, an attacker will not be able to tamper with the balance stored in location
is not. Since that capability is not leaked to an attacker, an attacker will not be able to tamper with the balance stored in location  .\(\boxdot \)
.\(\boxdot \)
4 RSC via Bisimulation
If the source language has a verification system that enforces robust safety, proving that a compiler attains RSC can be simpler than that of Sect. 3—it may not require a back translation. To demonstrate this, we consider a specific class of monitors, namely those that enforce type invariants on a specific set of locations. Our source language,  , is similar to
, is similar to  but it has a type system that accepts only those source programs whose traces the source monitor never rejects. Our compiler
but it has a type system that accepts only those source programs whose traces the source monitor never rejects. Our compiler  is directed by typing derivations, and its proof of RSC establishes a specific cross-language invariant on program execution, rather than a backtranslation. A second, independent goal of this section is to show that RSC is compatible with concurrency. Consequently, our source and target languages include constructs for forking threads.
is directed by typing derivations, and its proof of RSC establishes a specific cross-language invariant on program execution, rather than a backtranslation. A second, independent goal of this section is to show that RSC is compatible with concurrency. Consequently, our source and target languages include constructs for forking threads.
4.1 The Source Language 
 extends
extends  with concurrency, so it has a fork statement
with concurrency, so it has a fork statement  , processes and process soups [19]. Components define a set of safety-relevant locations
, processes and process soups [19]. Components define a set of safety-relevant locations  , so
, so  and heaps carry type information, so
and heaps carry type information, so  .
.  also specifies a type for each safety-relevant location, so
also specifies a type for each safety-relevant location, so  .
.
 has an unconventional type system that enforces robust type safety [1, 14, 31, 34, 45, 58], which means that no context can cause the static types of sensitive heap locations to be violated at runtime. Using a special type
has an unconventional type system that enforces robust type safety [1, 14, 31, 34, 45, 58], which means that no context can cause the static types of sensitive heap locations to be violated at runtime. Using a special type  that is described below, a program component statically partitions heap locations it deals with into those it cares about (sensitive or “trusted” locations) and those it does not care about (“untrusted” locations). Call a value shareable if only untrusted locations can be extracted from it using the language’s elimination constructs. The type system then ensures that a program component only ever shares shareable values with the context. This ensures that the context cannot violate any invariants (including static types) of the trusted locations, since it can never gets direct access to them.
that is described below, a program component statically partitions heap locations it deals with into those it cares about (sensitive or “trusted” locations) and those it does not care about (“untrusted” locations). Call a value shareable if only untrusted locations can be extracted from it using the language’s elimination constructs. The type system then ensures that a program component only ever shares shareable values with the context. This ensures that the context cannot violate any invariants (including static types) of the trusted locations, since it can never gets direct access to them.
Technically, the type system considers the types  and the following typing judgements (
and the following typing judgements ( maps variables to types).
maps variables to types).

Type  stands for “untrusted” or “shareable” and contains all values that can be passed to the context. Every type that is not a subtype of
stands for “untrusted” or “shareable” and contains all values that can be passed to the context. Every type that is not a subtype of  is implicitly trusted and cannot be passed to the context. Untrusted locations are explicitly marked
is implicitly trusted and cannot be passed to the context. Untrusted locations are explicitly marked  at their allocation points in the program. Other types are deemed shareable via subtyping. Intuitively, a type is safe if values in it can only yield locations of type
at their allocation points in the program. Other types are deemed shareable via subtyping. Intuitively, a type is safe if values in it can only yield locations of type  by the language elimination constructs. For example,
by the language elimination constructs. For example,  is a subtype of
is a subtype of  . We write
. We write  to mean that
to mean that  is a subtype of
is a subtype of  .
.
Further,  contains an endorsement statement (
contains an endorsement statement ( ) that dynamically checks the top-level constructor of a value of type
) that dynamically checks the top-level constructor of a value of type  and gives it a more precise superficial type
and gives it a more precise superficial type  [24]. This allows a program to safely inspect values coming from the context. It is similar to existing type casts [48] but it only inspects one structural layer of the value (this simplifies the compilation).
[24]. This allows a program to safely inspect values coming from the context. It is similar to existing type casts [48] but it only inspects one structural layer of the value (this simplifies the compilation).
The operational semantics of  updates that of
updates that of  to deal with concurrency and endorsement. The latter performs a runtime check on the endorsed value [62].
to deal with concurrency and endorsement. The latter performs a runtime check on the endorsed value [62].
Monitors  check at runtime that the set of trusted heap locations
check at runtime that the set of trusted heap locations  have values of their intended static types. Accordingly, the description of the monitor includes a list of trusted locations and their expected types (in the form of an environment
have values of their intended static types. Accordingly, the description of the monitor includes a list of trusted locations and their expected types (in the form of an environment  ). The type
). The type  of any location in
of any location in  must be trusted, so
must be trusted, so  . To facilitate checks of the monitor, every heap location carries a type at runtime (in addition to a value). The monitor transitions should therefore be of the form
. To facilitate checks of the monitor, every heap location carries a type at runtime (in addition to a value). The monitor transitions should therefore be of the form  , but since
, but since  never changes, we write the transitions as
never changes, we write the transitions as  .
.
A monitor and a component agree if they have the same  :
:  . Other definitions (safety, robust safety and actions) are as in Sect. 2. Importantly, a well-typed component generates traces that are always accepted, so every component typed at
. Other definitions (safety, robust safety and actions) are as in Sect. 2. Importantly, a well-typed component generates traces that are always accepted, so every component typed at  is robustly safe.
is robustly safe.
Theorem 4
(Typability Implies Robust Safety in
 )
)

Richer Source Monitors. In  , source language monitors only enforce the property of type safety on specific memory locations (robustly). This can be generalized substantially to enforce arbitrary invariants other than types on locations. The only requirement is to find a type system (e.g., based on refinements or Hoare logics) that can enforce robust safety in the source (cf. [68]). Our compilation and proof strategy should work with little modification. Another easy generalization is allowing the set of locations considered by the monitor to grow over time, as in Sect. 3.
, source language monitors only enforce the property of type safety on specific memory locations (robustly). This can be generalized substantially to enforce arbitrary invariants other than types on locations. The only requirement is to find a type system (e.g., based on refinements or Hoare logics) that can enforce robust safety in the source (cf. [68]). Our compilation and proof strategy should work with little modification. Another easy generalization is allowing the set of locations considered by the monitor to grow over time, as in Sect. 3.
4.2 The Target Language 
Our target language,  , extends the previous target language
, extends the previous target language  , with support for concurrency (forking, processes and process soups), atomic co-creation of a protected location and its protecting capability (
, with support for concurrency (forking, processes and process soups), atomic co-creation of a protected location and its protecting capability ( ) and for examining the top-level construct of a value (
) and for examining the top-level construct of a value ( ) according to a pattern (
) according to a pattern ( ).
).

Monitors are also updated to consider a fixed set of locations (a heap  ), so
), so  . The atomic creation of capabilities is provided to match modern security architectures such as Cheri [71] (which implement capabilities at the hardware level). This atomicity is not strictly necessary and we prove that RSC is attained both by a compiler relying on it and by one that allocates a location and then protects it non-atomically. The former compiler (with this atomicity in the target) is a bit easier to describe, so for space reasons, we only describe that here and defer the other one to the companion report [61].
. The atomic creation of capabilities is provided to match modern security architectures such as Cheri [71] (which implement capabilities at the hardware level). This atomicity is not strictly necessary and we prove that RSC is attained both by a compiler relying on it and by one that allocates a location and then protects it non-atomically. The former compiler (with this atomicity in the target) is a bit easier to describe, so for space reasons, we only describe that here and defer the other one to the companion report [61].
4.3 Compiler from  to
to 
The high-level structure of the compiler,  , is similar to that of our earlier compiler
, is similar to that of our earlier compiler  (Sect. 3.3). However,
(Sect. 3.3). However,  is defined by induction on the type derivation of the component to be compiled. The case for allocation (presented below) explicitly uses type information to achieve security efficiently, protecting only those locations whose type is not
is defined by induction on the type derivation of the component to be compiled. The case for allocation (presented below) explicitly uses type information to achieve security efficiently, protecting only those locations whose type is not  .
.

New Monitor Relation. As monitors have changed, we also need a new monitor relation  . Informally, a source and a target monitor are related if the target monitor can always step whenever the target heap satisfies the types specified in the source monitor (up to renaming by the partial bijection \(\beta \)).
. Informally, a source and a target monitor are related if the target monitor can always step whenever the target heap satisfies the types specified in the source monitor (up to renaming by the partial bijection \(\beta \)).
We write  to mean that for each location
to mean that for each location  ,
,  . Given a partial bijection \(\beta \) from source to target locations, we say that a target monitor
. Given a partial bijection \(\beta \) from source to target locations, we say that a target monitor  is good, written
is good, written  , if for all
, if for all  and all
and all  such that
such that  , there is a
, there is a  such that
such that  . For a fixed partial bijection \(\beta _0\) between the domains of
. For a fixed partial bijection \(\beta _0\) between the domains of  and
and  , we say that the source monitor
, we say that the source monitor  and the target monitor
and the target monitor  are related, written
are related, written  , if
, if  for the
for the  in
in  . With this setup, we define RSC as in Sect. 2.
. With this setup, we define RSC as in Sect. 2.
Theorem 5
(Compiler
 attains
RSC
).
attains
RSC
).

To prove that  attains RSC we do not rely on a backtranslation. Here, we know statically which locations can be monitor-sensitive: they must all be trusted, i.e., must have a type
attains RSC we do not rely on a backtranslation. Here, we know statically which locations can be monitor-sensitive: they must all be trusted, i.e., must have a type  satisfying
satisfying  . Using this, we set up a simple cross-language relation and show it to be an invariant on runs of source and compiled target components. The relation captures the following:
. Using this, we set up a simple cross-language relation and show it to be an invariant on runs of source and compiled target components. The relation captures the following:
-
Heaps (both
 and
and  ) can be partitioned into two parts, a trusted part and an untrusted part;
) can be partitioned into two parts, a trusted part and an untrusted part; -
The trusted
 contains only locations whose type is trusted (
contains only locations whose type is trusted ( );
); -
The trusted
 contains only locations related to
contains only locations related to 
 and these point to related values; more importantly, every
and these point to related values; more importantly, every 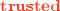

 is protected by a capability;
is protected by a capability; -
In the
 , any capability protecting a trusted location does not occur in attacker code, nor is it stored in an untrusted heap location.
, any capability protecting a trusted location does not occur in attacker code, nor is it stored in an untrusted heap location.
We need to prove that this relation is preserved by reductions both in compiled and in attacker code. The former follows from source robust safety (Theorem 4). The latter is simple since all trusted locations are protected with capabilities, attackers have no access to trusted locations, and capabilities are unforgeable and unguessable (by the semantics of  ). At this point, knowing that monitors are related, and that source traces are always accepted by source monitors, we can conclude that target traces are always accepted by target monitors too. Note that this kind of an argument requires all compilable source programs to be robustly safe and is, therefore, impossible for our first compiler
). At this point, knowing that monitors are related, and that source traces are always accepted by source monitors, we can conclude that target traces are always accepted by target monitors too. Note that this kind of an argument requires all compilable source programs to be robustly safe and is, therefore, impossible for our first compiler  . Avoiding the backtranslation results in a proof much simpler than that of Sect. 3.
. Avoiding the backtranslation results in a proof much simpler than that of Sect. 3.
5 Fully Abstract Compilation
Our next goal is to compare RSC to FAC at an intuitive level. We first define fully abstract compilation or FAC (Sect. 5.1). Then, we present an example of how FAC may result in inefficient compiled code and use that to present in Sect. 5.2 what would be needed to write a fully abstract compiler from  to
to  (the languages of our first compiler). We use this example to compare RSC and FAC concretely, showing that, at least on this example, RSC permits more efficient code and affords simpler proofs that FAC.
(the languages of our first compiler). We use this example to compare RSC and FAC concretely, showing that, at least on this example, RSC permits more efficient code and affords simpler proofs that FAC.
However, this does not imply that one should always prefer RSC to FAC blindly. In some cases, one may want to establish full abstraction for reasons other than security. Also, when the target language is typed [10, 11, 21, 50] or has abstractions similar to those of the source, full abstraction may have no downsides (in terms of efficiency of compiled code and simplicity of proofs) relative to RSC. However, in many settings, including those we consider, target languages are not typed, and often differ significantly from the source in their abstractions. In such cases, RSC is a worthy alternative.
5.1 Formalising Fully Abstract Compilation
As stated in Sect. 1, FAC requires the preservation and reflection of observational equivalence, and most existing work instantiates observational equivalence with contextual equivalence ( ). Contextual equivalence and FAC are defined below. Informally, two components
). Contextual equivalence and FAC are defined below. Informally, two components  and
and  are contextually equivalent if no context A interacting with them can tell them apart, i.e., they are indistinguishable. Contextual equivalence can encode security properties such as confidentiality, integrity, invariant maintenance and non-interference [6, 9, 53, 60]. We do not explain this well-known observation here, but refer the interested reader to the survey of Patrignani et al. [54]. Informally, a compiler
are contextually equivalent if no context A interacting with them can tell them apart, i.e., they are indistinguishable. Contextual equivalence can encode security properties such as confidentiality, integrity, invariant maintenance and non-interference [6, 9, 53, 60]. We do not explain this well-known observation here, but refer the interested reader to the survey of Patrignani et al. [54]. Informally, a compiler
 is fully abstract if it translates (only) contextually-equivalent source components into contextually-equivalent target ones.
is fully abstract if it translates (only) contextually-equivalent source components into contextually-equivalent target ones.
Definition 4
(Contextual equivalence and fully abstract compilation).

The security-relevant part of FAC is the \(\Rightarrow \) implication [29]. This part is security-relevant because the proof thesis concerns target contextual equivalence ( ). Unfolding the definition of
). Unfolding the definition of  on the right of the implication yields a universal quantification over all possible target contexts
on the right of the implication yields a universal quantification over all possible target contexts  , which captures malicious attackers. In fact, there may be target contexts
, which captures malicious attackers. In fact, there may be target contexts  that can interact with compiled code in ways that are impossible in the source language. Compilers that attain FAC with untyped target languages often insert checks in compiled code that detect such interactions and respond to them securely [60], often by halting the execution [6, 9, 29, 37, 39, 42, 53, 54]. These checks are often inefficient, but must be performed even if the interactions are not security-relevant. We now present an example of this.
that can interact with compiled code in ways that are impossible in the source language. Compilers that attain FAC with untyped target languages often insert checks in compiled code that detect such interactions and respond to them securely [60], often by halting the execution [6, 9, 29, 37, 39, 42, 53, 54]. These checks are often inefficient, but must be performed even if the interactions are not security-relevant. We now present an example of this.
Example 5
(Wrappers for heap resources). Consider a password manager written in an object-oriented language that is compiled to an assembly-like language. The password manager defines a \({\texttt {private}}\) \({\texttt {List}}\) object where it stores the passwords locally. Shown below are two implementations of the \({\texttt {newList}}\) method inside \({\texttt {List}}\) which we call  and
and  . The only difference between
. The only difference between  and
and  is that
is that  allocates two lists internally; one of these (\({\texttt {shadow}}\)) is used for internal purposes only.
allocates two lists internally; one of these (\({\texttt {shadow}}\)) is used for internal purposes only.

 and
and  are equivalent in a source language that does not allow pointer comparison (like our source languages). To attain FAC when the target allows pointer comparisons (as in our target languages), the pointers returned by \({\texttt {newList}}\) in the two implementations must be the same, but this is very difficult to ensure since the second implementation does more allocations. A simple solution to this problem is to wrap \({\texttt {ell}}\) in a proxy object and return the proxy [9, 47, 53, 59]. Compiled code needs to maintain a lookup table mapping the proxy to the original object and proxies must have allocation-independent addresses. Proxies work but they are inefficient due to the need to look up the table on every object access.\(\boxdot \)
are equivalent in a source language that does not allow pointer comparison (like our source languages). To attain FAC when the target allows pointer comparisons (as in our target languages), the pointers returned by \({\texttt {newList}}\) in the two implementations must be the same, but this is very difficult to ensure since the second implementation does more allocations. A simple solution to this problem is to wrap \({\texttt {ell}}\) in a proxy object and return the proxy [9, 47, 53, 59]. Compiled code needs to maintain a lookup table mapping the proxy to the original object and proxies must have allocation-independent addresses. Proxies work but they are inefficient due to the need to look up the table on every object access.\(\boxdot \)
In this example, FAC forces all privately allocated locations to be wrapped in proxies. However, RSC does not require this. Our target languages  and
and  support address comparison (addresses are natural numbers in their heaps) but
support address comparison (addresses are natural numbers in their heaps) but  and
and  just use capabilities to attain security efficiently while
just use capabilities to attain security efficiently while  relies on memory isolation. On the other hand, for attaining FAC, capabilities alone would be insufficient since they do not hide addresses. We explain this in detail in the next subsection.
relies on memory isolation. On the other hand, for attaining FAC, capabilities alone would be insufficient since they do not hide addresses. We explain this in detail in the next subsection.
Remarks. Our technical report lists many other cases of FAC forcing security-irrelevant inefficiency in compiled code [61]. All of these can be avoided by just replacing contextual equivalence with a different notion of equivalence in the statement of FAC. However, it is not clear how this can be done generally for any given kind of inefficiency, and what the security consequences of such instantiations of the statement of FAC are. On the other hand, RSC is uniform and it does not induce any of these inefficiencies.
A security issue that cannot be addressed just by tweaking equivalences is information leaks on side channels, as side channels are, by definition, not expressible in the language. Neither FAC nor RSC deals with side channels.
5.2 Towards a Fully Abstract Compiler from  to
to 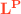
To further compare FAC and RSC, we now sketch what would be needed to construct a fully abstract compiler from  to
to  . In particular, this compiler should not suffer from the “attack” described in Example 5.
. In particular, this compiler should not suffer from the “attack” described in Example 5.
Inefficiency. We denote with  a (hypothetical) new compiler from
a (hypothetical) new compiler from  to
to  that attains FAC. We describe informally what code generated by this compiler would have to do. We know that fully abstract compilation preserves all source abstractions in the target language. One abstraction that distinguishes
that attains FAC. We describe informally what code generated by this compiler would have to do. We know that fully abstract compilation preserves all source abstractions in the target language. One abstraction that distinguishes  from
from  is that locations are abstract in
is that locations are abstract in  , but concrete natural numbers in
, but concrete natural numbers in  . Thus, locations allocated by compiled code must not be passed directly to the context as this would reveal the allocation order. Instead of passing the location
. Thus, locations allocated by compiled code must not be passed directly to the context as this would reveal the allocation order. Instead of passing the location  to the context, the compiler arranges for an opaque handle
to the context, the compiler arranges for an opaque handle  (that cannot be used to access any location directly) to be passed. Such an opaque handle is often called a mask or seal in the literature [66].
(that cannot be used to access any location directly) to be passed. Such an opaque handle is often called a mask or seal in the literature [66].
To ensure that masking is done properly,  can insert code at entry and exit points of compiled code, wrapping the compiled code in a way that enforces masking [32, 59]. The wrapper keeps a list
can insert code at entry and exit points of compiled code, wrapping the compiled code in a way that enforces masking [32, 59]. The wrapper keeps a list  of component-allocated locations that are shared with the context in order to know their masks. When a component-allocated location is shared, it is added to the list
of component-allocated locations that are shared with the context in order to know their masks. When a component-allocated location is shared, it is added to the list  . The mask of a location is its index in this list. If the same location is shared again it is not added again but its previous index is used. To implement lookup in
. The mask of a location is its index in this list. If the same location is shared again it is not added again but its previous index is used. To implement lookup in  we must compare capabilities too, so we need to add that expression to the target language. To ensure capabilities do not leak to the context, the second field of the pair is a constant capability
we must compare capabilities too, so we need to add that expression to the target language. To ensure capabilities do not leak to the context, the second field of the pair is a constant capability  which compiled code does not use otherwise. Clearly, this wrapping can increase the cost of all cross-component calls and returns.
which compiled code does not use otherwise. Clearly, this wrapping can increase the cost of all cross-component calls and returns.
However, this wrapping is not sufficient to attain FAC. A component-allocated location could be passed to the context on the heap, so before passing control to the context the compiled code needs to scan the whole heap where a location can be passed and mask all found component-allocated locations. Dually, when receiving control the compiled code must scan the heap to unmask any masked location so it can use the location. The problem now is determining what parts of the heap to scan and how. Specifically, the compiled code needs to keep track of all the locations (and related capabilities) that are shared, i.e., (i) passed from the context to the component and (ii) passed from the component to the context. Both keeping track of these locations as well as scanning them on every cross-component control transfer is likely to be very expensive.
Finally, masked locations cannot be used directly by the context to be read and written. Thus, compiled code must provide a  and a
and a  function that implement reading and writing to masked locations. The additional unmasking in these functions (as opposed to native reads and writes) adds to the inefficiency.
function that implement reading and writing to masked locations. The additional unmasking in these functions (as opposed to native reads and writes) adds to the inefficiency.
It should be clear as opposed to the RSC compiler  (Sect. 3), the FAC compiler
(Sect. 3), the FAC compiler  just sketched is likely to generate far more inefficient code.
just sketched is likely to generate far more inefficient code.
Proof Difficulty. Proving that  attains FAC can only be done by backtranslating traces, not contexts alone, since the newly-added target expressions cannot be directly backtranslated to valid source ones [7, 9, 59]. For this, we need a trace semantics that captures all information available to the context. This is often called a fully abstract trace semantics [38, 55, 56]. However, the trace semantics we defined for
attains FAC can only be done by backtranslating traces, not contexts alone, since the newly-added target expressions cannot be directly backtranslated to valid source ones [7, 9, 59]. For this, we need a trace semantics that captures all information available to the context. This is often called a fully abstract trace semantics [38, 55, 56]. However, the trace semantics we defined for  is not fully abstract, as its actions record the entire heap in every action, including private parts of the heap. Hence, we cannot use this trace semantics for proving FAC and so we design a new one. Building a fully abstract trace semantics for
is not fully abstract, as its actions record the entire heap in every action, including private parts of the heap. Hence, we cannot use this trace semantics for proving FAC and so we design a new one. Building a fully abstract trace semantics for  is challenging because we have to keep track of locations that have been shared with the context in the past. This substantially complicates both the definition of traces and the proofs that build on the definition.
is challenging because we have to keep track of locations that have been shared with the context in the past. This substantially complicates both the definition of traces and the proofs that build on the definition.
Finally, the source context that the backtranslation constructs from a target trace must simulate the shared part of the heap at every context switch. Since locations in the target may be masked, the source context has to maintain a map from the source locations to the corresponding masked target ones, which complicates the backtranslation and the proof substantially.
To summarize, it should be clear that the proof of  for
for  would be much harder than the proof of RSC for
would be much harder than the proof of RSC for  , even though the source and target languages are the same and so is the broad proof technique (backtranslation).
, even though the source and target languages are the same and so is the broad proof technique (backtranslation).
6 Related Work
Recent work [8, 33] presents new criteria for secure compilation that ensure preservation of subclasses of hyperproperties. Hyperproperties [25] are a formal representation of predicates on programs, i.e., they are predicates on sets of traces. Hyperproperties capture many security-relevant properties including not just conventional safety and liveness, which are predicates on traces, but also properties like non-interference, which is a predicate on pairs of traces. Modulo technical differences, our definition of RSC coincides with the criterion of “robust safety property preservation” in [8, 33]. We show, through concrete instances, that this criterion can be easily realized by compilers, and develop two proof techniques for establishing it. We further show that the criterion leads to more efficient compiled code than does FAC. Additionally, the criteria in [8, 33] assume that behaviours in the source and target are represented using the same alphabet. Hence, the definitions (somewhat unrealistically or ideally) do not require a translation of source properties to target properties. In contrast, we consider differences in the representation of behaviour in the source and in the target and this is accounted for in our monitor relation  . A slightly different account of this difference is presented by Patrignani and Garg [60] in the context of reactive black-box programs.
. A slightly different account of this difference is presented by Patrignani and Garg [60] in the context of reactive black-box programs.
Abate et al. [7] define a variant of robustly-safe compilation called RSCC specifically tailored to the case where (source) components can perform undefined behaviour. RSCC does not consider attacks from arbitrary target contexts but from compiled components that can become compromised and behave in arbitrary ways. To demonstrate RSCC, Abate et al. [7] rely on two backends for their compiler: software fault isolation and tag-based monitors. On the other hand, we rely on capability machines and memory isolation (the latter in the companion report). RSCC also preserves (a form of) safety properties and can be achieved by relying on a trace-based backtranslation; it is unclear whether proofs can be simplified when the source is verified and concurrent, as in our second compiler.
ASLR [6, 37], protected module architectures [9, 42, 53, 59], tagged architectures [39], capability machines [69] and cryptographic primitives [4, 5, 22, 26] have been used as targets for FAC. We believe all of these can also be used as targets of RSC-attaining compilers. In fact, some targets such as capability machines seem to be better suited to RSC than FAC, as we demonstrated.
Ahmed et al. prove full abstraction for several compilers between typed languages [10, 11, 50]. As compiler intermediate languages are often typed, and as these types often serve as the basis for complex static analyses, full abstraction seems like a reasonable goal for (fully typed) intermediate compilation steps. In the last few steps of compilation, where the target languages are unlikely to be typed, one could establish robust safety preservation and combine the two properties (vertically) to get an end-to-end security guarantee.
There are three other criteria for secure compilation that we would like to mention: securely compartmentalised compilation (SCC) [39], trace-preserving compilation (TPC) [60] and non-interference-preserving compilation (NIPC) [12, 15, 16, 27]. SCC is a re-statement of the “hard” part of full abstraction (the forward implication), but adapted to languages with undefined behaviour and a strict notion of components. Thus, SCC suffers from much of the same efficiency drawbacks as FAC. TPC is a stronger criterion than FAC, that most existing fully abstract compilers also attain. Again, compilers attaining TPC also suffer from the drawbacks of compilers attaining FAC.
NIPC preserves a single property: noninterference (NI). However, this line of work does not consider active target-level adversaries yet. Instead, the focus is on compiling whole programs. Since noninterference is not a safety property, it is difficult to compare NIPC to RSC directly. However, noninterference can also be approximated as a safety property [20]. So, in principle, RSC (with adequate massaging of observations) can be applied to stronger end-goals than NIPC.
Swamy et al. [67] embed an F\(^*\) model of a gradually and robustly typed variant of JavaScript into an F\(^*\) model of JavaScript. Gradual typing supports constructs similar to our endorsement construct in  . Their type-directed compiler is proven to attain memory isolation as well as static and dynamic memory safety. However, they do not consider general safety properties, nor a specific, general criterion for compiler security.
. Their type-directed compiler is proven to attain memory isolation as well as static and dynamic memory safety. However, they do not consider general safety properties, nor a specific, general criterion for compiler security.
Two of our target languages rely on capabilities for restricting access to sensitive locations from the context. Although capabilities are not mainstream in any processor, fully functional research prototypes such as Cheri exist [71]. Capability machines have previously been advocated as a target for efficient secure compilation [30] and preliminary work on compiling C-like languages to them exists, but the criterion applied is FAC [69].
7 Conclusion
This paper has examined robustly safe compilation (RSC), a soundness criterion for compilers with direct relevance to security. We have shown that the criterion is easily realizable and may lead to more efficient code than does fully abstract compilation wrt contextual equivalence. We have also presented two techniques for establishing that a compiler attains RSC. One is an adaptation of an existing technique, backtranslation, and the other is based on inductive invariants.
Notes
- 1.
Specifically, in this paper we use a
 font for
font for  elements, an
elements, an  font for
font for  elements and a
elements and a  font for elements common to both languages (to avoid repeating similar definitions twice). Thus,
font for elements common to both languages (to avoid repeating similar definitions twice). Thus,  is a source-level component,
is a source-level component,  is a target-level component and
is a target-level component and 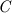 is generic notation for either a source-level or a target-level component.
is generic notation for either a source-level or a target-level component. - 2.
A callback is a call from the component to the context, so it generates label
 . A returnback is a return from such a callback, i.e., the context returning to the component, and it generates the label
. A returnback is a return from such a callback, i.e., the context returning to the component, and it generates the label  .
. - 3.
References
Abadi, M.: Secrecy by typing in security protocols. In: Abadi, M., Ito, T. (eds.) TACS 1997. LNCS, vol. 1281, pp. 611–638. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0014571
Abadi, M.: Protection in programming-language translations. In: Vitek, J., Jensen, C.D. (eds.) Secure Internet Programming. LNCS, vol. 1603, pp. 19–34. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48749-2_2
Abadi, M., Budiu, M., Erlingsson, Ú., Ligatti, J.: Control-flow integrity principles, implementations, and applications. ACM Trans. Inf. Syst. Secur. 13(1), 4:1–4:40 (2009)
Abadi, M., Fournet, C., Gonthier, G.: Authentication primitives and their compilation. In: Proceedings of the 27th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2000, pp. 302–315. ACM, New York (2000)
Abadi, M., Fournet, C., Gonthier, G.: Secure implementation of channel abstractions. Inf. Comput. 174, 37–83 (2002)
Abadi, M., Plotkin, G.D.: On protection by layout randomization. ACM Trans. Inf. Syst. Secur. 15, 8:1–8:29 (2012)
Abate, C., et al.: When good components go bad: formally secure compilation despite dynamic compromise. In: CCS 2018 (2018)
Abate, C., Blanco, R., Garg, D., Hriţcu, C., Patrignani, M., Thibault, J.: Journey beyond full abstraction: exploring robust property preservation for secure compilation. arXiv:1807.04603, July 2018
Agten, P., Strackx, R., Jacobs, B., Piessens, F.: Secure compilation to modern processors. In: 2012 IEEE 25th Computer Security Foundations Symposium, CSF 2012, pp. 171–185. IEEE (2012)
Ahmed, A., Blume, M.: Typed closure conversion preserves observational equivalence. In: Proceedings of the 13th ACM SIGPLAN International Conference on Functional Programming, ICFP 2008, pp. 157–168. ACM, New York (2008)
Ahmed, A., Blume, M.: An equivalence-preserving CPS translation via multi-language semantics. In: Proceedings of the 16th ACM SIGPLAN International Conference on Functional Programming, ICFP 2011, pp. 431–444. ACM, New York (2011)
Almeida, J.B., et al.: Jasmin: high-assurance and high-speed cryptography. In: ACM Conference on Computer and Communications Security, pp. 1807–1823. ACM (2017)
Alpern, B., Schneider, F.B.: Defining liveness. Inf. Process. Lett. 21(4), 181–185 (1985)
Backes, M., Hritcu, C., Maffei, M.: Union, intersection and refinement types and reasoning about type disjointness for secure protocol implementations. J. Comput. Secur. 22(2), 301–353 (2014)
Barthe, G., Grégoire, B., Laporte, V.: Secure compilation of side-channel countermeasures: the case of cryptographic “constant-time”. In: CSF 2018 (2018)
Barthe, G., Rezk, T., Basu, A.: Security types preserving compilation. Comput. Lang. Syst. Struct. 33, 35–59 (2007)
Bengtson, J., Bhargavan, K., Fournet, C., Gordon, A.D., Maffeis, S.: Refinement types for secure implementations. ACM Trans. Program. Lang. Syst. 33(2), 8:1–8:45 (2011)
Benton, N., Hur, C.-K.: Realizability and compositional compiler correctness for a polymorphic language. Technical report, MSR (2010)
Berry, G., Boudol, G.: The chemical abstract machine. Theor. Comput. Sci. 96(1), 217–248 (1992)
Boudol, G.: Secure information flow as a safety property. In: Degano, P., Guttman, J., Martinelli, F. (eds.) FAST 2008. LNCS, vol. 5491, pp. 20–34. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01465-9_2
Bowman, W.J., Ahmed, A.: Noninterference for free. In: Proceedings of the 20th ACM SIGPLAN International Conference on Functional Programming, ICFP 2015. ACM, New York (2015)
Bugliesi, M., Giunti, M.: Secure implementations of typed channel abstractions. In: Proceedings of the 34th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2007, pp. 251–262. ACM, New York (2007)
Carter, N.P., Keckler, S.W., Dally, W.J.: Hardware support for fast capability-based addressing. SIGPLAN Not. 29, 319–327 (1994)
Chong, S.: Expressive and enforceable information security policies. Ph.D. thesis, Cornell University, August 2008
Clarkson, M.R., Schneider, F.B.: Hyperproperties. J. Comput. Secur. 18(6), 1157–1210 (2010)
Corin, R., Deniélou, P.-M., Fournet, C., Bhargavan, K., Leifer, J.: A secure compiler for session abstractions. J. Comput. Secur. 16, 573–636 (2008)
Costanzo, D., Shao, Z., Gu, R.: End-to-end verification of information-flow security for C and assembly programs. In: PLDI, pp. 648–664. ACM (2016)
Devriese, D., Patrignani, M., Keuchel, S., Piessens, F.: Modular, fully-abstract compilation by approximate back-translation. Log. Methods Comput. Sci. 13(4) (2017). https://lmcs.episciences.org/4011
Devriese, D., Patrignani, M., Piessens, F.: Secure compilation by approximate back-translation. In: POPL 2016 (2016)
El-Korashy, A.: A formal model for capability machines - an illustrative case study towards secure compilation to CHERI. Master’s thesis, Universitat des Saarlandes (2016)
Fournet, C., Gordon, A.D., Maffeis, S.: A type discipline for authorization policies. ACM Trans. Program. Lang. Syst. 29(5), 141–156 (2007)
Fournet, C., Swamy, N., Chen, J., Dagand, P.-E., Strub, P.-Y., Livshits, B.: Fully abstract compilation to JavaScript. In: Proceedings of the 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2013, pp. 371–384. ACM, New York (2013)
Garg, D., Hritcu, C., Patrignani, M., Stronati, M., Swasey, D.: Robust hyperproperty preservation for secure compilation (extended abstract). ArXiv e-prints, October 2017
Gordon, A.D., Jeffrey, A.: Authenticity by typing for security protocols. J. Comput. Secur. 11(4), 451–519 (2003)
Gorla, D., Nestman, U.: Full abstraction for expressiveness: history, myths and facts. Math. Struct. Comput. Sci. 26(4), 639–654 (2016)
Hur, C.-K., Dreyer, D.: A Kripke logical relation between ML and assembly. SIGPLAN Not. 46, 133–146 (2011)
Jagadeesan, R., Pitcher, C., Rathke, J., Riely, J.: Local memory via layout randomization. In: Proceedings of the 2011 IEEE 24th Computer Security Foundations Symposium, CSF 2011, Washington, DC, USA, pp. 161–174. IEEE Computer Society (2011)
Jeffrey, A., Rathke, J.: Java JR: fully abstract trace semantics for a core Java language. In: Sagiv, M. (ed.) ESOP 2005. LNCS, vol. 3444, pp. 423–438. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31987-0_29
Juglaret, Y., Hriţcu, C., de Amorim, A.A., Pierce, B.C.: Beyond good and evil: formalizing the security guarantees of compartmentalizing compilation. In: 29th IEEE Symposium on Computer Security Foundations (CSF). IEEE Computer Society Press, July 2016. To appear
Kang, J., Kim, Y., Hur, C.-K., Dreyer, D., Vafeiadis, V.: Lightweight verification of separate compilation. In: POPL 2016, pp. 178–190 (2016)
Kuznetsov, V., Szekeres, L., Payer, M., Candea, G., Sekar, R., Song, D.: Code-pointer integrity. In: Proceedings of the 11th USENIX Conference on Operating Systems Design and Implementation, OSDI 2014, Berkeley, CA, USA, pp. 147–163. USENIX Association (2014)
Larmuseau, A., Patrignani, M., Clarke, D.: A secure compiler for ML modules. In: Feng, X., Park, S. (eds.) APLAS 2015. LNCS, vol. 9458, pp. 29–48. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26529-2_3
Leroy, X.: Formal certification of a compiler back-end or: programming a compiler with a proof assistant. In: POPL, pp. 42–54 (2006)
Leroy, X.: A formally verified compiler back-end. J. Autom. Reason. 43(4), 363–446 (2009)
Maffeis, S., Abadi, M., Fournet, C., Gordon, A.D.: Code-carrying authorization. In: Jajodia, S., Lopez, J. (eds.) ESORICS 2008. LNCS, vol. 5283, pp. 563–579. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-88313-5_36
McKeen, F., et al.: Innovative instructions and software model for isolated execution. In: HASP 2013, pp. 10:1–10:1. ACM (2013)
Morris Jr., J.H.: Protection in programming languages. Commun. ACM 16, 15–21 (1973)
Neis, G., Dreyer, D., Rossberg, A.: Non-parametric parametricity. SIGPLAN Not. 44(9), 135–148 (2009)
Neis, G., Hur, C.-K., Kaiser, J.-O., McLaughlin, C., Dreyer, D., Vafeiadis, V.: Pilsner: a compositionally verified compiler for a higher-order imperative language. In: Proceedings of the 20th ACM SIGPLAN International Conference on Functional Programming, ICFP 2015, pp. 166–178. ACM (2015)
New, M.S., Bowman, W.J., Ahmed, A.: Fully abstract compilation via universal embedding. In: Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, ICFP 2016, pp. 103–116. ACM, New York (2016)
Nielson, F., Nielson, H.R., Hankin, C.: Principles of Program Analysis. Springer, New York (1999). https://doi.org/10.1007/978-3-662-03811-6
Parrow, J.: General conditions for full abstraction. Math. Struct. Comput. Sci. 26(4), 655–657 (2014)
Patrignani, M., Agten, P., Strackx, R., Jacobs, B., Clarke, D., Piessens, F.: Secure compilation to protected module architectures. ACM Trans. Program. Lang. Syst. 37, 6:1–6:50 (2015)
Patrignani, M., Ahmed, A., Clarke, D.: Formal approaches to secure compilation a survey of fully abstract compilation and related work. ACM Comput. Surv. 51(6), 125:1–125:36 (2019)
Patrignani, M., Clarke, D.: Fully abstract trace semantics of low-level isolation mechanisms. In: Proceedings of the 29th Annual ACM Symposium on Applied Computing, SAC 2014, pp. 1562–1569. ACM (2014)
Patrignani, M., Clarke, D.: Fully abstract trace semantics for protected module architectures. Comput. Lang. Syst. Struct. 42(0), 22–45 (2015)
Patrignani, M., Clarke, D., Piessens, F.: Secure compilation of object-oriented components to protected module architectures. In: Shan, C. (ed.) APLAS 2013. LNCS, vol. 8301, pp. 176–191. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03542-0_13
Patrignani, M., Clarke, D., Sangiorgi, D.: Ownership types for the join calculus. In: Bruni, R., Dingel, J. (eds.) FMOODS/FORTE -2011. LNCS, vol. 6722, pp. 289–303. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21461-5_19
Patrignani, M., Devriese, D., Piessens, F.: On modular and fully abstract compilation. In: Proceedings of the 29th IEEE Computer Security Foundations Symposium, CSF 2016 (2016)
Patrignani, M., Garg, D.: Secure compilation and hyperproperties preservation. In: Proceedings of the 30th IEEE Computer Security Foundations Symposium, CSF 2017, Santa Barbara, USA (2017)
Patrignani, M., Garg, D.: Robustly safe compilation or, efficient, provably secure compilation. CoRR, abs/1804.00489 (2018)
Sabelfeld, A., Sands, D.: Declassification: dimensions and principles. J. Comput. Secur. 17(5), 517–548 (2009)
Schneider, F.B.: Enforceable security policies. ACM Trans. Inf. Syst. Secur. 3(1), 30–50 (2000)
Stark, I.: Names and higher-order functions. Ph.D. thesis, University of Cambridge, December 1994. Also available as Technical Report 363, University of Cambridge Computer Laboratory
Stewart, G., Beringer, L., Cuellar, S., Appel, A.W.: Compositional compcert. In: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, pp. 275–287. ACM, New York (2015)
Sumii, E., Pierce, B.C.: A bisimulation for dynamic sealing. In: Principles of Programming Languages, pp. 161–172 (2004)
Swamy, N., Fournet, C., Rastogi, A., Bhargavan, K., Chen, J., Strub, P.-Y., Bierman, G.: Gradual typing embedded securely in Javascript. SIGPLAN Not. 49(1), 425–437 (2014)
Swasey, D., Garg, D., Dreyer, D.: Robust and compositional verification of object capability patterns. In: Proceedings of the 2017 ACM SIGPLAN International Conference on Object-Oriented Programming, Systems, Languages, and Applications, OOPSLA 2017, 22–27 October 2017 (2017)
Tsampas, S., El-Korashy, A., Patrignani, M., Devriese, D., Garg, D., Piessens, F.: Towards automatic compartmentalization of C programs on capability machines. In: 2017 Workshop on Foundations of Computer Security, FCS 2017, 21 August 2017 (2017)
Volpano, D., Irvine, C., Smith, G.: A sound type system for secure flow analysis. J. Comput. Secur. 4, 167–187 (1996)
Woodruff, J., et al.: The CHERI capability model: revisiting RISC in an age of risk. In: Proceeding of the 41st Annual International Symposium on Computer Architecuture, ISCA 2014, Piscataway, NJ, USA, pp. 457–468. IEEE Press (2014)
Zdancewic, S.A.: Programming languages for information security. Ph.D. thesis, Cornell University (2002)
Acknowledgements
The authors would like to thank Dominique Devriese, Akram El-Korashy, Cătălin Hriţcu, Frank Piessens, David Swasey and the anonymous reviewers for useful feedback and discussions on an earlier draft.
This work was partially supported by the German Federal Ministry of Education and Research (BMBF) through funding for the CISPA-Stanford Center for Cybersecurity (FKZ: 13N1S0762).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Patrignani, M., Garg, D. (2019). Robustly Safe Compilation. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)






 and
and 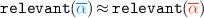

 to
to 
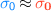 , and
, and 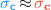 , and
, and and all
and all  with
with 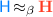 :
: iff
iff 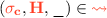 , and
, and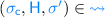 and
and  imply
imply  .
.

 to
to 
 and
and  ) can be partitioned into two parts, a trusted part and an untrusted part;
) can be partitioned into two parts, a trusted part and an untrusted part; contains only locations whose type is trusted (
contains only locations whose type is trusted ( );
); contains only locations related to
contains only locations related to 
 and these point to related values; more importantly, every
and these point to related values; more importantly, every 

 is protected by a capability;
is protected by a capability; , any capability protecting a trusted location does not occur in attacker code, nor is it stored in an untrusted heap location.
, any capability protecting a trusted location does not occur in attacker code, nor is it stored in an untrusted heap location. to
to 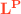
 font for
font for  elements, an
elements, an  font for
font for  elements and a
elements and a  font for elements common to both languages (to avoid repeating similar definitions twice). Thus,
font for elements common to both languages (to avoid repeating similar definitions twice). Thus,  is a source-level component,
is a source-level component,  is a target-level component and
is a target-level component and 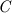 is generic notation for either a source-level or a target-level component.
is generic notation for either a source-level or a target-level component. . A returnback is a return from such a callback, i.e., the context returning to the component, and it generates the label
. A returnback is a return from such a callback, i.e., the context returning to the component, and it generates the label 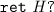 .
.