Abstract
A cornerstone of the theory of \(\lambda \)-calculus is that intersection types characterise termination properties. They are a flexible tool that can be adapted to various notions of termination, and that also induces adequate denotational models.
Since the seminal work of de Carvalho in 2007, it is known that multi types (i.e. non-idempotent intersection types) refine intersection types with quantitative information and a strong connection to linear logic. Typically, type derivations provide bounds for evaluation lengths, and minimal type derivations provide exact bounds.
De Carvalho studied call-by-name evaluation, and Kesner used his system to show the termination equivalence of call-by-need and call-by-name. De Carvalho’s system, however, cannot provide exact bounds on call-by-need evaluation lengths.
In this paper we develop a new multi type system for call-by-need. Our system produces exact bounds and induces a denotational model of call-by-need, providing the first tight quantitative semantics of call-by-need.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Duplications and erasures have always been considered as key phenomena in the \(\lambda \)-calculus—the \(\lambda I\)-calculus, where erasures are forbidden, is an example of this. The advent of linear logic [38] gave them a new, prominent logical status. Forbidding erasure and duplication enables single-use resources, i.e. linearity, but limits expressivity, as every computation terminates in linear time. Their controlled reintroduction via the non-linear modality  recovers the full expressive power of cut-elimination and allows a fine analysis of resource consumption. Duplication and erasure are therefore the key ingredients for logical expressivity, and—via Curry-Howard—for the expressivity of the \(\lambda \)-calculus. They are also essential to understand evaluation strategies.
recovers the full expressive power of cut-elimination and allows a fine analysis of resource consumption. Duplication and erasure are therefore the key ingredients for logical expressivity, and—via Curry-Howard—for the expressivity of the \(\lambda \)-calculus. They are also essential to understand evaluation strategies.
In a \(\lambda \)-term there can be many \(\beta \)-redexes, that is, places where \(\beta \)-reduction can be applied. In this sense, the \(\lambda \)-calculus is non-deterministic. Non-determinism does not affect the result of evaluation, if any, but it affects whether evaluation terminates, and in how many steps. There are two natural deterministic evaluation strategies, call-by-name (shortened to CbN) and call-by-value (CbV), which have dual behaviour with respect to duplication and erasure.
Call-by-Name = Silly Duplication + Wise Erasure. CbN never evaluates arguments of \(\beta \)-redexes before the redexes themselves. As a consequence, it never evaluates in subterms that will be erased. This is wise, and makes CbN a normalising strategy, that is, a strategy that reaches a result whenever one existsFootnote 1. A second consequence is that if the argument of the redex is duplicated then it may be evaluated more than once. This is silly, as it repeats work already done.
Call-by-Value = Wise Duplication + Silly Erasure. CbV, on the other hand, always evaluates arguments of \(\beta \)-redexes before the redexes themselves. Consequently, arguments are not re-evaluated—this is wise with respect to duplication—but they are also evaluated when they are going to be erased. For instance, on  , where \(\varOmega \) is the famous looping \(\lambda \)-term, CbV evaluation diverges (it keeps evaluating \(\varOmega \)) while CbN converges in one \(\beta \)-step (simply erasing \(\varOmega \)). This CbV treatment of erasure is clearly as silly as the duplicated work of CbN.
, where \(\varOmega \) is the famous looping \(\lambda \)-term, CbV evaluation diverges (it keeps evaluating \(\varOmega \)) while CbN converges in one \(\beta \)-step (simply erasing \(\varOmega \)). This CbV treatment of erasure is clearly as silly as the duplicated work of CbN.
Call-by-Need = Wise Duplication + Wise Erasure. It is natural to try to combine the advantages of both CbN and CbV. The strategy that is wise with respect to both duplications and erasures is usually called call-by-need (CbNeed), it was introduced by Wadsworth [57], and dates back to the ’70s. Despite being at the core of Haskell, one of the most-used functional programming languages, and—in its strong variant—being at work in the kernel of Coq as designed by Barras [16], the theory of CbNeed is much less developed than that of CbN or CbV.
One of the reasons for this is that it cannot be defined inside the \(\lambda \)-calculus without some hacking. Manageable presentations of CbNeed indeed require first-class sharing and micro-step operational semantics where variable occurrences are replaced one at a time (when needed), and not all at once as in the \(\lambda \)-calculus. Another reason is the less natural logical interpretation.
Linear Logic, Names, Values, and Needs. CbN and CbV have neat interpretations in linear logic. They correspond to two different representations of intuitionistic logic in linear logic, based on two different representations of implicationFootnote 2.
The logical interpretation of CbNeed—studied by Maraist et al. in [47]—is less neat than those of CbN and CbV. Within linear logic, CbNeed is usually understood as corresponding to the CbV representation where erasures are generalised to all terms, not only those under the scope of a  modality. So, it is seen as a sort of affine CbV. Such an interpretation however is unusual, because it does not match exactly with cut-elimination in linear logic, as for CbN and CbV.
modality. So, it is seen as a sort of affine CbV. Such an interpretation however is unusual, because it does not match exactly with cut-elimination in linear logic, as for CbN and CbV.
Call-by-Need, Abstractly. The main theorem of the theory of CbNeed is that it is termination equivalent to CbN, that is, on a fixed term, CbNeed evaluation terminates if and only if CbN evaluation terminates, and, moreover, they essentially produce the same result (up to some technical details that are irrelevant here). This is due to the fact that both strategies avoid silly divergent sequences such as that of \((\lambda x.\lambda y.y) \varOmega \). Termination equivalence is an abstract theorem stating that CbNeed erases as wisely as CbN. Curiously, in the literature there are no abstract theorems reflecting the dual fact that CbNeed duplicates as wisely as CbV—we provide one, as a side contribution of this paper.
Call-by-Need and Denotational Semantics. CbNeed is then usually considered as a CbV optimisation of CbN. In particular, every denotational model of CbN is also a model of CbNeed, and adequacy—that is the fact that the denotation of \(t\) is not degenerated if and only if \(t\) terminates—transfers from CbN to CbNeed.
Denotational semantics is invariant by evaluation, and so is insensitive to evaluation lengths by definition. It then seems that denotational semantics cannot distinguish between CbN and CbNeed. The aim of this paper is, somewhat counter-intuitively, to separate CbN and CbNeed semantically. We develop a type system whose type judgements induce a model—this is typical of intersection type systems—and whose type derivations provide exact bounds for CbNeed evaluation—this is usually obtained via non-idempotent intersection types. Unsurprisingly, the design of the type system requires a delicate mix of erasure and duplication and builds on the linear logic understanding of CbN and CbV.
Multi Types. Our typing framework is given by multi types, which is an alternative name for non-idempotent intersection typesFootnote 3. Multi types characterise termination properties exactly as intersection types, having moreover the advantages that they are closely related to (the relational semantics of) linear logic, their type derivations provide quantitative information about evaluation lengths, and the proof techniques are simpler—no need for the reducibility method.
The seminal work of de Carvalho [23] (appeared in 2007 but unpublished until 2018, see also [22]) showed how to use multi types to obtain exact bounds on evaluation lengths in CbN. Ehrhard adapted multi types to CbV [34], and very recently Accattoli and Guerrieri adapted de Carvalho’s study of exact bounds to Ehrhard’s system and CbV evaluation [8]. Kesner used de Carvalho’s CbN multi types to obtain a simple proof that CbNeed is termination equivalent to CbN [40] (first proved with other techniques by Maraist, Odersky, and Wadler [48] and Ariola and Felleisen [11] in the nineties), and then Kesner and coauthors continued exploring the theory of CbNeed via CbN multi types [14, 15, 42].
Kesner’s use of CbN multi types to study CbNeed is qualitative, as it deals with termination and not with exact bounds. For a quantitative study of CbNeed, de Carvalho’s CbN system cannot really be informative: CbN multi types provide bounds for CbNeed which cannot be exact because they already provide exact bounds for CbN, which generally takes more steps than CbNeed.
Multi Types by Need. In this paper we provide the first multi type system characterising CbNeed termination and whose minimal type derivations provide exact bounds for CbNeed evaluation lengths. The design of the type system is delicate, as we explain in Sect. 6. One of the key points is that, in contrast to Ehrhard’s system for CbV [34], multi types for CbNeed cannot be directly extracted by the relational semantics of linear logic, given that CbNeed does not have a clean representation in it. A by-product of our work is a new denotational semantics of CbNeed, the first one to precisely reflect its quantitative properties.
Beyond the result itself, the paper tries to stress how the key ingredients of our type system are taken from those for CbN and CbV and combined together. To this aim, we first present multi types for CbN and CbV, and only then we proceed to build the CbNeed system and prove its properties.
Along the way, we also prove the missing fundamental property of CbNeed, that is, that it duplicates as efficiently as CbV. The result dualizes the termination equivalence of CbN and CbNeed, which shows that CbNeed erases as wisely as CbN. Careful: the CbV system is correct but of course not complete with respect to CbNeed, because CbNeed may normalise when CbV diverges. The proof of the result is straightforward, because of our presentations of CbV and CbNeed. We adopt a liberal, non-deterministic formulation of CbV, and assuming (without loss of generality, see [1]) that garbage collection is always postponed. These two ingredients turn CbNeed into a fragment of CbV, obtaining the new fundamental result as a corollary of correctness of CbV multi types for CbV evaluation.
Technical Development. The paper is extremely uniform, technically speaking. The three evaluations are presented as strategies of Accattoli and Kesner’s Linear Substitution Calculus (shortened to LSC) [1, 6], a calculus with a simple but expressive form of explicit sharing. The LSC is strongly related to linear logic [2], and provides a neat and manageable presentation of CbNeed, introduced by Accattoli, Barenbaum, and Mazza in [3], and further developed by various authors in [4, 5, 10, 14, 15, 40, 42]. Our type systems count evaluation steps by annotating typing rules in the exact same way, and the proofs of correctness and completeness all follow the exact same structure. While the results for CbN are very minor variations with respect to those in the literature [7, 23], those for CbV are the first ones with respect to a presentation of CbV with sharing.
As it is standard for CbNeed, we restrict our study to closed terms and weak evaluation (that is, out of abstractions). The main consequence of this fact is that normal forms are particularly simple (sometimes called answers in the literature). Compared with other recent works dealing with exact bounds such as Accattoli, Graham-Lengrand, and Kesner [7] and Accattoli and Guerrieri [8] the main difference is that the size of normal forms is not taken into account by type derivations. This is because of the simple notions of normal forms in the closed and weak case, and not because the type systems are not accurate.
Related Work About CbNeed. Call-by-need was introduced by Wadsworth [57] in the ’70s. In the ’90s, it was first reformulated as operational semantics by Launchbury [46], Maraist, Odersky, and Wadler [48], and Ariola and Felleisen [11, 12], and then implemented by Sestoft [55] and further studied by Kutzner and Schmidt-Schauß [45]. More recent papers are Garcia, Lumsdaine, and Sabry [36], Ariola, Herbelin, and Saurin [13], Chang and Felleisen [26], Danvy and Zerny [29], Downen et al. [33], Pédrot and Saurin [53], and Balabonski et al. [14].
Related Work About Multi Types. Intersection types are a standard tool to study \(\lambda \)-calculi—see Coppo and Dezani [27, 28], Pottinger [54], and Krivine [44]. Non-idempotent intersection types, i.e. multi types, were first considered by Gardner [37], and then by Kfoury [43], Neergaard and Mairson [50], and de Carvalho [23]—a survey is Bucciarelli, Kesner, and Ventura [20].
Many recent works rely on multi types or relational semantics to study properties of programs and proofs. Beyond the cited ones, Diaz-Caro, Manzonetto, and Pagani [32], Carraro and Guerrieri [21], Ehrhard and Guerrieri [35], and Guerrieri [39] deal with CbV, while Bernadet and Lengrand [17], de Carvalho, Pagani, and Tortora de Falco [24] provide exact bounds. Further related work is by Bucciarelli, Ehrhard, and Manzonetto [18], de Carvalho and Tortora de Falco [25], Tsukada and Ong [56], Kesner and Vial [41], Piccolo, Paolini and Ronchi Della Rocca [52], Ong [51], Mazza, Pellissier, and Vial [49], Bucciarelli, Kesner and Ronchi Della Rocca [19]—this list is not exhaustive.
Proofs. Proofs are omitted. They can be found in the technical report [9].
2 Closed \(\lambda \)-Calculi
In this section we define the CbN, CbV, and CbNeed evaluation strategies. We present them in the context of the Accattoli and Kesner’s linear substitution calculus (LSC) [1, 6]. We mainly follow the uniform presentation of these strategies given by Accattoli, Barenbaum, and Mazza [3]. The only difference is that we adopt a non-deterministic presentation of CbV, subsuming both the left-to-right and the right-to-left strategies in [3], that makes our results slightly more general. Such a non-determinism is harmless: not only CbV evaluation is confluent, it even has the diamond property, so that all evaluations have the same length. Moreover, the non-deterministic presentation, together with the postponement of erasing steps discussed below, allows us to see CbNeed as a fragment of CbV, which shall provide a free proof that CbNeed duplicates as wisely as CbV.
Terms and Contexts. The set of terms \(\varLambda _{\mathtt{lsc}}\) of the LSC is given by the grammar below, where \(t[x{\leftarrow }s]\) is an explicit substitution (shortened to ES), that is a more compact notation for \(\mathtt{let}\ x=s\ \mathtt{in}\ t\) (intuitively, “\(t\) where \(x\) will be substituted by \(s\)”). Both \(\lambda x.t\) and \(t[x{\leftarrow }s]\) bind \(x\) in \(t\), with the usual notion of \(\alpha \)-equivalence.

The set \(\mathtt{fv}(t)\) of free variables of a term \(t\) is defined as expected, in particular,  . A term \(t\) is closed if \(\mathtt{fv}(t) = \emptyset \), open otherwise. As usual, terms are identified up to \(\alpha \)-equivalence.
. A term \(t\) is closed if \(\mathtt{fv}(t) = \emptyset \), open otherwise. As usual, terms are identified up to \(\alpha \)-equivalence.
Contexts are terms with exactly one occurrence of the hole \(\langle \cdot \rangle \), an additional constant. We shall use many different contexts. The most general ones are weak contexts \(W\) (i.e. not under abstractions). The (evaluation) contexts \(C\), \(V\) and \(E\)—used to define CbN, CbV and CbNeed evaluation strategies, respectively—are special cases of weak contexts (in fact, CbV contexts coincide with weak contexts, the consequences of that are discussed on p. 8). To define evaluation strategies, substitution contexts (i.e. lists of explicit substitutions) also play a role.

We write \(W\langle t\rangle \) for the term obtained by replacing the hole \(\langle \cdot \rangle \) in context \(W\) by the term \(t\). This plugging operation, as usual with contexts, can capture variables—for instance \(((\langle \cdot \rangle t)[x{\leftarrow }s])\langle x\rangle = (xt)[x{\leftarrow }s]\). We write \(W\langle \! \langle t \rangle \! \rangle \) when we want to stress that the context \(W\) does not capture the free variables of \(t\).
Micro-step Semantics. The rewriting rules decompose the usual small-step semantics for \(\lambda \)-calculi, by substituting linearly one variable occurrence at the time, and only when such an occurrence is in evaluation position. We emphasise this fact saying that we adopt a micro-step semantics. We now give the definitions, examples of evaluation sequences follow right next.
Formally, a micro-step semantics is defined by first giving its root-steps and then taking the closure of root-steps under suitable contexts.

where, in the root-step \(\mapsto _{\mathtt m}\) (resp. \(\mapsto _{{\mathtt e}_\mathrm{cbv}}\); \(\mapsto _{{\mathtt e}_\mathrm{need}}\)), if  for some \(n \in \mathbb {N}\), then \(\mathtt{fv}(s)\) (resp. \(\mathtt{fv}(V\langle \! \langle x \rangle \! \rangle )\); \(\mathtt{fv}(E\langle \! \langle x \rangle \! \rangle )\)) and \(\{y_1, \dots , y_n\}\) are disjoint. This condition can always be fulfilled by \(\alpha \)-equivalence.
for some \(n \in \mathbb {N}\), then \(\mathtt{fv}(s)\) (resp. \(\mathtt{fv}(V\langle \! \langle x \rangle \! \rangle )\); \(\mathtt{fv}(E\langle \! \langle x \rangle \! \rangle )\)) and \(\{y_1, \dots , y_n\}\) are disjoint. This condition can always be fulfilled by \(\alpha \)-equivalence.
The evaluation strategies \( \ {\xrightarrow {}}{}_{{\mathrm{cbn}}}^{} \) for CbN, \( \ {\xrightarrow {}}{}_{{\mathrm{cbv}}}^{} \) for CbV, and \( \ {\xrightarrow {}}{}_{{\mathrm{need}}}^{} \) for CbNeed, are defined as the closure of root-steps under CbN, CbV and CbNeed evaluation contexts, respectively (so, all evaluation strategies do not reduce under abstractions, since all such contexts are weak):

where the notation  means that, given a root-step \(\mapsto \), the evaluation \( \ {\xrightarrow {}}{}_{{}}^{} \) is defined as follows: \(t \ {\xrightarrow {}}{}_{{}}^{} s\) if and only if there are terms \(t'\) and \(s'\) and a context \(W\) such that \(t= W\langle t'\rangle \) and \(s= W\langle s'\rangle \) and \(t' \mapsto s'\).
means that, given a root-step \(\mapsto \), the evaluation \( \ {\xrightarrow {}}{}_{{}}^{} \) is defined as follows: \(t \ {\xrightarrow {}}{}_{{}}^{} s\) if and only if there are terms \(t'\) and \(s'\) and a context \(W\) such that \(t= W\langle t'\rangle \) and \(s= W\langle s'\rangle \) and \(t' \mapsto s'\).
Note that evaluations \( \ {\xrightarrow {}}{}_{{\mathrm{cbn}}}^{} \), \( \ {\xrightarrow {}}{}_{{\mathrm{cbv}}}^{} \) and \( \ {\xrightarrow {}}{}_{{\mathrm{need}}}^{} \) can equivalently be defined as \( \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} \cup \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbn}}}^{} \), \( \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} \cup \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbv}}}^{} \) and \( \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{need}}}^{} \cup \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{need}}}^{} \), respectively.
Given an evaluation sequence \(d:t \ {\xrightarrow {}}{}_{\mathrm{cbn}}^{*} s\) we note with \(|d|\) the length of \(d\), and with \(|d|_{{\mathtt m}}\) and \(|d|_{{\mathtt e}}\) the number of multiplicative and exponential steps in \(d\), respectively—and similarly for \( \ {\xrightarrow {}}{}_{{\mathrm{cbv}}}^{} \) and \( \ {\xrightarrow {}}{}_{{\mathrm{need}}}^{} \).
Erasing Steps. The reader may be surprised by our evaluation strategies, as none of them includes erasing steps, despite the absolute relevance of erasures pointed out in the introduction. There are no contradictions: in the LSC—in contrast to the \(\lambda \)-calculus—erasing steps can always be postponed (see [1]), and so they are often simply omitted. This is actually close to programming language practice, as the garbage collector acts asynchronously with respect to the evaluation flow. For the sake of clarity let us spell out the erasing rules—they shall nonetheless be ignored in the rest of the paper. In CbN and CbNeed every term is erasable, so the root erasing step takes the following form
and it is then closed by weak evaluation contexts.
In CbV only values are erasable; so, the root erasing step in CbV is:
and it is then closed by weak evaluation contexts.
Example 1
A good example to observe the differences between CbN, CbV, and CbNeed is given by the term  where
where  is the identity combinator. In CbN, it evaluates with 5 multiplicative steps and 5 exponential steps, as follows:
is the identity combinator. In CbN, it evaluates with 5 multiplicative steps and 5 exponential steps, as follows:

In CbV, \(t\) evaluates with 5 multiplicative steps and 5 exponential steps, for instance from right to left, as follows:

Note that the fact that CbN and CbV take the same number of steps is by chance, as they reduce different redexes: CbN never reduce the unneeded redex II associated to y, but it reduces twice the needed II redex associated to x, while CbV reduces both, but each one only once.
In CbNeed, \(t\) evaluates in 4 multiplicative steps and 4 exponential steps.

CbV Diamond Property. CbV contexts coincide with weak ones. As a consequence, our presentation of CbV is non-deterministic, as for instance one can have
but it is easily seen that diagrams can be closed in exactly one step (if the two reducts are different). For instance,
Moreover, the kind of steps is preserved, as the example illustrates. This is an instance of the strong form of confluence called diamond property. A consequence is that either all evaluation sequences normalise or all diverge, and if they normalise they have all the same length and the same number of steps of each kind. Roughly, the diamond property is a form of relaxed determinism. In particular, it makes sense to talk about the number of multiplicative/exponential steps to normal form, independently of the evaluation sequence. The proof of the property is an omitted routine check of diagrams.
Normal Forms. We use two predicates to characterise normal forms, one for both CbN and CbNeed normal forms, for which ES can contain whatever term, and one for CbV normal forms, where ES can only contain normal terms:

Proposition 1
(Syntactic characterization of closed normal forms). Let \(t\) be a closed term.
-
1.
CbN and CbNeed: For \(\mathsf {r}\in \{\mathrm{cbn}, \mathrm{need}\}\), \(t\) is \(\mathsf {r}\)-normal if and only if \(\mathsf{{normal}} ({t})\).
-
2.
CbV: \(t\) is \(\mathrm{cbv}\)-normal if and only if \({\mathsf{{normal}} _\mathrm{cbv}} ({t})\).
The simple structure of normal forms is the main point where the restriction to closed calculi plays a role in this paper.
From the syntactic characterization of normal forms (Proposition 1) it follows immediately that among closed terms, normal forms for CbN and CbNeed coincide, while normal forms for CbV are a subset of them. Such a subset is proper since the closed term \(I [x{\leftarrow }\delta \delta ]\) (where  and
and  ) is normal for CbN and CbNeed but not for CbV (and it cannot normalise in CbV).
) is normal for CbN and CbNeed but not for CbV (and it cannot normalise in CbV).
3 Preliminaries About Multi Types
In this section we define basic notions about multi types, type contexts, and (type) judgements that are shared by the three typing systems of the paper.
Multi-sets. The type systems are based on two layers of types, defined in a mutually recursive way, linear types \(L\) and finite multi-sets \(M\) of linear types. The intuition is that a linear type \(L\) corresponds to a single use of a term, and that an argument \(t\) is typed with a multi-set \(M\) of n linear types if it is going to end up (at most) n times in evaluation position, with respect to the strategy associated with the type system. The three systems differ on the definition of linear types, that is therefore not specified here, while all adopt the same notion of finite multi-set \(M\) of linear types (named multi type), that we now introduce:

where \([\ldots ]_{{}}\) denotes the multi-set constructor. The empty multi-set \([\,]\) (the multi type obtained for \(J = \emptyset \)) is called empty (multi) type and denoted by the special symbol \(\mathbf {0}\). An example of multi-set is \([L, L, {L'}]_{{}}\), that contains two occurrences of \(L\) and one occurrence of \({L'}\). Multi-set union is noted  .
.
Type Contexts. A type context  is a (total) map from variables to multi types such that only finitely many variables are not mapped to
is a (total) map from variables to multi types such that only finitely many variables are not mapped to  . The domain of
. The domain of  is the set
is the set  . The type context
. The type context  is empty if
is empty if  .
.
Multi-set union  is extended to type contexts point-wise, i.e.
is extended to type contexts point-wise, i.e.  for each variable \(x\). This notion is extended to a finite family of type contexts as expected, so that
for each variable \(x\). This notion is extended to a finite family of type contexts as expected, so that  denotes a finite union of type contexts—it stands for the empty context when \(J = \emptyset \). A type context
denotes a finite union of type contexts—it stands for the empty context when \(J = \emptyset \). A type context  is denoted by \(x_1 \,{:}\,M_1, \dots , x_n \,{:}\,M_n\) (for some \(n \in \mathbb {N}\)) if
is denoted by \(x_1 \,{:}\,M_1, \dots , x_n \,{:}\,M_n\) (for some \(n \in \mathbb {N}\)) if  and
and  for all \(1 \le i \le n\). Given two type contexts
for all \(1 \le i \le n\). Given two type contexts  and \(\varPi \) such that
and \(\varPi \) such that  , the type context
, the type context  is defined by
is defined by  if
if  ,
,  if \(x\in \mathtt{dom}({\varPi })\), and
if \(x\in \mathtt{dom}({\varPi })\), and  otherwise.
otherwise.
Judgements. Type judgements are of the form  or
or  (noted also \( {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{L}\) and \( {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{M}\), respectively, when
(noted also \( {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{L}\) and \( {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{M}\), respectively, when  is the empty context), where the indices \(m\) and \(e\) are natural numbers whose intended meaning is that \(t\) evaluates to normal form in \(m\) multiplicative steps and \(e\) exponential steps, with respect to the evaluation strategy associated with the type system.
is the empty context), where the indices \(m\) and \(e\) are natural numbers whose intended meaning is that \(t\) evaluates to normal form in \(m\) multiplicative steps and \(e\) exponential steps, with respect to the evaluation strategy associated with the type system.
To make clear in which type systems the judgement is derived, we write  if \(\varPhi \) is a derivation in the CbN system ending in the judgement
if \(\varPhi \) is a derivation in the CbN system ending in the judgement  , and similarly for CbV and CbNeed.
, and similarly for CbV and CbNeed.
4 Types by Name
In this section we introduce the CbN multi type system, together with intuitions about multi types. We also prove that derivations provide exact bounds on CbN evaluation sequences, and define the induced denotational model.
CbN Types. The system is essentially a reformulation of de Carvalho’s system \(\mathtt R\) [23], itself being a type-based presentation of the relational model of the CbN \(\lambda \)-calculus induced by relational model of linear logic via the CbN translation of \(\lambda \)-calculus into linear logic. Definitions:
-
CbN linear types are given by the following grammar:

Multi(-sets) types are defined as in Sect. 3, relatively to CbN linear types. Note the linear constant \(\mathsf{{normal}} \) (used to type abstractions, which are normal terms): it plays a crucial role in our quantitative analysis of CbN evaluation.
-
The CbN typing rules are in Fig. 1.
-
The \(\mathsf {many} \) rule: it has as many premises as the elements in the (possibly empty) set of indices J. When \(J = \emptyset \), the rule has no premises, and it types \(t\) with the empty multi type \(\mathbf {0}\). The \(\mathsf {many} \) rule is needed to derive the right premises of the rules \(\mathsf{app} \) and \(\mathsf{ES} \), that have a multi type \(M\) on their right-hand side. Essentially, it corresponds to the promotion rule of linear logic, that, in the CbN representation of the \(\lambda \)-calculus, is indeed used for typing the right subterm of applications and the content of explicit substitutions.
-
The size of a derivation
 is the sum \(m+ e\) of the indices. A quick look to the typing rules shows that indices on typing judgements are not needed, as \(m\) can be recovered as the number of \(\mathsf{app} \) rules, and \(e\) as the number of \(\mathsf {ax} \) rules. It is however handy to note them explicitly.
is the sum \(m+ e\) of the indices. A quick look to the typing rules shows that indices on typing judgements are not needed, as \(m\) can be recovered as the number of \(\mathsf{app} \) rules, and \(e\) as the number of \(\mathsf {ax} \) rules. It is however handy to note them explicitly.
Subtleties and Easy Facts. Let us overview some facts about our presentation of the type system.
-
1.
Introduction and destruction of multi-sets: multi-set are introduced on the right by the \(\mathsf {many} \) rule and on the left by \(\mathsf {ax} \). Moreover, on the left they are summed by \(\mathsf{app} \) and \(\mathsf{ES} \).
-
2.
Vacuous abstractions: the abstraction rule \(\mathsf{fun} \) can always abstract a variable \(x\); note that if \(M= \mathbf {0}\), then
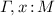 is equal to
is equal to  .
. -
3.
Relevance: No weakening is allowed in axioms. An easy induction on type derivations shows that
Lemma 1
(Type contexts and variable occurrences for CbN). Let  be a derivation. If \(x\not \in \mathtt{fv}(t)\) then
be a derivation. If \(x\not \in \mathtt{fv}(t)\) then  .
.
Lemma 1 implies that derivations of closed terms have empty type context. Note that there can be free variables of \(t\) not in  : the ones only occurring in subterms not touched by the evaluation strategy.
: the ones only occurring in subterms not touched by the evaluation strategy.
Key Ingredients. Two key points of the CbN system that play a role in the design of the CbNeed one in Sect. 6 are:
-
1.
Erasable terms and \(\mathbf {0}\): the empty multi type \(\mathbf {0}\) is the type of erasable terms. Indeed, abstractions that erase their argument—whose paradigmatic example is \(\lambda x.y\)—can only be typed with \(\mathbf {0} \multimap L\), because of Lemma 1. Note that in CbN every term—even diverging ones—can be typed with \(\mathbf {0}\) by rule \(\mathsf {many} \) (taking 0 premises), because, correctly, in CbN every term can be erased.
-
2.
Adequacy and linear types: all CbN typing rules but \(\mathsf {many} \) assign linear types. And \(\mathsf {many} \) is used only as right premise of the rules \(\mathsf{app} \) and \(\mathsf{ES} \), to derive \(M\). It is with respect to linear types, in fact, that the adequacy of the system is going to be proved: a term is CbN normalising if and only if it is typable with a linear type, given by Theorems 1 and 2 below.
Tight Derivations. A term may have several derivations, indexed by different pairs \((m, e)\). They always provide upper bounds on CbN evaluation lengths. The interesting aspect of our type systems, however, is that there is a simple description of a class of derivations that provide exact bounds for these quantities, as we shall show. Their definition relies on the \(\mathsf{{normal}} \) type constant.
Definition 1
(Tight derivations for CbN). A derivation  is tight (for CbN) if \(L= \mathsf{{normal}} \) and
is tight (for CbN) if \(L= \mathsf{{normal}} \) and  is empty.
is empty.
Example 2
Let us return to the term  used in Example 1 for explaining the difference in reduction lengths among the different strategies. We now give a derivation for it in the \(\text {CbN} \) type system.
used in Example 1 for explaining the difference in reduction lengths among the different strategies. We now give a derivation for it in the \(\text {CbN} \) type system.
First, let us shorten \(\mathsf{{normal}} \) to \(\mathsf {n}\). Then, we define \(\varPhi \) as the following derivation for the subterm \(\lambda x.{\lambda y.{xx}}\) of \(t\):

Now, we need two derivations for II, one of type \(\mathsf {n}\), given by \(\varPsi \) as follows

and one of type \([ \mathsf {n} ] \multimap \mathsf {n}\), given by \(\varXi \) as follows

Finally, we put \(\varPhi \), \(\varPsi \) and \(\varXi \) together in the following derivation \(\varTheta \) for \(t= (s(II)) (II)\), where  and
and 

Note that \(\varTheta \) is a tight derivation and the indices (5, 5) correspond to the number of \({\mathtt m}_\mathrm{cbn}\)-steps and \({\mathtt e}_\mathrm{cbn}\)-steps, respectively, from \(t\) to its \(\mathrm{cbn}\)-normal form, as shown in Example 1. Theorem 1 below shows that this is not by chance: tight derivations for CbN are minimal and provide exact bounds to evaluation lengths in CbN.
The next two subsections prove the two halves of the properties of the CbN type system, namely correctness and completeness.
4.1 CbN Correctness
Correctness is the fact that every typable term is CbN normalising. In our setting it comes with additional quantitative information: the indices \(m\) and \(e\) of a derivation  provide upper bounds on the length of the CbN evaluation of \(t\), that are exact when the derivation is tight.
provide upper bounds on the length of the CbN evaluation of \(t\), that are exact when the derivation is tight.
The proof technique is standard. Moreover, the correctness theorems for CbV and CbNeed in the next sections follow exactly the same structure. The proof relies on a quantitative subject reduction property showing that \(m\) decreases by exactly one at each \({\mathtt m}_\mathrm{cbn}\)-step, and similarly for \(e\) and \({\mathtt e}_\mathrm{cbn}\)-steps. In turn, subject reduction relies on a linear substitution lemma. Last, correctness for tight derivations requires a further property of normal forms.
Let us point out that correctness is stated with respect to closed terms only, but the auxiliary results have to deal with open terms, since they are proved by inductions (over predicates defined by induction) over the structure of terms.
Linear Substitution. The linear substitution lemma states that substituting over a variable occurrence as in the exponential rule consumes exactly one linear type and decreases of one the exponential index \(e\).
Lemma 2
(CbN linear substitution). If  then there is a splitting
then there is a splitting  such that for every derivation \(\varPsi \triangleright _{\mathrm{cbn}\!}\ {\varPi }\ {\pmb \vdash }_{}^{(m', e')} {t} \,{:}\,{{L'}}\) there is a derivation
such that for every derivation \(\varPsi \triangleright _{\mathrm{cbn}\!}\ {\varPi }\ {\pmb \vdash }_{}^{(m', e')} {t} \,{:}\,{{L'}}\) there is a derivation  .
.
The proof is by induction over CbN evaluation contexts.
Quantitative Subject Reduction. A key point of multi types is that the size of type derivations shrinks after every evaluation step, which is what allows to bound evaluation lengths. Remarkably, the size (defined as the sum of the indices) shrinks by exactly 1 at every evaluation step.
Proposition 2
(Quantitative subject reduction for CbN). Let  be a derivation.
be a derivation.
-
1.
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} s\) then \(m\ge 1\) and there exists a derivation
 .
. -
2.
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbn}}}^{} s\) then \(e\ge 1\) and there exists a derivation
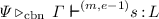 .
.
The proof is by induction on \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} s\) and \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbn}}}^{} s\), using the linear substitution lemma for the root exponential step.
Tightness and Normal Forms. Since the indices are always non-negative, quantitative subject reduction (Proposition 2) implies that they bound evaluation lengths. The bound is not necessarily exact, as derivations of normal forms can have strictly positive indices. If they are tight, however, they are indexed by (0, 0), as we now show. The proof of this fact (by induction on the predicate \(\mathsf{{normal}} \)) requires a slightly different statement, for the induction to go through.
Proposition 3
(\({\mathsf {normal}}\) typing of normal forms for CbN). Let \(t\) be such that \(\mathsf{{normal}} ({t})\), and  be a derivation. Then
be a derivation. Then  is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
The Tight Correctness Theorem. The theorem is then proved by a straightforward induction on the evaluation length relying on quantitative subject reduction (Proposition 2) for the inductive case, and the properties of tight typings for normal forms (Proposition 3) for the base case.
Theorem 1
(CbN tight correctness). Let \(t\) be a closed term. If \(\varPhi \triangleright _{\mathrm{cbn}\!}\ {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{L}\) then there is \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{cbn}}^{*} s\), with \(\mathsf{{normal}} ({s})\), \(|d|_{{\mathtt m}}\le m\) and \(|d|_{{\mathtt e}}\le e\). Moreover, if \(\varPhi \) is tight then \(|d|_{{\mathtt m}}= m\) and \(|d|_{{\mathtt e}}= e\).
Note that Theorem 1 implicitly states that tight derivations have minimal size among derivations.
4.2 CbN Completeness
Completeness is the fact that every CbN normalising term has a (tight) type derivation. As for correctness, the completeness theorem is always obtained via three intermediate steps, dual to those for correctness.
Normal Forms. The first step is to prove (by induction on the predicate \(\mathsf{{normal}} \)) that every normal form is typable, and is actually typable with a tight derivation.
Proposition 4
(Normal forms are tightly typable for CbN). Let \(t\) be such that \(\mathsf{{normal}} ({t})\). Then there is tight derivation \(\varPhi \triangleright _{\mathrm{cbn}\!}\ {}\ {\pmb \vdash }_{}^{(0, 0)} {t} \,{:}\,{\mathsf{{normal}}}\).
Linear Removal. In order to prove subject expansion, we have to first show that typability can also be pulled back along substitutions, via a linear removal lemma dual to the linear substitution lemma.
Lemma 3
(Linear removal for CbN). Let  , where \(x\notin \mathtt{fv}(s)\). Then there exist
, where \(x\notin \mathtt{fv}(s)\). Then there exist
-
a linear type \({L'}\) and two type contexts
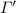 and \(\varPi \),
and \(\varPi \), -
a derivation
 , and
, and -
a derivation

such that
-
Type contexts:
 .
. -
Indices: \((m, e) = (m'+ m'', e'+ e''- 1)\).
Quantitative Subject Expansion. This property is the dual of subject reduction.
Proposition 5
(Quantitative subject expansion for CbN). Let  be a derivation.
be a derivation.
-
1.
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} s\) then there is a derivation
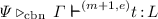 .
. -
2.
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbn}}}^{} \! s\) then there is a derivation
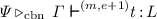 .
.
The proof is by induction on \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbn}}}^{} s\) and \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbn}}}^{} s\), using the linear removal lemma for the root exponential step.
The Tight Completeness Theorem. The theorem is proved by a straightforward induction on the evaluation length relying on quantitative subject expansion (Proposition 5) in the inductive case, and the existence of tight typings for normal forms (Proposition 4) in the base case.
Theorem 2
(CbN tight completeness). Let \(t\) be a closed term. If \(d:\!t\! \ {\xrightarrow {}}{}_{\mathrm{cbn}}^{*} s\) and \(\mathsf{{normal}} ({s})\) then there is a tight derivation \(\varPhi \triangleright _{\mathrm{cbn}\!\!\!\!}\ {}\ {\pmb \vdash }_{}^{(|d|_{{\mathtt m}}, |d|_{{\mathtt e}})} {t} \,{:}\,{\mathsf{{normal}}}\).
Back to Erasing Steps. Our system can be easily adapted to measure also garbage collection steps (the CbN erasing rule is just before Example 1). First, a new, third index g on judgements is necessary. Second, one needs to distinguish the erasing and non-erasing cases of the \(\mathsf{app} \) and \(\mathsf{ES} \) rules, discriminated by the \(\mathbf {0}\) type. For instance, the \(\mathsf{ES} \) rules are (the \(\mathsf{app} \) rules are similar):

The right premise of rule \(\mathsf{ES} _{\text {gc}} \) has been removed because the only way to introduce \(\mathbf {0}\) is via a \(\mathsf {many} \) rule with no premises. The index g bounds to the number of erasing steps. In the closed case, however, the bound cannot be, in general, exact. Variables typed with \(\mathbf {0}\) by  do not exactly match variables not appearing in the typed term (that is the condition triggering the erasing step), because a variable typed with \(\mathbf {0}\) may appear in the body of abstractions typed with the normal rule, as such bodies are not typed.
do not exactly match variables not appearing in the typed term (that is the condition triggering the erasing step), because a variable typed with \(\mathbf {0}\) may appear in the body of abstractions typed with the normal rule, as such bodies are not typed.
It is reasonable to assume that exact bounds for erasing steps can only by provided by a type system characterising strong evaluation, whose typing rules have to inspect abstraction bodies. These erasing typing rules are nonetheless going to play a role in the design of the CbNeed system in Sect. 6.
4.3 CbN Model
The idea to build the denotational model from the multi type system is that the interpretation (or semantics) of a term is simply the set of its type assignments, i.e. the set of its derivable types together with their type contexts. More precisely, let \(t\) be a term and \(x_1, \dots , x_n\) (with \(n \ge 0\)) be pairwise distinct variables. If \(\mathtt{fv}(t) \subseteq \{x_1, \dots , x_n\}\), we say that the list \(\vec {x} = (x_1, \dots , x_n)\) is suitable for \(t\). If \(\vec {x} = (x_1, \dots , x_n)\) is suitable for \(t\), the (relational) semantics of \(t\) for \(\vec {x}\) is

Subject reduction (Proposition 2) and expansion (Proposition 5) guarantee that the semantics \([\![t]\!]_{\vec {x}}^\text {CbN} \) of \(t\) (for any term \(t\), possibly open) is invariant by CbN evaluation. Correctness (Theorem 1) and completeness (Theorem 2) guarantee that, given a closed term \(t\), its interpretation \([\![t]\!]_{\vec {x}}^\text {CbN} \) is non-empty if and only if \(t\) is CbN normalisable, that is, they imply that relational semantics is adequate.
In fact, adequacy also holds with respect to open terms. The issue in that case is that the characterisation of tight derivations is more involved, see Accattoli, Graham-Lengrand and Kesner’s [7]. Said differently, weaker correctness and completeness theorems without exact bounds also hold in the open case. The same is true for the CbV and CbNeed systems of the next sections.
5 Types by Value
Here we introduce Ehrhard’s CbV multi type system [34] adapted to our presentation of CbV in the LSC, and prove its properties. The system is similar, and yet in many aspects dual, to the CbN one, in particular the grammar of types is different. Linear types for CbV are defined by:

Multi(-sets) types are defined as in Sect. 3, relatively to CbV linear types. Note that linear types now have a multi type both as source and as target, and that the \(\mathsf{{normal}} \) constant is absent—in CbV, its role is played by \(\mathbf {0}\).
The typing rules are in Fig. 2. It is a type-based presentation of the relational model of the CbV \(\lambda \)-calculus induced by relational model of linear logic via the CbV translation of \(\lambda \)-calculus into linear logic. Some remarks:
-
Right-hand types: all rules but \(\mathsf{fun} \) assign a multi type to the term on the right-hand side, and not a linear type as in CbN.
-
Abstractions and \(\mathsf {many} \): the \(\mathsf {many} \) rule has a restricted form with respect to the CbN one, it can only be applied to abstractions, that in turn are the only terms that can be typed with a linear type.
-
Indices: note as the indices are however incremented (on \(\mathsf {ax} \) and \(\mathsf{app} \)) and summed (in \(\mathsf {many} \) and \(\mathsf{ES} \)) exactly as in the CbN system.
Intuitions: The Empty Type \(\mathbf {0}\). The empty multi-set type \(\mathbf {0}\) plays a special role in CbV. As in CbN, it is the type of terms that can be erased, but, in contrast to CbN, not every term is erasable in CbV.
In the CbN multi type system every term, even a diverging one, is typable with \(\mathbf {0}\). On the one hand, this is correct, because in CbN every term can be erased, and erased terms can also be divergent, because they are never evaluated. On the other hand, adequacy is formulated with respect to non-empty types: a term terminates if and only if it is typable with a non-empty type.
In CbV, instead, terms have to be evaluated before being erased; and, of course, their evaluation has to terminate. Thus, terminating terms and erasable terms coincide. Since the multi type system is meant to characterise terminating terms, in CbV a term is typable if and only if it is typable with \(\mathbf {0}\), as we shall prove in this section. Then the empty type is not a degenerate type excluded for adequacy from the interesting types of a term, as in CbN, it rather is the type, characterising (adequate) typability altogether. And this is also the reason for the absence of the constant \(\mathsf{{normal}} \)—one way to see it is that in CbV \(\mathsf{{normal}} = \mathbf {0}\).
Note that, in particular, in a type judgement  the type context
the type context  may give the empty type to a variable \(x\) occurring in \(t\), as for instance in the axiom \(x\,{:}\,\mathbf {0}\vdash x\,{:}\,\mathbf {0}\)—this may seem very strange to people familiar with CbN multi types. We hope that instead, according to the provided intuition that \(\mathbf {0}\) is the type of termination, it would rather seem natural.
may give the empty type to a variable \(x\) occurring in \(t\), as for instance in the axiom \(x\,{:}\,\mathbf {0}\vdash x\,{:}\,\mathbf {0}\)—this may seem very strange to people familiar with CbN multi types. We hope that instead, according to the provided intuition that \(\mathbf {0}\) is the type of termination, it would rather seem natural.
Definition 2
(Tight derivation for CbV). A derivation  is tight (for CbV) if \(M= \mathbf {0}\) and
is tight (for CbV) if \(M= \mathbf {0}\) and  is empty.
is empty.
Example 3
Let’s consider again the term  of Example 1 (where
of Example 1 (where  ), for which a \(\text {CbN} \) tight derivation was given in Example 2, and let us type it in the \(\text {CbV} \) system with a tight derivation.
), for which a \(\text {CbN} \) tight derivation was given in Example 2, and let us type it in the \(\text {CbV} \) system with a tight derivation.
We define the following derivation \(\varPhi _{1}\) for the subterm  of \(t\)
of \(t\)

Note that  , which explains the shape of the type context in the conclusion of the \(\mathsf{app} \) rule. Next, we define the derivation \(\varPhi _{2}\) as follows
, which explains the shape of the type context in the conclusion of the \(\mathsf{app} \) rule. Next, we define the derivation \(\varPhi _{2}\) as follows

and the derivation \(\varPhi _{3}\) as follows

Finally, we put \(\varPhi _{1}\), \(\varPhi _{2}\) and \(\varPhi _{3}\) together in the following derivation \(\varPhi \) for \(t\)

Note that \(\varPhi \) is a tight derivation and the indices (5, 5) correspond to the number of \({\mathtt m}_\mathrm{cbv}\)-steps and \({\mathtt e}_\mathrm{cbv}\)-steps, respectively, from \(t\) to its \(\mathrm{cbv}\)-normal form, as shown in Example 1. Theorem 3 below shows that this is not by chance: tight derivations for CbV are minimal and provide exact bounds to evaluation lengths in \(\text {CbV} \).
Correctness (i.e. typability implies normalisability) and completeness (i.e. normalisability implies typability) of the CbV type system with respect to CbV evaluation (together with quantitative information about evaluation lengths) follow exactly the same pattern of the CbN case, mutatis mutandis.
5.1 CbV Correctness
Lemma 4
(CbV linear substitution). Let  and \(v\) be a value. There is a splitting
and \(v\) be a value. There is a splitting  such that, for any derivation
such that, for any derivation  , there is a derivation
, there is a derivation  .
.
Proposition 6
(Quantitative subject reduction for CbV). Let  be a derivation.
be a derivation.
-
1.
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbv}}}^{} t'\) then \(m\ge 1\) and there exists a derivation
 .
. -
2.
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbv}}}^{} t'\) then \(e\ge 1\) and there exists a derivation
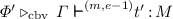 .
.
Proposition 7
(Tight typings for normal forms for CbV). Let  be a derivation, with \({\mathsf{{normal}} _\mathrm{cbv}} ({t})\). Then
be a derivation, with \({\mathsf{{normal}} _\mathrm{cbv}} ({t})\). Then  is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
Theorem 3
(CbV tight correctness). Let \(t\) be a closed term. If  then there is \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{cbv}}^{*} s\), with \({\mathsf{{normal}} _\mathrm{cbv}} ({s})\), \(|d|_{{\mathtt m}}\le m\) and \(|d|_{{\mathtt e}}\le e\). Moreover, if \(\varPhi \) is tight then \(|d|_{{\mathtt m}}= m\) and \(|d|_{{\mathtt e}}= e\).
then there is \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{cbv}}^{*} s\), with \({\mathsf{{normal}} _\mathrm{cbv}} ({s})\), \(|d|_{{\mathtt m}}\le m\) and \(|d|_{{\mathtt e}}\le e\). Moreover, if \(\varPhi \) is tight then \(|d|_{{\mathtt m}}= m\) and \(|d|_{{\mathtt e}}= e\).
5.2 CbV Completeness
Proposition 8
(Normal forms are tightly typable for CbV). Let \(t\) be such that \({\mathsf{{normal}} _\mathrm{cbv}} ({t})\). Then there exists a tight derivation \(\varPhi \triangleright _{\mathrm{cbv}\!}\ {}\ {\pmb \vdash }_{}^{(0, 0)} {t} \,{:}\,{\mathbf {0}}\).
Lemma 5
(Linear removal for CbV). Let  and \(v\) be a value, where \(x\notin \mathtt{fv}(v)\). Then, there exist
and \(v\) be a value, where \(x\notin \mathtt{fv}(v)\). Then, there exist
-
a multi type \(M'\) and two type contexts
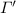 and \(\varPi \),
and \(\varPi \), -
a derivation
 and
and -
a derivation
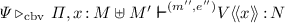
such that
-
Type contexts:
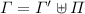 ,
, -
Indices: \((m, e) = (m'+ m'', e'+ e''- 1)\).
Proposition 9
(Quantitative subject expansion for CbV). Let  be a derivation.
be a derivation.
-
1.
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{cbv}}}^{} t'\) then there is a derivation
 .
. -
2.
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{cbv}}}^{} t'\) then there is a derivation
 .
.
Theorem 4
(CbV tight completeness). Let \(t\) be a closed term. If \(d:\! t \ {\xrightarrow {}}{}_{\mathrm{cbv}}^{*} \! s\) with \({\mathsf{{normal}} _\mathrm{cbv}} ({s})\), then there is a tight derivation \(\varPhi \triangleright _{\mathrm{cbv}\!}\ {}\ {\pmb \vdash }_{}^{(|d|_{{\mathtt m}}, |d|_{{\mathtt e}})} {t} \,{:}\,{\mathbf {0}}\).
CbV Model. The interpretation of terms with respect to the CbV system is defined as follows (where \(\vec {x} = (x_1, \dots , x_n)\) is a list of variables suitable for \(t\)):

Note that rule \(\mathsf{fun} \) assigns a linear type but the interpretation considers only multi types. The invariance and the adequacy of \([\![t]\!]_{\vec {x}}^\text {CbV} \) with respect to CbV evaluation are obtained exactly as for the CbN case.
6 Types by Need
CbNeed as a Blend of CbN and CbV. The multi type system for CbNeed is obtained by carefully blending ingredients from the CbN and CbV ones:
-
Wise erasures from CbN: in CbN wise erasures are induced by the fact that the empty multi type \(\mathbf {0}\) (the type of erasable terms) and the linear type \(\mathsf{{normal}} \) (the type of normalisable terms) are distinct and every term is typable with \(\mathbf {0}\) by using the \(\mathsf {many} \) rule with 0 premises. Adequacy is then formulated with respect to (non-empty) linear types.
-
Wise duplications from CbV: in CbV wise duplications are due to two aspects. First, only abstractions can be collected in multi-sets by rule \(\mathsf {many} \). This fact accounts for the evaluation of arguments to normal form—that is, abstractions—before being substituted. Second, terms are typed with multi types instead of linear types. Roughly, this second fact allows the first one to actually work because the argument is reduced once for a whole multi set of types, and not once for each element of the multi set, as in CbN.
It seems then that a type system for CbNeed can easily be obtained by basically adopting the CbV system plus
-
separating \(\mathbf {0}\) and \(\mathsf{{normal}} \), that is, adding \(\mathsf{{normal}} \) to the system;
-
modifying the \(\mathsf {many} \) rule by distinguishing two cases: with 0 premises it can assign \(\mathbf {0}\) to whatever term—as in CbN—otherwise it is forced to work on abstractions, as in CbV;
-
restricting adequacy to non-empty types.
Therefore, the grammar of linear types is:

Multi(-sets) types are defined as in Sect. 3, relatively to CbNeed linear types. The rules of this naïve system for CbNeed are in Fig. 3.
Issue with the Naïve System. Unfortunately, the naïve system does not work: tight derivations—defined as expected: empty type context and the term typed with \([ \mathsf{{normal}} ] \)—do not provide exact bounds. The problem is that the naïve blend of ingredients allows derivations of \(\mathbf {0}\) with strictly positive indices \(m\) and \(e\). Instead, derivations of \(\mathbf {0}\) should always have 0 in both indices—as is the case when they are derived with a \(\mathsf {many} _0\) rule with 0 premises—because they correspond to terms to be erased, that are not evaluated in CbNeed. For any term \(t\), indeed, one can for instance derive the following derivation \(\varPhi \):

Note that introducing \({} \vdash ^{(0,1)} x \,{:}\,\mathbf {0}\) with rule \(\mathsf {ax} \) rather than via \(\mathsf {many} _0\) (the typing context \(x\,{:}\,\mathbf {0}\) is equivalent to the empty type context) would give a derivation with final judgement \({} \vdash ^{(1,1)} (\lambda x.{x}) t \,{:}\,\mathbf {0}\)—thus, the system messes up both indices.
Such bad derivations of \(\mathbf {0}\) are not a problem per se, because in CbNeed one expects correctness and completeness to hold only for derivations of non-empty multi types. However, they do mess up also derivations of non-empty multi types because they can still appear inside tight derivations, as sub-derivations of sub-terms to be erased; consider for instance:

The term normalises in just 1 \({\mathtt m}_\mathrm{need}\)-step to \(I [y{\leftarrow }(\lambda x.{x}) t]\) but the multiplicative index of the derivation is 2. The mismatch is due to a bad derivation of \(\mathbf {0}\) used as right premise of an \(\mathsf{app} \) rule. Similarly, the induced typing of \(I [y{\leftarrow }(\lambda x.{x}) t]\) is an example of a bad derivation used as right premise of a rule \(\mathsf{ES} \):

The Actual Type System. Our solution to such an issue is to modify the system as to avoid derivations of \(\mathbf {0}\) to appear as right premises of rules \(\mathsf{app} \) and \(\mathsf{ES} \). We follow the schema of the rules for counting erasing steps given right after Theorem 2.
Therefore, we add two dedicated rules \(\mathsf{app} _{\text {gc}} \) and \(\mathsf{ES} _{\text {gc}} \), and constrain the right premise of rules \(\mathsf{app} \) and \(\mathsf{ES} \) to have a non-empty type. The system is in Fig. 4 and it is based on the same grammar of types of the naïve system. Note that rules \(\mathsf {many} \) and \(\mathsf {ax} \) can still introduce \(\mathbf {0}\). These \(\mathbf {0}\)s, however, can no longer mess up the indices of tight derivations, as we are going to show.
Note that the indices \(m\) and \(e\) are incremented and summed exactly as in the CbN and CbV type systems.
Definition 3
(Tight derivations for CbNeed). A derivation  is tight (for CbNeed) if \(M= [\mathsf{{normal}} ]\) and
is tight (for CbNeed) if \(M= [\mathsf{{normal}} ]\) and  is empty.
is empty.
Example 4
We return to the term  used in Example 1 and we give it a tight derivation in the \(\text {CbNeed} \) type system.
used in Example 1 and we give it a tight derivation in the \(\text {CbNeed} \) type system.
Again, we shorten \(\mathsf{{normal}} \) to \(\mathsf {n}\). Then, we define \(\varPsi \) as follows

and, shortening \([ \mathsf {n} ] \multimap [ \mathsf {n} ] \) to \([ \mathsf {n} ] ^{[ \mathsf {n} ] }\), we define \(\varTheta \) as follows

Finally, we put \(\varPsi \) and \(\varTheta \) together in the following derivation \(\varPhi \) for \(t\)

Note that the indices (4, 4) correspond exactly to the number of \({\mathtt m}_\mathrm{need}\)-steps and \({\mathtt e}_\mathrm{need}\)-steps, respectively, from \(t\) to its \(\mathrm{need}\)-normal form—as shown in Example 1—and that \(\varPhi \) is a tight derivation. Forthcoming Theorem 5 shows once again that this is not by chance: tight derivations for CbNeed are minimal and provides exact bounds to evaluation lengths in \(\text {CbNeed} \).
Remarkably, the technical development to prove correctness and completeness of the CbNeed type system with respect to CbNeed evaluation follows smoothly along the same lines of the two other systems, mutatis mutandis.
6.1 CbNeed Correctness
Lemma 6
(CbNeed linear substitution). Let  and \(v\) be a value. There is a splitting
and \(v\) be a value. There is a splitting  such that for any derivation \(\varPsi \triangleright _{\mathrm{need}\!}\ {\varPi } \vdash ^{(m', e')} v \,{:}\,O\) there exists
such that for any derivation \(\varPsi \triangleright _{\mathrm{need}\!}\ {\varPi } \vdash ^{(m', e')} v \,{:}\,O\) there exists  .
.
Proposition 10
(Quantitative subject reduction for CbNeed). Let  be a derivation such that
be a derivation such that  .
.
-
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{need}}}^{} s\) then \(m\ge 1\) and there is a derivation
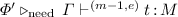 .
. -
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{need}}}^{} s\) then \(e\ge 1\) and there exists a derivation
 .
.
Note the condition \(M\ne \mathbf {0}\) in the statement of subject reduction, that is in contrast to the CbV system but akin to the CbN one. It is due to the way multi types are used as arguments, via rules \(\mathsf{ES} _{\text {gc}} \) and \(\mathsf{app} _{\text {gc}} \). The restriction is necessary: the CbNeed type system derives \({} \vdash ^{(0,1)} x[x{\leftarrow }\delta \delta ] \,{:}\,\mathbf {0}\), but \(x[x{\leftarrow }\delta \delta ]\) is not normalising for CbNeed evaluation. And it is expected, as it amounts to the fact that adequacy holds only with respect to non-empty types, as for CbN, and as stressed when introducing the CbNeed type system. The same restriction appears in Theorem 5, Proposition 13 and Theorem 6 below, for the same reason.
Proposition 11
(\([ \mathsf{{normal}} ] \) typings for normal forms for CbNeed). Let  be a derivation, with \(\mathsf{{normal}} ({t})\). Then
be a derivation, with \(\mathsf{{normal}} ({t})\). Then  is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
is empty, and so \(\varPhi \) is tight, and \(m= e= 0\).
Theorem 5
(CbNeed tight correctness). Let \(t\) be a closed term. If \(\varPhi \triangleright _{\mathrm{need}\!}\ {} \vdash ^{(m, e)} t \,{:}\,M\) where \(M\ne \mathbf {0}\), then there is \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\), with \(\mathsf{{normal}} ({s})\), \(|d|_{{\mathtt m}} \le m\) and \(|d|_{{\mathtt e}} \le e\). Moreover, if \(\varPhi \) is tight then \(|d|_{{\mathtt m}} = m\) and \(|d|_{{\mathtt e}} = e\).
6.2 CbNeed Completeness
Proposition 12
(Normal forms are tightly typable for CbNeed). Let \(t\) be such that \(\mathsf{{normal}} ({t})\). Then there is a tight derivation \(\varPhi \triangleright _{\mathrm{need}\!}\ {} \vdash ^{(0,0)} t \,{:}\,[ \mathsf{{normal}} ] \).
Lemma 7
(Linear removal for CbNeed). Let  be a derivation and \(v\) be a value, with \(x\notin \mathtt{fv}(v)\). Then there exist
be a derivation and \(v\) be a value, with \(x\notin \mathtt{fv}(v)\). Then there exist
-
a multi type \(M'\) and two type contexts
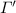 and \(\varPi \),
and \(\varPi \), -
a derivation
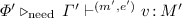 , and
, and -
a derivation
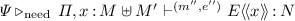
such that
-
Type contexts:
 .
. -
Indices: \((m, e) = (m'+ m'', e'+ e''- 1)\).
Proposition 13
(Quantitative subject expansion for CbNeed). Let  be a derivation such that
be a derivation such that  . Then,
. Then,
-
Multiplicative: if \(t \ {\xrightarrow {}}{}_{{{\mathtt m}_\mathrm{need}}}^{} s\) then there is a derivation
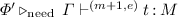 ,
, -
Exponential: if \(t \ {\xrightarrow {}}{}_{{{\mathtt e}_\mathrm{need}}}^{} s\) then there is a derivation
 .
.
Theorem 6
(CbNeed tight completeness). Let \(t\) be a closed term. If \(d:t \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\) and \(\mathsf{{normal}} ({s})\) then there exists a tight derivation \(\varPhi \triangleright _{\mathrm{need}\!}\ {} \vdash ^{(|d|_{{\mathtt m}},|d|_{{\mathtt e}})} t \,{:}\,[ \mathsf{{normal}} ] \).
CbNeed Model. The interpretation \([\![t]\!]_{\vec {x}}^\text {CbNeed} \) with respect to the CbNeed system is defined as the set (where \(\vec {x} = (x_1, \dots , x_n)\) is a list of variables suitable for \(t\)):
Note that the right multi type is required to be non-empty. The invariance and the adequacy of \([\![t]\!]_{\vec {x}}^\text {CbNeed} \) with respect to CbNeed evaluation are obtained exactly as for the CbN and CbV cases.
7 A New Fundamental Theorem for Call-by-Need
CbNeed Erases Wisely. In the literature, the theorem about CbNeed is the fact that it is operationally equivalent to CbN. This result was first proven independently by two groups, Maraist, Odersky, and Wadler [48], and Ariola and Felleisen [11], in the nineties, using heavy rewriting techniques.
Recently, Kesner gave a much simpler proof via CbN multi types [40]. She uses multi types to first show termination equivalence of CbN and CbNeed, from which she then infers operational equivalence. Termination equivalence means that a given term terminates in CbN if and only if terminates in CbNeed, and it is a consequence of our slogan that CbN and CbNeed both erase wisely.
With our terminology and notations, Kesner’s result takes the following form.
Theorem 7
(Kesner [40]). Let \(t\) be a closed term.
-
1.
Correctness: if \(\varPhi \triangleright _{\mathrm{cbn}\!}\ {}\ {\pmb \vdash }_{}^{(m, e)} {t} \,{:}\,{L}\) then there exists \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\), \(\mathsf{{normal}} ({s})\), \(|d|_{{\mathtt m}}\le m\) and \(|d|_{{\mathtt e}}\le e\).
-
2.
Completeness: if \(d:\! t\! \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\) and \(\mathsf{{normal}} ({s})\) then there is \(\varPhi \triangleright _{\mathrm{cbn}\!\!}\ {}\ {\pmb \vdash }_{}^{(m, e)} {t\!} \,{:}\,{\!\mathsf{{normal}}}\).
Note that, with respect to the other similar theorems in this paper, the result does not cover tight derivations and it does not provide exact bounds. In fact, the CbN system cannot provide exact bounds for CbNeed, because it does provide them for CbN evaluation, that in general is slower than CbNeed. Consider for instance the term \(t\) in Example 1 and its CbN tight derivation in Example 2: the derivation provides indices (5, 5) for \(t\) (and so \(t\) evaluates in 10 CbN steps), but \(t\) evaluates in 8 CbNeed steps. Closing such a gap is the main motivation behind this paper, achieved by the CbNeed multi type system in Sect. 6.
CbNeed Duplicates Wisely. Curiously, in the literature there are no dual results showing that CbNeed duplicates as wisely as CbV. One of the reasons is that it is a theorem that does not admit a simple formulation such as operational or termination equivalence, because CbNeed and CbV are not in such relationships. Morally, this is subsumed by the logical interpretation according to which CbNeed corresponds to an affine variant of the linear logic representation of CbV. Yet, it would be nice to have a precise, formal statement establishing that CbNeed duplicates as wisely as CbV—we provide it here.
Our result is that the CbV multi type system is correct with respect to CbNeed evaluation. In particular, the indices \((m, e)\) provided by a CbV type derivation provide bounds for CbNeed evaluation lengths. Two important remarks before we proceed with the formal statement:
-
Bounds are not exact: the indices of a CbV derivation do not generally provide exacts bounds for CbNeed, not even in the case of tight derivations. The reason is that CbNeed does not evaluate unneeded subterms (i.e. those typed with \(\mathbf {0}\)), while CbV does. Consider again the term \(t\) of Example 1, for instance, whose CbV tight derivation has indices (5, 5) (and so \(t\) evaluates in 10 CbV steps) but it CbNeed evaluates in 8 steps.
-
Completeness cannot hold: we prove correctness but not completeness simply because the CbV system is not complete with respect to CbNeed evaluation. Consider for instance \((\lambda x.I) \varOmega \): it is CbV untypable by Theorem 4, because it is CbV divergent, and yet it is CbNeed normalisable.
CbV Correctness with Respect to CbNeed. Pleasantly, our presentations of CbV and CbNeed make the proof of the result straightforward. It is enough to observe that, since we do not consider garbage collection and we adopt a non-deterministic formulation of CbV, CbNeed is a subsystem of CbV. Formally, if \(t \ {\xrightarrow {}}{}_{{\mathrm{need}}}^{} s\) then \(t \ {\xrightarrow {}}{}_{{\mathrm{cbv}}}^{} s\), as it is easily seen from the definitions (CbNeed reduces only some subterms of applications and ES, while CbV reduces all such subterms). The result is then a corollary of the correctness theorem for CbV.
Corollary 1
(CbV correctness w.r.t. CbNeed). Let \(t\) be a closed term and \(\varPhi \triangleright _{\mathrm{cbv}}\ {}\ {\pmb \vdash }_{}^{(m,e)} {t} \,{:}\,{M}\) be a derivation. Then there exists \(s\) such that \(d:t \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\) and \(\mathsf{{normal}} ({s})\), with \(|d|_{{\mathtt m}} \le m\) and \(|d|_{{\mathtt e}} \le e\).
Since the CbNeed system provides exact bounds (Theorem 5), we obtain that CbNeed duplicates as wisely as CbV, when the comparison makes sense, that is, on CbV normalisable terms.
Corollary 2
(CbNeed duplicates as wisely as CbV). Let \(d:t \ {\xrightarrow {}}{}_{\mathrm{cbv}}^{*} u\) with \({\mathsf{{normal}} _\mathrm{cbv}} ({u})\). Then there is \(d':t \ {\xrightarrow {}}{}_{\mathrm{need}}^{*} s\) with \(\mathsf{{normal}} ({s})\) and \(|d'|_{{\mathtt m}} \le |d|_{{\mathtt m}}\) and \(|d'|_{{\mathtt e}} \le |d|_{{\mathtt e}}\).
8 Conclusions
Contributions. This paper introduces a multi type system for CbNeed evaluation, carefully blending ingredients from multi type systems for CbN and CbV evaluation in the literature. Notably, it is the first type system whose minimal derivations—explicitly characterised—provide exact bounds for evaluation lengths. It also characterises CbNeed termination, and thus its judgements provide an adequate relational semantics.
The technical development is simple, and uniform with respect to those of CbN and CbV multi type systems. The typing rules count evaluation steps following exactly the same schema of the CbN and CbV rules. The proofs of correctness and completeness also follow exactly the same structure.
A further side contribution of the paper is a new fundamental result of CbNeed, formally stating that it duplicates as wisely as CbV. More precisely, the CbV multi type system is (quantitatively) correct with respect to CbNeed evaluation. Pleasantly, our presentations of CbV and CbNeed provide the result for free. This result dualizes the other fundamental theorem stating that CbNeed erases as wisely as CbN, usually formulated as termination equivalence, and recently re-proved by Kesner using CbN multi types [40].
Future Work. Recently, Barenbaum et al. extended CbNeed to strong evaluation [14], and it is natural to try to extend our type system as well. The definition of the system, in particular the extension of tight derivations to that setting, seems however far from being evident. Barembaum, Bonelli, and Mohamed also apply CbN multi types to a CbNeed calculus extended with pattern matching and fixpoints [15], that might be interesting to refine along the lines of our work.
An orthogonal direction is the study of the denotational models of CbNeed. It would be interesting to have a categorical semantics of CbNeed, as well as a categorical way of discriminating our quantitative precise model from the quantitatively lax one given by CbN multi types. It would also be interesting to obtain game semantics of CbNeed, hopefully satisfying a strong correspondence with our multi types in the style of what happens in CbN [30, 31, 51, 56].
A further, unconventional direction is to dualise the inception of the CbNeed type system trying to mix silly duplication from CbN and silly erasure from CbV, obtaining—presumably—a multi types system measuring a perpetual strategy.
Notes
- 1.
If a term \(t\) admits both converging and diverging evaluation sequences then the diverging sequences occur in erasable subterms of \(t\), which is why CbN avoids them.
- 2.
The CbN translation maps \(A\Rightarrow B\) to
 , while the CbV maps it to
, while the CbV maps it to 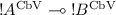 , or equivalently to
, or equivalently to 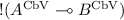 .
. - 3.
The new terminology is due to the fact that a non-idempotent intersection \(A \wedge A \wedge B \wedge C\) can be seen as a multi-set \([ A,A,B,C ] \).
References
Accattoli, B.: An abstract factorization theorem for explicit substitutions. In: 23rd International Conference on Rewriting Techniques and Applications (RTA 2012). LIPIcs, vol. 15, pp. 6–21 (2012). https://doi.org/10.4230/LIPIcs.RTA.2012.6
Accattoli, B.: Proof nets and the linear substitution calculus. In: Fischer, B., Uustalu, T. (eds.) ICTAC 2018. LNCS, vol. 11187, pp. 37–61. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-02508-3_3
Accattoli, B., Barenbaum, P., Mazza, D.: Distilling abstract machines. In: Proceedings of the 19th ACM SIGPLAN International Conference on Functional Programming (ICFP 2014), pp. 363–376 (2014). https://doi.org/10.1145/2628136.2628154
Accattoli, B., Barras, B.: Environments and the complexity of abstract machines. In: Proceedings of the 19th International Symposium on Principles and Practice of Declarative Programming (PPDP 2017), pp. 4–16. ACM (2017). https://doi.org/10.1145/3131851.3131855
Accattoli, B., Barras, B.: The negligible and yet subtle cost of pattern matching. In: Chang, B.-Y.E. (ed.) APLAS 2017. LNCS, vol. 10695, pp. 426–447. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-71237-6_21
Accattoli, B., Bonelli, E., Kesner, D., Lombardi, C.: A nonstandard standardization theorem. In: The 41st Annual Symposium on Principles of Programming Languages (POPL 2014), pp. 659–670. ACM (2014). https://doi.org/10.1145/2535838.2535886
Accattoli, B., Graham-Lengrand, S., Kesner, D.: Tight typings and split bounds. PACMPL 2(ICFP), 94:1–94:30 (2018). https://doi.org/10.1145/3236789
Accattoli, B., Guerrieri, G.: Types of fireballs. In: Ryu, S. (ed.) APLAS 2018. LNCS, vol. 11275, pp. 45–66. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-02768-1_3
Accattoli, B., Guerrieri, G., Leberle, M.: Types by Need (Extended Version). CoRR abs/1902.05945 (2019)
Accattoli, B., Sacerdoti Coen, C.: On the value of variables. Inf. Comput. 255, 224–242 (2017). https://doi.org/10.1016/j.ic.2017.01.003
Ariola, Z.M., Felleisen, M.: The call-by-need lambda calculus. J. Funct. Program. 7(3), 265–301 (1997)
Ariola, Z.M., Felleisen, M., Maraist, J., Odersky, M., Wadler, P.: The call-by-need lambda calculus. In: Conference Record of POPL 1995: 22nd Symposium on Principles of Programming Languages, pp. 233–246. ACM Press (1995). https://doi.org/10.1145/199448.199507
Ariola, Z.M., Herbelin, H., Saurin, A.: Classical call-by-need and duality. In: Ong, L. (ed.) TLCA 2011. LNCS, vol. 6690, pp. 27–44. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21691-6_6
Balabonski, T., Barenbaum, P., Bonelli, E., Kesner, D.: Foundations of strong call by need. PACMPL 1(ICFP), 20:1–20:29 (2017). https://doi.org/10.1145/3110264
Barenbaum, P., Bonelli, E., Mohamed, K.: Pattern matching and fixed points: resource types and strong call-by-need: extended abstract. In: Proceedings of the 20th International Symposium on Principles and Practice of Declarative Programming (PPDP 2018), pp. 6:1–6:12. ACM (2018). https://doi.org/10.1145/3236950.3236972
Barras, B.: Auto-validation d’un système de preuves avec familles inductives. Ph.D. thesis, Université Paris 7 (1999)
Bernadet, A., Graham-Lengrand, S.: Non-idempotent intersection types and strong normalisation. Logical Methods Comput. Sci. 9(4) (2013). https://doi.org/10.2168/LMCS-9(4:3)2013
Bucciarelli, A., Ehrhard, T., Manzonetto, G.: A relational semantics for parallelism and non-determinism in a functional setting. Ann. Pure Appl. Logic 163(7), 918–934 (2012). https://doi.org/10.1016/j.apal.2011.09.008
Bucciarelli, A., Kesner, D., Ronchi Della Rocca, S.: Inhabitation for non-idempotent intersection types. Logical Methods Comput. Sci. 14(3) (2018). https://doi.org/10.23638/LMCS-14(3:7)2018
Bucciarelli, A., Kesner, D., Ventura, D.: Non-idempotent intersection types for the lambda-calculus. Logic J. IGPL 25(4), 431–464 (2017). https://doi.org/10.1093/jigpal/jzx018
Carraro, A., Guerrieri, G.: A semantical and operational account of call-by-value solvability. In: Muscholl, A. (ed.) FoSSaCS 2014. LNCS, vol. 8412, pp. 103–118. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54830-7_7
de Carvalho, D.: Sémantiques de la logique linéaire et temps de calcul. Ph.D. thesis, Université Aix-Marseille II (2007)
de Carvalho, D.: Execution time of \(\lambda \)-terms via denotational semantics and intersection types. Math. Struct. Comput. Sci. 28(7), 1169–1203 (2018). https://doi.org/10.1017/S0960129516000396
de Carvalho, D., Pagani, M., Tortora de Falco, L.: A semantic measure of the execution time in linear logic. Theoret. Comput. Sci. 412(20), 1884–1902 (2011). https://doi.org/10.1016/j.tcs.2010.12.017
de Carvalho, D., Tortora de Falco, L.: A semantic account of strong normalization in linear logic. Inf. Comput. 248, 104–129 (2016). https://doi.org/10.1016/j.ic.2015.12.010
Chang, S., Felleisen, M.: The call-by-need lambda calculus, revisited. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 128–147. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_7
Coppo, M., Dezani-Ciancaglini, M.: A new type assignment for \(\lambda \)-terms. Arch. Math. Log. 19(1), 139–156 (1978). https://doi.org/10.1007/BF02011875
Coppo, M., Dezani-Ciancaglini, M.: An extension of the basic functionality theory for the \(\lambda \)-calculus. Notre Dame J. Formal Logic 21(4), 685–693 (1980). https://doi.org/10.1305/ndjfl/1093883253
Danvy, O., Zerny, I.: A synthetic operational account of call-by-need evaluation. In: 15th International Symposium on Principles and Practice of Declarative Programming (PPDP 2013), pp. 97–108. ACM (2013). https://doi.org/10.1145/2505879.2505898
Di Gianantonio, P., Honsell, F., Lenisa, M.: A type assignment system for game semantics. Theor. Comput. Sci. 398(1–3), 150–169 (2008). https://doi.org/10.1016/j.tcs.2008.01.023
Di Gianantonio, P., Lenisa, M.: Innocent game semantics via intersection type assignment systems. In: Computer Science Logic 2013 (CSL 2013). LIPIcs, vol. 23, pp. 231–247 (2013). https://doi.org/10.4230/LIPIcs.CSL.2013.231
Díaz-Caro, A., Manzonetto, G., Pagani, M.: Call-by-value non-determinism in a linear logic type discipline. In: Artemov, S., Nerode, A. (eds.) LFCS 2013. LNCS, vol. 7734, pp. 164–178. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35722-0_12
Downen, P., Maurer, L., Ariola, Z.M., Varacca, D.: Continuations, processes, and sharing. In: Proceedings of the 16th International Symposium on Principles and Practice of Declarative Programming (PPDP 2014), pp. 69–80. ACM (2014). https://doi.org/10.1145/2643135.2643155
Ehrhard, T.: Collapsing non-idempotent intersection types. In: Computer Science Logic (CSL 2012) - 26th International Workshop/21st Annual Conference of the EACSL. LIPIcs, vol. 16, pp. 259–273 (2012). https://doi.org/10.4230/LIPIcs.CSL.2012.259
Ehrhard, T., Guerrieri, G.: The bang calculus: an untyped lambda-calculus generalizing call-by-name and call-by-value. In: Proceedings of the 18th International Symposium on Principles and Practice of Declarative Programming (PPDP 2016), pp. 174–187. ACM (2016). https://doi.org/10.1145/2967973.2968608
Garcia, R., Lumsdaine, A., Sabry, A.: Lazy evaluation and delimited control. In: Proceedings of the 36th Symposium on Principles of Programming Languages (POPL 2009), pp. 153–164. ACM (2009). https://doi.org/10.1145/1480881.1480903
Gardner, P.: Discovering needed reductions using type theory. In: Hagiya, M., Mitchell, J.C. (eds.) TACS 1994. LNCS, vol. 789, pp. 555–574. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-57887-0_115
Girard, J.Y.: Linear logic. Theoret. Comput. Sci. 50, 1–102 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Guerrieri, G.: Towards a semantic measure of the execution time in call-by-value lambda-calculus. In: Proceedings of ITRS 2018 (2018, to appear)
Kesner, D.: Reasoning about call-by-need by means of types. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 424–441. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_25
Kesner, D., Vial, P.: Types as resources for classical natural deduction. In: 2nd International Conference on Formal Structures for Computation and Deduction (FSCD 2017). LIPIcs, vol. 84, pp. 24:1–24:17 (2017). https://doi.org/10.4230/LIPIcs.FSCD.2017.24
Kesner, D., Ríos, A., Viso, A.: Call-by-need, neededness and all that. In: Baier, C., Dal Lago, U. (eds.) FoSSaCS 2018. LNCS, vol. 10803, pp. 241–257. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89366-2_13
Kfoury, A.J.: A linearization of the lambda-calculus and consequences. J. Logic Comput. 10(3), 411–436 (2000). https://doi.org/10.1093/logcom/10.3.411
Krivine, J.L.: Lambda-Calculus, Types and Models. Ellis Horwood Series in Computers and Their Applications. Ellis Horwood, Upper Saddle River, NJ, USA (1993)
Kutzner, A., Schmidt-Schauß, M.: A non-deterministic call-by-need lambda calculus. In: Proceedings of the Third International Conference on Functional Programming (ICFP 1998), pp. 324–335. ACM (1998). https://doi.org/10.1145/289423.289462
Launchbury, J.: A natural semantics for lazy evaluation. In: Conference Record of the Twentieth Annual Symposium on Principles of Programming Languages (POPL 1993), pp. 144–154. ACM Press (1993). https://doi.org/10.1145/158511.158618
Maraist, J., Odersky, M., Turner, D.N., Wadler, P.: Call-by-name, call-by-value, call-by-need and the linear lambda calculus. Theor. Comput. Sci. 228(1–2), 175–210 (1999). https://doi.org/10.1016/S0304-3975(98)00358-2
Maraist, J., Odersky, M., Wadler, P.: The call-by-need lambda calculus. J. Funct. Program. 8(3), 275–317 (1998)
Mazza, D., Pellissier, L., Vial, P.: Polyadic approximations, fibrations and intersection types. PACMPL 2(POPL), 6:1–6:28 (2018). https://doi.org/10.1145/3158094
Neergaard, P.M., Mairson, H.G.: Types, potency, and idempotency: why nonlinearity and amnesia make a type system work. In: Proceedings of the Ninth International Conference on Functional Programming (ICFP 2004), pp. 138–149. ACM (2004). https://doi.org/10.1145/1016850.1016871
Ong, C.L.: Quantitative semantics of the lambda calculus: some generalisations of the relational model. In: 32nd Annual Symposium on Logic in Computer Science (LICS 2017), pp. 1–12. IEEE Computer Society (2017). https://doi.org/10.1109/LICS.2017.8005064
Paolini, L., Piccolo, M., Ronchi Della Rocca, S.: Essential and relational models. Math. Struct. Comput. Sci. 27(5), 626–650 (2017). https://doi.org/10.1017/S0960129515000316
Pédrot, P.-M., Saurin, A.: Classical by-need. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 616–643. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49498-1_24
Pottinger, G.: A type assignment for the strongly normalizable \(\lambda \)-terms. In: Seldin, J., Hindley, J. (eds.) To H.B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, pp. 561–578. Academic Press, Cambridge (1980)
Sestoft, P.: Deriving a lazy abstract machine. J. Funct. Program. 7(3), 231–264 (1997)
Tsukada, T., Ong, C.L.: Plays as resource terms via non-idempotent intersection types. In: Proceedings of the 31st Annual Symposium on Logic in Computer Science (LICS 2016), pp. 237–246. ACM (2016). https://doi.org/10.1145/2933575.2934553
Wadsworth, C.P.: Semantics and pragmatics of the lambda-calculus. Ph.D. thesis, University of Oxford (1971). Chapter 4
Acknowledgements
This work has been partially funded by the ANR JCJC grant COCA HOLA (ANR-16-CE40-004-01) and by the EPSRC grant EP/R029121/1 “Typed Lambda-Calculi with Sharing and Unsharing”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Accattoli, B., Guerrieri, G., Leberle, M. (2019). Types by Need. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)







 is the sum
is the sum 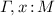 is equal to
is equal to  .
. .
.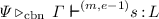 .
. and
and  , and
, and
 .
.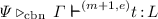 .
.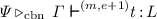 .
.
 .
.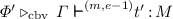 .
. and
and  and
and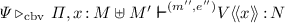
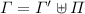 ,
, .
. .
.

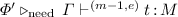 .
. .
. and
and 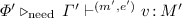 , and
, and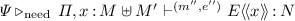
 .
.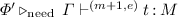 ,
, .
. , while the CbV maps it to
, while the CbV maps it to 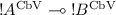 , or equivalently to
, or equivalently to 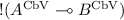 .
.