Abstract
Algebraic effects and handlers are a powerful abstraction mechanism to represent and implement control effects. In this work, we study their extension with parametric polymorphism that allows abstracting not only expressions but also effects and handlers. Although polymorphism makes it possible to reuse and reason about effect implementations more effectively, it has long been known that a naive combination of polymorphic effects and let-polymorphism breaks type safety. Although type safety can often be gained by restricting let-bound expressions—e.g., by adopting value restriction or weak polymorphism—we propose a complementary approach that restricts handlers instead of let-bound expressions. Our key observation is that, informally speaking, a handler is safe if resumptions from the handler do not interfere with each other. To formalize our idea, we define a call-by-value lambda calculus \(\lambda _\text {eff}^\text {let}\) that supports let-polymorphism and polymorphic algebraic effects and handlers, design a type system that rejects interfering handlers, and prove type safety of our calculus.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Algebraic effects [20] and handlers [21] are a powerful abstraction mechanism to represent and implement control effects, such as exceptions, interactive I/O, mutable states, and nondeterminism. They are growing in popularity, thanks to their success in achieving modularity of effects, especially the clear separation between their interfaces and their implementations. An interface of effects is given as a set of operations—e.g., an interface of mutable states consists of two operations, namely, put and get—with their signatures. An implementation is given by a handler \( H \), which provides a set of interpretations of the operations (called operation clauses), and a \( \mathsf {handle} \)–\( \mathsf {with} \) expression \(\mathsf {handle} \, M \, \mathsf {with} \, H \) associates effects invoked during the computation of \( M \) with handler \( H \). Algebraic effects and handlers work as resumable exceptions: when an effect operation is invoked, the run-time system tries to find the nearest handler that handles the invoked operation; if it is found, the corresponding operation clause is evaluated by using the argument to the operation invocation and the continuation up to the handler. The continuation gives the ability to resume the computation from the point where the operation was invoked, using the result from the operation clause. Another modularity that algebraic effects provide is flexible composition: multiple algebraic effects can be combined freely [13].
In this work, we study an extension of algebraic effects and handlers with another type-based abstraction mechanism—parametric polymorphism [22]. In general, parametric polymorphism is a basis of generic programming and enhance code reusability by abstracting expressions over types. This work allows abstracting not only expressions but also effect operations and handlers, which makes it possible to reuse and reason about effect implementations that are independent of concrete type representations. Like in many functional languages, we introduce polymorphism in the form of let-polymorphism for its practically desirable properties such as decidable typechecking and type inference.
As is well known, however, a naive combination of polymorphic effects and let-polymorphism breaks type safety [11, 23]. Many researchers have attacked this classical problem [1, 2, 10, 12, 14, 17, 23, 24], and their common idea is to restrict the form of let-bound expressions. For example, value restriction [23, 24], which is the standard way to make ML-like languages with imperative features and let-polymorphism type safe, allows only syntactic values to be polymorphic.
In this work, we propose a new approach to achieving type safety in a language with let-polymorphic and polymorphic effects and handlers: the idea is to restrict handlers instead of let-bound expressions. Since a handler gives an implementation of an effect, our work can be viewed as giving a criterion that suggests what effects can cooperate safely with (unrestricted) let-polymorphism and what effects cannot. Our key observation for type safety is that, informally speaking, an invocation of a polymorphic effect in a let-bound expression is safe if resumptions in the corresponding operation clause do not interfere with each other. We formalize this discipline into a type system and show that typeable programs do not get stuck.
Our contributions are summarized as follows.
-
We introduce a call-by-value, statically typed lambda calculus \(\lambda _\text {eff}^\text {let}\) that supports let-polymorphism and polymorphic algebraic effects and handlers. The type system of \(\lambda _\text {eff}^\text {let}\) allows any let-bound expressions involving effects to be polymorphic, but, instead, disallows handlers where resumptions interfere with each other.
-
To give the semantics of \(\lambda _\text {eff}^\text {let}\), we formalize an intermediate language \(\lambda _\text {eff}^{\varLambda }\) wherein type information is made explicit and define a formal elaboration from \(\lambda _\text {eff}^\text {let}\) to \(\lambda _\text {eff}^{\varLambda }\).
-
We prove type safety of \(\lambda _\text {eff}^\text {let}\) by type preservation of the elaboration and type soundness of \(\lambda _\text {eff}^{\varLambda }\).
We believe that our approach is complementary to the usual approach of restricting let-bound expressions: for handlers that are considered unsafe by our criterion, the value restriction can still be used.
The rest of this paper is organized as follows. Section 2 provides an overview of our work, giving motivating examples of polymorphic effects and handlers, a problem in naive combination of polymorphic effects and let-polymorphism, and our solution to gain type safety with those features. Section 3 defines the surface language \(\lambda _\text {eff}^\text {let}\), and Sect. 4 defines the intermediate language \(\lambda _\text {eff}^{\varLambda }\) and the elaboration from \(\lambda _\text {eff}^\text {let}\) to \(\lambda _\text {eff}^{\varLambda }\). We also state that the elaboration is type-preserving and that \(\lambda _\text {eff}^{\varLambda }\) is type sound in Sect. 4. Finally, we discuss related work in Sect. 5 and conclude in Sect. 6. The proofs of the stated properties and the full definition of the elaboration are given in the full version at https://arxiv.org/abs/1811.07332.
2 Overview
We start with reviewing how monomorphic algebraic effects and handlers work through examples and then extend them to a polymorphic version. We also explain why polymorphic effects are inconsistent with let-polymorphism, if naively combined, and how we resolve it.
2.1 Monomorphic Algebraic Effects and Handlers
Exception. Our first example is exception handling, shown in an ML-like language below.

Some and None are constructors of datatype  option. Line 1 declares an effect operation fail, which signals that an anomaly happens, with its signature \(\texttt {unit} \hookrightarrow \texttt {unit}\), which means that the operation is invoked with the unit value (), causes some effect, and may return the unit value. The function div100, defined in Lines 3–5, is an example that uses fail; it returns the number obtained by dividing 100 by argument x if x is not zero; otherwise, if x is zero, it raises an exception by calling effect operation fail.Footnote 1 In general, we write #op(\( M \)) for invoking effect operation op with argument \( M \). The function f (Lines 7–10) calls div_100 inside a handle–with expression, which returns Some n if div_100 returns integer n normally and returns None if it invokes fail.
option. Line 1 declares an effect operation fail, which signals that an anomaly happens, with its signature \(\texttt {unit} \hookrightarrow \texttt {unit}\), which means that the operation is invoked with the unit value (), causes some effect, and may return the unit value. The function div100, defined in Lines 3–5, is an example that uses fail; it returns the number obtained by dividing 100 by argument x if x is not zero; otherwise, if x is zero, it raises an exception by calling effect operation fail.Footnote 1 In general, we write #op(\( M \)) for invoking effect operation op with argument \( M \). The function f (Lines 7–10) calls div_100 inside a handle–with expression, which returns Some n if div_100 returns integer n normally and returns None if it invokes fail.
An expression of the form handle \( M \) with \( H \) handles effect operations invoked in \( M \) (which we call handled expression) according to the effect interpretations given by handler \( H \). A handler \( H \) consists of two parts: a single return clause and zero or more operation clauses. A return clause return x \(\rightarrow \) \( M' \) will be executed if the evaluation of \( M \) results in a value \( v \). Then, the value of \( M' \) (where x is bound to \( v \)) will be the value of the entire handle–with expression. For example, in the program above, if a nonzero number n is passed to f, the handle–with expression would return Some \((100{\slash }n)\) because div100 n returns \(100{\slash }n\). An operation clause \(\mathsf {op}\) x \(\rightarrow \) \( M' \) defines an implementation of effect op: if the evaluation of handled expression \( M \) invokes effect op with argument \( v \), expression \( M' \) will be evaluated after substituting \( v \) for x and the value of \( M' \) will be the value of the entire handle–with expression. In the program example above, if zero is given to f, then None will be returned because div100 0 invokes fail.
As shown above, algebraic effect handling is similar to exception handling. However, a distinctive feature of algebraic effect handling is that it allows resumption of the computation from the point where an effect operation was invoked. The next example demonstrates such an ability of algebraic effect handlers.
Choice. The next example is effect choose, which returns one of the given two arguments.

As usual, \( A_{{\mathrm {1}}} \times A_{{\mathrm {2}}} \) is a product type, (\( M_{{\mathrm {1}}} \), \( M_{{\mathrm {2}}} \)) is a pair expression, and fst is the first projection function. The first line declares that effect choose is for choosing integers. The handled expression #choose(1,2) + #choose(10,20) intuitively suggests that there would be four possible results—11, 21, 12, and 22—depending on which value each invocation of choose returns. The handler in this example always chooses the first element of a given pairFootnote 2 and returns it by using a resume expression, and, as a result, the expression in Lines 3–5 evaluates to 11.
A resumption expression resume \( M \) in an operation clause makes it possible to return a value of \( M \) to the point where an effect operation was invoked. This behavior is realized by constructing a delimited continuation from the point of the effect invocation up to the handle–with expression that deals with the effect and passing the value of \( M \) to the continuation. We illustrate it by using the program above. When the handled expression #choose(1,2) + #choose(10,20) is evaluated, continuation
 is constructed. Then, the body resume (fst x) of the operation clause is evaluated after binding x to the invocation argument (1,2). Receiving the value 1 of fst (1,2), the resumption expression passes it to the continuation c and c[1] = 1 + #choose(10,20) is evaluated under the same handler. Next, choose is invoked with argument (10,20). Similarly, continuation
is constructed. Then, the body resume (fst x) of the operation clause is evaluated after binding x to the invocation argument (1,2). Receiving the value 1 of fst (1,2), the resumption expression passes it to the continuation c and c[1] = 1 + #choose(10,20) is evaluated under the same handler. Next, choose is invoked with argument (10,20). Similarly, continuation
 is constructed and the operation clause for choose is executed again. Since fst (10,20) evaluates to 10, \(c'[\texttt {10}] = \texttt {1 + 10}\) is evaluated under the same handler. Since the return clause returns what it receives, the entire expression evaluates to 11.
is constructed and the operation clause for choose is executed again. Since fst (10,20) evaluates to 10, \(c'[\texttt {10}] = \texttt {1 + 10}\) is evaluated under the same handler. Since the return clause returns what it receives, the entire expression evaluates to 11.
Finally, we briefly review how an operation clause involving resumption expressions is typechecked [3, 13, 16]. Let us consider operation clause  for
for  of type signature
of type signature
 . The typechecking is performed as follows. First, argument x is assigned the domain type \( A \) of the signature as it will be bound to an argument of an effect invocation. Second, for resumption expression resume \( M' \) in \( M \), (1) \( M' \) is required to have the codomain type \( B \) of the signature because its value will be passed to the continuation as the result of the invocation and (2) the resumption expression is assigned the same type as the return clause. Third, the type of the body \( M \) has to be the same as that of the return clause because the value of
. The typechecking is performed as follows. First, argument x is assigned the domain type \( A \) of the signature as it will be bound to an argument of an effect invocation. Second, for resumption expression resume \( M' \) in \( M \), (1) \( M' \) is required to have the codomain type \( B \) of the signature because its value will be passed to the continuation as the result of the invocation and (2) the resumption expression is assigned the same type as the return clause. Third, the type of the body \( M \) has to be the same as that of the return clause because the value of  is the result of the entire handle–with expression. For example, the above operation clause for choose is typechecked as follows: first, argument x is assigned type
is the result of the entire handle–with expression. For example, the above operation clause for choose is typechecked as follows: first, argument x is assigned type
 ; second, it is checked whether the argument fst x of the resumption expression has int, the codomain type of choose; third, it is checked whether the body resume (fst x) of the clause has the same type as the return clause, i.e., int. If all the requirements are satisfied, the clause is well typed.
; second, it is checked whether the argument fst x of the resumption expression has int, the codomain type of choose; third, it is checked whether the body resume (fst x) of the clause has the same type as the return clause, i.e., int. If all the requirements are satisfied, the clause is well typed.
2.2 Polymorphic Algebraic Effects and Handlers
This section discusses motivation for polymorphism in algebraic effects and handlers. There are two ways to introduce polymorphism: by parameterized effects and by polymorphic effects.
The former is used to parameterize the declaration of an effect by types. For example, one might declare:

An invocation #choose involves a parameterized effect of the form  (where A denotes a type), according to the type of arguments: For example, #choose(true,false) has the effect bool choose and #choose(1,-1) has int choose. Handlers are required for each effect
(where A denotes a type), according to the type of arguments: For example, #choose(true,false) has the effect bool choose and #choose(1,-1) has int choose. Handlers are required for each effect  .
.
The latter is used to give a polymorphic type to an effect. For example, one may declare

In this case, the effect can be invoked with different types, but all invocations have the same effect choose. One can implement a single operation clause that can handle all invocations of choose, regardless of argument types. Koka supports both styles [16] (with the value restriction); we focus, however, on the latter in this paper. A type system for parameterized effects lifting the value restriction is studied by Kammar and Pretnar [14] (see Sect. 5 for comparison).
In what follows, we show a polymorphic version of the examples we have seen, along with brief discussions on how polymorphic effects help with reasoning about effect implementations. Other practical examples of polymorphic effects can be found in Leijen’s work [16].
Polymorphic Exception. First, we extend the exception effect fail with polymorphism.

The polymorphic type signature of effect \(\texttt {fail}^\forall \), given in Line 1, means that the codomain type \(\alpha \) can be any. Thus, we do not need to append the dummy value -1 to the invocation of \(\texttt {fail}^\forall \) by instantiating the bound type variable \(\alpha \) with int (the shaded part).
Choice. Next, let us make choose polymorphic.

The function random_walk implements random walk; it takes the current coordinate x, chooses whether it stops, and, if it decides to continue, recursively calls itself with a new coordinate. In the definition,
 is used twice with different types: bool and int. Lines 11–12 give
is used twice with different types: bool and int. Lines 11–12 give
 an interpretation, which calls rand to obtain a random float,Footnote 3 and returns either the first or the second element of y.
an interpretation, which calls rand to obtain a random float,Footnote 3 and returns either the first or the second element of y.
Typechecking of operation clauses could be extended in a straightforward manner. That is, an operation clause
 for an effect operation of signature
for an effect operation of signature  would be typechecked as follows: first, \(\alpha \) is locally bound in the clause and
would be typechecked as follows: first, \(\alpha \) is locally bound in the clause and  is assigned type
is assigned type  ; second, an argument of a resumption expression must have type
; second, an argument of a resumption expression must have type  (which may contain type variable \(\alpha \)); third,
(which may contain type variable \(\alpha \)); third,  must have the same type as that of the return clause (its type cannot contain \(\alpha \) as \(\alpha \) is local) under the assumption that resumption expressions have the same type as the return clause. For example, let us consider typechecking of the above operation clause for
must have the same type as that of the return clause (its type cannot contain \(\alpha \) as \(\alpha \) is local) under the assumption that resumption expressions have the same type as the return clause. For example, let us consider typechecking of the above operation clause for
 . First, the typechecking algorithm allocates a local type variable \(\alpha \) and assigns type \(\alpha \times \alpha \) to y. The body has two resumption expressions, and it is checked whether the arguments fst y and snd y have the codomain type \(\alpha \) of the signature. Finally, it is checked whether the body is typed at int assuming that the resumption expressions have type int. The operation clause meets all the requirements, and, therefore, it would be well typed.
. First, the typechecking algorithm allocates a local type variable \(\alpha \) and assigns type \(\alpha \times \alpha \) to y. The body has two resumption expressions, and it is checked whether the arguments fst y and snd y have the codomain type \(\alpha \) of the signature. Finally, it is checked whether the body is typed at int assuming that the resumption expressions have type int. The operation clause meets all the requirements, and, therefore, it would be well typed.
An obvious advantage of polymorphic effects is reusability. Without polymorphism, one has to declare many versions of choose for different types.
Another pleasant effect of polymorphic effects is that, thanks to parametricity, inappropriate implementations for an effect operation can be excluded. For example, it is not possible for an implementation of
 to resume with values other than the first or second element of y. In the monomorphic version, however, it is possible to resume with any integer, as opposed to what the name of the operation suggests. A similar argument applies to \(\texttt {fail}^\forall \); since the codomain type is \(\alpha \), which does not appear in the domain type, it is not possible to resume! In other words, the signature
to resume with values other than the first or second element of y. In the monomorphic version, however, it is possible to resume with any integer, as opposed to what the name of the operation suggests. A similar argument applies to \(\texttt {fail}^\forall \); since the codomain type is \(\alpha \), which does not appear in the domain type, it is not possible to resume! In other words, the signature  enforces that no invocation of \(\texttt {fail}^\forall \) will return.
enforces that no invocation of \(\texttt {fail}^\forall \) will return.
2.3 Problem in Naive Combination with Let-Polymorphism
Although polymorphic effects and handlers provide an ability to abstract and restrict effect implementations, one may easily expect that their unrestricted use with naive let-polymorphism, which allows any let-bound expressions to be polymorphic, breaks type safety. Indeed, it does.
We develop a counterexample, inspired by Harper and Lillibridge [11], below.

The function f first binds g to the invocation result of op. The expression #get_id() is given type \(\alpha \rightarrow \alpha \) and the naive let-polymorphism would assign type scheme \(\forall \alpha . \alpha \rightarrow \alpha \) to g, which makes both g true and g 0 (and thus the definition of f) well typed.
An intended use of f is as follows:

The operation clause for get_id resumes with the identity function \(\lambda \)z.z. It would be well typed under the typechecking procedure described in Sect. 2.2 and it safely returns 1.
However, the following strange expression

will get stuck, although this expression would be well typed: both
 and \(\lambda \)z2. z1 could be given type \(\alpha \rightarrow \alpha \) by assigning both z1 and z2 type \(\alpha \), which is the type variable local to this clause. Let us see how the evaluation gets stuck in detail. When the handled expression f () invokes effect get_id, the following continuation will be constructed:
and \(\lambda \)z2. z1 could be given type \(\alpha \rightarrow \alpha \) by assigning both z1 and z2 type \(\alpha \), which is the type variable local to this clause. Let us see how the evaluation gets stuck in detail. When the handled expression f () invokes effect get_id, the following continuation will be constructed:

Next, the body of the operation clause get_id is evaluated. It immediately resumes and reduces to

where

which is the continuation c under the same handler. The evaluation proceeds as follows (here,
 ):
):

Here, the hole in \(c'\) is filled by function (\(\lambda \)z2.true), which returns a Boolean value, though the hole is supposed to be filled by a function of \(\forall \alpha .\,\alpha \rightarrow \alpha \). This weird gap triggers a run-time error:

We stop here because true + 1 cannot reduce.
2.4 Our Solution
A standard approach to this problem is to restrict the form of let-bound expressions by some means such as the (relaxed) value restriction [10, 23, 24] or weak polymorphism [1, 12]. This approach amounts to restricting how effect operations can be used.
In this paper, we seek for a complementary approach, which is to restrict how effect operations can be implemented.Footnote 4 More concretely, we develop a type system such that let-bound expressions are polymorphic as long as they invoke only “safe” polymorphic effects and the notion of safe polymorphic effects is formalized in terms of typing rules (for handlers).
To see what are “safe” effects, let us examine the above counterexample to type safety. The crux of the counterexample is that
-
1.
continuation c uses g polymorphically, namely, as \(\texttt {bool} \rightarrow \texttt {bool}\) in g true and as \(\texttt {int} \rightarrow \texttt {int}\) in g 1;
-
2.
c is invoked twice; and
-
3.
the use of g as \(\texttt {bool} \rightarrow \texttt {bool}\) in the first invocation of c—where g is bound to
 —“alters” the type of \(\lambda \texttt {z2}.\) \(\texttt {z1}\) (passed to resume) from \(\alpha \rightarrow \alpha \) to \(\alpha \rightarrow \texttt {bool}\), contradicting the second use of g as \(\texttt {int} \rightarrow \texttt {int}\) in the second invocation of c.
—“alters” the type of \(\lambda \texttt {z2}.\) \(\texttt {z1}\) (passed to resume) from \(\alpha \rightarrow \alpha \) to \(\alpha \rightarrow \texttt {bool}\), contradicting the second use of g as \(\texttt {int} \rightarrow \texttt {int}\) in the second invocation of c.
The last point is crucial—if \(\lambda \texttt {z2}.\texttt {z1}\) were, say, \(\lambda \texttt {z2}.\texttt {z2}\), there would be no influence from the first invocation of c and the evaluation would succeed. The problem we see here is that the naive type system mistakenly allows interference between the arguments to the two resumptions by assuming that z1 and z2 share the same type.
Based on this observation, the typing rule for resumption is revised to disallow interference between different resumptions by separating their types: for each resume M in the operation clause for  , M has to have type \(B'\) obtained by renaming all type variables \(\alpha _i\) in B with fresh type variables \(\alpha _i'\). In the case of get_id, the two resumptions should be called with \(\beta \rightarrow \beta \) and \(\gamma \rightarrow \gamma \) for fresh \(\beta \) and \(\gamma \); for the first resume to be well typed, z1 has to be of type \(\beta \), although it means that the return type of \(\lambda \)z2.z1 (given to the second resumption) is \(\beta \), making the entire clause ill typed, as we expect. If a clause does not have interfering resumptions like
, M has to have type \(B'\) obtained by renaming all type variables \(\alpha _i\) in B with fresh type variables \(\alpha _i'\). In the case of get_id, the two resumptions should be called with \(\beta \rightarrow \beta \) and \(\gamma \rightarrow \gamma \) for fresh \(\beta \) and \(\gamma \); for the first resume to be well typed, z1 has to be of type \(\beta \), although it means that the return type of \(\lambda \)z2.z1 (given to the second resumption) is \(\beta \), making the entire clause ill typed, as we expect. If a clause does not have interfering resumptions like

or

it will be well typed.
3 Surface Language: \(\lambda _\mathbf {eff}^\mathbf {let}\)
We define a lambda calculus \(\lambda _\text {eff}^\text {let}\) that supports let-polymorphism, polymorphic algebraic effects, and handlers without interfering resumptions. This section introduces the syntax and the type system of \(\lambda _\text {eff}^\text {let}\). The semantics is given by a formal elaboration to intermediate calculus \(\lambda _\text {eff}^{\varLambda }\), which will be introduced in Sect. 4.
3.1 Syntax
The syntax of \(\lambda _\text {eff}^\text {let}\) is given in Fig. 1. Effect operations are denoted by \(\mathsf {op}\) and type variables by \(\alpha \), \(\beta \), and \(\gamma \). An effect, denoted by \(\epsilon \), is a finite set of effect operations. We write \( \langle \rangle \) for the empty effect set. A type, denoted by \( A \), \( B \), \( C \), and \( D \), is a type variable; a base type \(\iota \), which includes, e.g., \( \mathsf {bool} \) and \( \mathsf {int} \); or a function type  , which is given to functions that take an argument of type \( A \) and compute a value of type \( B \) possibly with effect \(\epsilon \). A type scheme \(\sigma \) is obtained by abstracting type variables. Terms, denoted by \( M \), consist of variables; constants (including primitive operations); lambda abstractions \( \lambda \! \, x . M \), which bind \( x \) in \( M \); function applications; let-expressions \(\mathsf {let} \, x = M_{{\mathrm {1}}} \, \mathsf {in} \, M_{{\mathrm {2}}} \), which bind \( x \) in \( M_{{\mathrm {2}}} \); effect invocations \( \texttt {\#} \mathsf {op} ( M ) \); \( \mathsf {handle} \)–\( \mathsf {with} \) expressions \(\mathsf {handle} \, M \, \mathsf {with} \, H \); and resumption expressions \(\mathsf {resume} \, M \). All type information in \(\lambda _\text {eff}^\text {let}\) is implicit; thus the terms have no type annotations. A handler \( H \) has a single return clause \(\mathsf {return} \, x \rightarrow M \), where \( x \) is bound in \( M \), and zero or more operation clauses of the form \(\mathsf {op} ( x ) \rightarrow M \), where \( x \) is bound in \( M \). A typing context \(\varGamma \) binds a sequence of variable declarations
, which is given to functions that take an argument of type \( A \) and compute a value of type \( B \) possibly with effect \(\epsilon \). A type scheme \(\sigma \) is obtained by abstracting type variables. Terms, denoted by \( M \), consist of variables; constants (including primitive operations); lambda abstractions \( \lambda \! \, x . M \), which bind \( x \) in \( M \); function applications; let-expressions \(\mathsf {let} \, x = M_{{\mathrm {1}}} \, \mathsf {in} \, M_{{\mathrm {2}}} \), which bind \( x \) in \( M_{{\mathrm {2}}} \); effect invocations \( \texttt {\#} \mathsf {op} ( M ) \); \( \mathsf {handle} \)–\( \mathsf {with} \) expressions \(\mathsf {handle} \, M \, \mathsf {with} \, H \); and resumption expressions \(\mathsf {resume} \, M \). All type information in \(\lambda _\text {eff}^\text {let}\) is implicit; thus the terms have no type annotations. A handler \( H \) has a single return clause \(\mathsf {return} \, x \rightarrow M \), where \( x \) is bound in \( M \), and zero or more operation clauses of the form \(\mathsf {op} ( x ) \rightarrow M \), where \( x \) is bound in \( M \). A typing context \(\varGamma \) binds a sequence of variable declarations  and type variable declarations \(\alpha \).
and type variable declarations \(\alpha \).
We introduce the following notations used throughout this paper. We write
 for
for
 where
where
 . We often omit indices (\( i \) and \( j \)) and index sets (
. We often omit indices (\( i \) and \( j \)) and index sets (
 and
and
 ) if they are not important: e.g., we often abbreviate
) if they are not important: e.g., we often abbreviate
 to
to
 or even to
or even to
 . Similarly, we use a bold font for other sequences (
. Similarly, we use a bold font for other sequences (
 for a sequence of types,
for a sequence of types,
 for a sequence of values, etc.). We sometimes write
for a sequence of values, etc.). We sometimes write
 to view the sequence \( \varvec{ \alpha } \) as a set by ignoring the order. Free type variables \( ftv ( \sigma ) \) in a type scheme \(\sigma \) and type substitution
to view the sequence \( \varvec{ \alpha } \) as a set by ignoring the order. Free type variables \( ftv ( \sigma ) \) in a type scheme \(\sigma \) and type substitution
 of
of
 for type variables
for type variables
 in \( B \) are defined as usual (with the understanding that the omitted index sets for
in \( B \) are defined as usual (with the understanding that the omitted index sets for
 and
and
 are the same).
are the same).
We suppose that each constant \( c \) is assigned a first-order closed type \( ty ( c ) \) of the form  and that each effect operation \(\mathsf {op}\) is assigned a signature of the form
and that each effect operation \(\mathsf {op}\) is assigned a signature of the form
 , which means that an invocation of \(\mathsf {op}\) with type instantiation
, which means that an invocation of \(\mathsf {op}\) with type instantiation
 takes an argument of
takes an argument of
 and returns a value of
and returns a value of
 . We also assume that, for
. We also assume that, for
 and
and
 .
.
3.2 Type System
The type system of \(\lambda _\text {eff}^\text {let}\) consists of four judgments: well-formedness of typing contexts \(\vdash \varGamma \); well formedness of type schemes \(\varGamma \vdash \sigma \); term typing judgment \(\varGamma ; R \vdash M : A \, | \, \epsilon \), which means that \( M \) computes a value of \( A \) possibly with effect \(\epsilon \) under typing context \(\varGamma \) and resumption type \( R \) (discussed below); and handler typing judgment \(\varGamma ; R \vdash H : A \, | \, \epsilon \Rightarrow B \, | \, \epsilon '\), which means that \( H \) handles a computation that produces a value of \( A \) with effect \(\epsilon \) and that the clauses in \( H \) compute a value of \( B \) possibly with effect \(\epsilon '\) under \(\varGamma \) and \( R \).
A resumption type \( R \) contains type information for resumption.
Definition 1
(Resumption type). Resumption types in \(\lambda _\text {eff}^\text {let}\), denoted by \( R \), are defined as follows:

If \( M \) is not a subterm of an operation clause, it is typechecked under \( R = \mathsf {none} \), which means that \( M \) cannot contain resumption expressions. Otherwise, suppose that \( M \) is a subterm of an operation clause \(\mathsf {op} ( x ) \rightarrow M' \) that handles effect \(\mathsf {op}\) of signature
 and computes a value of \( C \) possibly with effect \(\epsilon \). Then, \( M \) is typechecked under
and computes a value of \( C \) possibly with effect \(\epsilon \). Then, \( M \) is typechecked under  , which means that argument \( x \) to the operation clause has type \( A \) and that resumptions in \( M \) are effectful functions from \( B \) to \( C \) with effect \(\epsilon \). Note that type variables
, which means that argument \( x \) to the operation clause has type \( A \) and that resumptions in \( M \) are effectful functions from \( B \) to \( C \) with effect \(\epsilon \). Note that type variables
 occur free only in \( A \) and \( B \) but not in \( C \).
occur free only in \( A \) and \( B \) but not in \( C \).
Figure 2 shows the inference rules of the judgments (except for \(\varGamma \vdash \sigma \), which is defined by: \(\varGamma \vdash \sigma \) if and only if all free type variables in \(\sigma \) are bound by \(\varGamma \)). For a sequence of type schemes
 , we write
, we write
 if and only if every type scheme in
if and only if every type scheme in
 is well formed under \(\varGamma \).
is well formed under \(\varGamma \).
Well-formedness rules for typing contexts, shown at the top of Fig. 2, are standard. A typing context is well formed if it is empty
 or a variable in the typing context is associated with a type scheme that is well formed in the remaining typing context
or a variable in the typing context is associated with a type scheme that is well formed in the remaining typing context
 and a type variable in the typing context is not declared
and a type variable in the typing context is not declared
 . For typing context \(\varGamma \), \( dom ( \varGamma ) \) denotes the set of type and term variables declared in \(\varGamma \).
. For typing context \(\varGamma \), \( dom ( \varGamma ) \) denotes the set of type and term variables declared in \(\varGamma \).
Typing rules for terms are given in the middle of Fig. 2. The first six rules are standard for the lambda calculus with let-polymorphism and a type-and-effect system. If a variable \( x \) is introduced by a let-expression and has type scheme
 in \(\varGamma \), it is given type
in \(\varGamma \), it is given type
 , obtained by instantiating type variables
, obtained by instantiating type variables
 with well-formed types \( \varvec{ B } \). If \( x \) is bound by other constructors (e.g., a lambda abstraction), \( x \) is always bound to a monomorphic type and both \( \varvec{ \alpha } \) and \( \varvec{ B } \) are the empty sequence. Note that
with well-formed types \( \varvec{ B } \). If \( x \) is bound by other constructors (e.g., a lambda abstraction), \( x \) is always bound to a monomorphic type and both \( \varvec{ \alpha } \) and \( \varvec{ B } \) are the empty sequence. Note that
 gives any effect \(\epsilon \) to the typing judgment for \( x \). In general, \(\epsilon \) in judgment \(\varGamma ; R \vdash M : A \, | \, \epsilon \) means that the evaluation of \( M \) may invoke effect operations in \(\epsilon \). Since a reference to a variable involves no effect, it is given any effect; for the same reason, value constructors are also given any effect. The rule
gives any effect \(\epsilon \) to the typing judgment for \( x \). In general, \(\epsilon \) in judgment \(\varGamma ; R \vdash M : A \, | \, \epsilon \) means that the evaluation of \( M \) may invoke effect operations in \(\epsilon \). Since a reference to a variable involves no effect, it is given any effect; for the same reason, value constructors are also given any effect. The rule
 means that the type of a constant is given by (meta-level) function \( ty \). The typing rules for lambda abstractions and function applications are standard in the lambda calculus equipped with a type-and-effect system. The rule
means that the type of a constant is given by (meta-level) function \( ty \). The typing rules for lambda abstractions and function applications are standard in the lambda calculus equipped with a type-and-effect system. The rule
 gives lambda abstraction \( \lambda \! \, x . M \) function type
gives lambda abstraction \( \lambda \! \, x . M \) function type  if \( M \) computes a value of \( B \) possibly with effect \(\epsilon '\) by using \( x \) of type \( A \). The rule
if \( M \) computes a value of \( B \) possibly with effect \(\epsilon '\) by using \( x \) of type \( A \). The rule
 requires that (1) the argument type of function part \( M_{{\mathrm {1}}} \) be equivalent to the type of actual argument \( M_{{\mathrm {2}}} \) and (2) effect \(\epsilon '\) invoked by function \( M_{{\mathrm {1}}} \) be contained in the whole effect \(\epsilon \). The rule
requires that (1) the argument type of function part \( M_{{\mathrm {1}}} \) be equivalent to the type of actual argument \( M_{{\mathrm {2}}} \) and (2) effect \(\epsilon '\) invoked by function \( M_{{\mathrm {1}}} \) be contained in the whole effect \(\epsilon \). The rule
 allows weakening of effects.
allows weakening of effects.
The next two rules are mostly standard for algebraic effects and handlers. The rule
 is applied to effect invocations. Since \(\lambda _\text {eff}^\text {let}\) supports implicit polymorphism, an invocation \( \texttt {\#} \mathsf {op} ( M ) \) of polymorphic effect \(\mathsf {op}\) of signature
is applied to effect invocations. Since \(\lambda _\text {eff}^\text {let}\) supports implicit polymorphism, an invocation \( \texttt {\#} \mathsf {op} ( M ) \) of polymorphic effect \(\mathsf {op}\) of signature
 also accompanies implicit type substitution of well-formed types \( \varvec{ C } \) for \( \varvec{ \alpha } \). Thus, the type of argument \( M \) has to be \( A [ \varvec{ C } / \varvec{ \alpha } ] \) and the result of the invocation is given type \( B [ \varvec{ C } / \varvec{ \alpha } ] \). In addition, effect \(\epsilon \) contains \(\mathsf {op}\). The typeability of \( \mathsf {handle} \)–\( \mathsf {with} \) expressions depends on the typing of handlers
also accompanies implicit type substitution of well-formed types \( \varvec{ C } \) for \( \varvec{ \alpha } \). Thus, the type of argument \( M \) has to be \( A [ \varvec{ C } / \varvec{ \alpha } ] \) and the result of the invocation is given type \( B [ \varvec{ C } / \varvec{ \alpha } ] \). In addition, effect \(\epsilon \) contains \(\mathsf {op}\). The typeability of \( \mathsf {handle} \)–\( \mathsf {with} \) expressions depends on the typing of handlers
 , which will be explained below shortly.
, which will be explained below shortly.
The last typing rule
 is the key to gaining type safety in this work. Suppose that we are given resumption type
is the key to gaining type safety in this work. Suppose that we are given resumption type  . Intuitively,
. Intuitively,  is the type of the continuation for resumption and, therefore, argument \( M \) to \( \mathsf {resume} \) is required to have type \( B \). As we have discussed in Sect. 2, we avoid interference between different resumptions by renaming \( \varvec{ \alpha } \), the type parameters to the effect operation, to fresh type variables \( \varvec{ \beta } \), in typechecking \( M \). Freshness of \( \varvec{ \beta } \) will be ensured when well-formedness of typing contexts \(\varGamma _{{\mathrm {1}}} , \varGamma _{{\mathrm {2}}} , \varvec{ \beta } , \ldots \) is checked at the leaves of the type derivation. The type variables \( \varvec{ \alpha } \) in the type of \( x \), the parameter to the operation, are also renamed for \( x \) to be useful in \( M \). To see why this renaming is useful, let us consider an extension of the calculus with pairs and typechecking of an operation clause for \( \mathsf {choose}^{\forall } \) of signature
is the type of the continuation for resumption and, therefore, argument \( M \) to \( \mathsf {resume} \) is required to have type \( B \). As we have discussed in Sect. 2, we avoid interference between different resumptions by renaming \( \varvec{ \alpha } \), the type parameters to the effect operation, to fresh type variables \( \varvec{ \beta } \), in typechecking \( M \). Freshness of \( \varvec{ \beta } \) will be ensured when well-formedness of typing contexts \(\varGamma _{{\mathrm {1}}} , \varGamma _{{\mathrm {2}}} , \varvec{ \beta } , \ldots \) is checked at the leaves of the type derivation. The type variables \( \varvec{ \alpha } \) in the type of \( x \), the parameter to the operation, are also renamed for \( x \) to be useful in \( M \). To see why this renaming is useful, let us consider an extension of the calculus with pairs and typechecking of an operation clause for \( \mathsf {choose}^{\forall } \) of signature
 :
:
Variable \( x \) is assigned product type \( \alpha \times \alpha \) for fresh type variable \(\alpha \) and the body \(\mathsf {resume} \, ( \mathsf {fst} \, x )\) is typechecked under the resumption type  for some \(\epsilon \) and \( A \) (see the typing rules for handlers for details). To typecheck \(\mathsf {resume} \, ( \mathsf {fst} \, x )\), the argument \( \mathsf {fst} \, x \) is required to have type \(\beta \), freshly generated for this \( \mathsf {resume} \). Without applying renaming also to \( x \), the clause would not typecheck. Finally,
for some \(\epsilon \) and \( A \) (see the typing rules for handlers for details). To typecheck \(\mathsf {resume} \, ( \mathsf {fst} \, x )\), the argument \( \mathsf {fst} \, x \) is required to have type \(\beta \), freshly generated for this \( \mathsf {resume} \). Without applying renaming also to \( x \), the clause would not typecheck. Finally,
 also requires that (1) the typing context contains \( \varvec{ \alpha } \), which should have been declared at an application of the typing rule for the operation clause that surrounds this \( \mathsf {resume} \) and (2) effect \(\epsilon \), which may be invoked by resumption of a continuation, be contained in the whole effect \(\epsilon '\). The binding \( x \, \mathord {:} \, D \) in the conclusion means that parameter \( x \) to the operation clause is declared outside the resumption expression.
also requires that (1) the typing context contains \( \varvec{ \alpha } \), which should have been declared at an application of the typing rule for the operation clause that surrounds this \( \mathsf {resume} \) and (2) effect \(\epsilon \), which may be invoked by resumption of a continuation, be contained in the whole effect \(\epsilon '\). The binding \( x \, \mathord {:} \, D \) in the conclusion means that parameter \( x \) to the operation clause is declared outside the resumption expression.
The typing rules for handlers are standard [3, 13, 16]. The rule
 for a return clause \(\mathsf {return} \, x \rightarrow M \) checks that the body \( M \) is given a type under the assumption that argument \( x \) has type \( A \), which is the type of the handled expression. The effect \(\epsilon \) stands for effects that are not handled by the operation clauses that follow the return clause and it must be a subset of the effect \(\epsilon '\) that \( M \) may cause.Footnote 5 A handler having operation clauses is typechecked by
for a return clause \(\mathsf {return} \, x \rightarrow M \) checks that the body \( M \) is given a type under the assumption that argument \( x \) has type \( A \), which is the type of the handled expression. The effect \(\epsilon \) stands for effects that are not handled by the operation clauses that follow the return clause and it must be a subset of the effect \(\epsilon '\) that \( M \) may cause.Footnote 5 A handler having operation clauses is typechecked by
 , which checks that the body of the operation clause \(\mathsf {op} ( x ) \rightarrow M \) for \(\mathsf {op}\) of signature
, which checks that the body of the operation clause \(\mathsf {op} ( x ) \rightarrow M \) for \(\mathsf {op}\) of signature
 is typed at the result type \( B \), which is the same as the type of the return clause, under the typing context extended with fresh assigned type variables \( \varvec{ \alpha } \) and argument \( x \) of type \( C \), together with the resumption type
is typed at the result type \( B \), which is the same as the type of the return clause, under the typing context extended with fresh assigned type variables \( \varvec{ \alpha } \) and argument \( x \) of type \( C \), together with the resumption type  . The effect \( \epsilon \mathbin {\uplus } \{ \mathsf {op} \} \) in the conclusion means that the effect operation \(\mathsf {op}\) is handled by this clause and no other clauses (in the present handler) handle it. Our semantics adopts deep handlers [13], i.e., when a handled expression invokes an effect operation, the continuation, which passed to the operation clause, is wrapped by the same handler. Thus, resumption may invoke the same effect \(\epsilon '\) as the one possibly invoked by the clauses of the handler, hence
. The effect \( \epsilon \mathbin {\uplus } \{ \mathsf {op} \} \) in the conclusion means that the effect operation \(\mathsf {op}\) is handled by this clause and no other clauses (in the present handler) handle it. Our semantics adopts deep handlers [13], i.e., when a handled expression invokes an effect operation, the continuation, which passed to the operation clause, is wrapped by the same handler. Thus, resumption may invoke the same effect \(\epsilon '\) as the one possibly invoked by the clauses of the handler, hence  in the resumption type.
in the resumption type.
Finally, we show how the type system rejects the counterexample given in Sect. 2. The problem is in the following operation clause.
where \(\mathsf {op}\) has effect signature  . This clause is typechecked under resumption type
. This clause is typechecked under resumption type  for some \(\epsilon \). By
for some \(\epsilon \). By
 , the two resumption expressions are assigned two different type variables \(\gamma _{{\mathrm {1}}}\) and \(\gamma _{{\mathrm {2}}}\), and the arguments \( \lambda \! \, z_{{\mathrm {1}}} . ( \mathsf {resume} \, \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} ) ; z_{{\mathrm {1}}} \) and \( \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} \) are required to have
, the two resumption expressions are assigned two different type variables \(\gamma _{{\mathrm {1}}}\) and \(\gamma _{{\mathrm {2}}}\), and the arguments \( \lambda \! \, z_{{\mathrm {1}}} . ( \mathsf {resume} \, \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} ) ; z_{{\mathrm {1}}} \) and \( \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} \) are required to have  and
and  , respectively. However, \( \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} \) cannot because \( z_{{\mathrm {1}}} \) is associated with \(\gamma _{{\mathrm {1}}}\) but not with \(\gamma _{{\mathrm {2}}}\).
, respectively. However, \( \lambda \! \, z_{{\mathrm {2}}} . z_{{\mathrm {1}}} \) cannot because \( z_{{\mathrm {1}}} \) is associated with \(\gamma _{{\mathrm {1}}}\) but not with \(\gamma _{{\mathrm {2}}}\).
Remark. The rule
 allows only the type of the argument to an operation clause to be renamed. Thus, other variables bound by, e.g., lambda abstractions and let-expressions outside the resumption expression cannot be used as such a type. As a result, more care may be required as to where to introduce a new variable. For example, let us consider the following operation clause (which is a variant of the example of \( \mathsf {choose}^{\forall } \) above).
allows only the type of the argument to an operation clause to be renamed. Thus, other variables bound by, e.g., lambda abstractions and let-expressions outside the resumption expression cannot be used as such a type. As a result, more care may be required as to where to introduce a new variable. For example, let us consider the following operation clause (which is a variant of the example of \( \mathsf {choose}^{\forall } \) above).
The variable \( x \) is assigned \( \alpha \times \alpha \) first and the resumption requires \( y \) to be typed at fresh type variable \(\beta \). This clause would be rejected in the current type system because \( \mathsf {fst} \, x \) appears outside \( \mathsf {resume} \) and, therefore, \( y \) is given type \(\alpha \), not \(\beta \). This inconvenience may be addressed by moving down the let-binding in some cases: e.g., \(\mathsf {resume} \, ( \mathsf {let} \, y = \mathsf {fst} \, x \, \mathsf {in} \, y )\) is well typed.
4 Intermediate Language: \(\lambda _\mathbf {eff}^{\varLambda }\)
The semantics of \(\lambda _\text {eff}^\text {let}\) is given by a formal elaboration to an intermediate language \(\lambda _\text {eff}^{\varLambda }\), wherein type abstraction and type application appear explicitly. We define the syntax, operational semantics, and type system of \(\lambda _\text {eff}^\text {let}\) and the formal elaboration from \(\lambda _\text {eff}^\text {let}\) to \(\lambda _\text {eff}^{\varLambda }\). Finally, we show type safety of \(\lambda _\text {eff}^\text {let}\) via type preservation of the elaboration and type soundness of \(\lambda _\text {eff}^{\varLambda }\).
4.1 Syntax
The syntax of \(\lambda _\text {eff}^{\varLambda }\) is shown in Fig. 3. Values, denoted by \( v \), consist of constants and lambda abstractions. Polymorphic values, denoted by \( w \), are values abstracted over types. Terms, denoted by \( e \), and handlers, denoted by \( h \), are the same as those of \(\lambda _\text {eff}^\text {let}\) except for the following three points. First, type abstraction and type arguments are explicit in \(\lambda _\text {eff}^{\varLambda }\): variables and effect invocations are accompanied by a sequence of types and let-bound expressions, resumption expressions, and operation clauses bind type variables. Second, a new term constructor of the form \( \texttt {\#} \mathsf {op} ( \varvec{ \sigma } , w , E ) \) is added. It represents an intermediate state in which an effect invocation is capturing the continuation up to the closest handler for \(\mathsf {op}\). Here, \( E \) is an evaluation context [6] and denotes a continuation to be resumed by an operation clause handling \(\mathsf {op}\). In the operational semantics, an operation invocation \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v ) \) is first transformed to \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v , [\,] ) \) (where \( [\,] \) denotes the empty context or the identity continuation) and then it bubbles up by capturing its context and pushing it onto the third argument. Note that \( \varvec{ \sigma } \) and \( w \) of \( \texttt {\#} \mathsf {op} ( \varvec{ \sigma } , w , E ) \) become polymorphic when it bubbles up from the body of a type abstraction. Third, each resumption expression \(\mathsf {resume} \, \varvec{ \alpha } \, x . e \) declares distinct (type) variables \( \varvec{ \alpha } \) and \( x \) to denote the (type) argument to an operation clause, whereas a single variable declared at \(\mathsf {op} ( x ) \rightarrow M \) and implicit type variables are used for the same purpose in \(\lambda _\text {eff}^\text {let}\). For example, the \(\lambda _\text {eff}^\text {let}\) operation clause \( \mathsf {choose}^{\forall } ( x ) \rightarrow \mathsf {resume} \, ( \mathsf {fst} \, x )\) is translated to \( \varLambda \! \, \alpha . \mathsf {choose}^{\forall } ( x ) \rightarrow \mathsf {resume} \, \beta \, y .( \mathsf {fst} \, y )\). This change simplifies the semantics.
Evaluation contexts, denoted by \( E ^{ \varvec{ \alpha } } \), are standard for the lambda calculus with call-by-value, left-to-right evaluation except for two points. First, they contain the form \(\mathsf {let} \, x = \varLambda \! \, \varvec{ \alpha }. E ^{ \varvec{ \beta } } \, \mathsf {in} \, e_{{\mathrm {2}}} \), which allows the body of a type abstraction to be evaluated. Second, the metavariable \( E \) for evaluation contexts is indexed by type variables \( \varvec{ \alpha } \), meaning that the hole in the context appears under type abstractions binding \( \varvec{ \alpha } \). For example, \(\mathsf {let} \, x = \varLambda \! \, \alpha . \mathsf {let} \, y = \varLambda \! \, \beta . [\,] \, \mathsf {in} \, e_{{\mathrm {2}}} \, \mathsf {in} \, e_{{\mathrm {1}}} \) is denoted by \( E ^{\alpha ,\beta }\) and, more generally,  is denoted by
is denoted by
 . (Here,
. (Here,
 stands for the concatenation of the two sequences
stands for the concatenation of the two sequences  and
and  .) If \(\varvec{ \alpha } \) is not important, we simply write \( E \) for \( E ^{ \varvec{ \alpha } } \). We often use the term “continuation” to mean “evaluation context,” especially when it is expected to be resumed.
.) If \(\varvec{ \alpha } \) is not important, we simply write \( E \) for \( E ^{ \varvec{ \alpha } } \). We often use the term “continuation” to mean “evaluation context,” especially when it is expected to be resumed.
As usual, substitution
 of
of
 for
for
 in
in  is defined in a capture-avoiding manner. Since variables come along with type arguments, the case for variables is defined as follows:
is defined in a capture-avoiding manner. Since variables come along with type arguments, the case for variables is defined as follows:

Application of substitution
 to
to
 , where
, where
 , is undefined. We define free type variables
, is undefined. We define free type variables
 and
and
 and \( E \), respectively, as usual.
and \( E \), respectively, as usual.
4.2 Semantics
The semantics of \(\lambda _\text {eff}^{\varLambda }\) is given in the small-step style and consists of two relations: the reduction relation \( \rightsquigarrow \), which is for basic computation, and the evaluation relation \( \longrightarrow \), which is for top-level execution. Figure 4 shows the rules for these relations. In what follows, we write \( h ^\mathsf {return} \) for the return clause of handler \( h \), \( ops ( h ) \) for the set of effect operations handled by \( h \), and \( h ^{ \mathsf {op} } \) for the operation clause for \(\mathsf {op}\) in \( h \).
Most of the reduction rules are standard [13, 16]. A constant application \( c_{{\mathrm {1}}} \, c_{{\mathrm {2}}} \) reduces to \( \zeta ( c_{{\mathrm {1}}} , c_{{\mathrm {2}}} ) \)
 , where function \( \zeta \) maps a pair of constants to another constant. A function application \(( \lambda \! \, x . e ) \, v \) and a let-expression \(\mathsf {let} \, x = \varLambda \! \, \varvec{ \alpha } . v \, \mathsf {in} \, e \) reduce to \( e [ v / x ] \)
, where function \( \zeta \) maps a pair of constants to another constant. A function application \(( \lambda \! \, x . e ) \, v \) and a let-expression \(\mathsf {let} \, x = \varLambda \! \, \varvec{ \alpha } . v \, \mathsf {in} \, e \) reduce to \( e [ v / x ] \)
 and \( e [ \varLambda \! \, \varvec{ \alpha } . v / x ] \)
and \( e [ \varLambda \! \, \varvec{ \alpha } . v / x ] \)
 , respectively. If a handled expression is a value \( v \), the \( \mathsf {handle} \)–\( \mathsf {with} \) expression reduces to the body of the return clause where \( v \) is substituted for the parameter \( x \)
, respectively. If a handled expression is a value \( v \), the \( \mathsf {handle} \)–\( \mathsf {with} \) expression reduces to the body of the return clause where \( v \) is substituted for the parameter \( x \)
 . An effect invocation \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v ) \) reduces to \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v , [\,] ) \) with the identity continuation, as explained above
. An effect invocation \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v ) \) reduces to \( \texttt {\#} \mathsf {op} ( \varvec{ A } , v , [\,] ) \) with the identity continuation, as explained above
 ; the process of capturing its evaluation context is expressed by the rules
; the process of capturing its evaluation context is expressed by the rules
 ,
,
 ,
,
 ,
,
 , and
, and
 . The rule
. The rule
 can be applied only if the handler \( h \) does not handle \(\mathsf {op}\). The rule
can be applied only if the handler \( h \) does not handle \(\mathsf {op}\). The rule
 is applied to a let-expression where
is applied to a let-expression where  appears under a type abstraction with bound type variables
appears under a type abstraction with bound type variables  . Since
. Since  and \( w \) may refer to
and \( w \) may refer to  , the reduction result binds
, the reduction result binds  in both
in both
 and \( w \). We write
and \( w \). We write  for a sequence
for a sequence  , ...,
, ...,  of type schemes (where
of type schemes (where
 ).
).
The crux of the semantics is
 : it is applied when
: it is applied when  reaches the handler \( h \) that handles \(\mathsf {op}\). Since the handled term
reaches the handler \( h \) that handles \(\mathsf {op}\). Since the handled term  is constructed from an effect invocation
is constructed from an effect invocation  , if the captured continuation \( E \) binds type variables
, if the captured continuation \( E \) binds type variables  , the same type variables
, the same type variables  should have been added to
should have been added to  and \( v \) along the capture. Thus, the handled expression on the left-hand side of the rule takes the form
and \( v \) along the capture. Thus, the handled expression on the left-hand side of the rule takes the form  (with the same type variables
(with the same type variables  ).
).
The right-hand side of
 involves three types of substitution: continuation substitution
involves three types of substitution: continuation substitution  for resumptions, type substitution for
for resumptions, type substitution for  , and value substitution for \( x \). We explain them one by one below. In the following, let
, and value substitution for \( x \). We explain them one by one below. In the following, let  and
and  .
.
Continuation Substitution. Let us start with a simple case where the sequence  is empty. Intuitively, continuation substitution
is empty. Intuitively, continuation substitution  replaces a resumption expression
replaces a resumption expression  in the body \( e \) with \( E' [ v' ] \), where \( v' \) is the value of \( e' \), and substitutes
in the body \( e \) with \( E' [ v' ] \), where \( v' \) is the value of \( e' \), and substitutes
 and \( v \) (arguments to the invocation of \(\mathsf {op}\)) for
and \( v \) (arguments to the invocation of \(\mathsf {op}\)) for
 and \( z \), respectively. Therefore, assuming \( \mathsf {resume} \) does not appear in \( e' \), we define
and \( z \), respectively. Therefore, assuming \( \mathsf {resume} \) does not appear in \( e' \), we define
 to be
to be
 (for fresh \( y \)). Note that the evaluation of \( e' \) takes place outside of \( E \) so that an invocation of an effect in \( e' \) is not handled by handlers in \( E \). When
(for fresh \( y \)). Note that the evaluation of \( e' \) takes place outside of \( E \) so that an invocation of an effect in \( e' \) is not handled by handlers in \( E \). When
 is not empty,
is not empty,

(The differences from the simple case are shaded.) The idea is to bind
 that appear free in
that appear free in
 and \( v \) by type abstraction at \( \mathsf {let} \) and to instantiate with the same variables at
and \( v \) by type abstraction at \( \mathsf {let} \) and to instantiate with the same variables at
 , where
, where
 are bound by type abstractions in
are bound by type abstractions in
 .
.
Continuation substitution is formally defined as follows:
Definition 2
(Continuation substitution). Substitution of continuation
 for resumptions in \( e \), written
for resumptions in \( e \), written
 , is defined in a capture-avoiding manner, as follows (we describe only the important cases):
, is defined in a capture-avoiding manner, as follows (we describe only the important cases):

The second and third clauses (for a handler) mean that continuation substitution is applied only to return clauses.
Type and Value Substitution. The type and value substitutions
 and
and
 , respectively, in
, respectively, in
 are for (type) parameters in
are for (type) parameters in
 . The basic idea is to substitute
. The basic idea is to substitute
 for
for
 and
and  for
for  —similarly to continuation substitution. We erase free type variables
—similarly to continuation substitution. We erase free type variables
 in
in
 and \( v \) by substituting the designated base type \( \bot \) for all of them. (We write
and \( v \) by substituting the designated base type \( \bot \) for all of them. (We write
 and
and
 for the types and value, respectively, after the erasure.)
for the types and value, respectively, after the erasure.)
The evaluation rule is ordinary: Evaluation of a term proceeds by reducing a subterm under an evaluation context.
4.3 Type System
The type system of \(\lambda _\text {eff}^{\varLambda }\) is similar to that of \(\lambda _\text {eff}^\text {let}\) and has five judgments: well-formedness of typing contexts \(\vdash \varGamma \); well formedness of type schemes \(\varGamma \vdash \sigma \); term typing judgment \(\varGamma ; r \, \vdash e \, : A \, | \, \epsilon \); handler typing judgment \(\varGamma ; r \, \vdash h : A \, | \, \epsilon \Rightarrow B \, | \, \epsilon '\); and continuation typing judgment
 . The first two are defined in the same way as those of \(\lambda _\text {eff}^\text {let}\). The last judgment means that a term obtained by filling the hole of \( E \) with a term having \( A \) under \(\varGamma , \varvec{ \alpha } \) is typed at \( B \) under \(\varGamma \) and possibly involves effect \(\epsilon \). A resumption type \( r \) is similar to \( R \) but does not contain an argument variable.
. The first two are defined in the same way as those of \(\lambda _\text {eff}^\text {let}\). The last judgment means that a term obtained by filling the hole of \( E \) with a term having \( A \) under \(\varGamma , \varvec{ \alpha } \) is typed at \( B \) under \(\varGamma \) and possibly involves effect \(\epsilon \). A resumption type \( r \) is similar to \( R \) but does not contain an argument variable.
Definition 3
(Resumption type). Resumption types in \(\lambda _\text {eff}^{\varLambda }\), denoted by \( r \), are defined as follows:

The typing rules for terms, shown in Fig. 5, and handlers, shown in the upper half of Fig. 6, are similar to those of \(\lambda _\text {eff}^\text {let}\) except for a new rule
 , which is applied to an effect invocation
, which is applied to an effect invocation
 with a continuation. Let
with a continuation. Let
 . Since \(\mathsf {op}\) should have been invoked with
. Since \(\mathsf {op}\) should have been invoked with
 and \( v \) under type abstractions with bound type variables
and \( v \) under type abstractions with bound type variables
 , the argument \( v \) has type
, the argument \( v \) has type
 under the typing context extended with
under the typing context extended with
 . Similarly, the hole of
. Similarly, the hole of
 expects to be filled with the result of the invocation, i.e., a value of
expects to be filled with the result of the invocation, i.e., a value of
 . Since the continuation denotes the context before the evaluation, its result type matches with the type of the whole term.
. Since the continuation denotes the context before the evaluation, its result type matches with the type of the whole term.
The typing rules for continuations are shown in the lower half of Fig. 6. They are similar to the corresponding typing rules for terms except that a subterm is replaced with a continuation. In
 , the continuation \(\mathsf {let} \, x = \varLambda \! \, \varvec{ \alpha } . E \, \mathsf {in} \, e \) has type
, the continuation \(\mathsf {let} \, x = \varLambda \! \, \varvec{ \alpha } . E \, \mathsf {in} \, e \) has type
 because the hole of \( E \) appears inside the scope of \( \varvec{ \alpha } \).
because the hole of \( E \) appears inside the scope of \( \varvec{ \alpha } \).
4.4 Elaboration
This section defines the elaboration from \(\lambda _\text {eff}^\text {let}\) to \(\lambda _\text {eff}^{\varLambda }\). The important difference between the two languages from the viewpoint of elaboration is that, whereas the parameter of an operation clause is referred to by a single variable in \(\lambda _\text {eff}^\text {let}\), it is done by one or more variables in \(\lambda _\text {eff}^{\varLambda }\). Therefore, one variable in \(\lambda _\text {eff}^\text {let}\) is represented by multiple variables (required for each \( \mathsf {resume} \)) in \(\lambda _\text {eff}^{\varLambda }\). We use \( S \), a mapping from variables to variables, to make the correspondence between variable names. We write \( S \,\circ \, \{ x \, {\mapsto } \, y \} \) for the same mapping as \( S \) except that \( x \) is mapped to \( y \).
Elaboration is defined by two judgments: term elaboration judgment \( \varGamma ; R \vdash M : A \, | \, \epsilon \mathrel { \vartriangleright ^{ S } } e \), which denotes elaboration from a typing derivation of judgment \(\varGamma ; R \vdash M : A \, | \, \epsilon \) to \( e \) with \( S \), and handler elaboration judgment \( \varGamma ; R \vdash H : A \, | \, \epsilon \, \Rightarrow B \, | \, \epsilon ' \mathrel { \vartriangleright ^{ S } } h \), which denotes elaboration from a typing derivation of judgment \(\varGamma ; R \vdash H : A \, | \, \epsilon \Rightarrow B \, | \, \epsilon '\) to \( h \) with \( S \).
Selected elaboration rules are shown in Fig. 7; the complete set of the rules is found in the full version of the paper. The elaboration rules are straightforward except for the use of \( S \). A variable \( x \) is translated to \( S ( x )\)
 and, every time a new variable is introduced, \( S \) is extended: see the rules other than
and, every time a new variable is introduced, \( S \) is extended: see the rules other than
 and
and
 .
.
4.5 Properties
We show type safety of \(\lambda _\text {eff}^\text {let}\), i.e., a well-typed program in \(\lambda _\text {eff}^\text {let}\) does not get stuck, by proving (1) type preservation of the elaboration from \(\lambda _\text {eff}^\text {let}\) to \(\lambda _\text {eff}^{\varLambda }\) and (2) type soundness of \(\lambda _\text {eff}^{\varLambda }\). Term \( M \) is a well-typed program of \( A \) if and only if \( \emptyset ; \mathsf {none} \vdash M : A \, | \, \langle \rangle \).
The first can be shown easily. We write \( \emptyset \) also for the identity mapping for variables.
Theorem 1
(Elaboration is type-preserving). If \( M \) is a well-typed program of \( A \), then \( \emptyset ; \mathsf {none} \vdash M : A \, | \, \langle \rangle \mathrel { \vartriangleright ^{ \emptyset } } e \) and \( \emptyset ; \mathsf {none} \, \vdash e \, : A \, | \, \langle \rangle \) for some \( e \).
We show the second—type soundness of \(\lambda _\text {eff}^{\varLambda }\)—via progress and subject reduction [25]. We write \(\varDelta \) for a typing context that consists only of type variables. Progress can be shown as usual.
Lemma 1
(Progress). If \(\varDelta ; \mathsf {none} \, \vdash e \, : A \, | \, \epsilon \), then (1) \( e \longrightarrow e' \) for some \( e' \), (2) \( e \) is a value, or (3) \( e \, = \, \texttt {\#} \mathsf {op} ( \varvec{ \sigma } , w , E ) \) for some \(\mathsf {op} \, \in \, \epsilon \), \( \varvec{ \sigma } \), \( w \), and \( E \).
A key lemma to show subject reduction is type preservation of continuation substitution.
Lemma 2
(Continuation substitution). Suppose that
 and
and
 and
and
 .
.
-
1.
If
 , then
, then
 .
. -
2.
If
 , then
, then
 .
.
Using the continuation substitution lemma as well as other lemmas, we show subject reduction.
Lemma 3
(Subject reduction)
-
1.
If \(\varDelta ; \mathsf {none} \, \vdash e_{{\mathrm {1}}} \, : A \, | \, \epsilon \) and \( e_{{\mathrm {1}}} \rightsquigarrow e_{{\mathrm {2}}} \), then \(\varDelta ; \mathsf {none} \, \vdash e_{{\mathrm {2}}} \, : A \, | \, \epsilon \).
-
2.
If \(\varDelta ; \mathsf {none} \, \vdash e_{{\mathrm {1}}} \, : A \, | \, \epsilon \) and \( e_{{\mathrm {1}}} \longrightarrow e_{{\mathrm {2}}} \), then \(\varDelta ; \mathsf {none} \, \vdash e_{{\mathrm {2}}} \, : A \, | \, \epsilon \).
We write  if and only if \( e \) cannot evaluate further. Moreover, \( \longrightarrow ^{*} \) denotes the reflexive and transitive closure of the evaluation relation \( \longrightarrow \).
if and only if \( e \) cannot evaluate further. Moreover, \( \longrightarrow ^{*} \) denotes the reflexive and transitive closure of the evaluation relation \( \longrightarrow \).
Theorem 2
(Type soundness of \(\lambda _\mathbf {eff}^{\varLambda }\)). If \(\varDelta ; \mathsf {none} \, \vdash e \, : A \, | \, \epsilon \) and \( e \longrightarrow ^{*} e' \) and  , then (1) \( e' \) is a value or (2) \( e' \, = \, \texttt {\#} \mathsf {op} ( \varvec{ \sigma } , w , E ) \) for some \(\mathsf {op} \, \in \, \epsilon \), \( \varvec{ \sigma } \), \( w \), and \( E \).
, then (1) \( e' \) is a value or (2) \( e' \, = \, \texttt {\#} \mathsf {op} ( \varvec{ \sigma } , w , E ) \) for some \(\mathsf {op} \, \in \, \epsilon \), \( \varvec{ \sigma } \), \( w \), and \( E \).
Now, type safety of \(\lambda _\text {eff}^\text {let}\) is obtained as a corollary of Theorems 1 and 2.
Corollary 1
(Type safety of \(\lambda _\mathbf {eff}^\mathbf {let}\)). If \( M \) is a well-typed program of \( A \), there exists some \( e \) such that \( \emptyset ; \mathsf {none} \vdash M : A \, | \, \langle \rangle \mathrel { \vartriangleright ^{ \emptyset } } e \) and \( e \) does not get stuck.
5 Related Work
5.1 Polymorphic Effects and Let-Polymorphism
Many researchers have attacked the problem of combining effects—not necessarily algebraic—and let-polymorphism so far [1, 2, 10, 12, 14, 17, 23, 24]. In particular, most of them have focused on ML-style polymorphic references. The algebraic effect handlers dealt with in this paper seem to be unable to implement general ML-style references—i.e., give an appropriate implementation to a set of effect operations new with the signature
 , get with
, get with
 , and put with
, and put with
 for abstract datatype \( \alpha \, \mathsf {ref} \)—even without the restriction on handlers because each operation clause in a handler assigns type variables locally and it is impossible to share such type variables between operation clauses.Footnote 6 Nevertheless, their approaches would be applicable to algebraic effects and handlers.
for abstract datatype \( \alpha \, \mathsf {ref} \)—even without the restriction on handlers because each operation clause in a handler assigns type variables locally and it is impossible to share such type variables between operation clauses.Footnote 6 Nevertheless, their approaches would be applicable to algebraic effects and handlers.
A common idea in the literature is to restrict the form of expressions bound by polymorphic let. Thus, they are complementary to our approach in that they restrict how effect operations are used whereas we restrict how effect operations are implemented.
Value restriction [23, 24], a standard way adopted in ML-like languages, restricts polymorphic let-bound expressions to syntactic values. Garrigue [10] relaxes the value restriction so that, if a let-bound expression is not a syntactic value, type variables that appear only at positive positions in the type of the expression can be generalized. Although the (relaxed) value restriction is a quite clear criterion that indicates what let-bound expressions can be polymorphic safely and it even accepts interfering handlers, it is too restrictive in some cases. We give an example for such a case below.

In the definition of function f1, variable g is used polymorphically. Execution of this function under an appropriate handler would succeed, and in fact our calculus accepts it. By contrast, the (relaxed) value restriction rejects it because the let-bound expression
 is not a syntactic value and the type variable appear in both positive and negative positions, and so g is assigned a monomorphic type. A workaround for this problem is to make a function wrapper that calls either of fst or snd depending on the Boolean value chosen by
is not a syntactic value and the type variable appear in both positive and negative positions, and so g is assigned a monomorphic type. A workaround for this problem is to make a function wrapper that calls either of fst or snd depending on the Boolean value chosen by
 :
:

However, this workaround makes the program complicated and incurs additional run-time cost for the branching and an extra call to the wrapper function.
Asai and Kameyama [2] study a combination of let-polymorphism with delimited control operators shift/reset [4]. They allow a let-bound expression to be polymorphic if it invokes no control operation. Thus, the function f1 above would be rejected in their approach.
Another research line to restrict the use of effects is to allow only type variables unrelated to effect invocations to be generalized. Tofte [23] distinguishes between applicative type variables, which cannot be used for effect invocations, and imperative ones, which can be used, and proposes a type system that enforces restrictions that (1) type variables of imperative operations can be instantiated only with types wherein all type variables are imperative and (2) if a let-bound expression is not a syntactic value, only applicative type variables can be generalized. Leroy and Weis [17] allow generalization only of type variables that do not appear in a parameter type to the reference type in the type of a let-expression. To detect the hidden use of references, their type system gives a term not only a type but also the types of free variables used in the term. Standard ML of New Jersey (before ML97) adopted weak polymorphism [1], which was later formalized and investigated deeply by Hoang et al. [12]. Weak polymorphism equips a type variable with the number of function calls after which a value of a type containing the type variable will be passed to an imperative operation. The type system ensures that type variables with positive numbers are not related to imperative constructs, and so such type variables can be generalized safely. In this line of research, the function f1 above would not typecheck because generalized type variables are used to instantiate those of the effect signature, although it could be rewritten to an acceptable one by taking care not to involve type variables in effect invocation.

More recently, Kammar and Pretnar [14] show that parameterized algebraic effects and handlers do not need the value restriction if the type variables used in an effect invocation are not generalized. Thus, as the other work that restricts generalized type variables, their approach would reject function f1 but would accept f3.
5.2 Algebraic Effects and Handlers
Algebraic effects [20] are a way to represent the denotation of an effect by giving a set of operations and an equational theory that capture their properties. Algebraic effect handlers, introduced by Plotkin and Pretnar [21], make it possible to provide user-defined effects. Algebraic effect handlers have been gaining popularity owing to their flexibility and have been made available as libraries [13, 15, 26] or as primitive features of languages, such as Eff [3], Koka [16], Frank [18], and Multicore OCaml [5]. In these languages, let-bound expressions that can be polymorphic are restricted to values or pure expressions.
Recently, Forster et al. [9] investigate the relationships between algebraic effect handlers and other mechanisms for user-defined effects—delimited control shift0 [19] and monadic reflection [7, 8]—conjecturing that there would be no type-preserving translation from a language with delimited control or monadic reflection to one with algebraic effect handlers. It would be an interesting direction to export our idea to delimited control and monadic reflection.
6 Conclusion
There has been a long history of collaboration between effects and let-polymorphism. This work focuses on polymorphic algebraic effects and handlers, wherein the type signature of an effect operation can be polymorphic and an operation clause has a type binder, and shows that a naive combination of polymorphic effects and let-polymorphism breaks type safety. Our novel observation to address this problem is that any let-bound expression can be polymorphic safely if resumptions from a handler do not interfere with each other. We formalized this idea by developing a type system that requires the argument of each resumption expression to have a type obtained by renaming the type variables assigned in the operation clause to those assigned in the resumption. We have proven that a well-typed program in our type system does not get stuck via elaboration to an intermediate language wherein type information appears explicitly.
There are many directions for future work. The first is to address the problem, described at the end of Sect. 3, that renaming the type variables assigned in an operation clause to those assigned in a resumption expression is allowed for the argument of the clause but not for variables bound by lambda abstractions and let-expressions outside the resumption expression. Second, we are interested in incorporating other features from the literature on algebraic effect handlers, such as dynamic resources [3] and parameterized algebraic effects, and restriction techniques that have been developed for type-safe imperative programming with let-polymorphism such as (relaxed) value restriction [10, 23, 24]. For example, we would like to develop a type system that enforces the non-interfering restriction only to handlers implementing effect operations invoked in polymorphic computation. We also expect that it is possible to determine whether implementations of an effect operation have no interfering resumption from the type signature of the operation, as relaxed value restriction makes it possible to find safely generalizable type variables from the type of a let-bound expression [10]. Finally, we are also interested in implementing our idea for a language with effect handlers such as Koka [16] and in applying the idea of analyzing handlers to other settings such as dependent typing.
Notes
- 1.
Here, “; -1” is necessary to make the types of both branches the same; it becomes unnecessary when we introduce polymorphic effects.
- 2.
We can think of more practical implementations, which choose one of the two arguments by other means, say, random values.
- 3.
One might implement rand as another effect operation.
- 4.
We compare our approach with the standard approaches in Sect. 5 in detail.
- 5.
Thus, handlers in \(\lambda _\text {eff}^\text {let}\) are open [13] in the sense that a \( \mathsf {handle} \)–\( \mathsf {with} \) expression does not have to handle all effects caused by the handled expression.
- 6.
One possible approach to dealing with ML-style references is to extend algebraic effects and handlers so that a handler for parameterized effects can be connected with dynamic resources [3].
References
Appel, A.W., MacQueen, D.B.: Standard ML of New Jersey. In: Maluszyński, J., Wirsing, M. (eds.) PLILP 1991. LNCS, vol. 528, pp. 1–13. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54444-5_83
Asai, K., Kameyama, Y.: Polymorphic delimited continuations. In: Shao, Z. (ed.) APLAS 2007. LNCS, vol. 4807, pp. 239–254. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76637-7_16
Bauer, A., Pretnar, M.: Programming with algebraic effects and handlers. J. Log. Algebr. Methods Program. 84(1), 108–123 (2015). https://doi.org/10.1016/j.jlamp.2014.02.001
Danvy, O., Filinski, A.: Abstracting control. In: LISP and Functional Programming, pp. 151–160 (1990). https://doi.org/10.1145/91556.91622
Dolan, S., Eliopoulos, S., Hillerström, D., Madhavapeddy, A., Sivaramakrishnan, K.C., White, L.: Concurrent system programming with effect handlers. In: Wang, M., Owens, S. (eds.) TFP 2017. LNCS, vol. 10788, pp. 98–117. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89719-6_6
Felleisen, M., Hieb, R.: The revised report on the syntactic theories of sequential control and state. Theor. Comput. Sci. 103(2), 235–271 (1992). https://doi.org/10.1016/0304-3975(92)90014-7
Filinski, A.: Representing monads. In: Proceedings of the 21st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 446–457 (1994). https://doi.org/10.1145/174675.178047
Filinski, A.: Monads in action. In: Proceedings of the 37th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2010, pp. 483–494 (2010). https://doi.org/10.1145/1706299.1706354
Forster, Y., Kammar, O., Lindley, S., Pretnar, M.: On the expressive power of user-defined effects: effect handlers, monadic reflection, delimited control. PACMPL 1(ICFP), 13:1–13:29 (2017). https://doi.org/10.1145/3110257
Garrigue, J.: Relaxing the value restriction. In: Kameyama, Y., Stuckey, P.J. (eds.) FLOPS 2004. LNCS, vol. 2998, pp. 196–213. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24754-8_15
Harper, R., Lillibridge, M.: Polymorphic type assignment and CPS conversion. Lisp Symb. Comput. 6(3–4), 361–380 (1993)
Hoang, M., Mitchell, J.C., Viswanathan, R.: Standard ML-NJ weak polymorphism and imperative constructs. In: Proceedings of the Eighth Annual Symposium on Logic in Computer Science, LICS 1993 (1993)
Kammar, O., Lindley, S., Oury, N.: Handlers in action. In: ACM SIGPLAN International Conference on Functional Programming, ICFP 2013, pp. 145–158 (2013). https://doi.org/10.1145/2500365.2500590
Kammar, O., Pretnar, M.: No value restriction is needed for algebraic effects and handlers. J. Funct. Program. 27, e7 (2017). https://doi.org/10.1017/S0956796816000320
Kiselyov, O., Ishii, H.: Freer monads, more extensible effects. In: Proceedings of the 8th ACM SIGPLAN Symposium on Haskell, Haskell 2015, pp. 94–105 (2015). https://doi.org/10.1145/2804302.2804319
Leijen, D.: Type directed compilation of row-typed algebraic effects. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, pp. 486–499 (2017). http://dl.acm.org/citation.cfm?id=3009872
Leroy, X., Weis, P.: Polymorphic type inference and assignment. In: Proceedings of the 18th Annual ACM Symposium on Principles of Programming Languages, pp. 291–302 (1991). https://doi.org/10.1145/99583.99622
Lindley, S., McBride, C., McLaughlin, C.: Do be do be do. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, pp. 500–514 (2017). http://dl.acm.org/citation.cfm?id=3009897
Materzok, M., Biernacki, D.: A dynamic interpretation of the CPS hierarchy. In: Jhala, R., Igarashi, A. (eds.) APLAS 2012. LNCS, vol. 7705, pp. 296–311. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35182-2_21
Plotkin, G.D., Power, J.: Algebraic operations and generic effects. Appl. Categ. Struct. 11(1), 69–94 (2003). https://doi.org/10.1023/A:1023064908962
Plotkin, G.D., Pretnar, M.: Handlers of algebraic effects. In: Castagna, G. (ed.) ESOP 2009. LNCS, vol. 5502, pp. 80–94. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00590-9_7
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: IFIP Congress, pp. 513–523 (1983)
Tofte, M.: Type inference for polymorphic references. Inf. Comput. 89(1), 1–34 (1990). https://doi.org/10.1016/0890-5401(90)90018-D
Wright, A.K.: Simple imperative polymorphism. Lisp Symb. Comput. 8(4), 343–355 (1995)
Wright, A.K., Felleisen, M.: A syntactic approach to type soundness. Inf. Comput. 115(1), 38–94 (1994). https://doi.org/10.1006/inco.1994.1093
Wu, N., Schrijvers, T., Hinze, R.: Effect handlers in scope. In: Proceedings of the 2014 ACM SIGPLAN Symposium on Haskell, Haskell 2014, pp. 1–12 (2014). https://doi.org/10.1145/2633357.2633358
Acknowledgments
We would like to thank the anonymous reviewers for their valuable comments. This work was supported in part by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST (Sekiyama), and JSPS KAKENHI Grant Number JP15H05706 (Igarashi).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Sekiyama, T., Igarashi, A. (2019). Handling Polymorphic Algebraic Effects. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)





 —“alters” the type of
—“alters” the type of 






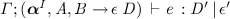 , then
, then
 .
. , then
, then
 .
.