Abstract
Modern software is no more developed in a single programming language. Instead, programmers tend to exploit cross-language interoperability mechanisms to combine code stemming from different languages, and thus yielding fully-fledged multi-language programs. Whilst this approach enables developers to benefit from the strengths of each single-language, on the other hand it complicates the semantics of such programs. Indeed, the resulting multi-language does not meet any of the semantics of the combined languages. In this paper, we broaden the boundary functions-based approach à la Matthews and Findler to propose an algebraic framework that provides a constructive mathematical notion of multi-language able to determine its semantics. The aim of this work is to overcome the lack of a formal method (resp., model) to design (resp., represent) a multi-language, regardless of the inherent nature of the underlying languages. We show that our construction ensures the uniqueness of the semantic function (i.e., the multi-language semantics induced by the combined languages) by proving the initiality of the term model (i.e., the abstract syntax of the multi-language) in its category.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Two elementary arguments lie at the heart of the multi-language paradigm: the large availability of existing programming languages, along with a very high number of already written libraries, and software that, in general, needs to interoperate. Although there is consensus in claiming that there is no best programming language regardless of the context [4, 8], it is equally true that many of them are conceived and designed in order to excel for specific tasks. Such examples are R for statistical and graphical computation, Perl for data wrangling, Assembly and C for low-level memory management, etc. “Interoperability between languages has been a problem since the second programming language was invented” [8], so it is hardly surprising that developers have focused on the design of cross-language interoperability mechanisms, enabling programmers to combine code written in different languages. In this sense, we speak of multi-languages.
The field of cross-language interoperability has been driven more by practical concerns than by theoretical questions. The current scenario sees several engines and frameworks [13, 28, 29, 44, 47] (among others) to mix programming languages but only [30] discusses the semantic issues related to the multi-language design from a theoretical perspective. Moreover, the existing interoperability mechanisms differ considerably not only from the viewpoint of the combined languages, but also in terms of the approach used to provide the interoperation. For instance, Nashorn [47] is a JavaScript interpreter written in Java to allow embedding JavaScript in Java applications. Such engineering design works in a similar fashion of embedded interpreters [40, 41].Footnote 1 On the contrary, Java Native Interface (JNI) framework [29] enables the interoperation of Java with native code written in C,
 , or Assembly through external procedure calls between languages, mirroring the widespread mechanism of foreign function interfaces (FFI) [14], whereas theoretical papers follow the more elegant approach of boundary functions (or, for short, boundaries) in the style of Matthews and Findler’s multi-language semantics [30]. Simply put, boundaries act as a gate between single-languages. When a value needs to flow on the other language, they perform a conversion so that it complies to the other language specifications.
, or Assembly through external procedure calls between languages, mirroring the widespread mechanism of foreign function interfaces (FFI) [14], whereas theoretical papers follow the more elegant approach of boundary functions (or, for short, boundaries) in the style of Matthews and Findler’s multi-language semantics [30]. Simply put, boundaries act as a gate between single-languages. When a value needs to flow on the other language, they perform a conversion so that it complies to the other language specifications.
The major issue concerning this new paradigm is that multi-language programs do not obey any of the semantics of the combined languages. As a consequence, any method of formal reasoning (such as static program analysis or verification) is neutralized by the absence of a semantics specification. In this paper, we propose an algebraic framework based on the mechanism of boundary functions [30] that unambiguously yields the syntax and the semantics of the multi-language regardless the combined languages.
The Lack of a Multi-Language Framework. The notion of multi-language is employed naively in several works in literature [2, 14, 21, 30, 35,36,37, 49] to indicate the embedding of two programming languages into a new one, with its own syntax and semantics.
The most recurring way to design a multi-language is to exploit a mechanism (like embedded interpreters, FFI, or boundary functions) able to regulate both control flow and value conversion between the underlying languages [30], thus adequate to provide cross-language interoperability [8]. The full construction is usually carried out manually by language designers, which define the multi-language by reusing the formal specifications of the single-languages [2, 30, 36, 37] and by applying the selected mechanism for achieving the interoperation. Inevitably, therefore, all these resulting multi-languages notably differ one from another.
These different ways to achieve a cross-language interoperation are all attributable to the lack of a formal description of multi-language that does not provide neither a method for language designers to conceive new multi-languages nor any guarantee on the correctness of such constructions.
The Proposed Framework: Roadmap and Contributions. Matthews and Findler [30] propose boundary functions as a way to regulate the flow of values between languages. They show their approach on different variants of the same multi-language obtained by mixing ML [33] and Scheme [9], representing two “syntactically sugared” versions of the simply-typed and untyped lambda calculi, respectively.
Rather than showing the embedding of two fixed languages, we extend their approach to the much broader class of order-sorted algebras [19] with the aim of providing a framework that works regardless of the inherent nature of the combined languages. There are a number of reasons to choose order-sorted algebras as the underlying framework for generalizing the multi-language construction. From the first formulation of initial algebra semantics [17], the algebraic approach to program semantics [16] has become a cornerstone in the theory of programming languages [27]. Order-sorted algebras provide a mathematical tool for representing formal systems as algebraic structures through a systematic use of the notion of sort and subsort to model different forms of polymorphism [18, 19], a key aspect when dealing with multi-languages sharing operators among the single-languages. They were initially proposed to ensure a rigorous model-theoretic semantics for error handling, multiple inheritance, retracts, selectors for multiple constructors, polymorphism, and overloading. In the years, several uses [3, 6, 11, 24, 25, 38, 39, 52] and different variants [38, 43, 45, 51] have been proposed for order-sorted algebras, making them a solid starting point for the development of a new framework. In particular, results on rewriting logic [32] extend easily to the order-sorted case [31], thus facilitating a future extension of this paper towards the operational semantics world. Improvements of the order-sorted algebra framework have also been proposed to model languages together with their type systems [10] and to extend order-sorted specification with high-order functions [38] (see [48] and [18] for detailed surveys).
In this paper, we propose three different multi-language constructions according to the semantic properties of boundary functions. The first one models a general notion of multi-language that do not require any constraints on boundaries (Sect. 3). We argue that when such generality is superfluous, we can achieve a neater approach where boundary functions do not need to be annotated with sorts. Indeed, we show that when the cross-language conversion of a term does not depend on the sort at which the term is considered (i.e., when boundaries are subsort polymorphic) the framework is powerful enough to apply the correct conversion (Sect. 4.1). This last construction is an improvement of the original notion of boundaries in [30]. From a practical point of view, it allows programmers to avoid to explicitly deal with sorts when writing code, a non-trivial task that could introduce type cast bugs in real world languages. Finally, we provide a very specific notion of multi-language where no extra operator is added to the syntax (Sect. 4.2). This approach is particularly useful to extend a language in a modular fashion and ensuring the backward compatibility with “old” programs. For each one of these variants we prove an initiality theorem, which in turn ensures the uniqueness of the multi-language semantics and thereby legitimating the proposed framework. Moreover, we show that the framework guarantees a fundamental closure property on the construction: The resulting multi-language admits an order-sorted representation, i.e., it falls within the same formal model of the combined languages. Finally, we model the multi-language designed in [30] in order to show an instantiation of the framework (Sect. 6).
2 Background
All the algebraic background of the paper is firstly stated in [15, 17, 19]. We briefly introduce here the main definitions and results, and we illustrate them on a simple running example.
Given a set of sorts S, an S-sorted set A is a family of sets indexed by S, i.e.,  . Similarly, an S-sorted function
. Similarly, an S-sorted function  is a family of functions
is a family of functions  . We stick to the convention of using s and w as metavariables for sorts in S and \(S^*\), respectively, and we use the \(\mathbb {blackboard}\) \(\mathbb {bold}\) typeface to indicate a specific sort in S. In addition, if A is an S-sorted set and \(w = s_1\ldots s_n \in S^+\), we denote by \(A_w\) the cartesian product \(A_{s_1} \times \cdots \times A_{s_n}\). Likewise, if f is an S-sorted function and \(a_i \in A_{s_i}\) for \(i = 1, \ldots , n\), then the function
. We stick to the convention of using s and w as metavariables for sorts in S and \(S^*\), respectively, and we use the \(\mathbb {blackboard}\) \(\mathbb {bold}\) typeface to indicate a specific sort in S. In addition, if A is an S-sorted set and \(w = s_1\ldots s_n \in S^+\), we denote by \(A_w\) the cartesian product \(A_{s_1} \times \cdots \times A_{s_n}\). Likewise, if f is an S-sorted function and \(a_i \in A_{s_i}\) for \(i = 1, \ldots , n\), then the function  is such that \(f_w(a_1, \ldots , a_n) = (f_{s_1}(a_1), \ldots , f_{s_n}(a_n))\). Given \(P \subseteq S\), the restriction of an S-sorted function f to P is denoted by
is such that \(f_w(a_1, \ldots , a_n) = (f_{s_1}(a_1), \ldots , f_{s_n}(a_n))\). Given \(P \subseteq S\), the restriction of an S-sorted function f to P is denoted by  and it is the P-sorted function
and it is the P-sorted function  . Finally, if
. Finally, if  is a function, we still use the symbol g to denote the direct image map of g (also called the additive lift of g), i.e., the function
is a function, we still use the symbol g to denote the direct image map of g (also called the additive lift of g), i.e., the function
 such that
such that  . Analogously, if \(\le \) is a binary relation on a set A (with elements \(a \in A\)), we use the same relation symbol to denote its pointwise extension, i.e., we write \(a_1 \ldots a_n \le a'_1\ldots a'_n\) for \(a_1 \le a'_1, \ldots , a_n \le a'_n\).
. Analogously, if \(\le \) is a binary relation on a set A (with elements \(a \in A\)), we use the same relation symbol to denote its pointwise extension, i.e., we write \(a_1 \ldots a_n \le a'_1\ldots a'_n\) for \(a_1 \le a'_1, \ldots , a_n \le a'_n\).
The basic notions underpinning the order-sorted algebra framework are the definitions of signature, that models symbols forming terms of the language, and algebra, that provides an algebraic meaning to symbols.
Definition 1
(Order-Sorted Signature). An order-sorted signature is a triple  , where S is a set of sorts, \(\le \) is a binary relation on S, and \(\varSigma \) is an \(S^* \times S\)-sorted set
, where S is a set of sorts, \(\le \) is a binary relation on S, and \(\varSigma \) is an \(S^* \times S\)-sorted set  , satisfying the following conditions:
, satisfying the following conditions:
-
(1os)
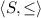 is a poset; and
is a poset; and -
(2os) \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and \(w_1 \le w_2\) imply \(s_1 \le s_2\).
If \(\sigma \in \varSigma _{w, s}\) (or,  and \(\sigma :s\) when \(w = \varepsilon \), as shorthands), we call \(\sigma \) an operator (symbol) or function symbol, w the arity, s the sort, and (w, s) the rank of \(\sigma \); if \(w = \varepsilon \), we say that \(\sigma \) is a constant (symbol). We name \(\le \) the subsort relation and \(\varSigma \) a signature when
and \(\sigma :s\) when \(w = \varepsilon \), as shorthands), we call \(\sigma \) an operator (symbol) or function symbol, w the arity, s the sort, and (w, s) the rank of \(\sigma \); if \(w = \varepsilon \), we say that \(\sigma \) is a constant (symbol). We name \(\le \) the subsort relation and \(\varSigma \) a signature when  is clear from the context. We abuse notation and write \(\sigma \in \varSigma \) when \(\sigma \in \bigcup _{w, s}\varSigma _{w, s}\).
is clear from the context. We abuse notation and write \(\sigma \in \varSigma \) when \(\sigma \in \bigcup _{w, s}\varSigma _{w, s}\).
Definition 2
(Order-Sorted Algebra). An order-sorted  -algebra \(\mathcal {A}\) over an order-sorted signature
-algebra \(\mathcal {A}\) over an order-sorted signature  is an S-sorted set A of interpretation domains (or, carrier sets or semantic domains)
is an S-sorted set A of interpretation domains (or, carrier sets or semantic domains)  , together with interpretation functions
, together with interpretation functions  (or, if \(w = \varepsilon \),
(or, if \(w = \varepsilon \),  )Footnote 2 for each \(\sigma \in \varSigma _{w, s}\), such that:
)Footnote 2 for each \(\sigma \in \varSigma _{w, s}\), such that:
-
(1oa) \(s \le s'\) implies \(A_s \subseteq A_{s'}\); and
-
(2oa) \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and \(w_1 \le w_2\) imply that
 for each \(a \in A_{w_1}\).
for each \(a \in A_{w_1}\).
An important property of signatures, related to polymorphism, is regularity. Its relevance lies in the possibility of linking each term to a unique least sort (see Proposition 2.10 in [19]).
Definition 3
(Regularity of an Order-Sorted Signature). An order-sorted signature  is regular if for each \(\sigma \in \varSigma _{\tilde{w}, \tilde{s}}\) and for each lower bound \(w_0 \le \tilde{w}\) the set
is regular if for each \(\sigma \in \varSigma _{\tilde{w}, \tilde{s}}\) and for each lower bound \(w_0 \le \tilde{w}\) the set  has minimum. This minimum is called least rank of \(\sigma \) with respect to \(w_0\).
has minimum. This minimum is called least rank of \(\sigma \) with respect to \(w_0\).
The freely generated algebra \(\mathcal {T}_\varSigma \) over a given signature  provides the notion of term with respect to
provides the notion of term with respect to  .
.
Definition 4
(Order-Sorted Term Algebra). Let  be an order-sorted signature. The order-sorted term
be an order-sorted signature. The order-sorted term  -algebra \(\mathcal {T}_\varSigma \) is an order-sorted algebra such that:
-algebra \(\mathcal {T}_\varSigma \) is an order-sorted algebra such that:
-
The S-sorted set
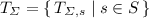 is inductively defined as the least family satisfying:
is inductively defined as the least family satisfying:-
(1ot)
\(\varSigma _{\varepsilon , s} \subseteq T_{\varSigma , s}\);
-
(2ot)
\(s \le s'\) implies \(T_{\varSigma , s} \subseteq T_{\varSigma , s'}\); and
-
(3ot)
\(\sigma \in \varSigma _{w, s}\), \(w = s_1\ldots s_n \in S^+\), and \(t_i \in T_{\varSigma , s_i}\) for \(i = 1, \ldots , n\) imply
 .
.
-
(1ot)
-
For each \(\sigma \in \varSigma _{w, s}\) the interpretation function
 is defined as
is defined as-
(4ot)
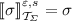 if \(\sigma \in \varSigma _{\varepsilon , s}\); and
if \(\sigma \in \varSigma _{\varepsilon , s}\); and -
(5ot)
 if \(\sigma \in \varSigma _{w, s}\), \(w = s_1\ldots s_n \in S^+\), and \(t_i \in T_{\varSigma , s_i}\) for \(i = 1, \ldots , n\).
if \(\sigma \in \varSigma _{w, s}\), \(w = s_1\ldots s_n \in S^+\), and \(t_i \in T_{\varSigma , s_i}\) for \(i = 1, \ldots , n\).
-
(4ot)
Homomorphisms between algebras capture the compositionality nature of semantics: The meaning of a term is determined by the meanings of its constituents. They are defined as order-sorted functions that preserve the interpretation of operators.
Definition 5
(Order-Sorted Homomorphism). Let \(\mathcal {A}\) and \(\mathcal {B}\) be  -algebras. An order-sorted
-algebras. An order-sorted  -homomorphism from \(\mathcal {A}\) to \(\mathcal {B}\), denoted by
-homomorphism from \(\mathcal {A}\) to \(\mathcal {B}\), denoted by  , is an S-sorted function
, is an S-sorted function  such that:
such that:
-
(1oh)
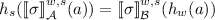 for each \(\sigma \in \varSigma _{w, s}\) and \(a \in A_w\); and
for each \(\sigma \in \varSigma _{w, s}\) and \(a \in A_w\); and -
(2oh)
\(s \le s'\) implies \(h_s(a) = h_{s'}(a)\) for each \(a \in A_s\).
The class of all the order-sorted  -algebras and the class of all order-sorted
-algebras and the class of all order-sorted  -homomorphisms form a category denote by
-homomorphisms form a category denote by  . Furthermore, the homomorphism definition determines the property of the term algebra \(\mathcal {T}_\varSigma \) of being an initial object in its category whenever the signature is regular. Since initiality is preserved by isomorphisms, it allows to identify \(\mathcal {T}_\varSigma \) with the abstract syntax of the language. If \(\mathcal {T}_\varSigma \) is initial, the homomorphism leaving \(\mathcal {T}_\varSigma \) and going to an algebra \(\mathcal {A}\) is called the semantic function (with respect to \(\mathcal {A}\)).
. Furthermore, the homomorphism definition determines the property of the term algebra \(\mathcal {T}_\varSigma \) of being an initial object in its category whenever the signature is regular. Since initiality is preserved by isomorphisms, it allows to identify \(\mathcal {T}_\varSigma \) with the abstract syntax of the language. If \(\mathcal {T}_\varSigma \) is initial, the homomorphism leaving \(\mathcal {T}_\varSigma \) and going to an algebra \(\mathcal {A}\) is called the semantic function (with respect to \(\mathcal {A}\)).
Example. Let \(L_1\) and \(L_2\) be two formal languages (see Fig. 1). The former is a language to construct simple mathematical expressions: \(n \in \mathbb {N}\) is the metavariable for natural numbers, while e inductively generates all the possible additions (Fig. 1a). The latter is a language to build strings over a finite alphabet of symbols  :
:  is the metavariable for atoms (or, characters), whereas s concatenates them into strings (Fig. 1b). A term in \(L_1\) and \(L_2\) denotes an element in the sets
is the metavariable for atoms (or, characters), whereas s concatenates them into strings (Fig. 1b). A term in \(L_1\) and \(L_2\) denotes an element in the sets  and
and  , accordingly to equations in Fig. 2a and b, respectively.
, accordingly to equations in Fig. 2a and b, respectively.
The syntax of the language \(L_1\) can be modeled by an order-sorted signature  defined as follows:
defined as follows:
 , a set with sorts
, a set with sorts
 (stands for expressions) and
(stands for expressions) and
 (stands for natural numbers); \(\le _1\) is the reflexive relation on \(S_1\) plus
(stands for natural numbers); \(\le _1\) is the reflexive relation on \(S_1\) plus
 (natural numbers are expressions); and the operators in \(\varSigma _1\) are
(natural numbers are expressions); and the operators in \(\varSigma _1\) are
 and
and
 . Similarly, the signature
. Similarly, the signature  models the syntax of the language \(L_2\): the set
models the syntax of the language \(L_2\): the set
 carries the sort for strings
carries the sort for strings
 and the sort for atomic symbols (or, characters)
and the sort for atomic symbols (or, characters)
 the subsort relation \(\le _2\) is the reflexive relation on \(S_2\) plus
the subsort relation \(\le _2\) is the reflexive relation on \(S_2\) plus
 (characters are one-symbol strings); and the operator symbols in \(\varSigma _2\) are
(characters are one-symbol strings); and the operator symbols in \(\varSigma _2\) are
 ,
,
 and
and
 . Semantics of \(L_1\) and \(L_2\) can be embodied by algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) over the signatures
. Semantics of \(L_1\) and \(L_2\) can be embodied by algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) over the signatures  and
and  , respectively. We set the interpretation domains of \(\mathcal {A}_1\) to
, respectively. We set the interpretation domains of \(\mathcal {A}_1\) to
 and those of \(\mathcal {A}_2\) to
and those of \(\mathcal {A}_2\) to
 . Moreover, we define the interpretation functions as follows (the juxtaposition of two or more strings denotes their concatenation, and we use \(\hat{a}\) as metavariable ranging over
. Moreover, we define the interpretation functions as follows (the juxtaposition of two or more strings denotes their concatenation, and we use \(\hat{a}\) as metavariable ranging over  ):
):

Since  and
and  are regular, then \(\mathcal {A}_1\) and \(\mathcal {A}_2\) induce the semantic functions
are regular, then \(\mathcal {A}_1\) and \(\mathcal {A}_2\) induce the semantic functions  and
and  , providing semantics to the languages.
, providing semantics to the languages.
3 Combining Order-Sorted Theories
The first step towards a multi-language specification is the choice of which terms of one language can be employed in the others [30, 35, 36]. For instance, a multi-language requirement could demand to use ML expressions in place of Scheme expressions and, possibly, but not necessarily, vice versa (such a multi-language is designed in [30]). A multi-language signature is an amenable formalism to specify the compatibility relation between syntactic categories across two languages.
Definition 6
(Multi-Language Signature). A multi-language signature is a triple  , where
, where  and
and  are order-sorted signatures, and \(\le \) is a binary relation on \(S = S_1 \cup S_2\), such that satisfies the following condition:
are order-sorted signatures, and \(\le \) is a binary relation on \(S = S_1 \cup S_2\), such that satisfies the following condition:
-
(1s)
\(s, s' \in S_i\) implies \(s \le s'\) if and only if \(s \le _i s'\), for \(i = 1,2\).
To make the notation lighter, we introduce the following binary relations on S: \(s \ltimes s'\) if \(s \le s'\) but neither \(s \le _1 s'\) nor \(s \le _2 s'\), and \(s \preccurlyeq s'\) if \(s \le s'\) but not \(s \ltimes s'\).
In the following, we always assume that the sets of sorts \(S_1\) and \(S_2\) of the order-sorted signatures  and
and  are disjoint.Footnote 3 Condition (1s) requires the multi-language subsort relation \(\le \) to preserve the original subsort relations \(\le _1\) and \(\le _2\) (i.e., \(\mathord {\le } \cap S_i \times S_i = \mathord {\le _i}\)). The join relation \(\ltimes \) provides a compatibility relation between sortsFootnote 4 in
are disjoint.Footnote 3 Condition (1s) requires the multi-language subsort relation \(\le \) to preserve the original subsort relations \(\le _1\) and \(\le _2\) (i.e., \(\mathord {\le } \cap S_i \times S_i = \mathord {\le _i}\)). The join relation \(\ltimes \) provides a compatibility relation between sortsFootnote 4 in  and
and  . More precisely, \(S_i \ni s \ltimes s' \in S_j\) suggests that we want to use terms in \(T_{\varSigma _i, s}\) in place of terms in \(T_{\varSigma _j, s'}\), whereas the intra-language subsort relation \(\preccurlyeq \) shifts the standard notion of subsort from the order-sorted to the multi-language world. In a nutshell, the relation \(\mathord {\le } = \mathord {\preccurlyeq } \cup \mathord {\ltimes }\) can only join (through \(\ltimes \)) the underlying languages without introducing distortions (indeed, \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\)).
. More precisely, \(S_i \ni s \ltimes s' \in S_j\) suggests that we want to use terms in \(T_{\varSigma _i, s}\) in place of terms in \(T_{\varSigma _j, s'}\), whereas the intra-language subsort relation \(\preccurlyeq \) shifts the standard notion of subsort from the order-sorted to the multi-language world. In a nutshell, the relation \(\mathord {\le } = \mathord {\preccurlyeq } \cup \mathord {\ltimes }\) can only join (through \(\ltimes \)) the underlying languages without introducing distortions (indeed, \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\)).
The role of an algebra is to provide an interpretation domain for each sort, as well as the meaning of every operator symbol in a given signature. When moving towards the multi-language context, the join relation \(\ltimes \) may add subsort constraints between sorts belonging to different signatures. Consequently, if \(s \ltimes s'\), a multi-language algebra has to specify how values of sort s may be interpreted as values of sort \(s'\). These specifications are called boundary functions [30] and provide an algebraic meaning to the subsort constraints added by \(\ltimes \). Henceforth, we define \(S = S_1 \cup S_2\), \(\varSigma = \varSigma _1 \cup \varSigma _2\), and, given \((w, s) \in S_i^* \times S_i\), we denote by \(\varSigma ^i_{w, s}\) the (w, s)-sorted component in \(\varSigma _i\).
Definition 7
(Multi-Language Algebra). Let  be a multi-language signature. A multi-language
be a multi-language signature. A multi-language  -algebra \(\mathcal {A}\) is an S-sorted set A of interpretation domains (or, carrier sets or semantic domains)
-algebra \(\mathcal {A}\) is an S-sorted set A of interpretation domains (or, carrier sets or semantic domains)  , together with interpretation functions
, together with interpretation functions  for each \(\sigma \in \varSigma _{w, s}\), and with a \(\ltimes \)-sorted set \(\alpha \) of boundary functions
for each \(\sigma \in \varSigma _{w, s}\), and with a \(\ltimes \)-sorted set \(\alpha \) of boundary functions  , such that the following constraint holds:
, such that the following constraint holds:
-
(1a)
the projected algebra \(\mathcal {A}_i\), where \(i = 1,2\), specified by the carrier set
 and interpretation functions
and interpretation functions  for each \(\sigma \in \varSigma ^i_{w,s}\), must be an order-sorted
for each \(\sigma \in \varSigma ^i_{w,s}\), must be an order-sorted 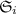 -algebra.
-algebra.
If \(\mathcal {M}\) is an algebra, we adopt the convention of denoting by M (standard math font) its carrier set and by \(\mu \) (Greek math font) its boundary functions whenever possible. Condition (1a) is the semantic counterpart of condition (1s): It requires the multi-language to carry (i.e., preserve) the underlying languages order-sorted algebras, whereas the boundary functions model how values can flow between languages.
Given two multi-language  -algebras \(\mathcal {A}\) and \(\mathcal {B}\) we can define morphisms between them that preserve the sorted structure of the underlying projected algebras.
-algebras \(\mathcal {A}\) and \(\mathcal {B}\) we can define morphisms between them that preserve the sorted structure of the underlying projected algebras.
Definition 8
(Multi-Language Homomorphism). Let \(\mathcal {A}\) and \(\mathcal {B}\) be multi-language  -algebras with sets of boundary functions \(\alpha \) and \(\beta \), respectively. A multi-language
-algebras with sets of boundary functions \(\alpha \) and \(\beta \), respectively. A multi-language  -homomorphism
-homomorphism  is an S-sorted function
is an S-sorted function  such that:
such that:
-
(1h)
the restriction
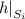 is an order-sorted
is an order-sorted 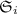 -homomorphism
-homomorphism  , for \(i = 1,2\); and
, for \(i = 1,2\); and -
(2h)
\(s \ltimes s'\) implies \(h_{s'} \circ \alpha _{s,s'} = \beta _{s,s'} \circ h_s\).
Conditions (1h) and (2h) are easily intelligible when the domain algebra is the abstract syntax of the language [15]: Simply put, both conditions require the semantics of a term to be a function of the meaning of its subterms, in the sense of [15, 46]. In particular, the second condition demands that boundary functions act as operators.Footnote 5
The identity homomorphism on a multi-language algebra \(\mathcal {A}\) is denoted by
 and it is the set-theoretic identity on the carrier set A of the algebra \(\mathcal {A}\). The composition of two homomorphisms
and it is the set-theoretic identity on the carrier set A of the algebra \(\mathcal {A}\). The composition of two homomorphisms  and
and  is defined as the sorted function composition
is defined as the sorted function composition  , thus
, thus
 and associativity follows easily by the definition of \(\circ \).
and associativity follows easily by the definition of \(\circ \).
Proposition 1
Multi-language homomorphisms are closed under composition.
Hence, as in the many-sorted and order-sorted case [15, 19], we have immediately the category of all the multi-language algebras over a multi-language signature:
Theorem 1
Let  be a multi-language signature. The class of all
be a multi-language signature. The class of all  -algebras and the class of all
-algebras and the class of all  -homomorphisms form a category denoted by
-homomorphisms form a category denoted by  .
.
3.1 The Initial Term Model
In this section, we introduce the concepts of (multi-language) term and (multi-language) semantics in order to show how a multi-language algebra yields a unique interpretation for any regular (see Definition 11) multi-language specification.
Multi-language terms should comprise all of the underlying languages terms, plus those obtained by the merging of the two languages according to the join relation \(\ltimes \). In particular, we aim for a construction where subterms of sort \(s'\) may have been replaced by terms of sort s, whenever \(s \ltimes s'\) (we recall that s and \(s'\) are two syntactic categories of different languages due to Definition 6). Nonetheless, we must be careful not to add ambiguities during this process: A term t may belong to both  and
and  term algebras but with different meanings
term algebras but with different meanings  and
and  (assuming that \(\mathcal {A}_1\) and \(\mathcal {A}_2\) are algebras over
(assuming that \(\mathcal {A}_1\) and \(\mathcal {A}_2\) are algebras over  and
and  , respectively). When t is included in the multi-language, we lose the information to determine which one of the two interpretations choose, thus making the (multi-language) semantics of t ambiguous. The same problem arises whenever an operator \(\sigma \) belongs to both languages with different interpretation functions. The simplest solution to avoid such issues is to add syntactical notations to make explicit the context of the language in which we are operating.
, respectively). When t is included in the multi-language, we lose the information to determine which one of the two interpretations choose, thus making the (multi-language) semantics of t ambiguous. The same problem arises whenever an operator \(\sigma \) belongs to both languages with different interpretation functions. The simplest solution to avoid such issues is to add syntactical notations to make explicit the context of the language in which we are operating.
Definition 9
(Associated Signature). The associated signature to the multi-language signature  is the ordered triple
is the ordered triple  , where \(S = S_1 \cup S_2\), \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\), and
, where \(S = S_1 \cup S_2\), \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\), and

It is trivial to prove that an associated signature is indeed an order-sorted signature, thus admitting a term algebra \(\mathcal {T}_\varPi \). All the symbols forming terms in \(\mathcal {T}_\varPi \) carry the source language information as a subscript, and all the new operators \(\hookrightarrow _{s,s'}\) specify when a term of sort s is used in place of a term of sort \(s'\). Although \(\mathcal {T}_\varPi \) seems a suitable definition for multi-language terms, it is not a multi-language algebra according to Definition 7. However, we can exploit the construction of \(\mathcal {T}_\varPi \) in order to provide a fully-fledged multi-language algebra able to generate multi-language terms.
Definition 10
(Multi-Language Term Algebra). The multi-language term algebra \(\mathcal {T}\) over a multi-language signature  with boundary functions \(\tau \) is defined as follows:
with boundary functions \(\tau \) is defined as follows:
-
(1t)
\(s \in S\) implies \(T_s = T_{\varPi ,s}\);
-
(2t)
\(\sigma \in \varSigma ^i_{w,s}\) implies
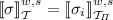 for \(i = 1,2\); and
for \(i = 1,2\); and -
(3t)
\(s \ltimes s'\) implies
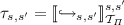 .
.
Proving that \(\mathcal {T}\) satisfies Definition 7 is easy and omitted. \(\mathcal {T}\) and \(\mathcal {T}_\varPi \) share the same carrier sets (condition (1t)), and each single-language operator \(\sigma \in \varSigma ^i_{w, s}\) is interpreted as its annotated version \(\sigma _i\) in \(\mathcal {T}_\varPi \) (condition (2t)). Furthermore, the multi-language operators \(\hookrightarrow _{s, s'}\) no longer belong to the signature (they do not belong neither to  nor to
nor to  ) but their semantics is inherited by the boundary functions \(\tau \) (condition (3t)), while their syntactic values are still in the carrier sets of the algebra (this construction is highly technical and very similar to the freely generated \(\varSigma (X)\)-algebra over a set of variables X, see [15]).
) but their semantics is inherited by the boundary functions \(\tau \) (condition (3t)), while their syntactic values are still in the carrier sets of the algebra (this construction is highly technical and very similar to the freely generated \(\varSigma (X)\)-algebra over a set of variables X, see [15]).
Note that this is exactly the formalization of the ad hoc multi-language specifications in [2, 30, 36, 37]: [2, 36, 37] exploit distinct colors to disambiguate the source language of the operators, whereas [30] use different font styles for different languages. Moreover, boundary functions in [30] conceptually match the introduced operators \(\hookrightarrow _{s, s'}\).
The last step in order to finalize the framework is to provide semantics for each term in \(\mathcal {T}\). As with the order-sorted case, we need a notion of regularity for proving the initiality of the term algebra in its category, which in turn ensures a single eligible (initial algebra) semantics.
Definition 11
(Regularity). A multi-language signature  is regular if its associated signature
is regular if its associated signature  is regular.
is regular.
Proposition 2
The associated signature  of a multi-language signature
of a multi-language signature  is regular if and only if
is regular if and only if  and
and  are regular.
are regular.
The last proposition enables to avoid checking the multi-language regularity whenever the regularity of the order-sorted signatures is known.
Theorem 2
(Initiality of \(\mathcal {T}\)). The multi-language term algebra \(\mathcal {T}\) over a regular multi-language signature  is initial in the category
is initial in the category  .
.
Initiality of \(\mathcal {T}\) is essential to assign a unique mathematical meaning to each term, as in the order-sorted case: Given a multi-language algebra \(\mathcal {A}\), there is only one way of interpreting each term \(t \in \mathcal {T}\) in \(\mathcal {A}\) (satisfying the homomorphism conditions).
Definition 12
((Multi-Language) Semantics). Let \(\mathcal {A}\) be a multi-language algebra over a regular multi-language signature  . The (multi-language) semantics of a (multi-language) term \(t \in \mathcal {T}\) induced by \(\mathcal {A}\) is defined as
. The (multi-language) semantics of a (multi-language) term \(t \in \mathcal {T}\) induced by \(\mathcal {A}\) is defined as

The last equation is well-defined since h is the unique multi-language homomorphism  and for each \(t \in \mathcal {T}\) there exists a least sort
and for each \(t \in \mathcal {T}\) there exists a least sort  such that
such that  (see Prop. 2.10 in [19]).
(see Prop. 2.10 in [19]).
Example. Suppose we are interested in a multi-language over the signatures  and
and  specified in the example given in the background section such that satisfies the following properties:
specified in the example given in the background section such that satisfies the following properties:
-
Terms denoting natural numbers can be used in place of characters
 according to the function
according to the function
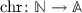 that maps the natural number n to the character symbol
that maps the natural number n to the character symbol  (we are assuming a total lexicographical order
(we are assuming a total lexicographical order  on
on  );
); -
Terms denoting strings can be used in place of natural numbers \(n \in \mathbb {N}\) according to the function
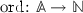 , which is the inverse of
, which is the inverse of 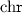 restricted the initial segment on natural numbers
restricted the initial segment on natural numbers 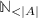 .
.
In order to achieve such a multi-language specification, we can simply provide a join relation \(\ltimes \) on S and a boundary function \(\alpha _{s, s'}\) for each extra-language subsort relation \(s \ltimes s'\) introduced by \(\ltimes \). We define the join relation and the boundary functions as follows:

The multi-language  -algebra \(\mathcal {A}\) can now be obtained by joining the projected algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) with the set of boundary functions \(\alpha \). The term algebra \(\mathcal {T}\) over
-algebra \(\mathcal {A}\) can now be obtained by joining the projected algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) with the set of boundary functions \(\alpha \). The term algebra \(\mathcal {T}\) over  provides all the multi-language terms, and Theorem 2 ensures a unique denotation of each \(t \in \mathcal {T}\) in \(\mathcal {A}\). For instance, the term
provides all the multi-language terms, and Theorem 2 ensures a unique denotation of each \(t \in \mathcal {T}\) in \(\mathcal {A}\). For instance, the term

is syntactically equivalent to the following but with a less pedantic notation, where language subscripts are replaced by colors (
 for one, and
for one, and
 for two) and prefix notation is replaced by infix notation
for two) and prefix notation is replaced by infix notation

and it denotes the natural numbers 765:

(see the proof of Prop. 2.10 in [19] to check how to compute the least sort of a term).
4 Refining the Construction
The construction in Sect. 3 does not set any constraint on boundary functions, thus giving a great deal of flexibility to language designers. For instance, they can provide boundary functions that act differently with respect to the intra-language subsort relation \(\preccurlyeq \): According to the previous example, it would have been possible to define
 to employ different value conversion specifications for terms in
to employ different value conversion specifications for terms in
 , based on whether they are used as natural numbers (
, based on whether they are used as natural numbers (
 ) or as expressions (
) or as expressions (
 ). However, when this amount of flexibility is not needed, we can refine the previous construction by reducing the amount of syntax introduced by the associated signature. In this section we examine
). However, when this amount of flexibility is not needed, we can refine the previous construction by reducing the amount of syntax introduced by the associated signature. In this section we examine
-
the case where boundary functions satisfy the monotonicity conditions of order-sorted algebra operators (Sect. 4.1); and
-
the case where boundary functions commutes with the semantics of operator symbols (Sect. 4.2).
In both cases, we prove that the introduced refinements do not affect the initiality of the term algebra, thereby providing unambiguous semantics to the multi-language.
4.1 Subsort Polymorphic Boundary Functions
In Sect. 3, the join relation constraints \(s \ltimes s'\) are turned in syntactical operators \(\hookrightarrow _{s, s'}\) in the associated signature  . We now show how to handle all the syntactical overhead introduced by \(\ltimes \) with a single polymorphic operator \(\hookrightarrow \) whenever the boundary functions satisfy the monotonicity conditions of the order-sorted algebras [19]. Such conditions require a subsort relation \(s_1 \le s_2\) between the sorts of a polymorphic operator \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\), assuming that \(w_1 \le w_2\). In our case, \(\sigma = \hookrightarrow \), and thus we extend Definition 6 with the following ad hoc constraint (2s\(^{*}\)):
. We now show how to handle all the syntactical overhead introduced by \(\ltimes \) with a single polymorphic operator \(\hookrightarrow \) whenever the boundary functions satisfy the monotonicity conditions of the order-sorted algebras [19]. Such conditions require a subsort relation \(s_1 \le s_2\) between the sorts of a polymorphic operator \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\), assuming that \(w_1 \le w_2\). In our case, \(\sigma = \hookrightarrow \), and thus we extend Definition 6 with the following ad hoc constraint (2s\(^{*}\)):
Definition 6\(^{*}\) (SP Multi-Language Signature). A subsort polymorphic (SP) multi-language signature is a multi-language signature  such that
such that
-
(2s\(^{*}\)) \(s_1 \ltimes s'_1\), \(s_2 \ltimes s'_2\), and \(s_1 \preccurlyeq s_2\) imply \(s'_1 \preccurlyeq s'_2\).
Furthermore, order-sorted algebras demand consistency of the interpretation functions of a subsort polymorphic operator on the smaller domain, which results in the following condition (2a\(^{*}\)) on boundary functions (that extends Definition 7):
Definition 7\(^{*}\) (SP Multi-Language Algebra). Let  be a SP multi-language signature. A subsort polymorphic (SP) multi-language
be a SP multi-language signature. A subsort polymorphic (SP) multi-language  -algebra is a multi-language
-algebra is a multi-language  -algebra \(\mathcal {A}\) such that
-algebra \(\mathcal {A}\) such that
-
(2a\(^{*}\)) \(s_1 \ltimes s'_1\), \(s_2 \ltimes s'_2\), and \(s_1 \preccurlyeq s_2\) imply that \(\alpha _{s_1,s'_1}(a) = \alpha _{s_2,s'_2}(a)\) for each \(a \in A_{s_1}\).
The notion of homomorphism in this new context does not change (an homomorphism between two
 algebras is still an S-sorted function decomposable in two order-sorted homomorphisms that commutes with boundaries), whereas the associated signature to an
algebras is still an S-sorted function decomposable in two order-sorted homomorphisms that commutes with boundaries), whereas the associated signature to an
 multi-language signature merely differs from Definition 9 for having a unique polymorphic operator \(\hookrightarrow \) instead of a family of parametrized symbols
multi-language signature merely differs from Definition 9 for having a unique polymorphic operator \(\hookrightarrow \) instead of a family of parametrized symbols  .
.
Definition 9\(^{*}\) (SP Associated Signature). The subsort polymorphic (SP) associated signature to the SP multi-language signature  is the ordered triple
is the ordered triple  , where \(S = S_1 \cup S_2\), \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\), and
, where \(S = S_1 \cup S_2\), \(\mathord {\preccurlyeq } = \mathord {\le _1} \cup \mathord {\le _2}\), and

Since the associated signature is the basis for the term algebra, we need to modify the condition (3t) in Definition 9:
Definition 10\(^{*}\) (SP Multi-Language Term Algebra). The subsort polymorphic (SP) multi-language term algebra \(\mathcal {T}\) over a SP multi-language signature  with boundary functions \(\tau \) is defined as follows:
with boundary functions \(\tau \) is defined as follows:
-
(1t) \(s \in S\) implies \(T_s = T_{\varPi ,s}\);
-
(2t) \(\sigma \in \varSigma ^i_{w,s}\) implies
 for \(i = 1,2\); and
for \(i = 1,2\); and -
(3t\(^{*}\)) \(s \ltimes s'\) implies
 .
.
Signature regularity is still defined as in Definition 11 and Proposition 2 still holds for the extended version developed in this section. As a result, the
 multi-language term
multi-language term  -algebra \(\mathcal {T}\) is still initial in the category
-algebra \(\mathcal {T}\) is still initial in the category  of
of
 multi-language algebras over the
multi-language algebras over the
 multi-language signature
multi-language signature  .
.
Theorem 3
Let  be a
be a
 multi-language signature. The class of all
multi-language signature. The class of all

 -algebras and the class of all
-algebras and the class of all  -homomorphisms form a category denoted by
-homomorphisms form a category denoted by  .
.
Theorem 4
(Initiality of \(\mathcal {T}\)). The
 multi-language term algebra \(\mathcal {T}\) over a regular
multi-language term algebra \(\mathcal {T}\) over a regular
 multi-language signature
multi-language signature  is initial in the category
is initial in the category  .
.
The semantics of a term t induced by a
 multi-language algebra \(\mathcal {A}\) is defined in the same way of Definition 12, thanks to the initiality result:
multi-language algebra \(\mathcal {A}\) is defined in the same way of Definition 12, thanks to the initiality result:  . The main advantage of dealing with
. The main advantage of dealing with
 multi-language terms is that the framework is able to determine the correct interpretation function of the operator \(\hookrightarrow \), making the subscript notation developed in the previous section superfluous. This also means that programmers are exempted from explicitly annotating multi-language programs with sorts, a non-trivial task in the general case that could introduce type cast bugs.
multi-language terms is that the framework is able to determine the correct interpretation function of the operator \(\hookrightarrow \), making the subscript notation developed in the previous section superfluous. This also means that programmers are exempted from explicitly annotating multi-language programs with sorts, a non-trivial task in the general case that could introduce type cast bugs.
Example. The boundary functions of the previous example are subsort polymorphic:
 for each character
for each character  , and
, and
 by definition. Thus, the equivalent of the term t (see Eq. 1) in the
by definition. Thus, the equivalent of the term t (see Eq. 1) in the
 term algebra is
term algebra is

or, according to the previous notation,

and denoting the same natural number 765.
4.2 Semantic-Only Boundary Functions
In the previous section, we have shown how to handle the flow of values across different languages with a single polymorphic operator. Now, we present a new multi-language construction where neither extra operators are added to the associated signature, nor single-language operators have to be annotated with subscripts indicating their original language. Thus, the resulting multi-language syntax comprises only symbols in \(\varSigma _1 \cup \varSigma _2\). Such a construction is achieved by:
-
Imposing commutativity conditions on algebras, making homomorphisms transparently inherit the semantics of boundary functions. The framework is therefore able to apply the correct value conversion function whenever is necessary, without the need for an explicit syntactical operator \(\hookrightarrow \).
-
Requiring a new form of cross-language polymorphism able to cope with shared operators among languages. The initiality of term algebras is preserved by modifying the notion of signature in a way that every operator admits a least sort.
The variant of the framework presented in this section is particularly useful when designing the extension of a language in a modular fashion. For instance, if the signature  models the syntax of a simple functional language (for an example, see [15, p. 77]) without an explicit encoding for string values, and
models the syntax of a simple functional language (for an example, see [15, p. 77]) without an explicit encoding for string values, and  is a language for manipulating strings (similar to the language \(L_2\) of the running example of this paper), we can exploit the construction presented below in order to embed
is a language for manipulating strings (similar to the language \(L_2\) of the running example of this paper), we can exploit the construction presented below in order to embed  into
into  .
.
Signature. The main issue that can arise at this stage of multi-language signature is the presence of shared operators in \(\varSigma _1\) and \(\varSigma _2\). Contrary to the previous cases where such ambiguity is solved by adding subscripts in the associated signature, the trade off here is requiring ad hoc or subsort polymorphism across signatures.
Definition 6\(^{\star }\) (SO Multi-Language Signature). A semantic-only (SO) multi-language signature is a multi-language signature  such that
such that
-
(2s\(^{\star }\))
 is a poset; and
is a poset; and -
(3s\(^{\star }\)) \(\sigma \in \varSigma ^i_{w_1, s_1} \cap \varSigma ^j_{w_2, s_2}\) and \(w_1 \ltimes w_2\) imply \(s_1 \ltimes s_2\) with \(i, j = 1, 2\) and \(i \ne j\).
Condition (2s\(^{\star }\)) forces the subsort relation to be directed, avoiding symmetricity of syntactic categories (this is typical when modeling language extensions), while condition (3s\(^{\star }\)) shifts the monotonicity condition of order-sorted signature to syntactically equal operators in \(\varSigma _1 \cap \varSigma _2\).
The associated signature is defined without adding extra symbols in the signature, i.e., \(\varPi = \varSigma _1 \cup \varSigma _2\), and deliberately confounding the relations \(\ltimes \) and \(\preccurlyeq \) in \(\le \):
Definition 9\(^{\star }\) (SO Associated Signature). The SO associated signature to the SO multi-language signature  is the ordered triple
is the ordered triple  , where \(S = S_1 \cup S_2\), \(\mathord {\le } = \mathord {\preccurlyeq } \cup \mathord {\ltimes }\), and \(\varPi = \varSigma _1 \cup \varSigma _2\).
, where \(S = S_1 \cup S_2\), \(\mathord {\le } = \mathord {\preccurlyeq } \cup \mathord {\ltimes }\), and \(\varPi = \varSigma _1 \cup \varSigma _2\).
The embedding of \(\ltimes \) in \(\le \) (i.e., \(\mathord {\ltimes } \subseteq \mathord {\le }\)) in the associated signature enables the order-sorted term algebra construction to automatically build multi-language terms, without the need for an explicit operator \(\hookrightarrow \) that acts as a bridge between syntactic categories. It is easy to see that the term algebra over the associated signature is precisely the symbols-free version of multi-language described at the beginning.
Unfortunately, multi-language regularity does not follow anymore from single-languages regularity and vice versa (see Figs. 3 and 4)Footnote 6. More formally, Proposition 2 does not hold in this new context:
-
Suppose
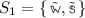 ,
,
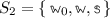 , \(\le _1\) and \(\le _2\) to be the reflexive relations on \(S_1\) and \(S_2\), respectively, plus
, \(\le _1\) and \(\le _2\) to be the reflexive relations on \(S_1\) and \(S_2\), respectively, plus
 , and
, and
 . If the join relation \(\ltimes \) is defined as
. If the join relation \(\ltimes \) is defined as
 and
and
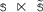 , the resulting associated signature is no longer regular, although
, the resulting associated signature is no longer regular, although 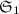 and
and 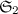 are regular (Fig. 3a). In Fig. 3b, it is easy to see that
are regular (Fig. 3a). In Fig. 3b, it is easy to see that
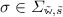 and
and
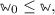 but the set
but the set
 does not have a least element w.r.t.
does not have a least element w.r.t. 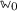 .
. -
On the other hand, let
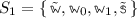 ,
,
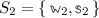 , \(\le _1\) and \(\le _2\) be the reflexive relations on \(S_1\) and \(S_2\), respectively, plus
, \(\le _1\) and \(\le _2\) be the reflexive relations on \(S_1\) and \(S_2\), respectively, plus
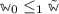 and
and
 , and
, and
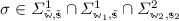 . If the join relation \(\ltimes \) is defined as
. If the join relation \(\ltimes \) is defined as
 , and
, and
 , the resulting associated signature is regular (Fig. 4a), although
, the resulting associated signature is regular (Fig. 4a), although  is not: given
is not: given
 and
and
 , the set
, the set
 has least element
has least element
 w.r.t.
w.r.t.
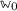 (Fig. 4b).
(Fig. 4b).
A positive result can be obtained by recalling that regularity is easier to check when  satisfies the descending chain condition (
satisfies the descending chain condition (
 ):
):
Lemma 1
(Regularity over DCC poset [19]). An order-sorted signature \(\varSigma \) over a
 poset
poset  is regular if and only if whenever \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and there is some \(w_0 \le w_1, w_2\), then there is some \(w \le w_1, w_2\) such that \(\sigma \in \varSigma _{w, s}\) and \(w_0 \le w\).
is regular if and only if whenever \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and there is some \(w_0 \le w_1, w_2\), then there is some \(w \le w_1, w_2\) such that \(\sigma \in \varSigma _{w, s}\) and \(w_0 \le w\).
At this point, we can relate the
 of the poset
of the poset  in the associated signature of
in the associated signature of  to the
to the
 of
of  and
and  :
:
Proposition 3
Let  be the associated signature of
be the associated signature of  . Then,
. Then,  is
is
 if and only if
if and only if  and
and  are
are
 .
.
As a result, whenever we know that  and
and  are
are
 , we can check the regularity of
, we can check the regularity of  by employing the Lemma 1 without checking whether
by employing the Lemma 1 without checking whether  is
is
 .
.
Algebra. In this multi-language construction, the boundary functions behaviour is no more bounded to syntactical operators as in the previous sections, but it is inherited by homomorphisms. A necessary condition to accomplish this aim is the commutativity of interpretation functions with boundary functions:
Definition 7\(^{\star }\) (SO Multi-Language Algebra). Let  be an
be an
 multi-language signature. A semantic-only (SO) multi-language
multi-language signature. A semantic-only (SO) multi-language  -algebra is an SP multi-language
-algebra is an SP multi-language  -algebra \(\mathcal {A}\) such that
-algebra \(\mathcal {A}\) such that
-
(3a\(^{\star }\)) \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and \(w_1 \ltimes w_2\) imply that
 for each \(a \in A_{w_1}\).
for each \(a \in A_{w_1}\).
Note that \(\sigma \in \varSigma _{w_1, s_1} \cap \varSigma _{w_2, s_2}\) and \(w_1 \ltimes w_2\) imply \(s_1 \ltimes s_2\) by condition (3s\(^{\star }\)). The notion of homomorphism remains unchanged from Definition 8 (to understand how the homomorphisms inherit the boundary functions behaviour, see the proof of Theorem 6).
The term algebra is defined similarly to Definition 10, except for boundary functions:
Definition 10\(^{\star }\) (SO Multi-Language Term Algebra). The semantic-only (SO) multi-language term algebra \(\mathcal {T}\) over an SO multi-language signature  with boundary functions \(\tau \) is defined as follows:
with boundary functions \(\tau \) is defined as follows:
-
(1t\(^{\star }\)) \(s \in S\) implies \(T_s = T_{\varPi , s}\);
-
(2t\(^{\star }\)) \(\sigma \in \varSigma _{w, s}\) implies
 ; and
; and -
(3t\(^{\star }\)) \(s \ltimes s'\) implies
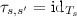 .
.
Since the subsort relation \(\le \) includes the join relation \(\ltimes \), \(s \ltimes s'\) implies \(T_{\varPi ,s} = T_s \subseteq T_{s'} = T_{\varPi ,s'}\). Thus, the boundary function \(\tau _{s,s'}\) can be defined as the identity on the smaller domain (note that it trivially satisfies the commutativity condition (3a\(^{\star }\))).
Proposition 4
Let  be an
be an
 multi-language signature. Then, the
multi-language signature. Then, the
 multi-language term
multi-language term  -algebra is a proper
-algebra is a proper
 multi-language algebra.
multi-language algebra.
Theorem 5
Let  be a
be a
 multi-language signature. The class of all
multi-language signature. The class of all

 -algebras and the class of all
-algebras and the class of all  -homomorphisms form a category denoted by
-homomorphisms form a category denoted by  .
.
We can now prove the initiality of \(\mathcal {T}\) in its category.
Theorem 6
(Initiality of \(\mathcal {T}\)). Let  be a regular multi-language signature. Then, the term algebra \(\mathcal {T}\) is an initial object in the category
be a regular multi-language signature. Then, the term algebra \(\mathcal {T}\) is an initial object in the category  .
.
Thanks to the initiality of the term algebra, the definition of term semantics is the same of Definition 12.
Example. Let \(\mathcal {A}_1\) and \(\mathcal {A}_2\) be two order-sorted algebras over the signatures  and
and  , respectively, as formalized in the example in Sect. 3. Suppose we are interested in a new multi-language \(\mathcal {A}\) over
, respectively, as formalized in the example in Sect. 3. Suppose we are interested in a new multi-language \(\mathcal {A}\) over  and
and  such that any string expressions t of sort
such that any string expressions t of sort
 in
in  can denote the natural number
can denote the natural number  when embedded in
when embedded in  terms. For instance, we require that
terms. For instance, we require that
 and
and
 , but
, but
 (parentheses in the last term have only been used to disambiguate the parsing result).
(parentheses in the last term have only been used to disambiguate the parsing result).
Since the requirements demand to use string expressions in place of natural numbers, the join relation \(\ltimes \) shall define
 and ensure transitivity, hence
and ensure transitivity, hence
 ,
,
 , and
, and
 .
.
The signatures  and
and  are trivially regular. However, by merging
are trivially regular. However, by merging  and
and  , we are causing subsort polymorphism on the symbol \(\texttt {+}\), which is used as sum operator in \(\mathcal {A}_1\) and as concatenation operator in \(\mathcal {A}_2\), and therefore we have to check the regularity: Let
, we are causing subsort polymorphism on the symbol \(\texttt {+}\), which is used as sum operator in \(\mathcal {A}_1\) and as concatenation operator in \(\mathcal {A}_2\), and therefore we have to check the regularity: Let
 , and
, and
 . Given \(\texttt {+} \in \varSigma _{w_1,s_1} \cap \varSigma _{w_2,s_2}\) and the lower bound
. Given \(\texttt {+} \in \varSigma _{w_1,s_1} \cap \varSigma _{w_2,s_2}\) and the lower bound
 , then there exists
, then there exists
 such that \(w \le w_1, w_2\) and \(\texttt {+} \in \varSigma _{w,s}\), where
such that \(w \le w_1, w_2\) and \(\texttt {+} \in \varSigma _{w,s}\), where
 (we have employed Lemma 1 thanks to Proposition 3). Analogously, when \(w_0 = w_1, w_2\) the relative least rank is
(we have employed Lemma 1 thanks to Proposition 3). Analogously, when \(w_0 = w_1, w_2\) the relative least rank is
 .
.
The multi-language  -algebra \(\mathcal {A}\) is now defined by joining the projected algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) and by defining boundary functions \(a_{s, s'}\) for each \(s \ltimes s'\) such that convert strings in naturals (their length) when strings are used in place of naturals:
-algebra \(\mathcal {A}\) is now defined by joining the projected algebras \(\mathcal {A}_1\) and \(\mathcal {A}_2\) and by defining boundary functions \(a_{s, s'}\) for each \(s \ltimes s'\) such that convert strings in naturals (their length) when strings are used in place of naturals:

The above definition of boundary functions satisfy both conditions (2a\(^{*}\)) and (3a\(^{\star }\)).
The initiality theorem yields the semantic homomorphism from \(\mathcal {T}\) to \(\mathcal {A}\). For instance, suppose we want to compute the semantics of the term

The least sorts of t, \(t_1\), and \(t_2\) are
 , and
, and
 , respectively. The operator \(\texttt {+}\) belongs to both
, respectively. The operator \(\texttt {+}\) belongs to both
 and
and
 , and its least rank w.r.t. the lower bound
, and its least rank w.r.t. the lower bound
 is
is
 . By Definition 12 we have
. By Definition 12 we have

At this point, since
 and
and
 , then the least rank of the root symbol + of \(t_1\) w.r.t. the lower bound
, then the least rank of the root symbol + of \(t_1\) w.r.t. the lower bound
 is
is
 , thus
, thus

Similarly,
 and
and
 . Then, the least rank of the root symbol + of \(t_2\) w.r.t. the lower bound
. Then, the least rank of the root symbol + of \(t_2\) w.r.t. the lower bound
 is
is
 and therefore we have
and therefore we have

Finally,

as desired.
We can observe that without any syntactical operator the framework is still able to apply the correct boundary functions to move values across languages.
5 Reduction to Order-Sorted Algebra
The constructions in the previous sections beg the question whether a multi-language algebra admits an equivalent order-sorted representation. Conceptually, it would mean that being a multi-language is essentially a matter of perspective: By forgetting how the multi-language has been constructed, what is left is simply an ordinary language. Mathematically speaking, it requires us to exhibit a reduction functor F from the multi-language category to an order-sorted one, such that there is an isomorphism \(\phi \) between the carrier sets of the multi-language term  -algebra \(\mathcal {T}\) and \(F(\mathcal {T})\), and such that
-algebra \(\mathcal {T}\) and \(F(\mathcal {T})\), and such that
 for each \(t \in \mathcal {T}\) and for each multi-language
for each \(t \in \mathcal {T}\) and for each multi-language  -algebra \(\mathcal {A}\).
-algebra \(\mathcal {A}\).
In the following, we denote the reduction functor by F, \(F^*\), and \(F^\star \) accordingly whether its domain is the category  ,
,  , and
, and  , respectively.
, respectively.
In the case of  and
and  categories, the construction of F and \(F^*\) is very simple, and we illustrate it only for the plain multi-language algebras of Sect. 3: Let \(\mathcal {A}\) be a multi-language
categories, the construction of F and \(F^*\) is very simple, and we illustrate it only for the plain multi-language algebras of Sect. 3: Let \(\mathcal {A}\) be a multi-language  -algebra. Then, we define the order-sorted
-algebra. Then, we define the order-sorted  -algebra \(\mathcal {A}_\varPi \) (called the associated order-sorted algebra of \(\mathcal {A}\)) by setting
-algebra \(\mathcal {A}_\varPi \) (called the associated order-sorted algebra of \(\mathcal {A}\)) by setting
-
\((1\pi )\) \(A_{\varPi , s} = A_s\) for each \(s \in S\);
-
\((2\pi )\)
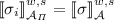 for each \(\sigma \in \varSigma ^i_{w,s}\) and \(i = 1,2\); and
for each \(\sigma \in \varSigma ^i_{w,s}\) and \(i = 1,2\); and -
\((3\pi )\)
 for each \(s \ltimes s'\).
for each \(s \ltimes s'\).
If \(\mathcal {A}\) and \(\mathcal {B}\) are multi-language  -algebras, and h is a multi-language
-algebras, and h is a multi-language  -homomorphism from \(\mathcal {A}\) to \(\mathcal {B}\), the functor F maps \(\mathcal {A}\) and \(\mathcal {B}\) to their associated order-sorted algebras \(\mathcal {A}_\varPi \) and \(\mathcal {B}_\varPi \) and the homomorphism h to itself. Since \(A_\varPi = A\), the isomorphism \(\phi \) is the identity function.
-homomorphism from \(\mathcal {A}\) to \(\mathcal {B}\), the functor F maps \(\mathcal {A}\) and \(\mathcal {B}\) to their associated order-sorted algebras \(\mathcal {A}_\varPi \) and \(\mathcal {B}_\varPi \) and the homomorphism h to itself. Since \(A_\varPi = A\), the isomorphism \(\phi \) is the identity function.
Theorem 7
 is a functor for every multi-language signature
is a functor for every multi-language signature  . Moreover,
. Moreover,  for each \(t \in \mathcal {T}\) and for each multi-language
for each \(t \in \mathcal {T}\) and for each multi-language  -algebra \(\mathcal {A}\).
-algebra \(\mathcal {A}\).
If \(\mathcal {A}\) is an
 multi-language
multi-language  -algebra, the construction of the reduction functor \(F^*\) is similar to the definition of F. The only difference is the equation in the condition (3\(\pi \)) that turns into
-algebra, the construction of the reduction functor \(F^*\) is similar to the definition of F. The only difference is the equation in the condition (3\(\pi \)) that turns into
-
(3\(\pi ^*\))
 for each \(s \ltimes s'\).
for each \(s \ltimes s'\).
Finally, the definition of \(F^\star \) starting from the category  of
of
 multi-language algebras is slightly different. We define \(F^\star \) as a map from the multi-language category
multi-language algebras is slightly different. We define \(F^\star \) as a map from the multi-language category  to the order-sorted category
to the order-sorted category  . We denote the reduction of a multi-language algebra \(\mathcal {A}\) and a homomorphism
. We denote the reduction of a multi-language algebra \(\mathcal {A}\) and a homomorphism  as
as  and
and  . The order-sorted algebra
. The order-sorted algebra  has the same carrier sets of the multi-language algebra \(\mathcal {A}\), i.e.,
has the same carrier sets of the multi-language algebra \(\mathcal {A}\), i.e.,  , and interpretation functions
, and interpretation functions
 . Furthermore, we define
. Furthermore, we define  . Intuitively, the algebra
. Intuitively, the algebra  is formally defined simply by forgetting about the boundary functions, while the homomorphism
is formally defined simply by forgetting about the boundary functions, while the homomorphism  inherits their semantics from h. Again, the isomorphism \(\phi \) is the identity.
inherits their semantics from h. Again, the isomorphism \(\phi \) is the identity.
Theorem 8
 is a functor for every
is a functor for every
 multi-language signature
multi-language signature  . Moreover,
. Moreover,  for each \(t \in \mathcal {T}\) and for each
for each \(t \in \mathcal {T}\) and for each
 multi-language
multi-language  -algebra \(\mathcal {A}\).
-algebra \(\mathcal {A}\).
Unfortunately, even though \(\mathcal {T}\) is an initial algebra in its category,  is not: Given two multi-language algebras \(\mathcal {A}\) and \(\mathcal {A}'\) that differ only in the boundary functions (we denote by \(\alpha \) and \(\alpha '\) the families of boundary functions of \(\mathcal {A}\) and \(\mathcal {A}'\), respectively) they both get mapped by \(F^\star \) to the same order-sorted algebra
is not: Given two multi-language algebras \(\mathcal {A}\) and \(\mathcal {A}'\) that differ only in the boundary functions (we denote by \(\alpha \) and \(\alpha '\) the families of boundary functions of \(\mathcal {A}\) and \(\mathcal {A}'\), respectively) they both get mapped by \(F^\star \) to the same order-sorted algebra  . Thus, if
. Thus, if  and
and  are the unique homomorphisms going from \(\mathcal {T}\) to \(\mathcal {A}\) and \(\mathcal {A}'\), the functor F maps them to two different order-sorted homomorphisms
are the unique homomorphisms going from \(\mathcal {T}\) to \(\mathcal {A}\) and \(\mathcal {A}'\), the functor F maps them to two different order-sorted homomorphisms  and
and  both leaving
both leaving  and going to
and going to  , hence losing the uniqueness property. However, this does not pose a problem once fixed a family of boundary functions:
, hence losing the uniqueness property. However, this does not pose a problem once fixed a family of boundary functions:
Theorem 9
Let \(\mathcal {T}\) be the multi-language term  -algebra and \(\mathcal {A}\) be an order-sorted
-algebra and \(\mathcal {A}\) be an order-sorted  -algebra. Given a family of boundary functions
-algebra. Given a family of boundary functions  such that satisfies condition (3a\(^{\star }\)), there exists a unique order-sorted
such that satisfies condition (3a\(^{\star }\)), there exists a unique order-sorted
 -homomorphism
-homomorphism  commuting with \(\alpha \), i.e., if \(s \ltimes s'\), then \(h^\alpha _{s'}(t) = \alpha _{s, s'}(h^\alpha _s(t))\) for each \(t \in T_s\).
commuting with \(\alpha \), i.e., if \(s \ltimes s'\), then \(h^\alpha _{s'}(t) = \alpha _{s, s'}(h^\alpha _s(t))\) for each \(t \in T_s\).
The reduction theorems presented in this section have a strong consequence: all the already known results for the order-sorted algebras can be lifted to the multi-language world.
6 An Example of Multi-Language Construction
The first theoretical paper addressing the problem of multi-language construction is [30]. The authors study the so-called natural embedding (a more realistic improvement of the lump embedding [7, 30, 34, 40]), in which Scheme terms can be converted to equivalent ML terms, and vice versa.Footnote 7 The novelty in their approach is how they succeed to define boundaries in order to translate values from Scheme to ML. Indeed, the latter does not admit an equivalent representation for each Scheme function. Their solution is to “represent a Scheme procedure in ML at type \(\tau _1\rightarrow \tau _2\) by a new procedure that takes an argument of type \(\tau _1\), converts it to a Scheme equivalent, runs the original Scheme procedure on that value, and then converts the result back to ML at type \(\tau _2\)”.
Our goal here is not to discuss a fully explained presentation of ML and Scheme languages in the form of order-sorted algebras, but rather to show how we can model the natural embedding construction in our framework. Doing so, we provide a sketchy formalization of Scheme and ML syntax and semantics, and we redirect the reader to [30] for all the languages details.
To provide the semantics of Scheme, we follow the same approach of Goguen et al. [15] where the denotational semantics of the simple applicative language (SAL) introduced by Reynolds [42] is given by means of an algebra, exploiting the initiality theorem. Such a language is a “syntactically sugared” version of the untyped lambda calculus with the fixpoint operator, which in turn is very similar to Scheme.
Let  be a set of variables and
be a set of variables and  be the naturals lattice with \(\top \) and \(\bot \) adjoined. From [46], there exists a complete lattice V such that satisfies the isomorphism
be the naturals lattice with \(\top \) and \(\bot \) adjoined. From [46], there exists a complete lattice V such that satisfies the isomorphism
 , where \(+\) is the disjoint union with minimum and maximum elements identified, and
, where \(+\) is the disjoint union with minimum and maximum elements identified, and
 is the complete lattice of Scott-continuous functions from V to V. Given
is the complete lattice of Scott-continuous functions from V to V. Given
 , we define the injections
, we define the injections
 and \(i_\xi = \phi ^{-1} \circ j_\xi \), and the projection
and \(i_\xi = \phi ^{-1} \circ j_\xi \), and the projection  such that
such that
 . The set of all Scheme environments is the lattice of all total functions \(\text {P}= X\rightarrow V\) with componentwise ordering \(\rho \sqsubseteq \rho '\) if and only if \(\rho (x) \sqsubseteq \rho '(x)\) in V for all \(x \in X\). Furthermore, we define auxiliary functions (see [15] for a more detailed explanation) in order to provide the semantics of the language (in the following, \(x \in X\) and
. The set of all Scheme environments is the lattice of all total functions \(\text {P}= X\rightarrow V\) with componentwise ordering \(\rho \sqsubseteq \rho '\) if and only if \(\rho (x) \sqsubseteq \rho '(x)\) in V for all \(x \in X\). Furthermore, we define auxiliary functions (see [15] for a more detailed explanation) in order to provide the semantics of the language (in the following, \(x \in X\) and  ):
):
-
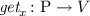 , \(\textit{get}_x(\rho ) = \rho (x)\) (evaluation function);
, \(\textit{get}_x(\rho ) = \rho (x)\) (evaluation function); -
 , \(\textit{val}_{n}(\rho ) = n\) (n-constant function);
, \(\textit{val}_{n}(\rho ) = n\) (n-constant function); -
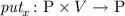 , \(\textit{put}_x(\rho , v) = \rho [v/x]\), where
, \(\textit{put}_x(\rho , v) = \rho [v/x]\), where
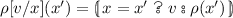 (environment updating);
(environment updating); -
 ,
,
 (function application);
(function application); -
 ,
,
 (natural predicate);
(natural predicate); -
 ,
,
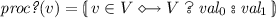 (function predicate);
(function predicate); -
given
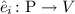 for \(1 \le i \le k\), then
for \(1 \le i \le k\), then  is defined by
is defined by  (target-tupling); and
(target-tupling); and -
given D, \(D'\) and \(D''\), then
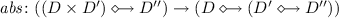 is defined by \(((\textit{abs}(f))(x))(y) = f(x, y)\) (abstraction); and
is defined by \(((\textit{abs}(f))(x))(y) = f(x, y)\) (abstraction); and -
 (conditional function),
(conditional function), 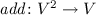 (addition), and
(addition), and  (subtraction)
(subtraction) 
The definition of \(\textit{sub}\) is analogous to the function \(\textit{add}\), with the only difference that, in the second case, \(\textit{sub}(v_1, v_2) = v_1 -_{\mathbb {N}} v_2\), where
 for each \(v_1, v_2 \in \mathbb {N}\).
for each \(v_1, v_2 \in \mathbb {N}\).
The semantics of the language is obtained by defining an algebra \(\mathcal {H}\) over a signature  ,Footnote 8 then the initiality yields the unique homomorphism from the term algebra. A Scheme term denotes a continuous function in the semantic domain
,Footnote 8 then the initiality yields the unique homomorphism from the term algebra. A Scheme term denotes a continuous function in the semantic domain
 . The interpretation functions of the operators are defined by the following equations:
. The interpretation functions of the operators are defined by the following equations:

For the sake of simplicity, we made a minor change to the language presented in [30]. They have an extra operator wrong to print an error message in case of an illegal operation, due to the lack of a type system. For instance, the sum of two functions produces the error wrong "non-number". To avoid to add cases almost everywhere in the definition of the interpretation functions, we let ill-typed terms to denote the value \(\bot \) without an explicit encoding of the error message. Furthermore, we denote by  the function application.
the function application.
The ML-like language defined in [30] is an extended version of the simply-typed lambda calculus. As before, we provide its semantics by defining an algebra \(\mathcal {M}\) over an order-sorted signature
 .
.
Let \(\text {I}\) (should read ‘iota’) be a set of base types and K a \(\text {I}\)-sorted set of base values  . We inductively define the set of simple types \(\text {T}\): If \(\iota \) is a base type, then it is a simple type; If \(\tau , \tau '\) are simple types, then \((\tau )\rightarrow (\tau ')\) is a simple type (henceforth we omit the parentheses). We abuse notation and extend K to the
. We inductively define the set of simple types \(\text {T}\): If \(\iota \) is a base type, then it is a simple type; If \(\tau , \tau '\) are simple types, then \((\tau )\rightarrow (\tau ')\) is a simple type (henceforth we omit the parentheses). We abuse notation and extend K to the  -sorted set of simple values
-sorted set of simple values  where \(K_{\tau \rightarrow \tau '} = K_\tau \rightarrow K_{\tau '}\).
where \(K_{\tau \rightarrow \tau '} = K_\tau \rightarrow K_{\tau '}\).
The set of all ML environments is defined as the set of all total functions \(\varDelta = Y \rightarrow K\), where  is a set of variables disjoint from X (this assumption comes from [30]) and \(K = \bigcup _{\tau \in \text {T}} K_\tau \). We instantiate
is a set of variables disjoint from X (this assumption comes from [30]) and \(K = \bigcup _{\tau \in \text {T}} K_\tau \). We instantiate
 and
and
 . The poset
. The poset
 carries all the simple types (i.e., \(\text {T}\subseteq S_2\)) and the sort
carries all the simple types (i.e., \(\text {T}\subseteq S_2\)) and the sort
 ; \(\le _2\) is the reflexive relation on \(S_2\) plus
; \(\le _2\) is the reflexive relation on \(S_2\) plus
 for each \(\tau \in \text {T}\). An ML term of type \(\tau \) denotes a total function in \(M_\tau = \varDelta \rightarrow K_\tau \), and we define
for each \(\tau \in \text {T}\). An ML term of type \(\tau \) denotes a total function in \(M_\tau = \varDelta \rightarrow K_\tau \), and we define
 . Due to the Turing-incompleteness of such a language, we do not need all the mathematical machinery of [15, 46] to formalize its semantics.
. Due to the Turing-incompleteness of such a language, we do not need all the mathematical machinery of [15, 46] to formalize its semantics.

Until now, we have just formalized the single-languages. The multi-language \(\mathcal {A}\) that combines Scheme and ML is obtained by requiring
 and
and
 in order to use ML terms in place of Scheme terms and vice versa. However, in the simplest version of the natural embedding, “the system has stuck states, since a boundary might receive a value of an inappropriate shape” [30]. They restore the type-soundness by first employing dynamic checks, and then by decoupling error-handling from the value conversion through the use of higher-order contracts [12]. We limit ourselves here to describe the first version; the subsequent refinements can be embodied by further complicating the semantics of the boundary functions (we do not have forced any constraints on them).
in order to use ML terms in place of Scheme terms and vice versa. However, in the simplest version of the natural embedding, “the system has stuck states, since a boundary might receive a value of an inappropriate shape” [30]. They restore the type-soundness by first employing dynamic checks, and then by decoupling error-handling from the value conversion through the use of higher-order contracts [12]. We limit ourselves here to describe the first version; the subsequent refinements can be embodied by further complicating the semantics of the boundary functions (we do not have forced any constraints on them).
Since we need a value representing the notion of stuck state in ML, we have to extend the algebra \(\mathcal {M}\). This is particularly easy by exploiting the underlying framework: We make \(\mathcal {M}^\bot \) into an order-sorted  -algebra by defining \(M_{\tau }^\bot = \varDelta ^\bot \rightarrow K_{\tau }^\bot \), where \(\varDelta ^\bot = Y \rightarrow K^\bot \), \(K^\bot = \bigcup _{\tau \in \text {T}} K_\tau ^\bot \), and
-algebra by defining \(M_{\tau }^\bot = \varDelta ^\bot \rightarrow K_{\tau }^\bot \), where \(\varDelta ^\bot = Y \rightarrow K^\bot \), \(K^\bot = \bigcup _{\tau \in \text {T}} K_\tau ^\bot \), and  , and the
, and the  -sorted injection \(\phi \) from \(M_\tau \) to \(M_\tau ^\bot \) such that \(\varphi (\hat{t}) = \hat{t}\). Now, \(\mathcal {M}^\bot \) becomes an algebra by letting \(\varphi \) to be an order-sorted
-sorted injection \(\phi \) from \(M_\tau \) to \(M_\tau ^\bot \) such that \(\varphi (\hat{t}) = \hat{t}\). Now, \(\mathcal {M}^\bot \) becomes an algebra by letting \(\varphi \) to be an order-sorted  -homomorphism (this in turn forces
-homomorphism (this in turn forces  ) and letting the interpretation functions to denote the value \(\bot \) in the remaining non-yet defined cases (namely, they compute the value \(\bot \) whenever one of their arguments is \(\bot \)).
) and letting the interpretation functions to denote the value \(\bot \) in the remaining non-yet defined cases (namely, they compute the value \(\bot \) whenever one of their arguments is \(\bot \)).
The boundary function
 moves the Scheme value
moves the Scheme value  in \(M_\tau \):
in \(M_\tau \):

where
 and
and

Vice versa,
 moves values from ML to Scheme. Its definition is analogous to the previous case:
moves values from ML to Scheme. Its definition is analogous to the previous case:
 where \(\hat{n} = \delta \mapsto n\), and
where \(\hat{n} = \delta \mapsto n\), and

These definitions adhere the conversion approach of the natural embedding in [30]: If \(\hat{e}\) is the value denoted by a natural number in Scheme, then it is converted—aside from cases deriving from ill-typed terms—by
 to the corresponding constant function denoting the same natural value in ML. Otherwise, if \(\hat{e}\) is the value denoted by a Scheme function, then it is mapped by
to the corresponding constant function denoting the same natural value in ML. Otherwise, if \(\hat{e}\) is the value denoted by a Scheme function, then it is mapped by
 to the ML function with variable x at type \(\tau \rightarrow \tau '\) such that converts its argument of type \(\tau \) to the Scheme equivalent by its conversion through
to the ML function with variable x at type \(\tau \rightarrow \tau '\) such that converts its argument of type \(\tau \) to the Scheme equivalent by its conversion through
 to x. Then it runs the original procedure \(\hat{e}\) on it and convert back the result by
to x. Then it runs the original procedure \(\hat{e}\) on it and convert back the result by
 .
.
Since the given boundary functions are subsort polymorphic, we can improve the construction and handle all the value conversions with a single polymorphic operator as explained in Sect. 4.1.
7 Concluding Remarks
In this paper, we have addressed the problem of providing a formal semantics to the combination of programming languages, the so-called multi-languages. We have introduced a new algebraic framework for modeling this new paradigm, and we have constructively shown how to attain a multi-language specification by only stipulate (1) how the syntactic categories of the single-languages have to be combined and (2) how the values may flow from one language to the other. We have proved the suitability of the framework to unambiguously yield the algebraic semantics of each multi-language term, while simultaneously preserving the single-languages semantics. We have also proved that combining languages is a close operation, i.e., that every multi-language admits an equivalent order-sorted representation. In particular, we have focused our study on the semantic properties of boundary functions in order to provide three different notions of multi-language designed to suit both general and specific cases.
To the best of our knowledge, this is the first attempt to provide a formal semantics of a multi-language independently from the combined languages.
Related Works. Cross-language interoperability is a well-researched area both from theoretical and practical points of view. The most related work to our approach is undoubtedly [30], which provides operational semantics to a combined language obtained by embedding a Scheme-like language into an ML-like language. Such an outcome is achieved by introducing boundaries, syntactic constructs that model the flow of values from one language to the other. Ours boundary functions draw heavily from their work. Nonetheless, we shift them to a semantic level, in order to several variants of multi-language constructions.
[7, 21, 36, 40, 53] take a similar line and combine typed and untyped languages (Lua and ML [40], Java and PLT Scheme [21], or Assembly and a typed functional language [36]), focusing on typing issues and values exchanging techniques. Instead of focusing on a particular problem, we adopt a rather general framework to model languages. This choice abstracts away many low-level details, allowing us to reason on semantic concerns in more general terms, without having to fix any particular pair of languages.
A lot of work has been done on multi-language runtime mechanisms: [20] provides a type system for a fragment of Microsoft Intermediate Language (IL) used by the .NET framework, that allows programmers to write components in several languages (C#, Visual Basic, VBScript, ...) which are then translated to IL. [22] proposes a virtual machine that can execute the composition of dynamically typed programming languages (Ruby and JavaScript) and statically typed one (C). [4, 5] describes a multi-language runtime mechanism achieved by combining single-language interpreters of (different versions of) Python and Prolog.
Future Works. From our perspective, the research presented in this paper opens up on three directions. Firstly, future works should aim to provide an operational semantics to the formalization of multi-languages. Rewriting logic seems the most reasonable approach to unifying the denotational world, presented in this paper, to the operational one [31]. This line of research is particularly useful in order to move towards an implementation of an automatic tool able to combine languages such that the resulting multi-language guarantees the results proved in the paper.
Secondly, future research applies to use the multi-language model in order to study the problem of analyzing multi-language programs. In particular, we aim at investigating how it is possible to obtain analyses of multi-language programs by merging already existing analyses of the single combined languages.
Finally, further studies should investigate the problem of compiling multi-languages. Current compilers are closed tools, non-parametric on language constructs (for instance, we cannot compile a single if-then-else term of a standard language like C or Java unless it is plugged into a valid program). Several works on typing [1, 20, 26], compiling [2, 37], and running [23, 50] multi-language programs already exist, but without providing a formal notion of multi-language. It would be beneficial to study how their approaches can be applied to the formal framework developed in this paper.
Notes
- 1.
- 2.
To be pedantic, we should introduce the one-point domain
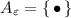 and then define
and then define  .
. - 3.
This hypothesis is non-restrictive: We can always perform a renaming of the sorts.
- 4.
Sorts may be understood as syntactic categories, in the sense of formal grammars. Given a context-free grammar G, it is possible to define a many-sorted signature \(\varSigma _G\) where non-terminals become sorts and such that each term t in the term algebra \(\mathcal {T}_{\varSigma _G}\) is isomorphic to the parse tree of t with respect to G (see [15] for details).
- 5.
- 6.
An (horizontal) arrow from an arity symbol w to a sort s labelled with an operator symbol \(\sigma \) is an alternative shorthand for
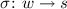 . A (vertical) single line between two sorts s below \(s'\) labelled with a binary relation \(\le \) means that \(s\le s'\) (if the binary relation is the join relation \(\ltimes \) the line is doubled). A dotted rectangle around operators is a graphical representation of the set of ranks (w, s) that must have a minimum element (red arrows) in order for the signature to be regular.
. A (vertical) single line between two sorts s below \(s'\) labelled with a binary relation \(\le \) means that \(s\le s'\) (if the binary relation is the join relation \(\ltimes \) the line is doubled). A dotted rectangle around operators is a graphical representation of the set of ranks (w, s) that must have a minimum element (red arrows) in order for the signature to be regular. - 7.
To be specific, the authors combine “an extended model of the untyped call-by-value lambda calculus, which is used as a stand-in for Scheme, and an extended model of the simply-typed lambda calculus, which is used as a stand-in for ML”.
- 8.
We do not define
 explicitly since it can be inferred by the algebra equations below.
explicitly since it can be inferred by the algebra equations below.
References
Abadi, M., Cardelli, L., Pierce, B.C., Plotkin, G.D.: Dynamic typing in a statically typed language. ACM Trans. Program. Lang. Syst. 13(2), 237–268 (1991)
Ahmed, A., Blume, M.: An equivalence-preserving CPS translation via multi-language semantics. SIGPLAN Not. 46(9), 431–444 (2011)
Alencar, A.J., Goguen, J.A.: Object-oriented specification case studies. In: Lano, K., Haughton, H. (eds.) Specification in OOZE with Examples, pp. 158–183. Prentice Hall International (UK) Ltd., Hertfordshire (1994)
Barrett, E., Bolz, C.F., Tratt, L.: Unipycation: a case study in cross-language tracing. In: Proceedings of the 7th ACM Workshop on Virtual Machines and Intermediate Languages, pp. 31–40. ACM, New York (2013)
Barrett, E., Bolz, C.F., Tratt, L.: Approaches to interpreter composition. Comput. Lang. Syst. Struct. 44, 199–217 (2015)
Beierle, C., Meyer, G.: Run-time type computations in the Warren abstract machine. J. Log. Program. 18(2), 123–148 (1994)
Benton, N.: Embedded interpreters. J. Funct. Program. 15(4), 503–542 (2005)
Chisnall, D.: The challenge of cross-language interoperability. Commun. ACM 56(12), 50–56 (2013)
Dybvig, R.K.: The Scheme Programming Language, 4th edn. The MIT Press, Cambridge (2009)
Erwig, M.: Specifying type systems with multi-level order-sorted algebra. In: Nivat, M., Rattray, C., Rus, T., Scollo, G. (eds.) Algebraic Methodology and Software Technology (AMAST 1993). WORKSHOPS COMP., pp. 177–184. Springer, London (1994). https://doi.org/10.1007/978-1-4471-3227-1_17
Erwig, M., Güting, R.H.: Explicit graphs in a functional model for spatial databases. IEEE Trans. Knowl. Data Eng. 6(5), 787–804 (1994)
Findler, R.B., Felleisen, M.: Contracts for higher-order functions. In: Proceedings of the Seventh ACM SIGPLAN International Conference on Functional Programming, ICFP 2002, pp. 48–59. ACM, New York (2002)
Flanagan, D.: JavaScript: The Definitive Guide. O’Reilly Media Inc., Sebastopol (2006)
Furr, M., Foster, J.S.: Checking type safety of foreign function calls. SIGPLAN Not. 40(6), 62–72 (2005)
Goguen, J.A., Thatcher, J.W., Wagner, E.G., Wright, J.B.: Initial algebra semantics and continuous algebras. J. ACM 24(1), 68–95 (1977)
Goguen, J.: Tossing algebraic flowers down the great divide (1999)
Goguen, J.A.: Semantics of computation. In: Manes, E.G. (ed.) Category Theory Applied to Computation and Control. LNCS, vol. 25, pp. 151–163. Springer, Heidelberg (1975). https://doi.org/10.1007/3-540-07142-3_75
Goguen, J.A., Diaconescu, R.: An oxford survey of order sorted algebra. Math. Struct. Comput. Sci. 4(3), 363–392 (1994)
Goguen, J.A., Meseguer, J.: Order-sorted algebra I: equational deduction for multiple inheritance, overloading, exceptions and partial operations. Theor. Comput. Sci. 105(2), 217–273 (1992)
Gordon, A.D., Syme, D.: Typing a multi-language intermediate code. In: Conference Record of POPL 2001: The 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, London, UK, 17–19 January 2001, pp. 248–260. ACM, New York (2001)
Gray, K.E.: Safe cross-language inheritance. In: Vitek, J. (ed.) ECOOP 2008. LNCS, vol. 5142, pp. 52–75. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70592-5_4
Grimmer, M., Schatz, R., Seaton, C., Würthinger, T., Luján, M.: Cross-language interoperability in a multi-language runtime. ACM Trans. Program. Lang. Syst. 40(2), 8:1–8:43 (2018)
Grimmer, M., Seaton, C., Schatz, R., Würthinger, T., Mössenböck, H.: High-performance cross-language interoperability in a multi-language runtime. In: Proceedings of the 11th Symposium on Dynamic Languages, DLS 2015, Part of SPLASH 2015, Pittsburgh, PA, USA, 25–30 October 2015, pp. 78–90. ACM, New York (2015)
Haxthausen, A.E.: Order-sorted algebraic specifications with higher-order functions. Theor. Comput. Sci. 183(2), 157–185 (1997)
Hearn, A.C., Schrüfer, E.: A computer algebra system based on order-sorted algebra. J. Symb. Comput. 19(1), 65–77 (1995)
Henglein, F., Rehof, J.: Safe polymorphic type inference for scheme: translating scheme to ML. In: Proceedings of the Seventh International Conference on Functional Programming Languages and Computer Architecture, FPCA 1995, La Jolla, California, USA, 25–28 June 1995, pp. 192–203. ACM, New York (1995)
Johann, P., Ghani, N.: Initial algebra semantics is enough!. In: Della Rocca, S.R. (ed.) TLCA 2007. LNCS, vol. 4583, pp. 207–222. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73228-0_16
Juneau, J., Baker, J., Wierzbicki, F., Soto, L., Ng, V.: The Definitive Guide to Jython: Python for the Java Platform, 1st edn. Apress, Berkely (2010)
Liang, S.: Java Native Interface: Programmer’s Guide and Reference, 1st edn. Addison-Wesley Longman Publishing Co., Inc., Boston (1999)
Matthews, J., Findler, R.B.: Operational semantics for multi-language programs. SIGPLAN Not. 42(1), 3–10 (2007)
Meseguer, J., Rosu, G.: The rewriting logic semantics project. Electr. Notes Theor. Comput. Sci. 156(1), 27–56 (2006)
Meseguer, J.: Conditional rewriting logic as a unified model of concurrency. Theor. Comput. Sci. 96(1), 73–155 (1992)
Milner, R., Tofte, M., Macqueen, D.: The Definition of Standard ML. MIT Press, Cambridge (1997)
Ohori, A., Kato, K.: Semantics for communication primitives in a polymorphic language. In: Proceedings of the 20th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 1993, pp. 99–112. ACM, New York (1993)
Osera, P.M., Sjöberg, V., Zdancewic, S.: Dependent interoperability. In: Proceedings of the Sixth Workshop on Programming Languages Meets Program Verification, PLPV 2012, pp. 3–14. ACM, New York (2012)
Patterson, D., Perconti, J., Dimoulas, C., Ahmed, A.: FunTAL: reasonably mixing a functional language with assembly. SIGPLAN Not. 52(6), 495–509 (2017)
Perconti, J.T., Ahmed, A.: Verifying an open compiler using multi-language semantics. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 128–148. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_8
Poigné, A.: Parametrization for order-sorted algebraic specification. J. Comput. Syst. Sci. 40(2), 229–268 (1990)
Qian, Z.: Another look at parameterization for order-sorted algebraic specifications. J. Comput. Syst. Sci. 49(3), 620–666 (1994)
Ramsey, N.: Embedding an interpreted language using higher-order functions and types. In: Proceedings of the 2003 Workshop on Interpreters, Virtual Machines and Emulators, IVME 2003, pp. 6–14. ACM, New York (2003)
Ramsey, N.: ML module mania: a type-safe, separately compiled, extensible interpreter. Electron. Notes Theor. Comput. Sci. 148(2), 181–209 (2006)
Reynolds, J.C.: Definitional interpreters for higher-order programming languages. In: Proceedings of the ACM Annual Conference - Volume 2, ACM 1972, pp. 717–740. ACM, New York (1972)
Robinson, E.: Variations on algebra: monadicity and generalisations of equational therories. Form. Asp. Comput. 13(3), 308–326 (2002)
Rogers, J.: Microsoft JScript.Net Programming. Sams, Indianapolis (2001)
Schmidt-Schauß, M. (ed.): Computational Aspects of an Order-Sorted Logic with Term Declarations. LNCS, vol. 395. Springer, Heidelberg (1989). https://doi.org/10.1007/BFb0024065
Scott, D.S., Strachey, C.: Toward a Mathematical Semantics for Computer Languages, vol. 1. Oxford University Computing Laboratory, Programming Research Group, Oxford (1971)
Sharan, K.: Scripting in Java: Integrating with Groovy and JavaScript, 1st edn. Apress, Berkely (2014)
Stell, J.G.: A framework for order-sorted algebra. In: Kirchner, H., Ringeissen, C. (eds.) AMAST 2002. LNCS, vol. 2422, pp. 396–411. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45719-4_27
Tan, G., Morrisett, G.: Ilea: Inter-language analysis across Java and C. SIGPLAN Not. 42(10), 39–56 (2007)
Trifonov, V., Shao, Z.: Safe and principled language interoperation. In: Swierstra, S.D. (ed.) ESOP 1999. LNCS, vol. 1576, pp. 128–146. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-49099-X_9
Waldmann, U.: Semantics of order-sorted specifications. Theor. Comput. Sci. 94(1), 1–35 (1992)
Wieringa, R.J.: A formalization of objects using equational dynamic logic. In: Delobel, C., Kifer, M., Masunaga, Y. (eds.) DOOD 1991. LNCS, vol. 566, pp. 431–452. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-55015-1_23
Wrigstad, T., Nardelli, F.Z., Lebresne, S., Östlund, J., Vitek, J.: Integrating typed and untyped code in a scripting language. In: Hermenegildo, M.V., Palsberg, J. (eds.) Proceedings of the 37th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2010, Madrid, Spain, 17–23 January 2010, pp. 377–388. ACM (2010)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Buro, S., Mastroeni, I. (2019). On the Multi-Language Construction. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)




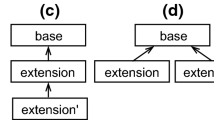
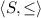 is a poset; and
is a poset; and for each
for each 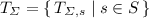 is inductively defined as the least family satisfying:
is inductively defined as the least family satisfying: .
. is defined as
is defined as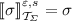 if
if  if
if 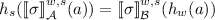 for each
for each 

 and interpretation functions
and interpretation functions  for each
for each 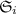 -algebra.
-algebra.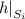 is an order-sorted
is an order-sorted 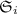 -homomorphism
-homomorphism  , for
, for 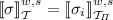 for
for 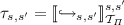 .
. according to the function
according to the function
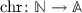 that maps the natural number n to the character symbol
that maps the natural number n to the character symbol  (we are assuming a total lexicographical order
(we are assuming a total lexicographical order  on
on  );
);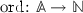 , which is the inverse of
, which is the inverse of  restricted the initial segment on natural numbers
restricted the initial segment on natural numbers 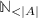 .
. for
for  .
. is a poset; and
is a poset; and

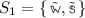 ,
,
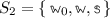 ,
,  , and
, and
 . If the join relation
. If the join relation  and
and
 , the resulting associated signature is no longer regular, although
, the resulting associated signature is no longer regular, although 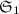 and
and 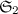 are regular (Fig.
are regular (Fig. 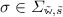 and
and
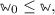 but the set
but the set
 does not have a least element w.r.t.
does not have a least element w.r.t. 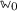 .
.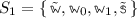 ,
,
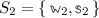 ,
, 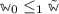 and
and
 , and
, and
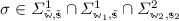 . If the join relation
. If the join relation  , and
, and
 , the resulting associated signature is regular (Fig.
, the resulting associated signature is regular (Fig.  is not: given
is not: given
 and
and
 , the set
, the set
 has least element
has least element
 w.r.t.
w.r.t.
 (Fig.
(Fig.  for each
for each  ; and
; and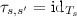 .
.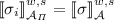 for each
for each  for each
for each  for each
for each 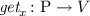 ,
,  ,
, 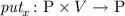 ,
, 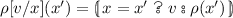 (environment updating);
(environment updating); ,
,
 (function application);
(function application);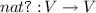 ,
,
 (natural predicate);
(natural predicate); ,
,
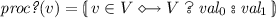 (function predicate);
(function predicate);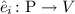 for
for  is defined by
is defined by  (target-tupling); and
(target-tupling); and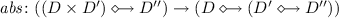 is defined by
is defined by  (conditional function),
(conditional function),  (addition), and
(addition), and  (subtraction)
(subtraction) 
 for each
for each 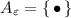 and then define
and then define  .
.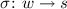 . A (vertical) single line between two sorts s below
. A (vertical) single line between two sorts s below  explicitly since it can be inferred by the algebra equations below.
explicitly since it can be inferred by the algebra equations below.