Abstract
Normal form bisimulation, also known as open bisimulation, is a coinductive technique for higher-order program equivalence in which programs are compared by looking at their essentially infinitary tree-like normal forms, i.e. at their Böhm or Lévy-Longo trees. The technique has been shown to be useful not only when proving metatheorems about \(\lambda \)-calculi and their semantics, but also when looking at concrete examples of terms. In this paper, we show that there is a way to generalise normal form bisimulation to calculi with algebraic effects, à la Plotkin and Power. We show that some mild conditions on monads and relators, which have already been shown to guarantee effectful applicative bisimilarity to be a congruence relation, are enough to prove that the obtained notion of bisimilarity, which we call effectful normal form bisimilarity, is a congruence relation, and thus sound for contextual equivalence. Additionally, contrary to applicative bisimilarity, normal form bisimilarity allows for enhancements of the bisimulation proof method, hence proving a powerful reasoning principle for effectful programming languages.
Thanks to the ANR projects 14CE250005 ELICA and 16CE250011 REPAS.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The study of program equivalence has always been one of the central tasks of programming language theory: giving satisfactory definitions and methodologies for it can be fruitful in contexts like program verification and compiler optimisation design, but also helps in understanding the nature of the programming language at hand. This is particularly true when dealing with higher-order languages, in which giving satisfactory notions of program equivalence is well-known to be hard. Indeed, the problem has been approached in many different ways. One can define program equivalence through denotational semantics, thus relying on a model. One could also proceed following the route traced by Morris [51], and define programs to be contextually equivalent when they behave the same in every context, this way taking program equivalence as the largest adequate congruence.
Both these approaches have their drawbacks, the first one relying on the existence of a (not too coarse) denotational model, the latter quantifying over all contexts, and thus making concrete proofs of equivalence hard. Among the many alternative techniques the research community has been proposing along the years, one can cite logical relations and applicative bisimilarity [1, 4, 8], both based on the idea that equivalent higher-order terms should behave the same when fed with any (pair of related) inputs. This way, terms are compared mimicking any possible action a discriminating context could possibly perform on the tested terms. In other words, the universal quantification on all possible contexts, although not explicitly present, is anyway implicitly captured by the bisimulation or logical game.
Starting from the pioneering work by Böhm, another way of defining program equivalence has been proved extremely useful not only when giving metatheorems about \(\lambda \)-calculi and programming languages, but also when proving concrete programs to be (contextually) equivalent. What we are referring to, of course, is the notion of a Böhm tree of a \(\lambda \)-term \(e\) (see [5] for a formal definition), which is a possibly infinite tree representing the head normal h form of \(e\), if \(e\) has one, but also analyzing the arguments to the head variable of h in a coinductive way. The celebrated Böhm Theorem, also known as Separation Theorem [11], stipulates that two terms are contextually equivalent if and only if their respective (appropriately \(\eta \)-equated) Böhm trees are the same.
The notion of equivalence induced by Böhm trees can be characterised without any reference to trees, by means of a suitable bisimilarity relation [37, 65]. Additionally, Böhm trees can also be defined when \(\lambda \)-terms are not evaluated to their head normal form, like in the classical theory of \(\lambda \)-calculus, but to their weak head normal form (like in the call-by-name [37, 65]), or to their eager normal form (like in the call-by-value \(\lambda \)-calculus [38]). In both cases, the notion of program equivalence one obtains by comparing the syntactic structure of trees, admits an elegant coinductive characterisation as a suitable bisimilarity relation. The family of bisimilarity relations thus obtained goes under the generic name of normal form bisimilarity.
Real world functional programming languages, however, come equipped not only with higher-order functions, but also with computational effects, turning them into impure languages in which functions cannot be seen merely as turning an input to an output. This requires switching to a new model, which cannot be the usual, pure, \(\lambda \)-calculus. Indeed, program equivalence in effectful \(\lambda \)-calculi [49, 56] have been studied by way of denotational semantics [18, 20, 31], logical relations [10, 14], applicative bisimilarity [13, 16, 36], and normal form bisimilarity [20, 41]. While the denotational semantics, logical relation semantics, and applicative bisimilarity of effectful calculi have been studied in the abstract [15, 25, 30], the same cannot be said about normal form bisimilarity. Particularly relevant for our purposes is [15], where a notion of applicative bisimilarity for generic algebraic effects, called effectful applicative bisimilarity, based on the (standard) notion of a monad, and on the (less standard) notion of a relator [71] or lax extension [6, 26], is introduced.
Intuitively, a relator is an abstraction axiomatising the structural properties of relation lifting operations. This way, relators allow for an abstract description of the possible ways a relation between programs can be lifted to a relation between (the results of) effectful computations, the latter being described throughout monads and algebraic operations. Several concrete notions of program equivalence, such as pure, nondeterministic and probabilistic applicative bisimilarity [1, 16, 36, 52] can be analysed using relators. Additionally, besides their prime role in the study of effectful applicative bisimilarity, relators have also been used to study logic-based equivalences [67] and applicative distances [23] for languages with generic algebraic effects.
The main contribution of [15] consists in devising a set of axioms on monads and relators (summarised in the notions of a \({\varSigma }\)-continuous monad and a \({\varSigma }\)-continuous relator) which are both satisfied by many concrete examples, and that abstractly guarantee that the associated notion of applicative bisimilarity is a congruence.
In this paper, we show that an abstract notion of normal form (bi)simulation can indeed be given for calculi with algebraic effects, thus defining a theory analogous to [15]. Remarkably, we show that the defining axioms of \({\varSigma }\)-continuous monads and \({\varSigma }\)-continuous relators guarantee the resulting notion of normal form (bi)similarity to be a (pre)congruence relation, thus enabling compositional reasoning about program equivalence and refinement. Given that these axioms have already been shown to hold in many relevant examples of calculi with effects, our work shows that there is a way to “cook up” notions of effectful normal form bisimulation without having to reprove congruence of the obtained notion of program equivalence: this comes somehow for free. Moreover, this holds both when call-by-name and call-by-value program evaluation is considered, although in this paper we will mostly focus on the latter, since the call-by-value reduction strategy is more natural in presence of computational effectsFootnote 1.
Compared to (effectful) applicative bisimilarity, as well as to other standard operational techniques—such as contextual and CIU equivalence [47, 51], or logical relations [55, 61]—(effectful) normal form bisimilarity has the major advantage of being an intensional program equivalence, equating programs according to the syntactic structure of their (possibly infinitary) normal forms. As a consequence, in order to deem two programs as normal form bisimilar, it is sufficient to test them in isolation, i.e. independently of their interaction with the environment. This way, we obtain easier proofs of equivalence between (effectful) programs. Additionally, normal form bisimilarity allows for enhancements of the bisimulation proof method [60], hence qualifying as a powerful and effective tool for program equivalence.
Intensionality represents a major difference between normal form bisimilarity and applicative bisimilarity, where the environment interacts with the tested programs by passing them arbitrary input arguments (thus making applicative bisimilarity an extensional notion of program equivalence). Testing programs in isolation has, however, its drawbacks. In fact, although we prove effectful normal form bisimilarity to be a sound proof technique for (effectful) applicative bisimilarity (and thus for contextual equivalence), full abstraction fails, as already observed in the case of the pure \(\lambda \)-calculus [3, 38] (nonetheless, it is worth mentioning that full abstraction results are known to hold for calculi with a rich expressive power [65, 68]).
In light of these observations, we devote some energy to studying some concrete examples which highlight the weaknesses of applicative bisimilarity, on the one hand, and the strengths of normal form bisimilarity, on the other hand.
This paper is structured as follows. In Sect. 2 we informally discuss examples of (pairs of) programs which are operational equivalent, but whose equivalence cannot be readily established using standard operational methods. Throughout this paper, we will show how effectful normal form bisimilarity allows for handy proofs of such equivalences. Section 3 is dedicated to mathematical preliminaries, with a special focus on (selected) examples of monads and algebraic operations. In Sect. 4 we define our vehicle calculus \({\varLambda }_{\varSigma }\), an untyped \(\lambda \)-calculus enriched with algebraic operations, to which we give call-by-value monadic operational semantics. Section 5 introduces relators and their main properties. In Sect. 6 we introduce effectful eager normal form (bi)similarity, the call-by-value instantiation of effectful normal form (bi)similarity, and its main metatheoretical properties. In particular, we prove effectful eager normal form (bi)similarity to be a (pre)congruence relation (Theorem 2) included in effectful applicative (bi)similarity (Proposition 5). Additionally, we prove soundness of eager normal bisimulation up-to context (Theorem 3), a powerful enhancement of the bisimulation proof method that allows for handy proof of program equivalence. Finally, in Sect. 6.4 we briefly discuss how to modify our theory to deal with call-by-name calculi.
2 From Applicative to Normal Form Bisimilarity
In this section, some examples of (pairs of) programs which can be shown equivalent by effectful normal form bisimilarity will be provided, giving evidence on the flexibility and strength of the proposed technique. We will focus on examples drawn from fixed point theory, simply because these, being infinitary in nature, are quite hard to be dealt with “finitary” techniques like contextual equivalence or applicative bisimilarity.
Example 1
Our first example comes from the ordinary theory of pure, untyped \(\lambda \)-calculus. Let us consider Curry’s and Turing’s call-by-value fixed point combinators Y and Z:
It is well known that Y and Z are contextually equivalent, although proving such an equivalence from first principles is doomed to be hard. For that reason, one usually looks at proof techniques for contextual equivalence. Here we consider applicative bisimilarity [1]. As in the pure \(\lambda \)-calculus applicative bisimilarity coincides with the intersection of applicative similarity and its converse, for the sake of the argument we discuss which difficulties one faces when trying to prove Z to be applicatively similar to Y.
Let us try to construct an applicative simulation  relating Y and Z. Clearly we need to have
relating Y and Z. Clearly we need to have  . Since Y evaluates to \(\lambda y.{{\varDelta }{\varDelta }}\), and Z evaluates to \(\lambda y. y(\lambda z.{\varTheta }{\varTheta } yz)\), in order for
. Since Y evaluates to \(\lambda y.{{\varDelta }{\varDelta }}\), and Z evaluates to \(\lambda y. y(\lambda z.{\varTheta }{\varTheta } yz)\), in order for  to be an applicative simulation, we need to show that for any value \(v\),
to be an applicative simulation, we need to show that for any value \(v\),  . Since the result of the evaluation of \({\varDelta }[v/y]{\varDelta }[v/y]\) is the same of \(v(\lambda z.{\varDelta }[v/y]{\varDelta }[v/y]z)\), we have reached a point in which we are stuck: in order to ensure
. Since the result of the evaluation of \({\varDelta }[v/y]{\varDelta }[v/y]\) is the same of \(v(\lambda z.{\varDelta }[v/y]{\varDelta }[v/y]z)\), we have reached a point in which we are stuck: in order to ensure  , we need to show that
, we need to show that  . However, the value \(v\) being provided by the environment, no information on it is available. That is, we have no information on how \(v\) tests its input program. In particular, given any context \(\mathcal {C}[-]\), we can consider the value \(\lambda x.\mathcal {C}[x]\), meaning that proving Y and Z to be applicatively bisimilar is almost as hard as proving them to be contextually equivalent from first principles.
. However, the value \(v\) being provided by the environment, no information on it is available. That is, we have no information on how \(v\) tests its input program. In particular, given any context \(\mathcal {C}[-]\), we can consider the value \(\lambda x.\mathcal {C}[x]\), meaning that proving Y and Z to be applicatively bisimilar is almost as hard as proving them to be contextually equivalent from first principles.
As we will see, proving Z to be normal form similar to Y is straightforward, since in order to test \(\lambda y.{{\varDelta }{\varDelta }}\) and \(\lambda y. y(\lambda z.{\varTheta }{\varTheta } yz)\), we simply test their subterms \({\varDelta } {\varDelta }\) and \(y(\lambda z.{\varTheta }{\varTheta } yz)\), thus not allowing the environment to influence computations.
Example 2
Our next example is a refinement of Example 1 to a probabilistic setting, as proposed in [66] (but in a call-by-name setting). We consider a variation of Turing’s call-by-value fixed point combinator which, at any iteration, can probabilistically decide whether to start another iteration (following the pattern of the standard Turing’s fixed point combinator) or to turn for good into Y, where Y and \({\varDelta }\) are defined as in Example 1:
Notice that the constructor \(\mathbin {\mathbf {or}}\) behaves as a (fair) probabilistic choice operator, hence acting as an effect producer. It is natural to ask whether these new versions of Y and Z are still equivalent. However, following insights from previous example, it is not hard to see the equivalence between Y and Z cannot be readily proved by means of standard operational methods such as probabilistic contextual equivalence [16], probabilistic CIU equivalence and logical relations [10], and probabilistic applicative bisimilarity [13, 16]. All the aforementioned techniques require to test programs in a given environment (such as a whole context or an input argument), and are thus ineffective in handling fixed point combinators such as Y and Z.
We will give an elementary proof of the equivalence between Y and Z in Example 17, and a more elegant proof relying on a suitable up-to context technique in Example 18. In [66], the call-by-name counterparts of Y and Z are proved to be equivalent using probabilistic environmental bisimilarity. The notion of an environmental bisimulation [63] involves both an environment storing pairs of terms played during the bisimulation game, and a clause universally quantifying over pairs of terms in the evaluation context closure of such an environmentFootnote 2, thus making environmental bisimilarity a rather heavy technique to use. Our proof of the equivalence of Y and Z is simpler: in fact, our notion of effectful normal form bisimulation does not involve any universal quantification over all possible closed function arguments (like applicative bisimilarity), or their evaluation context closure (like environmental bisimilarity), or closed instantiation of uses (like CIU equivalence).
Example 3
Our third example concerns call-by-name calculi and shows how our notion of normal form bisimilarity can handle even intricate recursion schemes. We consider the following argument-switching probabilistic fixed point combinators:
We easily see that P and Q satisfy the following (informal) program equations:
Again, proving the equivalence between P and Q using applicative bisimilarity is problematic. In fact, testing the applicative behaviour of P and Q requires to reason about the behaviour of e.g. \(e(P ef)\), which in turn requires to reason about the (arbitrary) term \(e\), on which no information is provided. The (essentially infinitary) normal forms of P and Q, however, can be proved to be essentially the same by reasoning about the syntactical structure of P and Q. Moreover, our up-to context technique enables an elegant and concise proof of the equivalence between P and Q (Sect. 6.4).
Example 4
Our last example discusses the use of the cost monad as an instrument to facilitate a more intensional analysis of programs. In fact, we can use the ticking operation \(\mathbf {tick}\) to perform cost analysis. For instance, we can consider the following variation of Curry’s and Turing’s fixed point combinator of Example 1, obtained by adding the operation symbol \(\mathbf {tick}\) after every \(\lambda \)-abstraction.
Every time a \(\beta \)-redex \((\lambda x.{\mathbf {tick}(e)})v\) is reduced, the ticking operation \(\mathbf {tick}\) increases an imaginary cost counter of a unit. Using ticking, we can provide a more intensional analysis of the relationship between Y and Z, along the lines of Sands’ improvement theory [62].
3 Preliminaries: Monads and Algebraic Operations
In this section we recall some basic definitions and results needed in the rest of the paper. Unfortunately, there is no hope to be comprehensive, and thus we assume the reader to be familiar with basic domain theory [2] (in particular with the notions of \(\omega \)-complete (pointed) partial order—\(\omega \)-cppo, for short—monotone, and continuous functions), basic order theory [19], and basic category theory [46]. Additionally, we assume the reader to be acquainted with the notion of a Kleisli triple [46] \(\mathbb {T}= \langle T, \eta , -^{\dagger } \rangle \). As it is customary, we use the notation \(f^{\dagger }: TX \rightarrow TY\) for the Kleisli extension of \(f: X \rightarrow TY\), and reserve the letter \(\eta \) to denote the unit of \(\mathbb {T}\). Due to their equivalence, oftentimes we refer to Kleisli triples as monads.
Concerning notation, we try to follow [46] and [2], with the only exception that we use the notation \((x_n)_n\) to denote an \(\omega \)-chain  in a domain
in a domain  . The notation \(\mathbb {T}= \langle T, \eta , -^{\dagger } \rangle \) for an arbitrary Kleisli triple is standard, but it is not very handy when dealing with multiple monads at the same time. To fix this issue, we sometimes use the notation
. The notation \(\mathbb {T}= \langle T, \eta , -^{\dagger } \rangle \) for an arbitrary Kleisli triple is standard, but it is not very handy when dealing with multiple monads at the same time. To fix this issue, we sometimes use the notation  to denote a Kleisli triple. Additionally, when unambiguous we omit subscripts. Finally, we denote by \(\mathsf {Set}\) the category of sets and functions, and by \(\mathsf {Rel}\) the category of sets and relations. We reserve the symbol \(1\) to denote the identity function. Unless explicitly stated, we assume functors (and monads) to be functors (and monads) on \(\mathsf {Set}\). As a consequence, we write functors to refer to endofunctors on \(\mathsf {Set}\).
to denote a Kleisli triple. Additionally, when unambiguous we omit subscripts. Finally, we denote by \(\mathsf {Set}\) the category of sets and functions, and by \(\mathsf {Rel}\) the category of sets and relations. We reserve the symbol \(1\) to denote the identity function. Unless explicitly stated, we assume functors (and monads) to be functors (and monads) on \(\mathsf {Set}\). As a consequence, we write functors to refer to endofunctors on \(\mathsf {Set}\).
We use monads to give operational semantics to our calculi. Following Moggi [49, 50], we model notions of computation as monads, meaning that we use monads as mathematical models of the kind of (side) effects computations may produce. The following are examples of monads modelling relevant notions of computation. Due to space constraints, we omit several interesting examples such as the output, the exception, and the nondeterministic/powerset monad, for which the reader is referred to e.g. [50, 73].
Example 5
(Partiality). Partial computations are modelled by the partiality (also called maybe) monad  . The carrier \(MX\) of
. The carrier \(MX\) of  is defined as \(\{just\ x \mid x \in X\} \cup \{\bot \}\), where \(\bot \) is a special symbol denoting divergence. The unit and Kleisli extension of
is defined as \(\{just\ x \mid x \in X\} \cup \{\bot \}\), where \(\bot \) is a special symbol denoting divergence. The unit and Kleisli extension of  are defined as follows:
are defined as follows:

Example 6
(Probabilistic Nondeterminism). In this example we assume sets to be countableFootnote 3. The (discrete) distribution monad  has carrier
has carrier  , whereas the maps
, whereas the maps  and
and  are defined as follows (where \(y \ne x\)):
are defined as follows (where \(y \ne x\)):

Oftentimes, we write a distribution \(\mu \) as a weighted formal sum. That is, we write \(\mu \) as the sumFootnote 4 \(\sum _{i \in I} p_i \cdot x_i\) such that \(\mu (x) = \sum _{x_i = x} p_i\).  models probabilistic total computations, according to the rationale that a (total) probabilistic program evaluates to a distribution over values, the latter describing the possible results of the evaluation. Finally, we model probabilistic partial computations using the monad
models probabilistic total computations, according to the rationale that a (total) probabilistic program evaluates to a distribution over values, the latter describing the possible results of the evaluation. Finally, we model probabilistic partial computations using the monad  . The carrier of
. The carrier of  is defined as \(DMX \triangleq D(MX)\), whereas the unit
is defined as \(DMX \triangleq D(MX)\), whereas the unit  is defined in the obvious way. For \(f: X \rightarrow DMY\), define:
is defined in the obvious way. For \(f: X \rightarrow DMY\), define:

It is easy to see that  is isomorphic to the subdistribution monad.
is isomorphic to the subdistribution monad.
Example 7
(Cost). The cost (also known as ticking or improvement [62]) monad  has carrier
has carrier  . The unit of \(\mathbb {C}\) is defined as
. The unit of \(\mathbb {C}\) is defined as  , whereas Kleisli extension is defined as follows:
, whereas Kleisli extension is defined as follows:

The cost monad is used to model the cost of (partial) computations. An element of the form \(just\ (n, x)\) models the result of a computation outputting the value x with cost n (the latter being an abstract notion that can be instantiated to e.g. the number of reduction steps performed). Partiality is modelled as the element \(\bot \), according to the rationale that we can assume all divergent computations to have the same cost, so that such information need not be explicitly written (for instance, measuring the number of reduction steps performed, we would have that divergent computations all have cost \(\infty \)).
Example 8
(Global states). Let \(\mathcal {L}\) be a set of public location names. We assume the content of locations to be encoded as families of values (such as numerals or booleans) and denote the collection of such values as \(\mathcal {V}\). A store (or state) is a function \(\sigma : \mathcal {L}\rightarrow \mathcal {V}\). We write \(S\) for the set of stores \(\mathcal {V}^\mathcal {L}\). The global state monad  has carrier \(GX \triangleq (X \times S)^{S}\), whereas
has carrier \(GX \triangleq (X \times S)^{S}\), whereas  and
and  are defined by:
are defined by:

where \(\alpha (\sigma ) = (x',\sigma ')\). It is straightforward to see that we can combine the global state monad with the partiality monad, obtaining the monad  whose carrier is \((M\otimes G) X \triangleq M(X \times S)^S\). In a similar fashion, we see that we can combine the global state monad with
whose carrier is \((M\otimes G) X \triangleq M(X \times S)^S\). In a similar fashion, we see that we can combine the global state monad with  and \(\mathbb {C}\), as we are going to see in Remark 1.
and \(\mathbb {C}\), as we are going to see in Remark 1.
Remark 1
The monads  and
and  of Example 6 and Example 8, respectively, are instances of two general constructions, namely the sum and tensor of effects [28]. Although these operations are defined on Lawvere theories [29, 40], here we can rephrase them in terms of monads as follows.
of Example 6 and Example 8, respectively, are instances of two general constructions, namely the sum and tensor of effects [28]. Although these operations are defined on Lawvere theories [29, 40], here we can rephrase them in terms of monads as follows.
Proposition 1
Given a monad  , define the sum
, define the sum  of \(\mathbb {T}\) and
of \(\mathbb {T}\) and  and the tensor
and the tensor  of \(\mathbb {T}\) and
of \(\mathbb {T}\) and  , as the triples
, as the triples  and
and  , respectively. The carriers of the triples are defined as \(TMX \triangleq T(MX)\) and \((T\otimes G)X \triangleq T(S \times X)^S\), whereas the maps
, respectively. The carriers of the triples are defined as \(TMX \triangleq T(MX)\) and \((T\otimes G)X \triangleq T(S \times X)^S\), whereas the maps  and
and  are defined as
are defined as  and
and  , respectively. Finally, define:
, respectively. Finally, define:

where, for a function \(f: X \rightarrow TMY\) we define \(f_{M}: MX \rightarrow TMY\) as  , \(f_{M}(just\ x) \triangleq f(x)\), and \(\mathsf {curry}\) and \(\mathsf {uncurry}\) are defined as usual. Then
, \(f_{M}(just\ x) \triangleq f(x)\), and \(\mathsf {curry}\) and \(\mathsf {uncurry}\) are defined as usual. Then  and
and  are monads.
are monads.
Proving Proposition 1 is a straightforward exercise (the reader can also consult [28]). We notice that tensoring  with
with  we obtain a monad for probabilistic imperative computations, whereas tensoring
we obtain a monad for probabilistic imperative computations, whereas tensoring  with \(\mathbb {C}\) we obtain a monad for imperative computations with cost.
with \(\mathbb {C}\) we obtain a monad for imperative computations with cost.
3.1 Algebraic Operations
Monads provide an elegant way to structure effectful computations. However, they do not offer any actual effect constructor. Following Plotkin and Power [56,57,58], we use algebraic operations as effect producers. From an operational perspective, algebraic operations are those operations whose behaviour is independent of their continuations or, equivalently, of the environment in which they are evaluated. Intuitively, that means that e.g. \(E[e_1 \mathbin {\mathbf {or}}e_2]\) is operationally equivalent to \(E[e_1] \mathbin {\mathbf {or}}E[e_2]\), for any evaluation context \(E\). Examples of algebraic operations are given by (binary) nondeterministic and probabilistic choices as well as primitives for rising exceptions and output operations.
Syntactically, algebraic operations are given via a signature \({\varSigma }\) consisting of a set of operation symbols (uninterpreted operations) together with their arity (i.e. their number of operands). Semantically, operation symbols are interpreted as algebraic operations on monads. To any n-ary operation symbolFootnote 5 \((\mathbf {op}: n) \in {\varSigma }\) and any set X we associate a map \([\![ \mathbf {op} ]\!]_X: (TX)^n \rightarrow TX\) (so that we equip \(TX\) with a \({\varSigma }\)-algebra structure [12]) such that \(f^{\dagger }\) is \({\varSigma }\)-algebra morphism, meaning that for any \(f: X \rightarrow TY\), and elements  we have
we have 
Example 9
The partiality monad  usually comes with no operation, as the possibility of divergence is an implicit feature of any Turing complete language. However, it is sometimes useful to add an explicit divergence operation (for instance, in strongly normalising calculi). For that, we consider the signature
usually comes with no operation, as the possibility of divergence is an implicit feature of any Turing complete language. However, it is sometimes useful to add an explicit divergence operation (for instance, in strongly normalising calculi). For that, we consider the signature  . Having arity zero, the operation \(\underline{{\varOmega }}\) acts as a constant, and has semantics \([\![ \underline{{\varOmega }} ]\!] = \bot \). Since
. Having arity zero, the operation \(\underline{{\varOmega }}\) acts as a constant, and has semantics \([\![ \underline{{\varOmega }} ]\!] = \bot \). Since  , we see that \(\underline{{\varOmega }}\) in indeed an algebraic operation on
, we see that \(\underline{{\varOmega }}\) in indeed an algebraic operation on  .
.
For the distribution monad  we define the signature
we define the signature  . The intended semantics of a program \(e_1 \mathbin {\mathbin {\mathbf {or}}} e_2\) is to evaluate to \(e_i\) (\(i \in \{1,2\}\)) with probability 0.5. The interpretation of \(\mathbin {\mathbf {or}}\) is defined by \([\![ \mathbin {\mathbf {or}} ]\!](\mu ,\nu )(x) \triangleq 0.5 \cdot \mu (x) + 0.5 \cdot \nu (x)\). It is easy to see that \(\mathbin {\mathbf {or}}\) is an algebraic operation on
. The intended semantics of a program \(e_1 \mathbin {\mathbin {\mathbf {or}}} e_2\) is to evaluate to \(e_i\) (\(i \in \{1,2\}\)) with probability 0.5. The interpretation of \(\mathbin {\mathbf {or}}\) is defined by \([\![ \mathbin {\mathbf {or}} ]\!](\mu ,\nu )(x) \triangleq 0.5 \cdot \mu (x) + 0.5 \cdot \nu (x)\). It is easy to see that \(\mathbin {\mathbf {or}}\) is an algebraic operation on  , and that it trivially extends to
, and that it trivially extends to  .
.
Finally, for the cost monad \(\mathbb {C}\) we define the signature \({\varSigma }_{\mathbb {C}} \triangleq \{\mathbf {tick}: 1\}\). The intended semantics of \(\mathbf {tick}\) is to add a unit to the cost counter:
The framework we have just described works fine for modelling operations with finite arity, but does not allow to handle operations with infinitary arity. This is witnessed, for instance, by imperative calculi with global stores, where it is natural to have operations of the form \(\mathbf {get}_{\ell }(x.k)\) with the following intended semantics: \(\mathbf {get}_{\ell }(x.k)\) reads the content of the location \(\ell \), say it is a value \(v\), and continue as \(k[v/x]\). In order to take such operations into account, we follow [58] and work with generalised operations.
A generalised operation (operation, for short) on a set X is a function \(\omega : P \times X^I \rightarrow X\). The set P is called the parameter set of the operation, whereas the (index) set I is called the arity of the operation. A generalised operation \(\omega : P \times X^I \rightarrow X\) thus takes as arguments a parameter \(p\) (such as a location name) and a map \(\kappa : I \rightarrow X\) giving for each index \(i \in I\) the argument \(\kappa (i)\) to pass to \(\omega \). Syntactically, generalised operations are given via a signature \({\varSigma }\) consisting of a set of elements of the form \(\mathbf {op}: P\,\rightsquigarrow \,I\) (the latter being nothing but a notation denoting that the operation symbols \(\mathbf {op}\) has parameter set P and index set I). Semantically, an interpretation of an operation symbol \(\mathbf {op}: P\,\rightsquigarrow \,I\) on a monad \(\mathbb {T}\) associates to any set X a map \([\![ \mathbf {op} ]\!]_X: P\times (TX)^I \rightarrow TX\) such that for any \(f: X \rightarrow TY\), \(p\in P\), and \(\kappa : I \rightarrow TX\):
If \(\mathbb {T}\) comes with an interpretation for operation symbols in \({\varSigma }\), we say that \(\mathbb {T}\) is \({\varSigma }\)-algebraic.
It is easy to see by taking the one-element set \(1 = \{*\}\) as parameter set and a finite set as arity set, generalised operations subsume finitary operations. For simplicity, we use the notation \(\mathbf {op}: n\) in place of \(\mathbf {op}: 1\,\rightsquigarrow \,n\), and write  in place of
in place of  .
.
Example 10
For the global state monad we consider the signature  . From a computational perspective, such operations are used to build programs of the form \(\mathbf {set}_{\ell }(v, e)\) and \(\mathbf {get}_{\ell }(x.e)\). The former stores the value \(v\) in the location \(\ell \) and continues as \(e\), whereas the latter reads the content of the location \(\ell \), say it is \(v\), and continue as \(e[v/x]\). Here \(e\) is used as the description of a function \(\kappa _e\) from values to terms defined by \(\kappa _e(v) \triangleq e[v/x]\). The interpretation of the new operations on
. From a computational perspective, such operations are used to build programs of the form \(\mathbf {set}_{\ell }(v, e)\) and \(\mathbf {get}_{\ell }(x.e)\). The former stores the value \(v\) in the location \(\ell \) and continues as \(e\), whereas the latter reads the content of the location \(\ell \), say it is \(v\), and continue as \(e[v/x]\). Here \(e\) is used as the description of a function \(\kappa _e\) from values to terms defined by \(\kappa _e(v) \triangleq e[v/x]\). The interpretation of the new operations on  is standard:
is standard:
Straightforward calculations show that indeed \(\mathbf {set}_{\ell }\) and \(\mathbf {get}_{\ell }\) are algebraic operations on  . Moreover, such operations can be easily extended to the partial global state monad
. Moreover, such operations can be easily extended to the partial global state monad  as well as to the probabilistic (partial) global store monad
as well as to the probabilistic (partial) global store monad  . These extensions share a common pattern, which is nothing but an instance of the tensor of effects. In fact, given a \({\varSigma }_{\mathbb {T}}\)-algebraic monad \(\mathbb {T}\) we can define the signature
. These extensions share a common pattern, which is nothing but an instance of the tensor of effects. In fact, given a \({\varSigma }_{\mathbb {T}}\)-algebraic monad \(\mathbb {T}\) we can define the signature  as
as  , and observe that the
, and observe that the  is
is  -algebraic. We refer the reader to [28] for details. Here we simply notice that we can define the interpretation
-algebraic. We refer the reader to [28] for details. Here we simply notice that we can define the interpretation  of \(\mathbf {op}: P\,\rightsquigarrow \,\mathcal {V}\) on
of \(\mathbf {op}: P\,\rightsquigarrow \,\mathcal {V}\) on  as
as  where \([\![ \mathbf {op} ]\!]^{\scriptscriptstyle \mathbb {T}}\) is the interpretation of \(\mathbf {op}\) on \(\mathbb {T}\) (the interpretations of \(\mathbf {set}_{\ell }\) and \(\mathbf {get}_{\ell }\) are straightforward).
where \([\![ \mathbf {op} ]\!]^{\scriptscriptstyle \mathbb {T}}\) is the interpretation of \(\mathbf {op}\) on \(\mathbb {T}\) (the interpretations of \(\mathbf {set}_{\ell }\) and \(\mathbf {get}_{\ell }\) are straightforward).
Monads and algebraic operations provide mathematical abstractions to structure and produce effectful computations. However, in order to give operational semantics to, e.g., probabilistic calculi [17] we need monads to account for infinitary computational behaviours. We thus look at \({\varSigma }\)-continuous monads.
Definition 1
A \({\varSigma }\)-algebraic monad \(\mathbb {T}= \langle T, \eta , -^{\dagger }\rangle \) is \({\varSigma }\)-continuous (cf. [24]) if to any set X is associated an order  and an element \(\bot _X \in TX\) such that
and an element \(\bot _X \in TX\) such that  is an \(\omega \)-cppo, and for all \((\mathbf {op}: P\,\rightsquigarrow \,I) \in {\varSigma }\), \(f,f_n,g: X \rightarrow TY\), \(\kappa , \kappa _n, \nu : I \rightarrow TX\),
is an \(\omega \)-cppo, and for all \((\mathbf {op}: P\,\rightsquigarrow \,I) \in {\varSigma }\), \(f,f_n,g: X \rightarrow TY\), \(\kappa , \kappa _n, \nu : I \rightarrow TX\),  , we have \(f^{\dagger }(\bot ) = \bot \) and:
, we have \(f^{\dagger }(\bot ) = \bot \) and:

When clear from the context, we will omit subscripts in \(\bot _X\) and  .
.
Example 11
The monads  ,
,  ,
,  , and \(\mathbb {C}\) are \({\varSigma }\)-continuous. The order on \(MX\) and \(\mathbb {C}\) is the flat ordering
, and \(\mathbb {C}\) are \({\varSigma }\)-continuous. The order on \(MX\) and \(\mathbb {C}\) is the flat ordering  defined by
defined by  , whereas the order on \(DMX\) is defined by
, whereas the order on \(DMX\) is defined by  . Finally, the order on \(GMX\) is defined pointwise from the flat ordering on \(M(X \times S)\).
. Finally, the order on \(GMX\) is defined pointwise from the flat ordering on \(M(X \times S)\).
Having introduced the notion of a \({\varSigma }\)-continuous monad, we can now define our vehicle calculus \({\varLambda }_{\varSigma }\) and its monadic operational semantics.
4 A Computational Call-by-value Calculus with Algebraic Operations
In this section we define the calculus \({\varLambda }_{\varSigma }\). \({\varLambda }_{\varSigma }\) is an untyped \(\lambda \)-calculus parametrised by a signature of operation symbols, and corresponds to the coarse-grain [44] version of the calculus studied in [15]. Formally, terms of \({\varLambda }_{\varSigma }\) are defined by the following grammar, where \(x\) ranges over a countably infinite set of variables and \(\mathbf {op}\) is a generalised operation symbol in \({\varSigma }\).

A value is either a variable or a \(\lambda \)-abstraction. We denote by \({\varLambda }\) the collection of terms and by \(\mathcal {V}\) the collection of values of \({\varLambda }_{\varSigma }\). For an operation symbol \(\mathbf {op}: P\,\rightsquigarrow \,I\), we assume that set I to be encoded by some subset of \(\mathcal {V}\) (using e.g. Church’s encoding). In particular, in a term of the form \(\mathbf {op}(p, x.e)\), \(e\) acts as a function in the variable \(x\) that takes as input a value. Notice also how parameters \(p\in P\) are part of the syntax. For simplicity, we ignore the specific subset of values used to encode elements of I, and simply write \(\mathbf {op}: P\,\rightsquigarrow \,\mathcal {V}\) for operation symbols in \({\varSigma }\).
We adopt standard syntactical conventions as in [5] (notably the so-called variable convention). The notion of a free (resp. bound) variable is defined as usual (notice that the variable \(x\) is bound in \(\mathbf {op}(p, x.e)\)). As it is customary, we identify terms up to renaming of bound variables and say that a term is closed if it has no free variables (and that it is open, otherwise). Finally, we write \(f[e/x]\) for the capture-free substitution of the term \(e\) for all free occurrences of \(x\) in \(f\). In particular, \(\mathbf {op}(p, x'.f)[e/x] \) is defined as \(\mathbf {op}(p, x'.f[e/x])\).
Before giving \({\varLambda }_{\varSigma }\) call-by-value operational semantics, it is useful to remark a couple of points. First of all, testing terms according to their (possibly infinitary) normal forms obviously requires to work with open terms. Indeed, in order to inspect the intensional behaviour of a value \(\lambda x.{e}\), one has to inspect the intensional behaviour of \(e\), which is an open term. As a consequence, contrary to the usual practice, we give operational semantics to both open and closed terms. Actually, the very distinction between open and closed terms is not that meaningful in this context, and thus we simply speak of terms. Second, we notice that values constitute a syntactic category defined independently of the operational semantics of the calculus: values are just variables and \(\lambda \)-abstractions. However, giving operational semantics to arbitrary terms we are interested in richer collections of irreducible expressions, i.e. expressions that cannot be simplified any further. Such collections will be different accordingly to the operational semantics adopted. For instance, in a call-by-name setting it is natural to regard the term \(x((\lambda x.{x}) v)\) as a terminal expression (being it a head normal form), whereas in a call-by-value setting \(x((\lambda x.{x}) v)\) can be further simplified to \(xv\), which in turn should be regarded as a terminal expression.
We now give \({\varLambda }_{\varSigma }\) a monadic call-by-value operational semantics [15], postponing the definition of monadic call-by-name operational semantics to Sect. 6.4. Recall that a (call-by-value) evaluation context [22] is a term with a single hole \([-]\) defined by the following grammar, where \(e\in {\varLambda }\) and \(v\in \mathcal {V}\):

We write \(E[e]\) for the term obtained by substituting the term \(e\) for the hole \([-]\) in \(E\).
Following [38], we define a stuck term as a term of the form \(E[xv]\). Intuitively, a stuck term is an expression whose evaluation is stuck. For instance, the term \(e\triangleq y(\lambda x.{x})\) is stuck. Obviously, \(e\) is not a value, but at the same time it cannot be simplified any further, as \(y\) is a variable, and not a \(\lambda \)-abstraction. Following this intuition, we define the collection \(\mathcal {E}\) of eager normal forms (enfs hereafter) as the collection of values and stuck terms. We let letters  range over elements in \(\mathcal {E}\).
range over elements in \(\mathcal {E}\).
Lemma 1
Any term \(e\) is either a value \(v\), or can be uniquely decomposed as either \(E[vw]\) or \(E[\mathbf {op}(p, x.f)]\).
Operational semantics of \({\varLambda }_{\varSigma }\) is defined with respect to a \({\varSigma }\)-continuous monad \(\mathbb {T}= \langle T, \eta , -^{\dagger }\rangle \) relying on Lemma 1. More precisely, we define a call-by-value evaluation function \([\![ - ]\!]\) mapping each term to an element in \(T\mathcal {E}\). For instance, evaluating a probabilistic term \(e\) we obtain a distribution over eager normal forms (plus bottom), the latter being either values (meaning that the evaluation of \(e\) terminates) or stuck terms (meaning that the evaluation of \(e\) went stuck at some point).
Definition 2
Define the  -indexed family of maps \([\![ - ]\!]_{n}: {\varLambda } \rightarrow T\mathcal {E}\) as follows:
-indexed family of maps \([\![ - ]\!]_{n}: {\varLambda } \rightarrow T\mathcal {E}\) as follows:

The monad \(\mathbb {T}\) being \({\varSigma }\)-continuous, we see that the sequence \(([\![ e ]\!]_{n})_{n}\) forms an \(\omega \)-chain in \(T\mathcal {E}\), so that we can define \([\![ e ]\!]\) as \(\bigsqcup _{n} [\![ e ]\!]_{n}\). Moreover, exploiting \({\varSigma }\)-continuity of \(\mathbb {T}\) we see that \([\![ - ]\!]\) is continuous.
We compare the behaviour of terms of \({\varLambda }_{\varSigma }\) relying on the notion of an effectful eager normal form (bi)simulation, the extension of eager normal form (bi)simulation [38] to calculi with algebraic effects. In order to account for effectful behaviours, we follow [15] and parametrise our notions of equivalence and refinement by relators [6, 71].
5 Relators
The notion of a relator for a functor \(T\) (on \(\mathsf {Set}\)) [71] (also called lax extension of \(T\) [6]) is a construction lifting a relation  between two sets X and Y to a relation
between two sets X and Y to a relation  between \(TX\) and \(TY\). Besides their applications in categorical topology [6] and coalgebra [71], relators have been recently used to study notions of applicative bisimulation [15], logic-based equivalence [67], and bisimulation-based distances [23] for \(\lambda \)-calculi extended with algebraic effects. Moreover, several forms of monadic lifting [25, 32] resembling relators have been used to study abstract notions of logical relations [55, 61].
between \(TX\) and \(TY\). Besides their applications in categorical topology [6] and coalgebra [71], relators have been recently used to study notions of applicative bisimulation [15], logic-based equivalence [67], and bisimulation-based distances [23] for \(\lambda \)-calculi extended with algebraic effects. Moreover, several forms of monadic lifting [25, 32] resembling relators have been used to study abstract notions of logical relations [55, 61].
Before defining relators formally, it is useful to recall some background notions on (binary) relations. The reader is referred to [26] for further details. We denote by \(\mathsf {Rel}\) the category of sets and relations, and use the notation  for a relation
for a relation  between sets X and Y. Given relations
between sets X and Y. Given relations  and
and  , we write
, we write  for their composition, and
for their composition, and  for the identity relation on X. Finally, we recall that for all sets \(X, Y\), the hom-set \(\mathsf {Rel}(X, Y)\) has a complete lattice structure, meaning that we can define relations both inductively and coinductively.
for the identity relation on X. Finally, we recall that for all sets \(X, Y\), the hom-set \(\mathsf {Rel}(X, Y)\) has a complete lattice structure, meaning that we can define relations both inductively and coinductively.
Given a relation  , we denote by
, we denote by  its dual (or opposite) relations and by \(-_{\circ }: \mathsf {Set}\rightarrow \mathsf {Rel}\) the graph functor mapping each function \(f: X \rightarrow Y\) to its graph
its dual (or opposite) relations and by \(-_{\circ }: \mathsf {Set}\rightarrow \mathsf {Rel}\) the graph functor mapping each function \(f: X \rightarrow Y\) to its graph  . The functor \(-_{\circ }\) being faithful, we will often write \(f: X \rightarrow Y\) in place of
. The functor \(-_{\circ }\) being faithful, we will often write \(f: X \rightarrow Y\) in place of  . It is useful to keep in mind the pointwise reading of relations of the form \(g^{\circ } \circ \mathbin {\mathcal {S}}\circ f\), for a relation
. It is useful to keep in mind the pointwise reading of relations of the form \(g^{\circ } \circ \mathbin {\mathcal {S}}\circ f\), for a relation  and functions \(f: X \rightarrow Z\), \(g: Y \rightarrow W\):
and functions \(f: X \rightarrow Z\), \(g: Y \rightarrow W\):
Given  , we can thus express a generalised monotonicity condition in a pointfree fashion using the inclusion
, we can thus express a generalised monotonicity condition in a pointfree fashion using the inclusion  Finally, since we are interested in preorder and equivalence relations, we recall that a relation
Finally, since we are interested in preorder and equivalence relations, we recall that a relation  is reflexive if
is reflexive if  , transitive if
, transitive if  , and symmetric if
, and symmetric if  . We can now define relators formally.
. We can now define relators formally.
Definition 3
A relator for a functor \(T\) (on \(\mathsf {Set}\)) is a set-indexed family of maps  satisfying conditions (rel 1)–(rel 4). We say that \({\varGamma }\) is conversive if it additionally satisfies condition (rel 5).
satisfying conditions (rel 1)–(rel 4). We say that \({\varGamma }\) is conversive if it additionally satisfies condition (rel 5).
Conditions (rel 1), (rel 2), and (rel 4) are rather standardFootnote 6. As we will see, condition (rel 4) makes the defining functional of (bi)simulation relations monotone, whereas conditions (rel 1) and (rel 2) make notions of (bi)similarity reflexive and transitive. Similarly, condition (rel 5) makes notions of bisimilarity symmetric. Condition (rel 3), which actually consists of two conditions, states that relators behave as expected when acting on (graphs of) functions. In [15, 43] a kernel preservation condition is required in place of (rel 3). Such a condition is also known as stability in [27]. Stability requires the equality  to hold. It is easy to see that a relator always satisfies stability (see Corollary III.1.4.4 in [26]).
to hold. It is easy to see that a relator always satisfies stability (see Corollary III.1.4.4 in [26]).
Relators provide a powerful abstraction of notions of ‘relation lifting’, as witnessed by the numerous examples of relators we are going to discuss. However, before discussing such examples, we introduce the notion of a relator for a monad or lax extension of a monad. In fact, since we modelled computational effects as monads, it seems natural to define the notion of a relator for a monad (and not just for a functor).
Definition 4
Let \(\mathbb {T}= \langle T, \eta , -^{\dagger } \rangle \) be a monad, and \({\varGamma }\) be a relator for \(T\). We say that \({\varGamma }\) is a relator for \(\mathbb {T}\) if it satisfies the following conditions:
Finally, we observe that the collection of relators is closed under specific operations (see [43]).
Proposition 2
Let \(T, U\) be functors, and let \(UT\) denote their composition. Moreover, let \({\varGamma }, {\varDelta }\) be relators for \(T\) and \(U\), respectively, and \(\{{\varGamma }_i\}_{i \in I}\) be a family of relators for \(T\). Then:
-
1.
The map \({\varDelta }{\varGamma }\) defined by
 is a relator for \(UT\).
is a relator for \(UT\). -
2.
The maps \(\bigwedge _{i \in I}{\varGamma }_i\) and \({\varGamma }^{\circ }\) defined by
 and \({\varGamma }^{\circ }\mathbin {\mathcal {R}}\triangleq ({\varGamma }\mathbin {\mathcal {R}}^{\circ })^{\circ }\), respectively, are relators for \(T\).
and \({\varGamma }^{\circ }\mathbin {\mathcal {R}}\triangleq ({\varGamma }\mathbin {\mathcal {R}}^{\circ })^{\circ }\), respectively, are relators for \(T\). -
3.
Additionally, if \({\varGamma }\) is a relator for a monad \(\mathbb {T}\), then so are \(\bigwedge _{i \in I}{\varGamma }_i\) and \({\varGamma }^{\circ }\).
Example 12
For the partiality monad  we define the set-indexed family of maps
we define the set-indexed family of maps  as:
as:

The mapping  describes the structure of the usual simulation clause for partial computations, whereas
describes the structure of the usual simulation clause for partial computations, whereas  describes the corresponding co-simulation clause. It is easy to see that
describes the corresponding co-simulation clause. It is easy to see that  is a relator for
is a relator for  . By Proposition 2, the map
. By Proposition 2, the map  is a conversive relator for
is a conversive relator for  . It is immediate to see that the latter relator describes the structure of the usual bisimulation clause for partial computations.
. It is immediate to see that the latter relator describes the structure of the usual bisimulation clause for partial computations.
Example 13
For the distribution monad we define the relator  relying on the notion of a coupling and results from optimal transport [72]. Recall that a coupling for \(\mu \in D(X)\) and \(\nu \in D(Y)\) a is a joint distribution \(\omega \in D(X \times Y)\) such that: \( \mu = \sum _{y\in Y} \omega (-, y) \) and \( \nu = \sum _{x \in X} \omega (x,-). \) We denote the set of couplings of \(\mu \) and \(\nu \) by \({\varOmega }(\mu , \nu )\). Define the (set-indexed) map
relying on the notion of a coupling and results from optimal transport [72]. Recall that a coupling for \(\mu \in D(X)\) and \(\nu \in D(Y)\) a is a joint distribution \(\omega \in D(X \times Y)\) such that: \( \mu = \sum _{y\in Y} \omega (-, y) \) and \( \nu = \sum _{x \in X} \omega (x,-). \) We denote the set of couplings of \(\mu \) and \(\nu \) by \({\varOmega }(\mu , \nu )\). Define the (set-indexed) map  as follows:
as follows:

We can show that  is a relator for
is a relator for  relying on Strassen’s Theorem [69], which shows that
relying on Strassen’s Theorem [69], which shows that  can be characterised universally (i.e. using an universal quantification).
can be characterised universally (i.e. using an universal quantification).
Theorem 1
(Strassen’s Theorem [69]). For all \(\mu \in DX\), \(\nu \in DY\), and  , we have:
, we have:  .
.
As a corollary of Theorem 1, we see that  describes the defining clause of Larsen-Skou bisimulation for Markov chains (based on full distributions) [34]. Finally, we observe that
describes the defining clause of Larsen-Skou bisimulation for Markov chains (based on full distributions) [34]. Finally, we observe that  is a relator for
is a relator for  .
.
Example 14
For relations  ,
,  , let
, let  be defined as
be defined as  . We define the relator \(\hat{\mathbb {C}}: \mathsf {Rel}(X,Y) \rightarrow \mathsf {Rel}(CX, CY)\) for the cost monad \(\mathbb {C}\) as
. We define the relator \(\hat{\mathbb {C}}: \mathsf {Rel}(X,Y) \rightarrow \mathsf {Rel}(CX, CY)\) for the cost monad \(\mathbb {C}\) as  where \(\ge \) denotes the opposite of the natural ordering on
where \(\ge \) denotes the opposite of the natural ordering on  . It is straightforward to see that \(\hat{\mathbb {C}}\) is indeed a relator for \(\mathbb {C}\). The use of the opposite of the natural order in the definition of \(\hat{\mathbb {C}}\) captures the idea that we use \(\hat{\mathbb {C}}\) to measure complexity. Notice that \(\hat{\mathbb {C}}\) describes Sands’ simulation clause for program improvement [62].
. It is straightforward to see that \(\hat{\mathbb {C}}\) is indeed a relator for \(\mathbb {C}\). The use of the opposite of the natural order in the definition of \(\hat{\mathbb {C}}\) captures the idea that we use \(\hat{\mathbb {C}}\) to measure complexity. Notice that \(\hat{\mathbb {C}}\) describes Sands’ simulation clause for program improvement [62].
Example 15
For the global state monad  we define the map
we define the map  as
as  It is straightforward to see that
It is straightforward to see that  is a relator for
is a relator for  .
.
It is not hard to see that we can extend  to relators for
to relators for  ,
,  , and
, and  . In fact, Proposition 1 extends to relators.
. In fact, Proposition 1 extends to relators.
Proposition 3
Given a monad  and a relator \(\hat{\mathbb {T}}\) for \(\mathbb {T}\), define the sum
and a relator \(\hat{\mathbb {T}}\) for \(\mathbb {T}\), define the sum  of
of  and
and  as
as  . Additionally, define the tensor
. Additionally, define the tensor  of \(\hat{\mathbb {T}}\) and
of \(\hat{\mathbb {T}}\) and  by
by  if an only if
if an only if  . Then
. Then  is a relator for
is a relator for  , and
, and  is a relator for
is a relator for  .
.
Finally, we require relators to properly interact with the \({\varSigma }\)-continuous structure of monads.
Definition 5
Let \(\mathbb {T}= \langle T, \eta , -^{\dagger } \rangle \) be a \({\varSigma }\)-continuous monad and \({\varGamma }\) be relator for \(\mathbb {T}\). We say that \({\varGamma }\) is \({\varSigma }\)-continuous if it satisfies the following clauses—called the inductive conditions—for any \(\omega \)-chain  , element
, element  , elements
, elements  , and relation
, and relation  .
.

The relators  ,
,  , \(\hat{\mathbb {C}}\),
, \(\hat{\mathbb {C}}\),  ,
,  ,
,  are all \({\varSigma }\)-continuous. The reader might have noticed that we have not imposed any condition on how relators should interact with algebraic operations. Nonetheless, it would be quite natural to require a relator \({\varGamma }\) to satisfy condition (rel 9) below, for all operation symbol \(\mathbf {op}: P\,\rightsquigarrow \,I \in {\varSigma }\), maps \(\kappa , \nu : I \rightarrow TX\), parameter \(p\in P\), and relation
are all \({\varSigma }\)-continuous. The reader might have noticed that we have not imposed any condition on how relators should interact with algebraic operations. Nonetheless, it would be quite natural to require a relator \({\varGamma }\) to satisfy condition (rel 9) below, for all operation symbol \(\mathbf {op}: P\,\rightsquigarrow \,I \in {\varSigma }\), maps \(\kappa , \nu : I \rightarrow TX\), parameter \(p\in P\), and relation  .
.
Remarkably, if \(\mathbb {T}\) is \({\varSigma }\)-algebraic, then any relator for \(\mathbb {T}\) satisfies (rel 9) (cf. [15]).
Proposition 4
Let \(\mathbb {T}= \langle T,\eta ,-^{\dagger }\rangle \) be a \({\varSigma }\)-algebraic monad, and let \({\varGamma }\) be a relator for \(\mathbb {T}\). Then \({\varGamma }\) satisfies condition (rel 9).
Having defined relators and their basic properties, we now introduce the notion of an effectful eager normal form (bi)simulation.
6 Effectful Eager Normal Form (Bi)simulation
In this section we tacitly assume a \({\varSigma }\)-continuous monad \(\mathbb {T}= \langle T, \eta , -^{\dagger }\rangle \) and a \({\varSigma }\)-continuous relator \({\varGamma }\) for it be fixed. \({\varSigma }\)-continuity of \({\varGamma }\) is not required for defining effectful eager normal form (bi)simulation, but it is crucial to prove that the induced notion of similarity and bisimilarity are precongruence and congruence relations, respectively.
Working with effectful calculi, it is important to distinguish between relations over terms and relations over eager normal forms. For that reason we will work with pairs of relations of the form  , which we call \(\lambda \)-term relations (or term relations, for short). We use letters
, which we call \(\lambda \)-term relations (or term relations, for short). We use letters  to denote term relations. The collection of \(\lambda \)-term relations (i.e. \(\mathsf {Rel}({\varLambda }, {\varLambda }) \times \mathsf {Rel}(\mathcal {E}, \mathcal {E})\)) inherits a complete lattice structure from \(\mathsf {Rel}({\varLambda }, {\varLambda })\) and \(\mathsf {Rel}(\mathcal {E}, \mathcal {E})\) pointwise, hence allowing \(\lambda \)-term relations to be defined both inductively and coinductively. We use these properties to define our notion of effectful eager normal form similarity.
to denote term relations. The collection of \(\lambda \)-term relations (i.e. \(\mathsf {Rel}({\varLambda }, {\varLambda }) \times \mathsf {Rel}(\mathcal {E}, \mathcal {E})\)) inherits a complete lattice structure from \(\mathsf {Rel}({\varLambda }, {\varLambda })\) and \(\mathsf {Rel}(\mathcal {E}, \mathcal {E})\) pointwise, hence allowing \(\lambda \)-term relations to be defined both inductively and coinductively. We use these properties to define our notion of effectful eager normal form similarity.
Definition 6
A term relation  is an effectful eager normal form simulation with respect to \({\varGamma }\) (hereafter enf-simulation, as \({\varGamma }\) will be clear from the context) if the following conditions hold, where in condition (enf 4)
is an effectful eager normal form simulation with respect to \({\varGamma }\) (hereafter enf-simulation, as \({\varGamma }\) will be clear from the context) if the following conditions hold, where in condition (enf 4)  .
.
We say that relation \(\mathbin {\mathcal {R}}\) respects enfs if it satisfies conditions (enf 2)–(enf 4).
Definition 6 is quite standard. Clause (enf 1) is morally the same clause on terms used to define effectful applicative similarity in [15]. Clauses (enf 2) and (enf 3) state that whenever two enfs are related by \(\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}}\), then they must have the same outermost syntactic structure, and their subterms must be pairwise related. For instance, if \(\lambda x.{e} \mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} s\) holds, then \(s\) must the a \(\lambda \)-abstraction, i.e. an expression of the form \(\lambda x.{f}\), and \(e\) and \(f\) must be related by \(\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle {\varLambda }}}\).
Clause (enf 4) is the most interesting one. It states that whenever \(E[xv] \mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} s\), then \(s\) must be a stuck term \(E'[xv']\), for some evaluation context \(E'\) and value \(v'\). Notice that \(E[xv]\) and \(s\) must have the same ‘stuck variable’ \(x\). Additionally, \(v\) and \(v'\) must be related by \(\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}}\), and \(E\) and \(E'\) must be properly related too. The idea is that to see whether \(E\) and \(E'\) are related, we replace the stuck expressions \(xv\), \(xv'\) with a fresh variable \(z\), and test \(E[z]\) and \(E'[z]\) (thus resuming the evaluation process). We require \(E[z] \mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} E'[z]\) to hold, for some fresh variable \(z\). The choice of the variable does not really matter, provided it is fresh. In fact, as we will see, effectful eager normal form similarity \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) is substitutive and reflexive. In particular, if \(E[z] \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle \mathcal {E}}} E'[z]\) holds, then \(E[y] \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle \mathcal {E}}} E'[y]\) holds as well, for any variable \(y\not \in FV(E) \cup FV(E')\).
Notice that Definition 6 does not involve any universal quantification. In particular, enfs are tested by inspecting their syntactic structure, thus making the definition of an enf-simulation somehow ‘local’: terms are tested in isolation and not via their interaction with the environment. This is a major difference with e.g. applicative (bi)simulation, where the environment interacts with \(\lambda \)-abstractions by passing them arbitrary (closed) values as arguments.
Definition 6 induces a functional \(\mathbin {\mathcal {R}}\mapsto [\mathbin {\mathcal {R}}]\) on the complete lattice \(\mathsf {Rel}({\varLambda }, {\varLambda }) \times \mathsf {Rel}(\mathcal {E}, \mathcal {E})\), where \([\mathbin {\mathcal {R}}] = (\mathbin {[\mathbin {\mathcal {R}}]_{\scriptscriptstyle {\varLambda }}}, \mathbin {[\mathbin {\mathcal {R}}]_{\scriptscriptstyle \mathcal {E}}})\) is defined as follows (here \(\mathsf {I}_{\mathcal {X}}\) denotes the identity relation on variables, i.e. the set of pairs of the form \((x, x)\)):
It is easy to see that a term relation \(\mathbin {\mathcal {R}}\) is an enf-simulation if and only if \(\mathbin {\mathcal {R}}\subseteq [\mathbin {\mathcal {R}}]\). Notice also that although \(\mathbin {[\mathbin {\mathcal {R}}]_{\scriptscriptstyle \mathcal {E}}}\) always contains the identity relation on variables, \(\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}}\) does not have to: the empty relation \((\emptyset , \emptyset )\) is an enf-simulation. Finally, since relators are monotone (condition (rel 4)), \(\mathbin {\mathcal {R}}\mapsto [\mathbin {\mathcal {R}}]\) is monotone too. As a consequence, by Knaster-Tarski Theorem [70], it has a greatest fixed point which we call effectful eager normal form similarity with respect to \({\varGamma }\) (hereafter enf-similarity) and denote by \({\preceq ^{\scriptscriptstyle \mathsf {E}}} = (\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}}, \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle \mathcal {E}}})\). Enf-similarity is thus the largest enf-simulation with respect to \({\varGamma }\). Moreover, \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) being defined coinductively, it comes with an associated coinduction proof principle stating that if a term relation \(\mathbin {\mathcal {R}}\) is an enf-simulation, then it is contained in \(\preceq ^{\scriptscriptstyle \mathsf {E}}\). Symbolically: \({\mathbin {\mathcal {R}}} \subseteq [{\mathbin {\mathcal {R}}}] \implies {\mathbin {\mathcal {R}}} \subseteq {\preceq ^{\scriptscriptstyle \mathsf {E}}}\).
Example 16
We use the coinduction proof principle to show that \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) contains the \(\beta \)-rule, viz. \((\lambda x.{e})v\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} e[v/x]. \) For that, we simply observe that the term relation \((\{((\lambda x.{e})v, e[v/x])\}, \mathbin {\mathsf {I}_{\scriptscriptstyle \mathcal {E}}})\) is an enf-simulation. Indeed, \([\![ (\lambda x.{e})v ]\!] = [\![ e[v/x] ]\!]\), so that by (rel 1) we have \([\![ (\lambda x.{e})v ]\!] \mathbin {{\varGamma }{\mathbin {\mathsf {I}_{\scriptscriptstyle \mathcal {E}}}}} [\![ e[v/x] ]\!]\).
Finally, we define effectful eager normal form bisimilarity.
Definition 7
A term relation \(\mathbin {\mathcal {R}}\) is an effectful eager normal form bisimulation with respect to \({\varGamma }\) (enf-bisimulation, for short) if it is a symmetric enf-simulation. Eager normal bisimilarity with respect to \({\varGamma }\) (enf-bisimilarity, for short) \(\simeq ^{\scriptscriptstyle \mathsf {E}}\) is the largest symmetric enf-simulation. In particular, enf-bisimilarity (with respect to \({\varGamma }\)) coincides with enf-similarity with respect to \({\varGamma }\wedge {\varGamma }^{\circ }\).
Example 17
We show that the probabilistic call-by-value fixed point combinators Y and Z of Example 2 are enf-bisimilar. In light of Proposition 5, this allows us to conclude that Y and Z are applicatively bisimilar, and thus contextually equivalent [15]. Let us consider the relator  for probabilistic partial computations. We show \(Y \mathbin {\simeq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} Z\) by coinduction, proving that the symmetric closure of the term relation \(\mathbin {\mathcal {R}}= (\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle {\varLambda }}}, \mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}})\) defined as follows is an enf-simulation:
for probabilistic partial computations. We show \(Y \mathbin {\simeq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} Z\) by coinduction, proving that the symmetric closure of the term relation \(\mathbin {\mathcal {R}}= (\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle {\varLambda }}}, \mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}})\) defined as follows is an enf-simulation:
The term relation \(\mathbin {\mathcal {R}}\) is obtained from the relation \(\{(Y, Z)\}\) by progressively adding terms and enfs according to clauses (enf 1)–(enf 4) in Definition 6. Checking that \(\mathbin {\mathcal {R}}\) is an enf-simulation is straightforward. As an illustrative example, we prove that \({\varDelta }{\varDelta }z\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle {\varLambda }}} Zyz\) implies  . The latter amounts to show:
. The latter amounts to show:

where, as usual, we write distributions as weighted formal sums. To prove the latter, it is sufficient to find a suitable coupling of \([\![ {\varDelta }{\varDelta }z ]\!]\) and \([\![ Zyz ]\!]\). Define the distribution \(\omega \in D(M\mathcal {E}\times M\mathcal {E})\) as follows:
and assigning zero to all other pairs in \(M\mathcal {E}\times M\mathcal {E}\). Obviously \(\omega \) is a coupling of \([\![ {\varDelta }{\varDelta }z ]\!]\) and \([\![ Zyz ]\!]\). Additionally, we see that  implies
implies  , since both \(y(\lambda z.{\varDelta }{\varDelta }z)z\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} y(\lambda z.{\varDelta }{\varDelta }z)z, \) and \(y(\lambda z.{\varDelta }{\varDelta }z)z\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} y(\lambda z.Zyz)z\) hold.
, since both \(y(\lambda z.{\varDelta }{\varDelta }z)z\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} y(\lambda z.{\varDelta }{\varDelta }z)z, \) and \(y(\lambda z.{\varDelta }{\varDelta }z)z\mathbin {\mathbin {\mathcal {R}}_{\scriptscriptstyle \mathcal {E}}} y(\lambda z.Zyz)z\) hold.
As already discussed in Example 2, the operational equivalence between Y and Z is an example of an equivalence that cannot be readily established using standard operational methods—such as CIU equivalence or applicative bisimilarity—but whose proof is straightforward using enf-bisimilarity. Additionally, Theorem 3 will allow us to reduce the size of \(\mathbin {\mathcal {R}}\), thus minimising the task of checking that our relation is indeed an enf-bisimulation. To the best of the authors’ knowledge, the probabilistic instance of enf-(bi)similarity is the first example of a probabilistic eager normal form (bi)similarity in the literature.
6.1 Congruence and Precongruence Theorems
In order for \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) and \(\simeq ^{\scriptscriptstyle \mathsf {E}}\) to qualify as good notions of program refinement and equivalence, respectively, they have to allow for compositional reasoning. Roughly speaking, a term relation \(\mathbin {\mathcal {R}}\) is compositional if the validity of the relationship \(\mathcal {C}[e] \mathbin {\mathcal {R}}\mathcal {C}[e']\) between compound terms \(\mathcal {C}[e], \mathcal {C}[e']\) follows from the validity of the relationship \(e\mathbin {\mathcal {R}}e'\) between the subterms \(e, e'\). Mathematically, the notion of compositionality is formalised throughout the notion of compatibility, which directly leads to the notions of a precongruence and congruence relation. In this section we prove that \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) and \(\simeq ^{\scriptscriptstyle \mathsf {E}}\) are substitutive precongruence and congruence relations, that is preorder and equivalence relations closed under term constructors of \({\varLambda }_{\varSigma }\) and substitution, respectively. To prove such results, we generalise Lassen’s relational construction for the pure call-by-name \(\lambda \)-calculus [37]. Such a construction has been previously adapted to the pure call-by-value \(\lambda \)-calculus (and its extension with delimited and abortive control operators) in [9], whereas Lassen has proved compatibility of pure eager normal form bisimilarity via a CPS translation [38]. Both those proofs rely on syntactical properties of the calculus (mostly expressed using suitable small-step semantics), and thus seem to be hardly adaptable to effectful calculi. On the contrary, our proofs rely on the properties of relators, thereby making our results and techniques more modular and thus valid for a large class of effects.
We begin proving precongruence of enf-similarity. The central tool we use to prove the wished precongruence theorem is the so-called (substitutive) context closure [37] \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\) of a term relation \(\mathbin {\mathcal {R}}\), which is inductively defined by the rules in Fig. 1, where \(\mathsf {x} \in \{{\varLambda }, \mathcal {E}\}\), \(i \in \{1,2\}\), and \(z \not \in FV(E) \cup FV(E')\).
We easily see that \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\) is the smallest term relation that contains \(\mathbin {\mathcal {R}}\), it is closed under language constructors of \({\varLambda }_{\varSigma }\) (a property known as compatibility [5]), and it is closed under the substitution operation (a property known as substitutivity [5]). As a consequence, we say that a term relation \(\mathbin {\mathcal {R}}\) is a substitutive compatible relation if \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}} \subseteq \mathbin {\mathcal {R}}\) (and thus \(\mathbin {\mathcal {R}}= \mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\)). If, additionally, \(\mathbin {\mathcal {R}}\) is a preorder (resp. equivalence) relation, then we say that \(\mathbin {\mathcal {R}}\) is a substitutive precongruence (resp. substitutive congruence) relation.
We are now going to prove that if \(\mathbin {\mathcal {R}}\) is an enf-simulation, then so is \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\). In particular, we will infer that \(\mathbin {(\preceq ^{\scriptscriptstyle \mathsf {E}})^{\scriptscriptstyle \mathsf {SC}}}\) is a enf-simulation, and thus it is contained in \(\preceq ^{\scriptscriptstyle \mathsf {E}}\), by coinduction.
Lemma 2
(Main Lemma). If \(\mathbin {\mathcal {R}}\) be an enf-simulation, then so is \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\).
Proof
(sketch). The proof is long and non-trivial. Due to space constraints here we simply give some intuitions behind it. First, a routine proof by induction shows that since \(\mathbin {\mathcal {R}}\) respects enfs, then so does \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\). Next, we wish to prove that \(e\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}_{ \scriptscriptstyle {\varLambda }}} f\) implies \([\![ e ]\!] \mathbin {{\varGamma }{\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}_{ \scriptscriptstyle \mathcal {E}}}}} [\![ f ]\!]\). Since \({\varGamma }\) is inductive, the latter follows if for any \(n \ge 0\), \(e\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}_{ \scriptscriptstyle {\varLambda }}} f\) implies \([\![ e ]\!]_{n} \mathbin {{\varGamma }{\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}_{ \scriptscriptstyle \mathcal {E}}}}} [\![ f ]\!]\). We prove the latter implication by lexicographic induction on (1) the natural number n and (2) the derivation \(e\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}_{ \scriptscriptstyle {\varLambda }}} f\). The case for \(n = 0\) is trivial (since \({\varGamma }\) is inductive). The remaining cases are nontrivial, and are handled observing that \([\![ E[e] ]\!] = (s\mapsto [\![ E[s] ]\!])^{\dagger } [\![ e ]\!]\) and  . Both these identities allow us to apply condition (rel 8) to simplify proof obligations (usually relying on part (2) of the induction hypothesis as well). This scheme is iterated until we reach either an enf (in which case we are done by condition (rel 7)) or a pair of expressions on which we can apply part (1) of the induction hypothesis.
. Both these identities allow us to apply condition (rel 8) to simplify proof obligations (usually relying on part (2) of the induction hypothesis as well). This scheme is iterated until we reach either an enf (in which case we are done by condition (rel 7)) or a pair of expressions on which we can apply part (1) of the induction hypothesis.
Theorem 2
Enf-similarity (resp. bisimilarity) is a substitutive precongruence (resp. congruence) relation.
Proof
We show that enf-similarity is a substitutive precongruence relation. By Lemma 2, it is sufficient to show that \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) is a preorder. This follows by coinduction, since the term relations \(\mathsf {I}\) and \(\preceq ^{\scriptscriptstyle \mathsf {E}}\circ \preceq ^{\scriptscriptstyle \mathsf {E}}\) are enf-simulations (the proofs make use of conditions (rel 1) and (rel 2), as well as of substitutivity of \(\preceq ^{\scriptscriptstyle \mathsf {E}}\)).
Finally, we show that enf-bisimilarity is a substitutive congruence relation. Obviously \(\simeq ^{\scriptscriptstyle \mathsf {E}}\) is an equivalence relation, so that it is sufficient to prove \({\mathbin {(\simeq ^{\scriptscriptstyle \mathsf {E}})^{\scriptscriptstyle \mathsf {SC}}}} \subseteq {\simeq ^{\scriptscriptstyle \mathsf {E}}}\). That directly follows by coinduction relying on Lemma 2, provided that \(\mathbin {(\simeq ^{\scriptscriptstyle \mathsf {E}})^{\scriptscriptstyle \mathsf {SC}}}\) is symmetric. An easy inspection of the rules in Fig. 1 reveals that \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\) is symmetric, whenever \(\mathbin {\mathcal {R}}\) is.
6.2 Soundness for Effectful Applicative (Bi)similarity
Theorem 2 qualifies enf-bisimilarity and enf-similarity as good candidate notions of program equivalence and refinement for \({\varLambda }_{\varSigma }\), at least from a structural perspective. However, we gave motivations for such notions looking at specific examples where effectful applicative (bi)similarity is ineffective. It is then natural to ask whether enf-(bi)similarity can be used as a proof technique for effectful applicative (bi)similarity.
Here we give a formal comparison between enf-(bi)similarity and effectful applicative (bi)similarity, as defined in [15]. First of all, we rephrase the notion of an effectful applicative (bi)simulation of [15] to our calculus \({\varLambda }_{\varSigma }\). For that, we use the following notational convention. Let \({\varLambda }_0, \mathcal {V}_0\) denote the collections of closed terms and closed values, respectively. We notice that if \(e\in {\varLambda }_0\), then \([\![ e ]\!] \in T\mathcal {V}_0\). As a consequence, \([\![ - ]\!]\) induces a closed evaluation function \(|- |: {\varLambda }_0 \rightarrow T\mathcal {V}_0\) characterised by the identity \([\![ - ]\!] \circ \iota = T\iota \circ |- |\), where \(\iota : \mathcal {V}_0 \hookrightarrow \mathcal {E}\) is the obvious inclusion map. We can thus phrase the definition of effectful applicative similarity (with respect to a relator \({\varGamma }\)) as follows.
Definition 8
A term relation  is an effectful applicative simulation with respect to \({\varGamma }\) (applicative simulation, for short) if:
is an effectful applicative simulation with respect to \({\varGamma }\) (applicative simulation, for short) if:
As usual, we can define effectful applicative similarity with respect to \({\varGamma }\) (applicative similarity, for short), denoted by \({\preceq ^{\scriptscriptstyle \mathsf {A}}_0} = ({\mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle {\varLambda }_{0}}}},{\mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle \mathcal {V}_{0}}}})\), coinductively as the largest applicative simulation. Its associated coinduction proof principle states that if a relation is an applicative simulation, then it is contained in applicative similarity. Finally, we extend \(\preceq ^{\scriptscriptstyle \mathsf {A}}_0\) to arbitrary terms by defining the relation \(\preceq ^{\scriptscriptstyle \mathsf {A}}\ = (\mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle {\varLambda }}}, \mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle \mathcal {V}}})\) as follows: let \(e, f, w, u\) be terms and values with free variables among  . We let \(\bar{v}\) range over n-ary sequences of closed values
. We let \(\bar{v}\) range over n-ary sequences of closed values  . Define:
. Define:

The following result states that enf-similarity is a sound proof technique for applicative similarity.
Proposition 5
Enf-similarity \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) is included in applicative similarity \(\preceq ^{\scriptscriptstyle \mathsf {A}}\).
Proof
Let \({\preceq ^{ \mathsf {c}}} = (\preceq ^{ \mathsf {c}}_{\scriptscriptstyle {\varLambda }}, \preceq ^{ \mathsf {c}}_{\scriptscriptstyle \mathcal {V}})\) denote enf-similarity restricted to closed terms and values. We first show that \(\preceq ^{ \mathsf {c}}\) is an applicative simulation, from which follows, by coinduction, that it is included in \(\preceq ^{\scriptscriptstyle \mathsf {A}}_0\). It is easy to see that \(\preceq ^{ \mathsf {c}}\) satisfies condition (app 2). In order to prove that it also satisfies condition (app 1), we have to show that for all \(e, f\in {\varLambda }_{\circ }\), \(e\preceq ^{ \mathsf {c}}_{\scriptscriptstyle {\varLambda }}f\) implies \(|e | \mathbin {{\varGamma }{\preceq ^{ \mathsf {c}}_{\scriptscriptstyle \mathcal {V}}}} |f |\). Since \(e\preceq ^{ \mathsf {c}}_{\scriptscriptstyle {\varLambda }}f\) obviously implies \(\iota (e) \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} \iota (f)\), by (enf 1) we infer \([\![ \iota (e) ]\!] \mathbin {{\varGamma }{\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle \mathcal {V}}}}} [\![ \iota (f) ]\!]\), and thus \(T\iota |e | \mathbin {{\varGamma }{\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle \mathcal {V}}}}} T\iota |f |\). By stability of \({\varGamma }\), the latter implies \(|e | \mathbin {{\varGamma }{(\iota ^{\circ } \circ \mathbin {\preceq _{\scriptscriptstyle \mathcal {E}}} \circ \iota )}} |f |\), and thus the wished thesis, since \(\iota ^{\circ } \circ \mathbin {\preceq _{\scriptscriptstyle \mathcal {E}}} \circ \iota \) is nothing but \(\preceq ^{ \mathsf {c}}_{\scriptscriptstyle \mathcal {V}}\). Finally, we show that for all terms \(e, f\), if \(e\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} f\), then \(e\mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle {\varLambda }}} f\) (a similar result holds mutatis mutandis for values, so that we can conclude \({\preceq ^{\scriptscriptstyle \mathsf {E}}} \subseteq {\preceq ^{\scriptscriptstyle \mathsf {A}}}\)). Indeed, suppose \(FV(e) \cup FV(f) \subseteq \bar{x}\), then by substitutivity of \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) we have that \(e\mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} f\) implies \(e[\bar{v}/\bar{x}] \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} f[\bar{v}/\bar{x}]\), for all closed values \(\bar{v}\) (notice that since we are substituting closed values, sequential and simultaneous substitution coincide). That essentially means \(e[\bar{v}/\bar{x}] \preceq ^{ \mathsf {c}}_{\scriptscriptstyle {\varLambda }}f[\bar{v}/\bar{x}]\), and thus \(e[\bar{v}/\bar{x}] \mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle {\varLambda }_{0}}} f[\bar{v}/\bar{x}]\). We thus conclude \(e\mathbin {\preceq ^{\scriptscriptstyle \mathsf {A}}_{\scriptscriptstyle {\varLambda }}} f\).
Since in [15] it is shown that effectful applicative similarity (resp. bisimilarity) is contained in effectful contextual approximation (resp. equivalence), Proposition 5 gives the following result.
Corollary 1
Enf-similarity and enf-bisimilarity are sound proof techniques for contextual approximation and equivalence, respectively.
Although sound, enf-bisimilarity is not fully abstract for applicative bisimilarity. In fact, as already observed in [38], in the pure \(\lambda \)-calculus enf-bisimilarity is strictly finer than applicative bisimilarity (and thus strictly finer than contextual equivalence too). For instance, the terms \(xv\) and \((\lambda y.{xv})(xv)\) are obviously applicatively bisimilar but not enf-bisimilar.
6.3 Eager Normal Form (Bi)simulation Up-to Context
The up-to context technique [37, 60, 64] is a refinement of the coinduction proof principle of enf-(bi)similarity that allows for handier proofs of equivalence and refinement between terms. When exhibiting a candidate enf-(bi)simulation relation \(\mathbin {\mathcal {R}}\), it is desirable for \(\mathbin {\mathcal {R}}\) to be as small as possible, so to minimise the task of verifying that \(\mathbin {\mathcal {R}}\) is indeed an enf-(bi)simulation.
The motivation behind such a technique can be easily seen looking at Example 17, where we showed the equivalence between the probabilistic fixed point combinators Y and Z working with relations containing several administrative pairs of terms. The presence of such pairs was forced by Definition 7, although they appear somehow unnecessary in order to convince that Y and Z exhibit the same operational behaviour.
Enf-(bi)simulation up-to context is a refinement of enf-(bi)simulation that allows to check that a relation \(\mathbin {\mathcal {R}}\) behaves as an enf-(bi)simulation relation up to its substitutive and compatible closure.
Definition 9
A term relation  is an effectful eager normal form simulation up-to context with respect to \({\varGamma }\) (enf-simulation up-to context, hereafter) if satisfies the following conditions, where in condition (up-to 4) \(z\not \in FV(E) \cup FV(E')\).
is an effectful eager normal form simulation up-to context with respect to \({\varGamma }\) (enf-simulation up-to context, hereafter) if satisfies the following conditions, where in condition (up-to 4) \(z\not \in FV(E) \cup FV(E')\).
In order for the up-to context technique to be sound, we need to show that every enf-simulation up-to context is contained in enf-similarity. This is a direct consequence of the following variation of Lemma 2.
Lemma 3
If \(\mathbin {\mathcal {R}}\) is a enf-simulation up-to context, then \(\mathbin {\mathbin {\mathcal {R}}^{\scriptscriptstyle \mathsf {SC}}}\) is a enf-simulation.
Proof
The proof is structurally identical to the one of Lemma 2, where we simply observe that wherever we use the assumption that \(\mathbin {\mathcal {R}}\) is an enf-simulation, we can use the weaker assumption that \(\mathbin {\mathcal {R}}\) is an enf-simulation up-to context.
In particular, since by Lemma 2 we have that \({\preceq ^{\scriptscriptstyle \mathsf {E}}} = {\mathbin {(\preceq ^{\scriptscriptstyle \mathsf {E}})^{\scriptscriptstyle \mathsf {SC}}}}\), we see that enf-similarity is an enf-simulation up-to context. Additionally, by Lemma 3 it is the largest such. Since the same result holds for enf-bisimilarity and enf-bisimilarity up-to context, we have the following theorem.
Theorem 3
Enf-similarity is the largest enf-simulation up-to context, and enf-bisimilarity is the largest enf-bisimulation up-to context.
Example 18
We apply Theorem 3 to simplify the proof of the equivalence between Y and Z given in Example 17. In fact, it is sufficient to show that the symmetric closure of term relation \(\mathbin {\mathcal {R}}\) defined below is an enf-bisimulation up-to context.
Example 19
Recall the fixed point combinators with ticking operations Y and Z of Example 4. Let us consider the relator \(\hat{\mathbb {C}}\). It is not hard to see that Y and Z are not enf-bisimilar (that is because the ticking operation is evaluated at different moments, so to speak). Nonetheless, once we pass them a variable \(x_0\) as argument, we have \(Z x_{0} \mathbin {\preceq ^{\scriptscriptstyle \mathsf {E}}_{\scriptscriptstyle {\varLambda }}} Y x_0\). For, observe that the term relation \(\mathbin {\mathcal {R}}\) defined below is an enf-simulation up-context.
Intuitively, Y executes a tick first, and then proceeds iterating the evaluation of \({\varDelta }[x_0/y]{\varDelta }[x_0/y]\), the latter involving two tickings only. On the contrary, Z proceeds by recursively call itself, hence involving three tickings at any iteration, so to speak. Since \(\preceq ^{\scriptscriptstyle \mathsf {E}}\) is substitutive, for any value \(v\) we have \(Z v\preceq ^{\scriptscriptstyle \mathsf {E}}Y v\).
Theorem 3 makes enf-(bi)similarity an extremely powerful proof technique for program equivalence/refinement, especially because it is yet unknown whether there exist sound up-to context techniques for applicative (bi)similarity [35].
6.4 Weak Head Normal Form (Bi)simulation
So far we have focused on call-by-value calculi, since in presence of effects the call-by-value evaluation strategy seems the more natural one. Nonetheless, our framework can be easily adapted to deal with call-by-name calculi too. In this last section we spend some words on effectful weak head normal form (bi)similarity (whnf-(bi)similarity, for short). The latter is nothing but the call-by-name counterpart of enf-(bi)similarity. The main difference between enf-(bi)similarity and whnf-(bi)similarity relies on the notion of an evaluation context (and thus of a stuck term). In fact, in a call-by-name setting, \({\varLambda }_{\varSigma }\) evaluation contexts are expressions of the form \([-]e_1 \cdots e_n\), which are somehow simpler than their call-by-value counterparts. Such a simplicity is reflected in the definition of whnf-(bi)similarity, which allows to prove mutatis mutandis all results proved for enf-(bi)similarity (such results are, without much of a surprise, actually easier to prove).
We briefly expand on that. The collection of weak head normal forms (whnfs, for short) \(\mathcal {W}\) is defined as the union of \(\mathcal {V}\) and the collection of stuck terms, the latter being expressions of the form \(xe_1 \cdots e_n\). The evaluation function of Definition 2 now maps terms to elements in \(T\mathcal {W}\), and it is essentially obtained modifying Definition 2 defining \([\![ E[xe] ]\!]_{n+1} \triangleq \eta (E[xe])\) and \([\![ E[(\lambda x.{f})e] ]\!]_{n+1} \triangleq [\![ E[f[e/x]] ]\!]_{n}\). The notion of a whnf-(bi)simulation (and thus the notions of whnf-(bi)similarity) is obtained modifying Definition 6 accordingly. In particular, clauses (enf 2) and (enf 4) are replaced by the following clause, where we use the notation  to denote a (call-by-name) \(\lambda \)-term relation.
to denote a (call-by-name) \(\lambda \)-term relation.

A straightforward modifications of the rules in Fig. 1 allows to prove an analogous of Lemma 2 for whnf-simulations, and thus to conclude (pre)congruence properties of whnf-(bi)similarity. Additionally, such results generalise to whnf-(bi)simulation up to-context, the latter being defined according to Definition 9, so that we have an analogous of Theorem 3 as well. The latter allows to infer the equivalence of the argument-switching fixed point combinators of Example 3, simply by noticing that the symmetric closure of the term relation \(\mathbin {\mathcal {R}}= (\{(P, Q), (Pyz, Qzy), (Pzy, Qyz)\},\emptyset )\) is a whnf-bisimulation up-to context.
Finally, it is straightforward to observe that whnf-(bi)similarity is included in the call-by-name counterpart of effectful applicative (bi)similarity, but that the inclusion is strict. In fact, the (pure \(\lambda \)-calculus) terms \(xx\) and \(x(\lambda y.{xy})\) are applicatively bisimilar, but not whnf-bisimilar.
7 Related Work
Normal form (bi)similarity has been originally introduced for the call-by-name \(\lambda \)-calculus in [65], where it was called open bisimilarity. Open bisimilarity provides a coinductive characterisation of Lévy-Longo tree equivalence [42, 45, 53], and has been shown to coincide with the equivalence (notably weak bisimilarity) induced by Milner’s encoding of the \(\lambda \)-calculus into the \(\pi \)-calculus [48].
In [37] normal form bisimilarity relations characterising both Böhm and Lévy-Longo tree equivalences have been studied by purely operational means, providing new congruence proofs of the aforementioned tree equivalences based on suitable relational constructions. Such results have been extended to the call-by-value \(\lambda \)-calculus in [38], where the so-called eager normal form bisimilarity is introduced. The latter is shown to coincide with the Lévy-Longo tree equivalence induced by a suitable CPS translation [54], and thus to be a congruence relation. An elementary proof of congruence properties of eager normal form bisimilarity is given in [9], where Lassen’s relational construction [37] is extended to the call-by-value \(\lambda \)-calculus, as well as its extensions with delimited and abortive control operators. Finally, following [65], eager normal form bisimilarity has been recently characterised as the equivalence induced by a suitable encoding of the (call-by-value) \(\lambda \)-calculus in the \(\pi \)-calculus [21].
Concerning effectful extensions of normal form bisimilarity, our work seems to be rather new. In fact, normal form bisimilarity has been studied for deterministic extensions of the \(\lambda \)-calculus with specific non-algebraic effects, notably control operators [9], as well as control and state [68] (where full abstraction of the obtained notion of normal form bisimilarity is proved). The only extension of normal form bisimilarity to an algebraic effect the authors are aware of, is given in [39], where normal form bisimilarity is studied for a nondeterministic call-by-name \(\lambda \)-calculus. However, we should mention that contrary to normal form bisimilarity, both nondeterministic [20] and probabilistic [41] extensions of Böhm tree equivalence have been investigated (although none of them employ, to the best of the authors’ knowledge, coinductive techniques).
8 Conclusion
This paper shows that effectful normal form bisimulation is indeed a powerful methodology for program equivalence. Interestingly, the proof of congruence for normal form bisimilarity can be given just once, without the necessity of redoing it for every distinct notion of algebraic effect considered. This relies on the fact that the underlying monad and relator are \({\varSigma }\)-continuous, something which has already been proved for many distinct notions of effects [15].
Topics for further work are plentiful. First of all, a natural question is whether the obtained notion of bisimilarity coincides with contextual equivalence. This is known not to hold in the deterministic case [37, 38], but to hold in presence of control and state [68], which offer the environment the necessary discriminating power. Is there any (sufficient) condition on effects guaranteeing full abstraction of normal form bisimilarity? This is an intriguing question we are currently investigating. In fact, contrary to applicative bisimilarity (which is known to be unsound in presence of non-algebraic effects [33], such as local states), the syntactic nature of normal form bisimilarity seems to be well-suited for languages combining both algebraic and non-algebraic effects.
Another interesting topic for future research, is investigating whether normal form bisimilarity can be extended to languages having both algebraic operations and effect handlers [7, 59].
Notes
- 1.
Besides, as we will discuss in Sect. 6.4, the formal analysis of call-by-name normal form bisimilarity strictly follows the corresponding (more challenging) analysis of call-by-value normal form bisimilarity.
- 2.
Meaning that two terms \(e_1, e_2\) are tested for their applicative behaviour against all terms of the form \(E[e], E[e']\), for any pair of terms \((e, e')\) stored in the environment.
- 3.
Although this is not strictly necessary, for simplicity we work with distributions over countable sets only, as the sets of values and normal forms are countable.
- 4.
For simplicity, we write only those \(p_i\)s such that \(p_i > 0\).
- 5.
Here \(\mathbf {op}\) denotes the operation symbol, whereas \(n \ge 0\) denotes its arity.
- 6.
References
Abramsky, S.: The lazy lambda calculus. In: Turner, D. (ed.) Research Topics in Functional Programming, pp. 65–117. Addison Wesley, Boston (1990)
Abramsky, S., Jung, A.: Domain theory. In: Handbook of Logic in Computer Science, pp. 1–168. Clarendon Press (1994)
Abramsky, S., Ong, C.L.: Full abstraction in the lazy lambda calculus. Inf. Comput. 105(2), 159–267 (1993)
Appel, A., McAllester, D.: An indexed model of recursive types for foundational proof-carrying code. ACM Trans. Program. Lang. Syst. 23(5), 657–683 (2001)
Barendregt, H.: The lambda calculus: its syntax and semantics. In: Studies in Logic and the Foundations of Mathematics. North-Holland (1984)
Barr, M.: Relational algebras. Lect. Notes Math. 137, 39–55 (1970)
Bauer, A., Pretnar, M.: Programming with algebraic effects and handlers. J. Log. Algebr. Meth. Program. 84(1), 108–123 (2015)
Benton, N., Kennedy, A., Beringer, L., Hofmann, M.: Relational semantics for effect-based program transformations: higher-order store. In: Proceedings of PPDP 2009, pp. 301–312 (2009)
Biernacki, D., Lenglet, S., Polesiuk, P.: Proving soundness of extensional normal-form bisimilarities. Electr. Notes Theor. Comput. Sci. 336, 41–56 (2018)
Bizjak, A., Birkedal, L.: Step-indexed logical relations for probability. In: Pitts, A. (ed.) FoSSaCS 2015. LNCS, vol. 9034, pp. 279–294. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46678-0_18
Böhm, C.: Alcune proprietà delle forme \(\beta \eta \)-normali del \(\lambda k\)-calcolo. Pubblicazioni dell’Istituto per le Applicazioni del Calcolo 696 (1968)
Burris, S., Sankappanavar, H.: A Course in Universal Algebra. Graduate Texts in Mathematics. Springer, New York (1981)
Crubillé, R., Dal Lago, U.: On probabilistic applicative bisimulation and call-by-value \(\lambda \)-Calculi. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 209–228. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_12
Culpepper, R., Cobb, A.: Contextual equivalence for probabilistic programs with continuous random variables and scoring. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 368–392. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_14
Dal Lago, U., Gavazzo, F., Levy, P.: Effectful applicative bisimilarity: monads, relators, and Howe’s method. In: Proceedings of LICS 2017, pp. 1–12 (2017)
Dal Lago, U., Sangiorgi, D., Alberti, M.: On coinductive equivalences for higher-order probabilistic functional programs. In: Proceedings of POPL 2014, pp. 297–308 (2014)
Dal Lago, U., Zorzi, M.: Probabilistic operational semantics for the lambda calculus. RAIRO - Theor. Inf. Appl. 46(3), 413–450 (2012)
Danos, V., Harmer, R.: Probabilistic game semantics. ACM Trans. Comput. Logic 3(3), 359–382 (2002)
Davey, B., Priestley, H.: Introduction to Lattices and Order. Cambridge University Press, Cambridge (1990)
De Liguoro, U., Piperno, A.: Non deterministic extensions of untyped lambda-calculus. Inf. Comput. 122(2), 149–177 (1995)
Durier, A., Hirschkoff, D., Sangiorgi, D.: Eager functions as processes. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, pp. 364–373 (2018)
Felleisen, M., Hieb, R.: The revised report on the syntactic theories of sequential control and state. Theor. Comput. Sci. 103(2), 235–271 (1992)
Gavazzo, F.: Quantitative behavioural reasoning for higher-order effectful programs: applicative distances. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Oxford, UK, 09–12 July 2018, pp. 452–461 (2018)
Goguen, J.A., Thatcher, J.W., Wagner, E.G., Wright, J.B.: Initial algebra semantics and continuous algebras. J. ACM 24(1), 68–95 (1977)
Goubault-Larrecq, J., Lasota, S., Nowak, D.: Logical relations for monadic types. Math. Struct. Comput. Sci. 18(6), 1169–1217 (2008)
Hofmann, D., Seal, G., Tholen, W. (eds.): Monoidal Topology. A Categorical Approach to Order, Metric, and Topology. No. 153 in Encyclopedia of Mathematics and its Applications. Cambridge University Press (2014)
Hughes, J., Jacobs, B.: Simulations in coalgebra. Theor. Comput. Sci. 327(1–2), 71–108 (2004)
Hyland, M., Plotkin, G.D., Power, J.: Combining effects: sum and tensor. Theor. Comput. Sci. 357(1–3), 70–99 (2006)
Hyland, M., Power, J.: The category theoretic understanding of universal algebra: Lawvere theories and monads. Electr. Notes Theor. Comput. Sci. 172, 437–458 (2007)
Johann, P., Simpson, A., Voigtländer, J.: A generic operational metatheory for algebraic effects. In: Proceedings of LICS 2010, pp. 209–218. IEEE Computer Society (2010)
Jones, C.: Probabilistic non-determinism. Ph.D. thesis, University of Edinburgh, UK (1990)
Katsumata, S., Sato, T.: Preorders on monads and coalgebraic simulations. In: Pfenning, F. (ed.) FoSSaCS 2013. LNCS, vol. 7794, pp. 145–160. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37075-5_10
Koutavas, V., Levy, P.B., Sumii, E.: From applicative to environmental bisimulation. Electr. Notes Theor. Comput. Sci. 276, 215–235 (2011)
Larsen, K.G., Skou, A.: Bisimulation through probabilistic testing. In: Proceedings of POPL 1989, pp. 344–352 (1989)
Lassen, S.: Relational reasoning about contexts. In: Gordon, A.D., Pitts, A.M. (eds.) Higher Order Operational Techniques in Semantics, pp. 91–136 (1998)
Lassen, S.: Relational reasoning about functions and nondeterminism. Ph.D. thesis, Department of Computer Science, University of Aarhus, May 1998
Lassen, S.B.: Bisimulation in untyped lambda calculus: Böhm trees and bisimulation up to context. Electr. Notes Theor. Comput. Sci. 20, 346–374 (1999)
Lassen, S.B.: Eager normal form bisimulation. In: Proceedings of LICS 2005, pp. 345–354 (2005)
Lassen, S.B.: Normal form simulation for McCarthy’s Amb. Electr. Notes Theor. Comput. Sci. 155, 445–465 (2006)
Lawvere, W.F.: Functorial semantics of algebraic theories. Ph.D. thesis (2004)
Leventis, T.: Probabilistic Böhm trees and probabilistic separation. In: Proceedings of LICS (2018)
Levy, J.-J.: An algebraic interpretation of the \(\lambda \)\(\upbeta \)K-calculus and a labelled \(\lambda \)-calculus. In: Böhm, C. (ed.) \(\lambda \)-Calculus and Computer Science Theory. LNCS, vol. 37, pp. 147–165. Springer, Heidelberg (1975). https://doi.org/10.1007/BFb0029523
Levy, P.B.: Similarity quotients as final coalgebras. In: Hofmann, M. (ed.) FoSSaCS 2011. LNCS, vol. 6604, pp. 27–41. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19805-2_3
Levy, P., Power, J., Thielecke, H.: Modelling environments in call-by-value programming languages. Inf. Comput. 185(2), 182–210 (2003)
Longo, G.: Set-theoretical models of lambda calculus: theories, expansions, isomorphisms. Ann. Pure Appl. Logic 24, 153–188 (1983)
Mac Lane, S.: Categories for the Working Mathematician. GTM, vol. 5. Springer, New York (1971). https://doi.org/10.1007/978-1-4612-9839-7
Mason, I.A., Talcott, C.L.: Equivalence in functional languages with effects. J. Funct. Program. 1(3), 287–327 (1991)
Milner, R.: Functions as processes. Math. Struct. Comput. Sci. 2(2), 119–141 (1992)
Moggi, E.: Computational lambda-calculus and monads. In: Proceedings of LICS 1989, pp. 14–23. IEEE Computer Society (1989)
Moggi, E.: Notions of computation and monads. Inf. Comput. 93(1), 55–92 (1991)
Morris, J.: Lambda calculus models of programming languages. Ph.D. thesis, MIT (1969)
Ong, C.L.: Non-determinism in a functional setting. In: Proceedings of LICS 1993, pp. 275–286. IEEE Computer Society (1993)
Ong, C.: The lazy lambda calculus: an investigation into the foundations of functional programming. University of London, Imperial College of Science and Technology (1988)
Plotkin, G.: Call-by-name, call-by-value and the lambda-calculus. Theoret. Comput. Sci. 1(2), 125–159 (1975)
Plotkin, G.: Lambda-definability and logical relations. Technical report SAI-RM-4. University of Edinburgh, School of A.I. (1973)
Plotkin, G., Power, J.: Adequacy for algebraic effects. In: Honsell, F., Miculan, M. (eds.) FoSSaCS 2001. LNCS, vol. 2030, pp. 1–24. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45315-6_1
Plotkin, G., Power, J.: Notions of computation determine monads. In: Nielsen, M., Engberg, U. (eds.) FoSSaCS 2002. LNCS, vol. 2303, pp. 342–356. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45931-6_24
Plotkin, G.D., Power, J.: Algebraic operations and generic effects. Appl. Categorical Struct. 11(1), 69–94 (2003)
Plotkin, G.D., Pretnar, M.: Handling algebraic effects. Logical Methods Comput. Sci. 9(4), 1–36 (2013)
Pous, D., Sangiorgi, D.: Enhancements of the bisimulation proof method. In: Sangiorgi, D., Rutten, J. (eds.) Advanced Topics in Bisimulation and Coinduction. Cambridge University Press, New York (2012)
Reynolds, J.: Types, abstraction and parametric polymorphism. In: IFIP Congress, pp. 513–523 (1983)
Sands, D.: Improvement theory and its applications. In: Gordon, A.D., Pitts, A.M. (eds.) Higher Order Operational Techniques in Semantics, pp. 275–306. Publications of the Newton Institute, Cambridge University Press (1998)
Sangiorgi, D., Kobayashi, N., Sumii, E.: Environmental bisimulations for higher-order languages. ACM Trans. Program. Lang. Syst. 33(1), 5:1–5:69 (2011)
Sangiorgi, D.: A theory of bisimulation for the \(\phi \)-calculus. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 127–142. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57208-2_10
Sangiorgi, D.: The lazy lambda calculus in a concurrency scenario. Inf. Comput. 111(1), 120–153 (1994)
Sangiorgi, D., Vignudelli, V.: Environmental bisimulations for probabilistic higher-order languages. In: Proceedings of POPL 2016, pp. 595–607 (2016)
Simpson, A., Voorneveld, N.: Behavioural equivalence via modalities for algebraic effects. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 300–326. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_11
Støvring, K., Lassen, S.B.: A complete, co-inductive syntactic theory of sequential control and state. In: Proceedings of POPL 2007, pp. 161–172 (2007)
Strassen, V.: The existence of probability measures with given marginals. Ann. Math. Statist. 36(2), 423–439 (1965)
Tarski, A.: A lattice-theoretical fixpoint theorem and its applications. Pacific J. Math. 5(2), 285–309 (1955)
Thijs, A.: Simulation and fixpoint semantics. Rijksuniversiteit Groningen (1996)
Villani, C.: Optimal Transport: Old and New. Grundlehren der mathematischen Wissenschaften. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71050-9
Wadler, P.: Monads for functional programming. In: Program Design Calculi, Proceedings of the NATO Advanced Study Institute on Program Design Calculi, Marktoberdorf, Germany, 28 July – 9 August 1992, pp. 233–264 (1992)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Dal Lago, U., Gavazzo, F. (2019). Effectful Normal Form Bisimulation. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)




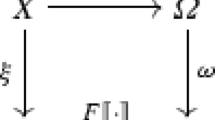
 is a relator for
is a relator for  and
and 
