Abstract
With the proliferation of contactless applications, obtaining reliable information about distance is becoming an important security goal, and specific protocols have been designed for that purpose. These protocols typically measure the round trip time of messages and use this information to infer a distance. Formal methods have proved their usefulness when analysing standard security protocols such as confidentiality or authentication protocols. However, due to their abstract communication model, existing results and tools do not apply to distance bounding protocols.
In this paper, we consider a symbolic model suitable to analyse distance bounding protocols, and we propose a new procedure for analysing (a bounded number of sessions of) protocols in this model. The procedure has been integrated in the Akiss tool and tested on various distance bounding and payment protocols (e.g. MasterCard, NXP).
This work has been partially supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 714955-POPSTAR).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In recent years, contactless communications have become ubiquitous. They are used in various applications such as access control cards, keyless car entry systems, payments, and many other applications which often require some form of authentication, and rely for this on security protocols. In addition, contactless systems aims to prevent against relay attacks in which an adversary mount an attack by simply forwarding messages he receives: ensuring physical proximity is a new security concern for all these applications.
Formal modelling and analysis techniques are well-adapted for verifying security protocols, and nowadays several verification tools exist, e.g. ProVerif [8], Tamarin [28]. They aim at discovering logical attacks, and therefore consider a symbolic model in which cryptographic primitives are abstracted by function symbols. Since its beginning in 80s, a lot of progress has been done in this area, and it is now a common good practice to formally analyse protocols using symbolic techniques in order to spot flaws possibly before their deployment, as it was recently done e.g. in TLS 1.3 [7, 17], or for an avionic protocol [9].
These symbolic techniques are based on the so-called Dolev Yao model [20]. In such a model, the attacker is supposed to control the entire network. He can send any message he is able to build using his current knowledge, and this message will reach its final destination instantaneously. This model is accurate enough to analyse many security protocols, e.g. authentication protocols, e-voting protocols, ...However, to analyse protocols that aim to prevent against relay attacks, some features need to be modelled in a more faithful way. Among them:
-
network topology: any pair of nodes can communicate but depending on their distance, exchanging messages take more or less time. We will simply assume that the time needed is proportional to the distance between the two agents, and that messages can not travel faster than the speed of the light.
-
timing constraints: protocols that aim to prevent against relay attacks typically rely on a rapid phase in which time measurements are performed. Our framework will allow us to model these time measurements through the use of timestamps put on each action.
There are some implications on the attacker model. Since communications take time, it may be interesting to consider several malicious nodes. We will assume that malicious nodes collaborate but again messages can not travel (even between malicious nodes) faster than the speed of the light.
Akiss in a Nutshell. The procedure we present in this paper builds on previous work by Chadha et al. [12], and its implementation in the tool Akiss. Akiss allows automated analysis of privacy-type properties (modelling as equivalences) when restricted to a bounded number of sessions. Cryptographic primitives may be defined through arbitrary convergent equational theories that have the finite variant property. This class includes standard cryptographic primitives as well as less commonly supported primitives such as blind signatures and zero knowledge proofs. Termination of the procedure is guaranteed for subterm convergent theories, but also achieved in practice on several examples outside this class.
The procedure behind Akiss is based on an abstract modelling of symbolic traces into first-order Horn clauses: each symbolic trace is translated into a set of Horn clauses called seed statements, and a dedicated resolution procedure is applied on this set to construct a set of statements which have a simple form: the so-called solved statements. Once the saturation of the set of seed statements is done, it is possible to decide, based solely on those solved statements, whether processes under study are equivalent or not.
Even if we are considering reachability properties (here authentication with physical proximity), in order to satisfy timing constraints, we may need to consider recipes that are discarded when performing a classical reachability analysis. Typically, in a classical reachability analysis, there is no need to consider two recipes that deduce the same message. The main advantage of Akiss is the fact that, since its original goal is to deal with equivalence, it considers more (actually almost all possible) recipes when performing the security analysis. Moreover, even if the tool has been designed to deal with equivalence-based properties, the first part of the Akiss procedure consists in computing a knowledge base which is in fact a finite representation of all possible traces (including recipes) executable by the process under study. We build on this saturation procedure in this work.
Our Contributions. We design a new procedure for verifying reachability properties for protocols written in a calculus sharing many similarities with the one introduced in [19], and that gives us a way to model faithfully distance bounding protocols. Our procedure follows the general structure of the original one described in [12]. We first model protocols as traces (see Sect. 3), and then translate them into Horn clauses (see Sect. 4). A direct generalisation would consist of keeping the saturation procedure unchanged, and simply modifying the algorithm to check the satisfiability of our additional timing constraints at the end. However, as discussed in Sect. 5, such a procedure would not be complete for our purposes. We therefore completely redesign the update function used during the saturation procedure using a new strategy to forbid certain steps that would otherwise systematically yield to non-termination in our final algorithm. Showing these statements are indeed unnecessary requires essential changes in the proofs of completeness of the original procedure.
This new saturation procedure yields an effective method for checking reachability properties in our calculus (see Sect. 6). Although termination of saturation is not guaranteed in theory, we have implemented our procedure and we have demonstrated its effectiveness on various examples. We report on our implementation and the various case studies we have performed in Sect. 7.
As we were unable to formally establish completeness of the procedure as implemented in the original Akiss tool (due to some mismatches between the procedure described in [12] and its implementation), we decided to bring the theory closer to the practice, and this explains several differences between our seed statements and those described originally in [12].
A full version of this paper including proofs is available at [18].
2 Background
We start by providing some background regarding distance bounding protocols. For illustrative purposes, we present a slightly simplified version of the TREAD protocol [2] together with the attack discovered by [26] (relying on the Tamarin prover). This protocol will be used along the paper as a running example.
2.1 Distance Bounding Protocols
Distance bounding protocols are cryptographic protocols that enable a verifier V to establish an upper bound on the physical distance to a prover P. They are typically based on timing the delay between sending out a challenge and receiving back the corresponding response. The first distance bounding protocol was proposed by Brands and Chaum [10], and since then various protocols have been proposed. In general, distance bounding protocols are made of two or three phases, the second one being a rapid phase during which the time measurement is performed. To improve accuracy, this challenge/response exchange during which the measurement is performed is repeated several times, and often performed at the bit level. Symbolic analysis does not allow us to reason at this level, and thus the rapid phase will be abstracted by a single challenge/response exchange, and operations done at bit level will be abstracted too.
For illustration purposes, we consider the TREAD protocol. As explained before, we ignore several details that are irrelevant to our symbolic security analysis, and we obtain the protocol described in Fig. 1. First, the prover generates a nonce \(\gamma \), and computes the signature \(\sigma \) with his own key. This signature is sent to V encrypted with the public key of V. Upon reception, the verifier decrypts the message and checks the signature. Then, the verifier sends a nonce m, and starts the rapid phase during which he sends a challenge c to the prover. The protocol ends successfully if the answer given by the prover is correct and arrived before a predefined threshold.
2.2 Attacks on Distance Bounding Protocols
Typically, an attack occurs when a verifier is deceived into believing it is co-located with a given prover whereas it is not. Attacker may replay, relay and build new messages, as well as predict some timed challenges. Since the introduction of distance bounding protocols, various kinds of attacks have emerged, e.g. distance fraud, mafia fraud, distance hijacking attack, ...For instance, a distance fraud only consider a dishonest prover who tries to authenticate remotely, whereas a distance hijacking scenario allows the dishonest prover to take advantage of honest agents in the neighbourhood of the verifier.
The TREAD protocol is vulnerable to a mafia fraud attack: an honest verifier v may end successfully a session with an honest prover p thinking that this prover p is in his vicinity whereas p is actually far away. The attack is described in Fig. 1. After learning \(\gamma \) and a signature \(\sigma =\mathsf {sign}(\gamma ,sk_p)\), the malicious agent i will be able to impersonate p. At the end, the verifier v will finish his session correctly thinking that he is playing with p (who is actually far away).
2.3 Symbolic Security Analysis
The first symbolic framework developed to analyse distance bounding protocols is probably the one proposed in [27]. Since then, several formal symbolic models have been proposed: e.g. a model based on multiset rewriting rules has been proposed in [5], another one based on strand spaces is available in [31]. However, these models do not come with a procedure allowing one to analyse distance bounding protocols in an automatic way. Recently, some attempts have been done to rely on existing automatic verification tools, e.g. ProVerif [13, 19] or Tamarin [26]. Those tools typically consider an unbounded number of sessions, and some approximations are therefore performed to tackle this problem well-known to be undecidable [21].
Here, following the long line of research on symbolic verification for a bounded number of sessions which is a problem well-known to be decidable [29, 32] and for which automatic verification tools have been developed (e.g. OFMC [6], Akiss [12]), we aim to extend this approach to distance bounding protocols.
3 A Security Model Dealing with Time and Location
We assume that our cryptographic protocols are modelled using a simple process calculus sharing some similarities with the applied-pi calculus [1], and strongly inspired by the calculus introduced in [19].
3.1 Term Algebra
As usual in symbolic models, we represent messages using a term algebra. We consider a set \(\mathcal {N}\) of names split into two disjoint sets: the set \(\mathcal {N}_\mathsf {pub}\) of public names which contains the set \(\mathcal {A}\) of agent names, and the set \(\mathcal {N}_\mathsf {priv}\) of private names. We consider the set \(\mathcal {X}\) of message variables, denoted \(x, y, \ldots \), as well as a set \(\mathcal {W}\) of handles: \(\mathcal {W}= \{\mathsf {w}_1, \mathsf {w}_2, \ldots \}\). Variables in \(\mathcal {X}\) model arbitrary data expected by the protocol, while variables in \(\mathcal {W}\) are used to store messages learnt by the attacker. Given a signature \(\varSigma \), i.e. a finite set of function symbols together with their arity, and a set of atomic data \(\mathcal {A}t\), we denote \(\mathcal {T}(\varSigma ,\mathcal {A}t)\) the set of terms built from \(\mathcal {A}t\) using function symbols in \(\varSigma \). Given a term u, we denote \( st (u)\) the set of the subterms occurring in u, and \( vars (u)\) the set of variables occurring in u. A term u is ground when \( vars (u) = \emptyset \). Then, we associate an equational theory \(\mathsf {E}\) to the signature \(\varSigma \) which consists of a finite set of equations of the form \(u =v\) with \(u,v \in \mathcal {T}(\varSigma ,\mathcal {X})\), and induces an equivalence relation over terms denoted \(=_\mathsf {E}\).
Example 1
\(\varSigma _\mathsf {ex}= \{\mathsf {aenc}, \mathsf {adec}, \mathsf {pk}, \mathsf {sign}, \mathsf {getmsg}, \mathsf {check}, \mathsf {ok}, \langle \; \rangle , \mathsf {proj}_1, \mathsf {proj}_2,\mathsf {h}\}\) allows us to model the cryptographic primitives used in the TREAD protocol presented in Sect. 2. The function symbols \(\mathsf {aenc}\) and \(\mathsf {adec}\) of arity 2 model asymmetric encryption, whereas \(\mathsf {sign}\), \(\mathsf {getmsg}\), \(\mathsf {check}\), and \(\mathsf {ok}\) are used to model signature. The term \(\mathsf {pk}(sk)\) represents the public key associated to the private key sk. We have function symbols to model pairs and projections, as well as a function \(\mathsf {h}\) of arity 3 to model hashes. The equational theory \(\mathsf {E}_\mathsf {ex}\) associated to the signature \(\varSigma _\mathsf {ex}\) is the relation induced by:
We consider equational theories that can be represented by a convergent rewrite system, i.e. we assume that there is a confluent and terminating rewrite system such that:
where \(t\mathord {\downarrow }\) denotes the normal form of t. Moreover, we assume that such a rewrite system has the finite variant property as introduced in [16]. This means that given a sequence \(t_1, \ldots , t_n\) of terms, it is possible to compute a finite set of substitutions, denoted \(\mathsf {variants}(t_1, \ldots , t_n)\), such that for any substitution \(\omega \), there exist \(\sigma \in \mathsf {variants}(t_1, \ldots , t_n)\) and \(\tau \) such that: \(t_1\omega \mathord {\downarrow }, \ldots , t_n\omega \mathord {\downarrow }= (t_1\sigma )\mathord {\downarrow }\tau , \ldots , (t_n\sigma )\mathord {\downarrow }\tau \). Many equational theories enjoy this property, e.g. symmetric/asymmetric encryptions, signatures and blind signatures, as well as zero-knowledge proofs.
Moreover, this finite variant property implies the existence of a finite and complete set of unifiers and gives us a way to compute it effectively. Given a set \(\mathcal {U}\) of equations between terms, a unifier (modulo a rewrite system \(\mathcal {R}\)) is a substitution \(\sigma \) such that \(s\sigma \mathord {\downarrow }= s'\sigma \mathord {\downarrow }\) for any equation \(s = s'\) in \(\mathcal {U}\). A set S of unifiers is said to be complete for \(\mathcal {U}\) if for any unifier \(\sigma \), there exists \(\theta \in S\) and \(\tau \) such that \(\sigma = \tau \circ \theta \). We denote \(\mathsf {csu}_\mathcal {R}(\mathcal {U})\) such a set. We will rely on these notions of \(\mathsf {variants}\) and \(\mathsf {csu}\) in our procedure (see Sect. 4).
Example 2
The finite variant property is satisfied by the rewrite system \(\mathcal {R}_\mathsf {ex}\) obtained by orienting from left to right equations in \(\mathsf {E}_\mathsf {ex}\).
Let \(\mathcal {U} = \{\mathsf {check}(t_\sigma , \mathsf {pk}(sk_p)) = \mathsf {ok}\}\) with \(t_\sigma = \mathsf {proj}_2(\mathsf {adec}(x, sk_v))\). We have that \(\{\theta \}\) with \(\theta = \{x \rightarrow \mathsf {aenc}(\langle x_1, \mathsf {sign}(x_2,sk_p)\rangle , \mathsf {pk}(sk_v))\}\) is a complete set of unifiers for \(\mathcal {U}\) (modulo \(\mathcal {R}_\mathsf {ex}\)). Now, considering the variants, let \(\sigma _1 = \{x \rightarrow \mathsf {aenc}(x_1, \mathsf {pk}(sk_v))\}\), \(\sigma _2 = \{x \rightarrow \mathsf {aenc}(\langle x_1, x_2\rangle , \mathsf {pk}(sk_v))\}\) and \( id \) be the identity substitution, we have that \(\{ id , \sigma _1, \sigma _2\}\) is a finite and complete set of variants (modulo \(\mathcal {R}_\mathsf {ex}\)) for the sequence \((x, t_\sigma )\).
An attacker builds her own messages by applying function symbols to terms she already knows and which are available through variables in \(\mathcal {W}\). Formally, a computation done by the attacker is a recipe, i.e. a term in \(\mathcal {T}(\varSigma , \mathcal {W}\cup \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+)\).
3.2 Timing Constraints
To model time, we will use non-negative real numbers \(\mathbb {R}^+\), and we may allow various operations (e.g. \(+\), −, \(\times \), ...). A time expression is constructed inductively by applying arithmetic symbols to time expressions starting with the initial set \(\mathbb {R}^+\) and an infinite set \(\mathcal {Z}\) of time variables. Then, a timing constraint is typically of the form \(t_1 \sim t_2\) with \(\sim \,\in \, \{<, \le , =\}\). We do not constraint the operators since our procedure is generic in this respect provided we have a way to decide whether a set of timing constraints is satisfiable or not. In practice, our tool (see Sect. 7) will only be able to consider simple linear timing constraints.
Example 3
When modelling distance bounding protocols, we will typically consider a timing constraint of the form \(z_2 - z_1 <t\) with \(z_1, z_2 \in \mathcal {Z}\) and \(t \in \mathbb {R}^+\). This constraint expresses that the time elapsed between the emission of a challenge and the receipt of the corresponding answer is at most t.
3.3 Process Algebra
We assume that cryptographic protocols are modelled using a simple process algebra. Following [12], we only consider a minimalistic core calculus. In particular, we do not introduce the new operator and we do not explicitly model the parallel operator. Since we only consider a bounded number of sessions (i.e. a calculus with no replication), this is at no loss of expressivity. We can simply assume that fresh names are generated from the beginning and parallel composition can be added as syntactic sugar to denote the set of all interleavings.
Syntax. We model a protocol as a finite set of traces. A trace T is a finite sequence (possibly empty and denoted \(\epsilon \) in this case) of pairs, i.e. \(T = (a_1,\mathsf {a}_1). \ldots . (a_n, \mathsf {a}_n)\) where each \(a_i \in \mathcal {A}\), and \(\mathsf {a}_i\) is an action of the form:
with \(x \in \mathcal {X}\), \(u, v, v' \in \mathcal {T}(\varSigma , \mathcal {N}\cup \mathbb {R}^+\cup \mathcal {X})\), \(z \in \mathcal {Z}\), and \(t_1 \sim t_2\) a timing constraint.
As usual, we have output and input actions. An input action acts as a binding construct for both x and z, whereas an output action acts as a binding construct for z only. For sake of clarity, we will omit the time variable z when we do not care of the precise time at which the input (resp. output) action has been performed. As usual, our calculus allows one to perform some tests on received messages, and it is also possible to extract a timestamp from a received message and perform some tests on this extracted value using timing constraints. Typically, this will allow us to model an agent that will stop executing the protocol in case an answer arrives too late.
We assume the usual definitions of free and bound variables for traces, and we assume that each variable is at most bound once. Note that, in the constructs presented above, the variables z, x are bound. Given a set \(\mathcal {V}\) of variables, a trace is locally closed w.r.t. \(\mathcal {V}\) if for any agent a, the trace obtained by considering actions executed by agent a does not contain free variables among those in \(\mathcal {V}\). Such an assumption, sometimes called origination [6, 15], is always satisfied when considering traces obtained by interleaving actions of a protocol. Therefore, we will only consider traces that are locally closed w.r.t. both \(\mathcal {X}\) and \(\mathcal {Z}\).
Contrary to the calculus introduced in [19] which assumes that there is at most one timer per thread, we are more flexible. This generalisation is not mandatory to analyse our case studies but it allows us to present our result on traces and greatly simplifies the theoretical development.
Example 4
Following our syntax, the trace corresponding to the role of the verifier played by v with p is modelled as follows:
where \(t_\gamma = \mathsf {proj}_1(\mathsf {adec}(x,sk_v))\), \(t_\sigma = \mathsf {proj}_2(\mathsf {adec}(x,sk_v))\), \(x,y \in \mathcal {X}\), \(z_1, z_2 \in \mathcal {Z}\), \({m,c, sk_v, sk_p \in \mathcal {N}_\mathsf {priv}}\), and \(t_0 \in \mathbb {R}^+\) is a fixed threshold.
Of course, when performing a security analysis, other traces have to be considered. Typically, we may want to consider several instances of each role, and we will have to generate traces corresponding to all the possible interleavings of the actions composing these roles.
Semantics. The semantics of a trace is given in terms of a labeled transition system over configurations of the form \((T;\varPhi ;t)\), and is parametrised by a topology reflecting the fact that interactions between agents depend on their location.
Definition 1
A topology is a tuple \(\mathcal {T}_0 = (\mathcal {A}_0,\mathcal {M}_0,\mathsf {Loc}_0)\) where \(\mathcal {A}_0 \subseteq \mathcal {A}\) is the finite set of agents composing the system, \(\mathcal {M}_0 \subseteq \mathcal {A}_0\) represents those that are malicious, and \(\mathsf {Loc}_0: \mathcal {A}_0 \rightarrow \mathbb {R}^3\) defines the position of each agent in the space.
In our model, the distance between two agents is given by the time it takes for a message to travel from one to another. We have that:
with \(||\cdot ||:\mathbb {R}^3\rightarrow \mathbb {R}\) the Euclidean norm and \(c_0\) the transmission speed. We suppose, from now on, that \(c_0\) is a constant for all agents, and thus an agent a can recover, at time \(t +\textsf {Dist}_{\mathcal {T}_0}(a,b)\), any message emitted by the agent b before \(t \in \mathbb {R}^+\).
Definition 2
Given a topology \(\mathcal {T}_0 = (\mathcal {A}_0, \mathcal {M}_0, \mathsf {Loc}_0)\), a configuration over \(\mathcal {T}_0\) is a tuple \((T;\varPhi ;t)\) where T is a trace locally closed w.r.t. \(\mathcal {X}\) and \(\mathcal {Z}\) composed of actions \((a, \mathsf {a})\) with \(a \in \mathcal {A}_0\), \(t \in \mathbb {R}^+\), and \(\varPhi =\{\mathsf {w}_1\xrightarrow {a_1,t_1}u_1, \ldots , \mathsf {w}_n\xrightarrow {a_n,t_n}u_n\}\) is an extended frame, i.e. a substitution such that \(\mathsf {w}_i\in \mathcal {W}\), \(u_i\in \mathcal {T}(\varSigma ,\mathcal {N}\cup \mathbb {R}^+)\), \(a_i\in \mathcal {A}_0\) and \(t_i\in \mathbb {R}^+\) for \(1 \le i \le n\).
Intuitively, T represents the trace that still remains to be executed; \(\varPhi \) represents the messages that have been outputted so far; and t is the global time.
Example 5
Continuing Example 4, we consider the topology \(\mathcal {T}_0 = (\mathcal {A}_0,\mathcal {M}_0,\mathsf {Loc}_0)\) depicted on the right where \(\mathcal {A}_0 = \{p, v, i\}\), and \(\mathcal {M}_0 = \{i\}\).

The precise location of each agent is not relevant, only the distance between them matters. Here \({\textsf {Dist}_{\mathcal {T}_0}(v,i) < t_0}\) whereas \({\textsf {Dist}_{\mathcal {T}_0}(v,p) \ge t_0}\).
A possible configuration is \(K_0 = (T_\mathsf {ex};\varPhi _0;0)\) with
We have that v is playing the verifier’s role with p (who is far away). We do not consider any prover’s role but we assume that p (acting as a prover) has started a session with i and thus the corresponding encryption (here \(\gamma \in \mathcal {N}_\mathsf {priv}\)) has been added to the knowledge of the attacker (handle \(\mathsf {w}_3\)). We also assume that \(sk_i \in \mathcal {N}_\mathsf {priv}\), the private key of the agent \(i \in \mathcal {M}_0\), is known by the attacker. A more realistic configuration would include other instances of the prover and the verifier roles and will probably give more knowledge to the attacker. This simple configuration is actually sufficient to retrieve the attack presented in Sect. 2.2.
We write \(\left. \lfloor \varPhi \rfloor \right. _{a}^{t}\) for the restriction of \(\varPhi \) to the agent a at time t, i.e.:
Our labeled transition system is given in Fig. 2 and relies on labels \(\ell \) which can be either equal to the unobservable \(\tau \) action or of the form \((a,\mathsf {a})\) with \(a \in \mathcal {A}\), and \(\mathsf {a}\in \{\mathsf {test}, \mathsf {eq}\} \cup \{\mathsf {in}(u), \mathsf {out}(u)~|~ u \in \mathcal {T}(\varSigma , \mathcal {N}\cup \mathbb {R}^+)\} \cup \{\mathsf {let}(v) ~|~ v \in \mathbb {R}^+\}\). The TIM rule allows time to elapse and is labeled with \(\tau \) (often omitted for sake of simplicity). The OUT rule allows an output action to be executed, and the outputted term will be added to the frame. Rule EQ is used to perform some tests, and those tests are evaluated modulo the equational theory. Then, the LET rule allows us to evaluate a term that is supposed to contain a real number, and could then be used in a timing constraint through the variable z. Then, we have a rule to evaluate a timing constraint. The IN rule allows an agent a to execute an input: the received message u has been sent at time \(t_b\) by an agent b who was in possession of the message at that time. In case b is a malicious agent, i.e. \(b \in \mathcal {M}_0\), the message u may have been forged through a recipe R, and b has to be in possession of all the necessary information at that time. The variable z is used to store the time at which this action has been executed.
Example 6
Continuing Example 5, we may consider the following execution which aims to mimic the trace developed in Sect. 2:
The first arrow corresponds to an application of the rule TIM with delay \(\delta _0 \ge \textsf {Dist}_{\mathcal {T}_0}(p,i) + \textsf {Dist}_{\mathcal {T}_0}(i,v)\). Then, the IN rule is triggered considering that the message \(t_\mathsf {aenc}= \mathsf {aenc}(\langle \gamma , \mathsf {sign}(\gamma ,sk_p)\rangle , \mathsf {pk}(sk_v))\) is sent by i at time \(t_i\) such that \(\textsf {Dist}_{\mathcal {T}_0}(p,i) \le t_i \le \delta _0 - \textsf {Dist}_{\mathcal {T}_0}(i,v)\). Such a message \(t_\mathsf {aenc}\) can indeed be forged by i at time \(t_i\) (using recipe \(R = \mathsf {aenc}(\mathsf {adec}(\mathsf {w}_3,\mathsf {w}_2),\mathsf {w}_1)\)) and thus be received by v at time \(\delta _0\). Then, tests performed by v are evaluated successfully, v outputs m, and we reach the configuration \(K_\mathsf {rapid}= (T_\mathsf {rapid};\varPhi _\mathsf {rapid};\delta _0)\) where:
-
\(T_\mathsf {rapid}= (v,\mathsf {out}^{z_1}(c)). (v,\mathsf {in}^{z_2}(y)). (v, [y=\mathsf {h}(c,m,\gamma )]).(v,[\![z_2 - z_1 < 2t_0]\!])\), and
-
\(\varPhi _\mathsf {rapid}= \varPhi _0 \uplus \{\mathsf {w}_4 \xrightarrow {v,\delta _0} m\}\).
We can pursue this execution as follows:
The second arrow is an application of the rule TIM with delay \(2 \textsf {Dist}_{\mathcal {T}_0}(v,i)\) so that \(\mathsf {h}(c,m,\gamma )\) can be received by v at time \(\delta _0 + 2 \textsf {Dist}_{\mathcal {T}_0}(v,i)\). Since \({\textsf {Dist}_{\mathcal {T}_0}(v,i) < t_0}\), the timing constraint is true and the last action can be executed.
The goal of this paper is to propose a new procedure for analysing a bounded number of sessions of distance bounding protocols. Once the topology is fixed, the existence of an attack can be directly encoded as a reachability property considering a finite set of traces. The following sections are thus dedicated to the study of the following problem:
-
Input: A trace T locally closed w.r.t. \(\mathcal {X}\) and \(\mathcal {Z}\), \(t_0 \in \mathbb {R}^+\), and a topology \(\mathcal {T}_0\).
-
Output: Do there exist \(\ell _1, \ldots , \ell _n\), \(\varPhi \), and t such that \((T;\emptyset ;t_0) \xrightarrow {\ell _1 \ldots , \ell _n}_{\mathcal {T}_0} (\epsilon ;\varPhi ;t)\)?
4 Modelling Using Horn Clauses
Following the approach developed in Akiss [12], our procedure is based on an abstract modelling of a trace in first-order Horn clauses. Our set of seed statements is more in line with what has been implemented in Akiss for optimisation purposes rather than what is presented in [12].
4.1 Preliminaries
We consider symbolic runs which are finite sequences of pairs with possibly a run variable typically denoted \(\mathsf {y}\) at its ends. We have that each pair \((a, \mathsf {a})\) is such that \(a \in \mathcal {A}\) and \(\mathsf {a}\) is an action of the form (with \(u\in \mathcal {T}(\varSigma , \mathcal {N}\cup \mathbb {R}^+\cup \mathcal {X})\)):
Excluding the special variable \(\mathsf {y}\), a symbolic run \((a_1, \mathsf {a}_1). \ldots . (a_n, \mathsf {a}_n)\), only contains variables from the set \(\mathcal {X}\). We say that it is locally closed if whenever a variable x occurs in an output action (resp. let action) \(\mathsf {a}_j\), then there exists an input action \(\mathsf {a}_i\) occurring before (i.e. \(i < j\)) such that \(a_i = a_j\) and \(x \in vars (\mathsf {a}_i)\). Symbolic runs are often denoted \(w, w', \ldots \), and we write \(w \sqsubseteq w'\) when the sequence w is a prefix of \(w'\). Given a symbolic run \(w_0\) whose sequence of outputs is \(\mathsf {out}(u_1) \cdot \ldots \cdot \mathsf {out}(u_n)\), we denote \(\phi (w_0) = \{\mathsf {w}_1 \rightarrow u_1, \ldots , \mathsf {w}_n \rightarrow u_n\}\).
We also consider symbolic recipes which are terms in \(\mathcal {T}(\varSigma , \mathcal {W}\cup \mathcal {N}_\mathsf {pub}\cup \mathcal {Y})\) where \(\mathcal {Y}\) is a set of recipe variables disjoint from \(\mathcal {X}\) and \(\mathcal {W}\). We use capital letters X, Y, and Z to range over \(\mathcal {Y}\).
Example 7
We consider the following symbolic run:
We have that \(\phi (w_0) = \{\mathsf {w}_1 \rightarrow m, \mathsf {w}_2 \rightarrow c\}\).
Our logic is based on two predicates expressing deduction and reachability without taking into account timing constraints. More formally, given a configuration \((T;\varPhi ;t)\), its untimed counterpart is \((T;\phi )\) where \(\phi \) is the untimed counterpart of \(\varPhi \), i.e. a frame of the form: \(\phi = \{\mathsf {w}_1 \rightarrow u_1, \ldots , \mathsf {w}_n \rightarrow u_n\}\). The relaxed semantics over untimed configurations is given in Fig. 3. Since time variables (from \(\mathcal {Z}\)) are not instantiated during a relaxed execution, in an untimed configuration \((T;\phi )\), the trace T is only locally closed w.r.t. \(\mathcal {X}\). Our predicates are:
-
a reachability predicate: \(\mathsf {r}_{w}\) holds when the run w is executable.
-
a deduction predicate: \(\mathsf {k}_{w} (R, u)\) holds if the message u can be built using the recipe \(R \in \mathcal {T}(\varSigma , \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\cup \mathcal {W})\) by an attacker using the outputs available after the execution of w (if this execution is possible).
Formally, we have that:
-
 if there exists \((T_n;\phi _n)\) such that
if there exists \((T_n;\phi _n)\) such that 
-
 if for all \((T_n;\phi _n)\) such that
if for all \((T_n;\phi _n)\) such that 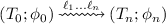 we have that \(R\phi _n\mathord {\downarrow }= u\).
we have that \(R\phi _n\mathord {\downarrow }= u\).
This semantics is extended as usual to first-order formulas built using the usual connectives (e.g. conjunction, quantification, ...)
Example 8
The frame \(\phi _0\) below is the untimed counterpart of \(\varPhi _0\):
We have that  where \(\phi _\mathsf {final}\) is the untimed counterpart of \(\varPhi _\mathsf {final}= \varPhi _{\mathsf {rapid}} \uplus \{\mathsf {w}_5 \xrightarrow {v,\delta _0} c\}\), and \(\mathsf {tr}\) is the same sequence of labels as the one developed in Example 6, i.e.
where \(\phi _\mathsf {final}\) is the untimed counterpart of \(\varPhi _\mathsf {final}= \varPhi _{\mathsf {rapid}} \uplus \{\mathsf {w}_5 \xrightarrow {v,\delta _0} c\}\), and \(\mathsf {tr}\) is the same sequence of labels as the one developed in Example 6, i.e.
4.2 Seed Statements
We consider particular Horn clauses which we call statements.
Definition 3
A statement is a Horn clause: \(H \Leftarrow \mathsf {k}_{w_1}(X_1, u_1), \ldots , \mathsf {k}_{w_n}(X_n, u_n)\) with \(H \in \{\mathsf {r}_{w_0}, \,\mathsf {k}_{w_0}(R, u)\}\) and such that:
-
\(w_0,\ldots , w_n\) are symbolic runs locally closed, \(w_i \sqsubseteq w_0\) for any \(i \in \{1,\ldots , n\}\);
-
\(u, u_1, \ldots , u_n\) are terms in \(\mathcal {T}(\varSigma ,\mathcal {N}\cup \mathbb {R}^+\cup \mathcal {X})\);
-
\(R \in \mathcal {T}(\varSigma ,\mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\cup \mathcal {W}\cup \{X_1,\ldots , X_n\}) \smallsetminus \mathcal {Y}\), and \(X_1, \dots , X_n\) are distinct variables from \(\mathcal {Y}\).
When \({H = \mathsf {k}_{w_0}(R, u)}\), we assume in addition that \( vars (u) \subseteq vars (u_1, \ldots , u_n)\) and \(R (\{X_i \rightarrow u_i\} \uplus \phi (w_0)) \mathord {\downarrow }= u\).
In the above definition, we implicitly assume that all variables are universally quantified, i.e., all statements are ground. By abuse of language we sometimes call \(\sigma \) a grounding substitution for a statement \(H \Leftarrow ( B_1, \ldots , B_n)\) when \(\sigma \) is grounding for each of the atomic formulas \(H, B_1, \ldots , B_n\). The skeleton of a statement f, denoted \(\mathsf {skl}(f)\), is the statement where recipes are removed. Our definition of statement is in line with the original one proposed in [12] but we state an additional invariant used to establish the completeness of our procedure.
In order to define our set of seed statements, we have to fix some naming conventions. Given a trace T of the form \((a_1, \mathsf {a}_1).(a_2,\mathsf {a}_2).\ldots .(a_n,\mathsf {a}_n)\), we assume w.l.o.g. the following naming conventions:
-
1.
if \(\mathsf {a}_i\) is a receive action, then \(\mathsf {a}_i = \mathsf {in}^{z_i}(x_i)\), and \(\ell _i =(a_i, \mathsf {in}(x_i))\);
-
2.
if \(\mathsf {a}_i\) is a send action, then \(\mathsf {a}_i= \mathsf {out}^{z_i}(u_i)\), and \(\ell _i = (a_i,\mathsf {out}(u_i))\);
-
3.
if \(\mathsf {a}_i\) is a test action, then \(\mathsf {a}_i = [v_i = v'_i]\), and \(\ell _i = (a_i,\mathsf {eq})\);
-
4.
if \(\mathsf {a}_i\) is a let action, then \(\mathsf {a}_i = [z'_i := v_i]\), and \(\ell _i = (a_i,\mathsf {let}(v_i))\).
-
5.
if \(\mathsf {a}_i\) is a timing constraint then \(\mathsf {a}_i = [\![t_i \sim t'_i]\!]\), and \(\ell _i = (a_i, \mathsf {test})\).
For each \(m \in \{0, \ldots , n\}\), the sets \(\mathsf {Rcv}(m)\), \(\mathsf {Snd}(m)\), \(\mathsf {Eq}(m)\), \(\mathsf {Let}(m)\), and \(\mathsf {Test}(m)\) respectively denote the set of indexes of the receive, send, equality, let, and test actions amongst \(\mathsf {a}_1, \ldots , \mathsf {a}_m\). We denote by |S| the cardinality of S.
Given a set \(\mathcal {C} \subseteq \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\), the set of seed statements associated to T and \(\mathcal {C}\), denoted \(\mathsf {seed}(T,\mathcal {C})\), is defined in Fig. 4. If \(\mathcal {C} = \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\), then \(\mathsf {seed}(T,\mathcal {C})\) is said to be the set of seed statements associated to T and in this case we write \(\mathsf {seed}(T)\) as a shortcut for \(\mathsf {seed}(T,\mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+)\). When computing seed statements, we compute complete sets of unifiers and complete sets of variants modulo \(\mathcal {R}\). This allows us to get rid of the rewrite system in the remainder of our procedure and then only consider unification modulo the empty equational theory. In this case, it is well-known that (when it exists) \(\mathsf {csu}_\emptyset (\mathcal {U})\) is uniquely defined up to some variable renaming, and we write \(\mathsf {mgu}(u_1,u_2)\) instead of \(\mathsf {csu}_{\emptyset }(\{u_1 = u_2\})\).
Example 9
Let \(T^+_\mathsf {ex}= T_0 \cdot T_\mathsf {ex}\) with \(T_0 = (i, \mathsf {out}(\mathsf {pk}(sk_v))).(i, \mathsf {out}(sk_i)).(p, \mathsf {out}(u))\) and \(u = \mathsf {aenc}(\langle \gamma , \mathsf {sign}(\gamma , sk_p)\rangle , \mathsf {pk}(sk_i))\). The set \(\mathsf {seed}(T^+_\mathsf {ex}, \emptyset )\) contains among others the statement \(f_1\), \(f_2\), \(f_3\), and \(f_4\) given below:
where \(w_0\) is given in Example 7, and \(w^5_0\) is the prefix of \(w_0\) of size 5.
Statement \(f_1\) expresses that the trace is executable (in the relaxed semantics) as soon as we are able to deduce the two terms requested in input, \(f_2\) says that the attacker knows the term u as soon as \(T_0\) has been executed. The two remaining statements model the fact that an attacker can apply the decryption algorithm on any terms he knows (statement \(f_3\)), and this will give him access to the plaintext when the right key is used (statement \(f_4\)).
4.3 Soundness and Completeness
We now show that as far as the timing constraints are ignored, the set \(\mathsf {seed}(T)\) is a sound and complete abstraction of a trace. Moreover, we have to ensure that the proof tree witnessing the existence of a given predicate in \(\mathcal {H}(\mathsf {seed}(T))\) matches with the relaxed execution we have considered. This is mandatory to establish the completeness of our procedure.
Definition 4
Given a set K of statements, \(\mathcal {H}(K)\) is the smallest set of ground facts such that:

Let \(B_i = \mathsf {k}_{w_i}(X_i,u_i)\) for \(i \in \{1, \ldots , n\}\), and \(w_0\) the world associated to H with \(v_1, \ldots , v_{k'}\) the terms occurring in input in \(w_0\). We say that such an instance of Conseq matches with  using \(R_1, \ldots , R_k\) as input recipes if \(w_0\sigma \sqsubseteq \ell _1, \ldots , \ell _p\), and there exist \(\hat{R}_1, \ldots , \hat{R}_{k'}\) such that:
using \(R_1, \ldots , R_k\) as input recipes if \(w_0\sigma \sqsubseteq \ell _1, \ldots , \ell _p\), and there exist \(\hat{R}_1, \ldots , \hat{R}_{k'}\) such that:
-
\(\hat{R}_j(\{X_i \rightarrow u_i~|~1 \le i\le n\} \uplus \phi (w_0))\mathord {\downarrow }= v_j\) for \(j \in \{1, \ldots , k'\}\); and
-
\(\hat{R}_j\sigma = R_i\) for \(j \in \{1, \ldots , k'\}\).
This notion of matching is extended to a proof tree \(\pi \) as expected, meaning that all the instances of Conseq used in \(\pi \) satisfy the property.
Actually, the completeness of our procedure will be established w.r.t. a subset of recipes, namely uniform recipes. We establish that an execution of a trace \(T_0\) which only involves uniform recipes has a counterpart in \(\mathcal {H}(\mathsf {seed}(T_0))\) which is uniform too.
Definition 5
Given a frame \(\phi \), a recipe R is uniform w.r.t. \(\phi \) if for any \(R_1, R_2 \in st (R)\) such that \(R_1\phi \mathord {\downarrow }= R_2\phi \mathord {\downarrow }\), we have that \(R_1 = R_2\).
Given a set K of statements, we say that a set \(\{\pi _1,\ldots ,\pi _n\}\) of proof trees in \(\mathcal {H}(K)\) is uniform if for any \(\mathsf {k}_{w}(R_1,t)\) and \(\mathsf {k}_{w}(R_2,t)\) that occur in \(\{\pi _1, \ldots , \pi _n\}\), we have that \(R_1 = R_2\).
We are now able to state our soundness and completeness result.
Theorem 1
Let \(T_0\) be a trace locally closed w.r.t. \(\mathcal {X}\).
-
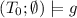 for any \(g\in \mathsf {seed}(T_0) \cup \mathcal {H}(\mathsf {seed}(T_0))\);
for any \(g\in \mathsf {seed}(T_0) \cup \mathcal {H}(\mathsf {seed}(T_0))\); -
If
 with input recipes \(R_1, \ldots , R_k\) that are uniform w.r.t. \(\phi \) then
with input recipes \(R_1, \ldots , R_k\) that are uniform w.r.t. \(\phi \) then-
1.
\(\mathsf {r}_{\ell _1, \ldots , \ell _p} \in \mathcal {H}(\mathsf {seed}(T_0))\); and
-
2.
if \(R\phi \mathord {\downarrow }= u\) for some recipe R uniform w.r.t. \(\phi \) then \(\mathsf {k}_{\ell _1, \ldots , \ell _p}(R, u) \in \mathcal {H}(\mathsf {seed}(T_0))\).
Moreover, we may assume that the proof tree witnessing these facts are uniform and match with \(\mathsf {exec}\) using \(R_1, \ldots , R_k\) as input recipes.
-
1.
5 Saturation
At a high level, our procedure consists of two steps:
-
1.
a saturation procedure which constructs a set of solved statements from the set \(\mathsf {seed}(T)\); and
-
2.
an algorithm which uses the solved statements obtained by saturation to check whether timing constraints are satisfied. This is needed to ensure that the execution obtained at step 1 is truly executable in our timed model.
5.1 Saturation Procedure
We start by describing our saturation procedure. It manipulates a set of statements called a knowledge base.
Definition 6
Given a statement \(f=(H \Leftarrow B_1, \ldots , B_n)\),
-
f is said to be solved if \(B_i = \mathsf {k}_{w_i}(X_i, x_i)\) with \(x_i \in \mathcal {X}\) for all \(i \in \{1, \ldots , n\}\).
-
f is said to be well-formed if whenever it is solved and \(H = \mathsf {k}_{w}(R, u)\), we have that \(u \not \in \mathcal {X}\).
A set of well-formed statements is called a knowledge base. If K is a knowledge base, \(\mathsf {solved}(K) = \{ f \in K \mid f \, is\, solved \}\).
We restrict the use of the resolution rule and we only apply it on a selected atom. To formalise this, we assume a selection function \(\mathsf {sel}\) which returns \(\bot \) when applied on a solved statement, and an atom \(\mathsf {k}_w(X,t)\) with \(t \not \in \mathcal {X}\) when applied on an unsolved statement. Resolution must be performed on this selected atom.

Example 10
Applying resolution between \(f_4\) and \(f_2\) (see Example 9), we obtain:
Then, we will derive \(\mathsf {k}_{T_0 \cdot \mathsf {y}}(\mathsf {adec}(\mathsf {w}_3,\mathsf {w}_2),\langle \gamma , \mathsf {sign}(\gamma ,sk_p)\rangle ) \Leftarrow \) and this solved statement (with others) will be used to perform resolution on \(f_1\) leading (after several resolution steps) to the statement:
Ultimately, we will derive \(\mathsf {r}_{T_0 \cdot w_0\sigma ' \cdot (v,\mathsf {test})} \Leftarrow \;\;\;\) with \(\sigma ' = \{x' \rightarrow \gamma \}\).
During saturation, the statement obtained by resolution is given to an update function which decides whether it has to be added or not into the knowledge base (possibly after some transformations). In original Akiss, many deduction statements are discarded during the saturation procedure. This is useful to avoid non-termination issues and it is not a problem since there is no need to derive the same term (from the deduction point of view) in more than one way. Now, considering that messages need time to reach a destination, a same message emitted twice at two different locations deserves more attention.
Example 11
Let \(T= (a_1,\mathsf {out}(k)).(a_2,\mathsf {out}(k)).(b,\mathsf {in}^{z}(x)).(b,[x = k]).(b, z < 2)\), and \(\mathcal {T}_0\) be a topology such that \(\textsf {Dist}_{\mathcal {T}_0}(a_1,b) = 10\) while \(\textsf {Dist}_{\mathcal {T}_0}(a_2,b) = 1\). The configuration \((T;\emptyset ;0)\) is executable but only considering \(\mathsf {w}_2\) as an input recipe for x. The recipe \(\mathsf {w}_1\) that produces the exact same term k is not an option (even if it is outputted before \(\mathsf {w}_2\)) since the agent \(a_1\) who outputs it is far away from b.
Whereas the original Akiss procedure will typically discard the statement \(\mathsf {k}(\mathsf {w}_2,k) \Leftarrow \;\) (by replacing it with an identical statement), we will keep it.
As illustrated by Example 11, we therefore need to consider more recipes (even if they deduce the same message) to accommodate timing constraints, but we have to do this in a way that does not break termination (in practice). To tackle this issue, we modified the canonicalization rule, as well as the update function to allow more deduction statements to be added in the knowledge base.
Definition 7
The canonical form \(f\mathord {\Downarrow }\) of a statement \(f = (H \Leftarrow B_1,\ldots , B_n)\) is the statement obtained by applying the Remove rule given below as many times as possible.

The intuition is that there is no need to consider several recipes (here X and Y) to deduce the same term t when such a recipe does not occur in the head of the statement.
Then, the update of K by f denoted \(K \Cup \{f\}\), is defined to be K if either \(\mathsf {skl}(f\mathord {\Downarrow })\) is not in normal form; or \(f\mathord {\Downarrow }\) is solved but not well-formed. Otherwise, \(K \Cup \{f\} = K \cup \{f\mathord {\Downarrow }\}\). To initiate our saturation procedure, we start with the initial knowledge base \(K_{\mathsf {init}}(S)\) associated to a set S of statements (typically \(\mathsf {seed}(T,\mathcal {C})\) for some well-chosen \(\mathcal {C}\)). Given a set S of statements, the initial knowledge base associated to S, denoted \(K_\mathsf {init}(S)\), is defined to be the empty knowledge base updated by the set S, i.e. \(K_\mathsf {init}(S) = (((\emptyset \Cup f_1) \Cup f_2) \Cup \ldots f_n\) where \(f_1, \ldots , f_n\) is an enumeration of the statements in S. In return, the saturation procedure produces a set \(\mathsf {sat}(K)\) which is actually a knowledge base.
Then, we can establish the soundness of our saturation procedure. This is relatively straightforward and follows the same lines as the original proof.
Proposition 1
Let \(T_0\) be a trace locally closed w.r.t. \(\mathcal {X}\), \(K = \mathsf {sat}(K_\mathsf {init}(T_0))\). We have that \((T_0;\emptyset ) \models g\) for any \(g\in \mathsf {solved}(K) \cup \mathcal {H}(\mathsf {solved}(K))\).
5.2 Completeness
Completeness is more involved. Indeed, we can not expect to retrieve all the recipes associated to a given term. To ensure termination (in practice) of our procedure, we discard some statements when updating the knowledge base, and we have to justify that those statements are indeed useless. Actually, we show that considering uniform recipes is sufficient when looking for an attack trace.
However, the notion of uniform recipe does not allow one to do the proof by induction. We therefore consider a more restricted notion that we call asap recipes. The idea is to deduce a term as soon as possible but this may depend on the agent who is performing the computation. We also rely on an ordering relation which is independent of the agent who is performing the computation, and which is compatible with our notion of asap w.r.t. any agent.
Given a relaxed execution  with input recipes \(R_1, \ldots , R_k\), we define the following relations:
with input recipes \(R_1, \ldots , R_k\), we define the following relations:
-
\(R <^{\mathsf {in}}_\mathsf {exec}\mathsf {w}\) when \(\ell _i = a, \mathsf {in}(u)\) with input recipe R and \(\ell _j = a, \mathsf {out}(u_j)\) with output recipe \(\mathsf {w}\) for some agent a with \(i < j\);
-
\(R' <^{\mathsf {sub}}_\mathsf {exec}R\) when \(R'\) is a strict subterm of R.
Then, \(<_{\mathsf {exec}}\) is the smallest transitive relation over recipes built on \( dom (\phi )\) that contains \(<^{\mathsf {in}}_\mathsf {exec}\) and \(<^{\mathsf {sub}}_\mathsf {exec}\). As usual, we denote \(\le _\mathsf {exec}\) the reflexive closure of \(<_\mathsf {exec}\).
Given a timed execution \(\mathsf {exec}= (T_0;\emptyset ;t_0) \xrightarrow {\ell _1,\ldots , \ell _n} (S;\varPhi ;t)\) with \(\varPhi = \{\mathsf {w}_1 \xrightarrow {a_1,t_1} u_1, \ldots , \mathsf {w}_n \xrightarrow {a_n,t_n} u_n\}\), we denote by \(\mathsf {agent}(\mathsf {w}_i)\) (resp. \(\mathsf {time}(\mathsf {w}_i)\)) the agent \(a_i\) (resp. the time \(t_i\)). The relation \(<^a_{\mathsf {exec}} \) over \( dom (\varPhi ) \times dom (\varPhi )\) with \(a \in \mathcal {A}\) is defined as follows: \(\mathsf {w}<^a_\mathsf {exec}\mathsf {w}' \) when:
-
either \(\mathsf {time}(\mathsf {w}) + \textsf {Dist}_{\mathcal {T}}(\mathsf {agent}(\mathsf {w}),a) < \mathsf {time}(\mathsf {w}') + \textsf {Dist}_{\mathcal {T}}(\mathsf {agent}(\mathsf {w}'),a)\);
-
or \(\mathsf {time}(\mathsf {w}) + \textsf {Dist}_{\mathcal {T}}(\mathsf {agent}(\mathsf {w}),a) = \mathsf {time}(\mathsf {w}') + \textsf {Dist}_{\mathcal {T}}(\mathsf {agent}(\mathsf {w}'),a)\), and the output \(\mathsf {w}\) occurs before \(\mathsf {w}'\) in the execution \(\mathsf {exec}\).
This order is extended on recipes as follows: \(R <^a_\mathsf {exec}R'\) when:
-
1.
either \(\mathsf {multi}_\mathcal {W}(R) <^a_\mathsf {exec}\mathsf {multi}_\mathcal {W}(R')\) where \(\mathsf {multi}_\mathcal {W}(R)\) is the multiset of variables \(\mathcal {W}\) occurring in R ordered using the multiset extension of \(<^a_\mathsf {exec}\) on variables;
-
2.
or \(\mathsf {multi}_\mathcal {W}(R) = \mathsf {multi}_\mathcal {W}(R')\) and \(|R| < |R'|\) where |R| is the size (number of symbols) occurring in R;
-
3.
or \(\mathsf {multi}_\mathcal {W}(R) = \mathsf {multi}_\mathcal {W}(R')\), \(|R| = |R'|\), and \(| st _\mathsf {eq}(R)| < | st _\mathsf {eq}(R')|\) where \( st _\mathsf {eq}(R)=\{(S,S')\in st (R) \times st (R) ~|~ S \ne S'\, \text { and }\, S\varPhi \mathord {\downarrow }= S'\varPhi \mathord {\downarrow }\}\) is the set of pairs of distinct syntactic subterms of R that deduce the same term.
We have that \(<_\mathsf {exec}^a\) is a well-founded order for any \(a\in \mathcal {A}\) which is compatible with \(<_\mathsf {exec}\), i.e. \(R <_\mathsf {exec}R'\) implies \(R <^a_\mathsf {exec}R'\) for any agent a.
We are now able to introduce our notion of asap recipe.
Definition 8
Let \(\mathcal {T}=(\mathcal {A}, \mathcal {M}, \mathsf {Loc})\) be a topology, and \(\mathsf {exec}= (T_0;\emptyset ;t_0) \xrightarrow {\ell _1,\ldots , \ell _n} (S;\varPhi ;t)\) be an execution. A recipe R is asap w.r.t. \(a\in \mathcal {A}\) and \(\mathsf {exec}\) if:
-
either \(R \in \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\cup \mathcal {W}\) and \(\not \exists R'\) such that \(R'<_\mathsf {exec}R\) and \(R'\varPhi \mathord {\downarrow }= R\varPhi \mathord {\downarrow }\);
-
or \(R = \mathsf {f}(R_1,\ldots , R_k)\) with \(\mathsf {f}\in \varSigma \) and \(\not \exists R'\) such that \(R' <^a_\mathsf {exec}R\) and \({R'\varPhi \mathord {\downarrow }= R\varPhi \mathord {\downarrow }}\).
We may note that our definition of being asap takes care about honest agents who are not allowed to forge messages from their knowledge using recipes not in \(\mathcal {W}\cup \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\). Hence, a recipe \(R \in \mathcal {W}\) is not necessarily replaced by a recipe \(R'\) even if \(R <^a_\mathsf {exec}R'\) and \({R'\varPhi \mathord {\downarrow }= R\varPhi \mathord {\downarrow }}\). Actually, such a recipe \(R'\) is not necessarily an alternative to R when \(a \not \in \mathcal {M}_0\).
Then, we can establish completeness of our saturation procedure w.r.t. these asap recipes.
Theorem 2
Let \(K = \mathsf {solved}(\mathsf {sat}(K_\mathsf {init}(T_0)))\). Let \(\mathsf {exec}= (T_0;\emptyset ;t_0) \xrightarrow {\ell _1, \ldots , \ell _p} (S;\varPhi ;t)\) be an execution with input recipes \(R_1, \ldots , R_k\) forged by \(b_1,\ldots , b_k\) and such that each \(R_j\) with \(j\in \{1,\ldots , k\}\) is asap w.r.t. \(b_j\) and \(\mathsf {exec}\). We have that:
-
\(\mathsf {r}_{\ell _1, \ldots , \ell _p} \in \mathcal {H}(K)\) with a proof tree matching \(\mathsf {exec}\) and \(R_1, \ldots , R_k\);
-
\(\mathsf {k}_{u_0}(R, R\phi \mathord {\downarrow }) \in \mathcal {H}(K)\) with a proof tree matching \(\mathsf {exec}\) and \(R_1, \ldots , R_k\) whenever \(u_0 = \ell _1,\ldots , \ell _{q-1}\) for some \(q\in \mathsf {Rcv}(p)\) and R is asap w.r.t. \(b_{|\mathsf {Rcv}(q)|}\) and \(\mathsf {exec}\).
Proof
(sketch). We have that asap recipes are uniform and we can therefore apply Theorem 1. This allows us to obtain a proof tree in \(\mathcal {H}(\mathsf {seed}(T_0))\). Then, by induction on the proof tree, we lift it from \(\mathcal {H}(\mathsf {seed}(T_0))\) to \(\mathcal {H}(K)\). The difficult part is when the statement obtained by resolution is not directly added in the knowledge base. It may have been modified by the rule Remove or even discarded by the update operator. In both cases, we derive a contradiction with the fact that we are considering asap recipes. \(\square \)
Example 12
Considering the relaxed execution starting from \((T_0 \cdot T_\mathsf {ex}, \emptyset )\) by performing the three outputs followed by the untimed version of the execution described in Example 6, we reach \((\epsilon ,\phi )\) using recipes \(R_1 = \mathsf {aenc}(\mathsf {adec}(\mathsf {w}_3,\mathsf {w}_2), \mathsf {w}_1)\) and \(R_2 = \mathsf {h}(\mathsf {w}_5,\mathsf {w}_4,\mathsf {proj}_1(\mathsf {adec}(\mathsf {w}_3,\mathsf {w}_2)))\). Let K be the set of solved statements obtained by saturation, we have that \(\mathsf {r}_{T_0 \cdot w_0\sigma ' \cdot (v,\mathsf {test})} \in \mathcal {H}(K)\) (see Example 10). Note that the symbolic run \(T_0 \cdot w_0\sigma ' \cdot (v,\mathsf {test})\) coincides with the labels used in the execution trace. Here, the proof tree is reduced to a leaf, and choosing \(\hat{R}_1 = R_1\), \(\hat{R}_2 = R_2\), gives us the matching we are looking for.
6 Algorithm
In this section, we first present our algorithm to verify whether a given timed configuration can be fully executed, and then discuss its correctness.
6.1 Description
Our procedure is given in Algorithm 1. We start with the set K of solved statements obtained by applying our saturation procedure on the trace T. We consider each reachability statement in K, and after instantiating the remaining variables with fresh constants using a bijection \(\rho \), we compute for each input \((a_i, \mathsf {in}(v_i))\) occurring in \(\ell '_1 \ldots , \ell '_n\) all the possible recipes that may lead to the term \(v_i\rho \) and store them in the set \(\overline{L_i}\). Actually, thanks to our soundness result (Proposition 1), we know that these recipes deduce the requested terms, and it only remains to check that the timing constraints are satisfied (lines 10–11).

We consider a trace T of the form \((a_1, \mathsf {a}_1).(a_2,\mathsf {a}_2).\ldots .(a_n,\mathsf {a}_n)\) locally closed w.r.t. \(\mathcal {X}\) and \(\mathcal {Z}\) and we assume the naming convention given in Sect. 4.2. Moreover, we denote by \(\mathsf {orig}(j)\) the index of the action in the trace T that performed the jth output, i.e. \(\mathsf {orig}(j)\) is the minimal k such that \(|\mathsf {Snd}(k)|=j\). The function \(\mathsf{Timing}\) takes as inputs the initial configuration, the recipes used to feed the inputs occurring in the trace, and the terms corresponding to these inputs. Note that all these terms may still contain variables from \(\mathcal {Z}\). This function computes a formula that represents all the timing constraints that have to be satisfied to ensure the executability of the trace in our timed model. More formally, \(\mathsf{Timing}((T;\emptyset ;t_0)), R_{i_1} \ldots R_{i_p}, u_{i_1} \ldots u_{i_p})\) is the conjunction of the formulas:
-
1.
\(z_1= t_0\), and \(z_i \le z_{i+1}\) for any \(1 \le i < n\);
-
2.
\(t_i \sim t'_i\) for any \(i \in \mathsf {Test}(n)\) with \(\mathsf {a}_i = [\![t_i \sim t'_i]\!]\);
-
3.
\(z'_i = v_i\{x_j \rightarrow u_j \mid j \in \mathsf {Rcv}(i)\}\mathord {\downarrow }\) for any \(i \in \mathsf {Let}(n)\);
-
4.
For any \(i \in \mathsf {Rcv}(n)\), we consider the formula:
-
\(z_{\mathsf {orig}(j)} + \textsf {Dist}_{\mathcal {T}_0}(a_{\mathsf {orig}(j)},a_i) \le z_i\) if \(R_i = \mathsf {w}_j\);
-
otherwise, we consider:
$$\begin{aligned} \bigvee \nolimits _{b \in \mathcal {M}_0} \big (\bigwedge \nolimits _{\{j \mid \mathsf {w}_j \in vars (R_i)\}} z_{\mathsf {orig}(j)} + \textsf {Dist}_{\mathcal {T}_0}(a_{\mathsf {orig}(j)},b) \le z_i - \textsf {Dist}_{\mathcal {T}_0}(b,a_i) \;\big ) \end{aligned}$$
-
The last step of our algorithm consists in checking whether the resulting formula \(\psi \) is satisfiable or not, i.e. whether there exists a mapping from \( vars (\psi )\) to \(\mathbb {R}^+\) such that the formula \(\psi \) is true. Of course, even if our procedure is generic w.r.t. to timing constraints, the procedure to check the satisfiability of \(\psi \) will depend on the constraints we consider. Actually, all the formulas encountered during our case studies are quite simple: they are expressed by equations of the form \(z' - z \le t\), and we therefore rely on the well-known Floyd-Warshall algorithm to solve them. When needed, we may rely on the simplex algorithm to solve more general linear constraints.
6.2 Termination Issues
First, we may note that to obtain an effective saturation procedure, it is important to start with a finite set of seed statements. Our set \(\mathsf {seed}(T)\) is infinite but as it was proved in [12], we can restrict ourselves to perform saturation using the finite set \(\mathsf {seed}(T,\mathcal {C}_T)\) where \(\mathcal {C}_T\) contains the public names and the real numbers occurring in the trace T. More formally, we have that:
Lemma 1
Let \(\mathcal {C}_T\) be the finite set of public names and real numbers occurring in T, and \(\mathcal {C}_{all} = \mathcal {N}_\mathsf {pub}\cup \mathbb {R}^+\). We have that:
Nevertheless, the saturation may not terminate. We could probably avoid some non-termination issues by improving our update operator. However, ensuring termination in theory is a rather difficult problem (the proof of termination for the original Akiss procedure for subterm convergent theories is quite complex [12] – more than 20 pages). We would like to mention that we never encountered non-termination issues in practice on our case studies.
Another issue is that, when computing the set \(\overline{L_i}\), we need to compute all the recipes R such that \(\mathsf {k}_w(R,u) \in \mathcal {H}(K)\) for a given term u. This can be achieved using a simple backward search and will terminate since K only contains solved statements that are well-formed. The naive recursive algorithm will therefore consider terms \(u_1, \ldots , u_n\) that are strict subterms of the initial term u. Note that statements that are not well-formed are discarded by our update operator: ensuring completeness of our saturation procedure when discarding statements that are not well-formed is the challenging part of our completeness proof.
6.3 Correctness of Our Algorithm
We consider a topology \(\mathcal {T}_0\) and a configuration \((T;\emptyset ;t_0)\) built on top of \(\mathcal {T}_0\) and such that T is locally closed w.r.t. both \(\mathcal {X}\) and \(\mathcal {Z}\).
Theorem 3
Let \(\mathcal {C}_T \subseteq \mathcal {N}_\mathsf {pub}\uplus \mathbb {R}^+\) be the finite set of public names and real numbers occurring in T. Let \(K = \mathsf {solved}(\mathsf {sat}(K_\mathsf {init}(\mathsf {seed}(T,\mathcal {C}_T))))\). We have that:
-
if Reachability\((K,t_0,\mathcal {T}_0)\) holds then \((T;\emptyset ;t)\) is executable in \(\mathcal {T}_0\);
-
if \((T;\emptyset ;t_0)\) is executable in \(\mathcal {T}_0\) then Reachability\((K,t_0,\mathcal {T}_0)\) holds.
Soundness (item 1 above) is relatively straightforward. Item 2 is more involved. Of course, our algorithm does not consider all the possible recipes for inputs. Some recipes are discarded from our analysis. Actually, it is sufficient to focus our attention on asap recipes. To justify that this is not an issue regarding completeness, we first establish the following result.
Lemma 2
Let \(\mathsf {exec}= K_0 \xrightarrow {\ell _1, \ldots , \ell _n}_{\mathcal {T}_0} (S; \varPhi ;t)\) be an execution. We may assume w.l.o.g. that \(\mathsf {exec}\) involves input recipes \(R_1,\ldots , R_k\) forged by agents \(b_1,\ldots , b_k\) and \(R_i\) is asap w.r.t. \(b_i\) and \(\mathsf {exec}\) for each \(i \in \{1, \ldots , k\}\).
Then, we may apply Theorem 2 (item 1) on this “asap execution” and deduce the existence of \(f = \mathsf {r}_{\ell '_1, \ldots , \ell '_n} \Leftarrow \mathsf {k}_{w_1}(X_1, x_1), \ldots , \mathsf {k}_{w_m}(X_m,x_m)\) in K and a substitution \(\sigma \) witnessing the fact that \(\mathsf {r}_{\ell _1, \ldots , \ell _n} = \mathsf {r}_{\ell '_1\sigma , \ldots , \ell '_n\sigma }\in \mathcal {H}(K)\). Moreover, we know that f and \(\sigma \) match with \(\mathsf {exec}\) and \(R_1, \ldots , R_k\). Considering the symbolic recipes \(\hat{R}_1, \ldots , \hat{R}_k\) witnessing this matching, and instantiating their variables with adequate fresh constants (using \(\rho \)), we can show that \(\hat{R}_1\rho , \ldots , \hat{R}_k\rho \) are recipes that allow to perform the timed execution \(\ell '_1\rho , \ldots , \ell '_n\rho \). Note that thanks the strong relationship we have between \(R_1, \ldots , R_k\) and \(\hat{R_1}, \ldots , \hat{R_k}\) (by definition of matching, \(R_i = \hat{R_i}\sigma \)), we know that the resulting timing constraints gathered in the formula \(\psi \) due to inputs are less restrictive, and the other ones are essentially unchanged. This allows us to ensure that the formula \(\psi \) will be satisfiable. Now, applying Lemma 2, we can assume w.l.o.g. that recipes involved in such a trace are asap, and thus according to Theorem 2 will be considered by our procedure, and put in \(\overline{L_{i_1}}, \ldots , \overline{L_{i_p}}\) at line 6 of Algorithm 1.
7 Implementation and Case Studies
We validate our approach by integrating our procedure in Akiss [12], and successfully used it on several case studies. All files related to the tool implementation and case studies are available at
7.1 Integration in Akiss
Our syntax is very close to the one presented in Sect. 3. For sake of simplicity, we sometimes omit timestamps on input/output actions. Regarding our timing constraints, our syntax only allows linear expressions of the form \(z_1 - z_2 \sim z_3\) with \(z_i\in \mathcal {Z}\cup \mathbb {R}^+\) and \(\sim \ \in \{=,<, \le \}\). These expressions are enough to model all our case studies. To ease the specification of protocols our tool support parallel composition of traces (\(T_1 \mid \mid T_2\)). This operator is syntactic sugar and can be translated to sets of traces in a straightforward way.
To mitigate the potential exponential blowup caused by this translation, we always favour let, equality, and test actions, as well as output actions when no timestamp occur on it. The second optimisation consists in executing input actions (without timestamps) in a raw. These optimisations will allow us to reduce the number of traces that have to be considered during our analysis, and are well-known to be sound when verifying reachability properties [4, 30].
Example 13
Let \(P = (a, \mathsf {in}(x_1)).(a,\mathsf {in}(x_2).(a,\mathsf {out}(u)) \mid \mid (b, \mathsf {in}(x_3)).(b,\mathsf {out}(v))\). Computing naively all the possible interleavings will give us 10 traces to analyse. The first optimisation will allow us to reduce this number to 3, and together with the second optimisation, this number falls to 2.
7.2 Case Studies
In this section we demonstrate that our tool can be effectively used to analyse distance bounding protocols and payment protocols. Our experiments have been done on a standard laptop and the results obtained confirm termination of the saturation procedure when analysing various protocols (\(\times \) stands for attack,  means that the protocol has been proved secure). We indicate the number of roles (running in parallel) we consider and the number of traces (due to all the possible interleaving of the roles) that have been analysed by the tool in order to conclude. Our algorithm stops as soon as an attack is found, and thus the number of possible interleavings is not relevant in this case.
means that the protocol has been proved secure). We indicate the number of roles (running in parallel) we consider and the number of traces (due to all the possible interleaving of the roles) that have been analysed by the tool in order to conclude. Our algorithm stops as soon as an attack is found, and thus the number of possible interleavings is not relevant in this case.
We only consider two distinct topologies: one to analyse mafia fraud scenarios (2 honest agents far away with a malicious agent close to each honest agent) and one to analyse distance hijacking for which 3 agents are considered (malicious agent in the neighbourhood of the verifier on which the security property is encoded is not allowed). This may seem restrictive but it has been shown to be sufficient to capture all the possible attacks [19]. Our results are consistent with the ones obtained in [13, 14, 19, 26].
Distance Bounding Protocols. As explained in Sect. 2 on the TREAD protocol, we ignore several details that are irrelevant to a security analysis performed in the symbolic model. Moreover, our procedure is not yet able to support the exclusive-or operator and thus it has been modelled in an abstract way when analysing the protocols BC and Swiss-Knife. When no attack was found for 2 roles, we consider more roles (and thus more traces). The fact that the performances degrade when considering additional roles is not surprising and is clearly correlated with the number of traces that have to be considered.
Payment Protocols. We have also analysed three payment protocols (and some of their variants) w.r.t. mafia fraud – the only relevant scenario for this kind of application (see [13]). It happens that these protocols are more complex to analyse than traditional distance bounding protocols. They often involve more complex messages, and a larger number of message exchanges. Moreover, in protocols MasterCard RRP and NXP, the threshold is not fixed in advance but received during the protocol execution. Due to this, these protocols fall outside the class of protocols that can be analysed by [19, 26]. To our knowledge only [13] copes with this issue by proposing a security analysis in two steps: they first establish that the value of the threshold can not be manipulated by the attacker, and then analyse the protocol considering a fixed threshold. Such a protocol can be encoded in a natural way in our calculus using the let instruction \([z := v]\) that allows one to extract a timing information from a message. We analysed these protocols considering one instance of each role.
Protocol | Mafia fraud | Distance hijacking | ||||
|---|---|---|---|---|---|---|
roles/tr | time | status | roles/tr | time | status | |
TREAD-Asym [2] | 2/− | 1 s | \(\times \) | 2/− | 1 s | \(\times \) |
SPADE [11] | 2/− | 2 s | \(\times \) | 2/− | 4 s | \(\times \) |
TREAD-Sym [2] | 4/7500 | 18 min |
| 2/− | 1 s | \(\times \) |
BC [10] | 4/5635 | 37 min |
| 2/− | 1 s | \(\times \) |
Swiss-Knife [25] | 3/1080 | 25 s |
| 3/7470 | 4 min |
|
HK [23] | 3/20 | 1 s |
| 3/20 | 1 s |
|
4/3360 | 58 s |
| 4/3360 | 47 s |
| |
5/30240 | 14 min |
| 5/30240 | 12 min |
| |
8 Conclusion
We presented a novel procedure for reasoning about distance bounding protocols which has been integrated in the Akiss tool. Even though termination is not guaranteed, the tool did terminate on all practical examples that we have tested.
Directions for future work include improving performances of our tool and this can be achieved by parallelising our algorithm (each trace can actually be analysed independently) and/or proposing new techniques to reduce the number of interleavings. Another interesting direction would be to add the exclusive-or operator which is often used in distance bounding protocols. This will require a careful analysis of the completeness proof developed in [3] to check whether their resolution strategy is compatible with the changes done here to accommodate timing constraints.
References
Abadi, M., Fournet, C.: Mobile values, new names, and secure communication. In: Proceedings of the 28th Symposium on Principles of Programming Languages (POPL 2001), pp. 104–115. ACM Press (2001)
Avoine, G., et al.: A terrorist-fraud resistant and extractor-free anonymous distance-bounding protocol. In: Proceedings of the 12th ACM Asia Conference on Computer and Communications Security (AsiaCCS 2017), pp. 800–814. ACM (2017)
Baelde, D., Delaune, S., Gazeau, I., Kremer, S.: Symbolic verification of privacy-type properties for security protocols with XOR. In: 2017 IEEE 30th Computer Security Foundations Symposium (CSF), pp. 234–248. IEEE (2017)
Baelde, D., Delaune, S., Hirschi, L.: A reduced semantics for deciding trace equivalence. Log. Methods Comput. Sci. 13(2), 1–48 (2017)
Basin, D., Capkun, S., Schaller, P., Schmidt, B.: Formal reasoning about physical properties of security protocols. ACM Trans. Inf. Syst. Secur. (TISSEC) 14(2), 16 (2011)
Basin, D.A., Mödersheim, S., Viganò, L.: OFMC: a symbolic model checker for security protocols. Int. J. Inf. Secur. 4(3), 181–208 (2005)
Bhargavan, K., Blanchet, B., Kobeissi, N.: Verified models and reference implementations for the TLS 1.3 standard candidate. In: Proceedings of the 38th IEEE Symposium on Security and Privacy (S&P 2017), pp. 483–502 (2017)
Blanchet, B.: Modeling and verifying security protocols with the applied pi calculus and ProVerif. Found. Trends Priv. Secur. 1(1–2), 1–135 (2016)
Blanchet, B.: Symbolic and computational mechanized verification of the ARINC823 avionic protocols. In: Proceedings of the 30th IEEE Computer Security Foundations Symposium (CSF 2017), pp. 68–82. IEEE (2017)
Brands, S., Chaum, D.: Distance-bounding protocols. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 344–359. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48285-7_30
Bultel, X., Gambs, S., Gerault, D., Lafourcade, P., Onete, C., Robert, J.: A prover-anonymous and terrorist-fraud resistant distance-bounding protocol. In: Proceedings of the 9th ACM Conference on Security & Privacy in Wireless and Mobile Networks, WISEC 2016, Darmstadt, Germany, 18–22 July 2016, pp. 121–133. ACM (2016)
Chadha, R., Cheval, V., Ciobâcă, Ş., Kremer, S.: Automated verification of equivalence properties of cryptographic protocol. ACM Trans. Comput. Logic 23(4), 23:1–23:32 (2016)
Chothia, T., de Ruiter, J., Smyth, B.: Modelling and analysis of a hierarchy of distance bounding attacks. In: Proceedings of the 27th USENIX Security Symposium (USENIX 2018), pp. 1563–1580. USENIX Association (2018)
Chothia, T., Garcia, F.D., de Ruiter, J., van den Breekel, J., Thompson, M.: Relay cost bounding for contactless EMV payments. In: Böhme, R., Okamoto, T. (eds.) FC 2015. LNCS, vol. 8975, pp. 189–206. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47854-7_11
Comon-Lundh, H., Cortier, V., Zălinescu, E.: Deciding security properties for cryptographic protocols. Application to key cycles. ACM Trans. Comput. Logic 11(2), 9 (2010)
Comon-Lundh, H., Delaune, S.: The finite variant property: how to get rid of some algebraic properties. In: Giesl, J. (ed.) RTA 2005. LNCS, vol. 3467, pp. 294–307. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-32033-3_22
Cremers, C., Horvat, M., Hoyland, J., Scott, S., van der Merwe, T.: A comprehensive symbolic analysis of TLS 1.3. In: Proceedings of the 24th ACM Conference on Computer and Communications Security (CCS 2017), pp. 1773–1788 (2017)
Debant, A., Delaune, S.: Symbolic verification of distance bounding protocols. Research report, Univ Rennes, CNRS, IRISA, France, February 2019
Debant, A., Delaune, S., Wiedling, C.: A symbolic framework to analyse physical proximity in security protocols. In: Proceedings of the 38th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2018). LIPICS (2018)
Dolev, D., Yao, A.: On the security of public key protocols. IEEE Trans. Inf. theory 29(2), 198–208 (1983)
Durgin, N., Lincoln, P., Mitchell, J., Scedrov, A.: Undecidability of bounded security protocols. In: Proceedings of the Workshop on Formal Methods and Security Protocols (FMSP 1999), Trento, Italy (1999)
EMVCo: EMV contactless specifications for payment systems, version 2.6 (2016)
Hancke, G.P., Kuhn, M.G.: An RFID distance bounding protocol. In: Proceedings of the 1st International Conference on Security and Privacy for Emerging Areas in Communications Networks (SECURECOMM 2005), pp. 67–73. IEEE (2005)
Janssens, P.: Proximity check for communication devices. US Patent 9,805,228, 31 October 2017
Kim, C.H., Avoine, G., Koeune, F., Standaert, F.-X., Pereira, O.: The Swiss-Knife RFID distance bounding protocol. In: Lee, P.J., Cheon, J.H. (eds.) ICISC 2008. LNCS, vol. 5461, pp. 98–115. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00730-9_7
Mauw, S., Smith, Z., Toro-Pozo, J., Trujillo-Rasua, R.: Distance-bounding protocols: verification without time and location. In: Proceedings of the 39th IEEE Symposium on Security and Privacy (S&P 2018), pp. 152–169 (2018)
Meadows, C., Poovendran, R., Pavlovic, D., Chang, L., Syverson, P.: Distance bounding protocols: authentication logic analysis and collusion attacks. In: Poovendran, R., Roy, S., Wang, C. (eds.) Secure Localization and Time Synchronization for Wireless Sensor and Ad Hoc Networks. ADIS, vol. 30, pp. 279–298. Springer, Boston (2007). https://doi.org/10.1007/978-0-387-46276-9_12
Meier, S., Schmidt, B., Cremers, C., Basin, D.: The TAMARIN prover for the symbolic analysis of security protocols. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 696–701. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_48
Millen, J., Shmatikov, V.: Constraint solving for bounded-process cryptographic protocol analysis. In: Proceedings of the 8th ACM Conference on Computer and Communications Security (CCS 2001). ACM Press (2001)
Mödersheim, S., Viganò, L., Basin, D.A.: Constraint differentiation: search-space reduction for the constraint-based analysis of security protocols. J. Comput. Secur. 18(4), 575–618 (2010)
Nigam, V., Talcott, C., Aires Urquiza, A.: Towards the automated verification of cyber-physical security protocols: bounding the number of timed intruders. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 450–470. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_23
Rusinowitch, M., Turuani, M.: Protocol insecurity with a finite number of sessions and composed keys is NP-complete. Theoret. Comput. Sci. 299(1–3), 451–475 (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Debant, A., Delaune, S. (2019). Symbolic Verification of Distance Bounding Protocols. In: Nielson, F., Sands, D. (eds) Principles of Security and Trust. POST 2019. Lecture Notes in Computer Science(), vol 11426. Springer, Cham. https://doi.org/10.1007/978-3-030-17138-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-17138-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17137-7
Online ISBN: 978-3-030-17138-4
eBook Packages: Computer ScienceComputer Science (R0)








 if there exists
if there exists 
 if for all
if for all 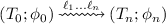 we have that
we have that 
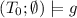 for any
for any  with input recipes
with input recipes 












