Abstract
Checked C is a new effort working toward a memory-safe C. Its design is distinguished from that of prior efforts by truly being an extension of C: Every C program is also a Checked C program. Thus, one may make incremental safety improvements to existing codebases while retaining backward compatibility. This paper makes two contributions. First, to help developers convert existing C code to use so-called checked (i.e., safe) pointers, we have developed a preliminary, automated porting tool. Notably, this tool takes advantage of the flexibility of Checked C’s design: The tool need not perfectly classify every pointer, as required of prior all-or-nothing efforts. Rather, it can make a best effort to convert more pointers accurately, without letting inaccuracies inhibit compilation. However, such partial conversion raises the question: If safety violations can still occur, what sort of advantage does using Checked C provide? We draw inspiration from research on migratory typing to make our second contribution: We prove a blame property that renders so-called checked regions blameless of any run-time failure. We formalize this property for a core calculus and mechanize the proof in Coq.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Vulnerabilities that compromise memory safety are at the heart of many attacks. Spatial safety, one aspect of memory safety, is ensured when any pointer dereference is always within the memory allocated to that pointer. Buffer overruns violate spatial safety, and still constitute a common cause of vulnerability. During 2012–2018, buffer overruns were the source of 9.7% to 18.4% of CVEs reported in the NIST vulnerability database [27], constituting the leading single cause of CVEs.
The source of memory unsafety starts with the language definitions of C and C++, which render out-of-bounds pointer dereferences “undefined.” Traditional compilers assume they never happen. Many efforts over the last 20 years have aimed for greater assurance by proving that accesses are in bounds, and/or preventing out-of-bounds accesses from happening via inserted dynamic checks [1,2,3,4,5,6,7,8,9,10, 12, 15, 16, 18, 22, 25, 26, 29]. This paper focuses on Checked C, a new, freely availableFootnote 1 language design for a memory-safe C [11], currently focused on spatial safety. Checked C draws substantial inspiration from prior safe-C efforts but differs in two key ways, both of which focus on backward compatibility with, and incremental improvement of, regular C code.
Mixing Checked and Legacy Pointers. First, as outlined in Sect. 2, Checked C permits intermixing checked (safe) pointers and legacy pointers. The former come in three varieties: pointers to single objects  ; pointers to arrays
; pointers to arrays  , and NUL-terminated arrays
, and NUL-terminated arrays  . The latter two have an associated clause that describes their known length in terms of constants and other program variables. The specified length is used to either prove pointer dereferences are safe or, barring that, serves as the basis of dynamic checks inserted by the compiler.
. The latter two have an associated clause that describes their known length in terms of constants and other program variables. The specified length is used to either prove pointer dereferences are safe or, barring that, serves as the basis of dynamic checks inserted by the compiler.
Importantly, checked pointers are represented as in normal C—no changes to pointer structure (e.g., by “fattening” a pointer to include its bounds) are imposed. As such, interoperation with legacy C is eased. Moreover, the fact that checked and legacy pointers can be intermixed in the same module eases the porting process, including porting via automated tools. For example, CCured [26] works by automatically classifying existing pointers and compiling them for safety. This classification is necessarily conservative. For example, if a function  is mostly called with safe pointers, but once with an unsafe one (e.g., a “wild” pointer in CCured parlance, perhaps constructed from an
is mostly called with safe pointers, but once with an unsafe one (e.g., a “wild” pointer in CCured parlance, perhaps constructed from an  ), then the classification of
), then the classification of  as unsafe will propagate backwards, poisoning the classification of the safe pointers, too. The programmer will be forced to change the code and/or pay a higher cost for added (but unnecessary) run-time checks.
as unsafe will propagate backwards, poisoning the classification of the safe pointers, too. The programmer will be forced to change the code and/or pay a higher cost for added (but unnecessary) run-time checks.
On the other hand, in the Checked C setting, if a function uses a pointer safely then its parameter can be typed that way. It is then up to a caller whose pointer arguments cannot also be made safe to insert a local cast. Section 5 presents a preliminary, whole-program analysis called checked-c-convert that utilizes the extra flexibility afforded by mixing pointers to partially convert a C program to a Checked C program. On a benchmark suite of five programs totaling more than 200K LoC, we find that thousands of pointer locations are made more precise than would have been if using a more conservative algorithm like that of CCured. The checked-c-convert tool is distributed with the publicly available Checked C codebase.
Avoiding Blame with Checked Regions. An important question is what “safety” means in a program with a mix of checked and unchecked pointers. In such a program, safety violations are still possible. How, then, does one assess that a program is safer due to checking some, but not all, of its pointers? Providing a formal answer to this question constitutes the core contribution of this paper.
Unlike past safe-C efforts, Checked C specifically distinguishes parts of the program that are and may not be fully “safe.” So-called checked regions differ from unchecked ones in that they can only use checked pointers—dereference or creation of unchecked pointers, unsafe casts, and other potentially dangerous constructs are disallowed. Using a core calculus for Checked C programs called CoreChkC, defined in Sect. 3, we prove in Sect. 4 these restrictions are sufficient to ensure that checked code cannot be blamed. That is, checked code is internally safe, and any run-time failure can be attributed to unchecked code, even if that failure occurs in a checked region. This proof has been fully mechanized in the Coq proof assistant.Footnote 2 Our theorem fills a gap in the literature on migratory typing for languages that, like Checked C, use an erasure semantics, meaning that no extra dynamic checks are inserted at checked/unchecked code boundaries [14]. Moreover, our approach is lighter weight than the more sophisticated techniques used by the RustBelt project [17], and constitutes a simpler first step toward a safe, mixed-language design. We say more in Sect. 6.
2 Overview of Checked C
We begin by describing the approach to using Checked C and presenting a brief overview of the language extensions, using the example in Fig. 1. For more about the language see Elliott et al. [11]. The approach works as follows:
-
1.
Programmers start with an existing unsafe C program and annotated header files for existing C libraries. The annotations describe the expected behavior of functions with respect to bounds.
-
2.
The programmers run a porting tool that modifies the unsafe C program to use the Checked C extensions. The tool identifies simple cases where
 can be used. This lets the programmers focus on pointers that need bounds declarations or that are used unsafely.
can be used. This lets the programmers focus on pointers that need bounds declarations or that are used unsafely. -
3.
The programmers add bounds declarations and checked regions to the remaining code. The programmers work incrementally, which lets the program be compiled and tested as it gradually becomes safer.
-
4.
The programmers use a C compiler extended to handle the Checked C extension to compile the program. The compiler inserts runtime null and bounds checks and optimizes them out if it can.
-
5.
At runtime, if a null check or bounds check fails, a runtime error is signaled and the process is terminated.
The programmers repeat steps 3–5 until as much code as possible (ideally, the entire program) has been made safe.
Checked Pointers. As mentioned in the introduction, Checked C supports three varieties of checked (safe) pointers: pointers to single objects  ; pointers to arrays
; pointers to arrays  , and NUL-terminated arrays
, and NUL-terminated arrays  . The
. The  field of
field of  , defined in Fig. 1(b), is an
, defined in Fig. 1(b), is an  ; its length is specified by
; its length is specified by  field in the same
field in the same  , as indicated by the
, as indicated by the  annotation.
annotation.  types are similar. The
types are similar. The  argument of the
argument of the  function in Fig. 1(c) is
function in Fig. 1(c) is  . This function overwrites the contents of
. This function overwrites the contents of  with those in the second argument
with those in the second argument  , an array whose length is specified by the third argument,
, an array whose length is specified by the third argument,  . Variables with checked pointer types or containing checked pointers must be initialized when they are declared.
. Variables with checked pointer types or containing checked pointers must be initialized when they are declared.
Checked Arrays. Checked C also supports a checked array type, which is designated by prefixing the dimension of an array declaration with the keyword  . For example,
. For example,  declares a 5-element integer array where accesses are always bounds checked. A checked array of \(\tau \) implicitly converts to an
declares a 5-element integer array where accesses are always bounds checked. A checked array of \(\tau \) implicitly converts to an  when accessing it. In our example, the array
when accessing it. In our example, the array  has an unchecked array type because the
has an unchecked array type because the  keyword is omitted.
keyword is omitted.
Checked and Unchecked Regions. Returning to  : If
: If  is too small (
is too small ( ) to hold the contents of
) to hold the contents of  , the function allocates a block from the static
, the function allocates a block from the static  array, whose free area starts at index
array, whose free area starts at index  . Designating a checked
. Designating a checked  from a pointer into the middle of the (unchecked) region array is not allowed in checked code, so it must be done within the designated
from a pointer into the middle of the (unchecked) region array is not allowed in checked code, so it must be done within the designated  block. Within such blocks the programmer has the full freedom of C, along with the ability to create and use checked pointers. Checked code, as designated by the
block. Within such blocks the programmer has the full freedom of C, along with the ability to create and use checked pointers. Checked code, as designated by the  annotation (e.g., as on the
annotation (e.g., as on the  function or on a block nested within unchecked code) may not use unchecked pointers or arrays. It also may not define or call functions without prototypes and variable argument functions.
function or on a block nested within unchecked code) may not use unchecked pointers or arrays. It also may not define or call functions without prototypes and variable argument functions.
Interface Types. Once  has allocated
has allocated  it calls
it calls  to transfer the data into it, from
to transfer the data into it, from  . Checked C permits normal C functions, such as those in an existing library, to be given an interface type. This is the type that Checked C code should use in a checked region. In an unchecked region, either the original type or the interface type may be used. This allows the function to be called with unchecked types or checked types. For
. Checked C permits normal C functions, such as those in an existing library, to be given an interface type. This is the type that Checked C code should use in a checked region. In an unchecked region, either the original type or the interface type may be used. This allows the function to be called with unchecked types or checked types. For  , this type is shown in Fig. 1(a).
, this type is shown in Fig. 1(a).
Interface types can also be attached to definitions within a Checked C file, not just prototypes declared for external libraries. Doing so permits the same function to be called from an unchecked region (with either checked or unchecked types) or a checked region (there it will always have the checked type). For example, if we wanted  to be callable from unchecked code with unchecked pointers, we could define its prototype as
to be callable from unchecked code with unchecked pointers, we could define its prototype as

Implementation Details. Checked C is implemented as an extension to the Clang/ LLVM compiler.Footnote 3 The clang front-end inserts run-time checks for the evaluation of lvalue expressions whose results are derived from checked pointers and that will be used to access memory. Accessing a  requires a null check, while accessing an
requires a null check, while accessing an  requires both null and bounds checks. The code for these checks is handed to the LLVM backend, which will remove checks if it can prove they will always pass. In general, such checks are the only source of Checked C run-time overhead. Preliminary experiments on some small, pointer-intensive benchmarks show running time overhead to be around 8.6%, on average [11].
requires both null and bounds checks. The code for these checks is handed to the LLVM backend, which will remove checks if it can prove they will always pass. In general, such checks are the only source of Checked C run-time overhead. Preliminary experiments on some small, pointer-intensive benchmarks show running time overhead to be around 8.6%, on average [11].
3 Formalism: CoreChkC
This section presents a formal language CoreChkC that models the essence of Checked C. The language is designed to be simple but nevertheless highlight Checked C’s key features: checked and unchecked pointers, and checked and unchecked code blocks. We prove our key theoretical result—checked code cannot be blamed for a spatial safety violation—in the next section.
3.1 Syntax
The syntax of CoreChkC is presented in Fig. 2. Types \(\tau \) classify word-sized objects while types \(\omega \) also include multi-word objects. The type \(\mathtt {ptr}^{m}{\omega }\) types a pointer, where m identifies its mode: mode c identifies a Checked C safe pointer, while mode u represents an unchecked pointer. In other words \(\mathtt {ptr}^{c}{\tau }\) is a checked pointer type  while \(\mathtt {ptr}^{u}{\tau }\) is an unchecked pointer type \(\tau \)
while \(\mathtt {ptr}^{u}{\tau }\) is an unchecked pointer type \(\tau \)  . Multiword types \(\omega \) include \(\mathtt {struct}\) records, and arrays of type \(\tau \) having size n, i.e., \(\mathtt {ptr}^{c}{\mathtt {array}~{n}~{\tau }}\) represents a checked array pointer type
. Multiword types \(\omega \) include \(\mathtt {struct}\) records, and arrays of type \(\tau \) having size n, i.e., \(\mathtt {ptr}^{c}{\mathtt {array}~{n}~{\tau }}\) represents a checked array pointer type  with bounds n. We assume \(\mathtt {struct}\)s are defined separately in a map D from struct names to their constituent field definitions.
with bounds n. We assume \(\mathtt {struct}\)s are defined separately in a map D from struct names to their constituent field definitions.
Programs are represented as expressions e; we have no separate class of program statements, for simplicity. Expressions include (unsigned) integers \(n^\tau \) and local variables x. Constant integers n are annotated with type \(\tau \) to indicate their intended type. As in an actual implementation, pointers in our formalism are represented as integers. Annotations help formalize type checking and the safety property it provides; they have no effect on the semantics except when \(\tau \) is a checked pointer, in which case they facilitate null and bounds checks. Variables x, introduced by let-bindings \(\mathtt {let}~x\, =\, e_1~\mathtt {in}\;{e_2}\), can only hold word-sized objects, so all \(\mathtt {struct}\)s can only be accessed by pointers.
Checked pointers are constructed using \(\mathtt {malloc}@{\omega }\), where \(\omega \) is the type (and size) of the allocated memory. Thus, \(\mathtt {malloc}@{\mathtt {int}}\) produces a pointer of type \(\mathtt {ptr}^{c}{\mathtt {int}}\) while \(\mathtt {malloc}@{(\mathtt {array}~{10}~{\mathtt {int}})}\) produces one of type \(\mathtt {ptr}^{c}{(\mathtt {array}~{10}~{\mathtt {int}})}\). Unchecked pointers can only be produced by the cast operator, \(\mathtt {(}{\tau }\mathtt {)}{e}\), e.g., by doing \(\mathtt {(}{\mathtt {ptr}^{u}{\mathtt {int}}}\mathtt {)}{\mathtt {malloc}@{\mathtt {int}}}\). Casts can also be used to coerce between integer and pointer types and between different multi-word types.
Pointers are read via the \(\mathtt {*}\) operator, and assigned to via the \(\mathtt {=}\) operator. To read or write \(\mathtt {struct}\) fields, a program can take the address of that field and read or write that address, e.g., \({x}\mathtt {\rightarrow }{f}\) is equivalent to \( \mathtt {*}{(\mathtt { \& }{x}\mathtt {\rightarrow }{f})}\). To read or write an array, the programmer can use pointer arithmetic to access the desired element, e.g., \(x\mathtt {[}i\mathtt {]}\) is equivalent to \(\mathtt {*}{(x + i)}\).
By default, CoreChkC expressions are assumed to be checked. Expression e in \(\mathtt {unchecked}\;{e}\) is unchecked, giving it additional freedom: Checked pointers may be created via casts, and unchecked pointers may be read or written.
Design Notes. CoreChkC leaves out many interesting C language features. We do not include an operation for freeing memory, since this paper is concerned about spatial safety, not temporal safety. CoreChkC models statically sized arrays but supports dynamic indexes; supporting dynamic sizes is interesting but not meaningful enough to justify the complexity it would add to the formalism. Making \(\mathtt {int}\)s unsigned simplifies handling pointer arithmetic. We do not model control operators or function calls, whose addition would be straightforward.Footnote 4 CoreChkC does not have a \(\mathtt {checked}\) e expression for nesting within \(\mathtt {unchecked}\) expressions, but supporting it would be easy.
3.2 Semantics
Figure 4 defines the small-step operational semantics for CoreChkC expressions in the form of judgment \(H; e \longrightarrow ^m H; r\). Here, H is a heap, which is a partial map from integers (representing pointer addresses) to type-annotated integers \(n^\tau \). Annotation m is the mode of evaluation, which is either c for checked mode or u for unchecked mode. Finally, r is a result, which is either an expression e, \(\mathtt {Null}\) (indicating a null pointer dereference), or \(\mathtt {Bounds}\) (indicating an out-of-bounds array access). An unsafe program execution occurs when the expression reaches a stuck state—the program is not an integer \(n^\tau \), and yet no rule applies. Notably, this could happen if trying to dereference a pointer n that is actually invalid, i.e., H(n) is undefined.
The semantics is defined in the standard manner using evaluation contexts E. We write \(E[e_0]\) to mean the expression that results from substituting \(e_0\) into the “hole” (\(\_\)) of context E. Rule C-Exp defines normal evaluation. It decomposes an expression e into a context E and expression \(e_0\) and then evaluates the latter via \(H; e_0 \leadsto H'; e_0'\), discussed below. The evaluation mode m is constrained by the \( mode (E)\) function, also given in Fig. 4. The rule and this function ensure that when evaluation occurs within e in some expression \(\mathtt {unchecked}~e\), then it does so in unchecked mode u; otherwise it may be in checked mode c. Rule C-Halt halts evaluation due to a failed null or bounds check.
The rules prefixed with E- are those of the computation semantics \(H; e_0 \leadsto H'; e_0'\). The semantics is implicitly parameterized by struct map D. The rest of this section provides additional details for each rule, followed by a discussion of CoreChkC ’s type system.
Rule E-Binop produces an integer \(n_3\) that is the sum of arguments \(n_1\) and \(n_2\). As mentioned earlier, the annotations \(\tau \) on literals \(n^\tau \) indicate the type the program has ascribed to n. When a type annotation is not a checked pointer, the semantics ignores it. In the particular case of E-Binop for example, addition \(n_1^{\tau _1} + n_2^{\tau _2}\) ignores \(\tau _1\) and \(\tau _2\) when \(\tau _1\) is not a checked pointer, and simply annotates the result with it. However, when \(\tau \) is a checked pointer, the rules use it to model bounds checks; in particular, dereferencing \(n^\tau \) where \(\tau \) is \(\mathtt {ptr}^{c}{(\mathtt {array}~{l}~{\tau _0})}\) produces \(\mathtt {Bounds}\) when \(l=0\) (more below). As such, when \(n_1\) is a non-zero, checked pointer to an array and \(n_2\) is an \(\mathtt {int}\), result \(n_3\) is annotated as a pointer to an array with its bounds suitably updated.Footnote 5 Checked pointer arithmetic on 0 is disallowed; see below.
Rules E-Deref and E-Assign confirm the bounds of checked array pointers: the length l must be positive for the dereference to be legal. The rule permits the program to proceed for non-checked or non-array pointers (but the type system will forbid them).
Rule E-Amper takes the address of a \(\mathtt {struct}\) field, according to the type annotation on the pointer, as long the pointer is not zero or not checked.
Rule E-Malloc allocates a checked pointer by finding a string of free heap locations and initializing each to 0, annotated to the appropriate type. Here, types(\(D,\omega \)) returns k types, where these are the types of the corresponding memory words; e.g., if \(\omega \) is a \(\mathtt {struct}\) then these are the types of its fields (looked up in D), while if \(\omega \) is an array of length k containing values of type \(\tau \), then we will get back k \(\tau \)’s. We require \(k \not = 0\) or the program is stuck (a situation precluded by the type system).
Rule E-Let uses a substitution semantics for local variables; notation \(e[x \mapsto n^\tau ]\) means that all occurrences of x in e should be replaced with \(n^\tau \).
Rule E-Unchecked returns the result of an unchecked block.
Rules with prefix X- describe failures due to bounds checks and null checks on checked pointers. These are analogues to the E-Assign, E-Deref, E-Binop, and E-Amper cases. The first two rules indicate a bounds violation for size-zero array pointers. The next two indicate an attempt to dereference a null pointer. The last two indicate an attempt to construct a checked pointer from a null pointer via field access or pointer arithmetic.
3.3 Typing
The typing judgment  says that expression e has type \(\tau \) under environment \(\varGamma \) and scope \(\sigma \) when in mode m. A scope \(\sigma \) is an additional environment consisting of a set of literals; it is used to type cyclic structures (in Rule T-PtrC, below) that may arise during program evaluation. The heap H and struct map D are implicit parameters of the judgment; they do not appear because they are invariant in derivations. \(\mathtt {unchecked}\) expressions are typed in mode u; otherwise we may use either mode.
says that expression e has type \(\tau \) under environment \(\varGamma \) and scope \(\sigma \) when in mode m. A scope \(\sigma \) is an additional environment consisting of a set of literals; it is used to type cyclic structures (in Rule T-PtrC, below) that may arise during program evaluation. The heap H and struct map D are implicit parameters of the judgment; they do not appear because they are invariant in derivations. \(\mathtt {unchecked}\) expressions are typed in mode u; otherwise we may use either mode.
\(\varGamma \) maps variables x to types \(\tau \), and is used in rules T-Var and T-Let as usual. Rule T-Base ascribes type \(\tau \) to literal \(n^\tau \). This is safe when \(\tau \) is \(\mathtt {int}\) (always). If \(\tau \) is an unchecked pointer type, a dereference is only allowed by the type system to be in unchecked code (see below), and as such any sort of failure (including a stuck program) is not a safety violation. When n is 0 then \(\tau \) can be anything, including a checked pointer type, because dereferencing n would (safely) produce \(\mathtt {Null}\). Finally, if \(\tau \) is \(\mathtt {ptr}^{c}{(\mathtt {array}~{0}~{\tau '})}\) then dereferencing n would (safely) produce \(\mathtt {Bounds}\).
Rule T-PtrC is perhaps the most interesting rule of CoreChkC. It ensures checked pointers of type \(\mathtt {ptr}^{c}{\omega }\) are consistent with the heap, by confirming the pointed-to heap memory has types consistent with \(\omega \), recursively. When doing this, we extend \(\sigma \) with \(n^\tau \) to properly handle cyclic heap structures; \(\sigma \) is used by RuleT-VConst.
To make things more concrete, consider the following program that constructs a cyclic cons cell, using a standard single-linked list representation:

After executing the program above, the heap would look something like the following, where n is the integer value of p. That is, the n-th location of the heap contains 0 (the default value for field \( val \) picked by \(\mathtt {malloc}\)), while the \((n+1)\)-th location, which corresponds to field \( next \), contains the literal n.

How can we type the pointer \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) in this heap without getting an infinite typing judgment?

That’s where the scope comes in, to break the recursion. In particular, using Rule T-PtrC and \(\mathtt {struct}~node\)’s definition, we would need to prove two things:

Since \(H(n+0) = 0\), as \(\mathtt {malloc}\) zeroes out its memory, we can trivially prove the first goal using Rule T-Base. However, the second goal is almost exactly what we set out to prove in the first place! If not for the presence of the scope \(\sigma \), the proof the n is typeable would be infinite! However, by adding \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) to the scope, we are essentially assuming it is well-typed to type its contents, and the desired result follows by Rule T-VConst.Footnote 6
A key feature of T-PtrC is that it effectively confirms that all pointers reachable from the given one are consistent; it says nothing about other parts of the heap. So, if a set of checked pointers is only reachable via unchecked pointers then we are not concerned whether they are consistent, since they cannot be directly dereferenced by checked code.
Back to the remaining rules, T-Amper and T-BinopInt are unsurprising. Rule T-Malloc produces checked pointers so long as the pointed-to type \(\omega \) is not zero-sized, i.e., is not \(\mathtt {array}~{0}~{\tau }\). Rule T-Unchecked introduces unchecked mode, relaxing access rules. Rule T-Cast enforces that checked pointers cannot be cast targets in checked mode.
Rules T-Deref and T-Assign type pointer accesses. These rules require unchecked pointers only be dereferenced in unchecked mode. Rule T-Index permits reading a computed pointer to an array, and rule T-IndAssign permits writing to one. These rules are not strong enough to permit updating a pointer to an array after performing arithmetic on it. In general, Checked C’s design permits overcoming such limitations through selective use of casts in unchecked code. (That said, our implementation is more flexible in this particular case.)
4 Checked Code Cannot Be Blamed
Our main formal result is that well-typed programs will never fail with a spatial safety violation that is due to a checked region of code, i.e., checked code cannot be blamed. This section presents the main result and outlines its proof. We have mechanized the full proof using the Coq proof assistant. The development is roughly 3500 lines long, including comments. It is freely available at https://github.com/plum-umd/checkedc/tree/master/coq.
4.1 Progress and Preservation
The blame theorem is proved using the two standard syntactic type-safety notions of Progress and Preservation, adapted for CoreChkC . Progress indicates that a (closed) well-typed program either is a value, can take a step (in either mode), or else is stuck in unchecked code. A program is in unchecked mode if its expression e only type checks in mode u, or its (unique) context E has mode u.
Theorem 1
(Progress). If  (under heap H) then one of the following holds:
(under heap H) then one of the following holds:
-
e is an integer \(n^\tau \)
-
There exists \(H'\), \(m'\), and r such that \(H; e \longrightarrow ^{m'} H'; r\) where r is either some \(e'\), \(\mathtt {Null}\), or \(\mathtt {Bounds}\).
-
\(m=u\) or \(e = E[e'']\) and \( mode (E) = u\) for some \(E, e''\).
Preservation indicates that if a well-typed program in checked mode takes a checked step then the resulting program is also well-typed in checked mode.
Theorem 2
(Preservation). If  (under a heap H) and \(H; e \longrightarrow ^{c} H'; r\) (for some \(H', r\)), then and \(r = e'\) implies \(H \vartriangleright H'\) and
(under a heap H) and \(H; e \longrightarrow ^{c} H'; r\) (for some \(H', r\)), then and \(r = e'\) implies \(H \vartriangleright H'\) and  (under heap \(H'\)).
(under heap \(H'\)).
We write \(H \vartriangleright H'\) to mean that for all \(n^\tau \) if  under H then
under H then  under \(H'\) as well.
under \(H'\) as well.
The proofs of both theorems are by induction on the typing derivation. The Preservation proof is the most delicate, particularly ensuring \(H \vartriangleright H'\) despite the creation or modification of cyclic data structures. Crucial to the proof were two lemmas dealing with the scope, weakening and strengthening.
The first lemma, scope weakening, allows us to arbitrarily extend a scope with any literal \(n_0^{\tau _0}\).
Lemma 1
(Weakening). If  then
then  , for all \(n_0^{\tau _0}\).
, for all \(n_0^{\tau _0}\).
Intuitively, this lemma holds because if a proof of  relies on the rule T-VConst, then that \(n_1^{\tau _1}\in \sigma \) for some \(n_1^{\tau _1}\). But then \(n_1^{\tau _1}\in (\sigma , n_0^{\tau _0})\) as well. Importantly, the scope \(\sigma \) is a set of \(n^\tau \) and not a map from n to \(\tau \). As such, if \(n'^{\tau '}\) is already present in \(\sigma \), adding \(n'^{\tau _0'}\) will not clobber it. Allowing the same literal to have multiple types is of practical importance. For example a pointer n to a struct could be annotated with the type of the struct, or the type of the first field of the struct, or \(\mathtt {int}\); all may safely appear in the environment.
relies on the rule T-VConst, then that \(n_1^{\tau _1}\in \sigma \) for some \(n_1^{\tau _1}\). But then \(n_1^{\tau _1}\in (\sigma , n_0^{\tau _0})\) as well. Importantly, the scope \(\sigma \) is a set of \(n^\tau \) and not a map from n to \(\tau \). As such, if \(n'^{\tau '}\) is already present in \(\sigma \), adding \(n'^{\tau _0'}\) will not clobber it. Allowing the same literal to have multiple types is of practical importance. For example a pointer n to a struct could be annotated with the type of the struct, or the type of the first field of the struct, or \(\mathtt {int}\); all may safely appear in the environment.
Consider the proof that \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) is well typed for the heap given in Sect. 3.3. After applying Rule T-PtrC, we used the fact that \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}} \in \sigma , n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) to prove that the \( next \) field of the struct is well typed. If we were to replace \(\sigma \) with another scope \(\sigma , n_0^{\tau _0}\) for some typed literal \(n_0^{\tau _0}\) (and as a result any scope that is a superset of \(\sigma \)), the inclusion \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}} \in \sigma , n_0^{\tau _0}, n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) still holds and our pointer is still well-typed.
Conversely, the second lemma, scope strengthening, allows us to remove a literal from a scope, if that literal is well typed in an empty context.
Lemma 2
(Strengthening). If  and
and  , then
, then  .
.
Informally, if the fact that \(n_2^{\tau _2}\) is in the scope is used in the proof of well-typedness of \(n_1^{\tau _1}\) to prove that \(n_2^{\tau _2}\) is well-typed for some scope \(\sigma \), then we can just use the proof that it is well-typed in an empty scope, along with weakening, to reach the same conclusion.
Looking back again at the proof of the previous section, we know that

While the proof of the latter fact relies on \(n^{\mathtt {ptr}^{c}{\mathtt {struct}~{node}}}\) being in scope, that would not be necessary if we knew (independently) that it was well-typed. That would essentially amount to unrolling the proof by one step.
4.2 Blame
With progress and preservation we can prove a blame theorem: Only unchecked code can be blamed as the ultimate reason for a stuck program.
Theorem 3
(Checked code cannot be blamed). Suppose  (under heap H) and there exists \(H_i\), \(m_i\), and \(e_i\) for \(1 \le i \le k\) such that \(H; e \longrightarrow ^{m_1} H_1; e_1 \longrightarrow ^{m_2} ... \longrightarrow ^{m_k} H_k; e_k \). If \(H_k; e_k\) is stuck then the source of the issue is unchecked code.
(under heap H) and there exists \(H_i\), \(m_i\), and \(e_i\) for \(1 \le i \le k\) such that \(H; e \longrightarrow ^{m_1} H_1; e_1 \longrightarrow ^{m_2} ... \longrightarrow ^{m_k} H_k; e_k \). If \(H_k; e_k\) is stuck then the source of the issue is unchecked code.
Proof
Suppose \(\cdot \vdash _{c} {e_k} : {\tau }\) (under heap \(H_k\)). By Progress, the only way the \(H_k; e_k\) can be stuck is if \(e_k = E[e'']\) and \( mode (E) = u\); i.e., the term’s redex is in unchecked code. Otherwise \(H_k; e_k\) is not well typed, i.e., \(\cdot \not \vdash _c e_k : \tau \) (under heap \(H_k\)). As such, one of the steps of the evaluation was in unchecked code, i.e., there must exist some i where \(1 \le i \le k\) and \(m_i = u\). This is because, by Preservation, a well-typed program in checked mode that takes a checked step always leads to a well-typed program in checked mode.
This theorem means that a code reviewer can focus on unchecked code regions, trusting that checked ones are safe.
5 Porting Assistance
Porting legacy code to use Checked C’s features can be tedious and time consuming. To assist the process, we developed a source-to-source translator called checked-c-convert that discovers some safely-used pointers and rewrites them to be checked. This algorithm is based on one used by CCured [26], but exploits Checked C’s allowance of mixing checked and unchecked pointers to make less conservative decisions.
The checked-c-convert translator works by (1) traversing a program’s abstract syntax tree (AST) to generate constraints based on pointer variable declaration and use; (2) solving those constraints; and (3) rewriting the program. These rewrites consist of promoting some declared pointer types to be checked, some parameter types to be bounds-safe interfaces, and inserting some casts. checked-c-convert aims to produce a well-formed Checked C program whose changes from the original are minimal and unsurprising. A particular challenge is to preserve syntactic structure of the program. A rewritten program should be recognizable by the author and it should be usable as a starting point for both the development of new features and additional porting. The checked-c-convert tool is implemented as a clang libtooling application and is freely available.
5.1 Constraint Logic and Solving
The basic approach is to infer a qualifier \(q_i\) for each defined pointer variable i. Inspired by CCured’s approach [26], qualifiers can be either  ,
,  and
and  , ordered as a lattice
, ordered as a lattice  . Those variables with inferred qualifier
. Those variables with inferred qualifier  can be rewritten into
can be rewritten into  types, while those with
types, while those with  are left as is. Those with the \( ARR \) qualifier are eligible to have
are left as is. Those with the \( ARR \) qualifier are eligible to have  type. For the moment we only signal this fact in a comment and do not rewrite because we cannot always infer proper bounds expressions.
type. For the moment we only signal this fact in a comment and do not rewrite because we cannot always infer proper bounds expressions.
Qualifiers are introduced at each pointer variable declaration, i.e., parameter, variable, field, etc. Constraints are introduced as a pointer is used, and take one of the following forms:
An expression that performs arithmetic on a pointer with qualifier \(q_i\), either via + or [], introduces a constraint \(q_{i} = ARR \). Assignments between pointers introduce aliasing constraints of the form \(q_{i} = q_{j}\). Casts introduce implication constraints based on the relationship between the sizes of the two types. If the sizes are not comparable, then both constraint variables in an assignment-based cast are constrained to \( UNK \) via an equality constraint. One difference from CCured is the use of negation constraints, which are used to fix a constraint variable to a particular Checked C type (e.g., due to an existing  annotation). These would cause problems for CCured, as they might introduce unresolvable conflicts. But Checked C’s allowance of checked and unchecked code can resolve them using explicit casts and bounds-safe interfaces, as discussed below.
annotation). These would cause problems for CCured, as they might introduce unresolvable conflicts. But Checked C’s allowance of checked and unchecked code can resolve them using explicit casts and bounds-safe interfaces, as discussed below.
One problem with unification-based analysis is that a single unsafe use might “pollute” the constraint system by introducing an equality constraint to \( UNK \) that transitively constrains unified qualifiers to \( UNK \) as well. For example, casting a  pointer to a
pointer to a  buffer to write to the network would cause all transitive uses of that pointer to be unchecked. The tool takes advantage of Checked C’s ability to mix checked and unchecked pointers to solve this problem. In particular, constraints for each function are solved locally, using separate qualifier variables for each external function’s declared parameters.
buffer to write to the network would cause all transitive uses of that pointer to be unchecked. The tool takes advantage of Checked C’s ability to mix checked and unchecked pointers to solve this problem. In particular, constraints for each function are solved locally, using separate qualifier variables for each external function’s declared parameters.
5.2 Algorithm
Our modular algorithm runs as follows:
-
1.
The AST for every compilation unit is traversed and constraints are generated based on the uses of pointer variables. Each pointer variable
 that appears at a physical location in the program is given a unique constraint variable \(q_i\) at the point of declaration. Uses of
that appears at a physical location in the program is given a unique constraint variable \(q_i\) at the point of declaration. Uses of  are identified with the constraint variable created at the point of declaration. A distinction is made for parameter and return variables depending on if the associated function definition is a declaration or a definition:
are identified with the constraint variable created at the point of declaration. A distinction is made for parameter and return variables depending on if the associated function definition is a declaration or a definition:-
Declaration: There may be multiple declarations. The constraint variables for the parameters and return values in the declarations are all constrained to be equal to each other. At call sites, the constraint variables used for a function’s parameters and return values come from those in the declaration, not the definition (unless there is no declaration).
-
Definition: There will only be one definition. These constraint variables are not constrained to be equal to the variables in the declarations. This enables modular (per function) reasoning.
-
-
2.
After the AST is traversed, the constraints are solved using a fast, unification-focused algorithm [26]. The result is a set of satisfying assignments for constraint variables \(q_i\).
-
3.
Then, the AST is re-traversed. At each physical location associated with a constraint variable, a re-write decision is made based on the value of the constraint variable. These physical locations are variable declaration statements, either as members of a
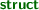 , function variable declarations, or parameter variable declarations. There is a special case, which is any constraint variable appearing at a parameter position, either at a function declaration/definition, or, a call site. That case is discussed in more detail next.
, function variable declarations, or parameter variable declarations. There is a special case, which is any constraint variable appearing at a parameter position, either at a function declaration/definition, or, a call site. That case is discussed in more detail next. -
4.
All of the re-write decisions are then applied to the source code.
5.3 Resolving Conflicts
Defining distinct constraint variables for function declarations, used at call-sites, and function definitions, used within that function, can result in conflicting solutions. If there is a conflict, then the declaration’s solution is safer than the definition, or the definition’s is safer than the declaration’s. Which case we are in can be determined by considering the relationship between the variables’ valuations in the qualifier lattice. There are three cases:
-
No imbalance: In this case, the re-write is made based on the value of the constraint variable in the solution to the unification.
-
Declaration (caller) is safer than definition (callee): In this case, there is nothing to do for the function, since the function does unknown things with the pointer. This case will be dealt with at the call site by inserting a cast.
-
Decalaration (caller) is less safe than definition (callee): In this case, there are call sites that are unsafe, but the function itself is fine. We can re-write the function declaration and definition with a bounds-safe interface.
Example: caller is safer than callee: Consider a function that makes unsafe use of the parameter within the body of the function, but a callee of the function passes an argument that is only ever used safely.

Here, we cannot make  safe since its use is outside Checked C’s type system. Relying on a unification-only approach, this fact would poison all arguments passed to
safe since its use is outside Checked C’s type system. Relying on a unification-only approach, this fact would poison all arguments passed to  too, i.e.,
too, i.e.,  in
in  . This is unfortunate, since
. This is unfortunate, since  is used safely inside of
is used safely inside of  . Our algorithm remedies this situation by doing the conversion and inserting a cast:
. Our algorithm remedies this situation by doing the conversion and inserting a cast:

The presence of the cast indicates to the programmer that perhaps there is something in  that should be investigated.
that should be investigated.
Example: caller less safe than callee: Now consider a function that makes safe use of the parameter within the body of the function, but a caller of the function might perform casts or other unsafe operations on an argument it passes.

If considered in isolation, the function  is safe and the parameter could be rewritten to
is safe and the parameter could be rewritten to  . However, it is used from an unsafe context. In an approach with pure unification, like CCured, this unsafe use at the call-site would pollute the classification at the definition. Our algorithm considers solutions and call sites and definitions independently. Here, the uses of
. However, it is used from an unsafe context. In an approach with pure unification, like CCured, this unsafe use at the call-site would pollute the classification at the definition. Our algorithm considers solutions and call sites and definitions independently. Here, the uses of  in
in  are less safe than those in the
are less safe than those in the  ’s definition so the rewriter would insert a bounds-safe interface for
’s definition so the rewriter would insert a bounds-safe interface for  :
:

The itype syntax indicates that  can be supplied by the caller as either an
can be supplied by the caller as either an  or a
or a  , but the function body will treat
, but the function body will treat  as a
as a  . (See Sect. 2 for more on interface types.)
. (See Sect. 2 for more on interface types.)
This approach has advantages and disadvantages. It favors making the fewest number of modifications across a project. An alternative to using interface types would be to change the parameter type to a  directly, and then insert casts at each call site. This would tell the programmer where potentially bogus pointer values were, but would also increase the number of changes made. Our approach does not immediately tell the programmer where the pointer changes need to be made. However, the Checked C compiler will do that if the programmer takes a bounds-safe interface and manually converts it into a non-interface
directly, and then insert casts at each call site. This would tell the programmer where potentially bogus pointer values were, but would also increase the number of changes made. Our approach does not immediately tell the programmer where the pointer changes need to be made. However, the Checked C compiler will do that if the programmer takes a bounds-safe interface and manually converts it into a non-interface  type. Every location that would require a cast will fail to type check, signaling to the programmer to have a closer look.
type. Every location that would require a cast will fail to type check, signaling to the programmer to have a closer look.
5.4 Experimental Evaluation
We carried out a preliminary experimental evaluation of the efficacy of checked-c-convert. To do so, we ran it on five targets—programs and libraries—and recorded how many pointer types the rewriter converted and how many casts were inserted. We chose these targets as they constitute legacy code used in commodity systems, and in security-sensitive contexts.
Running checked-c-convert took no more than 30 min to run, for each target. Table 1 contains the results. The first and last column indicate the target, its version, and the lines of code it contains (per cloc). The second column (\(\#\) of *) counts the number of pointer definitions or declarations in the program, i.e., places that might get rewritten when porting. The next three columns (\(\%\) _Ptr, Arr., Unk.) indicate the percentages of these that were determined to be PTR, ARR, or UNK, respectively, where only those in \(\%\) _Ptr induce a rewriting action. The results show that a fair number of variables can be automatically rewritten as safe, single pointers ( ). After investigation, there are usually two reasons that a pointer cannot be replaced with a
). After investigation, there are usually two reasons that a pointer cannot be replaced with a  : either some arithmetic is performed on the pointer, or it is passed as a parameter to a library function for which a bounds-safe interface does not exist.
: either some arithmetic is performed on the pointer, or it is passed as a parameter to a library function for which a bounds-safe interface does not exist.
The next two columns (Casts(Calls), Ifcs(Funcs)) examine how our rewriting algorithm takes advantage of Checked C’s support for incremental conversion. In particular, column 6 (Casts(Calls)) counts how many times we cast a safe pointer at the call site of a function deemed to use that pointer unsafely; in parentheses we indicate the total number of call sites in the program. Column 7 (Ifcs(Funcs)) counts how often a function definition or declaration has its type rewritten to use an interface type, where the total declaration/definition count is in parentheses. This rewriting occurs when the function itself uses at least one of its parameters safely, but at least one caller provides an argument that is deemed unsafe. Both columns together represent an improvement in precision, compared to unification-only, due to Checked C’s focus on backward compatibility.
This experiment represents the first step a developer would take to adopting Checked C into their project. The values converted into  by the re-writer need never be considered again during the rest of the conversion or by subsequent software assurance/bug finding efforts.
by the re-writer need never be considered again during the rest of the conversion or by subsequent software assurance/bug finding efforts.
6 Related Work
There has been substantial prior work that aims to address the vulnerability presented by C’s lack of memory safety. A detailed discussion of how this work compares to Checked C can be found in Elliott et al. [11]. Here we discuss approaches for automating C safety, as that is most related to work on our rewriting algorithm. We also discuss prior work generally on migratory typing, which aims to support backward compatible migration of an untyped/less-typed program to a statically typed one.
Security Mitigations. The lack of memory safety in C and C++ has serious practical consequences, especially for security, so there has been extensive research toward addressing it automatically. One approach is to attempt to detect memory corruption after it has happened or prevent an attacker from exploiting a memory vulnerability. Approaches deployed in practice include stack canaries [31], address space layout randomization (ASLR) [34], data-execution prevention (DEP), and control-flow integrity (CFI) [1]. These defenses have led to an escalating series of measures and counter-measures by attackers and defenders [32]. These approaches do not prevent data modification or data disclosure attacks, and they can be defeated by determined attackers who use those attacks. By contrast, enforcing memory safety avoids these issues.
Memory-Safe C. Another important line of prior work aims to enforce memory safety for C; here we focus on projects that aim to do so (mostly) automatically in a way related to our rewriting algorithm. CCured [26] is a source-to-source rewriter that transforms C programs to be safe automatically. CCured’s goal is end-to-end soundness for the entire program. It uses a whole-program analysis that divides pointers into fat pointers (which allow pointer arithmetic and unsafe casts) and thin pointers (which do not). The use of fat pointers causes problems interoperating with existing libraries and systems, making the CCured approach impractical when that is necessary. Other systems attempt to overcome the limitations of fat pointers by storing the bounds information in a separate metadata space [24, 25] or within unused bits in 64-bit pointers [19] (though this approach is unsound [13]). These approaches can add substantial overhead; e.g., Softbound’s overhead for spatial safety checking is 67%. Deputy [38] uses backward-compatible pointer representations with types similar to those in Checked C. It supports inference local to a function, but resorts to manual annotations at function and module boundaries. None of these systems permit intermixing safe and unsafe pointers within a module, as Checked C does, which means that some code simply needs to be rewritten rather than included but clearly marked within  blocks.
blocks.
Migratory Typing. Checked C is closely related to work supporting migratory typing [35] (aka gradual typing [30]). In that setting, portions of a program written in a dynamically typed language can be annotated with static types. For Checked C, legacy C plays the role of the dynamically typed language and checked regions play the role of statically typed portions. In migratory typing, one typically proves that a fully annotated program is statically type-safe. What about mixed programs? They can be given a semantics that checks static types at boundary crossings [21]. For example, calling a statically typed function from dynamically typed code would induce a dynamic check that the passed-in argument has the specified type. When a function is passed as an argument, this check must be deferred until the function is called. The delay prompted research on proving blame: Even if a failure were to occur within static code, it could be blamed on bogus values provided by dynamic code [36]. This semantics is, however, slow [33], so many languages opt for what Greenman and Felleisen [14] term the erasure semantics: No checks are added and no notion of blame is proved, i.e., failures in statically typed code are not formally connected to errors in dynamic code. Checked C also has erasure semantics, but Theorem 3 is able to lay blame with the unchecked code.
Rust. Rust [20] is a programming language, like C, that supports zero-cost abstractions, but like Checked C, aims to be safe. Rust programs may have designated  blocks in which certain rules are relaxed, potentially allowing run-time failures. As with Checked C, the question is how to reason about the safety of a program that contains any amount of unsafe code. The RustBelt project [17] proposes to use a semantic [23], rather than syntactic [37], account of soundness, in which (1) types are given meaning according to what terms inhabit them; (2) type rules are sound when interpreted semantically; and (3) semantic well typing implies safe execution. With this approach, unsafe code can be (manually) proved to inhabit the semantic interpretation of its type, in which case its use by type-checked code will be safe.
blocks in which certain rules are relaxed, potentially allowing run-time failures. As with Checked C, the question is how to reason about the safety of a program that contains any amount of unsafe code. The RustBelt project [17] proposes to use a semantic [23], rather than syntactic [37], account of soundness, in which (1) types are given meaning according to what terms inhabit them; (2) type rules are sound when interpreted semantically; and (3) semantic well typing implies safe execution. With this approach, unsafe code can be (manually) proved to inhabit the semantic interpretation of its type, in which case its use by type-checked code will be safe.
We view our approach as complementary to that of RustBelt, perhaps constituting the first step in mixed-language safety assurance. In particular, we employ a simple, syntactic proof that checked code is safe and unchecked code can always be blamed for a failure—no proof about any particular unsafe code is required. Stronger assurance that programs are safe despite using mixed code could employ the (more involved and labor-intensive) RustBelt approach.
7 Conclusions and Future Work
This paper has presented CoreChkC, a core formalism for Checked C, an extension to C aiming to provide spatial safety. CoreChkC models Checked C’s safe (checked) and unsafe (legacy) pointers; while these pointers can be intermixed, use of legacy pointers is severely restricted in checked regions of code. We prove that these restrictions are efficacious: checked code cannot be blamed in the sense that any spatial safety violation must be directly or indirectly due to an unsafe operation outside a checked region. Our formalization and proof are mechanized in the Coq proof assistant; this mechanization is available at https://github.com/plum-umd/checkedc/tree/master/coq.
The freedom to intermix safe and legacy pointers in Checked C programs affords flexibility when porting legacy code. We show this is true for automated porting as well. A whole-program rewriting algorithm we built is able to make more pointers safe than it would if pointer types were all-or-nothing; we do this by taking advantage of Checked C’s allowed casts and interface types. The tool implementing this algorithm, checked-c-convert, is distributed with Checked C at https://github.com/Microsoft/checkedc-clang.
As future work, we are interested in formalizing other aspects of Checked C, notably its subsumption algorithm and support for flow-sensitive typing (to handle pointer arithmetic), to prove that these aspects of the implementation are correct. We are also interested in expanding support for the rewriting algorithm, by using more advanced static analysis techniques to infer numeric bounds suitable for re-writing array types. Finally, we hope to automatically infer regions of code that could be enclosed within checked regions.
Notes
- 1.
- 2.
- 3.
- 4.
Function calls \(f(e')\) can be modeled by \(\mathtt {let}~x\, =\, e_1~\mathtt {in}\;{e_2}\), where we can view x as function f’s parameter, \(e_2\) as its body, and \(e_1\) as its actual argument. Calls to unchecked functions from checked code can thus be simulated by having an \(\mathtt {unchecked}\;{e}\) expression for \(e_2\).
- 5.
Here, \(l-n_2\) is natural number arithmetic: if \(n_2 > l\) then \(l-n_2 = 0\). This would have to be adjusted if the language contained subtraction, or else bounds information would be unsound.
- 6.
For readers familiar with coinduction [28], this proof technique is similar: to prove a coinductive property P one would assume P but need to use it productively in a subterm; similarly here, we can assume a pointer is well-typed when we attempt to type heap locations that are reachable from it.
References
Abadi, M., Budiu, M., Erlingsson, Ú., Ligatti, J.: Control-flow integrity. In: ACM Conference on Computer and Communications Security (2005)
Akritidis, P., Costa, M., Castro, M., Hand, S.: Baggy bounds checking: an efficient and backwards-compatible defense against out-of-bounds errors. In: Proceedings of the 18th Conference on USENIX Security Symposium (2009)
Austin, T.M., Breach, S.E., Sohi, G.S.: Efficient detection of all pointer and array access errors. In: SIGPLAN Not., vol. 29, no. 6, June 1994
Baratloo, A., Singh, N., Tsai, T.: Transparent run-time defense against stack smashing attacks. In: Proceedings of the Annual Conference on USENIX Annual Technical Conference (2000)
Bhatkar, S., DuVarney, D.C., Sekar, R.: Address obfuscation: an efficient approach to combat a broad range of memory error exploits. In: Proceedings of the 12th Conference on USENIX Security Symposium, vol. 12 (2003)
Condit, J., Hackett, B., Lahiri, S.K., Qadeer, S.: Unifying type checking and property checking for low-level code. In: POPL 2009: Proceedings of the 36th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. Association for Computing Machinery, New York (2009)
Condit, J., Harren, M., Anderson, Z., Gay, D., Necula, G.C.: Dependent types for low-level programming. In: Proceedings of European Symposium on Programming (ESOP 2007) (2007)
Cowan, C., et al.: Stackguard: automatic adaptive detection and prevention of buffer-overflow attacks. In: Proceedings of the 7th Conference on USENIX Security Symposium, vol. 7 (1998)
Dhurjati, D., Adve, V.: Backwards-compatible array bounds checking for C with very low overhead. In: Proceedings of the 28th International Conference on Software Engineering (2006)
Duck, G.J., Yap, R.H.C.: Heap bounds protection with low fat pointers. In: Proceedings of the 25th International Conference on Compiler Construction (2016)
Elliott, A.S., Ruef, A., Hicks, M., Tarditi, D.: Checked C: Making C safe by extension. In: Proceedings of the IEEE Conference on Secure Development (SecDev), September 2018
Frantzen, M., Shuey, M.: StackGhost: hardware facilitated stack protection. In: Proceedings of the 10th Conference on USENIX Security Symposium, vol. 10 (2001)
Gil, R., Okhravi, H., Shrobe, H.: There’s a hole in the bottom of the C: on the effectiveness of allocation protection. In: Proceedings of the IEEE Conference on Secure Development (SecDev), September 2018
Greenman, B., Felleisen, M.: A spectrum of type soundness and performance. Proc. ACM Program. Lang. 2(ICFP) (2018)
Grossman, D., Hicks, M., Jim, T., Morrisett, G.: Cyclone: a type-safe dialect of C. C/C++ Users J. 23(1), 112–139 (2005)
Jones, R.W.M., Kelly, P.H.J.: Backwards-compatible bounds checking for arrays and pointers in C programs. In: Kamkar, M., Byers, D. (eds.) Third International Workshop on Automated Debugging. Linkoping Electronic Conference Proceedings, Linkoping University Electronic Press, May 1997. http://www.ep.liu.se/ea/cis/1997/009/
Jung, R., Jourdan, J.H., Krebbers, R., Dreyer, D.: RustBelt: securing the foundations of the rust programming language. Proc. ACM Program. Lang. 2(POPL), 66 (2017)
Kiriansky, V., Bruening, D., Amarasinghe, S.P.: Secure execution via program shepherding. In: Proceedings of the 11th USENIX Security Symposium, pp. 191–206. USENIX Association, Berkeley (2002). http://dl.acm.org/citation.cfm?id=647253.720293
Kwon, A., Dhawan, U., Smith, J.M., Knight Jr., T.F., DeHon, A.: Low-fat pointers: compact encoding and efficient gate-level implementation of fat pointers for spatial safety and capability-based security. In: Proceedings of the 2013 ACM SIGSAC Conference on Computer & #38; Communications Security, CCS 2013, pp. 721–732. ACM, New York (2013). https://doi.org/10.1145/2508859.2516713, http://doi.acm.org/10.1145/2508859.2516713
Matsakis, N.D., Klock II, F.S.: The rust language. In: ACM SIGAda Annual Conference on High Integrity Language Technology (2014)
Matthews, J., Findler, R.B.: Operational semantics for multi-language programs. In: POPL (2007)
Microsoft Corporation: Control flow guard (2016). https://msdn.microsoft.com/en-us/library/windows/desktop/mt637065(v=vs.85).aspx. Accessed April 27 2016
Milner, R.: A theory of type polymorphism in programming. J. Comput. Syst. Sci. 17(3), 348–375 (1978)
Intel memory protection extensions (MPX) (2018). https://software.intel.com/en-us/isa-extensions/intel-mpx
Nagarakatte, S., Zhao, J., Martin, M.M., Zdancewic, S.: SoftBound: highly compatible and complete spatial memory safety for C. In: Proceedings of the 30th ACM SIGPLAN Conference on Programming Language Design and Implementation (2009)
Necula, G.C., Condit, J., Harren, M., McPeak, S., Weimer, W.: CCured: type-safe retrofitting of legacy software. ACM Trans. Program. Lang. Syst. (TOPLAS) 27(3), 477–526 (2005)
NIST vulnerability database. https://nvd.nist.gov. Accessed 17 May 2017
Sangiorgi, D., Rutten, J.: Advanced Topics in Bisimulation and Coinduction, vol. 52. Cambridge University Press, Cambridge (2011)
Serebryany, K., Bruening, D., Potapenko, A., Vyukov, D.: AddressSanitizer: a fast address sanity checker. In: Proceedings of the 2012 USENIX Conference on Annual Technical Conference (2012)
Siek, J.G., Taha, W.: Gradual typing for functional languages. In: Workshop on Scheme and Functional Programming (2006)
Steffen, J.L.: Adding run-time checking to the Portable C Compiler. Softw. Pract. Exper. 22(4), 305–316 (1992)
Szekeres, L., Payer, M., Wei, T., Song, D.: SoK: eternal war in memory. In: Proceedings of the 2013 IEEE Symposium on Security and Privacy (2013)
Takikawa, A., Feltey, D., Greenman, B., New, M.S., Vitek, J., Felleisen, M.: Is sound gradual typing dead? In: POPL (2016)
PaX Team: http://pax.grsecurity.net/docs/aslr.txt (2001)
Tobin-Hochstadt, S., et al.: Migratory typing: ten years later. In: 2nd Summit on Advances in Programming Languages (SNAPL 2017), vol. 71, pp. 17:1–17:17 (2017)
Wadler, P., Findler, R.B.: Well-typed programs can’t be blamed. In: Castagna, G. (ed.) ESOP 2009. LNCS, vol. 5502, pp. 1–16. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00590-9_1
Wright, A.K., Felleisen, M.: A syntactic approach to type soundness. Inf. Comput. 115(1), 38–94 (1994)
Zhou, F., et al.: SafeDrive: safe and recoverable extensions using language-based techniques. In: 7th Symposium on Operating System Design and Implementation (OSDI 2006). USENIX Association, Seattle (2006)
Acknowledgments
We would like to thank the anonymous reviewers for helpful comments on drafts of this paper, and Sam Elliott for contributions to the portions of the design and implementation of Checked C presented in this paper. This research was funded in part by the U.S. National Science Foundation under grants CNS-1801545 and EDU-1319147.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Ruef, A., Lampropoulos, L., Sweet, I., Tarditi, D., Hicks, M. (2019). Achieving Safety Incrementally with Checked C. In: Nielson, F., Sands, D. (eds) Principles of Security and Trust. POST 2019. Lecture Notes in Computer Science(), vol 11426. Springer, Cham. https://doi.org/10.1007/978-3-030-17138-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-17138-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17137-7
Online ISBN: 978-3-030-17138-4
eBook Packages: Computer ScienceComputer Science (R0)





 can be used. This lets the programmers focus on pointers that need bounds declarations or that are used unsafely.
can be used. This lets the programmers focus on pointers that need bounds declarations or that are used unsafely.




 that appears at a physical location in the program is given a unique constraint variable
that appears at a physical location in the program is given a unique constraint variable  are identified with the constraint variable created at the point of declaration. A distinction is made for parameter and return variables depending on if the associated function definition is a declaration or a definition:
are identified with the constraint variable created at the point of declaration. A distinction is made for parameter and return variables depending on if the associated function definition is a declaration or a definition: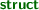 , function variable declarations, or parameter variable declarations. There is a special case, which is any constraint variable appearing at a parameter position, either at a function declaration/definition, or, a call site. That case is discussed in more detail next.
, function variable declarations, or parameter variable declarations. There is a special case, which is any constraint variable appearing at a parameter position, either at a function declaration/definition, or, a call site. That case is discussed in more detail next.