Abstract
A landmark security property of smart contracts is liquidity: in a non-liquid contract, it may happen that some funds remain frozen. The relevance of this issue is witnessed by a recent liquidity attack to the Ethereum Parity Wallet, which has frozen \({\sim }160M\) USD within the contract, making this sum unredeemable by any user. We address the problem of verifying liquidity of Bitcoin contracts. Focussing on BitML, a contracts DSL with a computationally sound compiler to Bitcoin, we study various notions of liquidity. Our main result is that liquidity of BitML contracts is decidable, in all the proposed variants. To prove this, we first transform the infinite-state semantics of BitML into a finite-state one, which focusses on the behaviour of any given set of contracts, abstracting the context moves. With respect to the chosen contracts, this abstraction is sound and complete. Our decision procedure for liquidity is then based on model-checking the finite space of states of the abstraction.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Decentralized ledgers like Bitcoin and Ethereum [19, 32] enable the trustworthy execution of smart contracts—computer protocols which regulate the exchange of assets among mutually untrusted users. The underlying protocols used to update the ledger (which defines the state of each contract) ensure that, even without trusted intermediaries, the execution of contracts is correct with respect to the contract rules. However, it may happen that the rules themselves are not correct with respect to the behaviour expected by the users. Indeed, all the attacks to smart contracts successfully carried out so far, which have plundered or frozen millions of USD in Ethereum [1,2,3, 8, 27, 30], exploit some discrepancy between the intended and the actual behaviour of a contract.
To counteract these attacks, the research community has recently started to formalize smart contracts and their security properties [22,23,24], and to develop automated verification tools based on these models [21, 27, 31, 35]. As a matter of fact, most of this research is targeted to Ethereum, the most widespread (and attacked) platform for smart contracts: for this reason, the security properties addressed by current tools focus on specific features of Solidity, the high-level language for smart contracts in Ethereum. For instance, some vulnerability patterns checked by these tools are reentrancy and mishandled exceptions, whose peculiar implementation in Solidity has led to attacks, like to one to the DAO [1]. Only a few tools verify general security properties of smart contracts, that would be meaningful also outside the realm of Ethereum. Among these works, [35] checks a property called liquidity, which holds when the contract always admits a trace where its balance is decreased (so, the funds stored within the contract do not remain frozen). This has been inspired from a recent attack to Ethereum [2], which has frozen \(\sim \)160M USD within a contract, exploiting a bug in a library. While being capable of classifying this particular contract as non-liquid, any contract where the adversary can lock some funds and redeem them at a later moment would be classified as liquid. Stronger notions of liquidity may rule out these unsafe contracts, e.g. by checking that funds are never frozen for all possible strategies of the adversary. Studying liquidity in a more general setting would be important for various reasons. First, taking into account adversaries would allow to detect more security issues w.r.t. those checked by the current verification tools. Second, platform-agnostic notions of liquidity could be applied to the forthcoming blockchain technologies, e.g. [20, 34]. Third, studying liquidity in simpler settings than Ethereum could simplify the verification problem, which is undecidable in Turing-powerful languages like those supported by Ethereum.
Contributions. We study several notions of liquidity for smart contracts, in a general setting where their behaviour is defined as a transition system. We then consider the special case where contracts are expressed in BitML, a high-level DSL for smart contracts which compiles into Bitcoin [14]. In such setting, we develop a verification technique for liquidity of smart contracts. We can summarise our main contributions as follows:
-
1.
We formalize a notion of liquidity (Definition 2), and we illustrate several meaningful variants. Our notion of liquidity takes into account both the contract and the strategy that a participant follows to perform contract actions. Roughly, a strategy is liquid when following it ensures that funds do not remain frozen within the contract, even in the presence of adversaries.
-
2.
We introduce an abstraction of the semantics of BitML which is finite-state (Theorem 1), and sound and complete w.r.t. the concrete (infinite-state) semantics, given a set of contracts under observation (Theorems 2 and 3).
-
3.
We devise a verification technique for liquidity in BitML. Our technique can establish whether a strategy is liquid for a given contract, and also to synthesise a liquid strategy, when it exists (Theorem 4).
Our finite-state abstraction is general-purpose: verifying liquidity is only one of its possible applications (some other applications are discussed in Sect. 6).
Related Works. Several recent works study security issues related to Ethereum smart contracts. A few papers address EVM, the bytecode language which is the target of compilation of Solidity. Among them, [27] introduces an operational semantics of a simplified version of EVM, and develops Oyente, a tool to detect some vulnerability patterns of EVM contracts through symbolic execution. Securify [35] checks vulnerability patterns by analysing dependency graphs extracted from EVM code. As mentioned before, this tool also addresses a form of liquidity, which essentially assumes a cooperating adversary. EtherTrust [21] is a framework for the static verification of EVM contracts, which can establish e.g. the absence of reentrancy vulnerabilities. This tool is based on the detailed formalisation of EVM provided in [22], which is validated against the official Ethereum test suite. The work [23] introduces an executable semantics of EVM, specified in the \(\mathbb {K}\) framework. The tool in [18] translates Solidity and EVM code into \(\mathsf {F}^*\), and use its verification tools to detect vulnerabilities of contracts; further, the tool verifies the equivalence between a Solidity program and an alleged compilation of it into EVM. The work [24] verifies EVM code through the Isabelle/HOL proof assistant [33], proving that, upon an invocation of a specific contract, only its owner can decrease the balance.
Smart contracts in Bitcoin have a completely different flavour compared to Ethereum, since they are usually expressed as cryptographic protocols, rather than as programs. Despite the limited expressiveness of the scripts in Bitcoin transactions [10], several kinds of contracts for Bitcoin have been proposed [9]: they range from lotteries [6, 7, 13, 29], to general multiparty computations [4, 17, 26], to contingent payments [11, 28], etc. All these works focus on proving the security of a fixed contract, unlike the above-mentioned works on Ethereum, where the goal is to verify arbitrary contracts. As far as we know, only a couple of works pursue this goal for Bitcoin. The tool in [25] analyses Bitcoin scripts, in order to find under which conditions the enclosing transaction can be redeemed. Compared to [25], our work verifies contracts spanning among many transactions, rather than single scripts. The work [5] models contracts as timed automata, and then uses the Uppaal model checker [16] to verify their properties. The contracts modelled as in [5] cannot be directly translated to Bitcoin, while in our approach we can exploit the BitML compiler to translate contracts to standard Bitcoin transactions. Note also that the properties considered in [5] are specific to the modelled contract, while in this work we are interested in verifying general properties of contracts, like liquidity.
2 Overview
In this section we briefly overview BitML; we then give some intuition about liquidity and our verification technique. Because of space limits, we refer to [14] for a detailed treatment of BitML, and to [12] for a more gentle introduction.
We assume a set of participants, ranged over by  , and a set of names, of two kinds:
, and a set of names, of two kinds:  denote deposits of
denote deposits of  , while \(\mathord {{a}_{}}, \mathord {{b}_{}}, \ldots \) denote secrets. We write
, while \(\mathord {{a}_{}}, \mathord {{b}_{}}, \ldots \) denote secrets. We write  (resp. \(\varvec{\mathord {{a}_{}}}\)) for a finite sequence of deposit (resp. secrets) names.
(resp. \(\varvec{\mathord {{a}_{}}}\)) for a finite sequence of deposit (resp. secrets) names.
2.1 BitML in a Nutshell
BitML is a domain-specific language for Bitcoin smart contracts, which allows participants to exchange cryptocurrency according to pre-agreed contract rules. In BitML, any participant can broadcast a contract advertisement  , where
, where  is the actual contract, specifying the rules to transfer bitcoins (
is the actual contract, specifying the rules to transfer bitcoins ( ), while
), while  is a set of preconditions to its execution.
is a set of preconditions to its execution.
Preconditions (Fig. 1, left) may require participants to deposit some  in the contract (either upfront or at runtime), or to commit to some secret. More in detail,
in the contract (either upfront or at runtime), or to commit to some secret. More in detail,  requires
requires  to own
to own  in a deposit
in a deposit  , and to spend it for stipulating a contract
, and to spend it for stipulating a contract  . Instead,
. Instead,  only requires
only requires  to pre-authorize the spending of
to pre-authorize the spending of  , which can be gathered by the contract at run-time. The precondition
, which can be gathered by the contract at run-time. The precondition  requires
requires  to commit to a secret \(\mathord {{a}_{}}\) before
to commit to a secret \(\mathord {{a}_{}}\) before  starts.
starts.
After  has been advertised, each participant can choose whether to accept it, or not. When all the preconditions
has been advertised, each participant can choose whether to accept it, or not. When all the preconditions  have been satisfied, and all the involved participants have accepted, the contract
have been satisfied, and all the involved participants have accepted, the contract  becomes stipulated. The contract starts its execution with a balance, initially set to the sum of the !-deposits required by its preconditions. Running
becomes stipulated. The contract starts its execution with a balance, initially set to the sum of the !-deposits required by its preconditions. Running  will affect this balance, when participants deposit/withdraw funds to/from the contract.
will affect this balance, when participants deposit/withdraw funds to/from the contract.
A contract  is a choice among zero or more branches. Each branch is a guarded contract (Fig. 1, right) which enables an action, and possibly proceeds with a continuation
is a choice among zero or more branches. Each branch is a guarded contract (Fig. 1, right) which enables an action, and possibly proceeds with a continuation  . The guarded contract
. The guarded contract  transfers the whole balance to
transfers the whole balance to  , while
, while  decomposes the contract into n parallel components
decomposes the contract into n parallel components  , each one with balance \(v_{i}\). The guarded contract
, each one with balance \(v_{i}\). The guarded contract  atomically performs the following: (i) spend all the ?-deposits
atomically performs the following: (i) spend all the ?-deposits  , adding their values to the contract balance; (ii) check that all the secrets \(\varvec{\mathord {{a}_{}}}\) have been revealed and satisfy the predicate \(\mathord {p_{}}\) (Fig. 2). When enabled, the above-mentioned actions can be fired by anyone, at anytime. To restrict who can execute actions and when, one can use the decoration
, adding their values to the contract balance; (ii) check that all the secrets \(\varvec{\mathord {{a}_{}}}\) have been revealed and satisfy the predicate \(\mathord {p_{}}\) (Fig. 2). When enabled, the above-mentioned actions can be fired by anyone, at anytime. To restrict who can execute actions and when, one can use the decoration  , which requires the authorization of
, which requires the authorization of  , and the decoration
, and the decoration  , which requires to wait until time \(t_{}\).
, which requires to wait until time \(t_{}\).
A Basic Example. As a first example, we express in BitML the timed commitment [6], a basic protocol to construct more complex contracts, like e.g. lotteries and other games [7]. In the timed commitment, a participant  wants to choose a secret, and promises to reveal it before some time \(t_{}\). The contract ensures that if
wants to choose a secret, and promises to reveal it before some time \(t_{}\). The contract ensures that if  does not reveal the secret in time, then she will pay a penalty of
does not reveal the secret in time, then she will pay a penalty of  to
to  (e.g., the opponent player in a game). In BitML, this is modelled as follows:
(e.g., the opponent player in a game). In BitML, this is modelled as follows:

The precondition requires  to pay upfront
to pay upfront  , and to commit to a secret \(\mathord {{a}_{}}\). The contract (hereafter, named
, and to commit to a secret \(\mathord {{a}_{}}\). The contract (hereafter, named  ) is a non-deterministic choice between two branches. Only
) is a non-deterministic choice between two branches. Only  can choose the first branch, by performing
can choose the first branch, by performing  (syntactic sugar for
(syntactic sugar for  ). Subsequently, anyone can transfer
). Subsequently, anyone can transfer  to
to  . Only after \(t_{}\), if the \(\texttt {reveal} \) has not been fired, any participant can fire
. Only after \(t_{}\), if the \(\texttt {reveal} \) has not been fired, any participant can fire  in the second branch, moving
in the second branch, moving  to
to  . So, before \(t_{}\),
. So, before \(t_{}\),  has the option to reveal \(\mathord {{a}_{}}\) (avoiding the penalty), or to keep it secret (paying the penalty). If no branch is taken by \(t_{}\), the first one who fires its
has the option to reveal \(\mathord {{a}_{}}\) (avoiding the penalty), or to keep it secret (paying the penalty). If no branch is taken by \(t_{}\), the first one who fires its  gets
gets  .
.
2.2 BitML Semantics
We briefly recall from [14] the semantics of BitML. The semantics is a labelled transition system between configurations of the following form:
-
 , representing the advertisement of contract
, representing the advertisement of contract  with preconditions
with preconditions  ;
; -
 , representing a stipulated contract, holding a current balance of
, representing a stipulated contract, holding a current balance of  . The name
. The name  uniquely identifies the contract in a configuration;
uniquely identifies the contract in a configuration; -
 representing a fund of
representing a fund of  owned by
owned by  , and with unique name
, and with unique name  ;
; -
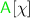 , representing
, representing  ’s authorizations to perform some operation \(\chi \). We refer to [14] for the syntax of authorizations (some of them are exemplified below);
’s authorizations to perform some operation \(\chi \). We refer to [14] for the syntax of authorizations (some of them are exemplified below); -
 , representing that
, representing that  has committed to a random secret \(\mathord {{a}_{}}\) with (secret) length N;
has committed to a random secret \(\mathord {{a}_{}}\) with (secret) length N; -
 , representing that
, representing that  has revealed her secret \(\mathord {{a}_{}}\) (with its length N).
has revealed her secret \(\mathord {{a}_{}}\) (with its length N). -
 is the parallel composition of two configurations (with identity \(0\));
is the parallel composition of two configurations (with identity \(0\)); -
 is a timed configuration, where \(t_{}\in \mathbb {N}\) is a global time.
is a timed configuration, where \(t_{}\in \mathbb {N}\) is a global time.
We now illustrate the BitML semantics by examples; when time is immaterial, we only show the steps of the untimed semantics. We omit labels on transitions.
Deposits. When  owns a deposit
owns a deposit  , she can use it in various ways: she can divide the deposit into two smaller deposits, or join it with another deposit of hers to form a larger one; the deposit can also be transferred to another participant, or destroyed. For instance, to donate a deposit
, she can use it in various ways: she can divide the deposit into two smaller deposits, or join it with another deposit of hers to form a larger one; the deposit can also be transferred to another participant, or destroyed. For instance, to donate a deposit  to
to  ,
,  must first issue the authorization
must first issue the authorization  ; then, anyone can transfer the money to
; then, anyone can transfer the money to  :
:

We assume that whenever a participant authorizes an operation on some deposit  , then she is also authorising a self-donation
, then she is also authorising a self-donation  of such deposit.Footnote 1
of such deposit.Footnote 1
Advertisement. Any participant can advertise a new contract  (with preconditions
(with preconditions  ). This is obtained by performing the step
). This is obtained by performing the step  .
.
Stipulation. Stipulation turns a contract advertisement into an active contract. For instance, let  . Given a contract
. Given a contract  , the stipulation of
, the stipulation of  is done in a few steps:
is done in a few steps:

Above, the funds in the deposit  are transferred to the newly created contract, to fulfill the precondition
are transferred to the newly created contract, to fulfill the precondition  . Instead, the deposit \(y_{}\) remains in the configuration, to be possibly spent after some time. The component
. Instead, the deposit \(y_{}\) remains in the configuration, to be possibly spent after some time. The component  represents the secret committed to by
represents the secret committed to by  , with its length N.
, with its length N.
Withdraw. Executing  terminates the contract, and transfers its whole balance to
terminates the contract, and transfers its whole balance to  by creating a fresh deposit owned by
by creating a fresh deposit owned by  :
:

Above,  is executed as a branch within a choice: as usual, taking a branch discards the other ones (denoted as
is executed as a branch within a choice: as usual, taking a branch discards the other ones (denoted as  ).
).
Split. The \(\texttt {split} \) primitive can be used to spawn several new concurrent contracts, dividing the balance among them. For instance:

Put & Reveal. A prefix  can be fired when the previously committed secret
can be fired when the previously committed secret  (satisfying the predicate
(satisfying the predicate  ) has been revealed, and the deposit
) has been revealed, and the deposit  is available in the configuration. For instance:
is available in the configuration. For instance:

In the first step,  reveals her secret
reveals her secret  . In the second step, any participant fires the prefix; doing so rakes the deposit
. In the second step, any participant fires the prefix; doing so rakes the deposit  within the contract.
within the contract.
Authorizations. When a branch is decorated by  it can be taken only after
it can be taken only after  has provided her authorization. For instance:
has provided her authorization. For instance:

In the first step,  authorizes to take the branch
authorizes to take the branch  . After that, any participant can fire such branch.
. After that, any participant can fire such branch.
Time. We always allow time \(t_{}\) to advance by a delay \(\delta >0\), through a transition \( {\varGamma _{}} \mid {t_{}} \xrightarrow {} {\varGamma _{}} \mid {t_{}+\delta } \). Advancing time can enable branches decorated with \(\texttt {after}\, t_{}\). For instance, if \(t_{0}+\delta \ge t_{}\), we have the following computation:

Runs and Strategies. A run \(\mathcal {R}_{}\) is a (possibly infinite) sequence:

where \(\ell _{i}\) are the transition labels, \(\varGamma _{0}\) contains only deposits, and \(t_{0}=0\). If \(\mathcal {R}_{}\) is finite, we write \(\varGamma _{\mathcal {R}_{}}\) for its last untimed configuration, and \(\delta _{\mathcal {R}_{}}\) for its last time. A strategy  is a PPTIME algorithm which allows
is a PPTIME algorithm which allows  to select which actions to perform (possibly, time delays), among those permitted by the BitML semantics. The choice among these actions is controlled by the adversary strategy
to select which actions to perform (possibly, time delays), among those permitted by the BitML semantics. The choice among these actions is controlled by the adversary strategy  , which acts on behalf of all the dishonest participants. Given the strategies of all participants (including
, which acts on behalf of all the dishonest participants. Given the strategies of all participants (including  ), there is a unique run conforming to all of them.
), there is a unique run conforming to all of them.
2.3 Liquidity
A desirable property of smart contracts is liquidity, which requires that the contract balance is always eventually transferred to some participant. In a non-liquid contract, funds can be frozen forever, unavailable to anyone, hence effectively destroyed. There are many possible flavours of liquidity, depending e.g. on which participants are assumed to be honest, and on which are their strategies. The simplest form of liquidity is to consider the case where everyone cooperates: i.e. a contract is liquid if there exists some strategy for each participant such that no funds are ever frozen. However, this notion does not capture the essence of smart contracts, i.e. to allow mutually untrusted participants to safely interact.
For instance, consider the following contract, where  and
and  contribute
contribute  each for a donation of
each for a donation of  to either
to either  or
or  (we omit the preconditions for brevity):
(we omit the preconditions for brevity):

In order to unlock the funds,  and
and  must agree on the recipient of the donation, by giving their authorization on the same branch. This contract would be liquid only by assuming the cooperation between
must agree on the recipient of the donation, by giving their authorization on the same branch. This contract would be liquid only by assuming the cooperation between  and
and  : indeed,
: indeed,  alone cannot guarantee that the
alone cannot guarantee that the  will eventually be donated, as
will eventually be donated, as  can choose a different recipient, or even refuse to give any authorization. Consequently, unless
can choose a different recipient, or even refuse to give any authorization. Consequently, unless  trusts
trusts  , it makes sense to consider this contract as non-liquid, from the point of view of
, it makes sense to consider this contract as non-liquid, from the point of view of  (and for similar reasons, also from that of
(and for similar reasons, also from that of  ).
).
Consider now the timed commitment contract discussed before:

This contract is liquid from  ’s point of view (even if
’s point of view (even if  is dishonest), because
is dishonest), because  can reveal the secret and then redeem the funds from the contract. The timed commitment is also liquid from
can reveal the secret and then redeem the funds from the contract. The timed commitment is also liquid from  ’s point of view: if
’s point of view: if  does not reveal the secret (making the first branch stuck), the funds in the contract can be redeemed through the second branch, after time \(t_{}\).
does not reveal the secret (making the first branch stuck), the funds in the contract can be redeemed through the second branch, after time \(t_{}\).
In a mutual timed commitment contract, where  and
and  have to exchange their secrets or pay a
have to exchange their secrets or pay a  penalty, achieving liquidity is a bit more challenging. We first consider a wrong attempt:
penalty, achieving liquidity is a bit more challenging. We first consider a wrong attempt:

Intuitively,  has only the following strategies, according to when she decides to reveal her secret \(\mathord {{a}_{}}\): (i)
has only the following strategies, according to when she decides to reveal her secret \(\mathord {{a}_{}}\): (i)  chooses to reveal \(\mathord {{a}_{}}\) unconditionally, and to perform the
chooses to reveal \(\mathord {{a}_{}}\) unconditionally, and to perform the  action. This strategy is not liquid: indeed, if
action. This strategy is not liquid: indeed, if  does not reveal \(\mathord {{b}_{}}\), the contract is stuck. (ii)
does not reveal \(\mathord {{b}_{}}\), the contract is stuck. (ii)  chooses to reveal \(\mathord {{a}_{}}\) only after
chooses to reveal \(\mathord {{a}_{}}\) only after  has revealed \(\mathord {{b}_{}}\). This strategy is not liquid: indeed, if
has revealed \(\mathord {{b}_{}}\). This strategy is not liquid: indeed, if  chooses not to reveal \(\mathord {{b}_{}}\), the contract will never advance. (iii)
chooses not to reveal \(\mathord {{b}_{}}\), the contract will never advance. (iii)  chooses to wait until
chooses to wait until  reveals secret \(\mathord {{b}_{}}\), or until time \(t'_{}\ge t_{}\), whichever comes first. If \(\mathord {{b}_{}}\) was revealed,
reveals secret \(\mathord {{b}_{}}\), or until time \(t'_{}\ge t_{}\), whichever comes first. If \(\mathord {{b}_{}}\) was revealed,  reveals \(\mathord {{a}_{}}\), and splits the contract balance between
reveals \(\mathord {{a}_{}}\), and splits the contract balance between  and
and  . Otherwise, if the deadline \(t'_{}\) is expired,
. Otherwise, if the deadline \(t'_{}\) is expired,  transfers the whole balance to
transfers the whole balance to  . Note that, although this strategy is liquid, it is not satisfactory for
. Note that, although this strategy is liquid, it is not satisfactory for  , since in the second case she will lose money.
, since in the second case she will lose money.
This example highlights a crucial point: participants’ strategies have to be taken into account when defining liquidity. Indeed, the mere fact that a liquid strategy exists does not imply that it is the ideal strategy for the honest participant. To fix this issue, we revise the mutual timed commitment as follows:

where \(t_{}< t'_{}\). Now,  has a liquid strategy where she does not pay the penalty. First,
has a liquid strategy where she does not pay the penalty. First,  reveals \(\mathord {{a}_{}}\) before time \(t_{}\). After that, if
reveals \(\mathord {{a}_{}}\) before time \(t_{}\). After that, if  reveals \(\mathord {{b}_{}}\), then
reveals \(\mathord {{b}_{}}\), then  can execute the \(\texttt {split} \), transferring
can execute the \(\texttt {split} \), transferring  to herself and
to herself and  to
to  (note that this does not require
(note that this does not require  ’s cooperation); otherwise, after time \(t'_{}\),
’s cooperation); otherwise, after time \(t'_{}\),  can withdraw
can withdraw  by executing the
by executing the  in the
in the  branch.
branch.
These examples, albeit elementary, show that detecting if a strategy is liquid for a contract is not straightforward, in general. The problem of determining a liquid strategy for a given contract seems even more demanding. Automatic techniques for the verification and inference of liquid strategies can be useful tools for the developers of smart contracts.
2.4 Verifying Liquidity
One of the main contributions of this paper is a verification technique for the liquidity of BitML contracts. Our technique is based on a more general result, i.e. a strict correspondence between the semantics of BitML in [14] (hereafter, called concrete semantics) and a new abstract semantics, which is finite-state (Theorem 1). Our abstraction is a correct and complete approximation of the concrete semantics with respect to a given set of contracts (Theorems 2 and 3). To obtain a finite-state abstraction, we need to cope with three sources of infiniteness of the concrete semantics of BitML: the unbounded passing of time, the advertisement/stipulation of new contracts, and the operations on deposits. Our abstraction replaces the time \(t_{}\) in concrete configurations with a finite number of time intervals \(T_{}= [t_{0},t_{1})\), and it disables the transitions to advertise new contracts. Further, the only operations on deposits allowed by the abstract semantics are the ones for transferring them to contracts and for destroying them. The latter is needed e.g. to properly model the situation where a participant spends a ?-deposit.
The intended use of our abstraction is to start from a configuration containing an arbitrary (but finite) set of contracts, and then analyse their possible evolutions in the presence of an honest participant and an adversary. This produces a finite set of (finite) traces, which we can model-check for liquidity. Soundness and completeness of the abstraction are exploited to prove that liquidity is decidable (Theorem 4). The computational soundness of the BitML compiler [14] guarantees that if a contract is verified to be liquid according to our analysis, this property is preserved when executing it on Bitcoin.
3 Liquidity
In this section we formalise a notion of liquidity of contracts, and we suggest some possible variants. Aiming at generality, liquidity is parameterised over (i) a set  of contract names, uniquely identifying the contracts under observation; (ii) a participant
of contract names, uniquely identifying the contracts under observation; (ii) a participant  (with her strategy
(with her strategy  ), which we assume to be the only honest participant in the system. Roughly, we want that the funds stored within the contracts
), which we assume to be the only honest participant in the system. Roughly, we want that the funds stored within the contracts  are eventually transferred to some participant, in any run conforming to
are eventually transferred to some participant, in any run conforming to  ’s strategy. The actual definition is a bit more complex, because the other participants may play against
’s strategy. The actual definition is a bit more complex, because the other participants may play against  , e.g. avoiding to reveal their secrets, or to give their authorizations for some branch.
, e.g. avoiding to reveal their secrets, or to give their authorizations for some branch.
We start by introducing an auxiliary partial function  that, given a contract name
that, given a contract name  and an extension \(\mathcal {R}_{}\) of a run \(\mathcal {R}_{0}\), determines the ancestor \(y_{}\) of
and an extension \(\mathcal {R}_{}\) of a run \(\mathcal {R}_{0}\), determines the ancestor \(y_{}\) of  in the last configuration of \(\mathcal {R}_{0}\), if any. Intuitively,
in the last configuration of \(\mathcal {R}_{0}\), if any. Intuitively,  means that \(y_{}\) has evolved into \(\mathcal {R}_{}\), eventually leading to
means that \(y_{}\) has evolved into \(\mathcal {R}_{}\), eventually leading to  (and possibly to other contracts).
(and possibly to other contracts).
In BitML, there are only two ways to make a contract evolve into another contract. First, a  can spawn new contracts, e.g.:
can spawn new contracts, e.g.:

Here, both \(y_{1}\) and \(y_{2}\) have  as ancestor. Second, \( \texttt {put} \& \texttt {reveal} \) reduces as follows:
as ancestor. Second, \( \texttt {put} \& \texttt {reveal} \) reduces as follows:

In this case, the ancestor of \(y_{}\) is  .
.
Definition 1
Let \(\mathcal {R}_{}\) be a run extending some run \(\mathcal {R}_{0}\), and let  be a contract name. We define
be a contract name. We define  by induction on the length of \(\mathcal {R}_{}\) in Fig. 3, where
by induction on the length of \(\mathcal {R}_{}\) in Fig. 3, where  denotes the set of contract names in \(\varGamma _{}\).
denotes the set of contract names in \(\varGamma _{}\).
Example 1
Let \(\mathcal {R}_{0}\) be a run with last configuration  , and let \(\mathcal {R}_{}\) be the following extension of \(\mathcal {R}_{0}\), where the contracts
, and let \(\mathcal {R}_{}\) be the following extension of \(\mathcal {R}_{0}\), where the contracts  and
and  are immaterial, but for the fact that they enable the displayed moves:
are immaterial, but for the fact that they enable the displayed moves:

We have that  , since the corresponding contracts have been obtained through a split of the ancestor y, which was in the last configuration of
, since the corresponding contracts have been obtained through a split of the ancestor y, which was in the last configuration of  . Instead,
. Instead,  is undefined, because its ancestor x is not in
is undefined, because its ancestor x is not in  . Further,
. Further,  , while
, while  is undefined.
is undefined.
We now formalise liquidity. Assume that we want to observe a single contract  , occurring in the last configuration of some run
, occurring in the last configuration of some run  (note that
(note that  has been stipulated at some point during
has been stipulated at some point during  ). A participant
). A participant  wants to know if the strategy
wants to know if the strategy  allows her to make
allows her to make  evolve so that funds are never frozen within the contract. We require that
evolve so that funds are never frozen within the contract. We require that  can do this without the help of the other participants, which therefore we model as a single adversary
can do this without the help of the other participants, which therefore we model as a single adversary  . More precisely, we say that
. More precisely, we say that  is liquid for
is liquid for  when, after any extension \(\mathcal {R}_{}\) of
when, after any extension \(\mathcal {R}_{}\) of  ,
,  can choose a sequence of moves so to make all the descendant contracts of
can choose a sequence of moves so to make all the descendant contracts of  terminate, transferring their funds to some participant (possibly not
terminate, transferring their funds to some participant (possibly not  ). Note that such moves can not reveal secrets of other participants, or generate authorizations for them:
). Note that such moves can not reveal secrets of other participants, or generate authorizations for them:  must be able to unfreeze the funds on her own, using her strategy. By contrast, \(\mathcal {R}_{}\) can also involve such moves, but it must conform to
must be able to unfreeze the funds on her own, using her strategy. By contrast, \(\mathcal {R}_{}\) can also involve such moves, but it must conform to  ’s strategy. The actual definition of liquidity generalises the above to sets
’s strategy. The actual definition of liquidity generalises the above to sets  of contract names.
of contract names.
Definition 2
(Liquidity). Let  be an honest participant, with strategy
be an honest participant, with strategy  , let
, let  be a run, and let
be a run, and let  be a set of contract names in
be a set of contract names in  . We say that
. We say that  is liquid w.r.t.
is liquid w.r.t.  in
in  if, for all finite extensions \(\mathcal {R}_{}\) of
if, for all finite extensions \(\mathcal {R}_{}\) of  conforming to
conforming to  and to some
and to some  , there exists an extension \(\mathcal {R}'_{}= \mathcal {R}_{}\xrightarrow {\ell _{1}} \cdots \xrightarrow {\ell _{n}}\) of \(\mathcal {R}_{}\) such that:
, there exists an extension \(\mathcal {R}'_{}= \mathcal {R}_{}\xrightarrow {\ell _{1}} \cdots \xrightarrow {\ell _{n}}\) of \(\mathcal {R}_{}\) such that:


Condition (1) requires that all the moves after \(\mathcal {R}_{}\) can be taken by  alone, conforming to her strategy. Condition (2) checks that \(\mathcal {R}'_{}\) no longer contains descendants of the contracts \(X_{0}\): since in BitML active contracts always store some funds, this is actually equivalent to checking that funds are not frozen.
alone, conforming to her strategy. Condition (2) checks that \(\mathcal {R}'_{}\) no longer contains descendants of the contracts \(X_{0}\): since in BitML active contracts always store some funds, this is actually equivalent to checking that funds are not frozen.
We remark that, although Definition 2 is instantiated on BitML, the basic concepts it relies upon (runs, strategies, termination of contracts) are quite general. Hence, our notion of liquidity, as well as the variants proposed below, can be applied to other languages for smart contracts, using their transition semantics.
Example 2
Recall the timed commitment contract  from Sect. 2. Assume that
from Sect. 2. Assume that  ’s strategy is to wait until time \(t_{}- 1\) (i.e., one time unit before the deadline), then reveal the secret and fire
’s strategy is to wait until time \(t_{}- 1\) (i.e., one time unit before the deadline), then reveal the secret and fire  . Let
. Let  be a run with final configuration
be a run with final configuration  , for some length N. We have that
, for some length N. We have that  is liquid w.r.t.
is liquid w.r.t.  in
in  , while it is not liquid w.r.t. the strategy where
, while it is not liquid w.r.t. the strategy where  does not reveal the secret, or reveals it without firing
does not reveal the secret, or reveals it without firing  . Indeed, under these strategies
. Indeed, under these strategies  alone cannot make x terminate.
alone cannot make x terminate.
Example 3
Consider the following two contracts, which both require as precondition that  put a deposit of
put a deposit of  and commits to a secret \(\mathord {{a}_{}}\), and where \(\mathord {p_{}}\) is an arbitrary predicate on \(\mathord {{a}_{}}\):
and commits to a secret \(\mathord {{a}_{}}\), and where \(\mathord {p_{}}\) is an arbitrary predicate on \(\mathord {{a}_{}}\):

Assume that  ’s strategy is to reveal the secret, and then fire any enabled
’s strategy is to reveal the secret, and then fire any enabled  . Under this strategy,
. Under this strategy,  is liquid, because one of the \(\texttt {reveal} \) branches is enabled, and the corresponding
is liquid, because one of the \(\texttt {reveal} \) branches is enabled, and the corresponding  is fired, transferring
is fired, transferring  either to
either to  or to
or to  . Instead, no strategy of
. Instead, no strategy of  can make
can make  liquid. If
liquid. If  does not reveal the secret, then the
does not reveal the secret, then the  are frozen; otherwise, if
are frozen; otherwise, if  reveals the secret, then only one of the two descendents of
reveals the secret, then only one of the two descendents of  can fire the \(\texttt {reveal} \), and so
can fire the \(\texttt {reveal} \), and so  remains frozen.
remains frozen.
Example 4
(Lottery). Consider a lottery between two players. The preconditions require  and
and  to commit to one secret each (\(\mathord {{a}_{}}\) and \(\mathord {{b}_{}}\), respectively), and to put a deposit of
to commit to one secret each (\(\mathord {{a}_{}}\) and \(\mathord {{b}_{}}\), respectively), and to put a deposit of  each (
each ( as a bet, and
as a bet, and  as a penalty for dishonest behaviour):
as a penalty for dishonest behaviour):

The contract splits the balance in three parts, of  each. The first part allows
each. The first part allows  to reveal \(\mathord {{b}_{}}\) and then redeem
to reveal \(\mathord {{b}_{}}\) and then redeem  ; otherwise, after the deadline
; otherwise, after the deadline  can redeem
can redeem  ’s penalty (as in the timed commitment). Similarly, the second part allows
’s penalty (as in the timed commitment). Similarly, the second part allows  to redeem
to redeem  by revealing \(\mathord {{a}_{}}\). To determine the winner we compare the secrets, in the subcontract
by revealing \(\mathord {{a}_{}}\). To determine the winner we compare the secrets, in the subcontract  :
:  wins if the secrets have the same length, otherwise
wins if the secrets have the same length, otherwise  wins. This lottery is fair, since: (i) if both players are honest, then they will reveal their secrets within the deadlines (redeeming
wins. This lottery is fair, since: (i) if both players are honest, then they will reveal their secrets within the deadlines (redeeming  each), and then they will have a 1 / 2 probability of winningFootnote 2; (ii) if a player is dishonest, not revealing the secret, then the other player has a positive payoff, since she can redeem
each), and then they will have a 1 / 2 probability of winningFootnote 2; (ii) if a player is dishonest, not revealing the secret, then the other player has a positive payoff, since she can redeem  .
.
Although fair,  is non-liquid w.r.t. any strategy of
is non-liquid w.r.t. any strategy of  . Indeed, if
. Indeed, if  does not reveal his secret, then the
does not reveal his secret, then the  stored in the
stored in the  subcontract are frozen. We can recover liquidity by replacing
subcontract are frozen. We can recover liquidity by replacing  with the following:
with the following:

where \(t'_{}> t_{}\). In this case, even if  does not reveal \(\mathord {{b}_{}}\),
does not reveal \(\mathord {{b}_{}}\),  can use a strategy firing any enabled
can use a strategy firing any enabled  at time \(t'_{}\), to unfreeze the
at time \(t'_{}\), to unfreeze the  stored in
stored in  .
.
We now present some variants of the notion of liquidity presented before.
Multiparty Liquidity. A straightforward generalisation of liquidity is to assume a set of honest participants (rather than just one). In this case, we can extend Definition 2 by requiring that the run \(\mathcal {R}_{}\) conforms to the strategies of all honest participants, and the moves in (1) can be taken by any honest participant.
We illustrate this notion through the following escrow contract between two participants  and
and  , where the precondition requires
, where the precondition requires  to deposit
to deposit  :
:

After the contract has been stipulated,  can choose to pay
can choose to pay  , by authorizing the first branch. Similarly,
, by authorizing the first branch. Similarly,  can allow
can allow  to take her money back, by authorizing the second branch. If they do not agree, any of them can invoke a mediator
to take her money back, by authorizing the second branch. If they do not agree, any of them can invoke a mediator  to resolve the dispute, invoking a
to resolve the dispute, invoking a  branch. There, the
branch. There, the  deposit is split in two parts:
deposit is split in two parts:  go to the mediator, while
go to the mediator, while  are assigned either to
are assigned either to  and
and  , depending on
, depending on  ’s choice.
’s choice.
Assuming that only  is honest, this contract does not admit any liquid strategy for
is honest, this contract does not admit any liquid strategy for  , according to Definition 2. This is because
, according to Definition 2. This is because  can invoke the mediator, who can refuse to act, freezing the funds within the contract. Similarly,
can invoke the mediator, who can refuse to act, freezing the funds within the contract. Similarly,  alone has no liquid strategy, as well as
alone has no liquid strategy, as well as  . Instead,
. Instead,  admits a liquid multiparty strategy for any pair of honest participants. For instance, if
admits a liquid multiparty strategy for any pair of honest participants. For instance, if  and
and  are honest, their strategies could be the following.
are honest, their strategies could be the following.  chooses whether to authorize the first branch or not; in the first case, she fires
chooses whether to authorize the first branch or not; in the first case, she fires  ; otherwise, if
; otherwise, if  gives his authorization within a certain deadline, then
gives his authorization within a certain deadline, then  withdraws
withdraws  ; if not, after the deadline
; if not, after the deadline  invokes
invokes  . The strategy of
. The strategy of  is to authorize some participant to redeem the
is to authorize some participant to redeem the  , and to fire all the
, and to fire all the  within
within  .
.
Strategyless Liquidity. Another variant of liquidity can be obtained by inspecting only the contract, neglecting  ’s strategy. In this case, we consider the contract as liquid when there exists some strategy of
’s strategy. In this case, we consider the contract as liquid when there exists some strategy of  which satisfies the constraints in Definition 2. For instance, the contract
which satisfies the constraints in Definition 2. For instance, the contract  is non-liquid from
is non-liquid from  ’s point of view, according to this notion, while it would be liquid for
’s point of view, according to this notion, while it would be liquid for  .
.
Quantitative Liquidity. Definition 2 requires that no funds remain frozen within the contract. However, in some cases  could accept the fact that a portion of the funds remain frozen, especially when these funds would be ideally assigned to other participants. Following this intuition, we could define a contract \(v_{}\)-liquid w.r.t.
could accept the fact that a portion of the funds remain frozen, especially when these funds would be ideally assigned to other participants. Following this intuition, we could define a contract \(v_{}\)-liquid w.r.t.  if at least \(v_{}\) bitcoins are guaranteed to be redeemable. If the contract uses only !-deposits, the special case where \(v_{}\) is the sum of all these deposits corresponds to the notion in Definition 2. For instance,
if at least \(v_{}\) bitcoins are guaranteed to be redeemable. If the contract uses only !-deposits, the special case where \(v_{}\) is the sum of all these deposits corresponds to the notion in Definition 2. For instance,  from Example 4 is non-liquid for any strategy of
from Example 4 is non-liquid for any strategy of  , but it is
, but it is  -liquid if
-liquid if  ’s strategy is to reveal her secret, and perform all the enabled
’s strategy is to reveal her secret, and perform all the enabled  . Instead,
. Instead,  is
is  -liquid, and then also liquid, under this strategy.
-liquid, and then also liquid, under this strategy.
A refinement of this variant could require that at least  are transferred to
are transferred to  , rather than to any participant. Under this notion, both
, rather than to any participant. Under this notion, both  and
and  would be
would be  -liquid for
-liquid for  . Further,
. Further,  would be
would be  -liquid in case
-liquid in case  wins the lottery.
wins the lottery.
Liquidity with Unknown Secrets. All the notions of liquidity proposed so far depend on the initial run  , which contains the lengths of the committed secrets. For instance, consider the run ending with the following configuration:
, which contains the lengths of the committed secrets. For instance, consider the run ending with the following configuration:

Since the length of \(\mathord {{b}_{}}\) is zero, the \(\texttt {reveal} \) branch cannot be taken, so  has a liquid strategy (e.g., fire the
has a liquid strategy (e.g., fire the  ). Instead, in an alternative initial run where
). Instead, in an alternative initial run where  chooses a secret of length 1,
chooses a secret of length 1,  has no liquid strategy, since
has no liquid strategy, since  can reveal the secret and then deny his authorization, freezing
can reveal the secret and then deny his authorization, freezing  .
.
In practice, when  performs the liquidity analysis, she does not know the secrets of other participants. To be safe,
performs the liquidity analysis, she does not know the secrets of other participants. To be safe,  should use a worst-case analysis, which would regard the contract
should use a worst-case analysis, which would regard the contract  as non-liquid. We can obtain such worst-case analysis by verifying liquidity (in the flavour of Definition 2) for all possible choices of the lengths of
as non-liquid. We can obtain such worst-case analysis by verifying liquidity (in the flavour of Definition 2) for all possible choices of the lengths of  ’s secrets. Although there is an infinite set of such lengths, each contract only checks a finite set of \(\texttt {if} \) conditions. Hence, the infinite set of lengths can be partitioned into a finite set of regions, which can be used as samples for the analysis. In this way, the basic liquidity analysis is performed a finite number of times.
’s secrets. Although there is an infinite set of such lengths, each contract only checks a finite set of \(\texttt {if} \) conditions. Hence, the infinite set of lengths can be partitioned into a finite set of regions, which can be used as samples for the analysis. In this way, the basic liquidity analysis is performed a finite number of times.
Similar worst-case analyses can be obtained for all the other above-mentioned variants of liquidity. An average-case analysis can be obtained by assuming to know the probability distribution of  ’s secrets lengths, partitioning secrets lengths like in the worst-case analysis.
’s secrets lengths, partitioning secrets lengths like in the worst-case analysis.
Other Variants. Mixing multiparty and strategyless liquidity, we obtain the notion of liquidity used in [35], in the context of Ethereum smart contracts. This notion considers a contract liquid if there exists a collaborative strategy of all participants that never freezes funds. Other variants may take into account the time when funds become liquid, the payoff of strategies (e.g., ruling out irrational adversaries), or fairness issues. Note indeed that Definition 2 already assumes a sort of fairness, by effectively forbidding the adversary to interfere when the honest participant attempts to unfreeze some funds. Technically, this is implemented in item (1) of Definition 2, requiring that the moves \(\ell _{1} \ldots \ell _{n}\) are performed atomically. Atomicity might be realistic in some settings, but not in others. For instance, in Ethereum a sequence \(\ell _{1} \ldots \ell _{n}\) of method calls can be performed atomically: this requires to deploy a new contract with a suitable method which performs the calls \(\ell _{1} \ldots \ell _{n}\) in sequence, and then to invoke it. BitML, instead, does not allow participants to perform an atomic sequence of moves: an honest participant could start to perform the sequence, but at some point in the middle the adversary interferes. To make the contract liquid, the honest participant must still have a way to unfreeze the funds from the contract. Of course, the adversary could interfere once again, and so on. This could lead to an infinite trace where each attempt by the honest player is hindered by the adversary. However, this is not an issue in BitML, for the following reason. Since the moves \(\ell _{1} \ldots \ell _{n}\) make the contract terminate, we can safely assume that each of these moves makes the contract progress (as moves which do not affect the contract can be avoided). Since a BitML contract can not progress forever without terminating (and unfreezing its funds), the honest participant just needs to be able to make a step at a time (with possible interferences by the adversary, which may affect the choice of the next step). Defining liquidity beyond BitML and Ethereum may require to rule out unfair runs, where the adversary prevents honest participants to perform the needed sequences of moves.
4 A Finite-State Semantics of BitML
The concrete BitML semantics is infinite-state because participants can always create new contracts and deposits, and can advance the current time (a natural number). In this section we introduce an abstract semantics for BitML, which focuses on both these features so to reduce the state space to a finite one. More specifically, for a concrete configuration \({\varGamma _{}} \mid {t_{}}\):
-
we abstract \(\varGamma _{}\) as an abstract configuration
 , where
, where 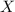 is the (finite) set of contract names under observation. Roughly,
is the (finite) set of contract names under observation. Roughly,  represents only the part of \(\varGamma _{}\) needed to run the contracts
represents only the part of \(\varGamma _{}\) needed to run the contracts  , discarding the other parts;
, discarding the other parts; -
we abstract \(t_{}\) as a time interval
 , where
, where  . The parameter \(\mathcal {T}_{}\) is a finite set of naturals, which intuitively represents all the deadlines occurring in the contracts
. The parameter \(\mathcal {T}_{}\) is a finite set of naturals, which intuitively represents all the deadlines occurring in the contracts  .
.
We start by defining the abstraction of configurations.
Definition 3
(Abstraction of configurations). We define the function  on concrete configurations in Fig. 4, where \(y^{\star }\) denotes a fixed name not present in any concrete configuration. We write
on concrete configurations in Fig. 4, where \(y^{\star }\) denotes a fixed name not present in any concrete configuration. We write  for
for  , where:
, where:

where we denote with  the set of deposit names in some \(\texttt {put} \) within
the set of deposit names in some \(\texttt {put} \) within  , and with
, and with  the set of secrets names in some \(\texttt {reveal} \) within
the set of secrets names in some \(\texttt {reveal} \) within  .
.
The abstraction removes from \(\varGamma _{}\) all the deposits not in  , all the (committed or revealed) secrets not in
, all the (committed or revealed) secrets not in  , and all the authorizations enabling branches of some contracts not in
, and all the authorizations enabling branches of some contracts not in  . All the other authorizations—but the deposit authorizations, which are handled in a special way—are removed. This is because, in the concrete semantics, deposits move into fresh ones which are no longer relevant for the contracts
. All the other authorizations—but the deposit authorizations, which are handled in a special way—are removed. This is because, in the concrete semantics, deposits move into fresh ones which are no longer relevant for the contracts  . Note that if we precisely tracked such irrelevant deposits and their authorizations, our abstract semantics would become infinite-state. To cope with this issue, the abstract semantics will render deposit moves as “destroy” moves, removing the now irrelevant deposits from the configuration. As anticipated in Sect. 2.2, an authorization of a deposit move can only be performed after a “self-donate” authorization
. Note that if we precisely tracked such irrelevant deposits and their authorizations, our abstract semantics would become infinite-state. To cope with this issue, the abstract semantics will render deposit moves as “destroy” moves, removing the now irrelevant deposits from the configuration. As anticipated in Sect. 2.2, an authorization of a deposit move can only be performed after a “self-donate” authorization  , which lets
, which lets  transfer the funds in x to another of her deposits. Our abstraction maps such
transfer the funds in x to another of her deposits. Our abstraction maps such  into an “abstract destroy” authorization
into an “abstract destroy” authorization  . In this way, in abstract configurations, deposits can be destroyed when, in concrete configurations, they are no longer relevant.
. In this way, in abstract configurations, deposits can be destroyed when, in concrete configurations, they are no longer relevant.
The abstraction of time  is parameterised over a finite set of naturals \(\mathcal {T}_{}\), which partitions \(\mathbb {N}\) into a finite set of non-overlapping intervalsFootnote 3. Each time \(t_{}\) is abstracted as
is parameterised over a finite set of naturals \(\mathcal {T}_{}\), which partitions \(\mathbb {N}\) into a finite set of non-overlapping intervalsFootnote 3. Each time \(t_{}\) is abstracted as  , which is the unique interval containing \(t_{}\).
, which is the unique interval containing \(t_{}\).
Definition 4
(Abstraction of time). Let \(\mathcal {T}_{}\in \wp _{ fin}(\mathbb {N})\). We define the function  as
as  where:
where:

Lemma 1
If  , then: (i)
, then: (i)  ; (ii)
; (ii)  is finite.
is finite.
Abstract Semantics. We now describe the abstract semantics of BitML (the detailed formalisation is deferred to Definition 7 in Appendix A). An abstract configuration is a term of the form  , where
, where  is a concrete untimed configuration, and
is a concrete untimed configuration, and  . We then define the relation
. We then define the relation  between abstract configurations by differences w.r.t. the concrete relation \(\xrightarrow {}\):
between abstract configurations by differences w.r.t. the concrete relation \(\xrightarrow {}\):
-
1.
the rule to advertise contracts is removed.
-
2.
the rules for deposits are replaced by two rules, which authorize and perform the destroy of deposits. In these rules we use the fixed name \(y^{\star }\), unlike the fresh names in the concrete semantics, so to avoid infinite branching.
-
3.
the rule for delays is replaced by a new rule, which allows for transitions
 . The delay \(\delta \) is the least positive integer which makes
. The delay \(\delta \) is the least positive integer which makes  (in the earliest moment) step to \(T'_{}\), i.e.
(in the earliest moment) step to \(T'_{}\), i.e. 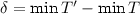 .
. -
4.
the rule for making a contract
 reduce to a deposit
reduce to a deposit  is replaced so that
is replaced so that 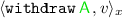 reduces to \(0\) (the empty configuration).
reduces to \(0\) (the empty configuration). -
5.
the rule for making branches
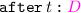 evolve is adapted to time intervals. The new rule requires that the current time interval \(T_{}\) is later than \(t_{}\).
evolve is adapted to time intervals. The new rule requires that the current time interval \(T_{}\) is later than \(t_{}\).
Abstract Runs. Given an arbitrary abstract configuration \({\varGamma _{0}} \mid {T_{0}}\), an abstract run \(\mathcal {R}^{\sharp }_{}\) is a (possibly infinite) sequence  . While concrete runs always start (at time 0) from configurations which contain only deposits, abstract runs can start from arbitrary configurations.
. While concrete runs always start (at time 0) from configurations which contain only deposits, abstract runs can start from arbitrary configurations.
Abstract Strategies. An abstract strategy  is a PPTIME algorithm which allows
is a PPTIME algorithm which allows  to select which actions to perform, among those permitted by the abstract semantics. Conformance between abstract runs and strategies is defined similarly to the concrete case [14].
to select which actions to perform, among those permitted by the abstract semantics. Conformance between abstract runs and strategies is defined similarly to the concrete case [14].
Concretisation of Strategies. Each abstract strategy  can be transformed into a concrete strategy
can be transformed into a concrete strategy  as follows. The transformation is parameterised over a concrete run
as follows. The transformation is parameterised over a concrete run  and a set of contract names
and a set of contract names  : intuitively,
: intuitively,  is the concrete counterpart of the initial abstract configuration \({\varGamma _{0}} \mid {T_{0}}\), and
is the concrete counterpart of the initial abstract configuration \({\varGamma _{0}} \mid {T_{0}}\), and  is the set of contracts under observation. The strategy
is the set of contracts under observation. The strategy  receives as input a concrete run \(\mathcal {R}_{}\), and it must output the next actions. If \(\mathcal {R}_{}\) is a prefix of
receives as input a concrete run \(\mathcal {R}_{}\), and it must output the next actions. If \(\mathcal {R}_{}\) is a prefix of  , the next move is chosen as in
, the next move is chosen as in  . The case where \(\mathcal {R}_{}\) is not an extension of
. The case where \(\mathcal {R}_{}\) is not an extension of  is immaterial. Assuming that \(\mathcal {R}_{}\) extends
is immaterial. Assuming that \(\mathcal {R}_{}\) extends  , we first abstract the part of \(\mathcal {R}_{}\) exceeding
, we first abstract the part of \(\mathcal {R}_{}\) exceeding  , so to obtain an abstract run \(\mathcal {R}^{\sharp }_{}\). This is done by abstracting every configuration in the run: times are abstracted with
, so to obtain an abstract run \(\mathcal {R}^{\sharp }_{}\). This is done by abstracting every configuration in the run: times are abstracted with  , while untimed configurations are abstracted with
, while untimed configurations are abstracted with  , where
, where  is the set of the descendants of
is the set of the descendants of  in the configuration at hand. The moves of \(\mathcal {R}_{}\) are mapped to abstract moves in a natural way: moves not affecting the descendents of
in the configuration at hand. The moves of \(\mathcal {R}_{}\) are mapped to abstract moves in a natural way: moves not affecting the descendents of  , nor their relevant deposits or secrets, are not represented in the abstract run. Once the abstract run \(\mathcal {R}^{\sharp }_{}\) has been constructed, we apply
, nor their relevant deposits or secrets, are not represented in the abstract run. Once the abstract run \(\mathcal {R}^{\sharp }_{}\) has been constructed, we apply  to obtain the next abstract actions.
to obtain the next abstract actions.  is defined as the concretisation of these actions. The concretisation of the adversary strategy
is defined as the concretisation of these actions. The concretisation of the adversary strategy  can be defined in a similar way.
can be defined in a similar way.
Theorem 1
Starting from any abstract configuration, the relation  is finitely branching, and it admits a finite number of runs.
is finitely branching, and it admits a finite number of runs.
A direct consequence of Theorem 1 is that the abstract semantics is finite-state, and that each abstract run is finite. This makes the abstract LTS amenable to model checking.
Correspondence Between the Semantics. We now establish a correspondence between the abstract and the concrete semantics of BitML. Assume that we have a concrete run  , representing the computation done so far. We want to observe the behaviour of a set of contracts
, representing the computation done so far. We want to observe the behaviour of a set of contracts  in \(\varGamma _{\mathcal {R}_{0}}\) (the last untimed configuration of
in \(\varGamma _{\mathcal {R}_{0}}\) (the last untimed configuration of  ). To this purpose, we run the abstract semantics, starting from an initial configuration \(\varGamma _{0}^{\sharp }\), whose untimed component is
). To this purpose, we run the abstract semantics, starting from an initial configuration \(\varGamma _{0}^{\sharp }\), whose untimed component is  . The time component is obtained by abstracting the last time
. The time component is obtained by abstracting the last time  in the concrete run. The parameter \(\mathcal {T}_{0}\) used to abstract time is any finite superset of the deadlines occurring in contracts
in the concrete run. The parameter \(\mathcal {T}_{0}\) used to abstract time is any finite superset of the deadlines occurring in contracts  within
within  . Hereafter we denote this set of deadlines as
. Hereafter we denote this set of deadlines as  (see Definition 8 in Appendix A).
(see Definition 8 in Appendix A).
When the contracts in  evolve, the run
evolve, the run  is extended to a run \(\mathcal {R}_{}\), which contains the descendents of
is extended to a run \(\mathcal {R}_{}\), which contains the descendents of  , i.e. those contracts whose origin belongs to
, i.e. those contracts whose origin belongs to  . These descendents are denoted with
. These descendents are denoted with  .
.
Definition 5
For all concrete runs  such that \(\mathcal {R}_{}\) extends
such that \(\mathcal {R}_{}\) extends  , and set of deposit names
, and set of deposit names  , we define the set of deposit names
, we define the set of deposit names  as follows:
as follows:

The following theorem states that the abstract semantics is a sound approximation of the concrete one. Every abstract run (conforming to  ’s abstract strategy
’s abstract strategy  ) has a corresponding concrete run (conforming to the concrete strategy derived from
) has a corresponding concrete run (conforming to the concrete strategy derived from  ). More precisely, each configuration \({\varGamma _{}^{\sharp }} \mid {T_{}}\) in the abstract run has a corresponding configuration in the concrete run, containing the concretization \(\varGamma _{}\) of \(\varGamma _{}^{\sharp }\), besides a term \(\varDelta _{}\) containing the parts unrelated to \(X_{0}\). Further, each move in the abstract run corresponds to an analogous move in the concrete run.
). More precisely, each configuration \({\varGamma _{}^{\sharp }} \mid {T_{}}\) in the abstract run has a corresponding configuration in the concrete run, containing the concretization \(\varGamma _{}\) of \(\varGamma _{}^{\sharp }\), besides a term \(\varDelta _{}\) containing the parts unrelated to \(X_{0}\). Further, each move in the abstract run corresponds to an analogous move in the concrete run.
Theorem 2
(Soundness). Let  be a concrete run, let
be a concrete run, let  , let
, let  , let
, let  , let
, let  . Let
. Let  and
and  be the abstract strategies of
be the abstract strategies of  and of
and of  , and let
, and let  and
and  be the corresponding concrete strategies. For each abstract run
be the corresponding concrete strategies. For each abstract run  conforming to
conforming to  and
and  , there exists a concrete run:
, there exists a concrete run:

such that: (i) \(\mathcal {R}_{}\) conforms to  and
and  ; (ii) \(\varDelta _{}\) contains all the subterms of
; (ii) \(\varDelta _{}\) contains all the subterms of  which are mapped to \(0\) when evaluating
which are mapped to \(0\) when evaluating  ; (iii)
; (iii)  , where
, where  ; (iv)
; (iv)  ; (v) the labels in \(\mathcal {R}_{}\) are the same as in \(\mathcal {R}^{\sharp }_{}\), except for the occurrences of \(y^{\star }\).
; (v) the labels in \(\mathcal {R}_{}\) are the same as in \(\mathcal {R}^{\sharp }_{}\), except for the occurrences of \(y^{\star }\).
Note that soundness only guarantees the existence of some concrete runs, which are a strict subset of all the possible concrete runs. For instance, the concrete semantics also allows the non-observed part \(\varDelta _{}\) to progress, and it contains configurations with a time \(t_{}\ne \min T_{}\), for any \(T_{}\) in any abstract run. Still, these concrete runs have an abstract counterpart, as established by the following completeness result (Theorem 3). This is almost dual to our soundness result (Theorem 2). Completeness maps concrete configurations to abstract ones using our abstraction functions for untimed configurations and time. Moreover, this run correspondence holds when the concrete strategy of  is derived from an abstract strategy, while no such restriction is required for the adversary strategy.
is derived from an abstract strategy, while no such restriction is required for the adversary strategy.
Theorem 3
(Completeness). Let  be a concrete run, let
be a concrete run, let  , let
, let  , let
, let  , and let
, and let  . Let
. Let  be the abstract strategy of
be the abstract strategy of  , and let
, and let  be the corresponding concrete strategy. For each concrete run
be the corresponding concrete strategy. For each concrete run  conforming to
conforming to  and to some
and to some  , there exists an abstract run:
, there exists an abstract run:

such that: (i) \(\mathcal {R}^{\sharp }_{}\) conforms to  and to some
and to some  ; (ii)
; (ii)  ; (iii) if
; (iii) if  and
and  , then there exists \(\ell '_{}\) such that
, then there exists \(\ell '_{}\) such that  where
where  and
and  .
.
Example 5
Let  , and let \(\mathcal {R}_{}\) be the following concrete run, where the prefix \(\cdots \) is immaterial (for simplicity, we also omit labels, times, and participants’ strategies):
, and let \(\mathcal {R}_{}\) be the following concrete run, where the prefix \(\cdots \) is immaterial (for simplicity, we also omit labels, times, and participants’ strategies):

By Theorem 3, this concrete run has the following corresponding abstract run w.r.t.  . The initial configuration \(\varGamma _{0}\) is abstracted w.r.t. \(X_{0}\) and
. The initial configuration \(\varGamma _{0}\) is abstracted w.r.t. \(X_{0}\) and  . This causes deposit
. This causes deposit  to be neglected in the abstraction.
to be neglected in the abstraction.

We now compare the two runs. The concrete authorization for a self-donate of \(y_{}\) is abstracted as an authorization for destroying \(y_{}\). Instead, the concrete authorization for donating \(y_{}\) to  has no abstract counterpart. The concrete reveal of secret
has no abstract counterpart. The concrete reveal of secret  and the subsequent contract move have identical abstract moves, which reach the abstract configuration \(\varGamma _{}^{\sharp }\). Technically, \(\varGamma _{}^{\sharp }\) is the result of abstracting the concrete configuration \(\varGamma _{}\) w.r.t.
and the subsequent contract move have identical abstract moves, which reach the abstract configuration \(\varGamma _{}^{\sharp }\). Technically, \(\varGamma _{}^{\sharp }\) is the result of abstracting the concrete configuration \(\varGamma _{}\) w.r.t.  and
and  : here, we no longer abstract w.r.t. \(X_{0}\), but instead use the set of its descendents
: here, we no longer abstract w.r.t. \(X_{0}\), but instead use the set of its descendents  . By contrast, the set
. By contrast, the set  is unchanged. Note that, if we instead abstracted with respect to \(X_{0}\), we would discard the contract
is unchanged. Note that, if we instead abstracted with respect to \(X_{0}\), we would discard the contract  , in which case we could not perform the abstract step, because the abstract semantics does not discard
, in which case we could not perform the abstract step, because the abstract semantics does not discard  . Similarly, if we instead used
. Similarly, if we instead used  we would discard the secret \(\mathord {{a}_{}}\) and the deposit \(y_{}\), invalidating the abstract steps. When \(\varGamma _{}\) performs the next move (a donation) this is abstracted as a destroy move. Finally, the last concrete
we would discard the secret \(\mathord {{a}_{}}\) and the deposit \(y_{}\), invalidating the abstract steps. When \(\varGamma _{}\) performs the next move (a donation) this is abstracted as a destroy move. Finally, the last concrete  move is mapped to an abstract
move is mapped to an abstract  move, which does not create the deposit \(x''_{}\).
move, which does not create the deposit \(x''_{}\).
5 Verifying Liquidity
In this section we devise a verification technique for liquidity of BitML contracts, exploiting our abstract semantics. The first step is to give an abstract counterpart of liquidity: this is done in Definition 6, which mimics Definition 2, replacing concrete objects with abstract ones.
Definition 6
(Abstract liquidity). Let  be an honest participant, with abstract strategy
be an honest participant, with abstract strategy  , let \(\mathcal {R}^{\sharp }_{0}\) be an abstract run, and let \(X_{0}\) be a set of contract names in \(\varGamma _{\mathcal {R}^{\sharp }_{0}}\). We say that \(X_{0}\) is \(\sharp \)-liquid w.r.t.
, let \(\mathcal {R}^{\sharp }_{0}\) be an abstract run, and let \(X_{0}\) be a set of contract names in \(\varGamma _{\mathcal {R}^{\sharp }_{0}}\). We say that \(X_{0}\) is \(\sharp \)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\) if for all extensions \(\mathcal {R}^{\sharp }_{}\) of \(\mathcal {R}^{\sharp }_{0}\) conforming to
in \(\mathcal {R}^{\sharp }_{0}\) if for all extensions \(\mathcal {R}^{\sharp }_{}\) of \(\mathcal {R}^{\sharp }_{0}\) conforming to  and to some
and to some  , there exists an extension \( \dot{\mathcal {R}^{\sharp }}_{}= \mathcal {R}^{\sharp }_{}\xrightarrow {\ell _{1}} \cdots \xrightarrow {\ell _{n}} \) of \(\mathcal {R}^{\sharp }_{}\) such that:
, there exists an extension \( \dot{\mathcal {R}^{\sharp }}_{}= \mathcal {R}^{\sharp }_{}\xrightarrow {\ell _{1}} \cdots \xrightarrow {\ell _{n}} \) of \(\mathcal {R}^{\sharp }_{}\) such that:


To verify liquidity of a set of contracts \(X_{0}\) in a concrete run  , we will choose \(\mathcal {R}^{\sharp }_{0}\) to be the run containing a single configuration \(\varGamma _{0}^{\sharp }\), obtained by abstracting with
, we will choose \(\mathcal {R}^{\sharp }_{0}\) to be the run containing a single configuration \(\varGamma _{0}^{\sharp }\), obtained by abstracting with  the last configuration of
the last configuration of  . In such case, the condition (4) above can be simplified by just requiring that
. In such case, the condition (4) above can be simplified by just requiring that  .
.
The following lemma states that abstract and concrete liquidity are equivalent. For this, it suffices that the abstraction is performed with respect to the contract names \(X_{0}\), and to the set of deadlines occurring in the contracts \(X_{0}\).
Lemma 2
(Abstract vs. concrete liquidity). Let  be a concrete run, let
be a concrete run, let  , and let
, and let  . Let
. Let  . Let
. Let  be an abstract strategy (w.r.t. \(\mathcal {T}_{0}\) and \(\varGamma _{0}^{\sharp }\)), and let
be an abstract strategy (w.r.t. \(\mathcal {T}_{0}\) and \(\varGamma _{0}^{\sharp }\)), and let  . Let \(\mathcal {R}^{\sharp }_{0}= \varGamma _{0}^{\sharp }\) (i.e., the run with no moves). Then:
. Let \(\mathcal {R}^{\sharp }_{0}= \varGamma _{0}^{\sharp }\) (i.e., the run with no moves). Then:

The following lemma states that if a contract is liquid w.r.t. some concrete strategy, then is also liquid w.r.t. some abstract strategy, and vice versa. Intuitively, this holds since if it is possible to make a contract evolve with a sequence of moves conforming to any concrete strategy, then the same moves can be also be generated by an abstract strategy.
Lemma 3
Let  be a concrete run, and let
be a concrete run, and let  . \(X_{0}\) is liquid w.r.t. some
. \(X_{0}\) is liquid w.r.t. some  in
in  iff \(X_{0}\) is liquid w.r.t.
iff \(X_{0}\) is liquid w.r.t.  in
in  , for some
, for some  .
.
Our main technical result follows. It states that liquidity is decidable, and that it is possible to automatically infer liquid strategies for a given contract.
Theorem 4
(Decidability of liquidity). Liquidity is decidable. Furthermore, for any  and \(X_{0}\), it is decidable whether there exists a strategy
and \(X_{0}\), it is decidable whether there exists a strategy  such that \(X_{0}\) is liquid w.r.t.
such that \(X_{0}\) is liquid w.r.t.  in
in  . If such strategy exists, then it can be automatically inferred given
. If such strategy exists, then it can be automatically inferred given  and \(X_{0}\).
and \(X_{0}\).
Proof
Let  be an honest participant with strategy
be an honest participant with strategy  , let
, let  be a concrete run, and let \(X_{0}\) be a set of contract names in
be a concrete run, and let \(X_{0}\) be a set of contract names in  . By Lemma 3, \(X_{0}\) is liquid w.r.t.
. By Lemma 3, \(X_{0}\) is liquid w.r.t.  iff there exists some abstract strategy
iff there exists some abstract strategy  such that \(X_{0}\) is liquid w.r.t.
such that \(X_{0}\) is liquid w.r.t.  . By Lemma 2, \(X_{0}\) is liquid w.r.t.
. By Lemma 2, \(X_{0}\) is liquid w.r.t.  iff \(X_{0}\) is \(\sharp \)-liquid w.r.t.
iff \(X_{0}\) is \(\sharp \)-liquid w.r.t.  . By Theorem 1, the abstract semantics is finite, and so the possible abstract strategies are finite. Therefore, \(\sharp \)-liquidity is decidable, and consequently also liquidity is decidable. Note that this procedure also finds a liquid strategy, if there exists one. \(\square \)
. By Theorem 1, the abstract semantics is finite, and so the possible abstract strategies are finite. Therefore, \(\sharp \)-liquidity is decidable, and consequently also liquidity is decidable. Note that this procedure also finds a liquid strategy, if there exists one. \(\square \)
6 Conclusions
We have developed a theory of liquidity for smart contracts, and a verification technique which is sound and complete for contracts expressed in BitML. Our finite-state abstraction can be applied, besides liquidity, to verify other properties of smart contracts. For instance, we could decide whether a strategy allows a participant to always terminate a contract within a certain deadline. Additionally, we could infer a strategy which guarantees that the contract terminates before a certain time (if any such strategy exists), or infer the strategy that terminates in the shortest time, etc. Although our theory is focussed on BitML, the various notions of liquidity we have proposed could be applied to more expressive languages for smart contracts, like e.g. Solidity (the high-level language used by Ethereum). To the best of our knowledge, the only form of liquidity verified so far in Ethereum is the “strategyless multiparty” variant, which only requires the existence of a cooperative strategy to unfreeze funds (this property is analysed, e.g., by the Securify tool [35]). Since Ethereum contracts are Turing-powerful, verifying their liquidity is not possible in a sound and complete manner; instead, the reduced expressiveness of BitML makes liquidity decidable in that setting.
Notes
- 1.
This assumption, while helpful to simplify the subsequent technical development, does not allow an adversary to steal money; at worst, the adversary can use the authorization to transfer the money back to the original owner.
- 2.
Note that
 could increase his probability to win the lottery by choosing a secret with length \(N>1\). However, doing so will make
could increase his probability to win the lottery by choosing a secret with length \(N>1\). However, doing so will make  lose his
lose his  deposit in the first part of \(\texttt {split} \), and so
deposit in the first part of \(\texttt {split} \), and so  ’s average payoff would be negative.
’s average payoff would be negative. - 3.
A specific choice of \(\mathcal {T}_{}\), which considers all the deadlines in the contracts
 under observation, is defined later on (Definition 8).
under observation, is defined later on (Definition 8).
References
Understanding the DAO attack, June 2016. http://www.coindesk.com/understanding-dao-hack-journalists/
Parity Wallet security alert, July 2017. https://paritytech.io/blog/security-alert.html
A Postmortem on the Parity Multi-Sig library self-destruct, November 2017. https://goo.gl/Kw3gXi
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, Ł.: Fair two-party computations via Bitcoin deposits. In: Böhme, R., Brenner, M., Moore, T., Smith, M. (eds.) FC 2014. LNCS, vol. 8438, pp. 105–121. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44774-1_8
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, Ł.: Modeling Bitcoin contracts by timed automata. In: Legay, A., Bozga, M. (eds.) FORMATS 2014. LNCS, vol. 8711, pp. 7–22. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10512-3_2
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on Bitcoin. In: IEEE S & P, pp. 443–458 (2014). First appeared on Cryptology ePrint Archive. http://eprint.iacr.org/2013/784
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on Bitcoin. Commun. ACM 59(4), 76–84 (2016)
Atzei, N., Bartoletti, M., Cimoli, T.: A survey of attacks on Ethereum Smart Contracts (SoK). In: Maffei, M., Ryan, M. (eds.) POST 2017. LNCS, vol. 10204, pp. 164–186. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54455-6_8
Atzei, N., Bartoletti, M., Cimoli, T., Lande, S., Zunino, R.: SoK: unraveling bitcoin smart contracts. In: Bauer, L., Küsters, R. (eds.) POST 2018. LNCS, vol. 10804, pp. 217–242. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89722-6_9
Atzei, N., Bartoletti, M., Lande, S., Zunino, R.: A formal model of Bitcoin transactions. In: Meiklejohn, S., Sako, K. (eds.) FC 2018. LNCS, vol. 10957, pp. 541–560. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-662-58387-6_29
Banasik, W., Dziembowski, S., Malinowski, D.: Efficient zero-knowledge contingent payments in cryptocurrencies without scripts. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 261–280. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_14
Bartoletti, M., Cimoli, T., Zunino, R.: Fun with Bitcoin smart contracts. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11247, pp. 432–449. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03427-6_32
Bartoletti, M., Zunino, R.: Constant-deposit multiparty lotteries on Bitcoin. In: Brenner, M., et al. (eds.) FC 2017. LNCS, vol. 10323, pp. 231–247. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70278-0_15
Bartoletti, M., Zunino, R.: BitML: a calculus for Bitcoin smart contracts. In: ACM SIGSAC CCS, pp. 83–100. ACM (2018)
Bartoletti, M., Zunino, R.: Verifying liquidity of Bitcoin contracts. Cryptology ePrint Archive, Report 2018/1125 (2018). https://eprint.iacr.org/2018/1125
Behrmann, G., David, A., Larsen, K.G.: A tutorial on Uppaal. In: Bernardo, M., Corradini, F. (eds.) SFM-RT 2004. LNCS, vol. 3185, pp. 200–236. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30080-9_7. http://www.it.uu.se/research/group/darts/papers/texts/new-tutorial.pdf
Bentov, I., Kumaresan, R.: How to use Bitcoin to design fair protocols. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 421–439. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_24
Bhargavan, K., et al.: Formal verification of smart contracts. In: PLAS (2016)
Buterin, V.: Ethereum: a next generation smart contract and decentralized application platform (2013). https://github.com/ethereum/wiki/wiki/White-Paper
Gilad, Y., Hemo, R., Micali, S., Vlachos, G., Zeldovich, N.: Algorand: scaling byzantine agreements for cryptocurrencies. In: Symposium on Operating Systems Principles, pp. 51–68 (2017)
Grishchenko, I., Maffei, M., Schneidewind, C.: Foundations and tools for the static analysis of Ethereum smart contracts. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10981, pp. 51–78. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96145-3_4
Grishchenko, I., Maffei, M., Schneidewind, C.: A semantic framework for the security analysis of Ethereum smart contracts. In: Bauer, L., Küsters, R. (eds.) POST 2018. LNCS, vol. 10804, pp. 243–269. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89722-6_10
Hildenbrandt, E., et al.: KEVM: a complete formal semantics of the Ethereum Virtual Machine. In: IEEE Computer Security Foundations Symposium (CSF), pp. 204–217. IEEE Computer Society (2018)
Hirai, Y.: Defining the Ethereum Virtual Machine for interactive theorem provers. In: Brenner, M., et al. (eds.) FC 2017. LNCS, vol. 10323, pp. 520–535. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70278-0_33
Klomp, R., Bracciali, A.: On symbolic verification of Bitcoin’s script language. In: Garcia-Alfaro, J., Herrera-Joancomartí, J., Livraga, G., Rios, R. (eds.) DPM/CBT -2018. LNCS, vol. 11025, pp. 38–56. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00305-0_3
Kumaresan, R., Bentov, I.: How to use Bitcoin to incentivize correct computations. In: ACM CCS, pp. 30–41 (2014)
Luu, L., Chu, D.H., Olickel, H., Saxena, P., Hobor, A.: Making smart contracts smarter. In: ACM CCS, pp. 254–269 (2016)
Maxwell, G.: The first successful zero-knowledge contingent payment (2016). https://bitcoincore.org/en/2016/02/26/zero-knowledge-contingent-payments-announcement/
Miller, A., Bentov, I.: Zero-collateral lotteries in Bitcoin and Ethereum. In: EuroS&P Workshops, pp. 4–13 (2017)
Miller, A., Cai, Z., Jha, S.: Smart contracts and opportunities for formal methods. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11247, pp. 280–299. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03427-6_22
Mythril (2018). https://github.com/ConsenSys/mythril
Nakamoto, S.: Bitcoin: a peer-to-peer electronic cash system (2008). https://bitcoin.org/bitcoin.pdf
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higherorderlogic, vol. 2283. Springer Science & Business Media, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Rocket, T.: Snowflake to avalanche: a novel metastable consensus protocol family for cryptocurrencies (2018). https://avalanchelabs.org/avalanche.pdf
Tsankov, P., Dan, A.M., Drachsler-Cohen, D., Gervais, A., Bünzli, F., Vechev, M.T.: Securify: practical security analysis of smart contracts. In: ACM CCS, pp. 67–82 (2018)
Acknowledgements
Massimo Bartoletti is partially supported by Aut. Reg. of Sardinia projects Sardcoin and Smart collaborative engineering. Roberto Zunino is partially supported by MIUR PON Distributed Ledgers for Secure Open Communities.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix
A Appendix
Lemma 4
Let \(\mathcal {R}_{0}, \mathcal {R}_{1}, \mathcal {R}_{2}\) be such that \(\mathcal {R}_{1}\) extends \(\mathcal {R}_{0}\) and \(\mathcal {R}_{2}\) extends \(\mathcal {R}_{1}\). Then:

Proof of Lemma 4 (sketch). By induction on \(\mathcal {R}_{1}\).
Definition 7
(Abstract semantics). Let  . An abstract configuration is a term of the form
. An abstract configuration is a term of the form  , where \(\varGamma _{}\) is a concrete untimed configuration, and
, where \(\varGamma _{}\) is a concrete untimed configuration, and  . We then define the relation
. We then define the relation  between abstract configurations by differences w.r.t. the concrete relation \(\xrightarrow {}\):
between abstract configurations by differences w.r.t. the concrete relation \(\xrightarrow {}\):
-
1.
the rule [C-Advertise] is removed.
-
2.
the rules for deposits are replaced by the following two rules:


-
3.
the rule [Delay] is replaced by the following:

-
4.
the rule [C-Withdraw] is replaced by the following:

-
5.
the rule [Timeout] is replaced by the following:

Definition 8
We define the function  from contracts to
from contracts to  as follows:
as follows:

Then, for any set of names  , we define the function
, we define the function  from concrete untimed configurations to \(\wp _{ fin}(\mathbb {N})\) as follows:
from concrete untimed configurations to \(\wp _{ fin}(\mathbb {N})\) as follows:

Lemma 5
If  , then
, then  .
.
Proof of Lemma 5 (sketch). When a move is performed, a contract becomes syntactically smaller, hence the set of deposit names and secret names within the contract becomes a subset.
Definition 9
(Abstract strategies). For any  and initial abstract configuration
and initial abstract configuration  with
with  , we define an abstract strategy
, we define an abstract strategy  as a PPTIME algorithm which takes as input an abstract run starting from
as a PPTIME algorithm which takes as input an abstract run starting from  and a randomness source, and gives as output a finite sequence of actions. Abstract strategies are subject to same constraints imposed to concrete ones.
and a randomness source, and gives as output a finite sequence of actions. Abstract strategies are subject to same constraints imposed to concrete ones.
Note that, since  can only output moves according to the abstract semantics, it can only choose delays \(\delta \) which jump from an interval \(T_{}\) to a subsequent interval
can only output moves according to the abstract semantics, it can only choose delays \(\delta \) which jump from an interval \(T_{}\) to a subsequent interval  , i.e.
, i.e.  .
.
Proof of Theorem 1 (sketch). The theorem immediately follows from the definition of our abstract semantics, which, compared to the concrete semantics, removes or abstracts all the BitML rules which can violate the statement. More precisely, using rule induction we observe that each abstract step makes the configuration syntactically “smaller”, ensuring termination. Further, we have a finite amount of rules, and each rule can only cause a finite amount of branches.
Proof of Theorem 2 (sketch). Essentially, the concrete run can perform the same moves of the abstract run, with the following minor changes. The abstract rules for destroying deposits (and the related authorizations) involve the name  , which are replaced by fresh names \(y_{}\) in the concrete run. Further, abstract delay moves change the abstract time \(T_{}\) to
, which are replaced by fresh names \(y_{}\) in the concrete run. Further, abstract delay moves change the abstract time \(T_{}\) to  : in the concrete run, instead, we make time move from
: in the concrete run, instead, we make time move from  to
to  . This makes the concrete and abstract timeout rules to agree on which branches
. This makes the concrete and abstract timeout rules to agree on which branches  are enabled.
are enabled.
Proof of Theorem 3 (sketch). Each concrete move corresponds to zero or more abstract moves: in the latter case, the concrete and abstract moves are related as follows: (i) contract moves are unchanged; (ii) all authorizations are unchanged, but for  (generated by [Dep-AuthDonate]) which is abstracted as
(generated by [Dep-AuthDonate]) which is abstracted as  ; (iii) deposit moves affecting a set Y of deposits are transformed to a sequence of [Dep-AbsDestroy] moves, destroying those deposits in Y which are present in the abstract configuration; (iv) reveal moves are unchanged; (v) delay moves are mapped to delay moves (not necessarily of the same duration).
; (iii) deposit moves affecting a set Y of deposits are transformed to a sequence of [Dep-AbsDestroy] moves, destroying those deposits in Y which are present in the abstract configuration; (iv) reveal moves are unchanged; (v) delay moves are mapped to delay moves (not necessarily of the same duration).
Proof of Lemma 3 (sketch). The lemma holds since  can be defined in terms of
can be defined in terms of  , in such a way to preserve the following invariant: each conforming run to
, in such a way to preserve the following invariant: each conforming run to  can be transformed into a concrete run conforming to
can be transformed into a concrete run conforming to  . Upon receiving a (conforming) abstract run, if some descendent of \(X_{0}\) is still present,
. Upon receiving a (conforming) abstract run, if some descendent of \(X_{0}\) is still present,  computes a corresponding concrete run and queries
computes a corresponding concrete run and queries  with it, learning the next concrete moves. Since \(X_{0}\) is liquid, the concrete strategy eventually must perform a move which is relevant for the contracts \(X_{0}\), and that move can then be chosen by
with it, learning the next concrete moves. Since \(X_{0}\) is liquid, the concrete strategy eventually must perform a move which is relevant for the contracts \(X_{0}\), and that move can then be chosen by  . If such move is then taken by the abstract adversary, the invariant is clearly preserved. If instead the adversary takes another move, we can extend the concrete run accordingly, and still preserve the invariant.
. If such move is then taken by the abstract adversary, the invariant is clearly preserved. If instead the adversary takes another move, we can extend the concrete run accordingly, and still preserve the invariant.
Liquidity for Finite LTS. We now give an alternative characterization of liquidity, which corresponds to Definition 2 on transition systems with finite traces, like the one obtained through the abstraction introduced in Sect. 4.
Definition 10
(Maximal run). We say that a run \(\mathcal {R}_{}\) is maximal w.r.t. a set of strategies  when \(\mathcal {R}_{}\xrightarrow {\ell _{}}\) implies \(\ell _{}\not \in \mathbf {\varSigma }(\mathcal {R}_{})\).
when \(\mathcal {R}_{}\xrightarrow {\ell _{}}\) implies \(\ell _{}\not \in \mathbf {\varSigma }(\mathcal {R}_{})\).
Definition 11
(Liquidity for finite LTS). Assume that  is the only honest participant, with strategy
is the only honest participant, with strategy  . We say that \(X_{0}\) is \(\sharp _{ fin}\)-liquid w.r.t.
. We say that \(X_{0}\) is \(\sharp _{ fin}\)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\) when, for all extensions \(\mathcal {R}^{\sharp }_{}\) of \(\mathcal {R}^{\sharp }_{0}\) conforming to
in \(\mathcal {R}^{\sharp }_{0}\) when, for all extensions \(\mathcal {R}^{\sharp }_{}\) of \(\mathcal {R}^{\sharp }_{0}\) conforming to  (and to some
(and to some  ), if \(\mathcal {R}^{\sharp }_{}\) is maximal w.r.t.
), if \(\mathcal {R}^{\sharp }_{}\) is maximal w.r.t.  and
and  , then
, then  .
.
Lemma 6
\(X_{0}\) is \(\sharp \)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\) iff \(X_{0}\) is \(\sharp _{ fin}\)-liquid w.r.t.
in \(\mathcal {R}^{\sharp }_{0}\) iff \(X_{0}\) is \(\sharp _{ fin}\)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\).
in \(\mathcal {R}^{\sharp }_{0}\).
Proof
For the “only if part”, assume that \(X_{0}\) is \(\sharp \)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\), and let \(\mathcal {R}^{\sharp }_{}\) be a maximal extension (w.r.t.
in \(\mathcal {R}^{\sharp }_{0}\), and let \(\mathcal {R}^{\sharp }_{}\) be a maximal extension (w.r.t.  ) of \(\mathcal {R}^{\sharp }_{0}\) conforming to
) of \(\mathcal {R}^{\sharp }_{0}\) conforming to  . By Definition 6, condition (3) can only hold for \(\dot{\mathcal {R}^{\sharp }}_{}= \mathcal {R}^{\sharp }_{}\). Hence, for all
. By Definition 6, condition (3) can only hold for \(\dot{\mathcal {R}^{\sharp }}_{}= \mathcal {R}^{\sharp }_{}\). Hence, for all  , by condition (4) it follows that
, by condition (4) it follows that  .
.
For the “if part”, assume that \(X_{0}\) is \(\sharp _{ fin}\)-liquid w.r.t.  in \(\mathcal {R}^{\sharp }_{0}\), and let \(\mathcal {R}^{\sharp }_{}\) be an extension of \(\mathcal {R}^{\sharp }_{0}\) conforming to
in \(\mathcal {R}^{\sharp }_{0}\), and let \(\mathcal {R}^{\sharp }_{}\) be an extension of \(\mathcal {R}^{\sharp }_{0}\) conforming to  . There are two cases:
. There are two cases:
-
If \(\mathcal {R}^{\sharp }_{}\) is maximal w.r.t.
 , then by Definition 11 it follows that
, then by Definition 11 it follows that  implies
implies  . Hence, conditions (3)–(4) of Definition 6 follow by choosing
. Hence, conditions (3)–(4) of Definition 6 follow by choosing  .
. -
If \(\mathcal {R}^{\sharp }_{}\) is not maximal w.r.t.
 , let \(\dot{\mathcal {R}^{\sharp }}_{}\) be the longest extension of \(\mathcal {R}^{\sharp }_{}\) made only by moves conforming to
, let \(\dot{\mathcal {R}^{\sharp }}_{}\) be the longest extension of \(\mathcal {R}^{\sharp }_{}\) made only by moves conforming to  . Let
. Let  be the strategy which (i) is equal to
be the strategy which (i) is equal to  on the prefix \(\mathcal {R}^{\sharp }_{}\), (ii) permits
on the prefix \(\mathcal {R}^{\sharp }_{}\), (ii) permits  ’s action on the extension, (iii) forbids any action after \(\dot{\mathcal {R}^{\sharp }}_{}\). By this construction, \(\dot{\mathcal {R}^{\sharp }}_{}\) is maximal w.r.t.
’s action on the extension, (iii) forbids any action after \(\dot{\mathcal {R}^{\sharp }}_{}\). By this construction, \(\dot{\mathcal {R}^{\sharp }}_{}\) is maximal w.r.t.  . So, by Definition 11 we have
. So, by Definition 11 we have  for all
for all  . Conditions (3)–(4) of Definition 6 follow by choosing \(\dot{\mathcal {R}^{\sharp }}_{}\). \(\square \)
. Conditions (3)–(4) of Definition 6 follow by choosing \(\dot{\mathcal {R}^{\sharp }}_{}\). \(\square \)
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Bartoletti, M., Zunino, R. (2019). Verifying Liquidity of Bitcoin Contracts. In: Nielson, F., Sands, D. (eds) Principles of Security and Trust. POST 2019. Lecture Notes in Computer Science(), vol 11426. Springer, Cham. https://doi.org/10.1007/978-3-030-17138-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-17138-4_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17137-7
Online ISBN: 978-3-030-17138-4
eBook Packages: Computer ScienceComputer Science (R0)







 , representing the advertisement of contract
, representing the advertisement of contract  with preconditions
with preconditions  ;
; , representing a stipulated contract, holding a current balance of
, representing a stipulated contract, holding a current balance of  . The name
. The name  uniquely identifies the contract in a configuration;
uniquely identifies the contract in a configuration; representing a fund of
representing a fund of  owned by
owned by  , and with unique name
, and with unique name  ;
; , representing
, representing  ’s authorizations to perform some operation
’s authorizations to perform some operation  , representing that
, representing that  has committed to a random secret
has committed to a random secret  , representing that
, representing that  has revealed her secret
has revealed her secret  is the parallel composition of two configurations (with identity
is the parallel composition of two configurations (with identity  is a timed configuration, where
is a timed configuration, where 
 , where
, where  is the (finite) set of contract names under observation. Roughly,
is the (finite) set of contract names under observation. Roughly,  represents only the part of
represents only the part of  , discarding the other parts;
, discarding the other parts; , where
, where  . The parameter
. The parameter  .
.
 . The delay
. The delay  (in the earliest moment) step to
(in the earliest moment) step to 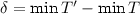 .
. reduce to a deposit
reduce to a deposit  is replaced so that
is replaced so that 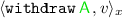 reduces to
reduces to 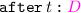 evolve is adapted to time intervals. The new rule requires that the current time interval
evolve is adapted to time intervals. The new rule requires that the current time interval  could increase his probability to win the lottery by choosing a secret with length
could increase his probability to win the lottery by choosing a secret with length  lose his
lose his  deposit in the first part of
deposit in the first part of  ’s average payoff would be negative.
’s average payoff would be negative. under observation, is defined later on (Definition
under observation, is defined later on (Definition 




 , then by Definition
, then by Definition  implies
implies  . Hence, conditions (
. Hence, conditions ( .
. , let
, let  . Let
. Let  be the strategy which (i) is equal to
be the strategy which (i) is equal to  on the prefix
on the prefix  ’s action on the extension, (iii) forbids any action after
’s action on the extension, (iii) forbids any action after  . So, by Definition
. So, by Definition  for all
for all  . Conditions (
. Conditions (