Abstract
There are different categorical approaches to variations of transition systems and their bisimulations. One is coalgebra for a functor G, where a bisimulation is defined as a span of G-coalgebra homomorphism. Another one is in terms of path categories and open morphisms, where a bisimulation is defined as a span of open morphisms. This similarity is no coincidence: given a functor G, fulfilling certain conditions, we derive a path-category for pointed G-coalgebras and lax homomorphisms, such that the open morphisms turn out to be precisely the G-coalgebra homomorphisms. The above construction provides path-categories and trace semantics for free for different flavours of transition systems: (1) non-deterministic tree automata (2) regular nondeterministic nominal automata (RNNA), an expressive automata notion living in nominal sets (3) multisorted transition systems. This last instance relates to Lasota’s construction, which is in the converse direction.
This research was supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST. The first author was supported by the DFG project MI 717/5-1. He expresses his gratitude for having been invited to Tokyo, which initiated the present work.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Coalgebras [25] and open maps [16] are two main categorical approaches to transition systems and bisimulations. The former describes the branching type of systems as an endofunctor, a system becoming a coalgebra and bisimulations being spans of coalgebra homomorphisms. Coalgebra theory makes it easy to consider state space types in different settings, e.g. nominal sets [17, 18] or algebraic categories [5, 11, 20]. The latter, open maps, describes systems as objects of a category and the execution types as particular objects called paths. In this case, bisimulations are spans of open morphisms. Open maps are particularly adapted to extend bisimilarity to history dependent behaviors, e.g. true concurrency [7, 8], timed systems [22] and weak (bi)similarity [9]. Coalgebra homomorphisms and open maps are then key concepts to describe bisimilarity categorically. They intuitively correspond to functional bisimulations, that is, those maps between states whose graph is a bisimulation.
We are naturally interested in the relationship between those two categorical approaches to transition systems and bisimulations. A reduction of open maps situations to coalgebra was given by Lasota using multi-sorted transition systems [19]. In this paper, we give the reduction in the other direction: from the category  of pointed TF-coalgebras and lax homomorphisms, we construct the path-category
of pointed TF-coalgebras and lax homomorphisms, we construct the path-category  and a functor
and a functor  such that
such that  -open morphisms coincide with strict homomorphisms, hence functional bisimulations. Here, T is a functor describing the branching behaviour and F describes the input type, i.e. the type of data that is processed (e.g. words or trees). This development is carried out with the case where T is a powerset-like functor, and covers transition systems allowing non-deterministic branching.
-open morphisms coincide with strict homomorphisms, hence functional bisimulations. Here, T is a functor describing the branching behaviour and F describes the input type, i.e. the type of data that is processed (e.g. words or trees). This development is carried out with the case where T is a powerset-like functor, and covers transition systems allowing non-deterministic branching.
The key concept in the construction of  are F-precise maps. Roughly speaking in set, a map \(f:X\mathbin {\longrightarrow }FY\) is F-precise if every \(y\in Y\) is used precisely once in f, i.e. there is a unique x such that y appears in f(x) and additionally y appears precisely once in f(x). Such an F-precise map represents one deterministic step (of shape F). Then a path
are F-precise maps. Roughly speaking in set, a map \(f:X\mathbin {\longrightarrow }FY\) is F-precise if every \(y\in Y\) is used precisely once in f, i.e. there is a unique x such that y appears in f(x) and additionally y appears precisely once in f(x). Such an F-precise map represents one deterministic step (of shape F). Then a path  is a finite sequence of deterministic steps, i.e. finitely many precise maps. J converts such a data into a pointed TF-coalgebra. There are many existing notions of paths and traces in coalgebra [4, 12, 13, 21], which lack the notion of precise map, which is crucial for the present work.
is a finite sequence of deterministic steps, i.e. finitely many precise maps. J converts such a data into a pointed TF-coalgebra. There are many existing notions of paths and traces in coalgebra [4, 12, 13, 21], which lack the notion of precise map, which is crucial for the present work.
Once we set up the situation  , we are on the framework of open map bisimulations. Our construction of
, we are on the framework of open map bisimulations. Our construction of  using precise maps is justified by the characterisation theorem:
using precise maps is justified by the characterisation theorem:  -open morphisms and strict coalgebra homomorphisms coincide (Theorems 3.20 and 3.24). This coincidence relies on the concept of path-reachable coalgebras, namely, coalgebras such that every state can be reached by a path. Under mild conditions, path-reachability is equivalent to an existing notion in coalgebra, defined as the non-existence of a proper sub-coalgebra (Sect. 3.5). Additionally, this characterization produces a canonical trace semantics for free, given in terms of paths (Sect. 3.6).
-open morphisms and strict coalgebra homomorphisms coincide (Theorems 3.20 and 3.24). This coincidence relies on the concept of path-reachable coalgebras, namely, coalgebras such that every state can be reached by a path. Under mild conditions, path-reachability is equivalent to an existing notion in coalgebra, defined as the non-existence of a proper sub-coalgebra (Sect. 3.5). Additionally, this characterization produces a canonical trace semantics for free, given in terms of paths (Sect. 3.6).
We illustrate our reduction with several concrete situations: different classes of non-deterministic top-down tree automata using analytic functors (Sect. 4.1), Regular Nondeterministic Nominal Automata (RNNA), an expressive automata notion living in nominal sets (Sect. 4.2), multisorted transition systems, used in Lasota’s work to construct a coalgebra situation from an open map situation (Sect. 4.3).
Notation. We assume basic categorical knowledge and notation (see e.g. [1, 3]). The cotupling of morphisms \(f:A\rightarrow C\), \(g:B\rightarrow C\) is denoted by \([f,g]:A+B\rightarrow C\), and the unique morphsim to the terminal object is \(!:X\rightarrow 1\) for every X.
2 Two Categorical Approaches for Bisimulations
We introduce the two formalisms involved in the present paper: the open maps (Sect. 2.1) and the coalgebras (Sect. 2.2). Those formalisms will be illustrated on the classic example of Labelled Transition Systems (LTSs).
Definition 2.1
Fix a set A, called the alphabet. A labelled transition system is a triple \((S,i,\varDelta )\) with S a set of states, \(i \in S\) the initial state, and \(\varDelta \subseteq S\times A\times S\) the transition relation. When \(\varDelta \) is obvious from the context, we write \(s\xrightarrow {~a}s'\) to mean \((s,a,s')\in \varDelta \).
For instance, the tuple \((\{0,\cdots ,n\},0,\{(k-1,a_k,k)~|~1\le k\le n\})\) is an LTS, and called the linear system over the word \(a_1\cdots a_n\in A^\star \). To relate LTSs, one considers functions that preserves the structure of LTSs:
Definition 2.2
A morphism of LTSs from \((S,i,\varDelta )\) to \((S',i', \varDelta ')\) is a function \(f:S \longrightarrow S'\) such that \(f(i) = i'\) and for every \((s,a,s')\in \varDelta \), \((f(s),a,f(s'))\in \varDelta '\). LTSs and morphisms of LTSs form a category, which we denote by  .
.
Some authors choose other notions of morphisms (e.g. [16]), allowing them to operate between LTSs with different alphabets for example. The usual way of comparing LTSs is by using simulations and bisimulations [23]. The former describes what it means for a system to have at least the behaviours of another, the latter describes that two systems have exactly the same behaviours. Concretely:
Definition 2.3
A simulation from \((S,i,\varDelta )\) to \((S',i',\varDelta ')\) is a relation \(R \subseteq S\times S'\) such that (1) \((i,i') \in R\), and (2) for every \(s\xrightarrow {~a}t\) and \((s,s') \in R\), there is \(t'\in S'\) such that \(s'\xrightarrow {~a}t'\) and \((t,t') \in R\). Such a relation R is a bisimulation if \(R^{-1} = \{(s',s) \mid (s,s') \in R\}\) is also a simulation.
Morphisms of LTSs are functional simulations, i.e. functions between states whose graph is a simulation. So how to model (1) systems, (2) functional simulations and (3) functional bisimulations categorically? In the next two sections, we will describe known answers to this question, with open maps and coalgebra. In both cases, it is possible to capture similarity and bisimilarity of two LTSs T and \(T'\). Generally, a simulation is a (jointly monic) span of a functional bisimulation and a functional simulation, and a bisimulation is a simulation whose converse is also a simulation, as depicted in Table 1. Consequently, to understand similarity and bisimilarity on a general level, it is enough to understand functional simulations and bisimulations.
2.1 Open Maps
The categorical framework of open maps [16] assumes functional simulations to be already modeled as a category  . For example, for
. For example, for  , objects are LTSs, and morphisms are functional simulations. Furthermore, the open maps framework assumes another category
, objects are LTSs, and morphisms are functional simulations. Furthermore, the open maps framework assumes another category  of ‘paths’ or ‘linear systems’, together with a functor J that tells how a ‘path’ is to be understood as a system:
of ‘paths’ or ‘linear systems’, together with a functor J that tells how a ‘path’ is to be understood as a system:
Definition 2.4
[16]. An open map situation is given by categories  (‘systems’ with ‘functional simulations’) and
(‘systems’ with ‘functional simulations’) and  (‘paths’) together with a functor
(‘paths’) together with a functor  .
.
For example with  , we pick
, we pick  to be the poset of words over A with prefix order. Here, the functor J maps a word \(w\in A^\star \) to the linear system over w, and \(w \le v\) to the evident functional simulation \(J(w\le v):Jw\mathbin {\longrightarrow }Jv\).
to be the poset of words over A with prefix order. Here, the functor J maps a word \(w\in A^\star \) to the linear system over w, and \(w \le v\) to the evident functional simulation \(J(w\le v):Jw\mathbin {\longrightarrow }Jv\).
In an open map situation  , we can abstractly represent the concept of a run in a system. A run of a path
, we can abstractly represent the concept of a run in a system. A run of a path  in a system
in a system  is simply defined to be an
is simply defined to be an  -morphism of type \(Jw\mathbin {\longrightarrow }T\). With this definition, each
-morphism of type \(Jw\mathbin {\longrightarrow }T\). With this definition, each  -morphism \(h:T\mathbin {\longrightarrow }T'\) (i.e. functional simulation) inherently transfers runs: given a run \(x:Jw\mathbin {\longrightarrow }T\), the morphism \(h\cdot x:Jw\mathbin {\longrightarrow }T'\) is a run of w in \(T'\). In the example open map situation
-morphism \(h:T\mathbin {\longrightarrow }T'\) (i.e. functional simulation) inherently transfers runs: given a run \(x:Jw\mathbin {\longrightarrow }T\), the morphism \(h\cdot x:Jw\mathbin {\longrightarrow }T'\) is a run of w in \(T'\). In the example open map situation  , a run of a path \(w=a_1\cdots a_n\in A^\star \) in an LTS \(T=(S,i,\varDelta )\) is nothing but a sequence of states \(x_0,\ldots ,x_n \in S\) such that \(x_0=i\) and \(x_{k-1}\xrightarrow {a_k} x_k\) holds for all \(1\le k \le n\).
, a run of a path \(w=a_1\cdots a_n\in A^\star \) in an LTS \(T=(S,i,\varDelta )\) is nothing but a sequence of states \(x_0,\ldots ,x_n \in S\) such that \(x_0=i\) and \(x_{k-1}\xrightarrow {a_k} x_k\) holds for all \(1\le k \le n\).
We introduce the concept of open map [16]. This is an abstraction of the property posessed by functional bisimulations. For LTSs \(T=(S,i,\varDelta )\) and \(T'=(S',i',\varDelta ')\), an  -morphism \(h:T\mathbin {\longrightarrow }T'\) is a functional bisimulation if the graph of h is a bisimulation. This implies the following relationship between runs in T and runs in \(T'\). Suppose that \(w\le w'\) holds in \(A^\star \), and a run x of w in T is given as in (1); here n, m are lengths of \(w,w'\) respectively. Then for any run \(y'\) of \(w'\) in \(T'\) extending \(h\cdot x\) as in (2), there is a run \(x'\) of \(w'\) extending x, and moreover its image by h coincides with \(y'\) (that is, \(h\cdot x'=y'\)). Such \(x'\) is obtained by repetitively applying the condition of functional bisimulation.
-morphism \(h:T\mathbin {\longrightarrow }T'\) is a functional bisimulation if the graph of h is a bisimulation. This implies the following relationship between runs in T and runs in \(T'\). Suppose that \(w\le w'\) holds in \(A^\star \), and a run x of w in T is given as in (1); here n, m are lengths of \(w,w'\) respectively. Then for any run \(y'\) of \(w'\) in \(T'\) extending \(h\cdot x\) as in (2), there is a run \(x'\) of \(w'\) extending x, and moreover its image by h coincides with \(y'\) (that is, \(h\cdot x'=y'\)). Such \(x'\) is obtained by repetitively applying the condition of functional bisimulation.
Observe that \(y'\) extending \(h\cdot x\) can be represented as \(y'\cdot J(w\le w')=h\cdot x\), and \(x'\) extending x as \(x'\cdot J(w\le w')=x\). From these, we conclude that if an  -morphism \(h:T\mathbin {\longrightarrow }T'\) is a functional bisimulation, then for any \(w\le w'\) in \(A^\star \) and run \(x:Jw\mathbin {\longrightarrow }T\) and \(y':Jw'\mathbin {\longrightarrow }T'\) such that \(y'\cdot J(w\le w')=h\cdot x\), there is a run \(x':Jw'\mathbin {\longrightarrow }T\) such that \(x'\cdot J(w\le w')=x\) and \(h\cdot x'=y'\) (the converse also holds if all states of T are reachable). This necessary condition of functional bisimulation can be rephrased in any open map situation, leading us to the definition of open map.
-morphism \(h:T\mathbin {\longrightarrow }T'\) is a functional bisimulation, then for any \(w\le w'\) in \(A^\star \) and run \(x:Jw\mathbin {\longrightarrow }T\) and \(y':Jw'\mathbin {\longrightarrow }T'\) such that \(y'\cdot J(w\le w')=h\cdot x\), there is a run \(x':Jw'\mathbin {\longrightarrow }T\) such that \(x'\cdot J(w\le w')=x\) and \(h\cdot x'=y'\) (the converse also holds if all states of T are reachable). This necessary condition of functional bisimulation can be rephrased in any open map situation, leading us to the definition of open map.
Definition 2.5
[16]. Let  be an open map situation. An
be an open map situation. An  -morphism \(h:T \longrightarrow T'\) is said to be open if for every morphism
-morphism \(h:T \longrightarrow T'\) is said to be open if for every morphism  making the square on the right commute, there is \(x'\) making the two triangles commute.
making the square on the right commute, there is \(x'\) making the two triangles commute.

Open maps are closed under composition and stable under pullback [16].
2.2 Coalgebras
The theory of G-coalgebras is another categorical framework to study bisimulations. The type of systems is modelled using an endofunctor  and a system is then a coalgebra for this functor, that is, a pair of an object S of
and a system is then a coalgebra for this functor, that is, a pair of an object S of  (modeling the state space), and of a morphism of type \(S \longrightarrow GS\) (modeling the transitions). For example for LTSs, the transition relation is of type \(\varDelta \subseteq S\times A\times S\). Equivalently, this can be defined as a function \(\varDelta :S \longrightarrow \mathcal {P} (A\times S)\), where \(\mathcal {P} \) is the powerset. In other words, the transition relation is a coalgebra for the Set-functor \(\mathcal {P} (A\times \_\!\_)\). Intuitively, this coalgebra gives the one-step behaviour of an LTS: S describes the state space of the system, \(\mathcal {P} \) describes the ‘branching type’ as being non-deterministic, \( A\times S\) describe the ‘computation type’ as being linear, and the function itself lists all possible futures after one-step of computation of the system. Now, changing the underlying category or the endofunctor allows to model different types of systems. This is the usual framework of coalgebra, as described for example in [25].
(modeling the state space), and of a morphism of type \(S \longrightarrow GS\) (modeling the transitions). For example for LTSs, the transition relation is of type \(\varDelta \subseteq S\times A\times S\). Equivalently, this can be defined as a function \(\varDelta :S \longrightarrow \mathcal {P} (A\times S)\), where \(\mathcal {P} \) is the powerset. In other words, the transition relation is a coalgebra for the Set-functor \(\mathcal {P} (A\times \_\!\_)\). Intuitively, this coalgebra gives the one-step behaviour of an LTS: S describes the state space of the system, \(\mathcal {P} \) describes the ‘branching type’ as being non-deterministic, \( A\times S\) describe the ‘computation type’ as being linear, and the function itself lists all possible futures after one-step of computation of the system. Now, changing the underlying category or the endofunctor allows to model different types of systems. This is the usual framework of coalgebra, as described for example in [25].
Initial states are modelled coalgebraically by a pointing to the carrier \(i:I\mathbin {\longrightarrow }S\) for a fixed object I in  , describing the ‘type of initial states’ (see e.g. [2, Sec. 3B]). For example, an initial state of an LTS is the same as a function from the singleton set \(I:=\{*\}\) to the state space S. This object I will often be the final object of
, describing the ‘type of initial states’ (see e.g. [2, Sec. 3B]). For example, an initial state of an LTS is the same as a function from the singleton set \(I:=\{*\}\) to the state space S. This object I will often be the final object of  , but we will see other examples later. In total, an I-pointed G-coalgebra is a
, but we will see other examples later. In total, an I-pointed G-coalgebra is a  -object S together with morphisms \(\alpha :S\mathbin {\longrightarrow }GS\) and \(i:I\mathbin {\longrightarrow }S\). E.g. an LTS is an I-pointed G-coalgebra for \(I=\{*\}\) and \(GX = \mathcal {P} (A\times X)\).
-object S together with morphisms \(\alpha :S\mathbin {\longrightarrow }GS\) and \(i:I\mathbin {\longrightarrow }S\). E.g. an LTS is an I-pointed G-coalgebra for \(I=\{*\}\) and \(GX = \mathcal {P} (A\times X)\).
In coalgebra, functional bisimulations are the first class citizens to be modelled as homomorphisms. The intuition is that those preserve the initial state, and preserve and reflect the one-step relation.
Definition 2.6
An I-pointed G-coalgebra homomorphism from \(I \xrightarrow {\,i\,} S \xrightarrow {\,\alpha \,} GS\) to \(I \xrightarrow {\,i'\,} S' \xrightarrow {\,\alpha '\,} GS'\) is a morphism \(f:S \longrightarrow S'\) making the right-hand diagram commute.

For instance, when \(G=\mathcal {P} (A\times \_\!\_)\), one can easily see that a function f is a G-coalgebra homomorphism iff it is a functional bisimulation. Thus, if we want to capture functional simulations in LTSs, we need to weaken the condition of homomorphism to the inequality \(Gf(\alpha (s))\subseteq \alpha '(f(s))\) (instead of equality). To express this condition for general G-coalgebras, we introduce a partial order \(\sqsubseteq _{X,Y}\) on each homset  in a functorial manner.
in a functorial manner.
Definition 2.7
A partial order on G-homsets is a functor  such that
such that  ; here,
; here,  is the forgetful functor from the category
is the forgetful functor from the category  of posets and monotone functions.
of posets and monotone functions.
The functoriality of \(\sqsubseteq \) amounts to that \(f_1\sqsubseteq f_2\) implies \(Gh\cdot f_1\cdot g\sqsubseteq Gh\cdot f_2\cdot g\).
Definition 2.8
Given a partial order on G-homsets, an I-pointed lax G-coalgebra homomorphism \(f:(S,\alpha ,i) \longrightarrow (S',\alpha ',i')\) is a morphism \(f:S\mathbin {\longrightarrow }S'\) making the right-hand diagram commute. The I-pointed G-coalgebras and lax homomorphisms form a category, denoted by  .
.

Conclusion 2.9
In  , with \(I=\{*\}\), \(G = \mathcal {P} (A\times \_\!\_)\), define the order \(f \sqsubseteq g\) in
, with \(I=\{*\}\), \(G = \mathcal {P} (A\times \_\!\_)\), define the order \(f \sqsubseteq g\) in  iff for every \(x \in X\), \(f(x) \subseteq g(x)\). Then
iff for every \(x \in X\), \(f(x) \subseteq g(x)\). Then  . In particular, we have an open map situation
. In particular, we have an open map situation

and the open maps are precisely the coalgebra homomorphisms (for reachable LTSs). In this paper, we will construct a path category  for more general I and G, such that the open morphisms are precisely the coalgebra homomorphisms.
for more general I and G, such that the open morphisms are precisely the coalgebra homomorphisms.
3 The Open Map Situation in Coalgebras
Lasota’s construction [19] transforms an open map situation  into a functor G (with a partial order on G-homsets), together with a functor
into a functor G (with a partial order on G-homsets), together with a functor  that sends open maps to G-coalgebra homomorphisms (see Sect. 4.3 for details). In this paper, we provide a construction in the converse direction for functors G of a certain shape.
that sends open maps to G-coalgebra homomorphisms (see Sect. 4.3 for details). In this paper, we provide a construction in the converse direction for functors G of a certain shape.
As exemplified by LTSs, it is a common pattern that G is the composition \(G=TF\) of two functors [12], where T is the branching type (e.g. partial, or non-deterministic) and F is the data type, or the ‘linear behaviour’ (words, trees, words modulo \(\alpha \)-equivalence). If we instantiate our path-construction to \(T=\mathcal {P} \) and \(F=A\times \_\!\_\), we obtain the known open map situation for LTSs (Conclusion 2.9).
Fix a category  with pullbacks, functors
with pullbacks, functors  , an object
, an object  and a partial order \(\sqsubseteq ^T\) on T-homsets. They determine a coalgebra situation
and a partial order \(\sqsubseteq ^T\) on T-homsets. They determine a coalgebra situation  where \(\sqsubseteq \) is the partial order on TF-homsets defined by \({\sqsubseteq _{X,Y}}={\sqsubseteq _{X,FY}^T}\). Under some conditions on T and F, we construct a path-category
where \(\sqsubseteq \) is the partial order on TF-homsets defined by \({\sqsubseteq _{X,Y}}={\sqsubseteq _{X,FY}^T}\). Under some conditions on T and F, we construct a path-category  and an open map situation
and an open map situation  where TF-coalgebra homomorphisms and
where TF-coalgebra homomorphisms and  -open morphisms coincide.
-open morphisms coincide.
3.1 Precise Morphisms
While the path category is intuitively clear for \(FX=A\times X\), it is not for inner functors F that model tree languages. For example for \(FX=A + X\times X\), a \(\mathcal {P} F\)-coalgebra models transition systems over binary trees with leaves labelled in A, instead of over words. Hence, the paths should be these kind of binary trees. We capture the notion of tree like shape (“every node in a tree has precisely one route to the root”) by the following abstract definition:
Definition 3.1
For a functor  , a morphism \(s:S\mathbin {\longrightarrow }FR\) is called F-precise if for all f, g, h the following implication holds:
, a morphism \(s:S\mathbin {\longrightarrow }FR\) is called F-precise if for all f, g, h the following implication holds:

Remark 3.2
If F preserves weak pullbacks, then a morphism s is F-precise iff it fulfils the above definition for \(g={\text { id }} \).
Example 3.3
Intuitively speaking, for a polynomial  -functor F, a map \(s:S\rightarrow FR\) is F-precise iff every element of R is mentioned precisely once in the definition of the map f. For example, for \(FX = A\times X + \{\bot \}\), the case needed later for LTSs, a map \(f:X\mathbin {\longrightarrow }FY\) is precise iff for every \(y \in Y\), there is a unique pair \((x,a) \in X\times A\) such that \(f(x) = (a,y)\). For \(FX=X\times X +\{\bot \}\) on
-functor F, a map \(s:S\rightarrow FR\) is F-precise iff every element of R is mentioned precisely once in the definition of the map f. For example, for \(FX = A\times X + \{\bot \}\), the case needed later for LTSs, a map \(f:X\mathbin {\longrightarrow }FY\) is precise iff for every \(y \in Y\), there is a unique pair \((x,a) \in X\times A\) such that \(f(x) = (a,y)\). For \(FX=X\times X +\{\bot \}\) on  , the map \(f:X\mathbin {\longrightarrow }FY\) in Fig. 1 is not F-precise, because \(y_2\) is used three times (once in \(f(x_2)\) and twice in \(f(x_3)\)), and \(y_3\) and \(y_4\) do not occur in f at all. However, \(f':X\mathbin {\longrightarrow }FY'\) is F-precise because every element of \(Y'\) is used precisely once in \(f'\), and we have that \(Fh\cdot f' = f\). Also note that \(f'\) defines a forest where X is the set of roots, which is closely connected to the intuition that, in the F-precise map \(f'\), from every element of \(Y'\), there is precisely one edge up to a root in X.
, the map \(f:X\mathbin {\longrightarrow }FY\) in Fig. 1 is not F-precise, because \(y_2\) is used three times (once in \(f(x_2)\) and twice in \(f(x_3)\)), and \(y_3\) and \(y_4\) do not occur in f at all. However, \(f':X\mathbin {\longrightarrow }FY'\) is F-precise because every element of \(Y'\) is used precisely once in \(f'\), and we have that \(Fh\cdot f' = f\). Also note that \(f'\) defines a forest where X is the set of roots, which is closely connected to the intuition that, in the F-precise map \(f'\), from every element of \(Y'\), there is precisely one edge up to a root in X.
So when transforming a non-precise map into a precise map, one duplicates elements that are used multiple times and drops elements that are not used. We will cover functors F for which this factorization pattern provides F-precise maps. If F involves unordered structure, this factorization needs to make choices, and so we restrict the factorization to a class \(\mathcal {S} \) of objects that have that choice-principle (see Example 4.5 later):
Definition 3.4
Fix a class of objects  closed under isomorphism. We say that F admits precise factorizations w.r.t. \(\mathcal {S} \) if for every \(f:S\rightarrow FY\) with \(S\in \mathcal {S} \), there exist \(Y'\in \mathcal {S} \), \(h:Y'\rightarrow Y\) and \(f':S\rightarrow FY'\) F-precise with \(Fh\cdot f' = f\).
closed under isomorphism. We say that F admits precise factorizations w.r.t. \(\mathcal {S} \) if for every \(f:S\rightarrow FY\) with \(S\in \mathcal {S} \), there exist \(Y'\in \mathcal {S} \), \(h:Y'\rightarrow Y\) and \(f':S\rightarrow FY'\) F-precise with \(Fh\cdot f' = f\).

For  , \(\mathcal {S} \) contains all sets. However for the category of nominal sets, \(\mathcal {S} \) will only contain the strong nominal sets (see details in Subsect. 4.2).
, \(\mathcal {S} \) contains all sets. However for the category of nominal sets, \(\mathcal {S} \) will only contain the strong nominal sets (see details in Subsect. 4.2).
Remark 3.5
Precise morphisms are essentially unique. If \(f_1:X\mathbin {\longrightarrow }FY_1\) and \(f_2:X\mathbin {\longrightarrow }FY_2\) are F-precise and if there is some \(h:Y_1\mathbin {\longrightarrow }Y_2\) with \(Fh\cdot f_1 = f_2\), then h is an isomorphism. Consequently, if \(f:S\mathbin {\longrightarrow }FY\) with \(S\in \mathcal {S} \) is F-precise and F-admits precise factorizations, then \(Y\in \mathcal {S} \).
Functors admitting precise factorizations are closed under basic constructions:
Proposition 3.6
The following functors admit precise factorizations w.r.t. \(\mathcal {S} \):
-
1.
Constant functors, if
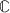 has an initial object 0 and \(0 \in \mathcal {S} \).
has an initial object 0 and \(0 \in \mathcal {S} \). -
2.
\(F\cdot F'\) if
 and
and 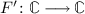 do so.
do so. -
3.
\(\prod \limits _{i\in I} F_i\), if all \((F_i)_{i\in I}\) do so and \(\mathcal {S} \) is closed under I-coproducts.
-
4.
\(\coprod \limits _{i\in I} F_i\), if all \((F_i)_{i\in I}\) do so,
 is I-extensive and \(\mathcal {S} \) is closed under I-coproducts.
is I-extensive and \(\mathcal {S} \) is closed under I-coproducts. -
5.
Right-adjoint functors, if and only if its left-adjoint preserves \(\mathcal {S} \)-objects.
Example 3.7
When  is infinitary extensive and \(\mathcal {S} \) is closed under coproducts, every polynomial endofunctor
is infinitary extensive and \(\mathcal {S} \) is closed under coproducts, every polynomial endofunctor  admits precise factorizations w.r.t. \(\mathcal {S} \). This is in particular the case for
admits precise factorizations w.r.t. \(\mathcal {S} \). This is in particular the case for  . In this case, we shall see later (Sect. 4.1) that many other
. In this case, we shall see later (Sect. 4.1) that many other  -functors, e.g. the bag functor \(\mathcal {B} \), where \(\mathcal {B} (X)\) is the set of finite multisets, have precise factorizations. In contrast, \(F=\mathcal {P} \) does not admit precise factorizations, and if \(f:X\mathbin {\longrightarrow }\mathcal {P} Y\) is \(\mathcal {P} \)-precise, then \(f(x) = \emptyset \) for all \(x\in X\).
-functors, e.g. the bag functor \(\mathcal {B} \), where \(\mathcal {B} (X)\) is the set of finite multisets, have precise factorizations. In contrast, \(F=\mathcal {P} \) does not admit precise factorizations, and if \(f:X\mathbin {\longrightarrow }\mathcal {P} Y\) is \(\mathcal {P} \)-precise, then \(f(x) = \emptyset \) for all \(x\in X\).
3.2 Path Categories in Pointed Coalgebras
We define a path for I-pointed TF-coalgebras as a tree according to F. Following the observation in Example 3.3, one layer of the tree is modelled by a F-precise morphism and hence a path in a TF-coalgebra is defined to be a finite sequence of \((F+1)\)-precise maps, where the \(\_\!\_+1\) comes from the dead states w.r.t. T; the argument is given later in Remark 3.23 when reachability is discussed. Since the \(\_\!\_+1\) is not relevant yet, we define  in the following and will use
in the following and will use  later. For simplicity, we write \(\varvec{X}_n\) for finite families \((X_k)_{0\le k < n}\).
later. For simplicity, we write \(\varvec{X}_n\) for finite families \((X_k)_{0\le k < n}\).
Definition 3.8
The category  consists of the following. An object is \((\varvec{P}_{n+1},\varvec{p}_n)\) for an
consists of the following. An object is \((\varvec{P}_{n+1},\varvec{p}_n)\) for an  with \(P_0 = I\) and \(\varvec{p}_n\) a family of F-precise maps \((p_k:P_k\mathbin {\longrightarrow }FP_{k+1})_{k<n}\). We say that \((\varvec{P}_{n+1},\varvec{p}_n)\) is a path of length n. A morphism \(\varvec{\phi }_{n+1}:(\varvec{P}_{n+1},\varvec{p}_{n}) \mathbin {\longrightarrow }(\varvec{Q}_{m+1},\varvec{q}_{m})\), \(m\ge n\), is a family \((\phi _k:P_k \mathbin {\longrightarrow }Q_k)_{k\le n}\) with \(\phi _0={{\text { id }} _{I}}\) and \(q_k\cdot \phi _k = F\phi _{k+1}\cdot p_k\) for all \(0 \le k \le n\).
with \(P_0 = I\) and \(\varvec{p}_n\) a family of F-precise maps \((p_k:P_k\mathbin {\longrightarrow }FP_{k+1})_{k<n}\). We say that \((\varvec{P}_{n+1},\varvec{p}_n)\) is a path of length n. A morphism \(\varvec{\phi }_{n+1}:(\varvec{P}_{n+1},\varvec{p}_{n}) \mathbin {\longrightarrow }(\varvec{Q}_{m+1},\varvec{q}_{m})\), \(m\ge n\), is a family \((\phi _k:P_k \mathbin {\longrightarrow }Q_k)_{k\le n}\) with \(\phi _0={{\text { id }} _{I}}\) and \(q_k\cdot \phi _k = F\phi _{k+1}\cdot p_k\) for all \(0 \le k \le n\).
Example 3.9
Paths for \(FX = A\times X + 1\) and \(I = \{*\}\) singleton are as follows. First, a map \(f:I \longrightarrow FX\) is precise iff (up-to isomorphism) either \(X = I\) and \(f(*) = (a, *)\) for some \(a \in A\); or \(X = \varnothing \) and \(f(*) = \bot \). Then a path is isomorphic to an object of the form: \(P_i = I\) for \(i \le k\), \(P_i = \varnothing \) for \(i > k\), \(p_i(*) = (a_i,*)\) for \(i < k\), and \(p_k(*) = \bot \). A path is the same as a word, plus some “junk”, concretely, a word in \(A^\star .\bot ^\star \). For LTSs, an object in  with \(FX=A\times X\) is simply a word in \(A^\star \). For a more complicated functor, Fig. 2 depicts a path of length 4, which is a tree for the signature with one unary, one binary symbol, and a constant. The layers of the tree are the sets \(\varvec{P}_4\). Also note that since every \(p_i\) is F-precise, there is precisely one route to go from every element of a \(P_k\) to \(*\).
with \(FX=A\times X\) is simply a word in \(A^\star \). For a more complicated functor, Fig. 2 depicts a path of length 4, which is a tree for the signature with one unary, one binary symbol, and a constant. The layers of the tree are the sets \(\varvec{P}_4\). Also note that since every \(p_i\) is F-precise, there is precisely one route to go from every element of a \(P_k\) to \(*\).
Remark 3.10
The inductive continuation of Remark 3.5 is as follows. Given a morphism \(\varvec{\phi }_{n+1}\) in  , since \(\phi _0\) is an isomorphism, then \(\phi _k\) is an isomorphism for all \(0\le k \le n\). If F admits precise factorizations and if \(I\in \mathcal {S} \), then for every path \((\varvec{P}_{n+1},\varvec{p}_{n})\), all \(P_k\), \(0\le k\le n\), are in \(\mathcal {S} \).
, since \(\phi _0\) is an isomorphism, then \(\phi _k\) is an isomorphism for all \(0\le k \le n\). If F admits precise factorizations and if \(I\in \mathcal {S} \), then for every path \((\varvec{P}_{n+1},\varvec{p}_{n})\), all \(P_k\), \(0\le k\le n\), are in \(\mathcal {S} \).
Remark 3.11
If in Definition 3.4, the connecting morphism \(h:Y'\mathbin {\longrightarrow }Y\) uniquely exists, then it follows by induction that the hom-sets of  are at most singleton. This is the case for all polynomial functors, but not the case for the bag functor on sets (discussed in Subsect. 4.1).
are at most singleton. This is the case for all polynomial functors, but not the case for the bag functor on sets (discussed in Subsect. 4.1).
Definition 3.12
The path poset  is the set
is the set  equipped with the order: for \(u:I\mathbin {\longrightarrow }F^n1\) and \(v:I\mathbin {\longrightarrow }F^m1\), we define \(u\le v\) if \(n \le m\) and \(F^n(!)\cdot v = u\).
equipped with the order: for \(u:I\mathbin {\longrightarrow }F^n1\) and \(v:I\mathbin {\longrightarrow }F^m1\), we define \(u\le v\) if \(n \le m\) and \(F^n(!)\cdot v = u\).

So \(u\le v\) if u is the truncation of v to n levels. This matches the morphisms in  that witnesses that one path is prefix of another:
that witnesses that one path is prefix of another:
Proposition 3.13
1. The functor  defined by \( I= P_0 \overset{p_0}{\rightarrow } FP_1\cdots \rightarrow F^{n}P_{n}\overset{F^{n}!}{\rightarrow }F^{n}1 \text { on }(\varvec{P}_{n+1},\varvec{p}_{n}) \) is full, and reflects isos.
defined by \( I= P_0 \overset{p_0}{\rightarrow } FP_1\cdots \rightarrow F^{n}P_{n}\overset{F^{n}!}{\rightarrow }F^{n}1 \text { on }(\varvec{P}_{n+1},\varvec{p}_{n}) \) is full, and reflects isos.
2. If F admits precise factorizations w.r.t. \(\mathcal {S} \) and \(I\in \mathcal {S} \), then  is sujective. 3. If additionally h in Definition 3.4 is unique, then
is sujective. 3. If additionally h in Definition 3.4 is unique, then  has a right-inverse.
has a right-inverse.
In particular, \(\mathsf {PathOrd} (I,F)\) is  up to isomorphism. In the instances, it is often easier to characterize \(\mathsf {PathOrd} (I,F)\). This also shows that
up to isomorphism. In the instances, it is often easier to characterize \(\mathsf {PathOrd} (I,F)\). This also shows that  contains the elements – understood as morphisms from I – of the finite start of the final chain of F: \( 1 \xleftarrow {!} F1 \xleftarrow {F!} F^21 \xleftarrow {F^2!} F^31 \xleftarrow {}\cdots . \)
contains the elements – understood as morphisms from I – of the finite start of the final chain of F: \( 1 \xleftarrow {!} F1 \xleftarrow {F!} F^21 \xleftarrow {F^2!} F^31 \xleftarrow {}\cdots . \)
Example 3.14
When \(FX = A\times X + 1\), \(F^n1\) is isomorphic to the set of words in \(A^\star .\bot ^\star \) of length n. Consequently, \(\mathsf {PathOrd} (I,F)\) is the set of words in \(A^\star .\bot ^\star \), equipped with the prefix order. In this case,  is an equivalence of categories.
is an equivalence of categories.
3.3 Embedding Paths into Pointed Coalgebras
The paths \((\varvec{P}_{n+1},\varvec{p}_n)\) embed into  as one expects it for examples like Fig. 2: one takes the disjoint union of the \(P_k\), one has the pointing \(I=P_0\) and the linear structure of F is embedded into the branching type T.
as one expects it for examples like Fig. 2: one takes the disjoint union of the \(P_k\), one has the pointing \(I=P_0\) and the linear structure of F is embedded into the branching type T.
During the presentation of the results, we require T, F, and I to have certain properties, which will be introduced one after the other. The full list of assumptions is summarized in Table 2:
(Ax1) – The main theorem will show that coalgebra homomorphisms in  are the open maps for the path category
are the open maps for the path category  . So from now on, we assume that
. So from now on, we assume that  has finite coproducts and to use the results from the previous sections, we fix a class
has finite coproducts and to use the results from the previous sections, we fix a class  such that \(F+1\) admits precise factorizations w.r.t. \(\mathcal {S} \) and that \(I\in \mathcal {S} \).
such that \(F+1\) admits precise factorizations w.r.t. \(\mathcal {S} \) and that \(I\in \mathcal {S} \).
(Ax2) – Recall, that a family of morphisms \((e_i:X_i \mathbin {\longrightarrow }Y)_{i\in I}\) with common codomain is called jointly epic if for \(f,g:Y\mathbin {\longrightarrow }Z\) we have that \(f\cdot e_i = g\cdot e_i~\forall i\in I\) implies \(f=g\). For  , this means, that every element \(y\in Y\) is in the image of some \(e_i\). Since we work with partial orders on T-homsets, we also need the generalization of this property if \(f\sqsubseteq g\) are of the form \(Y\mathbin {\longrightarrow }TZ'\).
, this means, that every element \(y\in Y\) is in the image of some \(e_i\). Since we work with partial orders on T-homsets, we also need the generalization of this property if \(f\sqsubseteq g\) are of the form \(Y\mathbin {\longrightarrow }TZ'\).
(Ax3) – In this section, we encode paths as a pointed coalgebra by constructing a functor  . For that we need to embed the linear behaviour \(FX+1\) into TFX. This is done by a natural transformation \([\eta ,\bot ]:{\text { Id }} +1\mathbin {\longrightarrow }T\), and we require that \(\bot :1\mathbin {\longrightarrow }T\) is a bottom element for \(\sqsubseteq \).
. For that we need to embed the linear behaviour \(FX+1\) into TFX. This is done by a natural transformation \([\eta ,\bot ]:{\text { Id }} +1\mathbin {\longrightarrow }T\), and we require that \(\bot :1\mathbin {\longrightarrow }T\) is a bottom element for \(\sqsubseteq \).
Example 3.15
For the case where T is the powerset functor \(\mathcal {P} \), \(\eta \) is given by the unit \(\eta _X(x) = \{x\}\), and \(\bot \) is given by empty sets \(\bot _X(*) = \varnothing \).
Definition 3.16
We have an inclusion functor  that maps a path \((\varvec{P}_{n+1},\varvec{p}_n)\) to an I-pointed TF-coalgebra on \(\coprod \varvec{P}_{n+1} := \coprod _{0\le k\le n} P_k\). The pointing is given by \(\mathsf {in} _0:I =P_0\mathbin {\longrightarrow }\coprod \varvec{P}_{n+1} \) and the structure by:
that maps a path \((\varvec{P}_{n+1},\varvec{p}_n)\) to an I-pointed TF-coalgebra on \(\coprod \varvec{P}_{n+1} := \coprod _{0\le k\le n} P_k\). The pointing is given by \(\mathsf {in} _0:I =P_0\mathbin {\longrightarrow }\coprod \varvec{P}_{n+1} \) and the structure by:

Example 3.17
In the case of LTSs, a path, or equivalently a word \(a_1...a_k.\bot ...\bot \in A^\star .\bot ^\star \), is mapped to the finite linear system over \(a_1...a_k\) (see Sect. 2.1), seen as a coalgebra (see Sect. 2.2).
Proposition 3.18
Given a morphism \([x_k]_{k\le n}:\coprod \varvec{P}_{n+1} \mathbin {\longrightarrow }X\) for some system \((X,\xi ,x_0)\) and a path \((\varvec{P}_{n+1},\varvec{p}_{n})\), we have

Also note that the pointing \(x_0\) of the coalgebra is necessarily the first component of any run in it. In a run \([x_k]_{k\le n}\), \(p_k\) corresponds to an edge from \(x_k\) to \(x_{k+1}\).
Example 3.19
For LTSs, since the \(P_k\) are singletons, \(x_k\) just picks the kth state of the run. The right-hand side of this lemma describes that this is a run iff there is a transition from the kth state and the \((k+1)-\)th state.
3.4 Open Morphisms Are Exactly Coalgebra Homomorphisms
In this section, we prove our main contribution, namely that  -open maps in
-open maps in  are exactly coalgebra homomorphisms. For the first direction of the main theorem, that is, that coalgebra homomorphisms are open, we need two extra axioms:
are exactly coalgebra homomorphisms. For the first direction of the main theorem, that is, that coalgebra homomorphisms are open, we need two extra axioms:
(Ax4) – describing that the order on  is point-wise. This holds for the powerset because every set is the union of its singleton subsets.
is point-wise. This holds for the powerset because every set is the union of its singleton subsets.
(Ax5) – describing that  admits a choice-principle. This holds for the powerset because whenever \(y \in h[x]\) for a map \(h:X\mathbin {\longrightarrow }Y\) and \(x\subseteq X\), then there is some \(\{x'\}\subseteq x\) with \(h(x') = y\).
admits a choice-principle. This holds for the powerset because whenever \(y \in h[x]\) for a map \(h:X\mathbin {\longrightarrow }Y\) and \(x\subseteq X\), then there is some \(\{x'\}\subseteq x\) with \(h(x') = y\).
Theorem 3.20
Under the assumptions of Table 2, a coalgebra homomorphism in  is
is  -open.
-open.
 , \(\sqsubseteq ^T\),
, \(\sqsubseteq ^T\), 
The converse is not true in general, because intuitively, open maps reflect runs, and thus only reflect edges of reachable states, as we have seen in Sect. 2.1. The notion of a state being reached by a path is the following:
Definition 3.21
A system \((X,\xi ,x_0)\) is path-reachable if the family of runs \([x_k]_{k\le n}:J(\varvec{P}_{n+1},\varvec{p}_n)\mathbin {\longrightarrow }(X,\xi ,x_0)\) (of paths from  ) is jointly epic.
) is jointly epic.
Example 3.22
For LTSs, this means that every state in X is reached by a run, that is, there is a path from the initial state to every state of X.
Remark 3.23
In Definition 3.21, it is crucial that we consider  and not
and not  for functors incorporating ‘arities \(\ge 2\)’. This does not affect the example of LTSs, but for \(I=1\), \(FX=X\times X\) and \(T=\mathcal {P} \) in
for functors incorporating ‘arities \(\ge 2\)’. This does not affect the example of LTSs, but for \(I=1\), \(FX=X\times X\) and \(T=\mathcal {P} \) in  , the coalgebra \((X,\xi ,x_0)\) on \(X=\{x_0,y_1,y_2,z_1,z_2\}\) given by \( \xi (x_0) = \{ (y_1,y_2) \}, ~~ \xi (y_1) = \{ (z_1,z_2) \}, ~~ \xi (y_2) = \xi (z_1) = \xi (z_2) = \emptyset \) is path-reachable for
, the coalgebra \((X,\xi ,x_0)\) on \(X=\{x_0,y_1,y_2,z_1,z_2\}\) given by \( \xi (x_0) = \{ (y_1,y_2) \}, ~~ \xi (y_1) = \{ (z_1,z_2) \}, ~~ \xi (y_2) = \xi (z_1) = \xi (z_2) = \emptyset \) is path-reachable for  . There is no run of a length 2 path from
. There is no run of a length 2 path from  , because \(y_2\) has no successors, and so there is no path to \(z_1\) or to \(z_2\).
, because \(y_2\) has no successors, and so there is no path to \(z_1\) or to \(z_2\).
Theorem 3.24
Under the assumptions of Table 2, if \((X,\xi ,x_0)\) is path-reachable, then an open morphism \(h:(X,\xi ,x_0) \mathbin {\longrightarrow }(Y,\zeta ,y_0)\) is a coalgebra homomorphism.
3.5 Connection to Other Notions of Reachability
There is another concise notion for reachability in the coalgebraic literature [2].
Definition 3.25
A subcoalgebra of \((X,\xi ,x_0)\) is a coalgebra homomorphism \(h:(Y,\zeta ,y_0) \mathbin {\longrightarrow }(X,\xi ,x_0)\) that is carried by a monomorphism \(h:X\rightarrowtail Y\). Furthermore \((X,\xi ,x_0)\) is called reachable if it has no proper subcoalgebra, i.e. if any subcoalgebra h is an isomorphism.
Under the following assumptions, this notion coincides with the path-based definition of reachability (Definition 3.21).
Assumption 3.26
For the present Subsect. 3.5, let  be cocomplete, have (epi,mono)-factorizations and wide pullbacks of monomorphisms.
be cocomplete, have (epi,mono)-factorizations and wide pullbacks of monomorphisms.
The first direction follows directly from Theorem 3.20:
Proposition 3.27
Every path-reachable \((X,\xi ,x_0)\) has no proper subcoalgebra.
For the other direction it is needed that TF preserves arbitrary intersections, that is, wide pullbacks of monomorphisms. In  , this means that for a family \((X_i\subseteq Y)_{i\in I}\) of subsets we have \(\bigcap _{i\in I} TFX_i = TF\bigcap _{i\in I} X_i\) as subsets of TFY.
, this means that for a family \((X_i\subseteq Y)_{i\in I}\) of subsets we have \(\bigcap _{i\in I} TFX_i = TF\bigcap _{i\in I} X_i\) as subsets of TFY.
Proposition 3.28
If, furthermore, for every monomorphism \(m:Y\mathbin {\longrightarrow }Z\), the function 
 reflects joins and if TF preserves arbitrary intersections, then a reachable coalgebra \((X,\xi ,x_0)\) is also path-reachable.
reflects joins and if TF preserves arbitrary intersections, then a reachable coalgebra \((X,\xi ,x_0)\) is also path-reachable.
All those technical assumptions are satisfied in the case of LTSs, and will also be satisfied in all our instances in Sect. 4.
3.6 Trace Semantics for Pointed Coalgebras
The characterization from Theorems 3.20 and 3.24 points out a natural way of defining a trace semantics for pointed coalgebras. Indeed, the paths category  provides a natural way of defining the runs of a system. A possible way to go from runs to trace semantics is to describe accepting runs as the subcategory
provides a natural way of defining the runs of a system. A possible way to go from runs to trace semantics is to describe accepting runs as the subcategory  . We can define the trace semantics of a system \((X,\xi ,x_o)\) as the set:
. We can define the trace semantics of a system \((X,\xi ,x_o)\) as the set:

Since  -open maps preserve and reflect runs, we have the following:
-open maps preserve and reflect runs, we have the following:
Corollary 3.29
 is a functor and if \(f:(X,\xi ,x_0) \longrightarrow (Y,\zeta ,y_0)\) is
is a functor and if \(f:(X,\xi ,x_0) \longrightarrow (Y,\zeta ,y_0)\) is  -open, then
-open, then  .
.
Let us look at two LTS-related examples (we will describe some others in the next section). First, for \(FX = A\times X\). The usual trace semantics is given by all the words in \(A^\star \) that are labelled of a run of a system. This trace semantics is obtained because \(\mathsf {PathOrd} (I,F) = \coprod _{n\ge 0} A^n\) and because  maps every path to its underlying word. Another example is given for \(FX = A\times X + \{\checkmark \}\), where \(\checkmark \) marks final states. In this case, a path in
maps every path to its underlying word. Another example is given for \(FX = A\times X + \{\checkmark \}\), where \(\checkmark \) marks final states. In this case, a path in  of length n is either a path that can still be extended or encodes less than n steps to an accepting state \(\checkmark \). This obtains the trace semantics containing the set of accepted words, as in automata theory, plus the set of possibly infinite runs.
of length n is either a path that can still be extended or encodes less than n steps to an accepting state \(\checkmark \). This obtains the trace semantics containing the set of accepted words, as in automata theory, plus the set of possibly infinite runs.
4 Instances
4.1 Analytic Functors and Tree Automata
In Example 3.7, we have seen that every polynomial  -functors, in particular the functor \(X \mapsto A\times X\), has precise factorizations with respect to all sets. This allowed us to see LTSs, modelled as \(\{*\}\)-pointed \(\mathcal {P} (A\times \_\!\_)\)-coalgebra, as an instance of our theory. This allowed us in particular to describe their trace semantics using our path category in Sect. 3.6. This can be extended to tree automata as follows. Assume given a signature \(\varSigma \), that is, a collection
-functors, in particular the functor \(X \mapsto A\times X\), has precise factorizations with respect to all sets. This allowed us to see LTSs, modelled as \(\{*\}\)-pointed \(\mathcal {P} (A\times \_\!\_)\)-coalgebra, as an instance of our theory. This allowed us in particular to describe their trace semantics using our path category in Sect. 3.6. This can be extended to tree automata as follows. Assume given a signature \(\varSigma \), that is, a collection  of disjoint sets. When \(\sigma \) belongs to \(\varSigma _n\), we say that n is the arity of \(\sigma \) or that \(\sigma \) is a symbol of arity n. A top-down non-deterministic tree automata as defined in [6] is then the same as a \(\{*\}\)-pointed \(\mathcal {P} F\)-coalgebra where F is the polynomial functor \(X \mapsto \coprod _{\sigma \in \varSigma _n} X^n\). For this functor, \(F^n(1)\) is the set of trees over \(\varSigma \sqcup \{*(0)\}\) of depth at most \(n+1\) such that a leaf is labelled by \(*\) if and only if it is at depth \(n+1\). Intuitively, elements of \(F^n(1)\) are partial runs of length n that can possibly be extended. Then, the trace semantics of a tree automata, seen as a pointed coalgebra, is given by the set of partial runs of the automata. In particular, this contains the set of accepted finite trees as those partial runs without any \(*\), and the set of accepted infinite trees, encoded as the sequence of their truncations of depth n, for every n.
of disjoint sets. When \(\sigma \) belongs to \(\varSigma _n\), we say that n is the arity of \(\sigma \) or that \(\sigma \) is a symbol of arity n. A top-down non-deterministic tree automata as defined in [6] is then the same as a \(\{*\}\)-pointed \(\mathcal {P} F\)-coalgebra where F is the polynomial functor \(X \mapsto \coprod _{\sigma \in \varSigma _n} X^n\). For this functor, \(F^n(1)\) is the set of trees over \(\varSigma \sqcup \{*(0)\}\) of depth at most \(n+1\) such that a leaf is labelled by \(*\) if and only if it is at depth \(n+1\). Intuitively, elements of \(F^n(1)\) are partial runs of length n that can possibly be extended. Then, the trace semantics of a tree automata, seen as a pointed coalgebra, is given by the set of partial runs of the automata. In particular, this contains the set of accepted finite trees as those partial runs without any \(*\), and the set of accepted infinite trees, encoded as the sequence of their truncations of depth n, for every n.
In the following, we would like to extend this to other kinds of tree automata by allowing some symmetries. For example, in a tree, we may not care about the order of the children. This boils down to quotient the set \(X^n\) of n-tuples, by some permutations of the indices. This can be done generally given a subgroup G of the permutation group \(\mathfrak {S}_n\) on n elements by defining \(X^n/G\) as the quotient of \(X^n\) under the equivalence relation: \((x_1, \ldots , x_n) \equiv _G (y_1, \ldots , y_n)\) iff there is \(\pi \in G\) such that for all i, \(x_i = y_{\pi (i)}\). Concretely, this means that we replace the polynomial functor F by a so-called analytic functor:
Definition 4.1
[14, 15]. An analytic  -functor is a functor of the form \(FX = \coprod _{\sigma \in \varSigma _n} X^{n}/G_\sigma \) where for every \(\sigma \in \varSigma _n\), we have a subgroup \(G_\sigma \) of the permutation group \(\mathfrak {S}_n\) on n elements.
-functor is a functor of the form \(FX = \coprod _{\sigma \in \varSigma _n} X^{n}/G_\sigma \) where for every \(\sigma \in \varSigma _n\), we have a subgroup \(G_\sigma \) of the permutation group \(\mathfrak {S}_n\) on n elements.
Example 4.2
Every polynomial functor is analytic. The bag-functor is analytic, with  has one operation symbol per arity and \(G_\sigma = \mathfrak {S}_{\mathsf {ar} (\sigma )}\) is the full permutation group on \(\mathsf {ar}(\sigma )\) elements. It is the archetype of an analytic functor, in the sense that for every analytic functor
has one operation symbol per arity and \(G_\sigma = \mathfrak {S}_{\mathsf {ar} (\sigma )}\) is the full permutation group on \(\mathsf {ar}(\sigma )\) elements. It is the archetype of an analytic functor, in the sense that for every analytic functor  , there is a natural transformation into the bag functor \(\alpha :F\mathbin {\longrightarrow }\mathcal {B} \). If F is given by \(\varSigma \) and \(G_\sigma \) as above, then \(\alpha _X\) is given by
, there is a natural transformation into the bag functor \(\alpha :F\mathbin {\longrightarrow }\mathcal {B} \). If F is given by \(\varSigma \) and \(G_\sigma \) as above, then \(\alpha _X\) is given by

Proposition 4.3
For an analytic  -functor F, the following are equivalent (1) a map \(f:X\mathbin {\longrightarrow }FY\) is F-precise, (2) \(\alpha _Y\cdot f\) is \(\mathcal {B} \)-precise, (3) every element of Y appears precisely once in the definition of f, i.e. for every \(y \in Y\), there is exactly one x in X, such that f(x) is the equivalence class of a tuple \((y_1, \ldots , y_n)\) where there is an index i, such that \(y_i = y\); and furthermore this index is unique. So every analytic functor has precise factorizations w.r.t.
-functor F, the following are equivalent (1) a map \(f:X\mathbin {\longrightarrow }FY\) is F-precise, (2) \(\alpha _Y\cdot f\) is \(\mathcal {B} \)-precise, (3) every element of Y appears precisely once in the definition of f, i.e. for every \(y \in Y\), there is exactly one x in X, such that f(x) is the equivalence class of a tuple \((y_1, \ldots , y_n)\) where there is an index i, such that \(y_i = y\); and furthermore this index is unique. So every analytic functor has precise factorizations w.r.t.  .
.
4.2 Nominal Sets: Regular Nondeterministic Nominal Automata
We derive an open map situation from the coalgebraic situation for regular nondeterministic nominal automata (RNNAs) [26]. They are an extension of automata to accept words with binders, consisting of literals  and binders \({|}_{a}\) for
and binders \({|}_{a}\) for  ; the latter is counted as length 1. An example of such a word of length 4 is \(a{|}_{c}bc\), where the last c is bound by \({|}_{c}\). The order of binders makes difference: \({|}_{a}{|}_{b}ab \ne {|}_{a}{|}_{b}ba\). RNNAs are coalgebraically represented in the category of nominal sets [10], a formalism about atoms (e.g. variables) that sit in more complex structures (e.g. lambda terms), and gives a notion of binding. Because the choice principles (Ax4) and (Ax5) are not satisfied by every nominal sets, we instead use the class of strong nominal sets for the precise factorization (Definition 3.4).
; the latter is counted as length 1. An example of such a word of length 4 is \(a{|}_{c}bc\), where the last c is bound by \({|}_{c}\). The order of binders makes difference: \({|}_{a}{|}_{b}ab \ne {|}_{a}{|}_{b}ba\). RNNAs are coalgebraically represented in the category of nominal sets [10], a formalism about atoms (e.g. variables) that sit in more complex structures (e.g. lambda terms), and gives a notion of binding. Because the choice principles (Ax4) and (Ax5) are not satisfied by every nominal sets, we instead use the class of strong nominal sets for the precise factorization (Definition 3.4).
Definition 4.4
[10, 24]. Fix a countably infinite set  , called the set of atoms. For the group
, called the set of atoms. For the group  of finite permutations on the set
of finite permutations on the set  , a group action \((X,\cdot )\) is a set X together with a group homomorphism
, a group action \((X,\cdot )\) is a set X together with a group homomorphism  , written in infix notation. An element \(x\in X\) is supported by
, written in infix notation. An element \(x\in X\) is supported by  , if for all
, if for all  with \(\pi (a) =a \ \forall a\in S\) we have \(\pi \cdot x = x\). A nominal set is a group action for
with \(\pi (a) =a \ \forall a\in S\) we have \(\pi \cdot x = x\). A nominal set is a group action for  such that every \(x\in X\) is finitely supported, i.e. supported by a finite
such that every \(x\in X\) is finitely supported, i.e. supported by a finite  . A map \(f:(X,\cdot )\mathbin {\longrightarrow }(Y,\star )\) is equivariant if for all \(x\in X\) and
. A map \(f:(X,\cdot )\mathbin {\longrightarrow }(Y,\star )\) is equivariant if for all \(x\in X\) and  we have \(f(\pi \cdot x) = \pi \star f(x)\). The category of nominal sets and equivariant maps is denoted by
we have \(f(\pi \cdot x) = \pi \star f(x)\). The category of nominal sets and equivariant maps is denoted by  . A nominal set \((X,\cdot )\) is called strong if for all \(x\in X\) and
. A nominal set \((X,\cdot )\) is called strong if for all \(x\in X\) and  with \(\pi \cdot x = x\) we have \(\pi (a) = a\) for all
with \(\pi \cdot x = x\) we have \(\pi (a) = a\) for all  .
.
Intuitively, the support of an element is the set of free literals. An equivariant map can forget some of the support of an element, but can never introduce new atoms, i.e.  . The intuition behind strong nominal sets is that all atoms appear in a fixed order, that is,
. The intuition behind strong nominal sets is that all atoms appear in a fixed order, that is,  is strong, but
is strong, but  (the finite powerset) is not. We set \(\mathcal {S} \) to be the class of strong nominal sets:
(the finite powerset) is not. We set \(\mathcal {S} \) to be the class of strong nominal sets:
Example 4.5
The  -functor of unordered pairs admits precise factorizations w.r.t. strong nominal sets, but not w.r.t. all nominal sets.
-functor of unordered pairs admits precise factorizations w.r.t. strong nominal sets, but not w.r.t. all nominal sets.
In the application, we fix the set  of distinct n-tuples of atoms (\(n\ge 0\)) as the pointing. The hom-sets
of distinct n-tuples of atoms (\(n\ge 0\)) as the pointing. The hom-sets  are ordered point-wise.
are ordered point-wise.
Proposition 4.6
Uniformly finitely supported powerset  satisfies (Ax2-5) w.r.t. \(\mathcal {S} \) the class of strong nominal sets.Footnote 1
satisfies (Ax2-5) w.r.t. \(\mathcal {S} \) the class of strong nominal sets.Footnote 1
As for F, we study an LTS-like functor, extended with the binding functor [10]:
Definition 4.7
For a nominal set X, define the \(\alpha \)-equivalence relation  on
on  by:
by:  Denote the quotient by
Denote the quotient by  . The assignment
. The assignment  extends to a functor, called the binding functor
extends to a functor, called the binding functor  .
.
RNNA are precisely \(\mathcal {P}_{\mathsf {ufs}} F\)-coalgebras for  [26]. In this paper we additionally consider initial states for RNNAs.
[26]. In this paper we additionally consider initial states for RNNAs.
Proposition 4.8
The binding functor  admits precise factorizations w.r.t. strong nominal sets and so does
admits precise factorizations w.r.t. strong nominal sets and so does  .
.
An element in  may be regarded as a word with binders under a context \(\varvec{a}\vdash w\), where
may be regarded as a word with binders under a context \(\varvec{a}\vdash w\), where  , all literals in w are bound or in \(\varvec{a}\), and w may end with \(\checkmark \). Moreover, two word-in-contexts \(\varvec{a}\vdash w\) and \(\varvec{a}'\vdash w'\) are identified if their closures are \(\alpha \)-equivalent, that is, \({|}_{a_1}\cdots {|}_{a_n}w={|}_{a'_1}\cdots {|}_{a'_n}w'\). The trace semantics of a RNNA T contains all the word-in-contexts corresponding to runs in T. This trace semantics distinguishes whether words are concluded by \(\checkmark \).
, all literals in w are bound or in \(\varvec{a}\), and w may end with \(\checkmark \). Moreover, two word-in-contexts \(\varvec{a}\vdash w\) and \(\varvec{a}'\vdash w'\) are identified if their closures are \(\alpha \)-equivalent, that is, \({|}_{a_1}\cdots {|}_{a_n}w={|}_{a'_1}\cdots {|}_{a'_n}w'\). The trace semantics of a RNNA T contains all the word-in-contexts corresponding to runs in T. This trace semantics distinguishes whether words are concluded by \(\checkmark \).
4.3 Subsuming Arbitrary Open Morphism Situations
Lasota [19] provides a translation of a small path-category  into a functor
into a functor  defined by
defined by  . So the hom-sets
. So the hom-sets  have a canonical order, namely the point-wise inclusion. This admits a functor
have a canonical order, namely the point-wise inclusion. This admits a functor  from
from  to
to  -coalgebras and lax coalgebra homomorphisms, and Lasota shows that
-coalgebras and lax coalgebra homomorphisms, and Lasota shows that  is
is  -open iff
-open iff  is a coalgebra homomorphism. In the following, we show that we can apply our framework to
is a coalgebra homomorphism. In the following, we show that we can apply our framework to  by a suitable decomposition
by a suitable decomposition  and a suitable object I for the initial state pointing. As usual in open map papers, we require that
and a suitable object I for the initial state pointing. As usual in open map papers, we require that  and
and  have a common initial object
have a common initial object  . Observe that we have
. Observe that we have  where
where

Lasota considers coalgebras without pointing, but one indeed has a canonical pointing as follows. For  , define the characteristic family
, define the characteristic family  by \(\chi ^P_Q = 1\) if \(P=Q\) and \(\chi ^P_Q = \emptyset \) if \(P\ne Q\). With this, we fix the pointing
by \(\chi ^P_Q = 1\) if \(P=Q\) and \(\chi ^P_Q = \emptyset \) if \(P\ne Q\). With this, we fix the pointing  .
.
Proposition 4.9
T, F and I satisfy the axioms from Table 2, with  .
.
The path category in  from our theory can be described as follows.
from our theory can be described as follows.
Proposition 4.10
An object of  is a sequence of composable
is a sequence of composable  -mor-
-mor-
phisms  .
.
5 Conclusions and Further Work
We proved that coalgebra homomorphisms for systems with non-deterministic branching can be seen as open maps for a canonical path-category, constructed from the computation type F. This limitation to non-deterministic systems is unsurprising: as we have proved in Sect. 4.3 on Lasota’s work [19], every open map situation can been encoded as a coalgebra situation with a powerset-like functor, so with non-deterministic branching. As a future work, we would like to extend this theory of path-categories to coalgebras for further kinds of branching, especially probabilistic and weighted. This will require (1) to adapt open maps to allow those kinds of branching (2) adapt the axioms from Table 2, by replacing the “+1” part of (Ax1) to something depending on the branching type.
Notes
- 1.
There are two variants of powersets discussed in [26]. The finite powerset \(\mathcal {P}_{\mathsf {f}} \) also fulfils the axioms. However, finitely supported powerset \(\mathcal {P}_{\mathsf {fs}}\) does not fulfil (Ax5).
References
Adámek, J., Herrlich, H., Strecker, G.E.: Abstract and concrete categories: the joy of cats. online and enhanced edition of the book published in 1990 by John Wiley and Sons (2004). http://katmat.math.uni-bremen.de/acc/acc.pdf
Adámek, J., Milius, S., Moss, L.S., Sousa, L.: Well-pointed coalgebras. Logical Methods Comput. Sci. 9(3), 1–51 (2013)
Awodey, S.: Category Theory, 2nd edn. Oxford University Press, Inc., New York (2010)
Beohar, H., Küpper, S.: On path-based coalgebras and weak notions of bisimulation. In: 7th Conference on Algebra and Coalgebra in Computer Science, CALCO 2017, Ljubljana, Slovenia, 12–16 June 2017, pp. 6:1–6:17 (2017). https://doi.org/10.4230/LIPIcs.CALCO.2017.6
Bonchi, F., Silva, A., Sokolova, A.: The power of convex algebras. In: Meyer, R., Nestmann, U. (eds.) 28th International Conference on Concurrency Theory (CONCUR 2017), Dagstuhl, Germany, vol. 85, pp. 23:1–23:18 (2017). https://doi.org/10.4230/LIPIcs.CONCUR.2017.23
Comon, H., et al.: Tree Automata Techniques and Applications (2007). http://tata.gforge.inria.fr
Dubut, J., Goubault, É., Goubault-Larrecq, J.: Natural homology. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015, Part II. LNCS, vol. 9135, pp. 171–183. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_14
Fahrenberg, U., Legay, A.: History-preserving bisimilarity for higher-dimensional automata via open maps. Electron. Notes Theor. Comput. Sci. 298, 165–178 (2013)
Fiore, M.P., Cattani, G.L., Winskel, G.: Weak bisimulation and open maps. In: 14th Annual IEEE Symposium on Logic in Computer Science (LICS 1999), pp. 67–76 (1999)
Gabbay, M., Pitts, A.M.: A new approach to abstract syntax involving binders. In: Longo, G. (ed.) Proceedings of the Fourteenth Annual IEEE Symposium on Logic in Computer Science, LICS 1999, pp. 214–224. IEEE Computer Society Press (1999)
Hansen, H.H., Klin, B.: Pointwise extensions of GSOS-defined operations. Math. Struct. Comput. Sci. 21(1), 321–361 (2011)
Hasuo, I., Jacobs, B., Sokolova, A.: Generic trace semantics via coinduction. Logical Methods Comput. Sci. 3(4), 1–36 (2007)
Jacobs, B., Sokolova, A.: Traces, executions and schedulers, coalgebraically. In: Kurz, A., Lenisa, M., Tarlecki, A. (eds.) CALCO 2009. LNCS, vol. 5728, pp. 206–220. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03741-2_15
Joyal, A.: Une théorie combinatoire des séries formelles. Adv. Math. 42(1), 1–82 (1981)
Joyal, A.: Foncteurs analytiques et espèces de structures. In: Labelle, G., Leroux, P. (eds.) Combinatoire énumérative. LNM, vol. 1234, pp. 126–159. Springer, Heidelberg (1986). https://doi.org/10.1007/BFb0072514
Joyal, A., Nielsen, M., Winskel, G.: Bisimulation from open maps. Inf. Comput. 127, 164–185 (1996)
Kozen, D., Mamouras, K., Petrişan, D., Silva, A.: Nominal Kleene coalgebra. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015, Part II. LNCS, vol. 9135, pp. 286–298. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_23
Kurz, A., Petrisan, D., Severi, P., de Vries, F.: Nominal coalgebraic data types with applications to lambda calculus. Logical Methods Comput. Sci. 9(4) (2013). https://doi.org/10.2168/LMCS-9(4:20)2013
Lasota, S.: Coalgebra morphisms subsume open maps. Theor. Comput. Sci. 280(1), 123–135 (2002)
Milius, S.: A sound and complete calculus for finite stream circuits. In: Proceedings of the 25th Annual Symposium on Logic in Computer Science (LICS 2010), pp. 449–458 (2010)
Milius, S., Pattinson, D., Schröder, L.: Generic trace semantics and graded monads. In: Moss, L.S., Sobocinski, P. (eds.) Proceedings of 6th Conference on Algebra and Coalgebra in Computer Science, CALCO 2015. Leibniz International Proceedings in Informatics, vol. 35, pp. 253–269 (2015). http://www8.cs.fau.de/_media/research:papers:traces-gm.pdf
Nielsen, M., Hune, T.: Bisimulation and open maps for timed transition systems. Fundam. Inform. 38, 61–77 (1999)
Park, D.: Concurrency and automata on infinite sequences. Theor. Comput. Sci. 104, 167–183 (1981)
Pitts, A.M.: Nominal Sets: Names and Symmetry in Computer Science. Cambridge Tracts in Theoretical Computer Science, vol. 57. Cambridge University Press, Cambridge (2013)
Rutten, J.: Universal coalgebra: a theory of systems. Theor. Comput. Sci. 249(1), 3–80 (2000)
Schröder, L., Kozen, D., Milius, S., Wißmann, T.: Nominal automata with name binding. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 124–142. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_8
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Wißmann, T., Dubut, J., Katsumata, Sy., Hasuo, I. (2019). Path Category for Free. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)







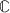 has an initial object 0 and
has an initial object 0 and  and
and 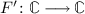 do so.
do so. is I-extensive and
is I-extensive and 