Abstract
Change structures, introduced by Cai et al., have recently been proposed as a semantic framework for incremental computation. We generalise change actions, an alternative to change structures, to arbitrary cartesian categories and propose the notion of change action model as a categorical model for (higher-order) generalised differentiation. Change action models naturally arise from many geometric and computational settings, such as (generalised) cartesian differential categories, group models of discrete calculus, and Kleene algebra of regular expressions. We show how to build canonical change action models on arbitrary cartesian categories, reminiscent of the Fàa di Bruno construction.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Incremental computation is the process of incrementally updating the output of some given function as the input is gradually changed, without recomputing the entire function from scratch. Recently, Cai et al. [6] introduced the notion of change structure to give a semantic account of incremental computation. Change structures have subsequently been generalised to change actions [2], and proposed as a model for automatic differentiation [16]. These developments raise a number of questions about the structure of change actions themselves and how they relate to more traditional notions of differentiation.
A change action \(A = ({|{A}|}, \varDelta A, \oplus _A, +_A, 0)\) is a set \({|{A}|}\) equipped with a monoid \((\varDelta A, +_A, 0_A)\) acting on it, via action \(\oplus _A : {|{A}|} \times \varDelta A \rightarrow {|{A}|}\). For example, every monoid \((S, +, 0)\) gives rise to a (so-called monoidal) change action \((S, S, +, +, 0)\). Given change actions A and B, consider functions \(f : {|{A}|} \rightarrow {|{B}|}\). A derivative of f is a function \(\partial f : {|{A}|} \times \varDelta A \rightarrow \varDelta B\) such that for all \(a \in {|{A}|}, \delta a \in \varDelta A\), \(f (a\oplus _A\delta a) = f(a) \oplus _B \partial f(a, \delta a).\) Change actions and differentiable functions (i.e. functions that have a regular derivative) organise themselves into categories (and indeed 2-categories) with finite (co)products, whereby morphisms are composed via the chain rule.
The definition of change actions (and derivatives of functions) makes no use of properties of \(\mathbf {Set}\) beyond the existence of products. We develop the theory of change actions on arbitrary cartesian categories and study their properties. A first contribution is the notion of a change action model, which is defined to be a coalgebra for a certain (copointed) endofunctor \(\mathrm {CAct}\) on the category \(\mathbf {Cat_\times }\) of (small) cartesian categories. The functor \(\mathrm {CAct}\) sends a category \(\mathbf {C}\) to the category \(\mathrm {CAct}(\mathbf {C})\) of (internal) change actions and differential maps on \(\mathbf {C}\).
There is a natural, extrinsic, notion of higher-order derivative in change action models. In such a model \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\), a \(\mathbf {C}\)-object A is associated (via \(\alpha \)) with a change action, the carrier object of whose monoid is in turn associated with a change action, and so on ad infinitum. We construct a “canonical” change action model, \(\mathrm {CAct_\omega }(\mathbf {C})\), that internalises such \(\omega \)-sequences that exhibit higher-order differentiation. Objects of \(\mathrm {CAct_\omega }(\mathbf {C})\) are \(\omega \)-sequences of “contiguously compatible” change actions; and morphisms are corresponding \(\omega \)-sequences of differential maps, each map being the canonical (via \(\alpha \)) derivative of the preceding in the \(\omega \)-sequence. We show that \(\mathrm {CAct_\omega }(\mathbf {C})\) is the final \(\mathrm {CAct}\)-coalgebra (relativised to change action models on \(\mathbf {C}\)). The category \(\mathrm {CAct_\omega }(\mathbf {C})\) may be viewed as a kind of Faà di Bruno construction [8, 10] in the more general setting of change action models.
Change action models capture many versions of differentiation that arise in mathematics and computer science. We illustrate their generality via three examples. The first, (generalised) cartesian differential categories (GCDC) [4, 10], are themselves an axiomatisation of the essential properties of the derivative. We show that a GCDC \(\mathbf {C}\)—which by definition associates every object A with a monoid \(L(A) = (L_0(A), +_A, 0_A)\)—gives rise to change action models in various non-trivial ways.
Secondly we show how discrete differentiation in both the calculus of finite differences [15] and Boolean differential calculus [22, 23] can be modelled using the full subcategory \(\mathbf {Grp}_{\mathbf {Set}}\) of \(\mathbf {Set}\) whose objects are groups. Our unifying formulation generalises these discrete calculi to arbitrary groups, and gives an account of the chain rule in these settings.
Our third example is differentiation of regular expressions. Recall that Kleene algebra \(\mathbb {K}\) is the algebra of regular expressions. We show that the algebra of polynomials over a commutative Kleene algebra is a change action model.
Outline. In Sect. 2 we present the basic definitions of change actions and differential maps, and show how they can be organised into categories. The theory of change action is extended to arbitrary cartesian categories \(\mathbf {C}\) in Sect. 3: we introduce the category \(\mathrm {CAct}(\mathbf {C})\) of internal change actions on \(\mathbf {C}\). In Sect. 4 we present change action models, and properties of the tangent bundle functors. In Sect. 5 we illustrate the unifying power of change action models via three examples. In Sect. 6, we study the category \(\mathrm {CAct_\omega }(\mathbf {C})\) of \(\omega \)-change actions and \(\omega \)-differential maps. Missing proofs are provided in an extended version of the present paper [1].
2 Change Actions
A change action is a tuple \(A = ({|{A}|}, \varDelta {A}, \oplus _A, +_A, 0_A)\) where \({|{A}|}\) and \(\varDelta {A}\) are sets, \((\varDelta {A}, +_A, 0_A)\) is a monoid, and \(\oplus _A : {|{A}|} \times \varDelta {A} \rightarrow {|{A}|}\) is an action of the monoid on \({|{A}|}\).Footnote 1 We omit the subscript from \(\oplus _A, +_A\) and \(0_A\) whenever we can.
Definition 1
(Derivative condition). Let \(A\) and \(B\) be change actions. A function \(f : {|{A}|} \rightarrow {|{B}|}\) is differentiable if there is a function \(\partial f : {|{A}|} \times \varDelta {A} \rightarrow \varDelta {B}\) satisfying \( f(a \oplus _A \delta {a}) = f(a) \oplus _B \partial f (a, \delta {a}), \) for all \(a \in {|{A}|}, \delta {a} \in \varDelta {A}\). We call \(\partial f\) a derivative for f, and write \(f : A \rightarrow B\) whenever f is differentiable.
Lemma 1
(Chain rule). Given \(f : A \rightarrow B\) and \(g : B \rightarrow C\) with derivatives \(\partial f\) and \(\partial g\) respectively, the function \(\partial (g \circ f) : {|{A}|} \times \varDelta {A} \rightarrow \varDelta {C}\) defined by  is a derivative for \(g \circ f : {|{A}|} \rightarrow {|{C}|}\).
is a derivative for \(g \circ f : {|{A}|} \rightarrow {|{C}|}\).
Proof
Unpacking the definition, we have \((g \circ f)(a) \oplus _C \partial (g \circ f)(a, \delta a) = g(f(a))\,\oplus _C\,\partial g(f(a), \partial f(a, \delta a)) = g(f(a)\,\oplus _B\,\partial f(a, \delta a)) = g(f(a \oplus _A \delta a))\), as desired. \(\square \)
Example 1
(Some useful change actions).
-
1.
If \((A, +, 0)\) is a monoid, \((A, A, +, +, 0)\) is a change action (called monoidal).
-
2.
For any set A,
 is a (trivial) change action.
is a (trivial) change action. -
3.
Let \(A \Rightarrow B\) be the set of functions from A from B, and \(\mathrm {ev}_{A, B} : A \times (A \Rightarrow B) \rightarrow B\) be the usual evaluation map. Then \((A, A \Rightarrow A, \mathrm {ev}_{A,A}, \circ , \mathrm {Id}_A)\) is a change action. If \(U \subseteq (A \Rightarrow A)\) contains the identity map and is closed under composition,
 is a change action.
is a change action.
Regular Derivatives. The preceding definitions neither assume nor guarantee a derivative to be additive (i.e. they may not satisfy \(\partial f(x, \varDelta {a} + \varDelta {b}) = \partial f(x, \varDelta {a}) + \partial f(x, \varDelta {b})\)), as they are in standard differential calculus. A strictly weaker condition that we will now require is regularity: if a derivative is additive in its second argument then it is regular, but not vice versa. Under some conditions, the converse is also true.
Definition 2
Given a differentiable map \(f : A \rightarrow B\), a derivative \(\partial f\) for f is regular if, for all \(a \in {|{A}|}\) and \(\delta {a}, \delta {b} \in \varDelta {A}\), we have \(f(a, 0_A) = 0_B\) and \(\partial f(a, \delta {a} +_A \delta {b}) = \partial f(a, \delta {a}) +_B \partial f(a \oplus _A \delta {a}, \delta {b})\).
Proposition 1
Whenever \(f : A \rightarrow B\) is differentiable and has a unique derivative \(\partial f\), this derivative is regular.
Proposition 2
Given \(f : A \rightarrow B\) and \(g : B \rightarrow C\) with regular derivatives \(\partial f\) and \(\partial g\) respectively, the derivative \(\partial (g \circ f) = \partial g \circ \langle {f \circ \pi _1}, {\partial f} \rangle \) is regular.
Two Categories of Change Actions. The study of change actions can be undertaken in two ways: one can consider functions that are differentiable (without choosing a derivative); alternatively, the derivative itself can be considered part of the morphism. The former leads to the category \(\mathbf {CAct^-}\), whose objects are change actions and morphisms are the differentiable maps.
The category \(\mathbf {CAct^-}\) was the category we originally proposed [2]. It is well-behaved, possessing limits, colimits, and exponentials, which is a trivial corollary of the following result:
Theorem 1
The category \(\mathbf {CAct^-}\) of change actions and differentiable morphisms is equivalent to \(\mathbf {PreOrd}\), the category of preorders and monotone maps.
The actual structure of the limits and colimits in \(\mathbf {CAct^-}\) is, however, not so satisfactory. One can, for example, obtain the product of two change actions \(A\) and \(B\) by taking their product in \(\mathbf {PreOrd}\) and turning it into a change action, but the corresponding monoid action map \(\oplus \) is not, in general, easily expressible, even if those for \(A\) and \(B\) are. Derivatives of morphisms in \(\mathbf {CAct^-}\) can also be hard to obtain, as exhibiting f as a morphism in \(\mathbf {CAct^-}\) merely proves it is differentiable but gives no clue as to how a derivative might be constructed.
A more constructive approach is to consider morphism as a function together with a choice of a derivative for it.
Definition 3
Given change actions \(A\) and \(B\), a differential map \(f: A \rightarrow B\) is a pair \(({|{f}|}, \partial f)\) where \({|{f}|}: {|{A}|} \rightarrow {|{B}|}\) is a function, and \(\partial f : {|{A}|} \times \varDelta A \rightarrow \varDelta B\) is a regular derivative for \({|{f}|}\).
The category \(\mathbf {CAct}\) has change actions as objects and differential maps as morphisms. The identity morphisms are \((\mathrm {Id}_A, \pi _1)\); given morphisms \(f: A \rightarrow B\) and \(g: B \rightarrow C\), define the composite  .
.
Finite products and coproducts exist in \(\mathbf {CAct}\) (see Theorems 2 and 4 for a more general statement). Whether limits and colimits exist in \(\mathbf {CAct}\) beyond products and coproducts is open.
Remark 1
If one thinks of changes (i.e. elements of \(\varDelta A\)) as morphisms between elements of \({|{A}|}\), then regularity resembles functoriality. This intuition is explored in [1, Appendix F], where we show that categories of change actions organise themselves into 2-categories.
3 Change Actions on Arbitrary Categories
The definition of change actions makes no use of any properties of \(\mathbf {Set}\) beyond the existence of products. Indeed, change actions can be characterised as just a kind of multi-sorted algebra, which is definable in any category with products.
The Category CAct(C). Consider the category \(\mathbf {Cat_\times }\) of (small) cartesian categories (i.e. categories with chosen finite products) and product-preserving functors. We can define an endofunctor \(\mathrm {CAct}: \mathbf {Cat_\times }\rightarrow \mathbf {Cat_\times }\) sending a category \(\mathbf {C}\) to the category of (internal) change actions on \(\mathbf {C}\).
The objects of \(\mathrm {CAct}(\mathbf {C})\) are tuples \(A = ({|{A}|}, \varDelta {A},\oplus _A, +_A, 0_A)\) where \({|{A}|}\) and \(\varDelta {A}\) are (arbitrary) objects in \(\mathbf {C}\), \((\varDelta {A}, +_A, 0_A)\) is a monoid object in \(\mathbf {C}\), and \(\oplus _A: {|{A}|} \times \varDelta {A} \rightarrow {|{A}|}\) is a monoid action in \(\mathbf {C}\), i.e. a \(\mathbf {C}\)-morphism satisfying, for all \(a: C \rightarrow {|{A}|}, \delta _1 a, \delta _2 a: C \rightarrow \varDelta {A}\):

Given objects \(A, B\) in \(\mathrm {CAct}(\mathbf {C})\), the morphisms of \(\mathrm {CAct}(A, B)\) are pairs \(f = ({|{f}|}, \partial f)\) where \({|{f}|} : {|{A}|} \rightarrow {|{B}|}\) and \(\partial f: {|{A}|} \times \varDelta {A} \rightarrow \varDelta {B}\) are morphisms in \(\mathbf {C}\), satisfying a diagrammatic version of the derivative condition:

Additionally, we require our derivatives to be regular, as in Definition 2, i.e. for all morphisms \(a : C \rightarrow {|{A}|}, \delta _1{a}, \delta _2{a}: C \rightarrow \varDelta {A}\), the following equations hold:
The chain rule can then be expressed naturally by pasting two instances of the previous diagram together:

Hence \(f \circ g = \langle {({|{g}|} \circ {|{f}|}) \circ \pi _1}, {\partial g \circ \langle {{|{f}|} \circ \pi _1}, {\partial f} \rangle } \rangle .\)
Now, given a product-preserving functor \(\mathrm {F} : \mathbf {C} \rightarrow \mathbf {D}\), there is a corresponding functor \(\mathrm {CAct}(\mathrm {F}) : \mathrm {CAct}(\mathbf {C}) \rightarrow \mathrm {CAct}(\mathbf {D})\) given by:

We can embed \(\mathbf {C}\) fully and faithfully into \(\mathrm {CAct}(\mathbf {C})\) via the functor \(\eta _{\mathbf {C}}\) which sends an object A of \(\mathbf {C}\) to the “trivial” change action \(A_\star = (A, \top , \pi _1, !, !)\) and every morphism \(f: A \rightarrow B\) of \(\mathbf {C}\) to the morphism (f, !). As before, this functor extends to a natural transformation from the identity functor to \(\mathrm {CAct}\).
Additionally, there is an obvious forgetful functor \(\varepsilon _{\mathbf {C}}: \mathrm {CAct}(\mathbf {C}) \rightarrow \mathbf {C}\), which defines the components of a natural transformation \(\varepsilon \) from the functor \(\mathrm {CAct}\) to the identity endofunctor \(\mathrm {Id}\).
Given \(\mathbf {C}\), we write \(\xi _{\mathbf {C}}\) for the functor \(\mathrm {CAct}(\varepsilon _{\mathbf {C}}): \mathrm {CAct}(\mathrm {CAct}(\mathbf {C})) \rightarrow \mathrm {CAct}(\mathbf {C})\).Footnote 2 Explicitly, this functor maps an object \((A, B, \oplus , +, 0)\) in \(\mathrm {CAct}(\mathrm {CAct}(\mathbf {C}))\) to the object \(({|{A}|}, {|{B}|}, {|{\oplus }|}, {|{+}|}, {|{0}|})\). Intuitively, \(\varepsilon _{\mathrm {CAct}(\mathbf {C})}\) prefers the “original” structure on objects, whereas \(\xi _{\mathbf {C}}\) prefers the “higher” structure. The equaliser of these two functors is precisely the category of change actions whose higher structure is the original structure.
Products and Coproducts in CAct(C). We have defined \(\mathrm {CAct}\) as an endofunctor on cartesian categories. This is well-defined: if \(\mathbf {C}\) has all finite (co)products, so does \(\mathrm {CAct}(\mathbf {C})\). Let \(A = ({|{A}|}, \varDelta A, \oplus _A, +_A, 0_A)\) and \(B = ({|{B}|}, \varDelta B, \oplus _B, +_B, 0_B)\) be change actions on \(\mathbf {C}\). We present their product and coproducts as follows.
Theorem 2
The following change action is the product of A and B in \(\mathrm {CAct}(\mathbf {C})\)

where  and
and  . The projections are \(\overline{\pi _1} = (\pi _1, \pi _1 \circ \pi _2)\)and \(\overline{\pi _2} = (\pi _2, \pi _2 \circ \pi _2),\) writing \(\overline{f}\) for maps f in \(\mathrm {CAct}\) to distinguish them from \(\mathbf {C}\)-maps.
. The projections are \(\overline{\pi _1} = (\pi _1, \pi _1 \circ \pi _2)\)and \(\overline{\pi _2} = (\pi _2, \pi _2 \circ \pi _2),\) writing \(\overline{f}\) for maps f in \(\mathrm {CAct}\) to distinguish them from \(\mathbf {C}\)-maps.
Theorem 3
The change action \(\overline{\top } = (\top , \top , \pi _1, \pi _1, \mathrm {Id}_\top )\) is the terminal object in \(\mathrm {CAct}(\mathbf {C})\), where \(\top \) is the terminal object of \(\mathbf {C}\). Furthermore, if A is a change action every point \({|{f}|}: \top \rightarrow {|{A}|}\) in \(\mathbf {C}\) is differentiable, with (unique) derivative \(0_A\).
Whenever we have a differential map \(f: A \times B \rightarrow C\) between change actions, we can compute its derivative \(\partial f\) by adding together its “partial” derivatives:Footnote 3.
Lemma 2
Let \(f: A \times B \rightarrow C\) be a differential map. Then
(The notational abuse is justified by the internal logic of a cartesian category.)
Theorem 4
If \(\mathbf {C}\) is distributive, with law \(\delta _{A, B, C}: (A \sqcup B) \times C \rightarrow (A \times C) \sqcup (B \times C)\), the following change action is the coproduct of A and B in \(\mathrm {CAct}(\mathbf {C})\)

where  , and
, and  . The injections are \( \overline{\iota _1} = (\iota _1, \langle {\pi _2}, {0_B} \rangle ) \) and \(\overline{\iota _2} = (\iota _2, \langle {0_A}, {\pi _2} \rangle ) \).
. The injections are \( \overline{\iota _1} = (\iota _1, \langle {\pi _2}, {0_B} \rangle ) \) and \(\overline{\iota _2} = (\iota _2, \langle {0_A}, {\pi _2} \rangle ) \).
Stable Derivatives and Additivity. We do not require derivatives to be additive in their second argument; indeed in many cases they are not. Under some simple conditions, however, (regular) derivatives can be shown to be additive.
Definition 4
Given a (internal) change action \(A\) and objects \({|{B}|}, {|{C}|}\) in a cartesian category \(\mathbf {C}\), a morphism \(u : {|{A}|} \times {|{B}|} \rightarrow {|{C}|}\) is stable whenever the diagram commutes:

If one thinks of \(\varDelta A\) as the object of “infinitesimal” transformations on \({|{A}|}\), then the preceding definition says that a morphism \(u: {|{A}|} \times {|{B}|} \rightarrow {|{C}|}\) is stable whenever infinitesimal changes on the input A do not affect its output.
Lemma 3
Let \(f = ({|{f}|}, \partial f)\) be a differential map in \(\mathrm {CAct}(\mathbf {C})\). If \(\partial f\) is stable, then it is additive in its second argumentFootnote 4, i.e. for all \(x, \delta _1 x, \delta _2 x\) we have:
Lemma 4
Let \(f = ({|{f}|}, \partial f)\) and \(g = ({|{g}|}, \partial g)\) be differential maps, with \(\partial g\) stable. Then \(\partial (g \circ f)\) is stable.
It is straightforward to see that the category \(\mathrm {Stab}(\mathbf {C})\) of change actions and differential maps with stable derivatives is a subcategory of \(\mathrm {CAct}(\mathbf {C})\).
4 Higher-Order Derivatives: The Extrinsic View
In this section we study categories in which every object is equipped with a change action, and every morphism specifies a corresponding differential map. This provides a simple way of characterising categories which are models of higher-order differentiation purely in terms of change actions.
Change Action Models. Recall that a copointed endofunctor is a pair \((\mathrm {F}, \sigma )\) where the endofunctor \(\mathrm {F}: \mathbf {C} \rightarrow \mathbf {C}\) is equipped with a natural transformation \(\sigma : \mathrm {F} \xrightarrow {.} \mathrm {Id}\). A coalgebra of a copointed endofunctor \((\mathrm {F}, \sigma )\) is an object A of \(\mathbf {C}\) together with a morphism \(\alpha : A \rightarrow \mathrm {F}A\) such that \(\sigma _A \circ \alpha = \mathrm {Id}_A\).
Definition 5
We call a coalgebra \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\) of the copointed endofunctor \((\mathrm {CAct}, \varepsilon )\) a change action model (on \(\mathbf {C})\).
Assumption. Throughout Sect. 4, we fix a change action model \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\).
Given an object A of \(\mathbf {C}\), the coalgebra \(\alpha \) specifies a (internal) change action \(\alpha (A) = (A, \varDelta A, \oplus _A, +_A, 0_A)\) in \(\mathrm {CAct}(\mathbf {C})\). (We abuse notation and write \(\varDelta A\) for the carrier object of the monoid specified in \(\alpha (A)\); similarly for \(+_A, \oplus _A\), and \(0_A\).) Given a morphism \(f: A \rightarrow B\) in \(\mathbf {C}\), there is an associated differential map \(\alpha (f) = (f, \partial f): \alpha (A) \rightarrow \alpha (B)\). Since \(\partial f: A \times \varDelta {A} \rightarrow \varDelta {B}\) is also a \(\mathbf {C}\)-morphism, there is a corresponding differential map \(\alpha (\partial f) = (\partial f, \partial ^2 f)\) in \(\mathrm {CAct}(\mathbf {C})\), where \(\partial ^2 f: (A \times \varDelta A) \times (\varDelta A \times \varDelta ^2A) \rightarrow \varDelta ^2 {B}\) is a second derivative for f. Iterating this process, we obtain an n-th derivative \(\partial ^n f\) for every \(\mathbf {C}\)-morphism f. Thus change action models offer a setting for reasoning about higher-order differentiation.
Tangent Bundles in Change Action Models. In differential geometry the tangent bundle functor, which maps every manifold to its tangent bundle, is an important construction. There is an endofunctor on change action models reminiscent of the tangent bundle functor, with analogous properties.
Definition 6
The tangent bundle functor  is defined as
is defined as  and
and  .
.
Notation. We use shorthand  .
.
The tangent bundle functor \(\mathrm {T}\) preserves products up to isomorphism, i.e. for all objects A, B of \(\mathbf {C}\), we have \(\mathrm {T}(A \times B) \cong \mathrm {T}A \times \mathrm {T}B\) and \(\mathrm {T}1 \cong 1\). In particular,  is an isomorphism. Consequently, given maps \(f: A \rightarrow B\) and \(g: A \rightarrow C\), then, up to the previous isomorphism, \(\mathrm {T}\langle {f}, {g} \rangle = \langle {\mathrm {T}f}, {\mathrm {T}g} \rangle \).
is an isomorphism. Consequently, given maps \(f: A \rightarrow B\) and \(g: A \rightarrow C\), then, up to the previous isomorphism, \(\mathrm {T}\langle {f}, {g} \rangle = \langle {\mathrm {T}f}, {\mathrm {T}g} \rangle \).
A consequence of the structure of products in \(\mathrm {CAct}(\mathbf {C})\) is that the map \(\oplus _{A \times B}\) inherits the pointwise structure in the following sense:
Lemma 5
Let \(\phi _{A, B}: \mathrm {T}A \times \mathrm {T}B \rightarrow \mathrm {T}(A \times B)\) be the canonical isomorphism described above. Then \(\oplus _{A \times B} \circ \phi _{A, B} = \oplus _A \times \oplus _B\).
It will often be convenient to operate directly on the functor \(\mathrm {T}\), rather than on the underlying derivatives. For these, the following results are useful:
Lemma 6
The following families of morphisms are natural transformations: 
 Additionally, the triple \((\mathrm {T}, \mathrm {z}, \mathrm {T}\oplus )\) defines a monad on \(\mathbf {C}\).
Additionally, the triple \((\mathrm {T}, \mathrm {z}, \mathrm {T}\oplus )\) defines a monad on \(\mathbf {C}\).
A particularly interesting class of change action models are those that are also cartesian closed. Surprisingly, this has as an immediate consequence that differentiation is itself internal to the category.
Lemma 7
(Internalisation of derivatives). Whenever \(\mathbf {C}\) is cartesian closed, there is a morphism \(\mathrm {d}_{A, B}: (A \Rightarrow B) \rightarrow (A \times \varDelta {A}) \Rightarrow \varDelta {B}\) such that, for any morphism \(f : 1 \times A \rightarrow B\), \(\mathrm {d}_{A, B} \circ \varLambda f = \varLambda (\partial f \circ \langle {\langle {\pi _1}, {\pi _{12}} \rangle }, {\langle {\pi _1}, {\pi _{22}} \rangle } \rangle )\).
Under some conditions, we can classify the structure of the exponentials in \((\mathrm {CAct}, \varepsilon )\)-coalgebras. This requires the existence of an infinitesimal object.Footnote 5
Definition 7
If \(\mathbf {C}\) is cartesian closed, an infinitesimal object D is an object of \(\mathbf {C}\) such that the tangent bundle functor \(\mathrm {T}\) is represented by the covariant Hom-functor \(D \Rightarrow (\cdot )\), i.e. there is a natural isomorphism \(\phi : (D \Rightarrow (\cdot )) \xrightarrow {.} \mathrm {T}\).
Lemma 8
Whenever there is an infinitesimal object in \(\mathbf {C}\), the tangent bundle \(\mathrm {T}(A \Rightarrow B)\) is naturally isomorphic to \(A \Rightarrow \mathrm {T}B\).
We would like the tangent bundle functor to preserve the exponential structure; in particular we would expect a result of the form \(\frac{\partial \,{(\lambda y . t)}}{\partial {x}} = \lambda y . \frac{\partial \,{t}}{\partial {x}}\), which is true in differential \(\lambda \)-calculus [11]. Unfortunately it seems impossible to prove in general that this equation holds, although weaker results are available. If the tangent bundle functor is representable, however, additional structure is preserved.
Theorem 5
The isomorphism between the functors \(\mathrm {T}(A \Rightarrow (\cdot ))\) and \(A \Rightarrow \mathrm {T}(\cdot )\) respects the structure of \(\mathrm {T}\), in the sense that the diagram commutes.

5 Examples of Change Action Models
Generalised Cartesian Differential Categories. Generalised cartesian differential categories (GCDC) [10]—a recent generalisation of cartesian differential categories [4]—are models of differential calculi. We show that change action models generalise GCDC in that GCDCs give rise to change action models in threeFootnote 6 different (non-trivial) ways. In this subsection let \(\mathbf {C}\) be a GCDC (we assume familiarity with the definitions and notations in [10]).
1. The Flat Model. Define the functor \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\) as follows. Let \(f : A \rightarrow B\) be a \(\mathbf {C}\)-morphism. Then  and
and  .
.
Theorem 6
The functor \(\alpha \) is a change action model.
2. The Kleisli Model. GCDCs admit a tangent bundle functor, defined analogously to the standard notion in differential geometry. Let \(f : A \rightarrow B\) be a \(\mathbf {C}\)-morphism. Define the tangent bundle functor \(\mathrm {T}: \mathbf {C} \rightarrow \mathbf {C}\) as:  , and
, and  . The functor \(\mathrm {T}\) is in fact a monad, with unit \(\eta = \langle {\mathrm {Id}}, {0_A} \rangle : A \rightarrow A \times L_0(A)\) and multiplication \(\mu : (A \times L_0(A)) \times L_0(A)^2 \rightarrow A \times L_0(A)\) defined by the composite:
. The functor \(\mathrm {T}\) is in fact a monad, with unit \(\eta = \langle {\mathrm {Id}}, {0_A} \rangle : A \rightarrow A \times L_0(A)\) and multiplication \(\mu : (A \times L_0(A)) \times L_0(A)^2 \rightarrow A \times L_0(A)\) defined by the composite:
Thus we can define the Kleisli category of this functor by \(\mathbf {C}_{\mathrm {T}}\) which has geometric significance as a category of generalised vector fields.
We define the functor \(\alpha _{\mathrm {T}}: \mathbf {C}_{\mathrm {T}} \rightarrow \mathrm {CAct}(\mathbf {C}_{\mathrm {T}})\): given a \(\mathbf {C}_{\mathrm {T}}\)-morphism \(f: A \rightarrow B\), set  and
and  .
.
Lemma 9
\(\alpha _{\mathrm {T}}\) is a change action model.
Remark 2
The converse is not true: in general the existence of a change action model on \(\mathbf {C}\) does not imply that \(\mathbf {C}\) satisfies the GCDC axioms. However, if one requires, additionally, \((\varDelta A, +_A, 0_A)\) to be commutative, with \(\varDelta (\varDelta A) = \varDelta A\) and \(\oplus _{\varDelta A} = +_A\) for all objects A, and some technical conditions (stability and uniqueness of derivatives), then it can be shown that \(\mathbf {C}\) is indeed a GCDC.
Difference Calculus and Boolean Differential Calculus. Consider the full subcategory \(\mathbf {Grp}_{\mathbf {Set}}\) of \(\mathbf {Set}\) whose objects are all the groupsFootnote 7. This is a cartesian closed category which can be endowed with the structure of a \((\mathrm {CAct}, \varepsilon )\)-coalgebra \(\alpha \) in a straightforward way.
Given a group \(A = (A, +, 0, -)\), define change action  Given a function \(f : A \rightarrow B\), define differential map
Given a function \(f : A \rightarrow B\), define differential map  where
where  Notice \( f(x) \oplus \partial f(x, \delta x) = f(x) + (-f(x) + f(x + \delta {x})) = f(x + \delta {x}) = f(x \oplus \delta {x}); \) hence \(\partial f\) is a derivative for f which is regular (but not necessarily additive), and \(\alpha (f)\) a map in \(\mathrm {CAct}(\mathbf {Grp}_{\mathbf {Set}})\). The following result is then immediate.
Notice \( f(x) \oplus \partial f(x, \delta x) = f(x) + (-f(x) + f(x + \delta {x})) = f(x + \delta {x}) = f(x \oplus \delta {x}); \) hence \(\partial f\) is a derivative for f which is regular (but not necessarily additive), and \(\alpha (f)\) a map in \(\mathrm {CAct}(\mathbf {Grp}_{\mathbf {Set}})\). The following result is then immediate.
Lemma 10
\(\alpha : \mathbf {Grp}_{\mathbf {Set}}\rightarrow \mathrm {CAct}(\mathbf {Grp}_{\mathbf {Set}})\) defines a change action model.
This result is significant: in the calculus of finite differences [15], the discrete derivative (or discrete difference operator) of a function \(f: \mathbb {Z}\rightarrow \mathbb {Z}\) is defined as  . In fact the discrete derivative \(\delta f\) is (an instance of) the derivative of f qua morphism in \(\mathbf {Grp}_{\mathbf {Set}}\), i.e. \(\delta f(x) = \partial f(x, 1)\).
. In fact the discrete derivative \(\delta f\) is (an instance of) the derivative of f qua morphism in \(\mathbf {Grp}_{\mathbf {Set}}\), i.e. \(\delta f(x) = \partial f(x, 1)\).
Finite difference calculus [13, 15] has found applications in combinatorics and numerical computation. Our formulation via change action model over \(\mathbf {Grp}_{\mathbf {Set}}\) has several advantages. First it justifies the chain rule, which seems new. Secondly, it generalises the calculus to arbitrary groups. To illustrate this, consider Boolean differential calculus [22, 23], a technique that applies methods from calculus to the space \(\mathbb {B}^n\) of vectors of elements of some Boolean algebra \(\mathbb {B}\).
Definition 8
Given a Boolean algebra \(\mathbb {B}\) and function \(f : \mathbb {B}^n \rightarrow \mathbb {B}^m\), the i-th Boolean derivative of f at \((u_1, \ldots , u_n) \in \mathbb {B}^n\) is the value  writing
writing  for exclusive-or.
for exclusive-or.
Now \(\mathbb {B}^n\) is a \(\mathbf {Grp}_{\mathbf {Set}}\)-object. Set  .
.
Lemma 11
The Boolean derivative of \(f : \mathbb {B}^n \rightarrow \mathbb {B}^m\) coincides with its derivative qua morphism in \(\mathbf {Grp}_{\mathbf {Set}}\): \(\frac{\partial f}{\partial x_i}(u_1, \ldots , u_n) = \partial f((u_1, \ldots , u_n), \top _i)\).
Polynomials over Commutative Kleene Algebras. The algebra of polynomials over a commutative Kleene algebra [14, 17] (see [12, 21] for work of a similar vein) is a change action model. Recall that Kleene algebra is the algebra of regular expressions [5, 9]. Formally a Kleene algebra \(\mathbb {K}\) is a tuple \((K, +, \cdot , {}^\star , 0, 1)\) such that \((K, +, \cdot , 0, 1)\) is an idempotent semiring under \(+\) satisfying, for all \(a, b, c \in K\):
where  . A Kleene algebra is commutative whenever \(\cdot \) is.
. A Kleene algebra is commutative whenever \(\cdot \) is.
Henceforth fix a commutative Kleene algebra \(\mathbb {K}\). Define the algebra of polynomials \(\mathbb {K}[\overline{x}]\) as the free extension of the algebra \(\mathbb {K}\) with elements \(\overline{x} = x_1, \ldots , x_n\). We write \(p(\overline{a})\) for the value of \(p(\overline{x})\) evaluated at \(\overline{x} \mapsto \overline{a}\). Polynomials, viewed as functions, are closed under composition: when \(p \in \mathbb {K}[\overline{x}], q_1, \ldots , q_n \in \mathbb {K}[\overline{y}]\) are polynomials, so is the composite \(p(q_1(\overline{y}), \ldots , q_n(\overline{y}))\).
Given a polynomial \(p = p(\overline{x})\), we define its i-th derivative \(\frac{\partial \,{p}}{\partial {x_i}}(\overline{x}) \in \mathbb {K}[\overline{x}]\):
Write \(\frac{\partial \,{p}}{\partial {x_i}}(\overline{e})\) to mean the result of evaluating the polynomial \(\frac{\partial \,{p}}{\partial {x_i}}(\overline{x})\) at \(\overline{x} \mapsto \overline{e}\).
Theorem 7
(Taylor’s formula [14]). Let \(p(x) \in \mathbb {K}[x]\). For all \(a, b \in \mathbb {K}[x]\), we have \(p(a + b) = p(a) + b \cdot \frac{\partial \,{p}}{\partial {x}}(a + b)\).
The category of finite powers of \(\mathbb {K}\), \(\mathbf {\mathbb {K}_\times }\), has all natural numbers n as objects. The morphisms \(\mathbb {K}_\times [m, n]\) are n-tuples of polynomials \((p_1, \ldots , p_n)\) where \(p_1, \ldots , p_n \in \mathbb {K}[x_1, \ldots , x_m]\). Composition of morphisms is the usual composition of polynomials.
Lemma 12
The category \(\mathbf {\mathbb {K}_\times }\) is a cartesian category, endowed with a change action model \(\alpha : \mathbf {\mathbb {K}_\times } \rightarrow \mathrm {CAct}(\mathbf {\mathbb {K}_\times })\) whereby  ,
,  ; for \(\overline{p} = (p_1(\overline{x}), \ldots , p_n(\overline{x})): \mathbb {K}^m \rightarrow \mathbb {K}^n\),
; for \(\overline{p} = (p_1(\overline{x}), \ldots , p_n(\overline{x})): \mathbb {K}^m \rightarrow \mathbb {K}^n\),  , where
, where  .
.
Remark 3
Interestingly derivatives are not additive in the second argument. Take \(p(x) = x^2\). Then \(\partial p(a, b+c) > \partial p (a, b) + \partial p (a, c)\). It follows that \(\mathbb {K}[\overline{x}]\) cannot be modelled by GCDC (because of axiom [CD.2]).
6 \(\omega \)-Change Actions and \(\omega \)-Differential Maps
A change action model \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\) is a category that supports higher-order differentials: each \(\mathbf {C}\)-object A is associated with an \(\omega \)-sequence of change actions—\( \alpha (A), \alpha (\varDelta A), \alpha (\varDelta ^2 A), \ldots \)—in which every change action is compatible with the neighbouring change actions. We introduce \(\omega \)-change actions as a means of constructing change action models “freely”: given a cartesian category \(\mathbf {C}\), the objects of the category \(\mathrm {CAct_\omega }(\mathbf {C})\) are all \(\omega \)-sequences of “contiguously compatible” change actions.
We work with \(\omega \)-sequences \([ {A_i} ]_{i \in \omega }\) and \([ {f_i} ]_{i \in \omega }\) of objects and morphisms in \(\mathbf {C}\). We write  for the k-th element of the \(\omega \)-sequence (similarly for \(\mathsf{p}_k([ {f_i} ]_{i \in \omega })\)), and omit the subscript ‘\(i \in \omega \)’ from \([ {A_i} ]_{i \in \omega }\) to reduce clutter. Given \(\omega \)-sequences \([ {A_i} ]\) and \([ {B_i} ]\) of objects of a cartesian category \(\mathbf {C}\), define \(\omega \)-sequences, product \([ {A_i} ] \times [ {B_i} ]\), left shift \(\varPi [ {A_i} ]\) and derivative space \(\mathbf {D}[ {A_i} ]\), by:
for the k-th element of the \(\omega \)-sequence (similarly for \(\mathsf{p}_k([ {f_i} ]_{i \in \omega })\)), and omit the subscript ‘\(i \in \omega \)’ from \([ {A_i} ]_{i \in \omega }\) to reduce clutter. Given \(\omega \)-sequences \([ {A_i} ]\) and \([ {B_i} ]\) of objects of a cartesian category \(\mathbf {C}\), define \(\omega \)-sequences, product \([ {A_i} ] \times [ {B_i} ]\), left shift \(\varPi [ {A_i} ]\) and derivative space \(\mathbf {D}[ {A_i} ]\), by:

Example 2
Given an \(\omega \)-sequence \([ {A_i} ]\), the first few terms of \(\mathbf {D}[ {A_i} ]\) are:
Definition 9
Given \(\omega \)-sequences \([ {A_i} ]\) and \([ {B_i} ]\), a pre-\(\omega \)-differential map between them, written \([ {f_i} ]: [ {A_i} ] \rightarrow [ {B_i} ]\), is an \(\omega \)-sequence \([ {f_i} ]\) such that for each j, \(f_j: \mathsf{p}_j \mathbf {D} [ {A_i} ] \rightarrow B_j\) is a \(\mathbf {C}\)-morphism.
We explain the intuition behind the derivative space \(\mathbf {D} [ {A_i} ]\). Take a morphism \(f: A \rightarrow B\), and set \(A_i = \varDelta ^i {A}\) (where  and
and  ). Since \(\varDelta \) distributes over product, the domain of the n-th derivative of f is \(\mathsf{p}_n \mathbf {D} [ {A_i} ]\).
). Since \(\varDelta \) distributes over product, the domain of the n-th derivative of f is \(\mathsf{p}_n \mathbf {D} [ {A_i} ]\).
Notation. Define  and
and  ; and define
; and define  and
and  .
.
Definition 10
Let \([ {f_i} ]: [ {A_i} ] \rightarrow [ {B_i} ]\) and \([ {g_i} ]: [ {B_i} ] \rightarrow [ {C_i} ]\) be pre-\(\omega \)-differential maps. The derivative sequence \(\mathbf {D}[ {f_i} ]\) is the \(\omega \)-sequence defined by:

Using the shorthand  , the composite \([ {g_i} ] \circ [ {f_i} ]: [ {A_i} ] \rightarrow [ {C_i} ]\) is the pre-\(\omega \)-differential map given by \(\mathsf{p}_j ([ {g_i} ] \circ [ {f_i} ]) = g_j \circ \mathsf{p}_0 (\mathbf {D}^j[ {f_i} ]). \) The identity pre-\(\omega \)-differential map \(\mathrm {Id}: [ {{A}_i} ] \rightarrow [ {{A}_i} ]\) is defined as:
, the composite \([ {g_i} ] \circ [ {f_i} ]: [ {A_i} ] \rightarrow [ {C_i} ]\) is the pre-\(\omega \)-differential map given by \(\mathsf{p}_j ([ {g_i} ] \circ [ {f_i} ]) = g_j \circ \mathsf{p}_0 (\mathbf {D}^j[ {f_i} ]). \) The identity pre-\(\omega \)-differential map \(\mathrm {Id}: [ {{A}_i} ] \rightarrow [ {{A}_i} ]\) is defined as:  .
.
Example 3
Consider \(\omega \)-sequences \([ {f_i} ]\) and \([ {g_i} ]\) as above. Then:
It follows that the first few terms of the composite \([ {g_i} ] \circ [ {f_i} ]\) are:
Notice that these correspond to iterations of the chain rule, assuming \(f_{i+1} = \partial f_i\) and \(g_{i+1} = \partial g_i\).
Proposition 3
For any pre-\(\omega \)-differential map \([ {f_i} ]\), \(\mathrm {Id}\circ [ {f_i} ] = [ {f_i} ] \circ \mathrm {Id}= [ {f_i} ]\).
Proposition 4
Composition of pre-\(\omega \)-differential maps is associative: given pre-\(\omega \)-differential maps \([ {f_i} ] : [ {{A}_i} ] \rightarrow [ {{B}_i} ]\), \([ {g_i} ] : [ {{B}_i} ] \rightarrow [ {{C}_i} ]\) and \([ {h_i} ]: [ {{C}_i} ] \rightarrow [ {{D}_i} ]\), then for all \(n \ge 0\), \( h_n \circ \mathsf{p}_0 \mathbf {D}^n ([ {g_i} ] \circ [ {f_i} ]) = (h_n \circ \mathsf{p}_0 \mathbf {D}^n [ {g_i} ]) \circ \mathsf{p}_0 \mathbf {D}^n [ {f_i} ]. \)
Definition 11
Given pre-\(\omega \)-differential maps \([ {f_i} ]: [ {A_i} ] \rightarrow [ {B_i} ], [ {g_i} ]: [ {A_i} ] \rightarrow [ {C_i} ]\), the pairing \(\langle {[ {f_i} ]}, {[ {g_i} ]} \rangle : [ {A_i} ] \rightarrow [ {B_i} ] \times [ {C_i} ] \) is the pre-\(\omega \)-differential map defined by: \(\mathsf{p}_j \langle {[ {f_i} ]}, {[ {g_i} ]} \rangle = \langle {f_j}, {g_j} \rangle . \) Define pre-\(\omega \)-differential maps  by
by  , and
, and  by
by  .
.
Definition 12
A pre-\(\omega \)-change action on a cartesian category \(\mathbf {C}\) is a quadruple \(\widehat{A} = ([ {A_i} ], [ {\widehat{\oplus ^A}_i} ], [ {\widehat{+^A}_i} ], [ {0^A_i} ]) \) where \([ {{A}_i} ]\) is an \(\omega \)-sequence of \(\mathbf {C}\)-objects, and for each \(j \ge 0\), \(\widehat{\oplus ^A}_j\) and \(\widehat{+^A}_j\) are \(\omega \)-sequences, satisfying
-
1.
\(\widehat{\oplus ^A}_j: \varPi ^j [ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^j[ {{A}_i} ]\) is a pre-\(\omega \)-differential map.
-
2.
\(\widehat{+^A}_j: \varPi ^{j + 1} [ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^{j+1}[ {{A}_i} ]\) is a pre-\(\omega \)-differential map.
-
3.
\(0^A_j: \top \rightarrow A_{j+1}\) is a \(\mathbf {C}\)-morphism.
-
4.
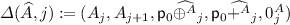 is a change action in \(\mathbf {C}\).
is a change action in \(\mathbf {C}\).
We extend the left-shift operation to pre-\(\omega \)-change actions by defining  . Then we define the change actions \(\mathbf {D}(\widehat{A}, j)\) inductively by:
. Then we define the change actions \(\mathbf {D}(\widehat{A}, j)\) inductively by:  and
and  . Notice that the carrier object of \(\mathbf {D}(\widehat{A}, j)\) is the j-th element of the \(\omega \)-sequence \(\mathbf {D}[ {A_i} ]\).
. Notice that the carrier object of \(\mathbf {D}(\widehat{A}, j)\) is the j-th element of the \(\omega \)-sequence \(\mathbf {D}[ {A_i} ]\).
Definition 13
Given pre-\(\omega \)-change actions \(\widehat{A}\) and \(\widehat{B}\) (using the preceding notation), a pre-\(\omega \)-differential map \([ {f_i} ]: [ {{A}_i} ] \rightarrow [ {{B}_i} ]\) is \(\omega \)-differential if, for each \(j \ge 0\), \((f_j, f_{j+1})\) is a differential map from the change action \(\mathbf {D}(\widehat{A}, j)\) to \(\varDelta (\widehat{B}, j)\). Whenever \([ {f_i} ]\) is an \(\omega \)-differential map, we write \(\widehat{f}: \widehat{A} \rightarrow \widehat{B}\).
We say that a pre-\(\omega \)-change action \(\widehat{A}\) is an \(\omega \)-change action if, for each \(i \ge 0\), \(\widehat{\oplus ^A}_i\) and \(\widehat{+^A}_i\) are \(\omega \)-differential maps.Footnote 8
Remark 4
The reason for requiring each \(\widehat{\oplus ^A}_i\) and \(\widehat{+^A}_i\) in an \(\omega \)-change object \(\widehat{A}\) to be \(\omega \)-differential is so that \(\widehat{A}\) is internally a change action in \(\mathrm {CAct_\omega }(\mathbf {C})\) (see Definition 15).
Lemma 13
Let \(\widehat{f}: \widehat{A} \rightarrow \widehat{B}\) and \(\widehat{g}: \widehat{B} \rightarrow \widehat{C}\) be \(\omega \)-differential maps. Qua pre-\(\omega \)-differential maps, their composite \([ {g_i} ] \circ [ {f_i} ]\) is \(\omega \)-differential. Setting  , it follows that composition of \(\omega \)-differential maps is associative.
, it follows that composition of \(\omega \)-differential maps is associative.
Lemma 14
For any \(\omega \)-change action \(\widehat{A}\), the pre-\(\omega \)-differential map \({\mathrm {Id}} : [ {{A}_i} ] \rightarrow [ {{A}_i} ]\) is \(\omega \)-differential. Hence \(\widehat{\mathrm {Id}} := \mathrm {Id}: \widehat{A} \rightarrow \widehat{A}\) satisfies the identity laws.
Definition 14
Given \(\omega \)-change actions \(\widehat{A}\) and \(\widehat{B}\), we define the product \(\omega \)-change action by:  where
where
-
1.

-
2.

-
3.

Notice that  is a change action in \(\mathbf {C}\) by construction.
is a change action in \(\mathbf {C}\) by construction.
Lemma 15
The pre-\(\omega \)-differential maps \(\pi _{\mathbf 1}, \pi _{\mathbf 2}\) are \(\omega \)-differential. Moreover, for any \(\omega \)-differential maps \(\widehat{f}: \widehat{A} \rightarrow \widehat{B}\) and \(\widehat{g}: \widehat{A} \rightarrow \widehat{C}\), the map  is \(\omega \)-differential, satisfying \(\widehat{\pi _{\mathbf 1}} \circ \langle {\widehat{f}}, {\widehat{g}} \rangle = \widehat{f}\) and \(\widehat{\pi _{\mathbf 2}} \circ \langle {\widehat{f}}, {\widehat{g}} \rangle = \widehat{g}. \)
is \(\omega \)-differential, satisfying \(\widehat{\pi _{\mathbf 1}} \circ \langle {\widehat{f}}, {\widehat{g}} \rangle = \widehat{f}\) and \(\widehat{\pi _{\mathbf 2}} \circ \langle {\widehat{f}}, {\widehat{g}} \rangle = \widehat{g}. \)
Definition 15
Define the functor \(\mathrm {CAct_\omega } : \mathbf {Cat_\times }\rightarrow \mathbf {Cat_\times }\) as follows.
-
\(\mathrm {CAct_\omega }(\mathbf {C})\) is the category whose objects are the \(\omega \)-change actions over \(\mathbf {C}\) and whose morphisms are the \(\omega \)-differential maps.
-
If \(\mathrm {F}: \mathbf {C} \rightarrow \mathbf {D}\) is a (product-preserving) functor, then \(\mathrm {CAct_\omega }(\mathrm {F}): \mathrm {CAct_\omega }(\mathbf {C}) \rightarrow \mathrm {CAct_\omega }(\mathbf {C})\) is the functor mapping the \(\omega \)-change action \( \left( [ {{A}_i} ], [ {[ {{\oplus }_i} ]_j} ],\right. \left. [ {[ {{+}_i} ]_j} ], [ {0_j} ]\right) \) to \( \left( [ {{\mathrm {F}A}_i} ], [ {[ {{\mathrm {F}\oplus }_i} ]_j} ], [ {[ {{\mathrm {F}+}_i} ]_j} ], [ {\mathrm {F}0_j} ]\right) \); and the \(\omega \)-differential map \([ {{f}_i} ]\) to \([ {{\mathrm {F}f}_i} ]\).
Theorem 8
The category \(\mathrm {CAct_\omega }(\mathbf {C})\) is cartesian, with product given in Definition 14. Moreover if \(\mathbf {C}\) is closed and has countable limits, \(\mathrm {CAct_\omega }(\mathbf {C})\) is cartesian closed.
Theorem 9
The category \(\mathrm {CAct_{\omega }}(\mathbf {C})\) is equipped with a canonical change action model: \(\gamma : \mathrm {CAct_\omega }(\mathbf {C}) \rightarrow \mathrm {CAct}(\mathrm {CAct_\omega }(\mathbf {C}))\).
Theorem 10
(Relativised final coalgebra). Let \(\mathbf {C}\) be a change action model. The canonical change action model \(\gamma : \mathrm {CAct_\omega }(\mathbf {C}) \rightarrow \mathrm {CAct}(\mathrm {CAct_\omega }(\mathbf {C}))\) is a relativisedFootnote 9 final coalgebra of \((\mathrm {CAct}, \varepsilon )\). i.e. for all change action models on \(\mathbf {C}\), \(\alpha : \mathbf {C} \rightarrow \mathrm {CAct}(\mathbf {C})\), there is a unique coalgebra homomorphism \(\alpha _\omega : \mathbf {C} \rightarrow \mathrm {CAct_\omega }(\mathbf {C})\), as witnessed by the commuting diagram:

Proof
We first exhibit the functor \(\alpha _\omega : \mathbf {C} \rightarrow \mathrm {CAct_\omega }(\mathbf {C})\).
Take a \(\mathbf {C}\)-morphism \(f : A \rightarrow B\). We define the \(\omega \)-differential map  , where
, where  is the \(\omega \)-change action determined by A under iterative actions of \(\alpha \). I.e. for each \(i \ge 0\):
is the \(\omega \)-change action determined by A under iterative actions of \(\alpha \). I.e. for each \(i \ge 0\):  (by abuse of notation, we write \(\varDelta A'\) to mean the carrier object of the monoid of the internal change action \(\alpha (A')\), for any \(\mathbf {C}\)-object \(A'\)); \(\widehat{\oplus }_j : \varPi ^j [ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^j[ {{A}_i} ]\) is specified by: \(\mathsf{p}_k \widehat{\oplus }_j\) is the monoid action morphism of \(\alpha (A_{j+k})\); \(\widehat{+}_j : \varPi ^{j+1}[ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^{j+1}[ {{A}_i} ]\) is specified by: \(\mathsf{p}_k \widehat{\oplus }_j\) is the monoid sum morphism of \(\alpha (A_{j+k})\); \(0_i\) is the zero object of \(\alpha (A_i)\).
(by abuse of notation, we write \(\varDelta A'\) to mean the carrier object of the monoid of the internal change action \(\alpha (A')\), for any \(\mathbf {C}\)-object \(A'\)); \(\widehat{\oplus }_j : \varPi ^j [ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^j[ {{A}_i} ]\) is specified by: \(\mathsf{p}_k \widehat{\oplus }_j\) is the monoid action morphism of \(\alpha (A_{j+k})\); \(\widehat{+}_j : \varPi ^{j+1}[ {{A}_i} ] \times \varPi ^{j+1}[ {{A}_i} ] \rightarrow \varPi ^{j+1}[ {{A}_i} ]\) is specified by: \(\mathsf{p}_k \widehat{\oplus }_j\) is the monoid sum morphism of \(\alpha (A_{j+k})\); \(0_i\) is the zero object of \(\alpha (A_i)\).
The \(\omega \)-sequence  is defined by induction:
is defined by induction:  ; assume \(f_n : (\mathbf {D} \widehat{A})_n \rightarrow B_n\) is defined and suppose \(\alpha (f_n) = (f_n, \partial f_n)\) then define
; assume \(f_n : (\mathbf {D} \widehat{A})_n \rightarrow B_n\) is defined and suppose \(\alpha (f_n) = (f_n, \partial f_n)\) then define  .
.
To see that the diagram commutes, notice that \(\gamma (\widehat{f}) = (\widehat{f}, \varPi \widehat{f})\) and \(\mathrm {CAct}(\alpha _\omega )\) maps \(\alpha (f) = (f, \partial f)\) to \((\widehat{f}, \widehat{\partial f})\); then observe that \(\varPi \widehat{f} = \widehat{\partial f}\) follows from the construction of \(\widehat{f}\).
Finally to see that the functor \(\alpha _\omega \) is unique, consider the \(\mathbf {C}\)-morphisms \(\partial ^n f\) \((n = 0, 1, 2, \cdots )\) where \(\alpha (\partial ^n f) = (\partial ^n f, \partial ^{n+1} f)\). Suppose \(\beta : \mathbf {C} \rightarrow \mathrm {CAct_\omega }(\mathbf {C})\) is another homomorphism. Thanks to the commuting diagram, we must have \(\varPi ^n \beta (f) = \beta (\partial ^n f)\), and so, in particular \((\beta (f))_n = (\varPi ^n \beta (f))_0 = (\beta (\partial ^n f))_0 = \partial ^n f\), for each \(n \ge 0\). Thus \(\widehat{f} = \beta (f)\) as desired. \(\square \)
Intuitively any change action model on \(\mathbf {C}\) is always a “subset” of the change action model on \(\mathrm {CAct_\omega }(\mathbf {C})\).
Theorem 11
The category \(\mathrm {CAct_\omega }(\mathbf {C})\) is the limit in \(\mathbf {Cat_\times }\) of the diagram.

7 Related Work, Future Directions and Conclusions
The present work directly expands upon work by the authors and others in [2], where the notion of change action was developed in the context of the incremental evaluation of Datalog programs. This work generalizes some results in [2] and addresses two significant questions that had been left open, namely: how to construct cartesian closed categories of change actions and how to formalize higher-order derivatives.
Our work is also closely related to Cockett, Seely and Cruttwell’s work on cartesian differential categories [3, 4, 7] and Cruttwell’s more recent work on generalised cartesian differential categories [10]. Both cartesian differential categories and change action models aim to provide a setting for differentiation, and the construction of \(\omega \)-change actions resembles the Faà di Bruno construction [8, 10] (especially its recent reformulation by Lemay [20]) which, given an arbitrary category \(\mathbf {C}\), builds a cofree cartesian differential category for it. The main difference between these two settings lies in the specific axioms required (change action models are significantly weaker: see Remark 2).
In this sense, the derivative condition is close to the Kock-Lawvere axiom from synthetic differential geometry [18, 19], which has provided much of the driving intuition behind this work, and making this connection precise is the subject of ongoing research.
In a different direction, the simplicity of products and exponentials in closed change action models (see Theorem 5) suggests that there should be a reasonable calculus for change action models. Exploring such a calculus and its connections to the differential \(\lambda \)-calculus [11] could lead to practical applications to languages for incremental computation or higher-order automatic differentiation [16].
In conclusion, change actions and change action models constitute a new setting for reasoning about differentiation that is able to unify “discrete” and “continuous” models, as well as higher-order functions. Change actions are remarkably well-behaved and show tantalising connections with geometry and 2-categories. We believe that most ad hoc notions of derivatives found in disparate subjects can be elegantly integrated into the framework of change action models. We therefore expect any further work in this area to have the potential of benefiting these notions of derivatives.
Notes
- 1.
Change actions are closely related to the notion of change structures introduced in [6] but differ from the latter in not being dependently typed or assuming the existence of an \(\ominus \) operator, and requiring \(\varDelta {A}\) to have a monoid structure compatible with the map \(\oplus \).
- 2.
One might expect \(\mathrm {CAct}\) to be a comonad with \(\varepsilon \) as a counit. But if this were the case, we would have \(\xi _{\mathbf {C}} = \varepsilon _{\mathrm {CAct}(\mathbf {C})}\), which is, in general, not true.
- 3.
Alternatively, one can define the (first) partial derivative of a map f(x, y) as a map \(\delta _1 f\) such that \(f(x \oplus \delta x, y) = f(x, y) \oplus \delta _1(x, y, \delta x)\). It can be shown that a map is differentiable iff its first and second derivatives exist.
- 4.
Note that the converse is not the case, i.e. a derivative can be additive but not stable.
- 5.
The concept of “infinitesimal object” is borrowed from synthetic differential geometry [18]. However, there is nothing intrinsically “infinitesimal” about such objects here.
- 6.
The third, the Eilenberg-Moore model, is presented in [1, Appendix D].
- 7.
We consider arbitrary functions, rather than group homomorphisms, since, according to this change action structure, every function between groups is differentiable.
- 8.
It is important to sequence the definitions appropriately. Notice that we only define \(\omega \)-differential maps once there is a notion of pre-\(\omega \)-change action, but pre-\(\omega \)-change actions need pre-\(\omega \)-differential maps to make sense of the monoidal sum \(\widehat{+}_j\) and action \(\widehat{\oplus }_j\).
- 9.
Here \(\mathrm {CAct}\) is restricted to the full subcategory of \(\mathbf {Cat}_\times \) with \(\mathbf {C}\) as the only object.
References
Alvarez-Picallo, M., Ong, C.H.L.: Change actions: models of generalised differentiation. arXiv preprint arXiv:1902.05465 (2019)
Alvarez-Picallo, M., Peyton-Jones, M., Eyers-Taylor, A., Ong, C.H.L.: Fixing incremental computation. In: European Symposium on Programming. Springer (2019, in press)
Blute, R., Ehrhard, T., Tasson, C.: A convenient differential category. arXiv preprint arXiv:1006.3140 (2010)
Blute, R.F., Cockett, J.R.B., Seely, R.A.: Cartesian differential categories. Theory Appl. Categories 22(23), 622–672 (2009)
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964). https://doi.org/10.1145/321239.321249
Cai, Y., Giarrusso, P.G., Rendel, T., Ostermann, K.: A theory of changes for higher-order languages: incrementalizing \(\lambda \)-calculi by static differentiation. ACM SIGPLAN Not. 49, 145–155 (2014)
Cockett, J.R.B., Cruttwell, G.S.H.: Differential structure, tangent structure, and SDG. Appl. Categorical Struct. 22(2), 331–417 (2014)
Cockett, J.R.B., Seely, R.A.G.: The Faà di Bruno construction. Theory Appl. Categories 25, 393–425 (2011)
Conway, J.H.: Regular Algebra and Finite Machines. Chapman and Hall, London (1971)
Cruttwell, G.S.: Cartesian differential categories revisited. Math. Struct. Comput. Sci. 27(1), 70–91 (2017)
Ehrhard, T., Regnier, L.: The differential lambda-calculus. Theor. Comput. Sci. 309(1–3), 1–41 (2003). https://doi.org/10.1016/S0304-3975(03)00392-X
Esparza, J., Kiefer, S., Luttenberger, M.: Newtonian program analysis. J. ACM 57(6), 33:1–33:47 (2010). https://doi.org/10.1145/1857914.1857917
Gleich, D.: Finite calculus: a tutorial for solving nasty sums. Stanford University (2005)
Hopkins, M.W., Kozen, D.: Parikh’s theorem in commutative Kleene algebra. In: 14th Annual IEEE Symposium on Logic in Computer Science, Trento, Italy, 2–5 July 1999, pp. 394–401 (1999). https://doi.org/10.1109/LICS.1999.782634
Jordan, C.: Calculus of Finite Differences, vol. 33. American Mathematical Society, New York (1965)
Kelly, R., Pearlmutter, B.A., Siskind, J.M.: Evolving the incremental lambda-calculus into a model of forward automatic differentiation (ad). arXiv preprint arXiv:1611.03429 (2016)
Kleene, S.C.: Representation of events in nerve nets and finite automata. In: Shannon, C.E., McCarthy, J. (eds.) Automata Studies, pp. 3–41. Princeton University Press, Princeton (1956)
Kock, A.: Synthetic Differential Geometry, 2nd edn. Cambridge University Press, Cambridge (2006)
Lavendhomme, R.: Basic Concepts of Synthetic Differential Geometry, vol. 13. Springer, Boston (2018). https://doi.org/10.1007/978-1-4757-4588-7
Lemay, J.S.: A tangent category alternative to the Faà di Bruno construction. arXiv preprint arXiv:1805.01774v1 (2018)
Lombardy, S., Sakarovitch, J.: How expressions can code for automata. In: 6th Latin American Symposium on Theoretical Informatics, LATIN 2004, Buenos Aires, Argentina, 5–8 April 2004, Proceedings, pp. 242–251 (2004). https://doi.org/10.1007/978-3-540-24698-5_28
Steinbach, B., Posthoff, C.: Boolean differential calculus. Synth. Lect. Digit. Circ. Syst. 12(1), 1–215 (2017)
Thayse, A. (ed.): Boolean Calculus of Differences. LNCS, vol. 101. Springer, Heidelberg (1981). https://doi.org/10.1007/3-540-10286-8
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Alvarez-Picallo, M., Ong, CH.L. (2019). Change Actions: Models of Generalised Differentiation. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)





 is a (trivial) change action.
is a (trivial) change action. is a change action.
is a change action.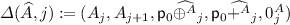 is a change action in
is a change action in 


